Barycentre Averaging for the Move-Split-Merge Time Series Distance

Measure

Christopher Holder

1 a

, David Guijo-Rubio

1,2 b

and Anthony Bagnall

3 c

School of Computing Sciences, University of East Anglia, Norwich, U.K.

Department of Computer Science and Numerical Analysis, University of C

ordoba, C

ordoba, Spain

School of Electronics and Computer Science, University of Southampton, Southampton, U.K.

Keywords:

Time Series Distances, Time Series Clustering, Move Split Merge, Barycentre Averaging, Dynamic

Barycentre Averaging, MSM Barycentre Averaging, DBA, MBA.

Abstract:

Distance functions play a core role in many time series machine learning algorithms for tasks such as cluster-

ing, classiﬁcation and regression. Time series often require bespoke distance functions because small offsets

in time can lead to large distances between series that are conceptually similar. Elastic distances compensate

for misalignment by creating a path through a cost matrix by warping and/or editing time series. Time series

are most commonly clustered with partitional algorithms such as k-means and k-medoids using elastic distance

measures such as Dynamic Time Warping (DTW). The distance is used to assign cases to the closest cluster

representative. k-means requires the averaging of time series to ﬁnd these representative centroids. If DTW is

used to assign membership, but the arithmetic mean is used to ﬁnd centroids, k-means performance degrades

signiﬁcantly. An averaging technique speciﬁc to DTW, called DTW Barycentre Averaging (DBA), overcomes

the averaging problem however, can only be used with DTW. As such alternative distance functions such as

Move-Split-Merge (MSM) are forced to use the arithmetic mean to compute new centroids and suffer similar

degraded performance as k-means-DTW without DBA. To address this we propose a averaging method for

MSM distance, MSM Barycentre Averaging (MBA) and show that when used to ﬁnd centroids it signiﬁcantly

improves MSM based k-means and is better than commonly used alternatives.

1 INTRODUCTION

Machine learning applied to time series data is a ex-

tensively studied area within the literature. One of

the key factors contributing to its advancement is the

improved ability to collect temporal data using cost-

effective sensor technology across various scientiﬁc

disciplines. Speciﬁcally, time series data can be sub-

jected to different tasks, each with its own objective.

Among these tasks, Time Series Classiﬁcation (TSC)

(Bagnall et al., 2017; Middlehurst et al., 2023) has

gained widespread attention, involving the prediction

of a discrete output value for a given time series. Fur-

thermore, if the aim is to predict a continuous output

value instead of a discrete one, the task is referred

to as Time Series Extrinsic Regression (TSER) (Tan

et al., 2021; Guijo-Rubio et al., 2023). Concerning

https://orcid.org/0000-0001-9571-3764

https://orcid.org/0000-0002-8035-4057

https://orcid.org/0000-0003-2360-8994

unsupervised tasks, Time Series Clustering (TSCL)

(Liao, 2005; Aghabozorgi et al., 2015) is particularly

well-known, aiming to group time series without the

need of labelled data. TSCL is the primary focus of

this work.

TSCL is used across multiple different diciplines.

It has been used to identify anomalous amplitude and

shape patterns in disease outbreak data (Li et al.,

2021) Climate researchers used TSCL to discover

common patterns preceding important paleoclimate

events (Nikolaou et al., 2015). TSCL has been used

extensivly in bioinformatics to group gene expression

patterns (McDowell et al., 2018). These applications

of TSCL demonstrate the versatility of this task across

several disciplines.

With respect the TSCL taxonomy, it can be ap-

proached from two main points of view: 1) extract-

ing features from the time series; and 2) employing

a standard clustering approach along with a time se-

ries distance measure. The majority of existing TSCL

techniques fall into the second category. These ap-

Holder, C., Guijo-Rubio, D. and Bagnall, A.

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure.

DOI: 10.5220/0012164900003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 51-62

ISBN: 978-989-758-671-2; ISSN: 2184-3228

proaches critically depend on the choice of an appro-

priate distance measure, combined with the clustering

approach used.

Measuring distance between time series is a prim-

itive operation that can be used for a range of

tasks such as classiﬁcation, clustering, regression and

query. Time series require bespoke distance func-

tions because small offsets between series can lead

to large distances between series that are conceptu-

ally similar. Elastic distances compensate for mis-

alignment by creating a path through a cost ma-

trix through either warping or editing time series.

The most common elastic distance is Dynamic Time

Warping (DTW) (Ratanamahatana and Keogh, 2005),

however, there have been numerous others proposed.

A recent comparison study that evaluated 9 com-

monly used elastic distances found that the MSM

distance measure was the best performing distance

function for the k-means clustering algorithm (Holder

et al., 2022). Unlike DTW, MSM satisﬁes the mathe-

matical conditions of a metric, meaning it can, for ex-

ample, exploit the triangle inequality for fast distance

calculations. Figure 1 shows the method for ﬁnding

the MSM distance between two series.

In addition to computing similarity, many TSCL

approaches must also choose or synthesise exemplars

to represent clusters. One of the most common tech-

niques to do this is averaging. k-means (Lloyd, 1982)

is one of the most commonly used TSCL approaches

in the literature and requires both to compute the dis-

tance between time series and the creation of syn-

thetic time series (by averaging) that represent a clus-

ter. Various methods have been proposed to compute

the average of a collection of time series (Brill et al.,

2019; Holznigenkemper and Seeger, 2023).

Our contribution is to propose a method for av-

eraging time series using MSM. Our method, MSM

Barycentre Averaging (MBA) is based on the approx-

imate barycentre averaging method which was made

popular for DTW using DTW Barycentre Averag-

ing (DBA) (Petitjean et al., 2011). We show that,

when integrated with k-means clustering, MBA sig-

niﬁcantly outperforms clusters created using either

DTW or MSM with arithmetic mean averaging and

DBA.

We have conducted all experiments with the aeon

time series machine learning toolkit

and we demon-

strate how to reproduce all our experiments with the

associated experimental code and notebook

The rest of this paper is structured as follows.

https://github.com/aeon-toolkit/aeon

https://github.com/time-series-machine-learning/tsml

-eval/blob/main/tsml eval/publications/y2023/distance bas

ed clustering/MBA.ipynb

In Section 2 we provide background into elastic dis-

tance functions and time series averaging. Section 2.3

describes our approach to averaging using MSM,

known as MSM Barycentre Averaging (MBA). In

Section 3.1, we present related works in TSCL litera-

ture. Our results are presented in Section 4 before we

conclude in Section 5.

2 BACKGROUND

Distance-based time series machine learning has been

a popular theme in time series classiﬁcation and clus-

tering research. There have been numerous exper-

imental evaluations of distance-based classiﬁcation,

such as (Ding et al., 2008; Lines and Bagnall, 2014).

For many years, the received wisdom was that DTW

was the best choice. For example, the ﬁrst sentence of

(Petitjean et al., 2016) is: “The last decade has seen

increasing acceptance that the nearest neighbour al-

gorithm with dynamic time warping as the distance

measure is the technique of choice for most time se-

ries classiﬁcation problems”. However, recent exper-

imental papers (Lines et al., 2018; Paparrizos et al.,

2020; Holder et al., 2022) have identiﬁed that MSM

is more effective for both classiﬁcation and cluster-

ing. Nevertheless, DTW is still by far the most widely

used elastic distance measure. Hence, we limit our

focus to DTW and MSM, as well as the standard Eu-

clidean Distance (ED), and direct the interested reader

to (Holder et al., 2022; Shifaz et al., 2023) for more

detailed background on elastic distances.

2.1 Time Series Elastic Distance

Functions

Suppose we want to measure the distance between

two time series (assumed to be equal lengths and uni-

variate), a = {a

,...,a

} and b = {b

,...,b

The ED, d

is the L2 norm between series,

(a,b) =

∑

i=1

− b

)

. (1)

puts no priority on the ordering of the series.

Elastic distance measures allow for possible misalign-

ment by attempting to optimally align two series. This

is done by either distorting indices or by editing the

series to add or remove values.

2.1.1 Dynamic Time Warping (DTW)

DTW mitigates distortions in the time axis by re-

aligning (also known as warping) the series to best

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

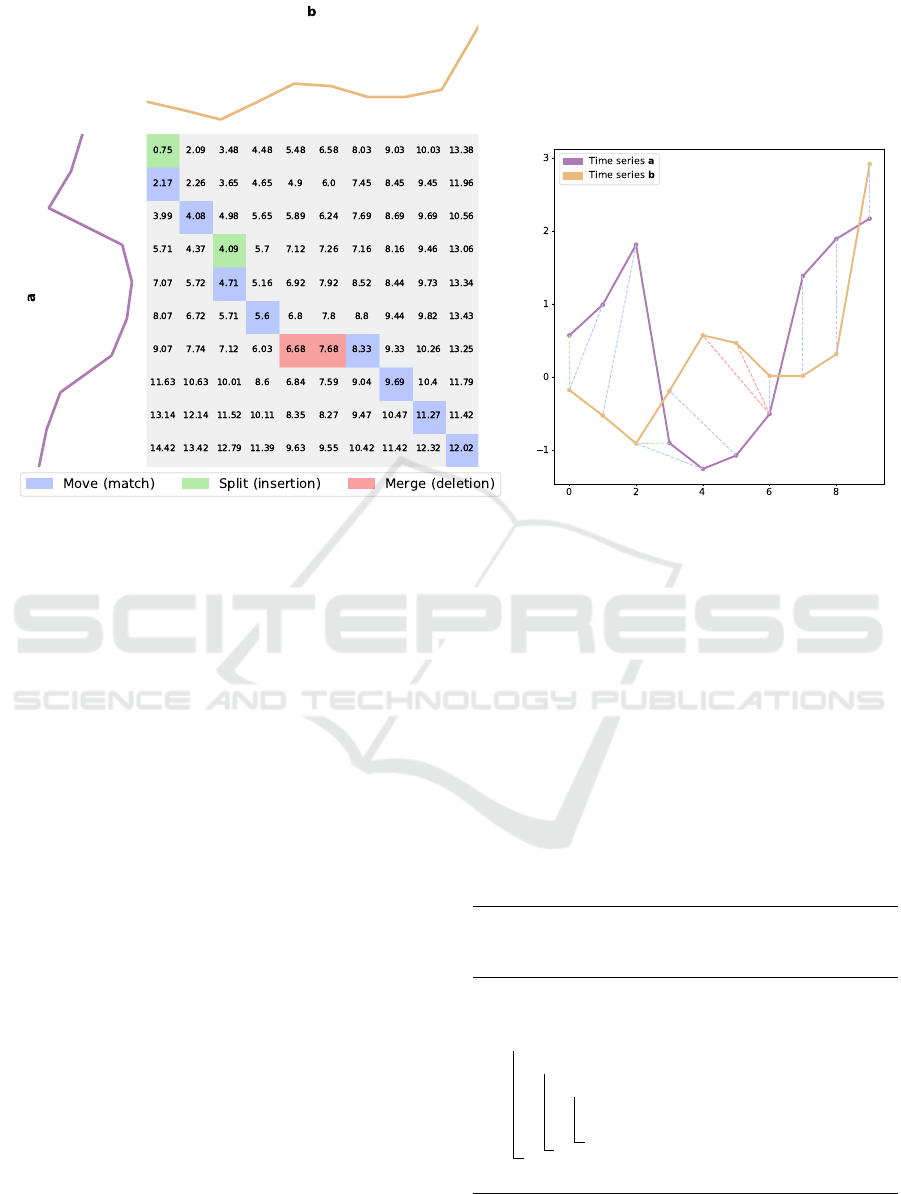
Figure 1: An example of MSM distance: cost matrix (left) to align series (right).

match each other. Let M(a,b) be the m × m point-

wise distance matrix between series a and b, where

i, j

= (a

− b

)

. A warping path

P =< (e

, f

),(e

, f

),...,(e

, f

) >

is a set of pairs of indices that deﬁne a traversal of

matrix M. A valid warping path must start at location

(1,1), end at point (m,m) and not backtrack, i.e. 0 ≤

i+1

− e

≤ 1 and 0 ≤ f

i+1

− f

≤ 1 for all 1 < i < m.

The DTW distance between series is the path through

M that minimises the total distance. The distance for

any path P of length s is

(a,b,M) =

∑

i=1

, f

. (2)

If P is the space of all possible paths, the DTW path

∗

is the path that has the minimum distance, hence

the DTW distance between series is

DTW

(a,b) = D

P∗

(a,b,M). (3)

The optimal warping path P

∗

can be found exactly

through the dynamic programming formulation de-

scribed in Algorithm 1. This can be a time-consuming

operation, and it is common to put a restriction on the

amount of warping allowed.

2.1.2 Move-Split-Merge (MSM)

At any step, elastic distances can use one of three

costs: diagonal, horizontal or vertical, in forming an

alignment. The alignment path is a series of moves

across the cost matrix. DTW assigns no explicit

penalty for moving off the diagonal. Instead, it uses

an implicit penalty (long paths have longer total dis-

tance) and a hard cut off on window size to stop large

warpings. An alternative family of distance func-

tions are based on the concept of edit distance (e.g.

Edit distance with Real Penalty (ERP) (Chen and Ng,

2004)). An edit distance, such as MSM, considers a

diagonal move as a match, a vertical move as an in-

sertion and an horizontal move as a deletion. MSM

(Algorithm 2) follows this structure, where move is

a match (diagonal), split is a insertion (vertical) and

merge is deletion (horizontal).

Algorithm 1: DTW (a,b, (both series of length m), w (win-

dow proportion, default value w ← 1), M (pointwise dis-

tance matrix)).

1 Let C be an (m + 1) × (m + 1) matrix

initialised to zero, indexed from zero.

2 for i ← 1 to m do

3 for j ← 1 to m do

4 if |i − j| < w · m then

5 C

i, j

← M

i, j

min(C

i−1, j−1

i−1, j

i, j−1

)

6 return C

m,m

Figure 1 shows the method for ﬁnding the MSM

distance between two time series. As can be ob-

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure

served, the three operations (match/insert/deletion)

are identiﬁed with different colours (blue/green/red)

and using the speciﬁc terminology of MSM distance

(move/split/merge).

The move operation in MSM uses the absolute dif-

ference rather than the squared euclidean distance for

matching in DTW. The cost of the split operation is

given by cost function C (Equation 4) with a call to

C(a

i−1

,c). If the value being inserted, b

, is be-

tween the two values a

and a

i−1

being split, the cost

is a constant value c. If not, the cost is c plus the

minimum deviation from the furthest point a

and the

previous point a

i−1

or b

. The delete/merge is given

by C(b

j−1

,c), which is simply the same oper-

ation as split but applied to the second series. Thus,

the cost of splitting and merging values depends on

the value itself and adjacent values.

C(a

i−1

,c) =











c if a

i−1

≤ a

≤ b

c if a

i−1

≥ a

≥ b

c + min(|a

− a

i−1

|,|a

− b

otherwise.

(4)

Algorithm 2 describes how to calculate the MSM

distance between two time series a and b. MSM sat-

isﬁes triangular inequality and is a metric. In Algo-

rithm 2 the ﬁrst return value is the MSM distance

between a and b, the second is the cost matrix used

to compute the MSM distance (this is used in Algo-

rithm 5).

Algorithm 2: MSM(a (of length m), b (of length m), c (min-

imum cost)).

1 Let CM be an m × m matrix initialised to zero.

2 CM

1,1

= |a

− b

3 for i ← 2 to m do

4 CM

i,1

= CM

i−1,1

+C(a

i−1

,c)

5 for i ← 2 to m do

6 CM

1,i

= CM

1,i−1

+C(b

,b + i − 1,c)

7 for i ← 2 to m do

8 for j ← 2 to m do

9 move ← CM

i−1, j−1

+ |a

− b

10 split ← CM

i−1, j

+C(a

i−1

,c)

11 merge ← CM

i, j−1

+C(b

j−1

,c)

12 CM

i, j

← min(move,split, merge)

13 return CM

m,m

,CM

2.2 Time Series Averaging Methods

Finding a consensus (average) representation of a set

of sequences has been described as the Holy Grail by

(Gusﬁeld, 1997). One of the main issues with averag-

ing sequences is that it is subjective. As such to de-

velop an algorithm to solve this problem it is normally

formulated as an optimisation problem (Brill et al.,

2019; Holznigenkemper and Seeger, 2023). If we are

not concerned with offset, then the simple arithmetic

average over time points will minimise the ED be-

tween time series. For algorithms such as k-means

this is the default approach. However, when using

this approach with elastic distances (i.e. cluster mem-

bership is assigned based on an elastic distance mea-

sure), the arithmetic mean centroid may misrepresent

the elements of a cluster. Simple averaging will tend

to blur the underlying series and result in worse k-

means clustering performance (Petitjean et al., 2016).

Similarly, if series of the same class are condensed

through arithmetic averaging, it is unlikely these ex-

emplars will be useful for classiﬁcation or regression.

As such many methods to average time series us-

ing DTW have been proposed. Initially NonLinear

Alignment and Averaging Filters (NLAAF) (Gupta

et al., 1996) was proposed. This method applies

a tournament scheme whereby sequences are paired

and averaged together step by step until only one ﬁ-

nal sequence remains. When two sequences are av-

eraged, the DTW alignment path between the two

series is computed and the point to point average is

taken using this alignment path. The main drawback

of this approach is it leads to a large growth in the av-

erage sequence produced (as every use of the averag-

ing method can lead to the length of the sequence al-

most doubling) (Petitjean et al., 2011). Another issue

with NLAAF is error propagation. Niennattrakul and

Ratanamahatana (2009) proposed Prioritised Shape

Averaging (PSA) which employs a hierarchical av-

eraging method reducing error propagation but also

leading to the same large sequence length growth as

NLAAF. Due to this growth of sequence, both are im-

practical for time series data (given complexities of

algorithms employed, such as DTW). Petitjean et al.

(2011) addresses both of these problems by propos-

ing DTW Barycentre Averaging (DBA) that uses the

optimal warping path to compute a series of the same

length while accounting for alignment of time series.

This will be explained further in Section 2.3.

2.3 Barycentre Averaging

DBA (Petitjean et al., 2011) was proposed to over-

come the limitations of other averaging methods for

time series outlined in Section 2.2. DBA uses a

heuristic strategy to compute a new series that min-

imises the DTW distance to cluster members rather

than the ED. The DBA process begins with an initial

centre, which is typically the medoids of the time se-

ries collection to be averaged. For each time series

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

in the collection, the optimal DTW warping path is

computed to the centre. Using these warping paths a

new centre is computed by determining which points

warped onto each element of the initial centre. The

mean is then calculated for each time point warped to

each other time point, taking into account how often

each time point was warped to. This process contin-

ues iteratively until there is no signiﬁcant change in

the sum of squared DTW distances to the centre, in-

dicating that the optimum centre has been achieved.

While the original proposal for DBA was only

for DTW, assuming an optimal alignment path can

be obtained from an elastic distance (and it aims to

minimise the dissimilarity between two series), any

distance could be used with (Petitjean et al., 2011)

barycentre averaging approach. Holder et al. (2022)

reviewed 9 different elastic distance measures for

TSCL and found the MSM distance signiﬁcantly out-

performed DTW across multiple clustering metrics.

As such this paper seeks to expand on these ﬁnding

by also using the best performing elastic distance in

the averaging stage of computation.

3 MSM BARYCENTRE AVERAGE

(MBA)

To change the distance measure used in the origi-

nal DBA, the optimal warping path needs to be re-

trieved from the distance computation, necessitating

the MSM algorithm to construct and return a cost ma-

trix, as seen in Algorithm 2. This optimal path is iden-

tiﬁed by backtracking through the cost matrix and fol-

lowing the trajectory that minimises the total distance,

as outlined in Algorithm 3. Given these traits, MSM

can feasibly be paired with barycentre averaging.

With this prerequisites the DBA algorithm has

been adapted and outlined in Algorithm 4 and 5. This

new algorithm computes the MSM Barycentre Aver-

age (MBA). Each step in the MBA algorithm will now

be outlined.

MSM medoids = arg min

∈C

∑

∈C

MSM(x

,cost).

(5)

Algorithm 4 takes a collection of time series, a num-

ber of max iterations and a minimum cost for MSM as

parameters and computes the MBA. Firstly an initial

centre is computed (line 1). This is done using the

MSM medoids given in Eq 5. Using this initial cen-

tre, a number of iterations are executed (max iters)

to reﬁne the centre (line 3). This is done using

Algorithm 5. Algorithm 5 begins by deﬁning two

values: num war ps to, which is an array that tracks

Algorithm 3: Compute path(CM (of size n × m)).

1 Let alignment be a list.

2 Let i = n − 1 and j = m − 1.

3 while i > 0 or j > 0 do

4 Append (i, j) to alignment.

5 if i == 0 then

6 j ← j − 1.

7 else if j == 0 then

8 i ← i − 1.

9 else

10 min index =

arg min((CM

i−1, j−1

,CM

i−1, j

,CM

i, j−1

)

11 if min index == 0 then

12 i ← i − 1, j ← j − 1.

13 else if min index == 1 then

14 i ← i − 1.

15 else

16 j ← j − 1.

17 Append (0,0) to alignment.

18 return alignment reversed.

Algorithm 4: MSM barycentre average(X (collection of

time series), max iters (max iterations before stop) c (min-

imum cost)).

1 centre ← MSM medoids(X )

2 for i ← 1 to max iters do

3 centre ← MSM BA update(centre,X, c)

4 return centre.

Algorithm 5: MSM BA update(centre (time series of size

m), X (collection of time series of size n × m), c (minimum

cost for MSM computation)).

1 Initialise num warps to as a zeros array of

size m.

2 Initialise alignment as a zeros array of size m.

3 for i ← 1 to n do

4 dist, CM ← MSM(X

, centre, c)

5 curr alignment ← compute path(CM)

6 for each ( j, k) in curr alignment do

7 alignment

← alignment

+ X

i, j

8 num warps to

← num warps to

9 new centre ← alignment/num warps to

10 return new centre

how many times a point is warped to (due to how

the optimal warping path is computed one point can

be warped to multiple times in a single path), and

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure

alignment, which is an array of length m which will

store the values of the new centre (line 1 and 2). Next,

for each value in the collection of time series X, it

computes the MSM Cost Matrix (CM) (Algorithm 2)

between X

and the centre (line 4). Using the com-

puted CM, the optimal alignment path can be found

in the form (line 5):

curr alignment =< (e

, f

),(e

, f

),...,(e

, f

) > .

Each tuple in the optimal alignment path is then

looped over (line 6) and the j

value in X

is added

to the value in alignment

(i.e. value j is warped to

the index k) (line 7). Furthermore num war ps to

incremented (line 8). Once each time series in the col-

lection X has been warped to, the new centre can be

computed by taking the mean of the alignments us-

ing num warps to, which tracked the number of time

each index was warped to (line 9). The new computed

centre is then returned (line 10).

The result of this adaptation, while subtle, leads to

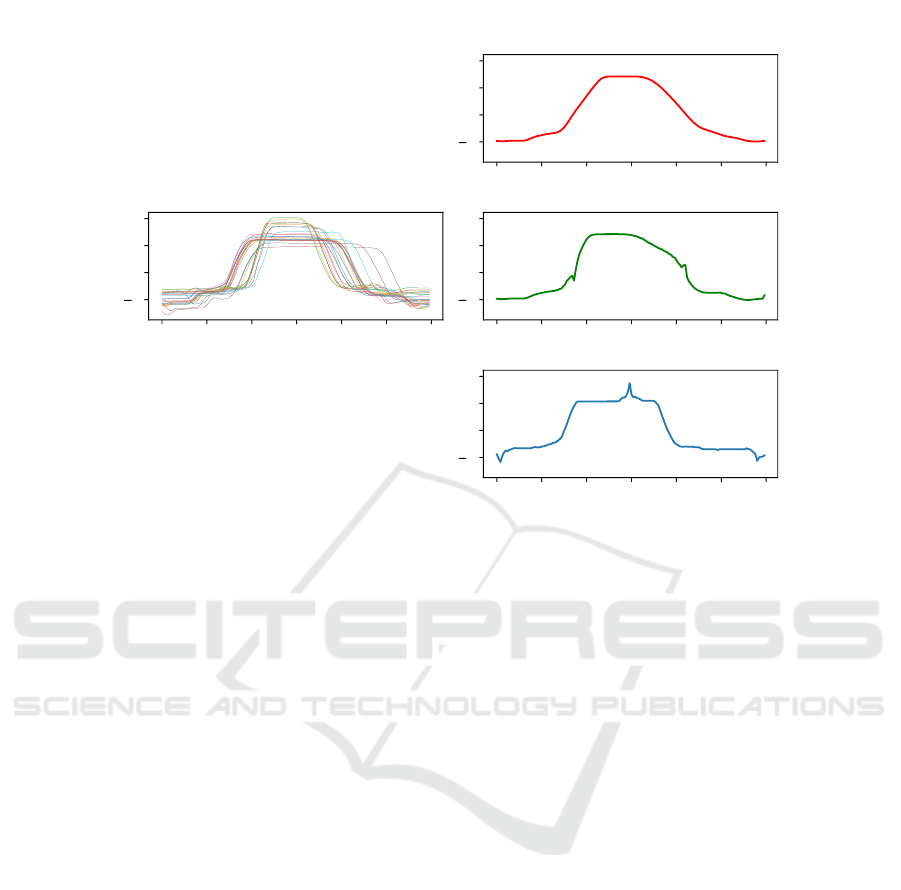
a much different resulting average as shown in Figure

2. This ﬁgure shows the average time series of the

whole set of time series with class 1 for the GunPoint

dataset. The discriminatory features are the small

peaks before and after the main peak. These represent

the moment when the actor is drawing and replacing

the gun. As can be observed, MSM is able to clearly

identify these discriminatory features, whereas both

arithmetic averaging or DTW do not.

3.1 Alternative TSCL Algorithms

To put the results of MBA into context we also ex-

plore alternative TSCL approaches. Most of the de-

velopments in TSCL are domain-speciﬁc, not being

focused on TSCL as a whole. Nevertheless, there

are a few approaches tackling TSCL as a whole.

The ﬁrst one is the U-shapelets technique (Zakaria

et al., 2012), which, instead of computing pairwise

distances, considers only relevant subsequences of

time series. This technique shares similarities with

its classiﬁcation counterpart (Hills et al., 2014). First

of all, subsequences are extracted from the data and

ranked based on their utility, which reﬂects their dis-

criminative power. This value attempts to maximise

the separation gap between two subsets of time se-

ries: one subset comprises time series with subse-

quences similar to the shapelet being evaluated, while

the other subset consists of the remaining time se-

ries. The subsequences with high utility, referred to as

shapelets, are retained. Once the ﬁnal set of shapelets

is achieved, a transformation matrix is built with cells

representing distances between U-shapelets and time

series. Finally, the standard k-means method is ap-

plied to the transformation matrix. The main advan-

tages of this approach are that U-shapelets mitigates

the sensitivity to noise and other irrelevant data, and

their ability to provide additional insights into the

data.

Another well-known approach is the Two-step

Time series Clustering (TTC) (Aghabozorgi et al.,

2014). This method ﬁrstly reduces the size of the

dataset using the concept of afﬁnity. For this, time

series are grouped according to similarity in time and

then applying an afﬁnity search technique. Subse-

quently, for each cluster a prototype is deﬁned ac-

cording to the afﬁnity of the time series belonging to

it. The second step of this approach involves comput-

ing the DTW distances between the subclusters pro-

totypes. This distance measurement aims to repre-

sent the dissimilarity between the subgroups, in such

a way that the complexity is reduced as much as possi-

ble. Finally, similar subclusters are merged by means

of the k-medoids standard clustering method.

In addition, one of the approaches in the state-of-

the-art of TSCL is the well-known k-shapes (Paparri-

zos and Gravano, 2015). It is a partitional clustering

algorithm that aims to create homogeneous and well-

separated clusters through an iterative process. In a

similar way to k-means, k-shapes also performs two

main processes: 1) the assignment step; and 2) the re-

ﬁnement step. For the ﬁrst one, k-shapes employs an

efﬁcient adaptation of the cross-correlation measure

known as Shape-Based Distance (SBD). In the reﬁne-

ment step, the centroids of the clusters are recom-

puted by solving an optimisation problem that min-

imises (or maximises) the sum of squared distances

(or squared similarities) to all the time series, found

signiﬁcantly better than computing the average time

series. A key advantage of k-shapes is that it groups

time series based on their shape similarity, regardless

of differences in amplitude and phase. Thus, it pre-

serves the shapes of the time series while measuring

the distance between them.

Finally, a range of deep learning approaches have

been recently compared and analysed in (Lafabregue

et al., 2022). This study represents the ﬁrst explo-

ration of deep learning techniques in TSCL. Hence,

three components have been studied: architecture,

clustering loss, and pretext loss. Through separate

assessments of each component it has been deter-

mined that a simple autoencoder architecture using a

reconstruction-based pretext loss is the best combina-

tion. Interestingly, the results also indicated that the

incorporation of clustering losses did not lead to a per-

formance increase. Therefore, its addition is not jus-

tiﬁed. Finally, authors discussed that more research is

required for improving the performance of these ap-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

0 25 50 75 100 125 150

Arithmetic averaging

0 25 50 75 100 125 150

Original time series

0 25 50 75 100 125 150

MBA

0 25 50 75 100 125 150

DBA

GunPoint - Class 1

Figure 2: Visual differences between arithmetic averaging, the MBA approach and the DBA technique.

proaches.

4 COMPARISON OF OUR

METHOD

This section details the experimental settings used as

well as the results obtained, highlighting some of the

most important aspects to be analysed.

4.1 Experimental Settings

We compare MBA to alternative approaches using the

112 univariate, equal-length time series in the UCR

archive (Dau et al., 2019) for clustering. We use the

provided default train/test splits for all experiments.

We z-normalise all datasets prior to clustering. In

addition each model takes a value of k as a param-

eter. We set the value of k equal to the number of

unique class labels for each dataset. To measure per-

formance, we use three measures of the cluster labels:

CLustering ACCuracy (CL-ACC), is calculated

by dividing the number of correct predictions by the

total number of cases, similar to classiﬁcation accu-

racy. To do this, once each value has been assigned to

a cluster the maximum accuracy from every permu-

tation of cluster and class value is taken. The cluster

that achieved the highest accuracy for each label is

then assigned that ground truth label (this is done us-

ing the Hungarian algorithm).

The Rand Index (RI) works by measuring the

similarity between two sets of labels such as the pre-

dicted and actual class values. The RI is the number

of pairs that agree on a label divided by the total num-

ber of pairs. One of the limiting factors of RI is that

the score is inﬂated, especially when the number of

clusters is high. The Adjusted Rand Index (ARI)

compensates for this by adjusting the RI based on the

expected scores on a purely random model.

The Mutual Information (MI) score, is a func-

tion that measures the agreement of the two cluster-

ings or a clustering and a true labelling, based on

entropy. Normalised Mutual Information (NMI)

rescales MI onto [0,1].

We compare the performance of the following 10

clustering algorithms:

1. k-means-DBA and k-means-MBA: k-means

clustering with DTW/MSM barycentre averaging

(i.e. DBA/MBA respectively), and DTW/MSM

distance assignment.

2. k-means-ED, k-means-DTW and k-means-

MSM: k-means clustering with arithmetic mean

for centres, and ED, DTW and MSM distance

assignment, respectively.

3. k-shapes (Paparrizos and Gravano, 2015).

4. TTC: Two-step Time series Clustering

(TTC) (Aghabozorgi and Wah, 2014)

5. k-medoids-ED, k-medoids-DTW and k-

medoids-MSM: k-medoids clustering with

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure

ED, DTW and MSM distance assignment,

respectively.

k-means, k-medoids and k-shapes at their core are

variations of Lloyds algorithm (Lloyd, 1982) and so

share many of the same parameters. As such this

means by keeping many of the same parameters con-

stant better insight can be gained when comparing

metric performance. The values used in our experi-

ment for Lloyds based models are given in table 1.

Max iters is a maximum number of iterations the

algorithm can run before forceful termination. This

limit will only ever be reached if the algorithm does

not converge (i.e. an iterations cluster values do not

change compared to the previous iteration). Our ex-

periments found many of the algorithm converged

(the cluster values did not change between iterations)

in under 20 iterations and so the limit of 300 is set

for redundancy. The init algo is the initialisation al-

gorithm used to select the initial centres. Our experi-

ment uses the most common initialisation technique:

random initialisation (MacQueen et al., 1967). This

technique consists of choosing the initial centres ran-

domly from the dataset. The rationale behind this is

that random selection is likely to pick points from

dense regions. Rerunning the model multiple times

with random initialisation and taking the best clus-

tering (as measured by the sum of distances to their

closest cluster centres) is the most common way of

initialising k-means (Bradley and Fayyad, 1998). The

number of reruns is deﬁned by n init which for our

experiment is set to 10 as this is the most common

value we could ﬁnd from other similar experiments

and is the default value for scikit-learn

k-means

clusterer.

The metric parameter is our ﬁrst independent vari-

able. These different metrics have been outlined in

Sections 2.1 and 2.3. Finally the centroid compu-

tation deﬁnes the technique used to compute a new

cluster centre from a collection of time series. MBA,

DBA and arithmetic mean have been deﬁned in Sec-

tion 2.3. MSM medoids is given in Eq 5 and DTW

medoids is similar but instead of using the MSM dis-

tance in Eq 5 the DTW distance is employed. Finally

shape extraction is a shape based averaging technique

using SBD.

Results are expressed using an adaptation of the

critical difference diagram (Dem

sar, 2006), replacing

the post-hoc Nemenyi test with a comparison of all

classiﬁers using pairwise Wilcoxon signed-rank tests,

and cliques formed using the Holm correction (Garc

ıa

and Herrera, 2008; Benavoli et al., 2016).

https://scikit-learn.org/stable/

Table 1: Lloyds based algorithm variation parame-

ters. For all models max iters = 300, n init=10 and

init algo=“random”.

metric centroid computation

k-means-MBA MSM MBA

k-means-MSM MSM arithmetic mean

k-means-DBA DTW DBA

k-means-DTW DTW arithmetic mean

k-means-ED ED arithmetic mean

k-shapes SBD SE

k-medoids-MSM MSM MSM medoid

k-medoids-DTW DTW DTW medoid

4.2 k-means Variants

Figures 3, 4 and 5 show the average ranks of the

ﬁve k-means clusters against our two benchmark al-

gorithms, k-shapes and TTC, for CL-ACC, ARI and

NMI. We had to exclude the HandOutlines dataset and

hence reduce the number of datasets in our study to

111, given the computational time required by this

dataset. The pattern of performance is the same for

the three measures: k-means-MBA is signiﬁcantly

better than the other six algorithms. This is our

primary support for using k-means-MBA. There is

some consistency in the clique membership. k-means-

MSM and k-means-DBA are always in the same

clique and TTC is signiﬁcantly better than k-shapes.

k-means-MSM (k-means with MSM using arithmetic

averaging to ﬁnd centroids) is not signiﬁcantly differ-

ent to k-means-DBA (k-means with DTW and DTW

barycentre averaging). Moreover, k-means-DTW (k-

means with DTW and arithmetic averaging) is the

worst performing algorithm and is signiﬁcantly worse

than k-means-ED (k-means with ED and arithmetic

averaging) (conﬁrming results presented in (Holder

et al., 2022)).

Figure 6 shows the scatter plot in terms of CL-

ACC of k-means-MBA against k-means-MSM. It

demonstrates the improvement provided by using

MBA.

Table 2 quantiﬁes the summary performance

statistics of these clusterers. Using MBA increase

MSM based k-means by approximately 2% for all

three metrics. The improvement does come at a cost:

both DBA and MBA take much longer than arithmetic

averaging. We run our experiments on a shared com-

puting cluster in parallel, but we can say that whilst

k-means-MSM and k-means-DTW take on average a

few minutes per problem, k-means-DBA and MBA

average over an hour.

Deep learning results presented in (Lafabregue

et al., 2022) are available from the associated web-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

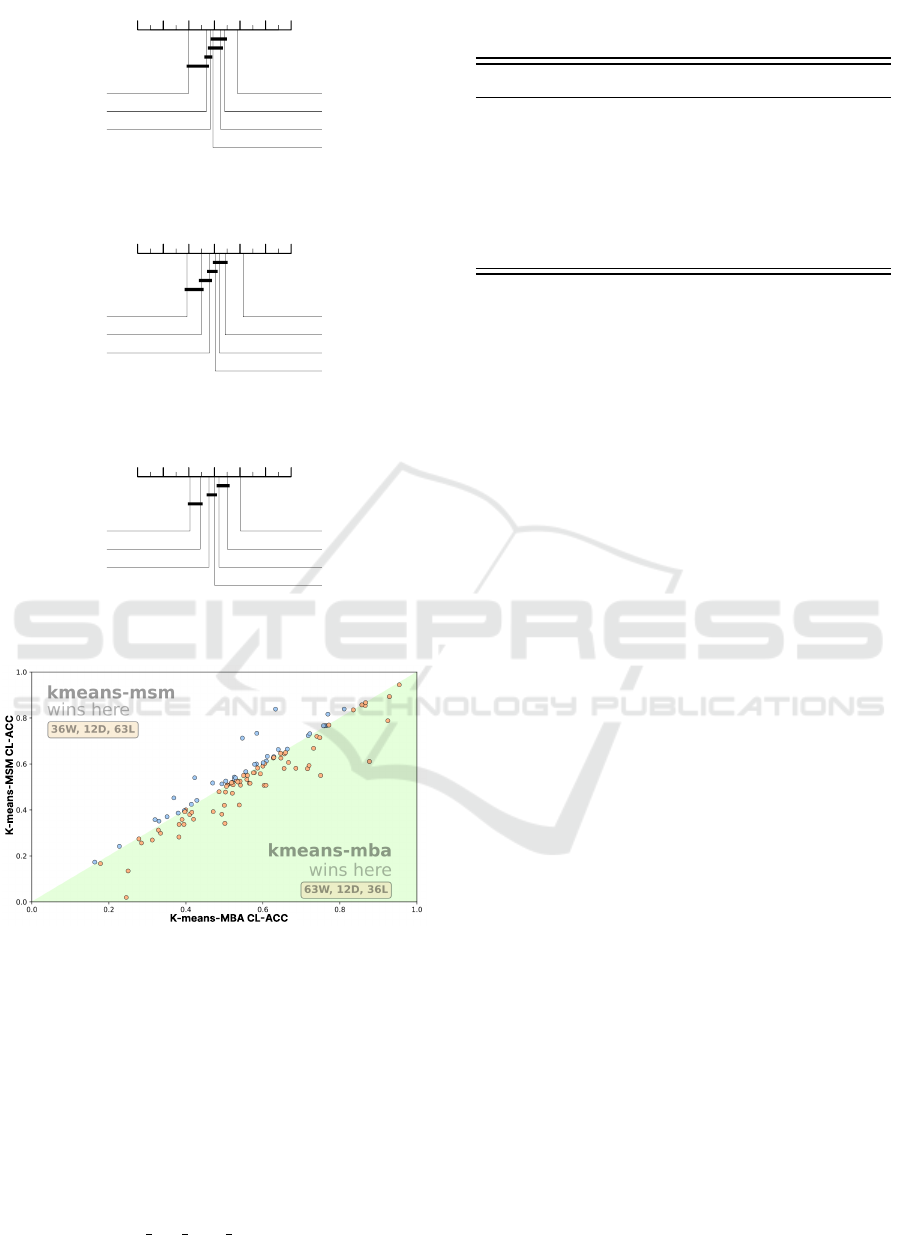
7 6 5 4 3 2 1

3.1081

k-means-MBA

3.6036

k-means-MSM

3.7568

TTC

4.0586

k-means-DBA

4.1667

k-means-ED

4.3063

k-shapes

k-means-DTW

Figure 3: Average ranks and cliques for CL-ACC for seven

clustering algorithms on 111 UCR datasets.

7 6 5 4 3 2 1

2.8739

k-means-MBA

3.5766

k-means-MSM

3.8018

k-means-DBA

3.9685

TTC

4.1937

k-means-ED

4.5135

k-shapes

5.0721

k-means-DTW

Figure 4: Average ranks and cliques for NMI for seven clus-

tering algorithms on 111 UCR datasets.

7 6 5 4 3 2 1

2.9775

k-means-MBA

3.4955

k-means-MSM

3.8243

k-means-DBA

3.991

TTC

4.2117

k-means-ED

4.5495

k-shapes

4.9505

k-means-DTW

Figure 5: Average ranks and cliques for ARI for seven clus-

tering algorithms on 111 UCR datasets.

Figure 6: CL-ACC scatter plot of k-means-MBA against k-

means-MSM. The yellow points show k-means-MBA was

better and the blue points show where k-means-MSM was

better.

site. They provide NMI results for over 300 different

clustering algorithms on the same UCR datasets we

use. These are not directly comparable, since they are

averaged over ﬁve runs and there may be other exper-

imental differences. However, they can give some in-

dication of relative performance. The best deep learn-

ing approach of the hundreds assessed, a cnn with

joint pretext loss and without clustering loss (key in

their results is res cnn joint None) achieved an aver-

age NMI of 0.3292. k-means-MBA obtained a com-

Table 2: Summary performance measures for k-means

based clustering.

CL-ACC ARI NMI

k-means-MBA 55.97% 23.91% 32.36%

k-means-MSM 54.07% 21.75% 29.87%

TTC 53.70% 22.38% 30.87%

k-means-DBA 53.96% 20.63% 29.86%

k-means-ED 51.59% 18.64% 27.31%

k-shapes 47.81% 11.24% 21.57%

k-means-DTW 48.95% 16.22% 23.30%

parable NMI of 0.3236.

4.3 k-means vs k-medoids

The alternative to using an elastic averaging technique

with k-means is to use k-medoids, which trade extra

memory to require fewer averaging operations. This

is because they require a precomputed pairwise dis-

tance matrix. This is not needed in k-means as only

distances to the generated centres each iteration are

needed. Holder et al. (2022) found that k-medoids

based on Lloyds algorithm was signiﬁcantly better

than k-means for seven elastic distance measures. If

we use k-means-MBA, then the performance differ-

ence is removed and on NMI and ARI measures,

k-means-MBA signiﬁcantly outperforms k-medoids-

MSM. Figures 7, 8 and 9 show the ranks by NMI, ac-

curacy and ARI of ﬁve k-means variants against three

k-medoids clusterers. The scatter plot of k-means-

MBA against k-medoids-MSM in terms of ARI is

shown in Figure 10.

As illustrated in Figures 7, 8, and 9, the choice

of elastic distance measure plays a critical role in the

performance of both k-means and k-medoids algo-

rithms. However, when we hold the distance met-

ric constant and solely vary the method for comput-

ing the cluster center - comparing k-medoids-MSM

against k-means-MBA we ﬁnd that MBA signiﬁcantly

enhances the quality of clustering across all evalua-

tion metrics. In addition this is true against the arith-

metic mean used in k-means-msm.

5 CONCLUSION

Distance functions play a crucial role in time series

machine learning, particularly with clustering where

it is commonly still used. A recent study found k-

medoids more effective than standard k-means on the

UCR data (Holder et al., 2022). However, k-medoids

has the problem of always requiring a complete dis-

tance matrix, and is usually slower than k-means. The

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure

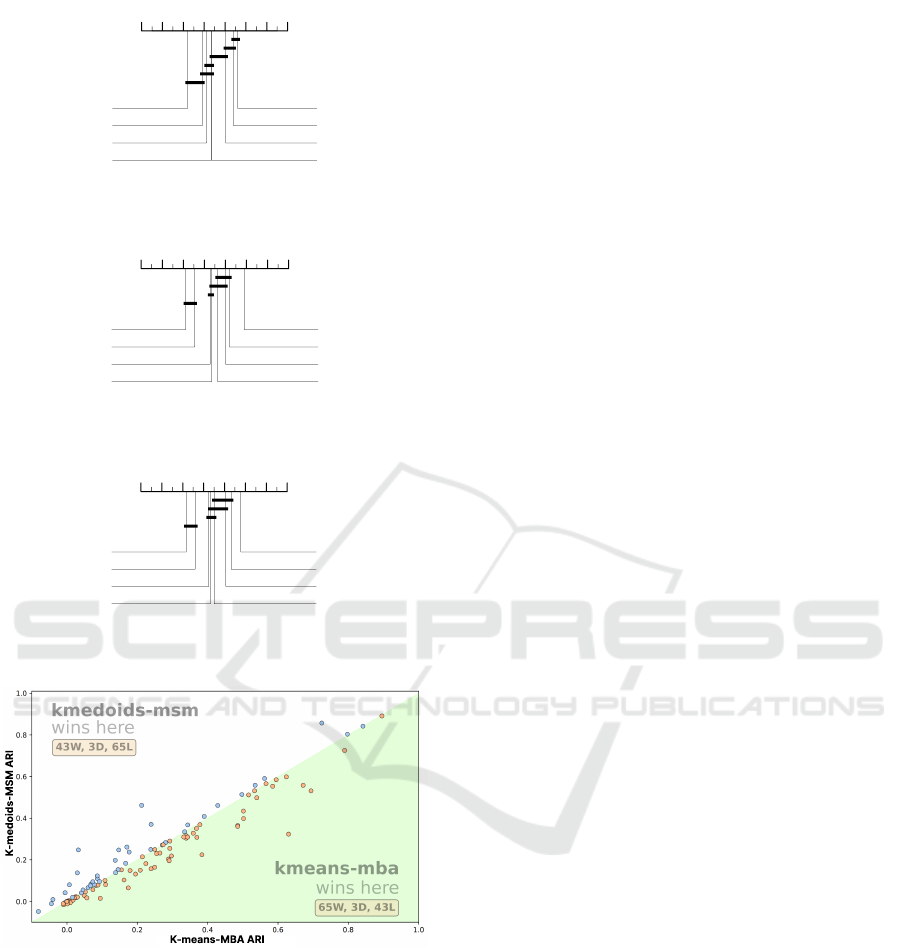
8 7 6 5 4 3 2 1

3.3919

k-means-MBA

3.5901

k-medoids-MSM

3.9685

k-means-MSM

4.6351

k-means-DBA

4.6396

k-means-ED

4.8829

k-medoids-DTW

5.0901

k-medoids-ED

5.8018

k-means-DTW

Figure 7: Average ranks and cliques for CL-ACC for ﬁve

k-means and three k-medoids methods.

8 7 6 5 4 3 2 1

3.0991

k-means-MBA

3.8063

k-medoids-MSM

k-means-MSM

4.3694

k-means-DBA

4.6577

k-medoids-DTW

4.7252

k-means-ED

5.4595

k-medoids-ED

5.8829

k-means-DTW

Figure 8: Average ranks and cliques for NMI for ﬁve k-

means and three k-medoids methods.

8 7 6 5 4 3 2 1

3.2207

k-means-MBA

3.6802

k-medoids-MSM

3.9369

k-means-MSM

4.4955

k-means-DBA

4.6757

k-medoids-DTW

4.7613

k-means-ED

5.3964

k-medoids-ED

5.8333

k-means-DTW

Figure 9: Average ranks and cliques for ARI for ﬁve k-

means and three k-medoids methods.

Figure 10: ARI scatter plot of k-means-MBA against k-

medoids-MSM. The yellow points show k-means-MBA was

better and the blue points show where k-medoids-MSM was

better.

problem with standard k-means is that arithmetic av-

eraging in the step to ﬁnd centroids loses the elastic

information. A solution for k-means-DTW based on

barycentre averaging was proposed in (Petitjean et al.,

2011), known as DTW Barycentre Averaging (DBA).

However, it was also shown in (Holder et al., 2022)

that DTW is less effective at ﬁnding good clusterings

than alternative elastic distances. We have adapted

the Move-Split-Merge (MSM) distance (Stefan et al.,

2013) to be used with k-means barycentre averaging.

We have shown (see Table 2, Figures 7, 9, 8) that

using MSM with Barycentre Averaging (MBA) sig-

niﬁcantly improves the results of k-means. k-means-

MBA is also signiﬁcantly better than the popular k-

shapes and Two-step Time series Clustering (TTC)

algorithms, and similar to the best deep learning ap-

proach found through experimenting with over 300

models (see end of Section 4.2). We believe k-means-

MBA offers a good alternative to k-medoids-MSM for

Time Series Clustering (TSCL).

In future work we would seek to improve the time

complexity of MBA by employing a techniques such

as a bounding windows for MBA. Additionally we

have set out a framework to adapt other elastic dis-

tances for barycentre averaging. This could lead to

experimentation using other distances such as Time

Warp Edit (TWE) (Marteau, 2009) which achieved

similar performance to MSM for k-means (Holder

et al., 2022). Finally we would like to investigate

the possibility of using different elastic distances with

our framework to create an ensemble elastic distance

k-means clusterer similar to the elastic ensemble clas-

siﬁer proposed in (Lines and Bagnall, 2015).

ACKNOWLEDGEMENTS

This work has been supported by EPSRC (grant

reference EP/W030756/1) and partially sub-

sidised by “Agencia Espa

nola de Investigaci

(Espa

na)” (grant reference: PID2020-115454GB-

C22/AEI/10.13039/501100011033). David Guijo-

Rubio’s research has been subsidised by the

University of C

ordoba through grants to Public

Universities for the requaliﬁcation of the Spanish

university system of the Ministry of Universities,

ﬁnanced by the European Union - NextGenerationEU

(grant reference: UCOR01MS). Some of the exper-

iments were carried out on the High Performance

Computing Cluster supported by the Research and

Specialist Computing Support service at the Uni-

versity of East Anglia. We would like to thank all

those responsible for helping maintain the time series

classiﬁcation archives and those contributing to open

source implementations of the algorithms.

REFERENCES

Aghabozorgi, S., Shirkhorshidi, A., and Wah, T. (2015).

Time-series clustering – a decade review. Information

Systems, 53:606–660.

Aghabozorgi, S. and Wah, T. Y. (2014). Clustering of

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

large time series datasets. Intelligent Data Analysis,

18:793–817.

Aghabozorgi, S., Ying Wah, T., Herawan, T., Jalab, H. A.,

Shaygan, M. A., and Jalali, A. (2014). A hybrid algo-

rithm for clustering of time series data based on afﬁn-

ity search technique. The Scientiﬁc World Journal,

2014.

Bagnall, A., Lines, J., Bostrom, A., Large, J., and Keogh,

E. (2017). The great time series classiﬁcation bake

off: a review and experimental evaluation of recent

algorithmic advances. Data Mining and Knowledge

Discovery, 31(3):606–660.

Benavoli, A., Corani, G., and Mangili, F. (2016). Should we

really use post-hoc tests based on mean-ranks? Jour-

nal of Machine Learning Research, 17:1–10.

Bradley, P. S. and Fayyad, U. M. (1998). Reﬁning ini-

tial points for k-means clustering. In Proceedings

of the Fifteenth International Conference on Machine

Learning, ICML ’98, page 91–99, San Francisco, CA,

USA. Morgan Kaufmann Publishers Inc.

Brill, M., Fluschnik, T., Froese, V., Jain, B., Niedermeier,

R., and Schultz, D. (2019). Exact mean computation

in dynamic time warping spaces. Data Mining and

Knowledge Discovery, 33:252–291.

Chen, L. and Ng, R. (2004). On the marriage of Lp-norms

and edit distance. In proceedings of the 30th Interna-

tional Conference on Very Large Data Bases.

Dau, H., Bagnall, A., Kamgar, K., Yeh, M., Zhu, Y.,

Gharghabi, S., Ratanamahatana, C., Chotirat, A., and

Keogh, E. (2019). The UCR time series archive.

IEEE/CAA Journal of Automatica Sinica, 6(6):1293–

1305.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. Journal of Machine Learning

Research, 7:1–30.

Ding, H., Trajcevski, G., Scheuermann, P., Wang, X., and

Keogh, E. (2008). Querying and mining of time series

data: Experimental comparison of representations and

distance measures. In proceedings of the 34th Inter-

national Conference on Very Large Data Bases.

Garc

ıa, S. and Herrera, F. (2008). An extension on “sta-

tistical comparisons of classiﬁers over multiple data

sets” for all pairwise comparisons. Journal of Ma-

chine Learning Research, 9:2677–2694.

Guijo-Rubio, D., Middlehurst, M., Arcencio, G., Silva,

D. F., and Bagnall, A. (2023). Unsupervised feature

based algorithms for time series extrinsic regression.

arXiv preprint arXiv:2305.01429.

Gupta, L., Molfese, D., Tammana, R., and Simos, P. (1996).

Nonlinear alignment and averaging for estimating the

evoked potential. IEEE Transactions on Biomedical

Engineering, 43(4):348–356.

Gusﬁeld, D. (1997). Algorithms on Strings, Trees, and Se-

quences: Computer Science and Computational Biol-

ogy. Cambridge University Press.

Hills, J., Lines, J., Baranauskas, E., Mapp, J., and Bagnall,

A. (2014). Classiﬁcation of time series by shapelet

transformation. Data Mining and Knowledge Discov-

ery, 28(4):851–881.

Holder, C., Middlehurst, M., and Bagnall, A. (2022).

A review and evaluation of elastic distance func-

tions for time series clustering. arXiv preprint

arXiv:2205.15181.

Holznigenkemper, J. and Seeger, C. K. B. (2023). On com-

puting exact means of time series using the move-

split-merge metric. Data Mining and Knowledge Dis-

covery, 37(2):595–626.

Lafabregue, B., Weber, J., Gancarski, P., and Forestier, G.

(2022). End-to-end deep representation learning for

time series clustering: a comparative study. Data Min-

ing and Knowledge Discovery, 36:29—-81.

Li, J., Izakian, H., Pedrycz, W., and Jamal, I. (2021).

Clustering-based anomaly detection in multivari-

ate time series data. Applied Soft Computing,

100:106919.

Liao, T. W. (2005). Clustering of time series data—a survey.

Pattern recognition, 38(11):1857–1874.

Lines, J. and Bagnall, A. (2014). Ensembles of elastic dis-

tance measures for time series classiﬁcation. In pro-

ceedings of the 14th SIAM International Conference

on Data Mining.

Lines, J. and Bagnall, A. (2015). Time series classiﬁcation

with ensembles of elastic distance measures. Data

Mining and Knowledge Discovery, 29:565–592.

Lines, J., Taylor, S., and Bagnall, A. (2018). Time se-

ries classiﬁcation with HIVE-COTE: The hierarchi-

cal vote collective of transformation-based ensembles.

ACM Transactions Knowledge Discovery from Data,

12(5):1–36.

Lloyd, S. P. (1982). Least squares quantization in pcm.

IEEE Trans. Inf. Theory, 28:129–136.

MacQueen, J. et al. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Proceed-

ings of the ﬁfth Berkeley symposium on mathematical

statistics and probability, volume 1, pages 281–297.

Marteau, P. (2009). Time warp edit distance with stiffness

adjustment for time series matching. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

31(2):306–318.

McDowell, I. C., Manandhar, D., Vockley, C. M., Schmid,

A. K., Reddy, T. E., and Engelhardt, B. E. (2018).

Clustering gene expression time series data using an

inﬁnite gaussian process mixture model. PLoS com-

putational biology, 14(1):e1005896.

Middlehurst, M., Sch

afer, P., and Bagnall, A. (2023). Bake

off redux: a review and experimental evaluation of

recent time series classiﬁcation algorithms. arXiv

preprint arXiv:2304.13029.

Nikolaou, A., Guti

errez, P. A., Dur

an, A., Dicaire,

I., Fern

andez-Navarro, F., and Herv

as-Mart

ınez, C.

(2015). Detection of early warning signals in paleo-

climate data using a genetic time series segmentation

algorithm. Climate Dynamics, 44:1919–1933.

Paparrizos, J. and Gravano, L. (2015). k-shape: Efﬁcient

and accurate clustering of time series. In Proceedings

of the 2015 ACM SIGMOD International Conference

on Management of Data, pages 1855–1870.

Paparrizos, J., Liu, C., Elmore, A., and Franklin, M.

(2020). Debunking four long-standing misconcep-

Barycentre Averaging for the Move-Split-Merge Time Series Distance Measure

tions of time-series distance measures. In proceed-

ings of the ACM SIGMOD international conference

on management of data.

Petitjean, F., Forestier, G., Webb, G. I., Nicholson, A. E.,

Chen, Y., and Keogh, E. (2016). Faster and more accu-

rate classiﬁcation of time series by exploiting a novel

dynamic time warping averaging algorithm. Knowl-

edge and Information Systems, 47:1–26.

Petitjean, F., Ketterlin, A., and Gancarski, P. (2011). A

global averaging method for dynamic time warping,

with applications to clustering. Pattern Recognition,

44:678–.

Ratanamahatana, C. and Keogh, E. (2005). Three myths

about dynamic time warping data mining. In pro-

ceedings of the 5th SIAM International Conference on

Data Mining.

Shifaz, A., Pelletier, C., Petitjean, F., and Webb, G. (2023).

Elastic similarity and distance measures for multivari-

ate time series. Knowledge and Information Systems,

65(6).

Stefan, A., Athitsos, V., and Das, G. (2013). The Move-

Split-Merge metric for time series. IEEE Transactions

on Knowledge and Data Engineering, 25(6):1425–

1438.

Tan, C. W., Bergmeir, C., Petitjean, F., and Webb, G.

(2021). Time series extrinsic regression. Data Min-

ing and Knowledge Discovery, 35:1032––1060.

Zakaria, J., Mueen, A., and Keogh, E. (2012). Cluster-

ing time series using unsupervised-shapelets. In 2012

IEEE 12th International Conference on Data Mining,

pages 785–794. IEEE.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval