A Genetic Algorithm for Marine Spatial Planning with Minimized

Conflict Between Planned Regions

Seo-Ah Yu

, Choong-Ki Kim

and Yong-Hyuk Kim

Dept. Comp. Sci, Kwangwoon University, Seoul, Republic of Korea

Divisions for Natural Environment, Korea Environment Institute, Seoul, Republic of Korea

Keywords: Genetic Algorithm, Multi-Objective Optimization, Marine Spatial Planning.

Abstract: To efficiently utilize marine space, numerous experiments have been conducted to optimize marine space.

We utilize a genetic algorithm (GA) to develop an optimal spatial plan for the Exclusive Economic Zone

(EEZ). The space can be allocated for six different uses, each with its own weight. Conflicts exist among

these uses. The objective is to maximize the fitness of the space by evaluating it at the cell level. This involves

maximizing the evaluation score, which is determined by the weighted sum of each cell's use, minimizing

conflicts, and reducing the number of clusters to ensure continuity of use. The basic allocation model, which

achieves the best quality among random solutions within the same running time as our GA, is used for

comparison. Experimental results showed that, when our method is compared to the basic model, the

evaluation scores increased by approximately 20%, except for one case of use ‘ecology’. Additionally,

conflicts between zones decreased, and the total fitness improved as the number of clusters decreased.

1 INTRODUCTION

As the population grows and the demand for resources

increases, it is important to allocate resources

efficiently to meet these demands. In particular, the

Food and Agriculture Organization of the United

Nations (FAO) predicts that the world's population

will reach 9 billion by 2050 (Liu., 2020).

If resources are not efficiently allocated, serious

environmental pollution problems and social conflicts

may result. The ocean is a repository of food and

resources. The ocean covers 70% of the Earth's

surface and is home to seven times more marine

organisms than land organisms. Therefore, interest in

marine spatial planning (MSP) is increasing every

year in each country.

MSP is a process and approach used to manage and

organize human activities in marine and coastal areas.

It involves the systematic and integrated planning of

various uses and activities, such as fisheries, tourism,

energy development, conservation, and shipping,

within the marine environment. The goal of MSP is to

achieve sustainable and efficient use of marine

https://orcid.org/0009-0001-4240-7760

https://orcid.org/0000-0002-8931-529X

https://orcid.org/0000-0002-0492-0889

resources while minimizing conflicts and negative

impacts on the marine ecosystem.

Europe is playing a leading role in the MSP field.

In the UK, the Marine and Coastal Access Act 2009

provides the legal basis for MSP. The Act was

adopted in 2009 and provides a comprehensive

marine planning framework for the protection,

management and use of the UK's coastal and marine

areas. The law emphasizes the sustainable

management and conservation of marine resources

and cooperation and coordination among various

stakeholders. In addition, in 2014, the EU adopted the

Legislation to create a common framework for MSP

in Europe. In Asia, the Republic of Korea enacted the

Marine Spatial Planning Act in 2018 to establish an

MSP process and regulate the utilization of specific

marine management areas. Other countries in Asia,

such as Thailand, Malaysia, and Indonesia, are also

conducting research and development on MSP.

When searching related papers, based on Google

Scholar site for the last 5 years, there were 2,110

papers related to MSP modelling. On the other hand,

papers related to MSP optimization technology were

Yu, S., Kim, C. and Kim, Y.

A Genetic Algorithm for Marine Spatial Planning with Minimized Conﬂict Between Planned Regions.

DOI: 10.5220/0012165000003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 179-185

ISBN: 978-989-758-674-3; ISSN: 2184-3236

179

Table 1: Region rate of each use.

Fishery Energy Resource Marine tour Harbor Ecology

Lower Bound 5% 5% 5% 5% 5% 5%

Upper Bound 20% 15% 10% 30% 30% 10%

Table 2: Weights of each use and constraints.

𝑤



𝑤



𝑤



𝑤







𝑤



𝑤

 

𝑤



𝑤







Weight 0.01 10.00 0.30 0.10 0.10 0.10 0.30 0.10

weak with 1,370 papers, and among them, papers

using genetic algorithm (GA) accounted for only 2%

with 32 papers. Prediction and prevention through

simulation and modelling are important, bur further -

optimization is required to establish direct policies.

Especially, GA excels in global exploration and can

be applied to various optimization problems. GAs can

be applied to a wide range of problem domains and do

not require prior knowledge about the problem

structure. They are versatile and adaptable to various

types of optimization problems, including continuous,

discrete, and combinatorial optimization. Also, GAs

have the ability to search the entire solution space,

making them suitable for global optimization

problems where finding the best possible solution is

the objective. They can overcome local optima and

escape from stagnant regions in the search space. In

addition, since multi-purpose optimization is

possible, it is powerful for resource allocation

problems that must satisfy various interests.

We try to make the optimal MSP with multiple

objectives using a novel GA. In this paper, unlike the

existing method, it is unique in that the map is

encoded in two dimensions and using block uniform

crossover applied to MSP. In addition, by mapping

the map for each use, multi-objective optimization

considering various uses is possible.

The structure of this paper is as follows: Section 2

introduces related work. Section 3 explains our GA

used in MSP. Section 4 analyses the experimental

results. And Section 5 concludes.

2 RELATED WORK

Numerous MSP studies have been conducted to

efficiently utilize marine space. In (Basirati et al.,

2021), the authors proposed a model that can achieve

multiple objectives simultaneously through multi-

objective integer linear optimization. The authors in

(Wang et al., 2022), the authors emphasized the

importance of MSP planning based on the collection

and analysis of data related to the status of marine

aquaculture in Shandong Province. By collecting and

analysing data on the location, scale, and types of

aquacultures, the study provides insights into the

current situation and spatial distribution of marine

aquaculture in the region. In (Boussarie et al., 2023),

the authors presented a framework for prioritizing

offshore wind farms and marine protected areas. In

(Janßen et al., 2019), the study discusses the

advantages and limitations of MARXAN. MARXAN

is a software, which is discrete optimization model. In

(Fotakis et al., 2012), the authors presented a study

that utilizes a spatial GA to solve the multi-objective

optimization problem in forest planning. The

algorithm is applied to address the challenges of

considering multiple objectives for forest

management and conservation. The spatial GA

arranges the genetic information of individuals in a

spatial manner to explore optimal solutions for the

multi-objective goals at hand. In (O'Reilly et al.,

2012), the paper focuses on the utilization of a GA to

determine optimal locations for offshore wind farm

siting. The GA serves as an optimization technique

for identifying the best positions to place wind

turbines in offshore areas. The study takes into

account various factors, including wind resources,

water depth, distance from the shore, and

environmental constraints. By employing the GA, the

researchers aim to maximize energy production while

minimizing the environmental impact and other

constraints associated with offshore wind farm siting.

In (Lubida et al., 2019), the authors focused on land-

use planning for achieving sustainable urban

development in Africa through a spatial and multi-

objective optimization approach. The study proposes

a method to plan and optimize land use considering

various sustainability-related objectives. It aims to

find efficient solutions that take into account

economic, environmental, and social factors in urban

development. The research contributes to providing

sustainable directions for urban development in the

African context. The authors in (Gissi et al., 2019),

the authors discuss the current state of marine spatial

planning.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

180

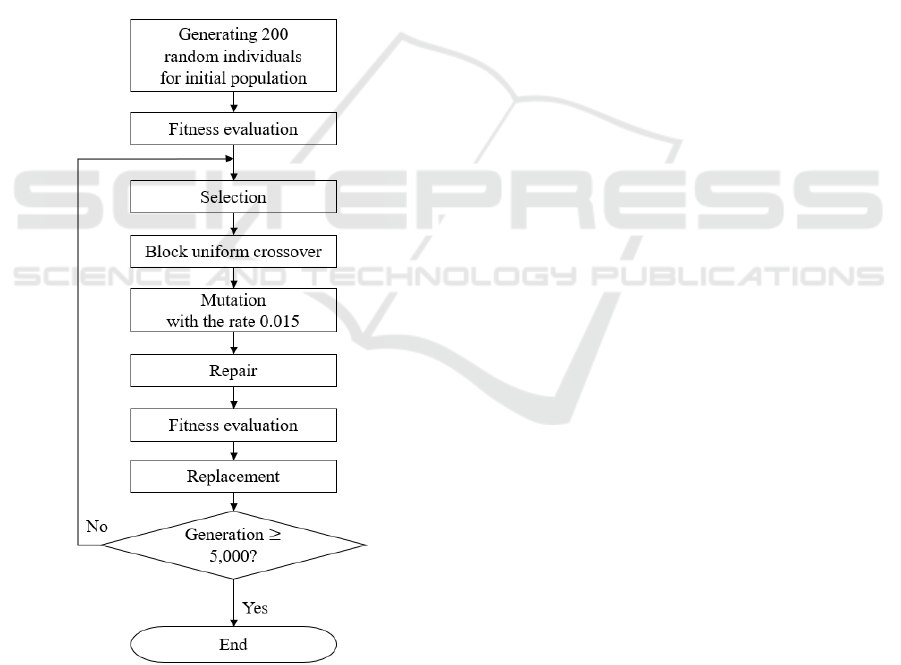
3 PROPOSED GENETIC

ALGORITHM

3.1 Algorithm Design

To evaluate the performance of the spatial planning

optimization using GA, I will designate the solution

derived from this method as “GA.” The population

size is 200, and there are 5,000 generations. A steady-

state GA is used where one solution replaces another

in each generation. The mutation rate is 0.015. The

crossover operation applies block uniform crossover,

which is an extension of one-point crossover in a 2-

dimensional space. The block uniform crossover

method is described in Section 3.2. The replacement

is performed only when the child has a better fitness

than its parent. Figure 1 illustrates the process of a

GA.

Figure 1: Flowchart of the proposed GA.

3.1.1 Block Uniform Crossover

The order of block uniform crossover is as follows:

First, a cutting line is randomly selected from the row

of the generated array(solution). Second, pick one

cutting line from the column. The location of the

cutting line is arbitrarily determined whenever an

intersection operation is performed. Third, child

solutions are generated by performing copying from

the parent solutions alternately for the four regions

thus created (Anderson et al., 1991). Block uniform

crossover is widely used in two-dimensional

problems (Im, C. H et al.,2003, Paik, K., 2011). Please

refer to the appendix for detailed explanations.

3.2 Experimental Design

In this experiment, the uses of marine space are

divided into six categories: fishery, energy, resource,

marine tour, harbour, and ecology. Each use has

minimum and maximum area ratios defined in Table

1. If these ratios are violated, repair operations are

conducted to adjust the area occupied within the

appropriate ratio. And each use is assigned a number

from 0 to 5. And we will call it as use number. The

weights for each use are determined based on expert

opinion, and that are presented in Table 2.

A domain map indicates feasible and infeasible

regions. A constraint matrix representing the degree

of conflict between different area use. Each use has a

use map. And in the use map, each cell is assigned an

evaluation number from 1 to 5. Note that it is different

from use number. The higher evaluation number, the

more appropriate the area for the use. For example, if

a cell is assigned a value of 5 on the ecology map, that

cell is an area very suitable for ecology. In Figure

2(a), ecology’s use map is represented.

To calculate fitness, first, the domain map is

checked to determine if the cell is available for use.

Unavailable cells are indicated as -1 in the domain

map. If a cell is available, use number is assigned to

the cell. It is a generated solution. For each use, a

solution, add up the evaluation number specified in

the use map. It becomes the evaluation score for that

each use. For example, if there are 3 cells assigned

ecology, use number 5, to the solution, and the

evaluation number at the ecology use map for each

cell is 1, 5, 3 the ecology evaluation score is 9. Total

evaluation value is obtained by summing the product

of the evaluation score and the weight.

The conflict number is assigned to 6 by 6 matrix.

Conflict score is obtained by add up conflict numbers

when other uses are adjacent. Conflict value is

obtained by multiplying the conflict score by the

conflict weight.

A Genetic Algorithm for Marine Spatial Planning with Minimized Conﬂict Between Planned Regions

181

Figure 2: An example map of ecology.

Table 3: Experimental results

Fitness Conflict #Clusters Fishery Energy Resource

Marine

Tour

Harbour Ecology

R(200)

Best 3852.84 2443.46 411.00 305.00 223.00 124.00 443.00 457.00 172.00

Ave 4009.83 2498.22 427.00 276.30 184.13 104.00 358.63 405.73 155.37

SD 62.08 38.41 6.26 18.09 22.45 10.96 26.64 30.18 7.47

R(5200)

Best 3579.91 2383.62 386.00 314.00 227.00 138.00 432.00 472.00 176.00

Ave 3848.54 2453.16 411.13 279.40 176.57 99.73 367.47 410.57 159.63

SD 65.41 34.07 6.47 26.69 19.23 15.00 30.57 28.14 7.01

Best 202.93 927.92 17.00 469.00 266.00 143.00 568.00 610.00 178.00

Ave 152.71 1057.67 22.37 417.43 199.87 102.10 492.83 565.00 127.40

SD 22.37 63.28 2.27 25.14 29.83 19.52 32.95 27.69 25.93

*Best : the highest value obtained among the 30 experiments. *R(200) : the quality of the best among initial population of the GA.

*Ave : the average value obtained among the 30 experiments. *R(5200) :

the best quality of random solutions achieved in the same

*SD :

the standard deviation of the values from the 30 experiments. time as in our GA.

The total cluster value is determined by

multiplying the number of clusters formed by the

allocated regions with the cluster weight. Regions of

the same area use are not considered as a single cluster

if they are not contiguous.

Finally, the fitness is calculated by subtracting the

conflict value and the cluster value from the

evaluation value. Figure 2(c) displays a fitness map

that highlights the areas in blue where ecology is

allocated. Equations (1)



(4) summarizes this

process.

𝑈  𝑓𝑖𝑠ℎ𝑒𝑟𝑦, 𝑒𝑛𝑒𝑟𝑔𝑦, 𝑟𝑒𝑠𝑜𝑢𝑟𝑐𝑒, 𝑚𝑎𝑟𝑖𝑛𝑒 𝑡𝑜𝑢𝑟, ℎ𝑜𝑟𝑏𝑜𝑢𝑟, 𝑒𝑐𝑜𝑙𝑜𝑔𝑦}

𝑉





∑

𝑤

∈

𝑆



(1)

𝑉



 𝑤



𝑆



(2)

𝑉



 𝑤



#𝑐𝑙𝑢𝑠𝑡𝑒𝑟𝑠

(3)

𝑓𝑖𝑡𝑛𝑒𝑠𝑠  𝑉



𝑉



𝑉



(4)

where 𝑉



is evaluation value, 𝑆



is evaluation score

for use 𝑖∈𝑈, 𝑉



is conflict value,

𝑆



conflict score, and 𝑉



is cluster value.

4 EXPERIMENTAL RESULTS

All the experiments are conducted using a computer

with processor AMD Ryzen Threadripper 2990WX

32-Core @ 1.75GHz with 64 GB of RAM. And OS is

Ubuntu 18.04.6 LTS. C++ is used to implement

the source code.

To make a comparison, the best solution obtained

from the pool of 5,200 solutions, each of which entails

randomly assigning zones. It will be denoted as

"R(5200)". To demonstrate that the solution derived

from the 5,200 solutions outperforms a smaller

subset, I will label the best solution from the initial

200 random solutions as "R(200)". This comparison

(a) An example use map, ecology (b) A plot that magnifies a section of

the ecology use map

highlights the ecology regions in

blue

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

182

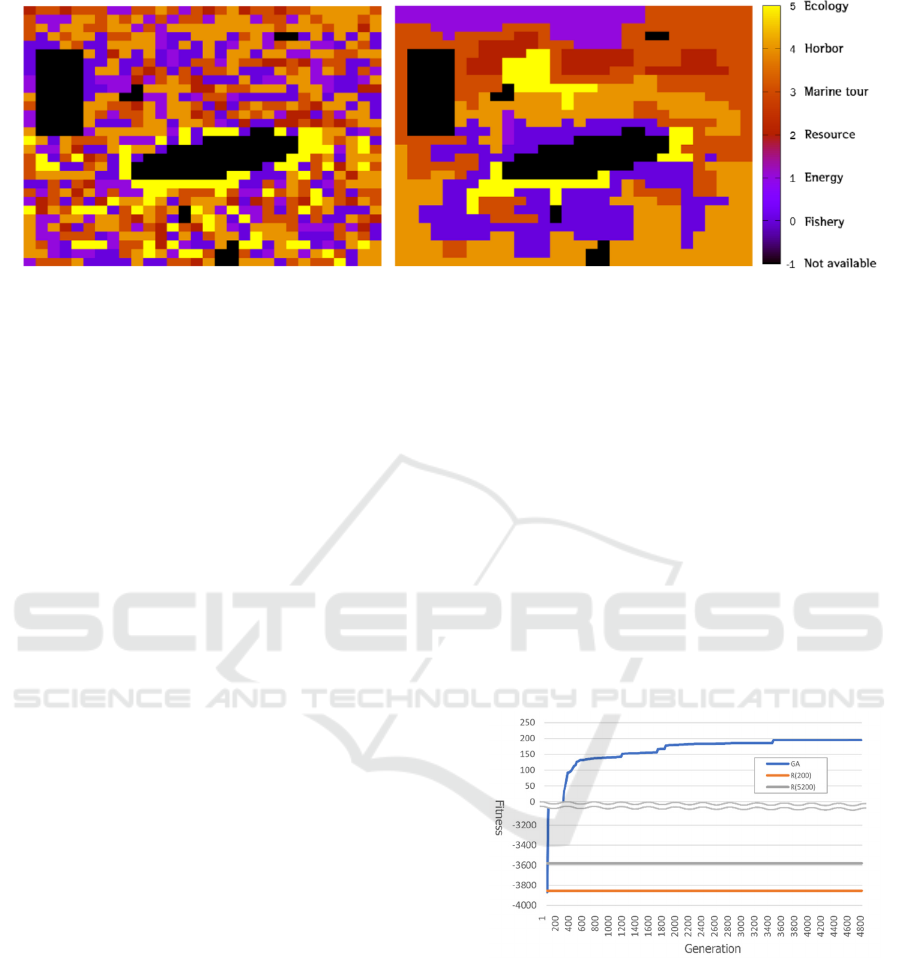
(a) R(5200) (b) Our genetic algorithm

Figure 3: Result maps.

will showcase the superiority of the obtained solution

from the larger set. The experiment was performed 30

times for each case. It took 516.32 seconds to

complete the optimization process for 5000

generations. It depends on the number of generations.

The optimization process took place in Jeju Island,

located in South Korea. The unit of measurement used

in the experiment corresponds to cells, with each cell

representing 3



3′ as latitude longitude, where 60'

means 1 degree.

Comparing the results of the GA and R(5200) in

Table 3’s average, it can be observed that the GA

achieved a reduction of approximately 57% in conflict

compared to Random. The evaluation scores for most

area use showed an increase. On the other hand, despite

the decrease in the evaluation score for ecology, these

exceptions can be seen as positive factors for

maintaining a balanced overall performance. This is

because the conflict value decreased, and the overall

fitness increased. Additionally, Figure 3(a)

demonstrates a significantly larger number of clusters

compared to Figure 3(b), indicating that optimization

has not been achieved. According to Table 3, the

number of clusters exhibited a reduction rate of

approximately 95% upon completion of the

optimization. The fitness of the Random solution

appears as negative, which is a result of being penalized

for a higher number of clusters and conflict levels. In

conclusion, based on Figure 4, it is evident that the

fitness of the “GA” results obtained through GA is

significantly higher, indicating that the optimization of

zone allocation through GA can be effectively utilized

in MSP process.

5 CONCLUSIONS

This study successfully optimized MSP with multiple

objectives using GA. The objective of optimization is

to maximize the overall fitness value. The experiments

showed higher fitness values compared to random

allocation of area use. By successfully applying GA to

MSP, it has become possible to achieve optimal and

automated planning that takes into account various

constraints. In this paper, the weights of each area use

were determined based on expert opinions, but it is also

possible to optimize by considering the weights based

on the expertise. In the future, we plan to observe trade-

off graphs between different area use. Given the

potential for environmental changes and social policy

modifications, spatial re-planning may be necessary.

Therefore, collaboration with monitoring technologies

that can incorporate such factors will be crucial.

Figure 4: Fitness plot of our GA.

ACKNOWLEDGEMENTS

This research was a part of the project titled Marine

ecosystem-based analysis and decision-making

support system development for marine spatial

planning (grant number 20170325), funded by the

Ministry of Ocean and Fisheries (Korea), supported

by Korea Institute of Marine Science & Technology

A Genetic Algorithm for Marine Spatial Planning with Minimized Conﬂict Between Planned Regions

183

Promotion. The project was implemented by the

Korea Environment Institute (project 2021-013(R)).

REFERENCES

Liu, S. Y. (2020). Artificial intelligence (AI) in agriculture.

IT Professional, 22(3), 14-15.

Basirati, M., Billot, R., Meyer, P., & Bocher, E. (2021). Exact

zoning optimization model for marine spatial planning

(msp). Frontiers in Marine Science, 8, 726187.

Wang, J., Yang, X., Wang, Z., Ge, D., & Kang, J. (2022).

Monitoring Marine Aquaculture and Implications for

Marine Spatial Planning—An Example from Shandong

Province, China. Remote Sensing, 14(3), 732.

Boussarie, G., Kopp, D., Lavialle, G., Mouchet, M., &

Morfin, M. (2023). Marine spatial planning to solve

increasing conflicts at sea: A framework for prioritizing

offshore windfarms and marine protected areas. Journal

of Environmental Management, 339, 117857.

Janßen, H., Göke, C., & Luttmann, A. (2019). Knowledge

integration in Marine Spatial Planning: a practitioners'

view on decision support tools with special focus on

Marxan. Ocean & Coastal Management, 168, 130-138.

Fotakis, D. G., Sidiropoulos, E., Myronidis, D., & Ioannou,

K. (2012). Spatial genetic algorithm for multi-objective

forest planning. Forest Policy and Economics, 21, 12-19.

O'Reilly, C. M., Grilli, A. R., & Potty, G. R. (2012,

December). Offshore wind farm siting using a genetic

algorithm. In 2012 International Conference on Green

Technologies (ICGT) (pp. 208-214). IEEE.

Lubida, A., Veysipanah, M., Pilesjo, P., & Mansourian, A.

(2019). Land-use planning for sustainable urban

development in Africa: A spatial and multi-objective

optimization approach. Geodesy and cartography,

45(1), 1-15.

Gissi, E., Fraschetti, S., & Micheli, F. (2019). Incorporating

change in marine spatial planning: A review.

Environmental Science & Policy, 92, 191-200.

Anderson, C. A., Jones, K. F., & Ryan, J. (1991). A two-

dimensional genetic algorithm for the Ising problem.

Complex Systems, 5(3), 327-334.

Im, C. H., Jung, H. K., & Kim, Y. J. (2003). Hybrid genetic

algorithm for electromagnetic topology optimization.

IEEE Transactions on Magnetics, 39(5), 2163-2169.

Paik, K. (2011). Optimization approach for 4-D natural

landscape evolution. IEEE transactions on evolutionary

computation, 15(5), 684-691.

APPENDIX

Comparing Methods with Respect to Each

Score and the Number of Clusters that

Constitutes Fitness

The graph presented in Figure 5(a) showcases the

comparison of experimental results, highlighting the

superiority of our GA. It focuses on two key

parameters: the conflict score and the number of

clusters. In this graph, lower values are considered

better, indicating improved performance.

Figure 5(b) displays the performance scores of

each use case. Higher values in this graph indicate

better overall performance.

Together, these two figures provide a

comprehensive visual representation of how our GA

outperforms other approaches in terms of conflict

resolution, cluster numbers, and overall evaluation

scores.

Block Uniform Crossover in Our Genetic

Algorithm

Figure 6 depicts the concept of block uniform

crossover, which serves as an extension of one-point

crossover into two dimensions. This technique

involves the following steps:

1. Random Selection: A row cutting line and a

column cutting line are randomly selected

within the solution space.

2. Division of Solution Space: The selected

cutting lines divide the solution space into

four distinct regions.

3. Offspring Generation: The offspring is

generated by performing alternating parent

copy operations within each of the four

regions. This means that for each region,

the genetic material from one parent is

copied into the offspring, while the other

parent's genetic material is copied into the

next region, and so on.

The benefits of block uniform crossover are

twofold. First, it allows for the exploration of a

broader solution space by creating diverse

combinations of genetic material from the parents.

This increases the chances of discovering novel and

potentially superior solutions. Second, by

incorporating genetic material from both parents,

block uniform crossover helps to preserve and

combine beneficial traits, potentially leading to

offspring with enhanced performance.

Overall, block uniform crossover serves as a

valuable tool within the GA framework, particularly

in two-dimensional problem domains.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

184

(a) Conflict scores and the numbers of clusters

(the lower, the better)

(b) Evaluation scores of uses

(the higher, the better)

Figure 5: Visual comparison of our experiments (values from Table 3).

Figure 6: Example of the block uniform crossover with one cutting line on each dimension.

row

column

A Genetic Algorithm for Marine Spatial Planning with Minimized Conﬂict Between Planned Regions

185