Multiphysics Simulation for the Optimization of an Optoelectronic-Based

Tactile Sensor

Gianluca Laudante

, Olga Pennacchio and Salvatore Pirozzi

Universit

a degli Studi della Campania “Luigi Vanvitelli”, Dipartimento di Ingegneria, Aversa (CE), Italy

Keywords:

Tactile Sensor, Multiphysics Simulation, Optics, Mechatronics.

Abstract:

Robotic systems are more and more present in various contexts such as industrial, domestic, logistic, health-

care, and others. For this reason, robots are being used for increasingly complex tasks which require skills like

dexterity and precision. These capabilities are achieved by means of sensory systems that give that robot the

perception of the environment. Sensors, before being produced and distributed, need to be suitably designed

in order to fulﬁl the speciﬁcs that a task requires. During the design process, simulation methods are really

important to analyze the characteristics of a designed product before actually producing it, so as to avoid waste

of time and money. This paper aims at proposing a method for simulating a tactile sensor based on optoelec-

tronic technology considering both the optical and mechanical interfaces, as well as their coupling. Also, it

exploits both simulation and experiment results in order to discuss the best choice for the shape to use for the

realization of reﬂective cells.

1 INTRODUCTION

Nowadays, robotics systems are increasingly used to

carry out complex tasks in cluttered environments,

where abilities such as dexterity and precision are es-

sential. To provide the robots with the necessary ca-

pabilities, sensory systems are required. These are

mainly cameras, useful for having an overall view of

the working scene, proximity and distance sensors,

for avoiding collisions with the environment, and tac-

tile sensors, which allow estimating the physical and

geometrical properties of the manipulated objects, in-

formation of paramount importance for the execution

of robotic grasping and manipulation tasks.

Tactile sensing, in particular, is receiving a lot of

interest in the last few years since it can bring new

possibilities for automating processes, currently car-

ried out by human workers, in several ﬁelds such as

logistics, people assistance, prosthetics, manufactur-

ing, automotive and aerospace industry. Thanks to

the growing interest, many new tactile sensors based

on different technologies are being developed. For

example, the Gelsight (Wang et al., 2021) and Tac-

Tip (Ward-Cherrier et al., 2018) sensors use high-

resolution RGB cameras to detect the deformation

of a deformable mechanical interface, the Contactile

sensor (Khamis et al., 2019) exploits optoelectronic

https://orcid.org/0000-0003-4009-8287

https://orcid.org/0000-0002-1237-0389

components to retrieve information about the contact,

while the GTac sensor (Lu et al., 2022), inspired by

the human sense of touch, integrates both piezoresis-

tive and Hall sensors in a multilayered structure. De-

spite the technological progress and the development

of these new sensors, the research in the analysis and

design of tactile sensors remains an open ﬁeld with

many investigated problems. Since all the aforemen-

tioned sensors present the combination of at least two

parts, i.e., an external mechanical interface and an

internal, usually electronic, component to transduce

deformations in a different signal depending on the

used technology, multiphysics modelling and simula-

tion are of paramount importance for improving and

optimizing the design and analysis processes.

To the best of the authors’ knowledge, in litera-

ture, there is a lack of methods for simulating both

the layers composing the tactile sensors, especially

for those based on optical technology like the one

considered in this work, and their coupling. In fact,

authors in (Amiri et al., 2022) simulate a GaN-based

integrated LED-photodetector system using only the

optical physics, in (Alqurashi et al., 2022) the optical

part of a low concentrator photovoltaic system is sim-

ulated, (Ferreira et al., 2022) studies the vertical p-n

junction photodiodes according to CMOS technology

through the optical-semiconductor interfaces, while

authors in (Cirillo et al., 2014) consider a FE analysis

of a silicone deformable interface using mechanical

physics. However, all these works do not take into ac-

Laudante, G., Pennacchio, O. and Pirozzi, S.

Multiphysics Simulation for the Optimization of an Optoelectronic-Based Tactile Sensor.

DOI: 10.5220/0012166900003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 101-110

ISBN: 978-989-758-670-5; ISSN: 2184-2809

101

count the coupling of the mechanical and the optical

interfaces. Indeed, the main objective of this paper is

the development of a simulation model for the design

and optimization of optic-based tactile sensors, con-

sidering the coupling of the optoelectronic layer and

the mechanical deformable layer.

The rest of the paper is structured as follows: Sec-

tion 2 reports the procedure used to reﬁne the opto-

electronic component parameters in order to obtain a

detailed optical model, also by means of comparison

between simulated data and the datasheet provided by

the manufacturer. This section also presents the me-

chanical model of the deformable layer, and the re-

sults of the coupling of the validated optical model

and the mechanical model to optimize the shapes of

the reﬂective cells on the basis of the sensor sensitiv-

ity. Section 3 reports some experimental tests using a

real sensor whose results are compared with the ones

from the simulations and among the different shapes

of the reﬂective cells, and, ﬁnally, section 4 provides

the conclusions and some possibilities for future ad-

vancements.

2 SIMULATION MODEL

The tactile sensor considered for this paper, reported

in detail in (Cirillo et al., 2021), is constituted by

a matrix of taxels, in which each taxel is based on

the use of a LED-phototransistor couple (integrated

within a single photo-reﬂector), and a deformable

layer positioned above the components.

This section describes how the models of the opto-

electronic component and the mechanical deformable

layer have been realized for the simulation of the com-

plete sensor, and reports the results obtained by the

simulation of the coupled model.

2.1 Optical Model

The following reports the analysis of the optoelec-

tronic device’s geometry, necessary to reproduce ad-

equately the optical component model in COMSOL

Multiphysics with the Ray Optics Module, and the

performance of the obtained model.

2.1.1 Component Analysis

The core component of the tactile sensor is the

NJL5908AR photo-reﬂector, currently manufactured

by Nisshinbo Micro Devices and it integrates into the

same case an infrared Light Emitting Diode (LED),

with the peak wavelength @925 nm and an optically

matched phototransistor. The dimensions of the com-

ponent are 1.06 ×1.46 ×0.5mm, as reported in the

datasheet (NJL5908AR Datasheet, 2015). Instead,

the dimensions of the LED emitting surface and pho-

totransistor receiving area have been estimated by

means of a high-resolution image (see Fig. 1), ac-

quired with an optical microscope (Model Dino-Lite

AM413T).

0.52 mm

0.3

Figure 1: Dimensions of LED emitting surface and photo-

transistor receiving area.

The phototransistor has a rectangular receiving

area equal to 0.52×0.3mm, while the external square

emitting area of the LED has a side equal to 0.25mm.

The central part of the LED does not emit rays, as vis-

ible from Fig. 1, and it is suitably modelled as it ap-

pears. The test conditions of the photo-reﬂector con-

sider the output current when the infrared signal from

LED is reﬂected by an aluminium surface, positioned

in front of the component. As reported in the photo-

reﬂector datasheet, the current in the phototransistor

changes when the distance z between the component

and the reﬂective surface varies from 0mm to 2.5 mm.

The characteristic is non-monotonic, and in particu-

lar, it increases if z varies from 0mm to 300µm, while

it decreases if z exceeds 300 µm. Besides, the cur-

rent follows a different trend when z is maintained

equal to 0.7mm and the aluminium plate is separately

moved on this ﬁxed plane along two orthogonal di-

rections, named x and y, until the space among the

reﬂective plane and the photo-reﬂector edges varies

from 0 mm to 1.5 mm. In order to allow the eval-

uation of optical model quality presented in the fol-

lowing, by means of a comparison of simulated data

with the ones from the datasheet, the main relations

exploited in the multiphysics simulator are here re-

called. By deﬁning with I

the output current from

the receiver and with P

the optical power incident

on it, its responsivity can be deﬁned as R =

. The

Quantum Efﬁciency (Q.E.), which considers the re-

lation among the incident photons and electron-hole

pairs that are responsible for the photo-current, can be

deﬁned as η =

hν

, where ν is the frequency of the

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

102

optical wave, e

is the constant value of the electron

charge and h is the Planck’s constant. By combining

the previous equations, it results that the responsivity

depends on the wavelength: R = η

hν

= η

, where

the constant c is the speed of light. Thus, when the

wavelength λ is ﬁxed, the responsivity R is constant.

As a consequence, the current I

and the power P

are

proportional, and the normalized current values re-

ported in the datasheet can be directly compared with

the normalized power values computed in the simu-

lation multiphysics environment, in order to evaluate

the accuracy of the optical component model.

2.1.2 Geometrical Optics

The Ray Optics Module exploits the Geometrical Op-

tics theory for the component modelling. The ray tra-

jectory is computed by solving the following six cou-

pled ﬁrst-order differential equations for the k and q

components

∂ω

∂k

= −

∂ω

∂q

(1)

where k is the wave vector, q is the position vec-

tor, ω is the angular frequency and t is the time.

Concerning the initial generation of rays from the

emitter surface, they are released by using the release

from boundary option. In detail, the ray release posi-

tions are related to a projected plane grid constituted

by a Number of points per release equal to N. Hence,

the ray initial direction can be speciﬁed, in different

modalities, by assigning values to the degrees of free-

dom corresponding to the wave vector k of each ray.

For the chosen Conical option the initial wave vec-

tor is sampled from a distribution in the wave vector

space at each release point. The Number of rays in

wave vector space is equal to N

. In 3D the initial

wave vector components (k

, k

) are sampled ac-

cording to the expressions

ωn

sinθ cos ϕ (2)

ωn

sinθ sin ϕ (3)

ωn

cosθ (4)

where

• ϕ is the azimuthal angle and it is uniformly dis-

tributed in [0,2π],

• θ is the polar angle and it can vary in [0,γ], with γ

the cone angle measured with respect to the verti-

cal z axis, orthogonal to the optical component,

• n is the refractive index of the material.

2.1.3 Photo-Reﬂector Model

The model of the optical component is built in COM-

SOL Multiphysics by using the Ray Optics Mod-

ule options described above, and the time-dependent

study Ray Tracing is used to solve the differential

equations in order to compute the ray trajectories.

First of all, in order to model the emitter, the release

from boundary option has been applied to the LED

emitting surface as experimentally measured from

Fig. 1, with a projected plane grid with N = 20 points

and N

= 3000 rays released from each point (see

Fig. 2). The cone angle γ, initially ﬁxed equal to 90

◦

during the model reﬁnement has been selected equal

to 88

◦

, by means of a trial and error procedure.

(a) (b)

Figure 2: LED model: (a) boundary selected as emitting

surface, and (b) projected plane grid with released rays.

Then, the aluminium plate is modelled as a rigid

plane with the bottom surface completely reﬂective,

by using the mirror option with the absorption coefﬁ-

cient α = 0. Instead, for the phototransistor, the wall

option is required to ﬁx the ray position and the wave

vector at the instant its surface is struck by a ray. At

last, the ray detector option is used to compute the

desired quantities related to the rays that struck the

receiving area of the phototransistor. In particular, the

interesting variables are the total number of the rays

sel

in the selected area and the total optical power P

transmitted to the detector. Figure 3 shows an exam-

ple of ray trajectories available during a simulation.

In order to simulate the optical component model

and compare the simulation data with the datasheet,

the described model has been solved by varying the

distance along the z−axis between the optical compo-

Figure 3: Ray trajectories with the reﬂective surface at a

distance z = 1.5mm, and at the instant time t = 6e −12 s.

Multiphysics Simulation for the Optimization of an Optoelectronic-Based Tactile Sensor

103

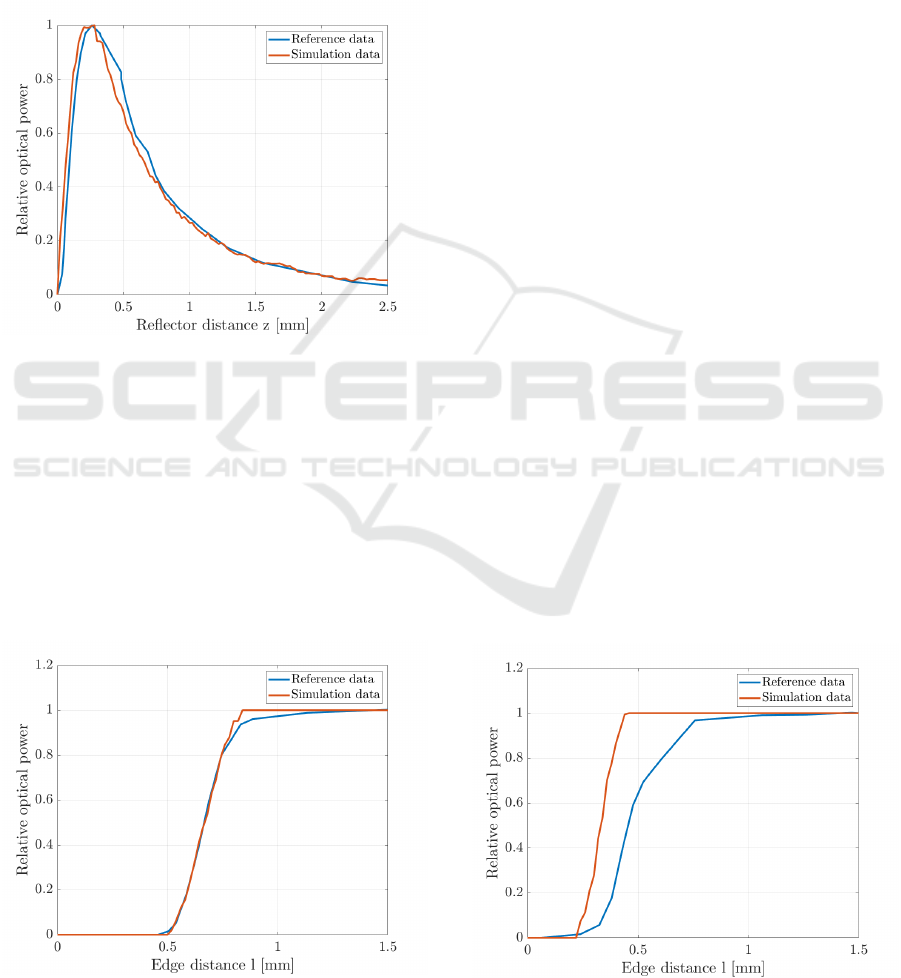
nent and the reﬂective surface from 0 mm to 2.5 mm

with a step of 0.02 mm, by using a parametric sweep

option. For each step, the optical power P

has been

computed and at the end of the sweeping phase the P

data have been normalized with respect to the max-

imum value and compared with the normalized pho-

tocurrent reported in the datasheet, according to the

observation detailed in Sec. 2.1.1. Figure 4 reports

the comparison between reference data and simula-

tion data. In order to completely verify the optical

Figure 4: Optical power along z−axis: comparison of ref-

erence data and simulation data.

component model, also the features corresponding to

the aluminium plate movements along x and y axes

have been simulated and compared with the datasheet.

Figures 5 and 6 show the optical power with respect to

the reﬂective surface edge distance. From the ﬁgures

it is evident that the model well reproduces the com-

ponent features along the x and z axis, while along the

y axis the reconstruction is qualitatively lower. How-

ever, for the following analysis, the fundamental rela-

tion is only the one along z axis.

Figure 5: Optical power along x−axis: comparison of ref-

erence data and simulation data.

2.2 Mechanical Model

In the following, the module exploited for the real-

ization of the model for the deformable layer of the

sensor is brieﬂy presented, and the geometry of the

realized mechanical structure is detailed.

2.2.1 Structural Mechanics Module

The Structural Mechanics Module solves the motion

equations with a constitutive model for the solid ma-

terial and it computes as results mechanical variables

(e.g., displacements, strain, etc.). It also allows the

reproduction of geometric nonlinearities, contact con-

ditions and loads. The analysis of the ﬁnite deforma-

tions is based on the total Lagrangian formulation, in

which the computed state is referred to the material

conﬁguration rather than to the current position in the

space. It can be formalized as x = X + u(X,t), where

x are the spatial coordinates, X are the material co-

ordinates and u are the displacements. A boundary

load can be deﬁned by specifying the application area

A, and the force components F

tot

= ( f

, f

) or the

force per unit area F

= F

tot

/A.

2.2.2 Deformable Layer Model

The geometry of the mechanical structure is com-

posed of 9 taxels, organized in a 3 ×3 matrix, and

numbered as reported in Fig. 7. The photo-reﬂector is

optically centered with respect to the taxel mechani-

cal geometry: the optical center is the mean point be-

tween the center of the LED and the center of the pho-

totransistor and it is aligned with the geometrical cen-

ter of the taxel structure. The deformable pad is the

hollow block obtained by removing the array of nine

smaller blocks with a spatial resolution of 3.55mm.

The hallow parts have different shapes, as shown

in Fig. 8. In the parallelepiped geometry, every sin-

Figure 6: Optical power along y−axis: comparison of ref-

erence data and simulation data.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

104

Figure 7: Taxel numbering used in the simulations.

gle cell has dimensions 2.55 ×2.55 × 1.55mm and

the distance between the optical component and the

reﬂective surface is 1.05 mm, by taking into account

that the component has a height of 0.5 mm. The

cylindrical taxel is obtained from the parallelepiped

case by using as a base the circle inscribed in the

parallelepiped base, with radius r = 1.275 mm, and

the same height equal to 1.55 mm. Analogously, the

hemispheric cell has radius r = 1.275 mm and r also

represents the distance between the emitting surface

of the optical component and the top of the dome.

The intermediate case is the spherical shape of ra-

dius R double with respect to the cylinder case, i.e.

R = 2r. With the equation h

= R −

√

−r

, it is

possible to compute the height of the spherical sec-

tion, that is 0.342mm. By ﬁxing the distance between

the photo-reﬂector emitting surface and the top of the

dome in this case equal to 1.1mm, the cylinder on

which the spherical section is built has a height of

1.258mm. The external dimensions of the whole pad

are 11.65 ×11.65 ×4.55 mm.

The material of the pad is selected from the avail-

able library as silicone with Young’s modulus equal

to 4.16MPa, which falls into Scale A durometer hard-

ness. From an optical point of view, the lateral walls

of taxels are modelled as totally absorbent (i.e., α =

1), while the above surfaces are simulated as com-

pletely reﬂective (i.e., α = 0) with isotropic scattering

(a) (b)

Figure 8: Tested shapes: (a) parallelepipeds, (b) cylinders,

condition. Regarding the mechanics, a variable total

force on the top surface of the whole pad is applied

and a ﬁxed constraint is deﬁned for the bottom of the

pad (i.e., u = 0 in all directions).

2.3 Coupled Model Results

The multiphysics coupling is realized by performing

the Ray Tracing analysis after the computation of the

structural deformation. In detail, the ﬁnal solutions

are obtained by means of a two-step analysis, repeated

with incremental values of applied external forces.

The ﬁrst step solves only the solid mechanics physics,

including the geometric nonlinearities, while the sec-

ond ray tracing step solves geometrical optics physics,

including the geometric nonlinearities in order to take

into account the deformed geometry, obtained from

the ﬁrst step. The external forces have been incre-

mentally applied to the deformable pad by means of a

parametric sweep option. By applying separate and

coupled force components, different analyses have

been carried out to evaluate taxel features. For each

considered taxel geometry, the optical power P

has

been computed with respect to force values in order

to quantify and compare the considered features. The

ﬁrst analysis has been carried out by applying to the

pad only a vertical force f

, with values from 0 N to

−20N with a step of 0.5 N. Figure 9 reports the op-

tical powers on the phototransistor surfaces with re-

spect to the force values in the parallelepiped case.

For the other geometries the same data have been

acquired, and the sensitivity with respect to f

has

been evaluated as the maximum slope of all curves,

for all considered shapes. The following maximum

sensitivity values have been obtained: 1.48e −4W/N

for the parallelepiped geometry, 1.11e −4 W/N in the

cylindrical case, 1.4e−4 W/N for the spherical shape,

2.48e −4 W/N in the hemispheric geometry. The sec-

ond type of analysis has been carried out to eval-

uate the sensitivity with respect to tangential force

components. To this aim, a constant normal force

equal to −8 N is applied on the boundary, and at the

same time variable tangential force components have

been applied from 0 N to a maximum value, depend-

ing on the simulation convergence with respect to

the taxel geometry. In detail, the simulation is con-

vergent with tangential components up to −11N in

the parallelepiped case, −13 N for the cylindrical and

the hemispheric shapes, −8 N for the spheres matrix.

Data similar to Fig. 9 can be considered in order to

evaluate the sensitivity with respect to a tangential

force applied along x or y directions. Obatined results

are: 2.48e −4 W/N for the parallelepiped geometry,

1.87e −4 W/N in the cylindrical case, 2.66e −4 W/N

Multiphysics Simulation for the Optimization of an Optoelectronic-Based Tactile Sensor

105

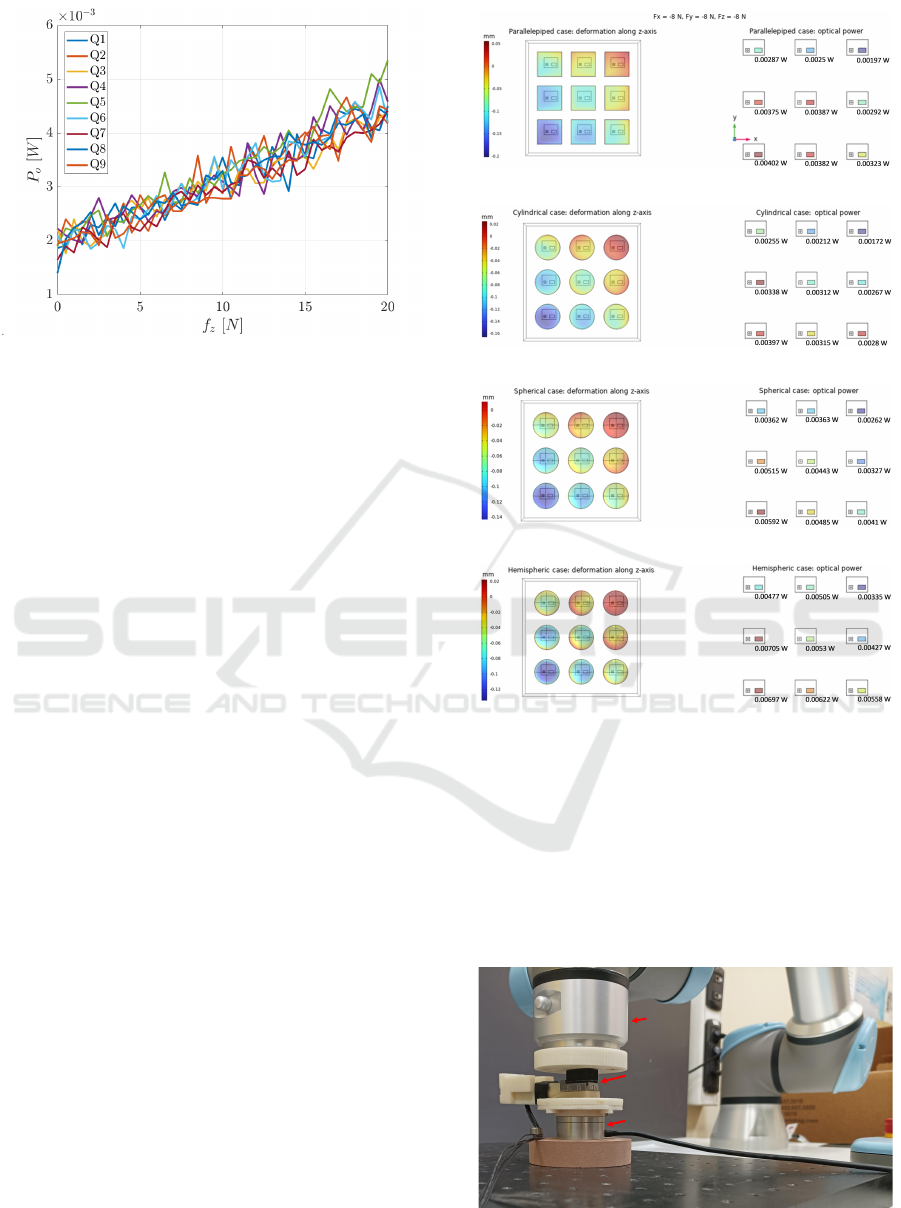
Figure 9: Optical powers with respect to the normal force

in the parallelepiped case.

for the spherical shape, 3.91e −4W/N in the hemi-

spheric geometry. Since the cylindrical case always

presents the lowest sensitivity, it has not been con-

sidered for the experimental comparison in the fol-

lowing section. Figure 10 allows additional observa-

tions about sensitivity, by showing how the taxel ma-

trix appears like a skew-symmetric matrix in terms of

mechanical displacement and optical power for some

simulation instants in presence of a tangential force

applied along the pad secondary diagonal. It is evi-

dent how the taxels 3 and 7 present the greater differ-

ence in values, the taxels 4 and 8 with respect to taxels

2 and 6 present a medium difference and the taxels on

the main diagonal are almost similar. This demon-

strates the relations among the force components, the

mechanical displacements and the optical power mea-

sured by photo-transistors. The matrix symmetry is

strictly related to force directions.

3 EXPERIMENTAL

EVALUATIONS

By considering the complexity of the deformable pad

both in terms of mechanical and optical features, also

an experimental evaluation of taxel performance has

been carried out. A suitable setup has been pre-

pared to evaluate some properties for the taxel: linear-

ity, sensitivity, hysteresis and repeatability. Linearity

and sensitivity are of paramount importance in sensor

characterization, but also hysteresis and repeatability

are computed. To obtain a complete sensor character-

ization, in this section experiments by applying only

normal forces and both normal and tangential com-

ponents have been considered. The setup is shown

in Fig. 11 and its main components are: a Robotous

(a)

(b)

(c)

(d)

Figure 10: Deformations along z−axis (left) and optical

powers (right), with a tangential force equal to −8N along

the secondary diagonal of taxel matrix: (a) parallelepiped

case, (b) cylindrical case, (c) spherical case, (d) hemispheric

case.

RFT40-SA01-D 6−axes force/torque sensor (used as

reference sensor), a 6 ×2 tactile sensor (equipped

with 3 pads with different taxel geometries) and an

UR5e robot manipulator (to apply external loads).

UR5e

tactile sensor

reference sensor

Figure 11: Experimental setup.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

106

For the experiments, a sensor with a matrix 6 ×2

has been used since the printed circuit board with op-

tical components was already available in the labora-

tory (see Fig. 12 for taxel numbering). This choice

does not limit the analysis in terms of linearity, sensi-

tivity, hysteresis and repeatability.

Figure 12: Taxel numbering used in the experiments.

The UR5e cobot is directly programmed by us-

ing its Graphical User Interface (GUI) available from

the teach pendant. It is used to apply the same force

components on the 3 different pads prepared with

the 3 different taxel shapes selected on the basis of

simulations (e.g., parallelepiped, spherical and hemi-

spheric). Figure 13 reports pictures of deformable

pads realized with silicone molding technique and

used in the experiments.

3.1 Sensor Characterization

As for simulations, two kinds of experiments have

been carried out in order to compare the tactile sen-

sor characteristics with respect to taxel shapes: the

ﬁrst by applying only normal force in order to evalu-

ate the sensor along the z axis and the second by ap-

plying also tangential components for the evaluation

along the x and y axes. In the ﬁrst experiment, the

robot is initially positioned almost in contact with the

pad, and then it is vertically moved of 1.1 mm along

z axis in 50 s (by resulting a velocity of 0.022 mm/s)

in order to apply a normal force to the pad. During

the linear movement in the operative space the robot

applies a normal force from 0 N to 10 N with a veloc-

ity of 0.2 N/s. Figure 14 reports the normal force f

signal from the reference sensor and the taxel voltage

variations ∆v

acquired during the experiment for the

parallelepiped case. From these data the sensitivity

(a) (b) (c)

Figure 13: Pad with different taxel geometries: paral-

lelepiped case (a), spherical case (b), and hemispheric case

(c).

for each taxel can be evaluated as the mean slope of

the force-voltage relation. It appears different for the

12 taxels, by varying from a minimum of 0.0196 V/N

achieved by the taxel 3 to a maximum of 0.0355 V/N

reached by the taxel 11. The taxel with maximum sen-

sitivity has been used to evaluate the other features,

since it corresponds to the worst case. In particular,

the hysteresis error has been evaluated as

∆v

incr

−∆v

decr

max

·100 (5)

where ∆v

incr

and ∆v

decr

are the voltage variations cor-

responding to two consecutive time ranges when the

force, in Fig. 14, increases and decreases respectively,

while v

max

is the maximum ∆v

value reached during

the experiment. Similarly, the repeatability error has

been evaluated as

∆v

−∆v

max

·100 (6)

where ∆v

and ∆v

are the voltage variations cor-

responding to the two time ranges when the force,

in Fig. 14, increases (or decreases). For the paral-

lelepiped case the hysteresis error is e

= 1.88% and

the repeatability error is e

= 2.08% for the taxel 11.

Figure 15 reports the graphs used for e

and e

com-

putation. For the spherical geometry, the same ac-

quired data are reported in Fig. 16. The minimum

sensitivity is 0.00467 V/N, reached by the taxel 10,

while the maximum one is 0.00716 V/N, achieved

by the taxel 11. Figure 17 reports data of taxel 11

for hysteresis and repeatability, and the computed er-

rors are e

= 6.87% and e

= 1.33%, respectively.

Finally, for the hemispheric shape the data are re-

ported in Fig. 18. The sensitivity ranges from a min-

imum of 0.00335 V/N for the taxel 1 to a maximum

of 0.00869 V/N for the taxel 8. As for previous case,

Fig. 19 reports data related to the taxel with the max-

imum sensitivity (taxel 8 for this shape) in order to

Figure 14: Parallelepiped case: (top) normal force applied

and (bottom) taxel voltage variations.

Multiphysics Simulation for the Optimization of an Optoelectronic-Based Tactile Sensor

107

Figure 15: Parallelepiped case: (left) data for hysteresis er-

ror and (right) data for repeatability error.

evaluate the hysteresis error e

= 10.3% and the re-

peatability error e

= 3.35%. The main important

feature highlighted from these experimental data with

respect to simulation data is the nonlinearity in the

force-voltage relations. In particular, while the paral-

lelepiped case is almost linear (see Fig. 15), the spher-

ical case shows a non negligible nonlinearity (see

Fig. 17) and the hemispheric case a high nonlinear-

ity (see Fig. 19). By evaluating the nonlinearity error

∆v

incr

−∆v

nom

max

·100, (7)

where ∆v

incr

is the voltage variations corresponding

to the ﬁrst time range when the force increases, and

∆v

nom

is the voltage variations corresponding to ideal

linear case, the following values are obtained: e

3.18% for the parallelepiped case, e

= 5.38% for the

spherical case, and e

= 11.7% for the hemispheric

one. Thus, the performance in terms of linearity are

clearly better for the parallelepiped case.

The comparison of characteristics along the x and

the y axes also has been carried out. In order to re-

produce simulated case, the robot, initially positioned

almost in contact with the pad, is vertically moved of

1.1mm along z axis in 50 s, by reaching a constant

normal force of about 10N. Then, the robot is moved

of 1 mm along x−axis and 1 mm along y−axis simul-

Figure 16: Spherical case: (top) normal force applied and

(bottom) taxel voltage variations.

Figure 17: Spherical case: (left) data for hysteresis error

and (right) data for repeatability error.

Figure 18: Hemispheric case: (top) normal force applied

and (bottom) taxel voltage variations.

taneously, by obtaining a diagonal tangential force.

Also in this case the velocity is 0.022mm/s and the

trajectory is executed forward and backward, in or-

der to obtain an increasing and decreasing phase for

the tangential force. The sensitivity with respect to

tangential force components have been evaluated on

the same taxels selected from the normal case (i.e.,

the ones with the maximum sensitivity with respect to

normal force). For the parallelepiped case, the taxel

11 presents a sensitivity along the x−axis equal to

0.0342V/N and along the y−axis equal to 0.0314V/N

(see Fig. 20). For the spherical geometry, the taxel 11

reaches a sensitivity of 0.00271V/N along the x−axis

and 0.00276 V/N along the y−axis (see Fig. 21). At

last, for the hemispheric case the taxel 8 presents a

sensitivity of 0.00668V/N along the x−axis and of

0.00569V/N along the y−axis (see Fig. 22).

Figure 19: Hemispheric case: (left) data for hysteresis error

and (right) data for repeatability error.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

108

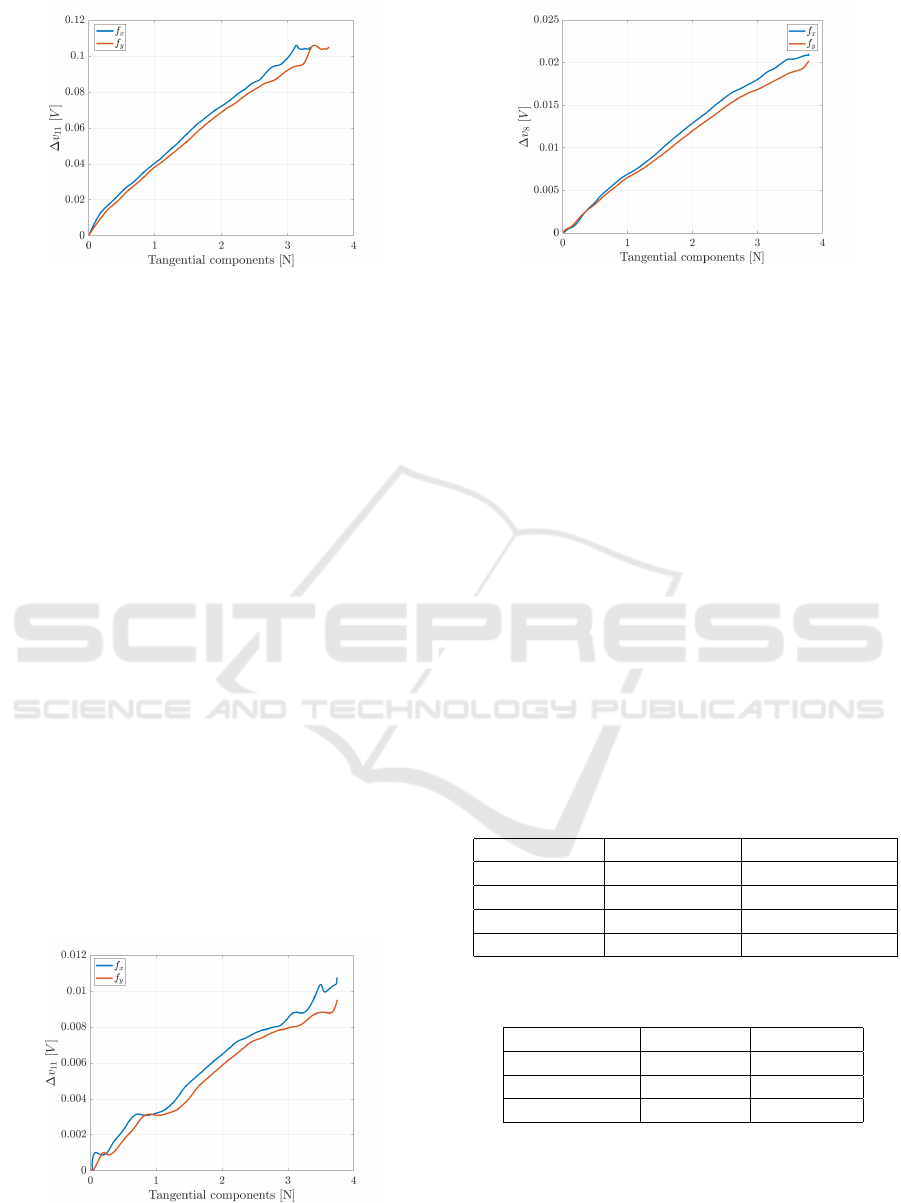
Figure 20: Parallelepiped case: voltage variations with re-

spect to tangential force components.

3.2 Comparison and Discussion

In order to compare simulation and experimental data

among the different shapes for the reﬂective cells,

the main important data have been summarized and

discussed in this section. First of all, the sensitiv-

ity with respect to both normal and tangential com-

ponents (see Tab. 1), estimated from simulation data,

show that the cylindrical shape presents the lower val-

ues (particularly for the tangential case) and hence

the experimental case has not been implemented to

reduce the case studies. Among the other cases the

sensitivity is almost of the same order. Obviously,

in simulation all taxels of the same shape present

the same features. Instead, by considering the ex-

perimental data, the taxel responses are different due

to realization processes of electronic and mechani-

cal components, hence it could be interesting to eval-

uate the minimum and maximum sensitivities. Ta-

ble 2 summarizes these sensitivities for the differ-

ent shapes. The absolute values cannot be directly

compared with simulated results, since the units are

different, but both cases (minimum and maximum)

show similar sensitivity for spherical and hemispher-

ical cases, while parallelepiped case is more sensitive

up to one order of magnitude. This difference with

Figure 21: Spherical case: voltage variations with respect

to tangential force components.

Figure 22: Hemispheric case: voltage variations with re-

spect to tangential force components.

simulation case probably depends on the mechanical

realization trough silicone moulds technique of pads

by means of 3D printed moulds: the ﬂat surface (in

parallelepiped case) can be perfectly realized, while

the spherical and hemispherical shapes are locally ap-

proximated with small discrete steps by the 3D print

technology. The sensitivities experimentally evalu-

ated with respect to tangential components, and re-

ported in Tab. 3, conﬁrm the same observations done

for normal force: the parallelepiped case shows a sen-

sitivity higher of one order of magnitude. Finally, the

main feature highlighted from the experiments is the

nonlinearity shown by the different shapes. As sum-

marized in Tab. 4, the spherical case presents a nonlin-

earity almost double with respect to the parallelepiped

case and the hemispheric case almost four times more.

As a consequence the parallelepiped case appears as

the best choice by considering its features also with

respect to current manufacturing processes.

Table 1: Simulations: sensitivity to normal and tangential

forces with respect to taxel shapes.

Normal[W/N] Tangential[W/N]

Parallelepiped 1.48e-4 2.48e-4

Cylindrical 1.11e-4 1.87e-4

Spherical 1.4e-4 2.66e-4

Hemispheric 2.48e-4 3.91e-4

Table 2: Experiments: minimum and maximum sensitivity

to normal force with respect to taxel shapes.

Min [V/N] Max [V/N]

Parallelepiped 0.0196 0.0355

Spherical 0.00467 0.00716

Hemispheric 0.00335 0.00869

4 CONCLUSIONS

This paper reported the steps followed for the real-

ization of the models of the two main parts compos-

Multiphysics Simulation for the Optimization of an Optoelectronic-Based Tactile Sensor

109

Table 3: Experiments: sensitivity to tangential force with

respect to taxel shapes.

along x [V/N] along y [V/N]

Parallelepiped 0.0342 0.0314

Spherical 0.00271 0.00276

Hemispheric 0.00668 0.00569

Table 4: Experiments: nonlinearity with respect to taxel

shapes.

Nonlinearity e

[%]

Parallelepiped 3.18

Spherical 5.38

Hemispheric 11.7

ing the considered optoelectronic-based tactile sen-

sor: the photoreﬂector and the deformable layer. The

simulation has been used to determine how differ-

ent shapes of the reﬂective cells inﬂuence the per-

formance of the sensor. In particular, four different

shapes have been considered: parallelepiped, cylin-

drical, spherical, and hemispheric. Some tests have

been carried out to check the response of the simu-

lated model to different stimuli. Then, similar tests

have been repeated in a real setup in order to compare

the evaluated taxel shapes. Data from both the simu-

lation results and the measurements from the real sen-

sor have been used to discuss the best choice for the

taxel shape, also by considering the limitations due

to manufacturing processes. The results for proper-

ties such as linearity and sensitivity show differences

between simulations and experiments probably due

to the following reasons: in the simulation, the con-

sidered walls are completely reﬂective or absorbent,

while the real pads have white and black walls that are

not totally reﬂective or absorbent; the molds used for

realizing the silicone pads, being 3D printed, present

imperfections (i.e., grooves, small steps) that make

the actual walls not smooth, differently from those

in the simulation model, particularly for hemispheric

and spherical cases. The consequence of this lack of

smoothness is that, in the real case, the ray reﬂections

are locally quite different from the simulated case.

Future studies will be devoted to enhancing the sim-

ulation model by taking into account the aforemen-

tioned imperfections, e.g., by modifying the mechani-

cal model of the deformable layer taking into account

the non-smooth surfaces due to the production pro-

cess, or by investigating the possibility to consider

different reﬂection modalities in the ray tracing tech-

nique.

ACKNOWLEDGMENTS

This work was partially supported by the European

Commission under the Horizon Europe research grant

INTELLIMAN, project ID: 101070136

REFERENCES

Alqurashi, M. M., Ganash, E. A., and Altuwirqi, R. M.

(2022). Simulation of a low concentrator photovoltaic

system using comsol. Applied Sciences, 12(7).

Amiri, P., Casals, O., Maur, M. A. d., and Prades, J. (2022).

Ray tracing simulation of a gan-based integrated led-

photodetector system. In 2022 Int. Conf. on Numeri-

cal Simulation of Optoelectronic Devices (NUSOD).

Cirillo, A., Cirillo, P., De Maria, G., Natale, C., and Pirozzi,

S. (2014). A FE analysis of a silicone deformable in-

terface for distributed force sensors. AIP Conference

Proceedings, 1599(1):485–488.

Cirillo, A., Costanzo, M., Laudante, G., and Pirozzi, S.

(2021). Tactile sensors for parallel grippers: Design

and characterization. Sensors, 21(5).

Ferreira, G. M., Silva, V., Minas, G., and Catarino, S. O.

(2022). Simulation study of vertical p-n junction pho-

todiodes’ optical performance according to cmos tech-

nology. Applied Sciences, 12(5).

Khamis, H., Xia, B., and Redmond, S. J. (2019). A novel

optical 3d force and displacement sensor – towards in-

strumenting the papillarray tactile sensor. Sensors and

Actuators A: Physical, 291:174–187.

Lu, Z., Gao, X., and Yu, H. (2022). Gtac: A

biomimetic tactile sensor with skin-like heteroge-

neous force feedback for robots. IEEE Sensors Jour-

nal, 22(14):14491–14500.

NJL5908AR Datasheet (2015). NJL5908AR Datasheet

Ver.2015-02-17. New Japan Radio Co. LTD, Tokyo,

Japan.

Wang, S., She, Y., Romero, B., and Adelson, E. (2021).

Gelsight wedge: Measuring high-resolution 3d con-

tact geometry with a compact robot ﬁnger. In 2021

IEEE Int. Conf. on Robotics and Automation (ICRA).

Ward-Cherrier, B., Pestell, N., Cramphorn, L., Winstone,

B., Giannaccini, M. E., Rossiter, J., and Lepora, N. F.

(2018). The tactip family: Soft optical tactile sen-

sors with 3d-printed biomimetic morphologies. Soft

Robotics, 5(2):216–227.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

110