A Clustering-Based Approach for Adaptive Control

Applied to a Hybrid Electric Vehicle

Rian Beck

, Sudarsan Kumar Venkatesan, Joram Meskens

Jeroen Willems

, Edward Kikken

and Bruno Depraetere

Flanders Make, Lommel, Belgium

ﬁ ﬂ

Keywords:

Adaptive Control, Clustering, Context-Adaptive Control, Machine Learning in Control Applications.

Abstract:

In this paper we present an approach to adapt the parameters of controllers during operation. It is targeted

at industrial adoption, relying on controllers of the same type currently in use, but adjusting their gains at

run-time based on varying system and / or environment conditions. As the key contribution of this paper we

present a method to discover what condition variations warrant a control adaptation for cases where this is

not known up front. The goal is not to achieve a better performance than other adaptive control schemes, but

to provide a different method of designing or deciding how to build adaptation logic. To achieve this we use

data-driven methods to, in an ofﬂine preprocessing step: (I) derive features that quantify system / environment

variations, (II) optimize the control parameters for the distinct feature values, (III) search for clusters in the

multi-dimensional space of both these features and control parameters, looking for sets of similar features as

well as control parameters to be used. Once a set of clusters is deﬁned, an online adaptive controller is then

synthesized by (I) building a classiﬁer to determine which cluster the currently observed conditions belong

to, and (II) selecting the optimal control parameters for that cluster. This paper provides a ﬁrst illustration of

the method, without theoretical analysis, on an example case of energy management for a hybrid electrical

vehicle, for which an Equivalent Consumption Minimization Strategy controller is built whose parameters are

adjusted as the detected cluster changes. The results show an increase in energy-efﬁciency of the adaptive

control method over the non-adaptive one in a variety of scenarios.

1 INTRODUCTION

The industrial need for reduced energy consumption,

increased throughput and increased production ac-

curacy leads to ever-increasing performance require-

ments for mechatronic systems and their controllers.

The historical approach of designing a single ﬁxed

controller that is robust against variability of system

dynamics or changes in the system environment will

result in sub-optimal performance to achieve the re-

quired robustness (e.g., plane fuel consumption re-

duces mass so dynamics change, hybrid electric ve-

hicle driving in different trafﬁc scenarios). There-

fore, adaptive control techniques that adjust control

actions when the system and / or environment change

https://orcid.org/0000-0003-4795-6133

https://orcid.org/0000-0002-1660-4285

https://orcid.org/0000-0002-2727-6096

https://orcid.org/0000-0002-5769-5814

https://orcid.org/0000-0003-2011-3857

have gained widespread attention in academia. Moti-

vated by the performance beneﬁts, these approaches

are even cautiously being adopted by industry where

they were typically not preferred before due to their

complexity, difﬁcult design and tuning, as well as, the

lack of industrial understanding and trust in more ad-

vanced control methods in general.

A survey of literature reveals a wide array of such

adaptive control techniques originating from classic

model-based control theory: MRAC (Kreisselmeier

and Anderson, 1986), approximate direct program-

ming (Powell, 2007), adaptive ECMS (Musardo

et al., 2005), gain scheduling (Leith and Leithead,

2000), adaptive pole placement (Elliott et al., 1985),

dual controllers (Åström and Wittenmark, 2013),

extremum-seeking controllers (Ariyur and Krstic,

2003), iterative learning controllers (Wang et al.,

2009), MIAC (Schreier, 2012), fuzzy adaptive con-

trollers (Yang et al., 2021), any many more. In the

past decade, advances in artiﬁcial intelligence (AI)

and machine learning (ML) are pushing data-based

162

Beck, R., Venkatesan, S., Meskens, J., Willems, J., Kikken, E. and Depraetere, B.

A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle.

DOI: 10.5220/0012171100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 162-171

ISBN: 978-989-758-670-5; ISSN: 2184-2809

adaptive control techniques such as the many variants

of Reinforcement Learning (RL) (Khan et al., 2012)

(e.g., Q-learning (Watkins and Dayan, 1992), SARSA

(Rummery and Niranjan, 1994), Monte-Carlo (Sut-

ton and Barto, 2018)) to the forefront. More re-

cently combinations of model-based and data-based

approaches are begin developed e.g., model-based

RL (Berkenkamp et al., 2017) and residual RL (Jo-

hannink et al., 2019) (Staessens et al., 2022). For

completeness, advanced model-based approaches like

Model Predictive Control (MPC) or explicit MPC are

also able adapt to changes, but these are not consid-

ered in this work, since they require good predictions

of the upcoming events or changes in the conditions,

in order to work well, which is not possible for the

considered case of a vehicle driving through various

trafﬁc conditions.

As can be seen in these references, this diverse set

of adaptive control techniques has been applied to a

multitude of engineering ﬁelds: robotics, aerospace,

automotive, process control and ranging from aca-

demic demonstrators to industrial cases. Under this

last category of combined model-based and data-

driven methods the proposed approach of this paper

ﬁts best, where we believe our method is a worth-

while extension to the available techniques, because

it is straightforward to implement and control actions

can be inspected a-priori and understood easily, there-

fore making it especially suitable for industrial appli-

cations where these topics matter most.

The approach described in this work relies on the

following assumptions: (I) The system under con-

sideration is a complex non-linear parameter-varying

system that operates in a varying environment. (II)

It is controlled by a parametric controller (e.g., PID).

(III) The optimal control parameter values change as

a function of the system and / or environment, and can

be found by means of optimization.

For such cases we propose to:

• Simulate or experimentally collect a broad set of

system and environment conditions, and for each

ﬁnd the optimal control parameter values.

• Look for clusters (with K-means) (Jain and

Dubes, 1988)) where both the optimal control val-

ues and the system / environment features are sim-

ilar. These clusters then indicate sets of system /

environment conditions, as well as the most ap-

propriate control parameter values to be used for

them.

• To get to an adaptive controller that performs on-

line adaptation of the control parameters we will

also train a classiﬁer to identify the system / en-

vironment conditions from measurements. Dur-

ing operation / run-time, this classiﬁer indicates

in which cluster the system / environment is, so

that an adaptive controller can be formed by us-

ing this information to select the optimal control

parameter values corresponding to this cluster.

Note that the work presented in this paper builds

upon previous work, where we already built an adap-

tive controller for the same use case as in this paper

(Venkatesan et al., 2021): the key improvement here

is the usage of data-driven clustering methods to de-

termine for what conditions adaptations are most ben-

eﬁcial, as opposed to the engineering insight based

division of conditions that was performed in the pre-

vious work.

To demonstrate the proposed approach a Hybrid

Electric Vehicle (HEV) use case is used. In an HEV,

the energy management controller decides how much

power is requested from the internal combustion en-

gine (ICE) and how much from the electromotor

(EM). At a given vehicle speed, it looks at the de-

sired wheel torque and considers how to best achieve

it: supplying all power with the ICE, only using the

EM, or a mix of the two. This is often called the HEV

power-split. Ideally, the controller selects the power-

split to maximize the fuel-efﬁciency of the vehicle.

To demonstrate our control approach, we will control

the power split using a widely used parametric Equiv-

alent Consumption Minimization Strategy (ECMS)

controller, see (De Jager et al., 2013; Gao et al., 2017;

Rezaei et al., 2017), knowing that the optimal ECMS

control parameter values will vary for different driv-

ing cycles. This ECMS will be augmented towards

an adaptive ECMS (A-ECMS) using the method de-

scribed before. Note that we are aware of other meth-

ods to improve an ECMS towards an A-ECMS (e.g.,

(Chasse et al., 2010; Onori and Serrao, 2011; Hus-

sain et al., 2019; Frank et al., 2017)), but the goal

of this case is purely demonstration of our approach.

Detailed comparison to other A-ECMS approaches is

for now left to future work.

The paper makes the following contributions:

• The usage of clustering to group similar control

parameters values to features derived from the

varying system / environment is detailed in Sec-

tion 2, and an example is provided on the use-case

in Section 4.

• The training of a classiﬁer to detect cluster mem-

bership at run-time to adjust control parameters

online is detailed in Section 2.

• The integration of the cluster classiﬁer with

the original parameter controller resulting in the

adaptive parametric controller can also be found

in Section 2.

A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle

163

• The validation of our adaptive controller approach

on a simulated HEV use case (detailed in Sec-

tion 3) can be found in Section 5.

2 PROPOSED ADAPTIVE

CONTROL APPROACH

In this paper we follow an approach to develop con-

trollers that adapt when the system dynamics, op-

erating conditions and / or the system environment

change. We aim for industrial adoption so to that end,

we restrict ourselves to an adaptive control scheme in

which classical non-adaptive controllers are used, but

a layer is added on top to adapt the parameter values

of these non-adaptive controllers to come to an adap-

tive control scheme. To keep things simple to analyze

for industrial use, we restrict ourselves in the adap-

tation logic layer to choosing between a ﬁnite num-

ber of conditions, each with its speciﬁc set of control

parameter values, and we choose which of the sets

to select. We furthermore aim to ﬁnd conditions for

which switching between them does not occur very

frequently, but instead once a condition is selected

the control values can remain ﬁxed to the values of

this condition for a substantial amount of control sam-

ples to prevent Zeno-like switching behavior. Exten-

sions towards a framework wherein adaption is not

restricted to the discrete selections but is done con-

tinuously, and as a consequence, also much more fre-

quently (down to every control sample) are possible,

but omitted in this paper to increase the ease of analy-

sis and the conﬁdence we expect industry would have

in the resulting controllers.

Deﬁnition 1. In the remainder of this work the term

’context’ is used to describe the current dynamics, op-

erating conditions and / or the system environment at

which the system is operating. We assume each spe-

ciﬁc context can be described by a set of feature val-

ues f that can be measured or estimated at run-time.

For an HEV possible context example features could

be: the change in vehicle mass, the mean slope of the

road over a time window and the ambient air temper-

ature.

To obtain the adaptive controller describe above,

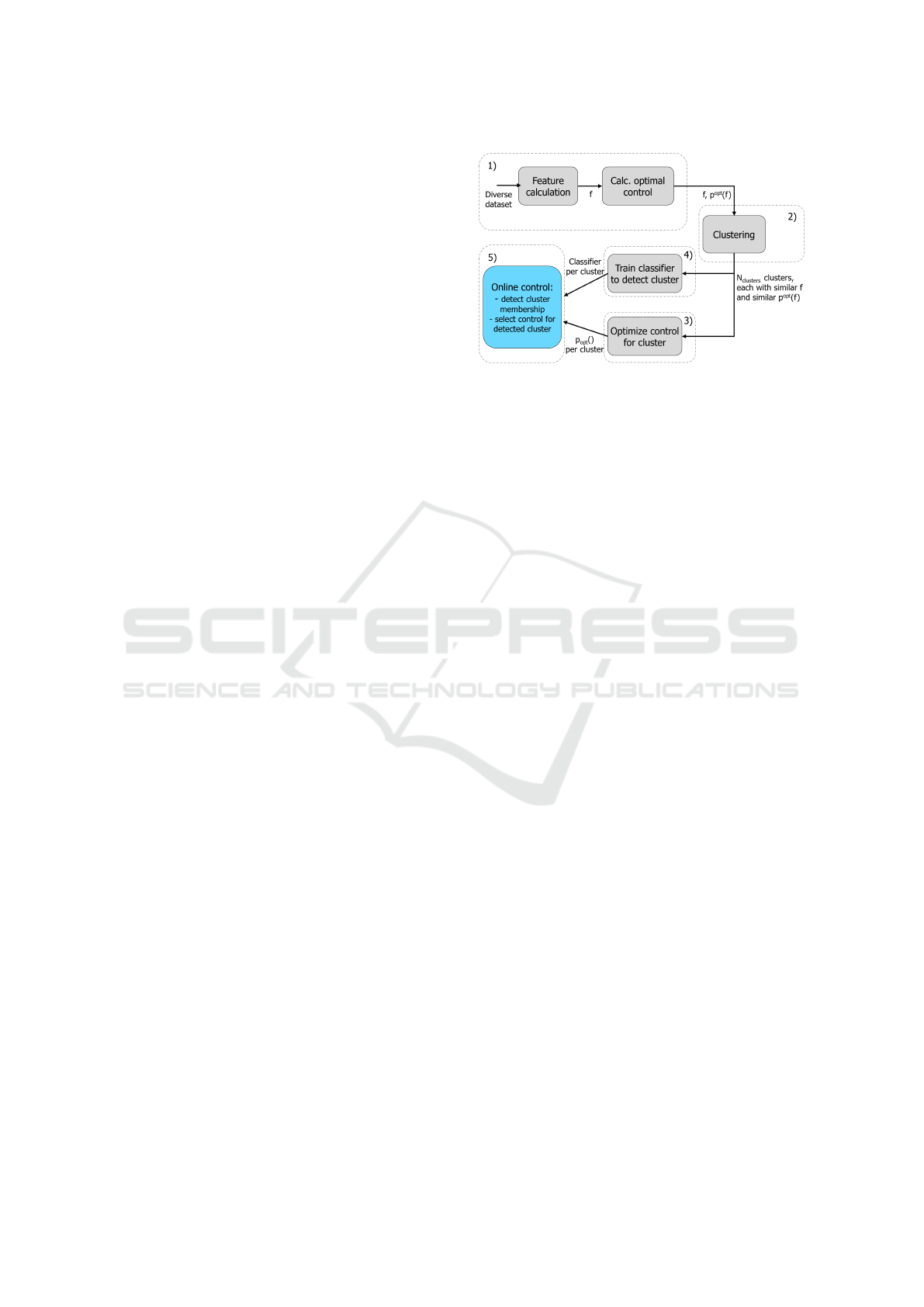
the following steps are taken, as shown also in Fig-

ure 1

1. Simulate or experimentally gather a data-set with

a variety of contexts, described by the duty cy-

cle and all sensor signals and a set of features f

derived from them, along with the control param-

eter values p

opt

( f ) that are optimal for each of the

given contexts.

Figure 1: Workﬂow for constructing the classiﬁer.

2. Use data-based clustering methods to form

clusters

groups with similar context features f

as well as similar optimal control parameters

opt

( f ).

3. Re-compute the optimal control parameters, but

now per cluster to get the cluster-optimal control

parameters p

opt,i

, where i ∈ [1, . . . , N

clusters

4. Train a classiﬁer to use context features f col-

lected at run-time to detect cluster membership

during operation.

5. Assemble the adaptive controller by combining

the outcome of the previous 2 bullets.

Firstly, we need data to apply the clustering meth-

ods to. This can be collected in the ﬁeld, or, like in this

paper, generated in a simulation environment. This

way, we ﬂexibly build a large data-set which contains

variable contexts. On top of that, we also calculate the

optimal control parameters for every sample in this

dataset, as will be described in the next section.

In the second step, this data is then used for the

clustering. This step, like the ﬁrst, is still done ofﬂine,

before deployment. In this step, we look for clusters

that have similar values for both optimal control pa-

rameters and context features. This can be done in a

large space, spanning multiple possible context fea-

tures, with the aim of ﬁnding a small set of clusters

with similar context features for which also the con-

trol parameters are similar. As a consequence, when-

ever a context is seen with similar context features

to those of a given cluster, a good choice would be

to also choose the control values that were present in

that speciﬁc cluster.

Remark 1. Ideally we would also include sensitivity

of the performance to changes in the control param-

eters. Now we look for points with similar context

features and similar control values, but we don’t ac-

count for how sensitive changes in control values are.

However, since this is harder to do, this was not (yet)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

164

done in this work, but the authors think it can be an

interesting avenue for future research.

In the third step, a single set of control parame-

ter values is optimized for each cluster from step two.

This does not need to be equal to the cluster mean val-

ues, but the values will of course be similar in value

to those of the points in the cluster.

In the fourth step we build an estimation algorithm

that can, online, i.e., during normal operation, detect

which of the clusters from the previous step most re-

sembles the current context the system will be oper-

ating in. This classiﬁer importantly relies only on the

features, and not on the control values.

In the ﬁfth step ﬁnally, a simple adaptive control

scheme is set up, that uses the classiﬁer to estimate the

cluster membership, and then selects the controller

parameters corresponding to the estimated cluster.

More details on these steps and the workﬂow will

be given in Section 4, when they are applied to the

considered HEV use case, which is ﬁrst described in

Section 3.

3 HYBRID ELECTRICAL

VEHICLE USE-CASE

As stated in the introduction, the energy management

controller decides the power-split. It looks at the de-

sired wheel torque, and decides the mix of torques

from the ICE and the EM to match it. Ideally, the

controller does so in a manner such that over the long

term, the efﬁciency is maximized.

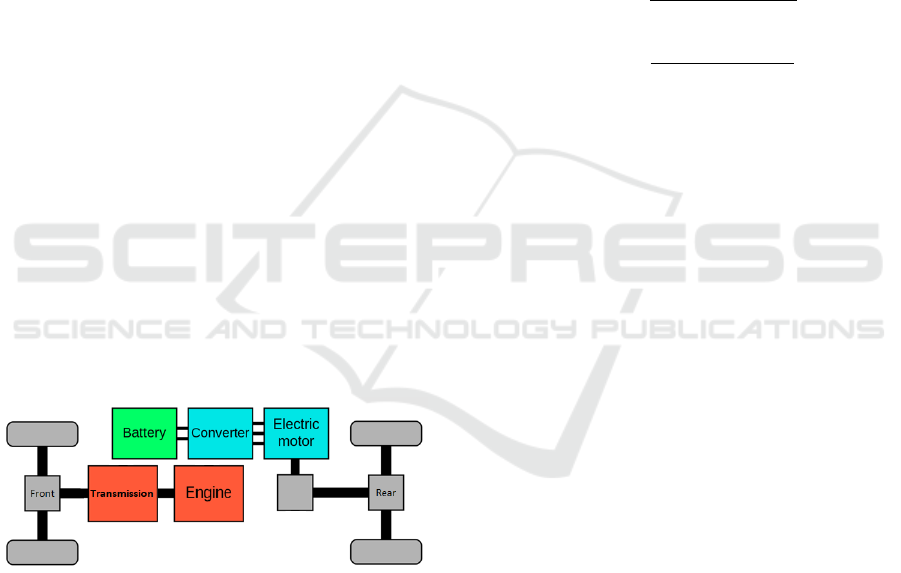
Figure 2: Layout of the HEV: consisting of an engine (ICE)

and an electromotor (EM).

3.1 Model of the HEV

The considered vehicle is a series-parallel-hybrid ve-

hicle with an EM and an ICE driving a 9 speed trans-

mission, as shown in Figure 2.

We model the HEV using a backwards-facing

quasi-static vehicle model: the drive cycle is the in-

put, deﬁned by vehicle velocity v(t), and from that we

calculate the corresponding torque T (t) at the wheels

calculated with an inertia and friction model. The

controller chooses the power-split between the torque

delivered by the ICE: T

ICE,wheels

(t), and that by the

EM / battery: T

bat,wheels

(t), such that

T (t) = T

ICE,wheels

(t) + T

bat,wheels

(t), (1)

and equivalently

P(t) = P

ICE,wheels

(t) + P

bat,wheels

(t). (2)

With these, the model then calculates the torques

at the ICE and the EM, based on drive ratios i

and

drivetrain efﬁciencies η

wheels to x

, where i

ICE

for the

ICE also depends on the selected gear (which for con-

venience is currently chosen with standard methods

not relying on ECMS):

ICE

(t) =

ICE,wheels

(t)

ICE

· η

wheels to ICE

, (3)

(t) =

bat,wheels

(t)

· η

wheels to EM

. (4)

From T

ICE

(t) we can then calculate the fuel rate

˙m

fuel

(t) of the ICE, according to:

˙m

fuel

(t) = f



ICE

(t), ω

ICE

(t)



, (5)

wherein ω

ICE

(t) = i

ICE

· v(t), and where f () is an em-

pirical map from which we extract the fuel rate using

2D-interpolation.

Similarly, we can calculate the change in battery

state-of-charge according to

SOC(t) = h



(t), ω

(t)



, (6)

wherein ω

(t) = i

· v(t), and where to calculate

h() we again use an empirical 2D efﬁciency map of

the EM, coupled with a simple battery model with a

loss resistance.

The maps f () and h() and the model parameters

used are those of a custom, modiﬁed version of a non-

hybrid Range Rover Evoque, which was made into a

hybrid-through-the-road using two in-wheel electro-

motors added at the rear wheels, as was described in

(Venkatesan et al., 2021). The resulting vehicle model

is made in MATLAB model as described in (Goos

et al., 2017).

In the remainder we will simplify notation. Since

we will always be looking at powersplits at the wheel

level, we will leave out the distinction between values

at the wheel level and those at the ICE or EM/bat-

tery. We will redeﬁne P

ICE

(t) and P

bat

(t) to indicate

the powers from both sources at the wheels, requir-

ing that P(t) = P

ICE

(t) + P

bat

(t). We will furthermore

leave out many dependencies from the notation, so

that we can denote the fuel rate as ˙m

fuel



ICE

(t)



A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle

165

3.2 ECMS Control Algorithm

As denoted previously, in this paper we consider

an ECMS controller. This choice is made since it

matches our requirements, i.e., we can make it adap-

tive by tuning its gains. Furthermore, it is a control

technique that is simple enough to facilitate industrial

adoption, and last, it is a well-known and often-used

approach, see e.g., (De Jager et al., 2013; Gao et al.,

2017; Rezaei et al., 2017).

Rooted in optimal control, ECMS is a class of sub-

optimal control methods that aims to approximate a

fully optimal solution. The power split is calculated

at each time step, without future predictions, consid-

ering only the current speed and desired load. The

calculation minimizes the expected equivalent con-

sumption, which is a combination of the modeled fuel

usage and the modeled electrical energy used, as ex-

plained previously. Since there is no need for future

predictions, and since the optimization is only done

over a single time-step, it can be solved very efﬁ-

ciently, and it can even be pre-computed for (a grid

of) all possible loads and speeds, and stored in a look-

up-table. This leads to it being very efﬁcient to imple-

ment, especially if compared to prediction based ap-

proaches such as for example dynamic programming

(DP) (Bellman, 1966). However, ECMS methods are

still able to sufﬁciently approximate optimal control

methods employing a longer prediction horizon, see

e.g., (De Jager et al., 2013; Frank et al., 2017; Onori

and Serrao, 2011). However in order to achieve this,

the control parameters of the ECMS need to be tuned

well. The tuning of the ECMS can be different for

each drive cycle. Therefore, in this paper, we will

look to adjust the tuning of the ECMS controller on-

line based on (estimated) context, and as stated above,

focus on discovering what contexts we need to adapt

to. In this paper, we consider an ECMS method that

has been broadly used to control the power split of

HEVs, see e.g., (De Jager et al., 2013; Gao et al.,

2017; Rezaei et al., 2017). Later on in this paper, we

will modify it to make it context-dependent.

The ECMS algorithm is optimization problem,

which calculates the combination of P

ICE

(t) and

bat

(t)) that minimizes a given cost J(t) at time instant

t, while meeting the total required power P

desired

(t):

ICE

(t)

opt

, P

bat

(t)

opt

= arg min

ICE

(t),P

bat

(t)

J(t), (7)

s.t. P

desired

(t) = P

ICE

(t) + P

bat

(t).

A commonly selected cost function J(t) is:

J(t) = ˙m

fuel



ICE

(t)



+ λP

bat

(t), (8)

wherein λ is the control parameter, which makes the

trade-off between the usage of the ICE and EM. In or-

der to obtain a well-tuned ECMS controller, λ needs

to be chosen properly. If λ is selected too high or too

low, the battery will ﬁll up or drain in the long run,

which can be undesired. Since this effect (and cor-

responding λ) is dependent on the considered drive

cycle, ECMS is often made charge sustainable by

making λ dependent on the state of charge. This is

done by splitting λ in λ

and λ

, where λ

regulates

the power split (as considered before), and λ

pro-

motes charge sustainability by penalizing the differ-

ence between the current SOC(t) and it’s reference

value SOC

ref

(which we set to 50%) (Onori and Ser-

rao, 2011; Rezaei et al., 2017). The following cost

function is then obtained, and will be considered in

the remainder of this paper:

J(t) = ˙m

fuel



ICE

(t)





+ λ

(SOC(t) − SOC

ref

)



bat

(t). (9)

To practically solve the optimization at every time

step, the ECMS uses the model described in Section

3.1 to predict ˙m

fuel

(t). We do this over a ﬁne grid

of discretized values for ∆SOC(t), since each deﬁnes

bat

(t) and through the constraint also P

ICE

(t), thus

allowing to evaluate J(t). We can thus essentially

solve the optimization without needing to explicitly

solve a numerical optimization, and we can even pre-

compute the solution for a large grid of speeds and

torques and interpolate to ﬁnd solutions that way. In

any case, once solved, the powers from the best solu-

tion are applied to the vehicle, and the next time step

the procedure is repeated.

In this paper the aim is to adapt both λ

and λ

depending on the context, with the aim to reduce the

overall energy consumption relative to the case when

they are kept constant.

3.3 Generation of Training and

Validation Data

In this section, we will describe the data used for

training and validation. The data-set is built using the

velocity proﬁles described by several standard driv-

ing cycles: WLTP, FTP, UDDS, CADC, Australia

SPC240, and US HWFET (Dieselnet, 2022).

Figure 3 shows all these cycles in a concatenated

form. These cycles are divided into segments, where

each belongs to one of 3 categories: urban, suburban

or highway, based on average velocity, as indicated in

the Figure. Every segment is in turn split up again in

even smaller sub-segments. These small sub-cycles

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

166

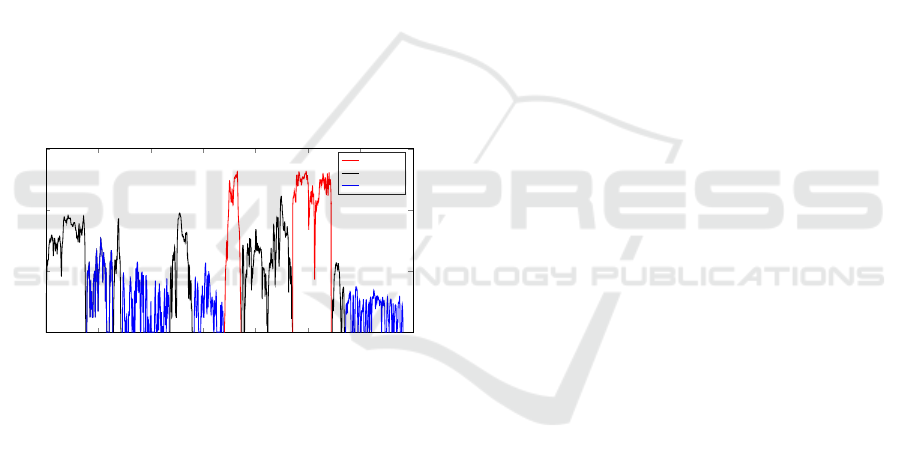
are then used as building blocks to construct a larger

set of training and validation velocity cycles, by con-

catenating several of them in varying order. Segments

are only concatenated when the velocity at the end of

segment one matches to the starting velocity of seg-

ment two, in order to avoid an unrealistic acceleration

proﬁle. Note that none of the sub-segments used for

validation are used for training and vice-versa. By

augmenting the original set of velocity cycles in this

way, a larger variety of training and validation scenar-

ios is obtained (more variation in length, more transi-

tions, etc.).

We know that clustering methods will perform

better when a more complete set of simulated sen-

sor signals is available, since it will allow for a more

diverse set of context features to be calculated. So

to generate our data-set we integrate the model from

Section 3.1 into the automotive simulator IPG Car-

Maker (IPG Automotive, 2022) and simulate the same

driving cycles. The new extended data-set then con-

tains the same vehicle speeds and torques as predicted

by our MATLAB model, but also additional simulated

signals (e.g., throttle and braking pedals, steering in-

put) from which additional features can be extracted.

0 1,000 2,000 3,000 4,000

5,000 6,000

7,000

100

150

Time [s]

Velocity [km/h]

Highway

Suburban

Urban

Figure 3: The considered velocity cycle data, which is man-

ually split into 3 categories: urban, suburban and highway.

4 CONTROL-CONTEXT

GROUPING

This section details the approach to group similar con-

trol parameter values to features derived from vary-

ing contexts, matching steps 1-4 outlined earlier. This

allows to later on adapt the control parameters as a

function of the observed context.

4.1 Computation of Optimal Control

Parameters

As mentioned in step 1) earlier, We need to calcu-

late optimal controller parameters for a variety of con-

texts, so they can later on be clustered together with

the context features. For each training cycle V

the complete training data set V consisting of N

cycles

cycles, we compute the optimal power split (i.e., the

control parameters λ

opt,k

and λ

opt,k

) using Dynamic

Programming (DP) (Goos et al., 2017) as:

opt,k

, λ

opt,k

=arg min

,λ

fuel

(t), (10)

s.t. P

desired

(t) = P

ICE

(t) + P

bat

(t),

desired

(t) = V

, k ∈ [1, . . . , N

cycles

Note that here we use DP to ﬁnd optimal values

for every cycle. We do this to generate training data

for our approach, but DP cannot easily be used di-

rectly online as an alternative, since the calculations

are very time consuming and rely on preview of the

entire upcoming cycles.

4.2 Extraction of Context Features

To complete step 1) we also need to extract and save

the features f to describe the context. To do so, we:

• Select a driving cycle V

from the complete data-

set V and extract all signals (e.g., speed, torque,

pedal positions, steering input, etc.).

• Deﬁne a time window of length N. Note that the

choice of N will need some iteration, depending

on the resulting clustering.

• For each signal compute aggregate (e.g., mean,

RMS, variance) context features f

for each win-

dow j that ﬁts within the driving cycle V

• For each time window j we also store the ac-

tive control parameters λ

1, j

= λ

opt,k

and λ

2, j

opt,k

. Note that these are constant for all win-

dows within the selected driving cycle V

, but will

change when moving to the next cycle.

• Move the the next driving cycle V

k+1

and con-

tinue until all driving cycles are processed.

Note that features computed over a window are as-

sociated with the last timestamp within this window,

thus looking at Figure 4, window 1’s features f

are

associated with timestep t

The steps above result in a set of aggregated con-

text features f

and a set of optimal control parameter

values λ

1, j

and λ

2, j

for every time window j in V .

These can then be represented by a point in a high di-

mensional space, spanning both the context features

and control parameter attributes.

A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle

167

Window 3

Window 2

Window 1

. . .

N+1

N+2

Time

. . .

Figure 4: Context features are computed over a window

in the past and linked to control parameters at the current

timestep.

4.3 Clustering of Context Features and

Control Parameters

Once the controller parameters and context features

are computed, we perform step 2), and group them

in such a way that the similarity within a group is as

high as possible, without ending up with a high num-

ber of groups. We have used K-means clustering to

do so, but before trying to form clusters in this highly

dimensional space, it is best to remove some context

features to only retain the relevant ones. The approach

used in this paper is to compute the ‘permutation fea-

ture importance’ (PFI) values for each context feature,

with respect to the controller parameters (Leo, 2001;

Venkatesan et al., 2021). Only features that have an

importance value above a set threshold are used for

clustering.

The number of clusters has to be given as an input

parameter to the clustering algorithm, but the ideal

number is not known beforehand and is use-case de-

pendent. Selecting the right number of clusters is

therefore an iterative process, and comes down to a

trade-off between having better control performance

(by being able to adapt to a more diverse set of con-

texts) and still maintaining sufﬁcient controller ro-

bustness / avoiding continuously switching between

context clusters. Furthermore, as described in Section

2, a lower number of clusters will result in an adaptive

controller which is easier to validate.

Remark 2. Other methods to avoid switching can

include deadbands or hysteresis controllers, or even

adding features to promote temporal similarity during

the clustering. For now we have not looked into these,

but we have restricted ourselves to using a small (2)

number of clusters.

In this paper we have chosen to use 2 clusters. An

example of the clustering outcome is depicted in Fig-

ure 5 where the 2 clusters are each indicated with a

different color. Both clustering methods which have

been used rely on the Scikit-learn (Buitinck et al.,

2013) machine learning toolbox in Python.

0.2

0.4

0.6

0.8

·10

−4

−6

−5

−4

−3

−2

100

150

Max velocity [km/h]

Figure 5: Example outcome of the clustering, yielding 2

clusters with similar controller parameters and context fea-

tures.

4.4 ECMS per Cluster

Since only a single set of controller parameters can

be used for a given cluster during on-line implemen-

tation, the controller parameters for each cluster must

be chosen to be as optimal as possible in all condi-

tions represented by this cluster i ∈ [1, . . . , N

clusters

Therefore, in step 3) the controller parameters are re-

optimized for each cluster before deployment, using

all data within the cluster. This is done by solving

the following optimization problem for each cluster i

(with time horizon t ∈ [t

start

, . . . ,t

end

]):

opt,i

, λ

opt,i

= arg min

,λ

fuel, eq.

, (11)

s.t. |SOC(t

start

) − SOC(t

end

)| ≤ ε,

where m

fuel, eq.

describes equivalent spent fuel and ε

is some small number to get a well-conditioned prob-

lem. This comprises the effective fuel spent, but also

a term to take into account the difference in chemical

energy due to differences in the ﬁnal SOC at t

end

the end of the horizon (duty cycle):

fuel, eq.

= m

fuel

end

) + ν · ∆SOC(t

end

), (12)

where ν is a factor expressing the average efﬁciencies

of ICE and EM. This is found by calculating the aver-

age value of ν(t) over the entire horizon:

ν(t)=











wh to EM

bat

wh to ICE

ICE

LHV

if ∆SOC(t) > 0,

wh to EM

bat

wh to ICE

ICE

LHV

otherwise,

(13)

where η denotes the efﬁciency of each component

(ICE, EM, battery), and Q

LHV

is the lower heat value

of the fuel. The constraint in Equation 11 ensures

(approximate) charge sustainability. The problem is

solved using the Matlab Global Optimization toolbox,

using the patternsearch algorithm (MathWorks, 2022).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

168

4.5 Integration with Classiﬁer

In order for the adaptive controller to be imple-

mentable on-line, it must know which cluster from

the training data best represents the current working

conditions. Because the desired controller parameters

are not known beforehand but depend on the cluster,

we cannot simply look for the closest cluster in the

full clustering space described in Section 4.3. There-

fore, in step 4) a random forest classiﬁer (a variant of

supervised learning), see e.g., (Ho, 1995), is built to

estimate the cluster membership, using only (a subset

of) the windowed context features as described above,

but not the controller parameters.

The considered workﬂow used to construct the

classiﬁer is shown in Figure 6. As described in Sec-

tion 4.2, features are extracted from timeseries data,

using windows of various lengths. Next, highly cor-

related features are removed using the Spearman rank

correlation analysis. Thereafter, similar to as done for

the clustering approach, we use a ’permutation fea-

ture importance’ (PFI) metric to select the most im-

portant features used for training the classiﬁer. Once

the classiﬁer has been trained, it can be used to pre-

dict the context during on-line operation, and select

the corresponding optimal control parameters. The

above workﬂow is implemented using the Scikit-learn

machine learning toolbox in Python (Buitinck et al.,

2013).

Figure 6: Workﬂow for constructing the classiﬁer.

4.6 Assembly of Resulting Adaptive

Controller

Given the building blocks of earlier sections, we can

now assemble the adaptive controller itself. Online

we continuously run the random forest classiﬁer from

the previous section, and using it estimate the cluster

j to which the current conditions are the most similar.

Based on that, we then take the values (λ

opt, j

, λ

opt, j

)

according to (11) which were optimized ofﬂine for

this cluster j, and use it to calculate the ECMS power-

split and thus P

ICE

(t)

opt

, P

bat

(t)

opt

according to (7) for

the current vehicle speed and desired wheel torque.

5 SIMULATION RESULTS AND

DISCUSSION

In this section we evaluate the performance of the pro-

posed adaptive controller on the validation data de-

scribed earlier.

First, we compare it to a benchmark ECMS (bm-

ECMS) controller with ﬁxed control parameters, with

and λ

chosen to be optimal, using the ECMS clus-

ter optimization approach detailed in Equation 11, but

given the complete training data-set V instead of only

the data in a single cluster.

In order to benchmark the controllers, we use

the equivalent fuel consumption, see Equation 11.

Table 1 compares the developed adaptive approach

(a-ECMS) to the benchmark ECMS for the training

and validation driving cycles. It can be seen that

for validation data the performance gain when using

our adaptive controller is 0.72% over the benchmark

ECMS with ﬁxed parameters. This gain is moreover

attained over the best possible ﬁxed ECMS controller,

optimized on our training data-set, which is already a

high-performance baseline. Given the amount of ve-

hicles on the road and in industrial settings, such a

gain could yield a signiﬁcant reduction of fuel usage

and exhaust gasses. Furthermore, this can be achieved

without the need for additional hardware since we are

only using existing sensor signals and requires only

limited additional computational power compared to

traditional ECMS.

Table 1: Comparison of proposed adaptive ECMS, to the

benchmark ECMS controller with ﬁxed parameters.

Cycle Description

a-ECMS

fuel, eq.

−m

bm-ECMS

fuel, eq.

bm-ECMS

fuel, eq.

Training data-set -1.28%

Validation data-set -0.72%

To further evaluate the developed controller, we

compare it to DP. As mentioned earlier in this paper,

DP is computationally heavy and hard to implement

online. However, when used ofﬂine with preview of

the entire duty cycle it can be seen as the best-case

controller and thus a lower bound on fuel consump-

tion. For comparing our adaptive ECMS to DP we do

not need to use the equivalent fuel deﬁned above. In-

stead we can directly evaluate the effective fuel spent

for a DP constrained to end up with the same SOC(t

)

as the adaptive ECMS. Table 2 shows the outcome,

indicating that the adaptive ECMS approaches the

DP to within 0.47%. The proposed approach has thus

cut the gap between ﬁxed ECMS and the upper bound

A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle

169

provided by DP roughly in half, achieving a

performance just closer to DP than to the ﬁxed

ECMS.

Table 2: Comparison of proposed adaptive ECMS using

clustering, to DP solution which is the best case solution.

Cycle Description

a-ECMS

fuel

−m

fuel

Training data-set 0.69%

Validation data-set 0.47%

6 CONCLUSIONS

A method for deriving an adaptive controller was pre-

sented focused on discovering the relevant changes in

system dynamics and / or environment conditions to

adapt to. A clustering based approach is used to detect

conditions where optimal control parameter values

differ signiﬁcantly and adaptation is beneﬁcial. Us-

ing these clusters an adaptive controller is then made

that during operation (I) determines what cluster the

current conditions reside in, and (II) selects the opti-

mal control parameters computed ofﬂine beforehand

for that cluster.

Owing to the generic nature of the clustering ap-

proach, the authors expect this technique to be useful

for many applications where adaptation of paramet-

ric controllers is needed, yet the dependencies or con-

texts to adapt to are not known. As more machines

are connected, and more (complex) sensors become

available, the authors expect applications where the

contexts to adapt to are not known up front to occur

ever more frequently.

On the considered HEV use case this approach

outperforms a non-adaptive but well-tuned ECMS

controller by 0.72%, and comes to within 0.47% of

the dynamic programming gold standard that cannot

be implemented as an online controller. This pro-

vides a proof-of-concept for the developed method to

design adaptive controllers, but we do not claim the

outcome outperforms other adaptive control schemes,

which is a topic still to be tackled in future research.

The proposed method is developed to be espe-

cially suitable for industrial usage since (I) it can be

added on top of existing parametric controllers, (II) its

implementation is limited in complexity, and (III) its

adaptations can be inspected before deployment and

are straightforward to understand. There are however

still a few remaining drawbacks as well. Currently

a training set is obtained from simulation, for which

we can calculate optimal control parameters for each

sample, but ﬁnding optimal control values for a large

experimental dataset will be harder to do. Further-

more, the grouping approach including the cluster-

ing still has many algorithm choices and factors to be

tuned which are less obvious for a typical application

engineer, like choosign the number of clusters, choos-

ing features, selecting window lengths, .. So while

the overall controller has been kept simple conceptu-

ally (combining a typical ECMS with an additional

routine to detect cluster and switch between ECMS

parameter sets), future work can look into improving

the design procedure itself.

Summarizing the previous, future work will focus

on:

• Improving the design procedure and the choices

made therein, comparing different clustering

methods, trying out more clusters, looking into

automatic feature extraction and selection using

e.g. tsfresh (Christ et al., 2018).

• Investigation of optimal data collection, hopefully

with reduced datasets, and optionally sparse ex-

perimental sets.

• Extending the clustering with additional ﬁxes to

avoid excessive parameter switches in time.

• Comparing the a-ECMS approach considered in

this paper with other adaptive approaches targeted

at HEVs.

• Validation of methods on different cases, possibly

with more complex variability in dynamics / envi-

ronment.

ACKNOWLEDGEMENTS

This work was carried out in the framework of Flan-

ders Make’s ICON project ’Context-Aware Control’

and also received funding from the Flemish Govern-

ment (AI Research Program). Flanders Make is the

Flemish strategic research centre for the manufactur-

ing industry.

REFERENCES

Ariyur, K. B. and Krstic, M. (2003). Real-time optimization

by extremum-seeking control. John Wiley & Sons.

Åström, K. J. and Wittenmark, B. (2013). Adaptive control.

Courier Corporation.

Bellman, R. (1966). Dynamic programming. Science,

153(3731):34–37.

Berkenkamp, F., Turchetta, M., Schoellig, A., and Krause,

A. (2017). Safe model-based reinforcement learning

with stability guarantees. Advances in neural infor-

mation processing systems, 30.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

170

Buitinck, L., Louppe, G., Blondel, M., Pedregosa, F.,

Mueller, A., Grisel, O., Niculae, V., Prettenhofer, P.,

Gramfort, A., Grobler, J., Layton, R., VanderPlas, J.,

Joly, A., Holt, B., and Varoquaux, G. (2013). API de-

sign for machine learning software: experiences from

the scikit-learn project. In ECML PKDD Workshop:

Languages for Data Mining and Machine Learning,

pages 108–122.

Chasse, A., Sciarretta, A., and Chauvin, J. (2010). Online

optimal control of a parallel hybrid with costate adap-

tation rule. IFAC proceedings volumes, 43(7):99–104.

Christ, M., Braun, N., Neuffer, J., and Kempa-Liehr, A. W.

(2018). Time series feature extraction on basis of scal-

able hypothesis tests (tsfresh–a python package). Neu-

rocomputing, 307:72–77.

De Jager, B., Van Keulen, T., and Kessels, J. (2013). Opti-

mal control of hybrid vehicles. Springer.

Dieselnet (2022). Emission test cycles,

http://dieselnet.com/standards/cycles/index.php.

Elliott, H., Cristi, R., and Das, M. (1985). Global stability

of adaptive pole placement algorithms. IEEE transac-

tions on automatic control, 30(4):348–356.

Frank, B. et al. (2017). Hybrid systems, optimal control and

hybrid vehicles.

Gao, A., Deng, X., Zhang, M., and Fu, Z. (2017). De-

sign and validation of real-time optimal control with

ecms to minimize energy consumption for parallel hy-

brid electric vehicles. Mathematical Problems in En-

gineering.

Goos, J., Criens, C., and Witters, M. (2017). Automatic

evaluation and optimization of generic hybrid vehi-

cle topologies using dynamic programming. IFAC-

PapersOnLine, 50(1):10065–10071.

Ho, T. K. (1995). Random decision forests. In Proceedings

of 3rd international conference on document analysis

and recognition, volume 1, pages 278–282. IEEE.

Hussain, S., Ali, M. U., Park, G.-S., Nengroo, S. H.,

Khan, M. A., and Kim, H.-J. (2019). A real-time

bi-adaptive controller-based energy management sys-

tem for battery–supercapacitor hybrid electric vehi-

cles. Energies, 12(24):4662.

IPG Automotive (2022). Carmaker,

https://ipg-automotive.com/en/products-

solutions/software/carmaker.

Jain, A. K. and Dubes, R. C. (1988). Algorithms for clus-

tering data. Prentice-Hall, Inc.

Johannink, T., Bahl, S., Nair, A., Luo, J., Kumar, A.,

Loskyll, M., Ojea, J. A., Solowjow, E., and Levine,

S. (2019). Residual reinforcement learning for robot

control. In 2019 International Conference on Robotics

and Automation (ICRA), pages 6023–6029. IEEE.

Khan, S. G., Herrmann, G., Lewis, F. L., Pipe, T., and Mel-

huish, C. (2012). Reinforcement learning and opti-

mal adaptive control: An overview and implementa-

tion examples. Annual reviews in control, 36(1):42–

59.

Kreisselmeier, G. and Anderson, B. (1986). Robust model

reference adaptive control. IEEE Transactions on Au-

tomatic Control, 31(2):127–133.

Leith, D. J. and Leithead, W. E. (2000). Survey of gain-

scheduling analysis and design. International journal

of control, 73(11):1001–1025.

Leo, B. (2001). Random forests. Machine Learning,

45(1):5–32.

MathWorks (2022). Global optimization toolbox user’s

guide. The MathWorks.

Musardo, C., Rizzoni, G., Guezennec, Y., and Staccia, B.

(2005). A-ecms: An adaptive algorithm for hybrid

electric vehicle energy management. European Jour-

nal of Control, 11(4-5):509–524.

Onori, S. and Serrao, L. (2011). On adaptive-ecms strate-

gies for hybrid electric vehicles. In Proceedings of

the international scientiﬁc conference on hybrid and

electric vehicles, Malmaison, France, volume 67.

Powell, W. B. (2007). Approximate Dynamic Program-

ming: Solving the curses of dimensionality, volume

703. John Wiley & Sons.

Rezaei, A., Burl, J. B., Zhou, B., and Rezaei, M. (2017).

A new real-time optimal energy management strategy

for parallel hybrid electric vehicles. IEEE Transac-

tions on Control Systems Technology, 27(2):830–837.

Rummery, G. A. and Niranjan, M. (1994). On-line Q-

learning using connectionist systems, volume 37. Uni-

versity of Cambridge, Department of Engineering

Cambridge, UK.

Schreier, M. (2012). Modeling and adaptive control of a

quadrotor. In 2012 IEEE international conference on

mechatronics and automation, pages 383–390. IEEE.

Staessens, T., Lefebvre, T., and Crevecoeur, G. (2022).

Adaptive control of a mechatronic system using con-

strained residual reinforcement learning. IEEE Trans-

actions on Industrial Electronics, 69(10):10447–

10456.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-

ing: An introduction. MIT press.

Venkatesan, S. K., Beck, R., Bengea, S., Meskens, J., and

Depraetere, B. (2021). Design framework for context-

adaptive control methods applied to vehicle power

management. In 2021 21st International Conference

on Control, Automation and Systems (ICCAS), pages

584–591.

Wang, Y., Gao, F., and Doyle III, F. J. (2009). Survey on it-

erative learning control, repetitive control, and run-to-

run control. Journal of Process Control, 19(10):1589–

1600.

Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine

learning, 8:279–292.

Yang, T., Sun, N., and Fang, Y. (2021). Adaptive fuzzy con-

trol for a class of mimo underactuated systems with

plant uncertainties and actuator deadzones: Design

and experiments. IEEE Transactions on Cybernetics,

52(8):8213–8226.

A Clustering-Based Approach for Adaptive Control Applied to a Hybrid Electric Vehicle

171