Adaptive Case Selection for Symbolic Regression in Grammatical

Evolution

Krishn Kumar Gupt

1 a

, Meghana Kshirsagar

2 b

, Douglas Mota Dias

2,3 c

Joseph P. Sullivan

1 d

and Conor Ryan

2 e

Technological University of the Shannon: Midlands Midwest, Moylish campus, Limerick, Ireland

Biocomputing and Development System Lab, University of Limerick, Ireland

Department of Electronics & Telecommunications, Rio de Janeiro State University, Rio de Janeiro, Brazil

Keywords:

Test Case Selection, Adaptive Selection, Symbolic Regression, Grammatical Evolution, Diversity,

Computational Efﬁciency.

Abstract:

The analysis of time efﬁciency and solution size has recently gained huge interest among researchers of Gram-

matical Evolution (GE). The voluminous data have led to slower learning of GE in ﬁnding innovative solu-

tions to complex problems. Few works incorporate machine learning techniques to extract samples from big

datasets. Most of the work in the ﬁeld focuses on optimizing the GE hyperparameters. This leads to the mo-

tivation of our work, Adaptive Case Selection (ACS), a diversity-preserving test case selection method that

adaptively selects test cases during the evolutionary process of GE. We used six symbolic regression synthetic

datasets with diverse features and samples in the preliminary experimentation and trained the models using

GE. Statistical Validation of results demonstrates ACS enhancing the efﬁciency of the evolutionary process.

ACS achieved higher accuracy on all six problems when compared to conventional ‘train/test split.’ It outper-

forms four out of six problems against the recently proposed Distance-Based Selection (DBS) method while

competitive on the remaining two. ACS accelerated the evolutionary process by a factor of 14X and 11X

against both methods, respectively, and resulted in simpler solutions. These ﬁndings suggest ACS can poten-

tially speed up the evolutionary process of GE when solving complex problems.

1 INTRODUCTION

Evolutionary Algorithms (EAs) (Slowik and Kwas-

nicka, 2020) have become popular in solving complex

optimization problems in various domains. Grammat-

ical Evolution (GE) (Ryan et al., 1998) is one such

algorithm that can evolve programs or models in any

language, which makes it versatile in solving different

kinds of problems such as program synthesis (O’Neill

et al., 2014), circuit design (Ryan et al., 2020; Gupt

et al., 2022a), symbolic regression (Ali. et al., 2021;

Gupt et al., 2022b; Murphy et al., 2021) etc.

Symbolic Regression (SR) is a problem where

a mathematical expression or formula is evolved

through an iterative process to ﬁt a given data set

https://orcid.org/0000-0002-1612-5102

https://orcid.org/0000-0002-8182-2465

https://orcid.org/0000-0002-1783-6352

https://orcid.org/0000-0003-0010-3715

https://orcid.org/0000-0002-7002-5815

(Zhang and Zhou, 2021). Unlike traditional regres-

sion analysis, where a pre-deﬁned functional form

is used to ﬁt the data, SR allows for discovering an

expression that best captures the underlying relation-

ships in the data. This expression can be in the form

of a mathematical formula or equation and can in-

volve various mathematical functions and operators.

This problem is ubiquitous in many ﬁelds, including

ﬁnance (Chen, 2012), clinical informatics (Cava et al.,

2020), and many ﬁelds of engineering (La Cava et al.,

2016a; Abdellaoui and Mehrkanoon, 2021).

One common approach to solving SR problems

is Genetic Programming (GP), where a population of

individuals gradually improves throughout an evolu-

tionary process (Koza, 1992). However, GE is also

a suitable candidate for this task and has been used

in several studies (Ali. et al., 2021; Gupt et al.,

2022b). We employ GE due to its versatility in

tackling real-world problems, incorporating domain-

speciﬁc knowledge and constraints into the grammar,

with plans to extend the proposed research to other

Gupt, K., Kshirsagar, M., Dias, D., Sullivan, J. and Ryan, C.

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution.

DOI: 10.5220/0012175900003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 195-205

ISBN: 978-989-758-674-3; ISSN: 2184-3236

195

problem domains in the future. During the evolution-

ary process, parents are chosen based on their ﬁtness,

often determined by performance on training data.

Evolutionary methods can be computationally ex-

pensive, especially when dealing with big datasets

in problems like real-world SR. Limited computing

resources further compound the computational com-

plexity and cost challenges in the design and testing

phase.

In this paper, we propose Adaptive Case Selection

(ACS) to minimize the training cost of GE while re-

taining the quality of the solutions. ACS is a diversity-

preserving test case selection approach that aids GE

by adaptive training case

selection during the evolu-

tionary process. This ensures cases are selected based

on their degree of dissimilarity, promoting high cov-

erage and a reduced computational cost. We compare

the solutions’ quality with the conventional ‘train/test

split’ and the state-of-the-art Distance-Based Selec-

tion (DBS) (Ryan. et al., 2021; Gupt et al., 2022a)

method on six well-known SR benchmarks. Further-

more, we analyze the time efﬁciency of the ACS over

the evolutionary process.

2 BACKGROUND

This section provides the GE background used to

evaluate the proposed ACS, and state-of-the-art DBS,

considered as one of the baselines. Following these,

it brieﬂy covers the recent research contributions to

case optimization focused on SR problems, which are

most relevant to this study.

2.1 Grammatical Evolution

Grammatical Evolution (GE) is an evolutionary algo-

rithm that combines GP with formal grammars. The

individuals in GE are represented as codons, which

are sequences of binary digits that map to a cor-

responding string in the Backus–Naur Form (BNF)

grammar. Grammar plays a crucial role in deﬁn-

ing individuals’ genetic makeup and characteristics in

the evolutionary process. During evolution, individu-

als are generated by applying the production rules of

grammar. These individuals are then evaluated using

a ﬁtness function that measures their performance on

a set of training data.

The ﬁtness evaluations in GE are typically com-

putationally expensive, as each individual needs to be

Dataset or test cases used for model training is referred

to as training data/cases, while those for testing the model’s

performance are termed testing data.

evaluated on all training cases. The size and complex-

ity of the training data can signiﬁcantly impact the ﬁt-

ness evaluation process and, hence, the performance

of GE.

2.2 Distance-Based Selection

DBS is a test case selection algorithm for selecting

data from a given set of test cases. It follows a greedy

approach during selection based on dissimilarity be-

tween test case pairs. Test case pairs with the highest

dissimilarity are selected ﬁrst, followed by pairs with

decreasing dissimilarity until the desired number of

test cases or a subset of the desired size is obtained.

While using DBS in conjunction with GE exhibits

promising results in enhancing solution quality and

reducing the computational cost, there is uncertainty

regarding the optimal subset size for a given prob-

lem (Gupt et al., 2022a). However, the algorithm of-

fers ﬂexibility in selecting an appropriate subset size

based on design budgets.

Despite its advantages, DBS has limitations when

compared to the proposed ACS. ACS explores the po-

tential of test case selection in both increasing and de-

creasing order of diversity and employs adaptive se-

lection based on the evolutionary budget, resulting in

a more thorough test case selection process. In con-

trast, DBS does not employ these strategies, which

may lead to a potentially signiﬁcant data loss.

2.3 Related Work

Balancing computational cost with solution quality

in EAs is challenging, and researchers must care-

fully evaluate trade-offs to determine the optimal ap-

proach. Several studies have used methods such as

adaptive population sizing (Lobo and Lima, 2007)

or parameter tuning (Huang et al., 2019) to help re-

duce the computational cost of EAs. However, tuning

hyper-parameters is tiresome and could take longer

to ﬁnd the optimal solution (Huang et al., 2019).

Some studies have used parallelization that could ef-

fectively improve the evolutionary time (Streichert

et al., 2005). This comes at the cost of high compu-

tational resources and communication overhead be-

tween processors. Another method that signiﬁcantly

improves time efﬁciency is ﬁtness approximation (Jin,

2005). Despite their beneﬁts, these approaches result

in longer evaluation times, high resource consump-

tion, or compromised solution quality.

Researchers have proposed various methods that

aim to reduce the computational expenses of the

evolutionary process. To reduce the evaluation fre-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

196

quency and cost, (Schmidt and Lipson, 2007)

suggested co-evolving the ﬁtness models where two

populations (the individuals and their ﬁtness models)

are evolved simultaneously. (Helmuth et al., 2014)

in their work proposed lexicase selection, a parent

selection method for evolutionary algorithms based

on the lexicographic ordering of test cases. The

approach works well for discrete error spaces but has

been shown to perform poorly for continuous-valued

problems that are common in system identiﬁcation

tasks. To address this issue, (La Cava et al., 2016b)

proposed e-lexicase selection, which redeﬁnes the

pass criteria for individuals on each test case more

effectively. This approach has been shown to improve

the performance of lexicase selection for continuous-

valued issues and has been successfully applied to

various system identiﬁcation tasks.

The authors in (Gonc¸alves and Silva, 2013) intro-

duced a method of randomly choosing a single train-

ing instance at each generation and balancing it peri-

odically using all training data. (Kordos and Blach-

nik, 2012) used a variety of instance selection algo-

rithms for regression problems, including Condensed

Nearest Neighbor (CNN) and Edited Nearest Neigh-

bor (ENN). These algorithms were modiﬁed for re-

gression problems and used Euclidean measures to

determine the difference between the output values of

two vectors for selection.

In a separate study, (Kordos and Łapa, 2018) used

the k-Nearest Neighbor (k-NN) algorithm and pre-

sented an instance selection approach for regression

tasks. Their method employs a multi-objective EA to

search for the optimal subset of the training dataset

efﬁciently. However, combining k-NN and multi-

objective EAs can increase the computational com-

plexity of the selection algorithm, making it a compu-

tationally expensive approach.

In another study, (Son and Kim, 2006) proposed

an algorithm where the dataset was divided into sev-

eral partitions, and the entropy value was calculated

for each attribute in every partition. Further, they used

the attribute with the lowest entropy to segment the

dataset and used Euclidean distance to ﬁnd the repre-

sentative cases that best capture the characteristics of

each partition. However, the approach is more suit-

able for pre-processing tasks like data mining rather

than SR.

To compare and choose training datasets, (Kaj-

danowicz et al., 2011) employed clustering to divide

the dataset into groups. Their selection method as-

sesses the distance between training and testing data,

favoring the selection of training data that exhibit

greater similarity to the testing data. This raises con-

cerns about biased training, as it predominantly uti-

lizes data that closely resemble the testing data for

training purposes.

Efﬁciently selecting a representative subset of

training cases signiﬁcantly impacts machine learning

model performance. However, this task is non-trivial,

leading to the present study’s motivation to evaluate

the efﬁcacy of the ACS algorithm in the selection and

adaptive use of training case subsets, offering opti-

mal search space coverage while substantially reduc-

ing computational costs.

3 ADAPTIVE CASE SELECTION

The Adaptive Case Selection algorithm proposed in

this paper selects training cases adaptively while eval-

uating the models during the evolutionary run. The

objective is to ﬁnd a balance between training time

and accuracy. The proposed ACS algorithm incor-

porates a Distance-Based Selection method to select

subsets of diverse training data. This approach helps

capture a broad range of features and patterns present

in the data.

In most problems, test cases or data instances are

typically distributed across a vast space. To apply

ACS, we ﬁrst group them using clustering (Kshirsagar

et al., 2022), a machine-learning technique of divid-

ing data into groups (clusters) based on similar char-

acteristics or patterns. K-Means clustering is used

with the Euclidean distance metric to group the cases.

Note that clustering is not a part of ACS; rather, it is a

pre-processing step. Once we have a stable group of

clusters, the selection is done by creating a distance

matrix for the data of each cluster. The distance is

used to select the data pair from each cluster.

The ACS method consists of two approaches for

selecting data from a larger dataset based on their di-

versity

. It measures diversity based on the Euclidean

distance between data points in each cluster. Data

pairs exhibiting greater Euclidean distance in a given

cluster are considered diverse, indicating a signiﬁcant

dissimilarity between them. Conversely, those with

a closer resemblance or smaller distances are less di-

verse. The selection strategy is discussed below.

• Incremental-ACS (Inc-ACS): This involves se-

lecting the data in increasing order of diversity.

This means that the least diverse data points are

selected ﬁrst, followed by increasingly diverse

ones.

• Decremental-ACS (Dec-ACS): This involves se-

lecting data in decreasing order of diversity. In

Diversity is considered as opposed to similarity (Chen,

2010; Gupt et al., 2022a)

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution

197

this case, we select the most diverse data points

ﬁrst, followed by increasingly less diverse ones.

To implement these approaches, we ﬁrst compute

a diversity score for each data point in the clusters.

This is done by calculating the Euclidean distance be-

tween each pair of data points in each cluster as

(p, q) =

∑

i=1

− p

)

(1)

where p and q are two test case points in Euclidean

n-space. Based on the diversity scores, we sort the

data points in ascending/descending order of diversity

and select the data pairs individually, starting from the

least/most diverse one. This is done to promote di-

versity (to represent a vast test case space) and max-

imum coverage. This is done for all clusters until

the required budget is fulﬁlled, and based on the data

size and computational budget, training subsets are

formed. For instance, if the desired number of sub-

sets S

is speciﬁed, the total data is divided into S

subsets of size S

≈ data/S

cases in each subset. Al-

ternatively, if the size of a subset S% is provided, the

data is split into S

= ⌈1/S%⌉ subsets, and selection

is performed accordingly. The steps are described in

Algorithm 1.

The two selection approaches, Inc/Dec-ACS, offer

the ﬂexibility of prioritizing the data based on require-

ments. The former approach may be helpful when we

want to ensure that we cover all the different types

of data in the dataset, starting from the less common

ones; the latter approach may be useful when we want

to focus ﬁrst on the most representative or informative

data points in the dataset while ignoring the less im-

portant ones. We test both approaches in this paper.

Once the subsets are formed, GE uses them as

training data and updates during the evolutionary pro-

cess based on Inc/Dec-ACS applied. The adaptive use

of these subsets also helps ensure the model can learn

from a wide range of training cases without overﬁt-

ting any particular data subset.

4 EXPERIMENTAL SETUP

To assess the efﬁcacy of the proposed ACS algo-

rithm, we tested the method on six problems from

symbolic regression. The selected problems are pop-

ular, frequently used in SR, and have recently been

used to evaluate various algorithms and tools (Ali.

et al., 2021; Gupt et al., 2022b; Murphy et al., 2021;

Youssef et al., 2021). While selecting these key prob-

lems, we tried considering benchmarks with differ-

ent levels of complexity. Ideally, they should be non-

trivial and orthogonal enough to uncover the strengths

Algorithm 1: Adaptive Case Selection.

Input: data: the size of the dataset,

clusters: k clusters of the dataset,

approach: Inc/Dec-ACS,

budget: S

or S%,

Output: subset: a list of data subsets

1 if S% is given then

2 Calculate S

= ⌈1/S%⌉ ;

3 end

4 Calculate S

≈ data/S

;

5 Initialize an empty list - subset[S

];

6 for each k do

7 Compute the distance matrix;

8 if Inc-ACS == 1 then

9 Sort data pairs by increasing

diversity;

10 else

11 if Dec-ACS == 1 then

12 Sort data pairs by decreasing

diversity;

13 end

14 end

15 for i in range(S

) do

16 if (i ̸= S

− 1) then

17 append top S

data points in

subset[i];

18 end

19 else

20 append remaining data to the

subset[i];

21 end

22 end

23 end

24 Return subset;

Table 1: Benchmark candidates used.

Dataset # Features # Instances

Keijzer-4 1 402

Keijzer-9 1 1102

Keijzer-10 2 10301

Keijzer-14 2 3741

Vladislavleva-5 3 3000

Vladislavleva-6 2 991

and weaknesses of the ACS algorithm being exam-

ined. A list of problems used in this paper is summa-

rized in Table 1.

For a given benchmark, we employed the conven-

tional ‘train/test split’ method, allocating the initial

70% of the total data for training and reserving the

remaining 30% as testing data. A total of 30 inde-

pendent runs are performed for each benchmark. The

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

198

solutions are tested against the testing data, and the

results are reported. We take an average of the best

test scores and use them as a baseline 1.

Further, we use DBS and consider its best results

as baseline 2. One issue in this approach is that it is

not known in advance which data sample will be use-

ful. Considering this, we select a number of subsets

using a decremental approach (Olvera-L

opez et al.,

2010), which begins with a large training data and

is reduced by omitting instances during the selection

process. For all six problems, we apply DBS on the

baseline 1 training data and select a range of subsets.

We select six subsets of different sizes, viz. 70%,

65%, 60%, 55%, 50%, and 45% of baseline 1 training

data and perform 30 independent runs on each sub-

set for each of the six benchmarks used. For ease of

understanding, we represent training data or a sub-

set of size 70% of baseline 1 selected using DBS as

DBS(70%), and so on. The best performing DBS sub-

set amongst them for a given benchmark is considered

for comparison, and we call it DBS* (the best result

of DBS).

While the training data size may vary for experi-

ments using different selection approaches, the testing

data is kept the same for a speciﬁc benchmark. The

total number of instances used in training data dur-

ing the different sets of experiments using baseline 1,

baseline 2 or DBS*, and ACS is given in Table 2.

The evolutionary process of GE works similarly

for all approaches, and GE parameters are kept the

same across all experiments as given in Table 3.

In the proposed ACS, we used S = 20%, meaning

a subset could hold a maximum of 20% of the base-

line 1 training data. This produced a total number of

subsets S

= 5. Running on a budget of 50 gener-

ations, we preferred to allow an equal run time for

each subset, and hence, the training subset is updated

with another subset after every 10 generations. How-

ever, to ensure that the best individuals or their off-

spring are retained in the evolutionary process across

generations, we analyzed a few runs across 50 genera-

tions. We observed the offspring’s genotype that was

carried throughout, thus preserving the evolutionary

prospects.

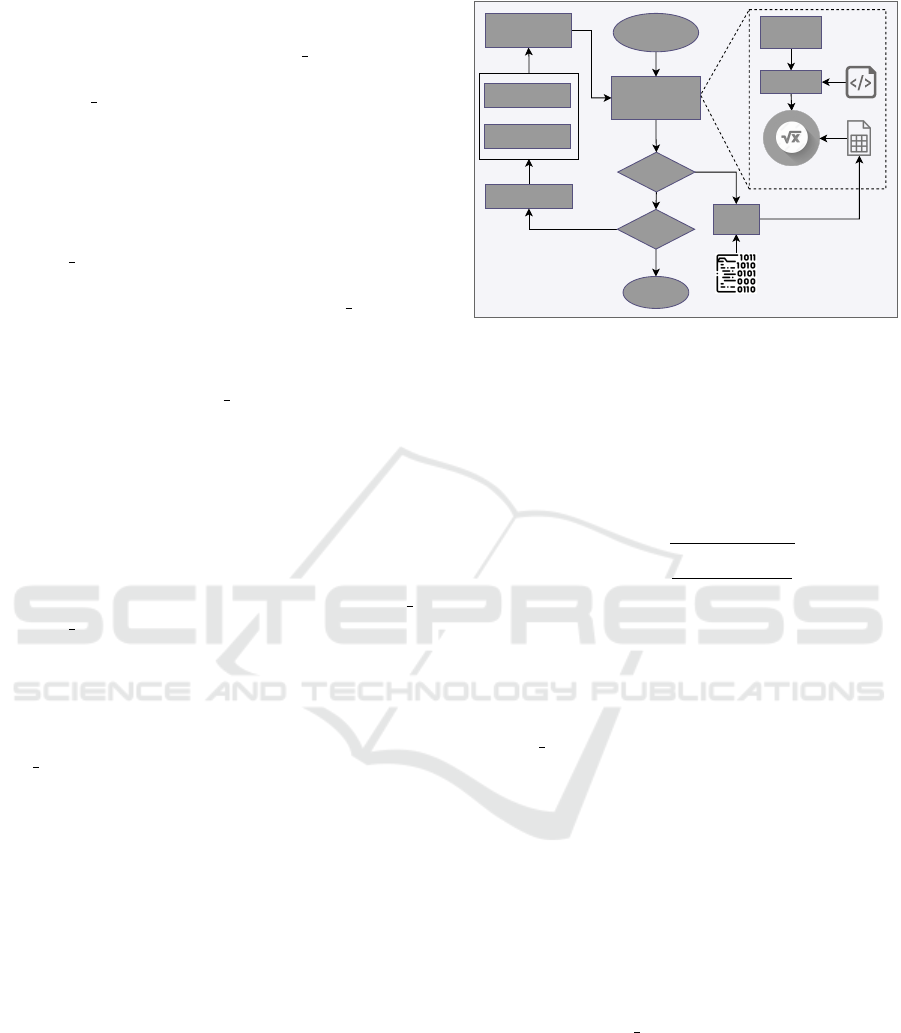
The GE training setup incorporating ACS is given

in Figure 1. The proposed algorithm with GE pro-

vides the ﬂexibility to choose the desired number of

subsets or size of subsets depending on the require-

ments like available budget or complexity of the prob-

lem, etc. For instance, in problems like approximate

circuits (Traiola et al., 2018) where a set of test cases

are not mandated to be fulﬁlled, or a certain level of

tolerance is allowed, the ACS can deprioritize those

cases and allocate them a lesser or even no training

ACS

Fitness

Evaluation

Genotype

Mapping

Mutation

Crossover

Selection

New

population

Grammar

Subset

Initialization

Stop ?

End

Data

Update

data?

Symbolic

Regression Model

Yes

Figure 1: Pipeline of the proposed approach using ACS.

budget. Also, depending on the problem at hand or

training strategy, different subsets can have different

evolutionary budgets.

We use Root Mean Square Error (RMSE) as the

ﬁtness function. This is one of the most commonly

used measures for evaluating the quality of predic-

tions and is represented as

RMSE =

∑

i=1

− O

)

. (2)

Here, P

and O

are the predicted and observed (ac-

tual) values for the i

observation, respectively, while

is the total number of observations. The trained

mathematical models are assessed using testing data,

and the RMSE score is calculated to compare with the

baseline 1 and DBS*.

The ACS algorithm is written in Python, incorpo-

rating libraries such as SciPy and SKlearn, which is

further used with libGE (Nicolau and Slattery, 2006),

a C++ library for GE. We used an Intel i5 CPU @

1.6GHz machine with 4 cores, 6 MB cache, and 8GB

of RAM.

5 RESULTS AND DISCUSSION

We performed 180 (30 runs/problem) independent

runs for the baseline 1, 1080 (30 runs on 6 subsets per

problem) runs for DBS where 6 different training sub-

sets were used per benchmark, and 180 runs each for

Inc-ACS and Dec-ACS. This section presents a graph-

ical representation of the average test scores from 30

independent runs performed on each distinct pair of

training data and benchmarks. In addition, we con-

duct a statistical analysis to assess the signiﬁcance of

our test results and provide time analysis of the GE

run time to measure the computational cost of the ap-

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution

199

Table 2: Training and testing size used in different experiments.

Benchmarks

Training size

Testing size

Baseline 1 DBS(70%) DBS(65%) DBS(60%) DBS(55%) DBS(50%) DBS(45%) ACS

Keijzer-4 282 199 185 170 157 141 128* 58 120

Keijzer-9 772 540 503* 464 426 386 349 155 330

Keijzer-10 7211 5049 4689 4328 3968 3606 3247* 1444 3090

Keijzer-14 2619 1835 1704 1572 1443 1310 1180* 525 1122

Vladislavleva-5 2100 1471 1366* 1261 1157 1051 946 422 900

Vladislavleva-6 694 488* 452 418 383 349 315 141 297

Table 3: Evolutionary parameters used.

Parameter Value

Number of Runs 30

Total Generations 50

Population Size 250

Selection Type Tournament

Crossover Type Effective

Crossover Probability 0.9

Mutation Probability 0.01

Initialisation Method Sensible

proaches used. We also compare the sizes of the best

solutions obtained from each experiment.

5.1 Test Score

We present a comparative analysis of the performance

of our proposed method using the ﬁtness score on test

data. Recall the baselines are deﬁned as follows:

• Baseline 1: the conventional ‘train/test split’

method

• Baseline 2: best score obtained from the six DBS

subsets used on each benchmark. For clarity, we

write the best of DBS as DBS* (indicated with *

in Table 2).

The graphs in Figure 2 depict the mean, median,

minimum, and maximum values from the average of

the best test scores.

Figure 2(a) presents the results from the

Keijzer-4 dataset. The mean test score of the

Inc-ACS approach is better than the baseline results.

For Keijzer-9, the test score of ACS approaches

is superior to both of the baselines as shown in

Figure 2(b). Figure 2(c) shows the test scores from

Keijzer-10 experiments. The mean best test score

obtained from the models trained using the ACS

approach appears superior to the considered baselines

in both of its instances.

As shown in Figure 2(d), the mean best test scores

of Keijzer-14 experiments obtained using the Dec-

ACS approach seem to be better than the considered

baselines. Although Inc-ACS performed better than

baseline 1, it appears similar to DBS*. However, the

differences between these scores are small; it may be

difﬁcult to determine which approach is the most ef-

fective based solely on the ﬁgure. In this case, we

analyzed the numerical data to clarify the results and

found the test score at Inc-ACS is comparable to the

DBS*.

Figure 2(e) presents the test score of the best solu-

tions for the Vladislavleva-5 problem. The best

test scores of Inc-ACS are better or similar to the

baselines. In the case of Vladislavleva-6, the mean

test score in all cases was observed to be superior, as

shown in Figure 2(f).

In each of the six SR benchmarks presented in this

research, we observe ACS producing better solutions

regarding test scores.

We employ statistical tests to analyze and deter-

mine the signiﬁcance of the results. The Shapiro-Wilk

Test, with a signiﬁcance level of α=0.05, was used to

evaluate normality. We discovered that the difference

between the data sample and the normal distribution is

big enough to be statistically signiﬁcant. The results

do not match the requirements for parametric tests.

The Wilcoxon Signed-Rank test

(a non-

parametric test) is thus employed to test the statistical

signiﬁcance with α=0.05.

A statistical difference between the two samples

must be conﬁrmed ﬁrst. We compare Inc-ACS and

Dec-ACS both with the baseline 1 and DBS*, test

with a null hypothesis (the test score of the baseline 1

and DBS* are equal to ACS approaches) and label the

outcome as equal/similar (=) if no statistically signif-

icant difference is noted. Otherwise, the following

hypotheses are tested, and results are marked as + to

indicate signiﬁcantly better results, as shown in Table

– Null Hypothesis: The test scores of base-

line 1/DBS* are better than the test scores of

ACS.

– Alternative Hypothesis: The test score of ACS is

better than the test scores of baseline 1/DBS*.

Normality is not an assumption for the Wilcoxon

Signed-Rank test! We only examine normality to see if a

more appropriate test could be applied

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

200

(a) Keijzer-4 (b) Keijzer-9 (c) Keijzer-10

(d) Keijzer-14 (e) Vladislavleva-5 (f) Vladislavleva-6

Figure 2: Mean best test score of best solutions obtained across 30 independent runs.

Table 4: Results of the Wilcoxon Signed-Rank test for six benchmarks considering a signiﬁcance level of α = 0.05. Values

shown are the mean best test score across 30 independent runs. The symbols +, =, - indicate, whether the corresponding

results for ACS are signiﬁcantly better, not signiﬁcantly different, or worse than the baseline. The last row summarizes this

information.

Benchmark

Baseline 1 DBS* Inc-ACS Dec-ACS

Score Score Score

Vs. baseline 1

p-value

Vs. DBS*

p-value

Score

Vs. baseline 1

p-value

Vs. DBS*

p-value

Keijzer-4 0.2052 0.21298 0.20302 2.2694E-3 + 3.06E-08 + 0.28625 1E0 - 1E0 -

Keijzer-9 0.68085 0.69296 0.57311 5.27E-10 + 1.49005E-06 + 0.42009 4.14E-10 + 1.29E-09 +

Keijzer-10 0.29691 0.133 0.06433 3.90E-10 + 3.90E-10 + 0.08394 3.90E-10 + 3.90E-10 +

Keijzer-14 0.66978 0.52197 0.52832 6.71E-10 + 0.650042 = 0.40789 3.89E-10 + 3.89E-10 +

Vladislavleva-5 1.17529 1.15988 1.16663 3.4040E-2 + 8.24293E-1 = 1.22414 1E0 - 1E0 -

Vladislavleva-6 4.47298 4.14764 3.88021 3.90E-10 + 3.89437e-10 + 4.0199 4.14E-10 + 4.13854e-10 +

#Better/#Same/#Worse – – – 6/0/0 4/2/0 – 4/0/2 4/0/2

We found the p-value below the signiﬁcance level

and rejected the null hypothesis on all of the six prob-

lems when comparing Inc-ACS with baseline 1. The

results were better on 4 and similar on 2 problems

(Keijzer-14 and Vladislavleva-5) when com-

pared with DBS*.

Similarly, Dec-ACS was found to be better than

existing methods at 4 (Keijzer-9, Keijzer-10,

Keijzer-14, and Vladislavleva-6) of the bench-

marks. Although the results are improved and equally

effective or viable in most of the cases of the used

problems, the choice of using the ACS algorithm for

such problems could come down due to factors like

time and computational cost.

5.2 Performance Analysis

We conduct a comprehensive performance analysis

of the ACS algorithm. We assess the algorithm’s

efﬁciency and ability to handle various input sizes

through a detailed time analysis. Additionally, we an-

alyze the solution size to gain insights into the effect

of ACS on the solutions generated.

5.2.1 Time Analysis

An important objective we aim for while proposing

the ACS algorithm is that a reduced amount of data

will reduce the ﬁtness evaluation and, hence, the com-

putational cost of the evolutionary run. While the pro-

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution

201

posed method is good for producing quality solutions,

it is also important that the computational efﬁciency

match or be better than the baseline level. The graph

in Figure 3 shows an average of the total run time

across 30 independent runs for six benchmarks.

For Keijzer-4 dataset, the GE run time has sig-

niﬁcantly reduced for ACS compared to baseline ap-

proaches used to evolve the solution.

Figure 3: Average time taken (along with std error) per GE

run using baselines and proposed ACS approaches.

For the Keijzer-9 problem, the average run time

is clearly improved for both approaches of ACS. The

improved time efﬁciency is clear and evident in the

case of Keijzer-10 and Keijzer-14.

A similar observation is made for

Vladislavleva-5 and Vladislavleva-6 datasets.

Note that the run time for SR benchmarks used in this

paper is denominated in seconds.

When compared to the baseline 1, the perfor-

mance of the GE using ACS has shown a remarkable

improvement, with a minimum of 1.5X speedup in

the case of Keijzer-9. At the same time, the cost-

cutting measures resulted in a maximum reduction in

Vladislavleva-6 with a speedup factor of 14.77X.

The proposed approach has outperformed DBS*, with

a minimum improvement of 1.33X in the case of

Keijzer-4 and a maximum cost-cutting reduction

with a speedup of 11.38X is recorded in the case of

Vladislavleva-6. A detailed quantitative analysis

is given in Table 5.

The time analysis presented in this paper has

demonstrated the ACS algorithm’s efﬁcacy in reduc-

ing the run time of the GE while retaining ﬁtness re-

sults comparable with the baselines. The results vali-

date the rationale behind the development of the ACS

algorithm, which shows consistent and signiﬁcant im-

provements in the overall computational efﬁciency of

the evolutionary algorithm. The ﬁndings are crucial

as computational efﬁciency is often a major concern

in real-world applications, where time and resource

constraints are paramount.

5.2.2 Solution Size

To ensure that bloat is not introduced, we present

a comparative analysis of the effective individual

size of the best solutions achieved through the ACS

method, as shown in Figure 4. We report the value for

effective size averaged over 30 runs.

The effective size of the best solutions produced

for Keizer-4 is shown in Figure 4(a). The mean

solution size produced using Inc-ACS and Dec-ACS

is comparable to or smaller than the baseline 1 and

DBS* in all instances. A similar result is observed

in the case of the Keijzer-9 problem as shown in

Figure 4(b). In the Keijzer-10 problem, the mean

effective size of the best solutions generated by ACS

is smaller in all scenarios as indicated in Figure 4(c).

Figure 4(d) presents the performance of the ACS

algorithm in comparison to baseline 1 and DBS* on

the Keijzer-14 dataset. Both approaches of ACS

perform better than DBS* in terms of solution size.

We observe a smaller solution size in Dec-ACS com-

pared to baseline 1 and DBS*. However, the mean ef-

fective solution size of the Inc-ACS approach appears

similar to baseline 1.

Figure 4(e) reveals the impact of different case se-

lection strategies on the size of solutions produced

for the Vladislavleva-5 problem. The ACS ap-

proaches have smaller mean effective solution sizes

than both of the considered baselines.

Figure 4(f) shows the results for the

Vladislavleva-6 problem where the mean ef-

fective size of the best solutions achieved using the

Dec-ACS is better than the baselines. A quantitative

analysis of the solutions’ size is reported in Table 6.

The models trained using the two approaches of

the ACS algorithm pose solution sizes that are smaller

or equal to the baseline 1 and DBS*. For instance,

Dec-ACS produced smaller solutions in all bench-

marks tested. One possible reason is that the ACS

utilizes a more efﬁcient mechanism to guide the evo-

lutionary search. This can be particularly important in

real-world applications where solutions must be im-

plemented and maintained. Smaller solutions are eas-

ier to evaluate, adding value to the algorithm regard-

ing computational efﬁciency and run time. Moreover,

smaller solutions or solutions with less bloat are less

prone to overﬁtting and, therefore, are more likely to

generalize to unseen data.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

202

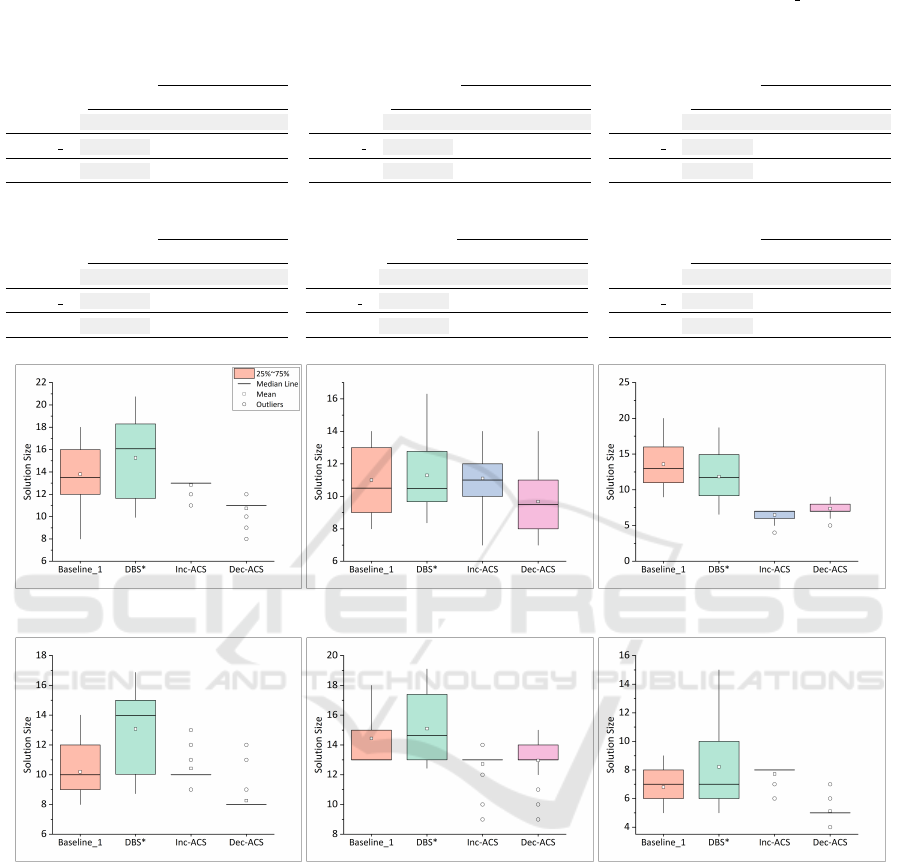
Table 5: Computational time analysis of six SR benchmarks. The tables display the GE run time for baseline 1, DBS*, and

the proposed Inc/Dec-ACS approaches averaged over 30 runs. The ACS methods are compared to both baselines, and the

resulting speedup factor is calculated.

(a) Keijzer-4

Inc-ACS Dec-ACS

Time (s) 1.666 1.366

Baseline 1 4.966 2.98X 3.63X

DBS* 2.233 1.33X 1.63X

(b) Keijzer-9

Inc-ACS Dec-ACS

Time (s) 2.366 3.33

Baseline 1 5.037 2.12X 1.51X

DBS* 4.7 1.98X 1.41X

Inc-ACS Dec-ACS

Time (s) 2.4 2.933

Baseline 1 23.666 9.68X 8.06X

DBS* 13.098 5.45X 4.46X

(d) Keijzer-14

Inc-ACS Dec-ACS

Time (s) 2.4 2.133

Baseline 1 8.4 3.5X 3.93X

DBS* 4.870 2.02X 2.28X

(e) Vladislavleva-5

Inc-ACS Dec-ACS

Time (s) 2.366 2.433

Baseline 1 4.633 2.8X 2.72X

DBS* 4.759 2.01X 1.95X

(f) Vladislavleva-6

Inc-ACS Dec-ACS

Time (s) 1.2 1.2

Baseline 1 17.733 14.77X 14.77X

DBS* 13.666 11.38X 11.38X

(a) Keijzer-4 (b) Keijzer-9 (c) Keijzer-10

(d) Keijzer-14 (e) Vladislavleva-5 (f) Vladislavleva-6

Figure 4: The mean effective individual size of the best solutions, averaged across 30 runs.

6 CONCLUSIONS

In this paper, we introduce ACS, an adaptive and

diversity-preserving algorithm, for selecting subsets

of training instances from SR datasets. We validate

it on six diverse SR problems with varying levels of

complexity in terms of features and instances. We

use two approaches, Inc-ACS and Dec-ACS, for se-

lecting the training instances in increasing and de-

creasing order of diversity. We compare the results

against the conventional ‘train/test split’ and existing

state-of-the-art DBS. The ACS algorithm produces

comparable or superior accuracy and quality solutions

across all six benchmarks. Hypothesis testing through

statistical analysis conﬁrms the effectiveness of the

ACS, producing comparatively better solutions than

the ‘train/test split’ method on 6/6 problems and 4/6

when compared to DBS*.

We conducted a run-time analysis to measure the

impact of the ACS algorithm on computational efﬁ-

ciency in evolutionary runs. Results showed that the

adaptive selection with reduced training data signif-

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution

203

Table 6: Analysis of the mean effective solution size of six SR benchmarks. The tables display the mean effective size of the

best individuals for baseline 1, DBS*, and the proposed Inc/Dec-ACS approaches averaged over 30 runs. The ACS methods

are compared to the baselines, and the resulting decrease in size factor is calculated.

(a) Keijzer-4

Inc-ACS Dec-ACS

Eff. Size 12.84 10.74

Baseline 1 13.8 1.07X 1.28X

DBS* 15.269 1.18X 1.42X

(b) Keijzer-9

Inc-ACS Dec-ACS

Eff. Size 11.1 9.68

Baseline 1 11 0.99X 1.13X

DBS* 11.293 1.01X 1.16X

Inc-ACS Dec-ACS

Eff. Size 6.5 7.38

Baseline 1 13.58 2.08X 1.84X

DBS* 11.846 1.82X 1.6X

(d) Keijzer-14

Inc-ACS Dec-ACS

Eff. Size 10.42 8.26

Baseline 1 10.2 0.97X 1.23X

DBS* 13.079 1.25X 1.58X

(e) Vladislavleva-5

Inc-ACS Dec-ACS

Eff. Size 12.72 12.96

Baseline 1 14.44 1.13X 1.11X

DBS* 15.097 1.18X 1.16X

(f) Vladislavleva-6

Inc-ACS Dec-ACS

Eff. Size 7.72 5.12

Baseline 1 6.8 0.88X 1.32X

DBS* 8.22 1.06X 1.6X

icantly decreased the ﬁtness evaluation time of GE,

producing solutions up to 14.77X and 11.38X faster

than baseline 1 and DBS*, respectively.

Additionally, the impact of the ACS method on the

size of solutions was investigated. In most instances,

solutions obtained incorporating the ACS approach

were shown to have effective solution sizes smaller

or similar to the state-of-the-art results indicating the

potential of ACS in producing efﬁcient solutions with

a smaller probability of creating bloat. Smaller solu-

tions with fewer bloats are important considerations

in EAs producing more efﬁcient and generalizable so-

lutions.

This paper’s experiments can serve as both an

early case study and a platform for selecting test cases

in other problem domains. The effectiveness of the

two ACS variants depends on the problem type, and

it would be interesting to explore which approach is

best for speciﬁc problem sets.

For future work, we plan to extend this research

and test the proposed algorithm on other domains like

Boolean problems. Additionally, we aim to increase

the robustness of ACS by making it self-adaptive by

choosing training subsets based on the population’s

ﬁtness score during run time.

ACKNOWLEDGEMENTS

This publication results from research conducted with

the ﬁnancial support of Science Foundation Ireland

under Grant # 16/IA/4605. The 3

author is also ﬁ-

nanced by the Coordenac¸

ao de Aperfeic¸oamento de

Pessoal de N

ıvel Superior - Brazil (CAPES), Finance

Code 001, and the Fundac¸

ao de Amparo

a Pesquisa

do Estado do Rio de Janeiro (FAPERJ).

REFERENCES

Abdellaoui, I. A. and Mehrkanoon, S. (2021). Symbolic

regression for scientiﬁc discovery: an application to

wind speed forecasting. In 2021 IEEE Symposium Se-

ries on Computational Intelligence (SSCI), pages 01–

08. IEEE.

Ali., M., Kshirsagar., M., Naredo., E., and Ryan., C. (2021).

Autoge: A tool for estimation of grammatical evo-

lution models. In Proceedings of the 13th Inter-

national Conference on Agents and Artiﬁcial Intelli-

gence - Volume 2: ICAART,, pages 1274–1281. IN-

STICC, SciTePress.

Cava, W. L., Lee, P. C., Ajmal, I., Ding, X., Solanki, P.,

Cohen, J. B., Moore, J. H., and Herman, D. S. (2020).

Application of concise machine learning to construct

accurate and interpretable EHR computable pheno-

types. medRxiv, pages 2020–12.

Chen, S.-H. (2012). Genetic algorithms and genetic pro-

gramming in computational ﬁnance. Springer Science

& Business Media.

Chen, T. Y. (2010). Fundamentals of test case selection: Di-

versity, diversity, diversity. In The 2nd International

Conference on Software Engineering and Data Min-

ing, pages 723–724. IEEE.

Gonc¸alves, I. and Silva, S. (2013). Balancing learning and

overﬁtting in genetic programming with interleaved

sampling of training data. In European Conference

on Genetic Programming, pages 73–84. Springer.

Gupt, K. K., Kshirsagar, M., Rosenbauer, L., Sullivan, J. P.,

Dias, D. M., and Ryan, C. (2022a). Predive: pre-

serving diversity in test cases for evolving digital cir-

cuits using grammatical evolution. In Proceedings of

the Genetic and Evolutionary Computation Confer-

ence Companion, pages 719–722.

Gupt, K. K., Raja, M. A., Murphy, A., Youssef, A., and

Ryan, C. (2022b). GELAB – the cutting edge of gram-

matical evolution. IEEE Access, 10:38694–38708.

Helmuth, T., Spector, L., and Matheson, J. (2014). Solv-

ing uncompromising problems with lexicase selec-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

204

tion. IEEE Transactions on Evolutionary Computa-

tion, 19(5):630–643.

Huang, C., Li, Y., and Yao, X. (2019). A survey of

automatic parameter tuning methods for metaheuris-

tics. IEEE transactions on evolutionary computation,

24(2):201–216.

Jin, Y. (2005). A comprehensive survey of ﬁtness approxi-

mation in evolutionary computation. Soft computing,

9(1):3–12.

Kajdanowicz, T., Plamowski, S., and Kazienko, P. (2011).

Training set selection using entropy based distance. In

2011 IEEE Jordan Conference on Applied Electrical

Engineering and Computing Technologies (AEECT),

pages 1–5. IEEE.

Kordos, M. and Blachnik, M. (2012). Instance selection

with neural networks for regression problems. In In-

ternational Conference on Artiﬁcial Neural Networks,

pages 263–270. Springer.

Kordos, M. and Łapa, K. (2018). Multi-objective evolution-

ary instance selection for regression tasks. Entropy,

20(10):746.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge, MA, USA.

Kshirsagar, M., Gupt, K. K., Vaidya, G., Ryan, C., Sullivan,

J. P., and Kshirsagar, V. (2022). Insights into incor-

porating trustworthiness and ethics in ai systems with

explainable ai. International Journal of Natural Com-

puting Research (IJNCR), 11(1):1–23.

La Cava, W., Danai, K., Spector, L., Fleming, P., Wright,

A., and Lackner, M. (2016a). Automatic identiﬁcation

of wind turbine models using evolutionary multiobjec-

tive optimization. Renewable Energy, 87:892–902.

La Cava, W., Spector, L., and Danai, K. (2016b). Epsilon-

lexicase selection for regression. In Proceedings of

the Genetic and Evolutionary Computation Confer-

ence 2016, pages 741–748.

Lobo, F. G. and Lima, C. F. (2007). Adaptive population

sizing schemes in genetic algorithms. Parameter set-

ting in evolutionary algorithms, 54:185–204.

Murphy, A., Youssef, A., Gupt, K. K., Raja, M. A., and

Ryan, C. (2021). Time is on the side of grammatical

evolution. In 2021 International Conference on Com-

puter Communication and Informatics (ICCCI), pages

1–7.

Nicolau, M. and Slattery, D. (2006). libGE. for version

0.27alpha1, 14 September 2006.

Olvera-L

opez, J. A., Carrasco-Ochoa, J. A., Mart

ınez-

Trinidad, J., and Kittler, J. (2010). A review of in-

stance selection methods. Artiﬁcial Intelligence Re-

view, 34(2):133–143.

O’Neill, M., Nicolau, M., and Agapitos, A. (2014). Exper-

iments in program synthesis with grammatical evo-

lution: A focus on integer sorting. In 2014 IEEE

Congress on Evolutionary Computation (CEC), pages

1504–1511. IEEE.

Ryan, C., Collins, J. J., and Neill, M. O. (1998). Gram-

matical evolution: Evolving programs for an arbitrary

language. In European Conference on Genetic Pro-

gramming, pages 83–96.

Ryan., C., Kshirsagar., M., Gupt., K. K., Rosenbauer.,

L., and Sullivan., J. (2021). Hierarchical Cluster-

ing Driven Test Case Selection in Digital Circuits.

In Proceedings of the 16th International Conference

on Software Technologies - ICSOFT, pages 589–596.

SciTePress.

Ryan, C., Tetteh, M. K., and Dias, D. M. (2020). Be-

havioural modelling of digital circuits in system ver-

ilog using grammatical evolution. In IJCCI, pages 28–

39.

Schmidt, M. D. and Lipson, H. (2007). Coevolving ﬁtness

models for accelerating evolution and reducing evalu-

ations. In Genetic Programming Theory and Practice

IV, pages 113–130. Springer.

Slowik, A. and Kwasnicka, H. (2020). Evolutionary al-

gorithms and their applications to engineering prob-

lems. Neural Computing and Applications, 32:12363–

12379.

Son, S.-H. and Kim, J.-Y. (2006). Data reduction for

instance-based learning using entropy-based parti-

tioning. In International Conference on Computa-

tional Science and Its Applications, pages 590–599.

Springer.

Streichert, F., Ulmer, H., and Zell, A. (2005). Parallelization

of multi-objective evolutionary algorithms using clus-

tering algorithms. In Evolutionary Multi-Criterion

Optimization: Third International Conference, EMO

2005, Guanajuato, Mexico, March 9-11, 2005. Pro-

ceedings 3, pages 92–107. Springer.

Traiola, M., Virazel, A., Girard, P., Barbareschi, M., and

Bosio, A. (2018). Testing approximate digital cir-

cuits: Challenges and opportunities. In 2018 IEEE

19th Latin-American Test Symposium (LATS), pages

1–6. IEEE.

Youssef, A., Gupt, K. K., Raja, M. A., Murphy, A., and

Ryan, C. (2021). Evolutionary computing based anal-

ysis of diversity in grammatical evolution. In 2021 In-

ternational Conference on Artiﬁcial Intelligence and

Smart Systems (ICAIS), pages 1688–1693.

Zhang, H. and Zhou, A. (2021). Rl-gep: symbolic regres-

sion via gene expression programming and reinforce-

ment learning. In 2021 International Joint Conference

on Neural Networks (IJCNN), pages 1–8. IEEE.

Adaptive Case Selection for Symbolic Regression in Grammatical Evolution

205