MOEA/D with Adaptive Mutation Operator Based on Walsh

Decomposition: Application to Nuclear Reactor Control Optimization

Baptiste Gasse

1,2

, S

ebastien Verel

and Jean-Michel Do

Universit

e Paris-Saclay, 91190 Gif-sur-Yvette, France

CEA, Service d’

Etudes des R

eacteurs et de Math

ematiques Appliqu

ees, 91191 Gif-sur-Yvette, France

Univ. Littoral C

ote d’Opale, UR 4491, LISIC, Laboratoire d’Informatique Signal et Image de la C

ote d’Opale,

Keywords:

Applied Computing Methodologies, Bi-Objective Optimization, Surrogate Model/ﬁtness Approximation,

Nuclear Reactor Physics.

Abstract:

France has a ﬂeet of nuclear reactors that makes up a signiﬁcant proportion of the electricity generation mix.

This over-representation of nuclear power compared with other energy sources leads reactors to operate in load

following mode in order to balance supply and demand on the electricity grid. The increasing penetration of

intermittent energies in the mix and the desire not to renew the entire current nuclear ﬂeet bring active research

into optimising the control of reactors operating in load following mode to allow them greater ﬂexibility. In

this study, we propose to solve a new bi-objective unit commitment problem using an MOEA/D algorithm

equipped with an adaptive mutation operator based on a Walsh surrogate model of a black-box function with a

high computation cost. The method consists of taking advantage of the linear effects associated with the prob-

lem variables thanks to the Walsh coefﬁcients to regularly update the mutation rate of the variation operator

and explore the problem’s search space more judiciously. We show that this method enables to penalize some

variables by decreasing their mutation probability without affecting the global performance of the search for

Pareto-optimal solutions, which makes it similar to an adaptive in-line ﬁtness landscape analysis.

1 INTRODUCTION

1.1 Context and Motivations

In France, the strategy adopted in terms of energy

transition is leading to a reﬂection on a change of

the national electricity production mix to achieve car-

bon neutrality by 2050. In 2022, 62.7% of elec-

tricity production was provided by nuclear reactors

in metropolitan France, 11.1% by hydroelectricity

sources, 12.7% by wind and solar power, and 13.5%

by fossil-ﬁred power stations, the vast majority of

which are gas-ﬁred. While the energy produced by the

ﬂeet of nuclear reactors is controllable, i.e. capable

of adapting their power output to ensure the supply-

demand balance of the electricity network, wind and

solar energy sources are intermittent since weather

conditions affect their load factor. This technological

difference coupled with the fact that the merit order

curve of the French electricity market gives consump-

tion priority to intermittent resources raises a growing

need for manoeuvrability for current nuclear reactors.

Indeed, research has shown that a high penetration of

intermittent energies in the electricity production mix

decorrelates the daily nuclear production proﬁle from

real electricity demand, implies reduced power varia-

tion times and, depending on the number of reactors

in operation in the coming years, decreases the nu-

clear ﬂeet’s load factor (Denholm and Hand, 2011;

Cany et al., 2018). Numerous works have studied the

issue from the point of view of economic constraints,

leading to unit commitment type optimization calcu-

lations in electricity mix scenarios with a high pene-

tration of intermittent energies without relying on fos-

sil plants (Xu et al., 2011; Jenkins et al., 2018; Ju

et al., 2019), but also with technical feasibility criteria

since power variations in a pressurized water reactor

(PWR) induce operating constraints linked to safety

rules. This article introduces a work that is in line

with this second approach.

The optimization problem at stake in this study

requires the use of a black-box function with a high

computation time, as around 45 minutes are needed

for the calculation of a single point in the objective

Gasse, B., Verel, S. and Do, J.

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization.

DOI: 10.5220/0012177200003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 75-85

ISBN: 978-989-758-674-3; ISSN: 2184-3236

space. In a context of limited computing resources,

this time constraint implies that the number of evalua-

tions can’t be too high even though the main goal is to

compare optimization methods with each other while

guaranteeing sufﬁcient statistics to interpret the re-

sults. The use of best direction search assistance in the

decomposition of the search space for the MOEA/D

algorithm using a surrogate model of the ﬁtness func-

tion has led to a slight gain in performance (Drouet

et al., 2020b), but the use of an adaptive mutation op-

erator for a reactor controlling simulator hasn’t been

tested yet. In this study, we propose a new adaptive

method based on a Walsh surrogate model of the ﬁt-

ness function to adapt regularly the mutation operator

of MOEA/D.

The paper is organised as follows. Firstly section

2 introduces related work in the ﬁelds of MOEA/D

adaptive methods, use of Walsh surrogate models for

optimization techniques and nuclear reactor optimiza-

tions for load following control mode. Section 3 is

reserved both for a review of nuclear reactor physics

notions useful for the understanding of PWR control,

and the deﬁnition of the optimization problem ad-

dressed in this study. Section 4 describes the method-

ology behind the adaptive bi-objective evolutionary

optimization algorithm using Walsh surrogate model

to update the mutation operator regularly. Finally,

section 5 describes the experimental setup and some

discussions of the results obtained with our method.

2 RELATED WORKS

Adaptive Evolutionary Algorithms: in (Shim et al.,

2012) a general optimization study using three evolu-

tionary algorithms of different natures has been con-

ducted. Authors found that using the ratio of promis-

ing solutions obtained by each optimizer at a given

generation to select the proportion of distributed solu-

tions for each algorithm at the next generation results

in a signiﬁcant performance improvement compared

with non-adaptive techniques. Adaptive weight ad-

justment techniques for MOEA/D has been conducted

in (Qi et al., 2014) in the case of complex Pareto

front to prevent the penalization of some regions in

the objective space during the optimization. More re-

cently, optimization methods involving an adaptation

of the mutation operator in an evolutionary algorithm

has been carried out in (Cruz-Salinas and Perdomo,

2017; Prieto and G

omez, 2020), where decision trees

and decomposition-based approaches helps to adapt

dynamically the mutation rates of genetic operators.

This multi-objective hybrid adaptive algorithm has

shown better performance on benchmark functions in

its ability to ﬁnd a well-covered and well-distributed

set of points on the Pareto Front.

Black-box Optimization: in (Dadkhahi et al.,

2022), two novel Fourier representations as surrogate

model for problems involving the use of black-box

functions over categorical variables has shown good

performance when combined with a variety of search

algorithms. One of the Fourier representation devel-

oped in this study is made of an abridged one-hot

encoded Boolean expansion recalling previous work

published in (Verel et al., 2018; Lepr

etre et al., 2019;

Derbel et al., 2023) which developed Walsh polyno-

mials as surrogate models for pseudo-Boolean opti-

mization problems. These studies have shown Walsh

surrogate models are relevant for benchmark prob-

lems and should be considered to improve the per-

formance of optimization algorithm for combinatorial

problems.

Nuclear Reactor Control Optimization: previous

works (Muniglia et al., 2018; Drouet et al., 2020b), on

optimising the control of nuclear reactors have shown

the existence of optimized sets of technical parame-

ters in order to minimize the axial destabilization of

the power proﬁle within the reactor core (see sect. 3)

as well as the use of liquid efﬂuents in load follow-

ing mode. These optimizations were carried out for

a ﬁxed transient and by exploring different parame-

ters for the movement of the control rods which are

inserted into the core during the power reduction. In

our study, we propose to jointly optimize rod param-

eters with the best way of distributing a ﬂeet transient

involving two nuclear reactors.

3 NUCLEAR REACTOR PHYSICS

3.1 Description of a French PWR

Reactor

This optimization study is conducted on a ﬂeet of

two 1300 MW nuclear reactors typical of the units

involved in load following of the French power grid.

Apart from the heat production medium, a nuclear re-

actor does not differ much from a conventional ther-

mal power plant in terms of electricity production.

There are three circuits : ﬁrst, the primary circuit,

where water passes through the reactor’s core from

bottom to top and is heated by the ﬁssion reactions

of uranium 235 nuclei. Once it reaches the top of the

core, the primary water is redirected to a steam gener-

ator where its heat is exchanged with the water of the

secondary circuit, which vaporizes. The steam thus

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

produced is expanded in the turbines, where thermal

energy is converted into mechanical energy. The ro-

tation of the shaft of the successive turbines makes

an alternator to rotate, which converts kinetic energy

into electricity. The role of the last circuit, called

the cooling circuit, is to evacuate the residual heat

which could not be converted into mechanical energy

by virtue of the second principle of thermodynamics.

Figure 1: Typical load map for 1300 MW French PWR

(left) and zoom on a single assembly provided with black

rods (right).

The core is roughly comparable to a cylinder 4

meters high and 3 meters in diameter. It is composed

of 193 fuel assemblies and 62 reﬂector assemblies

(see ﬁg. 1, left). The fuel assemblies all have the

same geometric pattern : 264 fuel pins about 4 me-

ters long that contain uranium oxide pellets (UOX)

over their entire height, and 25 guide tubes (see ﬁg. 1,

right). These tubes enable neutron-absorbing rods to

slide vertically in order to regulate the neutron popu-

lation, and thus the ﬁssion chain reaction. These rods

are placed at strategic points in the core for the sake

of a ﬂatten radial ﬂux distribution during power varia-

tions. The reﬂector assemblies, shaded in gray on the

ﬁgure 1 (left) limit the leakage of neutrons out of the

core as well as the wear of the vessel which ages with

irradiation.

3.2 Rods

Concerning the rods, the rate of captured neutrons in-

creases as they inserts into the core. Transiently, the

number of neutrons decreases in the core and conse-

quently the ﬁssion rate, which implies a decrease in

the power produced. The opposite occurs when rods

are extracted from the core. Rods are divided into two

groups:

• on the one hand, power shimming group of rods

(PSG) that compensates the power defect during

load variations, which is the change in core re-

activity due to moderator and fuel neutron feed-

backs. Four groups of rods compose PSG (ﬁg.

1, left) : grey rods (G1 and G2) and black rods

(N1 and N2), which differ by their respective neu-

tron absorption capacity. During a load drop, PSG

groups of rods don’t plunge into the core simulta-

neously but with constant overlaps to prevent too

much axial power imbalance. Let r

(resp. r

)

be the overlap value between groups G1 and G2

(resp. G2 and N1) : G2 moves as soon as G1 has

reached an insertion step value of r

as well as N1

moves when G2 exceeds r

inserted steps. The

position of the PSG is slaved to the net electrical

power of the nuclear power plant ;

• on the other hand, temperature regulation group

of rods (TRG) aims at respecting the temperature

program set by the operating technical speciﬁca-

tions all along the load transient. NPP operator in-

serts (resp. extracts) the TRG as soon as core wa-

ter is hotter (resp. colder) than the setpoint with a

dead band of 0.8°C. The operator can move TRG

rods all along a ﬁxed manoeuvring band whose

width is given in steps by the parameter b, 27 steps

for a typical P4 1300 MW reactor (Grard, 2014).

3.3 Boron

Soluble boron is a neutron poison diluted in core’s

primary water. Contrary to the rods its concentra-

tion adjustment is much slower than a rod step move-

ment and its effect are homogeneous in the core. In

G mode load follow control, it is mainly used to com-

pensate reactivity variations occurring during the evo-

lution of xenon concentration in the core, which is a

strong neutron absorber with a delayed dynamic at the

time scale of a load drop. Moreover, xenon equilib-

rium of production (mostly due to iodine decay) and

consumption (by neutron capture) is highly tied to the

variation of neutron ﬂux in the core. Not only a power

drop diminishes neutron ﬂux absolutely, it also redis-

tributes core’s axial power proﬁle due to combined

effects of rods insertion and an axially evolutionary

negative moderator temperature coefﬁcient. In case

of reactivity loss, the plant operator injects clear water

to dilute boron whereas he increases boron concentra-

tion in case of abnormal reactivity rise.

3.4 Control of Load Variations

3.4.1 Core Computer Simulator in

Load-Following Mode

G mode load control consists in the coordinated use

of both removable neutron absorbing rods and soluble

boron diluted in the water of the primary circuit. Basi-

cally, controlling a nuclear reactor consists in adjust-

ing the position of the rods and the boron concentra-

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization

tion to enable load variations while respecting safety

margins at all times. Much effort has been put into

simulating the operation of a nuclear reactor. Strate-

gies aiming at modeling a human behavior regarding

the interpretation of the observables of the core and

the decisions which result from it have been devel-

oped (Muniglia et al., 2016; Drouet et al., 2020a).

Similarly, PID controllers

performs well to optimize

the current control mode and minimize the power os-

cillations mainly related to the axial transients of the

xenon (Zeng et al., 2020; Raﬁei et al., 2021; Mah-

fudin et al., 2022). In this study, we choose to opt for

a model close to the real case G mode and we search

for an optimization focusing on variables that do not

intrinsically affect the behavior of the dummy opera-

tor for a corrective action using rods or boron. What-

ever the model of a ﬁctitious operator, safety rules im-

pose to guarantee the axial power stability of the core

during load following mode. The observable parame-

ter ∆I quantiﬁes it ; given the power produced in the

core’s upper half and lower half denoted P

and P

respectively, and P

rel

the relative power of the core :

∆I =

− P

+ P

rel

, given in % of core’s height. (1)

A plant operator must control the reactor during load

following so that ∆I remains within a margin of ±

5% of its value at its state before the power drop.

Maintaining a good axial power stability may lead the

operator to favor control of the neutron ﬂux by the

boron rather than by the rods, since they distort the

power proﬁle of the core more widely. However, re-

lying more extensively on boron adjustments in the

primary circuit means a rise in ﬂuid transfers leading

to the generation of more liquid waste one seeks to

minimize for technical, economic and environmental

concerns.

3.4.2 Optimization Problem Setting

Previous work has introduced solutions of better sets

of PSG overlaps and width of the TRG manoeuvring

band for a 6-6 hours transient (6 hours at 30% of nom-

inal power followed by 6 hours at full power) to guar-

antee a better stability against axial displacement of

the neutron ﬂux distribution as well as on the quantity

of liquid efﬂuents produced during the load transient

(Muniglia et al., 2018; Drouet et al., 2020a). Finding

the best set of operating levers whatever the ampli-

tude of load drops is a perspective of these studies.

PID controllers computes the corrective action by esti-

mating the (p)roportionnal, (i)ntegral and (d)erivative signal

error over time.

We introduce in this work the Nuclear Unit Commit-

ment Optimization Problem (NUCOP), which aims to

jointly ﬁnd the best distribution of a ﬂeet load tran-

sient to a group of two reactors while optimizing rods

parameters. Solving NUCOP would lead to judge the

better way of meeting grid’s needs with a given ﬂeet

of reactors while staying within safety rules and min-

imizing both objectives as it investigates two main is-

sues :

• an optimized way to involve both reactors to as-

sume the ﬂeet transient instead of letting a single

reactor doing a deep load drop (ﬁg. 2) ;

• the joint search of the best division of the ﬂeet

transient with the best set of PSG rods overlaps

and TRG manoeuvring band’s width adapted for

both reactors.

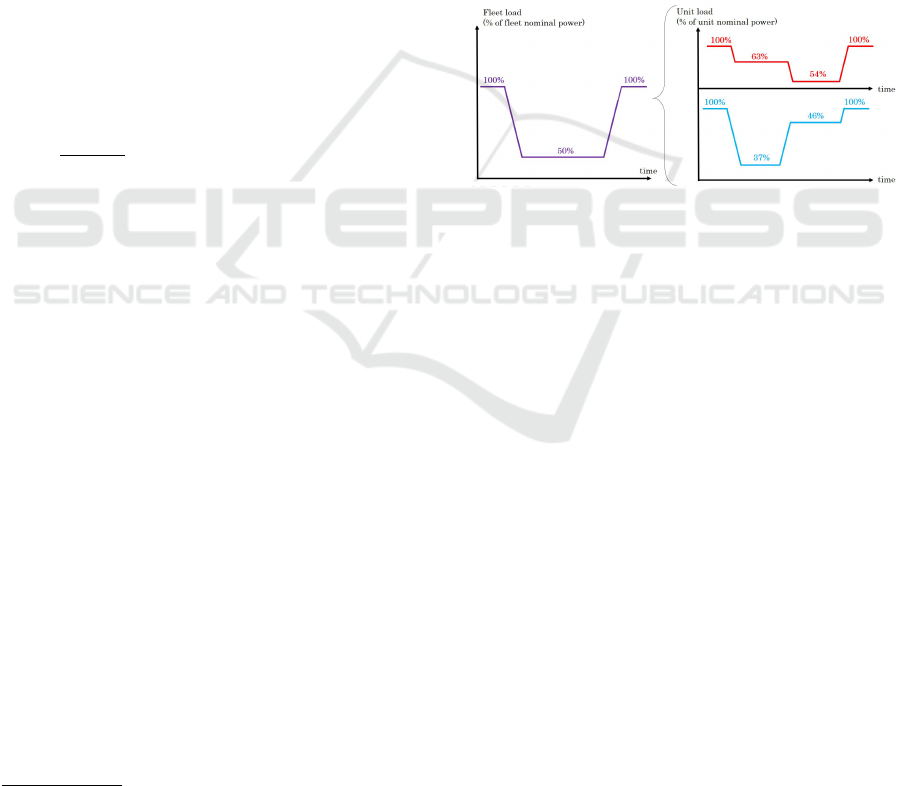
Figure 2: Example of a two-reactor distribution for the NU-

COP problem. Fleet transient on the left is divided into two

transients on the right. In this case, both reactors have the

same nominal power. Amplitudes are not to scale.

Search Space: NUCOP is a discrete and ex-

pensive bi-objective optimization problem with a 5-

dimensional search space of size ∼ 10

, conducted

on a ﬂeet composed of two French PWR reactors of

1300 MW each. First type of search space’s variables

are rods overlaps r

and r

as well as the width b

of the maneuvering band of TRG. These numerical

variables are counted into rod steps. Second type of

variables are categorical and identify the unit com-

mitment dispatch of the two-reactor ﬂeet. As shown

on ﬁgure 2, we enable each units to operate any load

drop as long as the whole ﬂeet drop reaches 50% of

ﬂeet’s nominal power. The ﬂeet drop is divided into

two time zones which leads to two variables of power

distribution d

and d

. For each d

we ﬁx 40 possible

possibilities for the power distribution. Search space

is summarized in table 1.

Fitness Space: Given the domain X =

{

,...,x

),x

∈ E

}

⊂ N

, the objective is to

ﬁnd all Pareto-optimal solutions x

∗

such as :

∗

= argmin

x∈X

f (x) (2)

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

Table 1: Search space sub-variables and their range. Brack-

ets [a,b] refers to the integer range

{

a,a + 1, ...,b

}

while

shorter notation [b] is for the

{

0,1,...,b

}

range.

Sub-variable Parameter Range

= [255]

b E

= [7,118]

= [39]

where f : X → R

is a black-box function computa-

tionally expensive to evaluate which returns a two ob-

jective values. Objective functions respectively stands

for the Euclidean distances in the 2D space of the gen-

erated liquid efﬂuents (V

), and the integral of ax-

ial power imbalance (∆I

,∆I

) during each transient

and for each reactor. The black-box ﬁtness function

is :

f : X → R

x 7→ z =



(x)







∆I

+∆I





(3)

4 OPTIMIZATION USING

ADAPTIVE MOEA/D WITH

WALSH SURROGATE

The NUCOP problem is a bi-objective black-box op-

timization problem. This kind of problem can be

solved with a variety of metaheuristic methods whose

goal is to ﬁnd the set of non-dominated solutions of

the problem. For a bi-objective minimization prob-

lem, a solution x is dominated by x

′

iff f

′

) ≤ f

(x)

and f

′

) ≤ f

(x), and if there is an i ∈ {1,2} such

that f

′

) < f

(x). A solution x

⋆

is non-dominated if

there is no other solution x such that x

⋆

is dominated

by x. The set of non-dominated solutions is called the

Pareto set, the image of this set by f constitutes the

Pareto front of the objective space. The metaheuristic

used for solving NUCOP is a variant of the MOEA/D

algorithm (Zhang and Li, 2007) which is an evolu-

tionary algorithm based on the decomposition of the

objective space into several directions.

4.1 MOEA/D for Solving NUCOP

Let Λ =

{

,...,λ

}

be the set of directions splitting

the objective space. MOEA/D consists in dividing the

bi-objective problem into Λ single objective subprob-

lems communicating with each other to enable a co-

operatively solving of the initial problem. Each sub-

problem aims at minimizing f along its respective as-

signed direction. The single objective function asso-

ciated to each direction λ

is the Chebyshev function

deﬁned as

g(z | λ

) = max

i∈{1,2}



q,i

ref

− z



(4)

where z

ref

is the reference point set to the minimal

values of objectives. We save in a buffer ﬁle each best

solutions found for each subproblem (namely for each

direction λ

). Each iteration of the algorithm (see Al-

gorithm 1) gives the ﬁtness values of a candidate so-

lution x in a direction λ

; we compute g(x | λ

) and

compare the result to solutions saved in the buffer ﬁle

whose directions are in the set T

(T ), which refers to

the T neighbouring directions of λ

. We replace any

solution of the buffer ﬁle whose corresponding direc-

tion is in T

(T ) by x iff x dominates it.

Algorithm 1: MOEA/D : master process.

1 for p ← 1 to N

proc

2 x

← Init. with latin hypercube sampler ;

3 λ

← Attribute a direction among Λ ;

4 Send x

to worker process p

5 end

6 z

ref

←Init. reference point ;

7 x

⋆

←Init. best x

for each direction λ

;

8 z

⋆

←Init. best f (x

) for each direction λ

;

9 S ←

0 ; // Set of evaluated solutions

10 while time left do

11 Receive (x

) from worker process p

from direction λ

;

12 S ← S ∪ {(x

)} ;

13 if z

dominates z

ref

then

14 z

ref

← z

; // update reference

15 end

16 for all directions λ

∈ T

(T ) do

17 if g(z

|λ

) ≤ g(z

⋆

|λ

) then

18 x

⋆

← x

;

19 z

⋆

← z

; // update best

known solutions buffer

file

20 end

21 end

22 x

← Mutate x

⋆

;

23 Send x

to worker process p ;

24 end

In addition, our MOEA/D algorithm beneﬁts from

a massive parallel architecture and follows a master-

workers procedure (algorithms 1 and 2). The com-

putation time to evaluate a candidate solution of NU-

COP is expensive (on average 45 minutes). Moreover,

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization

this computation time has a large variance according

to the rod parameters and ﬂeet’s transient distribution.

Because of limited computing resources, the master-

workers algorithm is asynchronous to avoid wasting

time between the evaluation of the ﬁrst and the last

worker associated to each direction.

Algorithm 2: MOEA/D: worker process.

1 Receive x

from master process ;

2 Compute z

= f (x

) ;

3 Send (x

) to master process ;

4.2 Walsh Surrogate Model

One way to face expensive ﬁtness evaluation is to use

a surrogate model in order to extract more informa-

tion from the costly black-box ﬁtness function, and to

better guide the search. Popular methods of assisted

optimization with surrogate models try to substitute

the original time-consuming black-box function with

a cheap approximation of it : the best solution given

by the surrogate function is then computed as the

next candidate through the real problem function. In

the context of discrete optimization, Walsh functions

have already been used as surrogate model for solv-

ing pseudo-boolean optimization problems (Lepr

etre

et al., 2019; Verel et al., 2018).

4.2.1 Walsh Functions

Notations : we reuse range notations described in ta-

ble 1. Also, ♯E refers to the cardinality of a set E.

The set of Walsh functions (W

)

k∈

[

−1

]

is a nor-

mal and orthogonal basis of the space of pseudo-

Boolean functions F

= { f :

{

0,1

}

→ R} with d be-

ing an integer (Walsh, 1923; Bethke, 1980),(Lepr

etre

et al., 2019; Verel et al., 2018). Expansions based

on Walsh functions are sometime called Fourier ex-

pansions as they have similar properties (O’Donnell,

2021). By virtue of basis properties, any f ∈ F

can

be written as a unique linear combination of Walsh

functions:

∀x ∈ {0,1}

, f (x) =

−1

∑

k=0

(x) (5)

where ω

∈ R is the coefﬁcient of the k-th Walsh func-

tion W

deﬁned by:

(x) = (−1)

∑

d−1

i=0

(6)

where k

∈ {0, 1} is the i

binary digit of the integer

k. As classical Fourier series for an analog signal, and

in order to reduce the number of terms in the series,

it is possible to truncate the Walsh expansion of f to

get a polynomial approximation function

f . We call

order of the k-th Walsh function the number of 1 in

the binary representation of k. The Walsh function of

order 0 is the constant term, Walsh functions of order

1 are linear functions as they only depend on 1 binary

variable, Walsh functions of order 2 are quadratic, and

so on. This leads to the following rearrangement of

the series:

f (x) =

−1

∑

k=0

(x) =

∑

n=0

∑

k with

ord(W

)=n

(x). (7)

It should be noted that Walsh’s surrogate model can

be viewed as a linear regression in a speciﬁc Hilber-

tian space.

4.2.2 One-Hot Encoded Boolean Representation

of the Search Space

We consider a one-hot encoded Boolean representa-

tion of any variable of x = (x

) using an

uniform partitioning of each range E

corresponding

to the domain of the variable x

(see tab. 1). We de-

ﬁne for each variable x

a binary digit sequence of size

♯E

− 1 (see eq. 8) such that at most one digit is equal

to 1. More formally, let be (E

i j

) an uniform partition

of E

into ♯E

sets of equal cardinality : E

♯E

j=0

i j

and E

i j

∩E

i j

0 for any j

̸= j

. The proposed one-

hot encoded strategy follows two rules (eq. 9). Firstly

the unique digit sequence with no 1 corresponds to

’s ﬁrst element

, secondly other elements are linked

to sequences that have exactly one 1 ; its position is

given by the value x

: if x

∈ E

i j

for j ∈ [1, ♯E

], then

the digit 1 is positioned at index j − 1 in the boolean

sequence. Other digits equal to 0.

: E

→

{

0,1

}

♯E

7→



i 0

,...,x

i(♯E

−1)



(8)

∀ j ∈ [♯E

− 1],x

i j

(

1 if x

∈ E

i( j+1)

0 otherwise.

(9)

The one-hot encoded Boolean representation

of the whole variable x = (x

,...,x

) results

from the concatenation of one-hot encoded

sequences corresponding to each variable x

h(x) = (h

),h

),...,h

)).

Example : let x = (185, 175, 27, 4, 36) a ran-

dom element of X . If ♯E

= 4 for all i then

All sets E

are sorted in ascending order so that con-

sidering the ﬁrst element of E

makes sense.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

for instance the uniform partitioning of r

pa-

rameter domain is E

= [255] = [63] ∪ [64,127] ∪

[128,191] ∪ [192, 255], which means that h(x

) =

(0010). Following this schemata with other subvari-

ables the complete Boolean sequence of x would be

(0010 0010 1000 1000 0001).

Such a one-hot encoded representation is common

with previous work proposed recently in (Dadkhahi

et al., 2022), used for Boolean Fourier representation

of any categorical variable. It is very practical as we

can remove many terms in the expression of f (x) (eq.

7) ; indeed, for any sub-variable x

, Walsh terms or

order n ≥ 2 involving more than two elements of the

same family (x

i j

) are inconsistent. Considering that

NUCOP is a d = 5 dimension problem (tab. 1) :

f (x)=ω

∑

n=1

∑

I∈



[1,d]



∑

J∈

♯I

c=1

[

♯E

−1

]

I,J

(x) (10)

where



[1,d]



is the set of subsets of cardinal n drawn

from the set [1, d] and

♯I

c=1

[♯E

− 1] is the carte-

sian product of all integer sets [♯E

− 1] with I

tak-

ing values in [1, d] according to the sum term explor-

ing each n-subset previously deﬁned. Finally, Walsh

functions W

I ,J

are given by

I ,J

(x) =

∏

(i, j)=(I

)

with c∈J1,#I K

(−1)

i j

. (11)

As mentioned in equation (7) we can sort the terms of

the series (10) according to their contribution in lin-

ear or interaction effects within the linear regression

equation that deﬁnes Walsh surrogate model. First-

order terms of (10) are all those whose Walsh function

I ,J

(x) involves a single x

i j

; second-order terms are

terms containing two terms in the product (11) ; and

so forth. We can write the truncated expansion

f (x)

of f (x) at order n = 2 by the Walsh decomposition

given in (10) :

f (x) =

∑

i∈[1,5]

∑

j∈[♯E

−1]

i j

(−1)

i j

∑

(i,i

′

)∈



J1, 5K



∑

( j, j

′

)∈[♯E

−1]×

[

♯E

′

−1

]

i j,i

′

(−1)

i j

′

(12)

Example : consider a Walsh decomposition model

based on x

and x

sub-variables of the NUCOP

search space. Let’s partition E

and E

with cardi-

nality ♯E

= 2 and ♯E

= 3 respectively. Approxima-

tion (12) of f (x) gives :

f (x)=

4,0

(−1)

4,0

4,1

(−1)

4,1

5,0

(−1)

5,0

5,1

(−1)

5,1

5,2

(−1)

5,2

4,0,5,0

(−1)

4,0

5,0

4,0,5,1

(−1)

4,0

5,1

4,0,5,2

(−1)

4,0

5,2

4,1,5,0

(−1)

4,1

5,0

4,1,5,1

(−1)

4,1

5,1

4,1,5,2

(−1)

4,1

5,2

. (13)

Following semantics proposed in (Dadkhahi et al.,

2022), we refer to the tuple (x

i j

)

j∈[♯E

−1]

as the de-

scendant of the parent variable x

of the solution x ∈

X . The completeness and uniqueness of the decom-

position (10) is justiﬁed by the fact that each W

I ,J

(x)

contains exactly one x

i j

descending from the parent

variable x

. The proof is given in Appendix of (Dad-

khahi et al., 2022).

4.3 Walsh Adaptive Method

As MOEA/D is an evolutionary algorithm, the mu-

tation step involves the use of a selection and a mu-

tation operator. Given a evaluated solution x and a

mutation rate vector P = (P

,...,P

)

, the ﬁrst one

performs a Bernoulli test with an expectancy value

of P

on each variable x

of x, so that sub-variable x

is mutated into ˜x

iff the test succeeds. Usually, P is

ﬁxed such as each sub-variable has the same prob-

ability to mutate, which means that each P

equals

to 1/d = 0.2. The second one is based on a vector

R = (R

,...,R

)

such that all mutated variables ˜x

are

chosen thanks to an uniform distribution in the real in-

terval [x

− R

⌊

− lb

⌋

+ R

⌊

− lb

⌋

], with ub

and lb

respectively being the upper bound and lower

bound values of x

Our adaptive method is based on an evolutionary

selection operator where vector P is regularly updated

during a run, following the evolution of the Walsh sur-

rogate model coefﬁcients. In this study, P updates

occur once all worker processors deployed for a run

of NUCOP resolution have returned a solution to the

master processor. The adaptive procedure starts by

computing the current Pareto optimal solutions that

will be used as the sample base for training the surro-

gate model. Then we use python library Scikit-Learn

(Pedregosa et al., 2011) to build a surrogate for each

one of the objectives under study, which consists in a

linear regression ﬁt using Lasso interpolator. As men-

tioned in (Lepr

etre et al., 2019) the use of Lasso is

motivated by the high number of Walsh coefﬁcients

in the decomposition, as it relies on the choice of

the partitioning mesh of each E

set. For instance, if

eight sets make a partition of the interval E

= [255],

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization

there will be a family (

1, j

)

j∈[7]

of eight coefﬁcients

associated with parameter r

in the Walsh surrogate

model. After ﬁtting the surrogate we get access to

all Walsh coefﬁcients that can be separated accord-

ing to the sub-variable they correspond with : taking

the L1-norm on coefﬁcients linked to the same x

, we

perform a normalization by the L1-norm of all Walsh

surrogate coefﬁcients (except for ω

which a constant

term). This reasoning leads to the calculation of two

new selection vectors

and

respectively for ob-

jective f

and f

, that involves a learning rate coefﬁ-

cients denoted l. For instance, in the case of objective



(1 − l)P

+ l

,∀i ∈ [4]



. (14)

The learning rate parameter inﬂuence the importance

given to the modiﬁcation of P

during iterations. In

this study, we have taken l = 0.2 for all runs because

of limited computational resources, but with more

computational budget it would possible to carry out

a parametric study on this parameter in order to as-

sess its effects on the study proposed here. We use

and

to update regularly the mutation rate vec-

tor of MOEA/D such as it is given by :

P =



(1 − l)P

+ l





,∀i ∈ [4]



. (15)

The underlying idea is to progressively favor the se-

lection of variables whose mutation is expected to

have more pronounced effects on the results given

by the black-box function. In short, we take advan-

tage of the interpretation of the coefﬁcients which im-

pact more the objective values in a linear regression

to adapt the selection operator of MOEA/D (see alg.

3).

Algorithm 3: Adaptive mutation operator.

1 Receive x

⋆

;

2 if n

mut

modulo M = 0 then

3 Fit Walsh surrogate model for each

objective of NUCOP with all known

solution ;

4 Update mutation rate P following

equation (15) ;

5 end

6 x

′

← Mutate x

⋆

obtained with ﬁxed

mutation range vector R and new P ;

7 n

mut

← n

mut

+ 1;

5 EXPERIMENTAL ANALYSIS

5.1 Experimental Setup

The experimental setup is as follows. We use 600

computational processors, distributed over 200 direc-

tions decomposing the objective space (3 per direc-

tion). The neighborhood of a direction is equal to the

total number of directions in the problem to enable

a total communication between directions following

recommendations of previous works working on the

optimization of rod parameters (Muniglia et al., 2018;

Drouet et al., 2020b). We use Chebyshev’s scalariza-

tion function to evaluate the dominance of one solu-

tion over another in the objective space. For each raw

ﬁt from the controlling simulator, we center-reduce

the ﬁt according to a normal distribution N (µ, σ)

whose parameters are derived from a totally random

sampling of the search space upstream of the NUCOP

optimization study. The proposed adaptive mutation

operator method is denoted AMOW for adaptive mu-

tation operator based on Walsh decomposition, and it

compared the baseline method FMO for ﬁxed muta-

tion operator. The AMOW method updates the mu-

tation operator every M = 600 evaluated solutions.

We train a Walsh surrogate model by evaluating cur-

rent non-dominated solutions that are taken to build a

training dataset with the corresponding ﬁtness values

as training targets. Each sample in the dataset is then

expressed as a feature of ﬁve features (r

, r

, b, d

and

) and two targets ( f

and f

). The construction of

the Walsh predictors made of all W

I ,J

leads to a non-

orthogonal and non-normal basis : as shown on ﬁgure

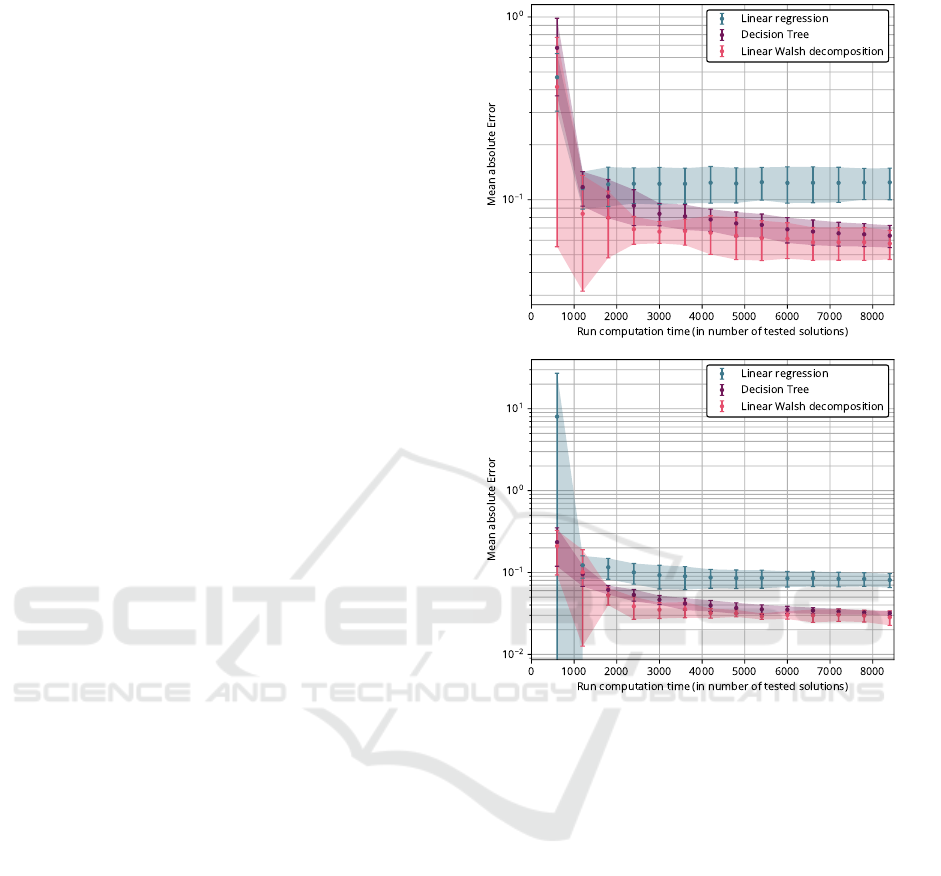
3 the transformation of the base vectors through the

Gram Schmidt algorithm slightly decreases the mean

absolute error observed on both objectives ; thus, re-

sults presented in the rest of this study were obtained

with the orthonormal basis of Walsh functions. It

should be noted that Walsh surrogate has similar per-

formance as decision tree method ; in any case such

a method is rejected as it does not give access to the

individual contribution of each research space’s sub-

variable.

We perform 10 runs that computes 9000 solutions

each. The performance assessment protocol is such

that we compare two by two runs that begin with

the same initial population given by an latin hyper-

cube sampling of the search space (see table 1 for

dimensions). In other words, there are 10 different

runs for each method FMO and method AMOW, and

we use only ten different population samples to be-

gin the each run. Performance indicators are given as

the mean value observed on all runs. Concerning the

NUCOP problem, we study a ﬂeet of two reactors :

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

one reactor has got fresh fuel whereas the other one

is at the middle of its fuel campaign. Calculations are

performed at the TGCC on Intel Skylake AVX-512

2.7GHz CPU units (GENCI, 2023).

5.2 Performance Analysis

Figure 4 shows the evolution of the coordinates of the

mutation rate vector P during the run. The optimiza-

tion process progressively reduces the probability that

b and r

sub-variables will be mutated for the next 600

iterations, thus favoring mutation of the other sub-

variables. In other words, we take advantage of a

quantiﬁcation of the linear effect induced by variation

of b on objectives thanks to Walsh’s model that priv-

ilege mutation of the other parameters with the hope

of exploring the ﬁtness landscape more effectively. In

the ﬁeld of nuclear reactor physics for power maneu-

vering, this result shows that there is less expected im-

provement in searching for the best width of the ma-

neuvering strip of TRG rods than in changing other

variables like rod overlaps and ﬂeet transient’s distri-

bution. The physical interpretation of these interac-

tions belongs to the ﬁeld of reactor physics that are

beyond the scope of this current study.

One notable result is that decreasing the chances

of mutating variable b does not seem to have much

impact on the diversity of solutions in the compromise

zone between the two objectives (ﬁgure 6). We be-

lieve the use of AMOW makes it possible to progres-

sively remove a variable from the NUCOP problem if

it turns out that its mutations are not likely to cause

a large variation of the black-box function, without

leading to a great loss of potential non-dominated so-

lutions. In the formalism of linear regression, this

amounts to discarding the terms with the weakest

main effects. Figure 6 also shows that best solutions

minimizing absolutely f

or f

were done with the

AMOW method. However these results must be qual-

iﬁed to the extent that most of the metrics usually used

for the comparison of optimization method seems to

favour the FMO non-adaptive method (hypervolume

metric is presented on ﬁgure 5). However, a Welsch t-

test made on the hypervolume metric gives a p-value

of 0.2606 meaning that we cannot statistically state

that either method leads to better performance on the

hypervolume metric. The use of AMOW seems more

relevant to get a better comprehension of the physics

of the ﬁtness function by reducing the search space

than for hoping to achieve a better approximation of

the optimal Pareto front.

Figure 3: Mean absolute error on f

(top) and f

(bottom)

obtained from different surrogate methods during a run.

The training dataset is updated each 600 tested solutions.

Points stand for mean values over all runs whereas shaded

areas stand for the 1σ conﬁdence interval (note that y-axis

scale is logarithmic so mean values are not centered in error

bars).

6 CONCLUSION AND

PERSPECTIVES

Modeling a nuclear reactor is complex and simulating

load following operations is costly in terms of com-

puting time. The joint optimization of the control rod

overlap settings, TRG maneuvering bandwidth and

the distribution of a ﬂeet transient over a group of

two reactors is an innovative problem whose resolu-

tion leads to new considerations on the possible gains

in nuclear power maneuverability. In this context, we

have implemented within a MOEA/D algorithm an

adaptive mutation rate based on a decomposition of

the ﬁtness function in the basis of Walsh functions.

This method favours the mutation of variables most

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization

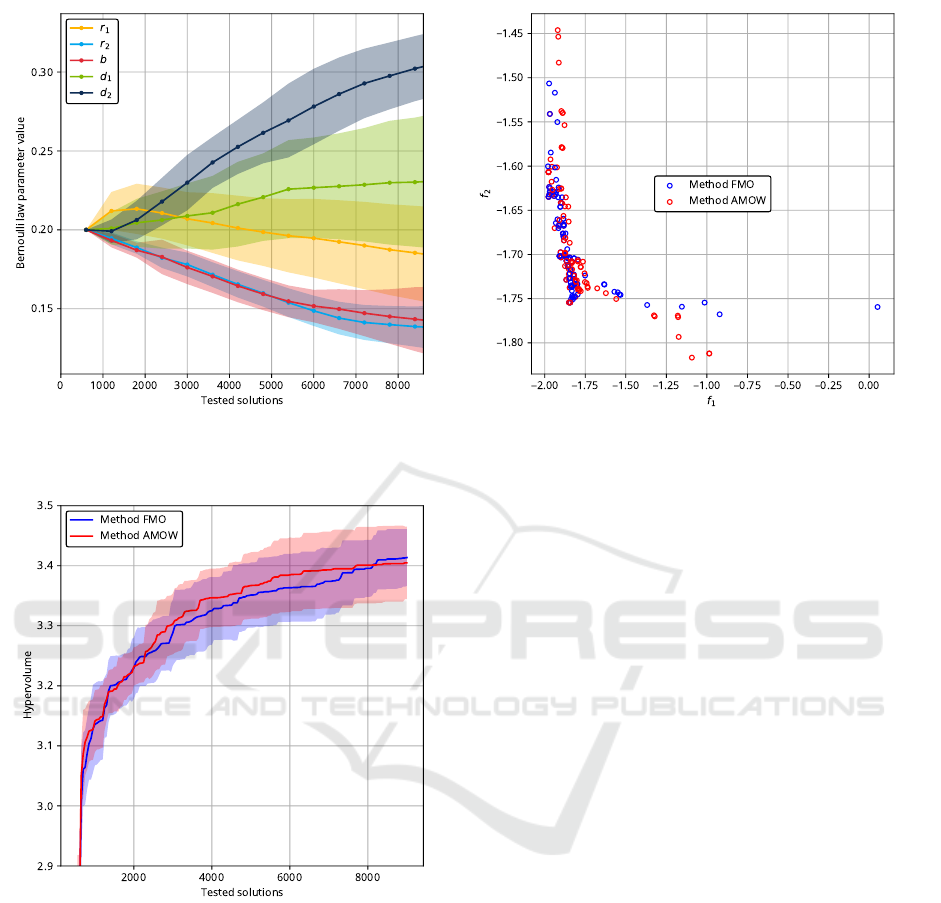
Figure 4: Evolution of mutation rate vector’s coordinates

during the run, using method AMOW. Interpretations of

points and shaded areas is the same as in the ﬁgure 3.

Figure 5: Evolution of hypervolume referenced to the ori-

gin of the objective space for method FMO (ﬁxed mutation

operator) and AMOW (adaptive mutation operator based on

Walsh decomposition). Hypervolume was computed thanks

to the library (L

opez-Ib

nez et al., 2010). Interpretations of

points and shaded areas is the same as in the ﬁgure 3.

likely to lead to greater goal variation at the expense

of those contributing least to the problem, as if a ﬁt-

ness landscape analysis is made in-line instead of be-

ing done before the optimization process. Naturally,

the adaptive method using the surrogate model is not

limited to load following operation in nuclear energy

context. Future works will test the proposed adaptive

method to others discrete expensive problems. Future

research works may involve developing an adaptive

Figure 6: Pareto fronts for all runs (method FMO in blue,

method AMOW in red).

mutation operator up to the second order of the Walsh

series decomposition, to take advantage of knowledge

of the interactions between variables in the problem,

and moreover mutation operators which mutate sev-

eral variables could also be designed in order to in-

crease the convergence rate of the optimization algo-

rithms for larger dimension problems.

ACKNOWLEDGEMENTS

Authors would like to thank the GENCI project for

access to the CCRT’s computing resources, which

were used during allocation campaign A0131013043

(GENCI, 2023).

REFERENCES

Bethke, A. D. (1980). Genetic algorithms as function opti-

mizers. PhD thesis, University of Michigan.

Cany, C., Mansilla, C., Mathonni

ere, G., and da Costa, P.

(2018). Nuclear contribution to the penetration of

variable renewable energy sources in a french decar-

bonised power mix. Energy, 150:544–555.

Cruz-Salinas, A. F. and Perdomo, J. G. (2017). Self-

adaptation of genetic operators through genetic pro-

gramming techniques. In Proceedings of the Genetic

and Evolutionary Computation Conference. ACM.

Dadkhahi, H., Rios, J., Shanmugam, K., and Das, P. (2022).

Fourier representations for black-box optimization

over categorical variables. Proceedings of the AAAI

Conference on Artiﬁcial Intelligence, 36(9):10156–

10165.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

Denholm, P. and Hand, M. (2011). Grid ﬂexibility and stor-

age required to achieve very high penetration of vari-

able renewable electricity. Energy Policy, 39(3):1817–

1830.

Derbel, B., Pruvost, G., Liefooghe, A., Verel, S., and

Zhang, Q. (2023). Walsh-based surrogate-assisted

multi-objective combinatorial optimization: A ﬁne-

grained analysis for pseudo-boolean functions. Ap-

plied Soft Computing, 136:110061.

Drouet, V., Do, J.-M., and Verel, S. (2020a). Optimization

of load-follow operations of a 1300mw pressurized

water reactor using evolutionnary algorithms. In In-

ternational Conference on Physics of Reactors: Tran-

sition to a Scalable Nuclear Future (PHYSOR 2020),

volume 247, pages 1–8/11001.

Drouet, V., Verel, S., and Do, J.-M. (2020b). Surrogate-

assisted asynchronous multiobjective algorithm for

nuclear power plant operations. In Proceedings of the

2020 Genetic and Evolutionary Computation Confer-

ence, GECCO ’20, page 1073–1081, New York, NY,

USA. Association for Computing Machinery.

GENCI (2023). http://www.genci.fr/.

Grard, H. (2014). Physique, fonctionnement et s

uret

e des

REP : Le r

eacteur en production. EDP Sciences.

Jenkins, J., Zhou, Z., Ponciroli, R., Vilim, R., Ganda, F., de

Sisternes, F., and Botterud, A. (2018). The beneﬁts

of nuclear ﬂexibility in power system operations with

renewable energy. Applied Energy, 222:872–884.

Ju, Y., Wang, J., Ge, F., Lin, Y., Dong, M., Li, D., Shi,

K., and Zhang, H. (2019). Unit commitment accom-

modating large scale green power. Applied Sciences,

9(8).

Lepr

etre, F., Verel, S., Fonlupt, C., and Marion, V. (2019).

Walsh functions as surrogate model for pseudo-

boolean optimization problems. In The Genetic

and Evolutionary Computation Conference (GECCO

2019), Proceedings of the Genetic and Evolution-

ary Computation Conference, pages 303–311, Prague,

Czech Republic. ACM.

opez-Ib

nez, M., Paquete, L., and St

utzle, T. (2010).

Exploratory analysis of stochastic local search al-

gorithms in biobjective optimization. In Bartz-

Beielstein, T., Chiarandini, M., Paquete, L., and

Preuss, M., editors, Experimental Methods for the

Analysis of Optimization Algorithms, pages 209–222.

Springer, Berlin, Germany.

Mahfudin, I., Ardiyanto, I., and Cahyadi, A. I. (2022).

Auto-tuning pid controller for nuscale nuclear reactor

using point reactor kinetics model simulator. In 2022

9th International Conference on Information Tech-

nology, Computer, and Electrical Engineering (ICI-

TACEE), pages 7–12.

Muniglia, M., Do, J.-M., Jean-Charles, L. P., Grard, H.,

Verel, S., and David, S. (2016). A multi-physics

pwr model for the load following. In Interna-

tional Congress on Advances in Nuclear Power Plants

(ICAPP).

Muniglia, M., Verel, S., Le Pallec, J.-C., and Do, J.-M.

(2018). A ﬁtness landscape view on the tuning of

an asynchronous master-worker ea for nuclear reactor

design. In Artiﬁcial Evolution, pages 30–46. Springer

International Publishing.

O’Donnell, R. (2021). Analysis of boolean functions.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Prieto, J. and G

omez, J. (2020). Hybrid adaptive evolution-

ary algorithm for multi-objective optimization. ArXiv,

abs/2004.13925.

Qi, Y., Ma, X., Liu, F., Jiao, L., Sun, J., and Wu, J. (2014).

MOEA/D with Adaptive Weight Adjustment. Evolu-

tionary Computation, 22(2):231–264.

Raﬁei, M., Ansarifar, G., Hadad, K., and Mohammadi, M.

(2021). Load-following control of a nuclear reactor

using optimized fopid controller based on the two-

point fractional neutron kinetics model considering re-

activity feedback effects. Progress in Nuclear Energy,

141:103936.

Shim, V. A., Tan, K. C., and Tan, K. K. (2012). A hybrid

adaptive evolutionary algorithm in the domination-

based and decomposition-based frameworks of multi-

objective optimization. In 2012 IEEE Congress on

Evolutionary Computation, pages 1–8.

Verel, S., Derbel, B., Liefooghe, A., Aguirre, H., and

Tanaka, K. (2018). A surrogate model based on walsh

decomposition for pseudo-boolean functions. In Par-

allel Problem Solving from Nature – PPSN XV, pages

181–193, Cham. Springer International Publishing.

Walsh, J. L. (1923). A closed set of normal orthogonal func-

tions. American Journal of Mathematics, 45:5–24.

Xu, Y., Wang, Z., Sun, W., Chen, S., Wu, Y., and Zhao, B.

(2011). Unit commitment model considering nuclear

power plant load following. APAP 2011 - Proceed-

ings: 2011 International Conference on Advanced

Power System Automation and Protection, 3.

Zeng, W., Jiang, Q., Xie, J., and Yu, T. (2020). A functional

variable universe fuzzy pid controller for load follow-

ing operation of pwr with the multiple model. Annals

of Nuclear Energy, 140:107174.

Zhang, Q. and Li, H. (2007). Moea/d: A multiob-

jective evolutionary algorithm based on decomposi-

tion. IEEE Transactions on evolutionary computation,

11(6):712–731.

MOEA/D with Adaptive Mutation Operator Based on Walsh Decomposition: Application to Nuclear Reactor Control Optimization