Statistical Analysis of Recent Rule Revision Effects for Tactical and

Strategic Elements in Curling

Yutaka Kondo

, Hitoshi Yanagi

, Michal Ptaszyns ki

2 b

, Shimpei Aihara

4 c

and Fumito Masui

2,4

Graduate School of Kitami Institute of Technology, 165, Kouen-cho, Kitami, Japan

Information Communication Group, Kitami Institute of Technology, 165, Kouen-cho, Kitami, Japan

Common Education Group, Kitami Institute of Technology, 165, Kouen-cho, Kitami, Japan

Department of Sport Science and Research, Japan Institute of Sport Sciences, Tokyo, Japan

Keywords:

Curling Informatics, Tactics and Strategies, Game Information, Game Score, Scoring Opportunity.

Abstract:

In this paper, PCA is performed on a set of tactical elements calculated by scoring opportunity analysis for the

men’s and women’s Japanese Championships 2017, 2022, and 2023 with different rules. Curling is a winter

sport called ”chess on ice”. Curling is considered as a system system consisting of multiple elements, which

can be divided into three categories: physical, human and tacti cal. Among these, strategic and tactical factors

are considered to be the most important in top-level competition. In addition, in the curling world, some rules

are sometimes changed in order t o improve players’ skills and tactics. In this study, we analyzed the changes

in tactical factors due to the rule changes. As a result, it is considered that the nautical zone rule is not effective

in men’s competitions. In the women’s competitions, scoring points by stealing became more important each

time the rules were changed.

1 INTRODUCTION

The ofﬁcial rules of curling were established in

Canada in 1838, and in recent years, the sport has

been played in 66 countries and regions that are mem-

bers of the World Curling Federation. Jap an is ranked

8th in the men’s world and 4th in the women’s world

and has performed well in world competitions. How-

ever, some issues must be solved to maintain the cur-

rent world ranking.

Considering curling as a system consisting of mul-

tiple factors, we can list physical factors (cha nges in

ice c onditions) , human factors (players’ conditions),

and tactical factors (knowledge of tactics and strat-

egy). Bradley (Bradley, 2009) points out that strate-

gic and tactical factors are the most important at the

top level. Various enhancement programs have been

developed to strengthen curling in Japan (Yanagi et

al., 2012; Takahashi, 2011; Masui et al., 2012). One

example of a method to improve team performance is

https://orcid.org/0009-0008-7432-9999

https://orcid.org/0000-0002-1910-9183

https://orcid.org/0000-0002-8513-0204

https://orcid.org/0000-0001-9979-8734

the info rmatics approach. In the past few years, many

examples of the use of ICT (In formation and Comm u-

nication Technology) to su pport sports have been re-

ported(Fujimura and Sugihara, 2004 ; Kagawa, 2006),

and curling is one of them (Masui et al., 2 012). One

example of ICT utilizatio n in baseball is Trackman. It

uses optically enhanced radar technology to measure

the tr ajectory of the entire ba ll.

In this study, as a part of the curling informatics

project, game plans in curling are analyzed based on

the scoring d ata. Curling is a highly tactical sport,

so much so that it is called ”chess on ice.” Therefore,

it is necessary to collect various tactics-related fac-

tors and make a precise tactical plan for each phase

of the game. I n addition , the ﬁrst and second turn-

ers switch at each end, and only one of the teams can

score points. Because of this unique rule structure

of curling, it is generally said that the latter team has

the advantage. Therefore, players must make e nd and

game plans for th eir pla y.

Masui et al. developed the digital scorebook

”iCE” to record tactical elements electro nically (Ma-

sui et al., 2012). Using the ”iCE”, it is currently pos-

sible to provide feedback to players on the direc tion

Kondo, Y., Yanagi, H., Ptaszynski, M., Aihara, S. and Masui, F.

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling.

DOI: 10.5220/0012178800003587

In Proceedings of the 11th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2023), pages 70-81

ISBN: 978-989-758-673-6; ISSN: 2184-3201

of rotation, type, and score (accuracy) of shots in each

game. However, research to analyze scoring patterns

and consider end and game plans has not progressed,

and feedback has not been returned to players.

In addition, there have been two signiﬁcant rule

changes in curling. Players must a dapt more quickly

to the changed rules and develop their e nd and game

plans. Th erefore, it is advantageous to analyze com-

petitions with different rules.

In this paper, we focu s on the Opportunities to

score and lose points in curling and c onsider the im-

pact of revising the ﬁrst-division rules on the tactical

elements. Speciﬁcally, we analyze scoring opportuni-

ties and collect tactical elements conside red necessary

among top-level players. Next, Principal Component

Analysis ( PCA) measures the inﬂuence of the tactical

factors obtained from the scoring o pportunities.

PCA is a type of multivariate analysis method, an

analytical techn ique developed in economics. PCA

can represent the characteristics of the data by redu c-

ing the numbe r of variables without losing the original

multivariate data as m uch as possible.

The outline of this paper is as follows. First, Sec-

tion 2 introduces related studies. In Section 3, ru le

changes in curling are introduc ed. Section 5 d escribes

Goal Scoring Opportunity Analysis and PCA (Princi-

pal Component Analysis) an a lysis me thods. Section 6

describes PCA. Section 7 introduces the analysis tar-

gets. In Section 8, we interpret the results of PCA.

Section 9 discusses the results. Finally, Section 10

conclud es the paper.

2 RELATED RESEARCH

As a previous study on support f or strengthening tac-

tical elemen ts, there is the curling infor matics concept

of Masui (Masui et al., 2012). As shown in Fig. 1, it

is an attempt to support the top teams in Japan and to

contribute to the improvement of the tactical skills of

the competitors. For this purp ose, we aim to develop

technologies and environments for recording, analyz-

ing, visualizing, and sharing match information.

As for tactical and competitive factors, studies on

game information analysis in curling have bee n con-

ducted. Otani (Otani et al., 2016) conducte d a cor-

relation analysis between shot accuracy and scoring

power at the world’s top level and found a po sitive

correlation between shot rate difference and scoring

difference. Hirata(Hirata et al., 2016) conducted a

correlation analysis of the difference in shot accu -

racy and the difference in ﬁnal score by position and

found a sexual correla tion for the force. However, no

correlation was fou nd for positions other th a n force.

Heo(Heo and Kim, 2013) developed a curling simu-

lator that can be u sed as a training tool to improve

performance in real competitions. The realistic curl-

ing simulation allows users to set up strategies and

tactics while imaginatively tr a ining in various situ-

ations without being limited by the training space.

Sung(Duda et al., 2001) analyzed the game results us-

ing b inomial logistic regression based on the posses-

sion of the ﬁrst and last stones at each end. The results

showed statistical signiﬁcance between the game re-

sults and the control of the last stone from the ﬁrst end

to th e tenth end, except for the second end.

Figure 1: The Concept of Curli ng Informatics.

3 CHANGE OF COMPETITION

RULES

Below are some of the changes in the rules and tactics

of curling.

3.1 Rules of Curling

In this section, we will introduce the basic rules of

curling and some special ru les tha t vary from age to

age.

3.1.1 Basic Rules

Curling is a sport where two teams play against each

other in an area called a ”sheet” made of ice. Each

team takes tu rns throwing eight stones to score points.

Points are awarded only to the team whose stone is

closest to the circle’s center called the house. One

point is awarded to th e team that scores a point for

each stone inside the nearest stone from the center of

the house of the team that failed to score a point.

In the ﬁrst end, the team with the lowest LSD (Last

Stone Draw) is the last team to score a p oint, and the

team with the highest LSD is th e ﬁrst te a m to score

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling

a point. After the second end, the team tha t scored

in the previous end is the ﬁrst to attack, and the team

that sco red in the pr evious end is the second to strike.

A blank end is an end in which neither team scores a

point. In this case, the ﬁrst and secon d teams do no t

switch.

3.1.2 Special Rules

Curling has special rules that signiﬁcantly inﬂuence

tactics, and the rules have been revised twice so far.

The free-guard zone rule has been in effect sinc e

1993. This rule states that if an opponent’s stone is

directly o r indirectly moved out of the playing area

before the ﬁfth throw of the end is made, the thrown

stone is removed, and the moved stone is returned by

the non-offending team to the position it was in before

the infraction took place.

This free guard zone rule was amended for the

2018-2019 seaso n to state that if an opponent d irectly

or indire ctly moves a n opponent’s sto ne out of the

playing area before the sixth throw of the second is

made, the thrown stone will be removed. The moved

stone will be returned by the non-o ffending team to

the position it was in before the violation was com mit-

ted. The rule is now that the thrown stone is removed,

and the moved stone is returned by the n on-offending

team to its position before the infraction. However,

players have started to use tactics to avoid violating

the rule by throwing shots (wick) to shift the oppo-

nent’s stones to the edge of the playing area. There-

fore, the No Tick Zone Rule was implemented for the

2022-2023 season. This rule prohibits a player from

moving an opponent’s ston e directly or indirectly in

the free guard zone and touching the center lin e to a

position outside the free guard zone or not touching

the center line be fore the sixth throw of the end. The

offending team may c hoose one option: (1) Remove

the thrown stones and return all stones to their original

position. (2) Leave all stones in place.

3.2 Curling Tactics

It is generally believed that the team with the rear end

has th e advantage of curling. Therefore, the theory o f

curling is that the ﬁrst team should limit the o pposing

team’s scor e to one point, and the second team should

score two or more p oints. Thus, curling is a sport in

which the offensive and defensive tactics are switched

between the ﬁrst and the second team.

The tactics of the ﬁrst and the second turn, often

seen in recent years, are as follows. The ﬁrst team

places a stone called a guard near the center line of

the free guard zone in front of the house (the yel-

low area in Figure2) on the ﬁrst throw. By ﬁlling the

center of the house with your team’s stones, you can

suppress your opponent’s sco ring. T he second team

throws a c ome-around, a shot to hid e behind the guard

stone thrown on the ﬁrst throw. The second throw is

shot to hide the guard stone behind the guard stone

thrown in the ﬁrst throw. The team attacking from

the rear throws a take-o ut shot to bounce the oppo-

nent’s rock in the center of the house, creating a space

in the center and scoring multiple go a ls, including the

stone thrown in the ﬁr st throw. From the middle of the

end of the game, the game proceeds according to the

phase. When the score difference is far, even if your

team is the second team, you should not try to score

points but rather reduce the risk of losing points. If the

team is not expected to score more than two or more

goals, the game may be played with a blank end, and

the game continues with the following end as a back-

placed game. This tactic is intended to reset the stones

and start the next end with the back en d again.

Figure 2: Free gard zone.

4 ANALYTICAL METHOD

In this study, we collect the tactical elements of eac h

team fr om the analysis of goal-scoring machines and

condu c t quantitative research on the inﬂuence of each

tactical e le ment on the tournament using PCA (Prin-

cipal Component Analysis). Based on the results of

PCA, changes in tactical elements due to rule changes

are discussed. Sec tion 5 describes the analysis of

Opportunities to score and lose points, Section 6 de-

scribes the PCA, and Section 7 describes the analysis

targets.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

5 SCORING OPPORTUNITY

ANALYSIS

Curling is a sport in which the tactics differ between

the ﬁrst and the second team, and on ly one of the

teams can score points. Therefore, it is cruc ial to clar-

ify the pattern of goals scored by the ﬁrst and second

teams.

In the analysis of scoring opportunities, the score

of each game is recorded, and the tactical factors are

calculated for each tourn ament. The ta c tical factors

are score(Scorling), lost poin ts(Lost), ﬁrst turn(First

Turn), second turn(Second Turn), ﬁrst blank

end(BECFirst), secon d blank end(BECSecond),

number of steals(Steal), number of steals con-

ceded(Stolen), Last Stone Efﬁciency(LSEff), and

Force Efﬁciency(FEff). These tactical elements are

those emphasized by world-class te a ms. Section

5.1 describes the collection and recording of game

informa tion, and Sec tion 5.2 describes the analysis

for each tou rnament.

5.1 Collecting and Recording Match

Information

The scoresheet shown in Fig.1.3 analyzes each game.

The team nam e , LSD (L ast Stone Draw), and score

are entered on the score sheet. LSD is an abbreviation

for Last Stone Draw. Before the game, both teams

throw one pitch counterclockwise and clockwise to a

circle called a house, and the total distance from the

circle’s center is recorded. Team n a mes, LSD, and

scores are entered man ually by referring to the match

informa tion on the tournament’s ofﬁcial website. The

ﬁrst or the second team is assigned to the ﬁrst or the

second team for each end based on the enter e d LSD

record and the score. HMR(HAMMER) in the ﬁrst

line of Fig. 2 indica te s which team was the second

in each end. R su ggests that team A was the second

team, and Y shows that team B was the second team.

The number of blank ends, steals, LSEff, and FEff

are also tabulated for ea ch game. LSEff is the ratio

of the number of ends that scored two or more points

in the second round. FEff is the ratio of the number

of endpoints in which the opponent scored only one

point in the ﬁrst turn. LSEff and FEff are indic es for

quantitatively calculating whether the theory of curl-

ing is generally followed. The formulas for calculat-

ing LSEff and FEff are given below. In the formula,

the number of multi-score ends in the 2nd h a lf is given

as ”Multi-score ends in 2nd half,” and the number of

defensive ends in the 1st half is given as ”Number of

defensive ends”.

LSE f f =

Multi-score e nds in 2nd half

(Steal-BECSecond)

FE f f =

Number of defensive ends

(First Turn-BECFirst-Steal)

Figure 3: Match information for one game.

5.2 Analysis of Each Tournament

The information of each match is comp iled and an-

alyzed for each tournament. Here, we create a table

of average goals sco red p er end, a graph of the per-

centage of goals scored, a graph of the rate of goals

scored, a table of nu mber of ends with multiple goals

scored per end, a table of number of ends with 3 or

more goals scored per end, and so on. In this table, ten

tactical elem ents (Scoring, Lost, First Turn, Secon d

Turn, BECFirst, BECSecond, Steal, Stolen, LSEff,

FEff) are calculated as the average value per game.

The reason for calculating the average per game is that

the number of games played in a tournament varies

from tea m to team.

6 PCA(PRINCIPAL COMPONENT

ANALYSIS)

The concept of PCA for the case of two variables is

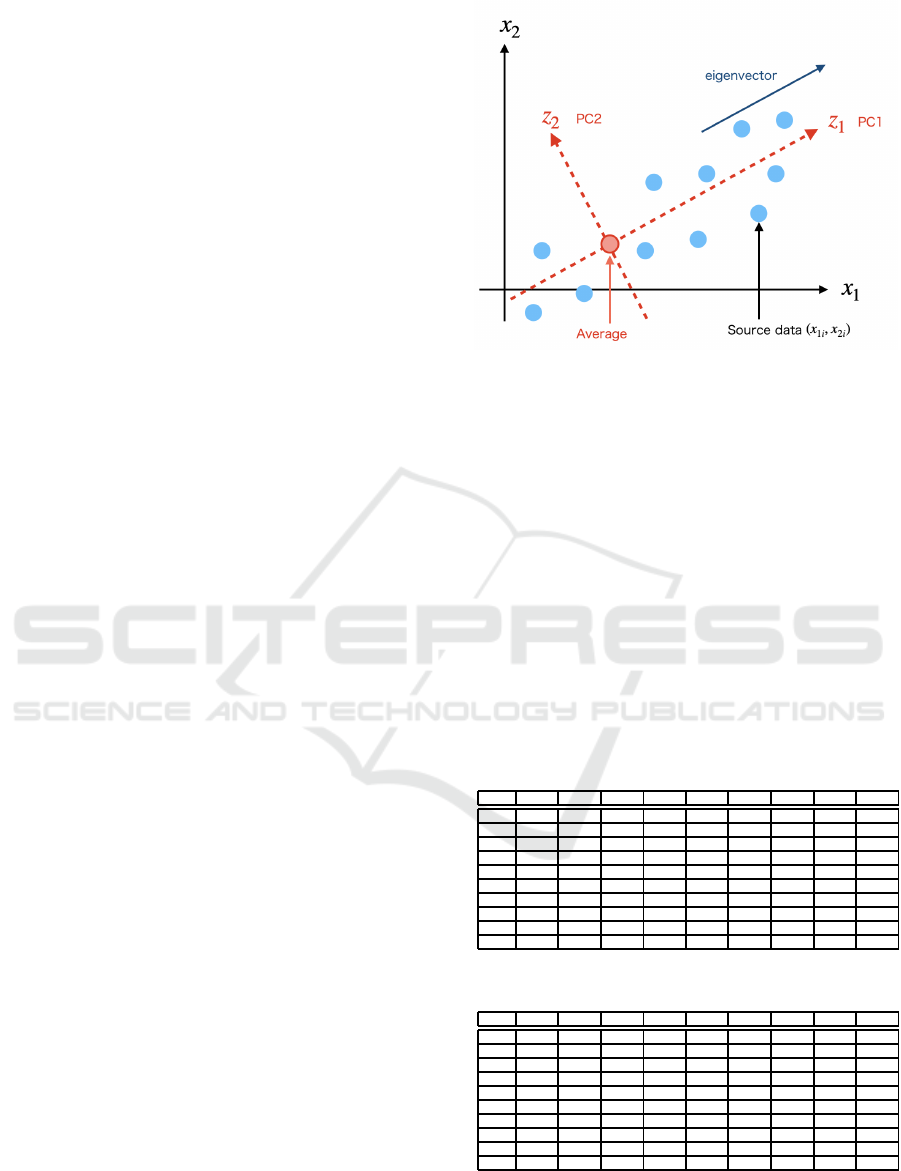
shown in Fig.4. PCA is a type of multivariate anal-

ysis tha t compresses the original data into a smaller

number of princ ipal components, taking into account

the correlatio n and variance among the variables in

the data set. Th e principa l compone nts are cho sen

such tha t the variance of the original data is maxi-

mized, and the next principal c omponent represents

the remainin g direction with the largest variance of

the original data. A simple m e thod for calculating

principal compone nts is described below. See the Ap-

pendix for details.

For the entire data set, a d-dimensional mean vec-

tor µ and a d × d covariance matrix Σ are com-

puted. Next, eigenvectors and eigenvalues are com-

puted and arranged in decreasing order of eigenvalue.

These eigenvectors are called eig e nvectore

with

eigenvalueλ

, eigenvectore

with eigenvalueλ

,... and

select the k eigenvectors with the largest eigenval-

ues. In many cases, there are only a few large eigen-

values, which means that k is the eigendimension of

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling

the subspace governing the ”sig nal” and the remain-

ing d -k dimensions generally contain noise. We then

form a dxk matrix A with k eigenvectors as columns.

The representation of the data in terms of princi-

pal compon ents consists of projec ting the data onto

the k-dime nsional subspace as follows (Satomi et al.,

2009).

′

= F

(x) = A

(x −µ)

On the other hand, since the objective of PCA is

to represent the original amount of informatio n with

as little information as possible, the number of prin-

cipal components employed is important. As a rule

of thumb,(1)the eigenvalue should be greater than

1, and (2)the cumulative contribution rate should be

greater than 80However, depending on the interpr e ta -

tion m e thod, principal c omponents may be taken even

when the eigenvalues are not greater than 1. The de-

termination of the number of principal components

should be conside red according to the results of the

analysis.

Eigenvalues represent the degree of chara c te ristic

variability of the original data through diagonaliza-

tion (c onversion to a diagonal matrix) of the covari-

ance m a trix. Speciﬁcally, eigenvalues are an impor-

tant measu re of h ow much directional variation the

correspo nding eigenvector has in the data, depending

on its magnitude. Th e contribution ratio is a measure

of how well each principal componen t explains the

variability in the original data. The cumulative contri-

bution rate is a cumulative measure of the contribution

rate, and the larger the value, the more infor mation on

the origina l data is explained. The principal compo-

nents obtained in PCA are expressed as a linear c om-

bination of th e original variables. The load ings are

coefﬁcients that indicate how much each original vari-

able co ntributes to the linear combination of its prin-

cipal components. In order to capture the relation-

ship between the prin cipal componen ts and the orig-

inal variables, co rrelation coefﬁcients are computed

between the principal components and each variable,

which are interp reted as loadings.

7 SUBJECT OF ANALYSIS

The analysis covered men’s and women’s matches of

the Japan Championships 2017 (JC2017), the Japan

Championships 2022 (JC2022), and the Japan Cham-

pionships 2023 (JC2023) , which w ere held bef ore the

free guard zone rule was revised after the revision, re-

spectively. Table1-6 displays the 10 tac tica l elements

calculated by the goal-scoring opportunity ana lysis

for each team. The columns repr esent the respective

Figure 4: PCA concept.

teams, which are not shown in this paper. The rows

represent the following 10 tactical eleme nts. Here,

the average score is abbreviated as Sc(Scorling), the

average g oals scored is abbreviated as Lo(Lost), the

number of turns taken by the ﬁrst team is abbrevi-

ated as Ft(First Turn), th e number of turns taken by

the second team is abbreviated as St(Second Turn),

the number of blank ends by the ﬁrst team is abbrevi-

ated as Bf(Blank End for the First Attack), the num-

ber of blank ends by the second team is abbreviated

as Bs(Blank End for the Second Attack), the number

of steals is abbreviated as Stl(Steal), the number of

steals suffered is ab breviated as Std(Stealed), LSEff

is abbreviated a s LS(Last Stone Efﬁciency), a nd FEff

is a bbreviated as FE(Force Efﬁciency).

Table 1: Tactics elements(Japan Championship Men 2017).

A1 B1 C1 D1 E1 F1 G1 H1 I1

Sc 9.6 7.36 6.82 5.91 5.22 4.88 5.38 5.38 4.88

Lo 4.00 5.64 6.09 6.27 6.44 7.75 7.75 7.88 5.63

Ft 4.60 5.27 4.82 4.73 4.44 3.88 4.63 4.13 4.25

St 3.80 3.91 4.55 5.00 4.56 4.75 4.88 5.13 4.88

Bf 0.70 0.73 0.55 0.36 0.78 0.00 0.38 0.50 1.13

Bs 0.20 0.45 0.55 0.45 1.00 0.63 0.38 1.00 0.63

Stl 1.40 1.27 0.82 1.36 1.00 0.75 0.88 0.75 1.00

Std 0.60 0.55 0.82 1.27 0.89 1.25 1.50 1.25 1.63

LS 0.60 0.48 0.37 0.22 0.27 0.16 0.28 0.33 0.19

FE 0.72 0.66 0.57 0.61 0.60 0.39 0.58 0.43 0.56

Table 2: Tactics elements(Japan Championship Men 2022).

A2 B2 C2 D2 E2 F2 G2 H2 I2

Sc 8.18 7.90 7.70 6.33 6.50 5.13 5.38 3.25 3.75

Lo 4.82 4.50 5.10 5.89 5.13 6.63 6.88 9.38 8.63

Ft 5.09 4.60 4.00 5.11 4.88 3.63 3.63 3.50 4.38

St 3.91 4.40 4.90 3.78 4.00 5.13 4.88 4.13 4.13

Bf 0.82 0.60 0.10 1.00 0.63 0.38 0.38 0.50 1.00

Bs 0.55 0.80 1.20 0.33 0.75 0.75 0.50 0.25 0.13

Stl 1.36 1.50 0.90 1.00 1.63 0.63 0.38 0.50 0.50

Std 0.27 0.70 0.30 0.56 0.75 1.75 1.50 1.75 1.63

LS 0.66 0.53 0.59 0.41 0.58 0.23 0.20 0.10 0.12

FE 0.60 0.73 0.59 0.61 0.50 0.50 0.45 0.42 0.39

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

Table 3: Tactics elements(Japan Championship Men 2023).

A3 B3 C3 D3 E3 F3 G3 H3 I3

Sc 8.60 7.36 7.70 7.33 7.25 6.13 5.13 3.50 3.50

Lo 4.70 4.91 5.30 5.67 5.38 8.38 7.50 9.25 8.13

Ft 4.90 4.82 3.80 4.56 4.25 3.88 4.13 3.63 3.88

St 3.90 4.18 4.70 3.89 4.13 4.50 4.75 3.88 4.25

Bf 0.60 0.55 0.10 0.22 0.75 0.00 0.25 0.25 0.63

Bs 0.40 0.64 0.90 0.00 0.50 0.25 0.50 0.00 0.00

Stl 1.60 1.55 1.00 1.56 0.88 0.38 0.38 0.63 0.38

Std 0.50 0.82 0.90 0.78 0.88 0.88 0.88 1.50 1.88

LS 0.63 0.50 0.59 0.39 0.48 0.40 0.25 0.09 0.15

FE 0.64 0.68 0.61 0.64 0.61 0.39 0.51 0.11 0.35

Table 4: Tactics el ements(Japan Championship Women

2017).

a1 b1 c1 d1 e1 f1 g1 h1 i1

Sc 6.91 8.50 8.00 7.70 6.13 6.38 3.75 3.38 5.00

Lo 4.09 4.50 5.80 5.20 6.63 7.00 7.63 9.25 9.00

Ft 4.91 4.10 4.90 4.60 4.50 3.88 3.38 3.50 4.14

St 3.91 4.50 4.00 3.90 4.63 4.75 4.63 3.63 5.14

Bf 1.00 0.10 0.50 0.50 0.75 0.00 0.25 0.00 0.43

Bs 0.64 0.80 0.20 0.20 0.63 0.50 0.63 0.00 0.14

Stl 1.09 1.30 1.50 1.20 1.00 1.13 0.38 1.13 0.71

Std 0.36 0.50 0.90 0.60 1.25 1.25 1.50 1.88 2.29

LS 0.49 0.48 0.52 0.37 0.28 0.26 0.14 0.08 0.21

FE 0.83 0.60 0.59 0.64 0.40 0.63 0.58 0.32 0.50

Table 5: Tactics el ements(Japan Championship Women

2022).

a2 b2 c2 d2 e2 f2 g2 h2 i2

Sc 7.30 7.91 7.20 7.44 6.00 5.38 6.00 5.50 2.25

Lo 4.40 4.64 4.90 6.22 6.75 5.75 6.75 7.00 11.25

Ft 4.50 4.91 4.10 5.11 3.75 4.25 4.75 4.50 2.75

St 4.70 3.73 4.20 4.11 5.38 4.63 3.88 4.25 4.25

Bf 0.10 0.73 0.40 0.56 0.25 0.38 0.75 0.63 0.00

Bs 0.80 0.36 0.70 0.22 0.38 0.38 0.50 0.25 0.13

Stl 1.80 1.36 1.10 1.56 0.75 1.25 1.00 0.88 0 .38

Std 0.60 0.55 0.60 1.11 2.00 1.63 0.63 1.25 2.50

LS 0.44 0.43 0.40 0.40 0.34 0.20 0.29 0.38 0.03

FE 0.76 0.67 0.65 0.60 0.58 0.64 0.49 0.67 0.07

8 ANALYSIS RESULTS

In this section, we present and discuss the PCA re-

sults for each conference in the tables7-12. The table

lists the eigenvalues, principal component loadings,

contribution rates, and cumulative contribution rates

for each principal component. The number of princi-

pal components to be interpreted is determined with

referenc e to the cumulative contribution rate. For in-

terpretation, the loadings of each component are u sed

as a refe rence.

8.1 Japan Championship 2017 Men

Table 7 shows the results of the analysis of the Japan

Championship 2017 men’s race. T his time, we have

obtained up to the third principal component whose

cumulative contribution rate is 0.8 or mor e , which is

the standard for the nu mber of principal components

as described in (2) of 6 chapter. Since the cumulative

contribution rate up to the third principal compon ent

is 85. 9%, we consider that we h ave effectively pro-

cessed 10 variables.

Table 6: Tactics elements(Japan Championship Women

2023).

a3 b3 c3 d3 e3 f3 g3 h3 i3

Sc 9.00 7.18 8.60 8.33 8.50 6.25 5.38 4.38 2.00

Lo 4.80 7.00 5.60 4.78 5.75 7.75 7.13 7.50 11.63

Ft 4.70 4.82 5.00 5.33 4.50 4.50 4.13 3.50 2.63

St 4.20 4.45 4.10 3.11 4.63 4.75 4.50 5.38 4.75

Bf 0.30 0.45 0.30 0.78 0.38 0.13 0.50 0.50 0.13

Bs 0.60 0.36 0.10 0.22 0.63 0.25 0.38 0.88 0.13

Stl 2.00 1.27 2.00 2.44 1.38 1.00 0.63 0.38 0.25

Std 0.60 1.00 1.30 0.78 0.88 1.25 1.38 2.00 3.00

LS 0.49 0.43 0.43 0.57 0.58 0.31 0.33 0.19 0.03

FE 0.28 0.53 0.72 0.69 0.61 0.48 0.69 0.40 0.26

The ﬁrst principal componen t is m ainly related to

the score, with a value of more than 0.3 or -0.3, which

can be interpreted as a principal component relate d to

the goals scored . In curling , the team that scores the

most points is the ﬁrst team to attack in the next end,

so the loadings on the number of ends for the second

team a re also large.

The second principal comp onent, BECFirst(Blank

End for the First Attack) had a larger value than the

other components. BECFirst is considered to have the

effect of preventing the ﬁrst team from preventing the

second team from scoring a goal. I n other words, the

second principa l component can be interpreted as a

defensive principal component for the ﬁrst team.

The third principal component, BECSec-

ond(Blank End for the Second) is larger than the

other compon e nts. BECSecond is considered to

be a factor that the rear-angle team choosing the

scoring opportunities. In other words, the third prin-

cipal compon e nt can be interpreted as an offensive

principal component for the rear-attacking team.

Table 7: Analysis Results(Japan Championship Men 2017).

PC1 PC2 PC3

Eigenvalue 6.321 1.285 0.986

Load

Scorling 0.366 -0.240 -0.033

Lost -0.34 9 -0.258 -0.052

First Turn 0.299 0.035 0.079

Second Turn -0.3 61 0.173 0. 228

BECFirst 0.158 0.762 -0.193

BECSecond -0. 241 0.281 -0.656

Steal 0.302 0. 156 0.371

Stolen -0.32 0 0.234 0.4 74

LSEff 0.347 -0.195 -0.279

FEff 0.356 0.259 0.172

Contribution Rate 63.2% 12.9% 9.9%

Cumulative

Contribution

Rate

63.2% 76.1% 85.9%

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling

8.2 Japan Championship 2022 Men

Table 8 shows the results of the analysis for the Japan

Championships 2022 men . Since the cumulative con-

tribution rate up to the second principal compon ent

was 90.5%, we obtained the L oad(loadings) up to the

second principal component.

In the ﬁrst principal component, the factors related

to the score were high, except for those related to the

number of ends. Similarly to the men’s Japan Cham-

pionship 2017, the ﬁrst principal component can be

interpreted as the principal component related to the

score.

The second prin cipal component was higher than

the other components in terms of Second Turn and

BECFirst(Blank End for the First Turn). The ﬁrst

team aims to pr event the second team from scoring

by creating blank ends. The second team aims to cre-

ate scoring opportunities and to score more tha n two

points. Thus, the second principal component can be

interpreted as a p rincipal co mponent that represents

offense and defense in the end.

Table 8: Analysis Results(Japan Championship Men 2022).

PC1 PC2

Eigenvalue 6.084 2.968

Load

Scorling -0.390 0.101

Lost 0.386 -0.114

First Turn -0.294 -0.38 5

Second Turn 0.088 0.534

BECFirst -0.001 -0.55 7

BECSecond -0.223 0.462

Steal -0.364 -0.11 8

Stolen 0.378 0.040

LSEff -0.396 0.034

FEff -0.350 0.055

Contribution Rate 60.8% 29.7%

Cumulative Contribution Rate 60.8% 90.5%

8.3 Japan Championship 2023 Men

Table 9 shows the results of the analysis for the Japan

Championship 2023 men. Since the cumulative con-

tribution rate up to the second principal compon ent

was 82.5%, we obtained the L oad(loadings) up to the

second principal component.

The ﬁrst principal component can be interpreted

as the principal comp onent related to the score as in

the Japan c hampionship men 2017,2022.

The second principal component is the number of

back e ndings, which is higher than the other compo-

nents. The second principal compone nt can be in-

terpreted as an offensive principal component for the

team that pla ys in the rear end.

Table 9: Analysis Results(Japan Championship Men 2023).

PC1 PC2

Eigenvalue 6.115 2.139

Load

Scorling -0.390 0.078

Lost 0.391 0.034

First Turn -0.332 -0.287

Second Turn 0.045 0.637

BECFirst -0.108 -0.418

BECSecond -0.242 0.450

Steal -0.337 -0.276

Stolen 0.342 -0.149

LSEff -0.374 0.156

FEff -0.376 0.07 1

Contribution Rate 61.2% 21.4%

Cumulative Contribution Rate 61.2% 82.5%

8.4 Japan Championship 2017 Women

Table 10 shows the re sults of the analysis for the

Japan Championship 2017 women. The loadings up

to the third principal component were obtained since

the cumulative contribution up to the third pr incipal

component was 86.4%.

The ﬁrst principal component can be interpreted

as the principal compon ent related to the score as in

the men’s competition.

For the second principal comp onent, Second

Turn(the number of back-end ends) and BECSec-

ond(Blank End for the Second) were higher than

those of the o ther components. These two co mpo-

nents can also be interpreted as offensive p rincipal

components of the latter team.

Table 10: Analysis Results(Japan Championship Women

2017).

PC1 PC2 PC3

Eigenvalue 5.838 1.670 1.134

Load

Scorling -0.374 0.0198 0.237

Lost 0.400 0.125 -0.078

First Turn -0.345 0.162 -0.393

Second Turn 0 .132 -0.572 0.065

BECFirst -0.218 -0.095 -0.767

BECSecond -0.21 9 -0.547 0.248

Steal -0.274 0.483 0.304

Stolen 0.386 0.039 -0.163

LSEff -0.395 0.053 0.045

FEff -0. 297 -0.290 -0.091

Contribution Rate 58.4% 16.7% 11.3%

Cumulative

Contribution

Rate

58.4% 75.1% 86.4%

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

BECFirst(Blank End for the ﬁrst Attack) was

higher in the third prin cipal component when the ﬁrst

attack was made. From this result, the thir d pr incipal

component can be interpreted as a defensive principal

component for th e ﬁrst offensive team.

8.5 Japan Championship 2022 Women

Table 11 shows the re sults of the analysis for the

Japan Championship 2022 women. Since the cumula-

tive contribution ra te up to the secon d principal com-

ponen t was 84.0%, we obtained the loadings up to the

second principal component.

The ﬁrst pr incipal component is considered to be

the principal compon ent related to the score.

The second prin cipal component was higher than

the other factors in the BECFirst(Blank End for the

ﬁrst attack). Therefore, the second principal compo-

nent is considered to be a defensive principal co mpo-

nent in the ﬁrst turn.

Table 11: Analysis Results(Japan Championship Women

2022).

PC1 PC2

Eigenvalue 6.580 1.825

Load

Scorling -0.375 0.038

Lost 0.371 -0.169

First Turn -0.345 -0.25 8

Second Turn 0.103 0.621

BECFirst -0.216 -0.53 0

BECSecond -0.248 0.400

Steal -0.327 0.114

Stolen 0.355 0.130

LSEff -0.357 0.081

FEff -0.352 0.202

Contribution Rate 65.8% 18.3%

Cumulative Contribution Rate 65.8% 84.0%

8.6 Japan Championship 2023 Women

Table 12 shows the re sults of the analysis for the

Japan Championship 2023 women. Since the cumu -

lative contribution up to the second principal compo-

nent was 82.0%, we obtained the L oad(loadings) up

to the second principal co mponent.

The ﬁrst principal component can be interpreted

as the principal component related to the score.

The second prin cipal component was higher than

the other factors in the BECSecond(Blank E nd for the

second attack). BECSecond(Blank End for the sec-

ond attack) has the effect of inc reasing the scoring op-

portunities of the team in the back-offense. Therefore,

it can be interpreted as an offensive principal c ompo-

nent.

Table 12: Analysis Results(Japan Championship Women

2023).

PC1 PC2

Eigenvalue 6.637 1.562

Load

Scorling -0.366 0.105

Lost 0.365 -0.223

First Turn -0.374 -0.031

Second Turn 0.299 0.413

BECFirst -0.228 0.117

BECSecond 0.020 0.790

Steal -0.353 -0.153

Stolen 0.358 -0.212

LSEff -0.373 0.101

FEff -0.242 -0.227

Contribution Rate 66.4% 15.6%

Cumulative Contribution Rate 66.4% 82.0%

9 DISCUSSION

In this section, the re sults of our analysis of the

changes in tactical elements due to the revised rules

are presented. In or der to focus on the changes in

the tactical factors obtained from the Opportunities to

score and lo se points, we use a chart in which the prin-

cipal component loadings of the three tournaments are

superimposed. The principal component loadings of

the ﬁrst principal compo nent are exp ressed in terms

of magnitude, and we focus on the combinations with

the highest principal component loadings. In the sec-

ond principal component, we focus on the changes in

the highest component.

9.1 Men’s Load Changes

Figure 5 will be an overlay of the p rincipal com-

ponen t loading s of the ﬁrst principal component for

the Japanese Championships 20 17, 2022, and 2023

men. Here, each principal comp onent loadings are

expressed in absolute values.

The principal compon ent loadings f rom the Japan

Championships 2017 to the Japan Championships

2022 are highe r for the four factors of Scorling,

Lost, Steal, Stolen, and LSEff(Last Stone Efﬁciency).

These are mainly related to points scored and points

lost. We consider that the increase of one more pitch -

ing order in which stones in the free guard zone can

be thrown out of the playing area has made it e asier to

score points. Since the principal component loadings

of the number of steals have also increased, it can be

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling

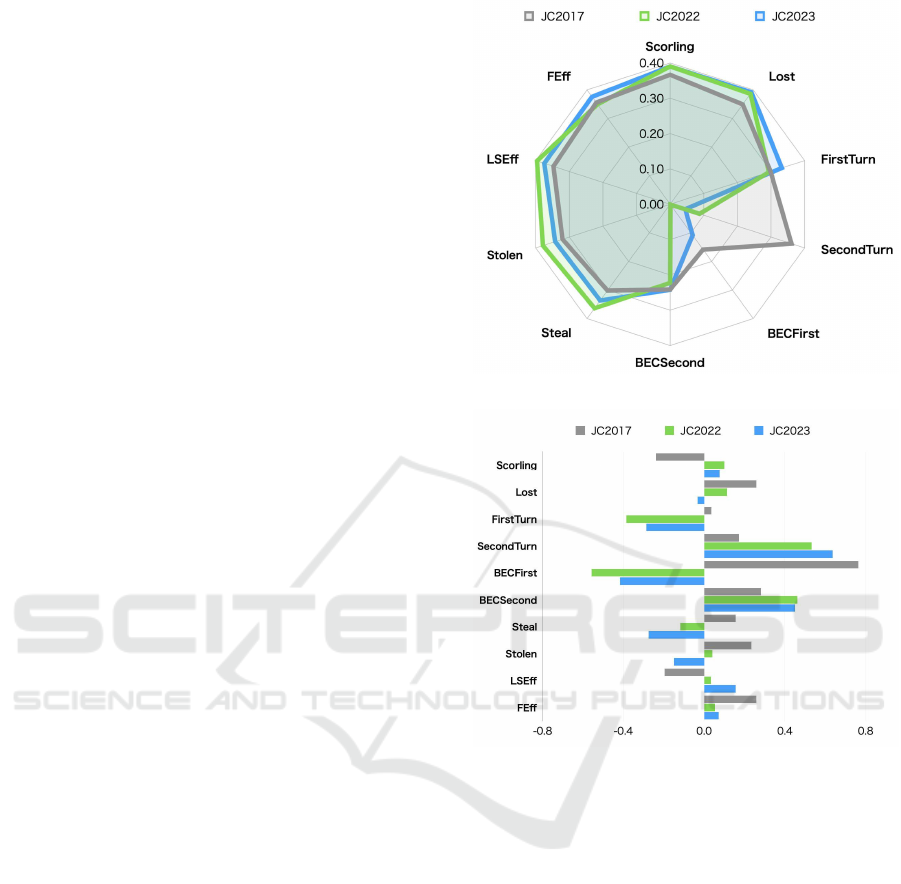
seen that scoring in the ﬁr st end is also imp ortant, al-

though it is generally con sidered that the second end

is more advantageous. Two factors, Sec ond Turn and

BECSecond(Blank End for th e Second), were lower

than those of the ﬁrst endings. This indicates that the

number of blank ends is no longer important for the

players to win the back end and to win the ﬁrst end.

Therefore, we can consider that the advantage in the

back end ha s decreased, and that the advantage in the

ﬁrst end has slightly increased.

From Japan Championships 2022 to Japan Cham -

pionships 2023, three factors were slightly higher:

First Turn, BECSecond(Blank End for the Second),

and FEff(Force Efﬁciency). Since these factors were

slightly higher, we consider that it became more im-

portant to limit the opponent’s score to one point in

the ﬁrst end. In the back end, it is not necessarily

to aim for multiple go als, but to aim at the blank end

when it is difﬁcult to score goals, and to aim for multi-

ple goals when it is easy to score goals, which is con-

sidered to be an important tactic. The four factors of

Second Turn, Steal, Stolen, and the LSEff(Last Stone

Efﬁciency) were lower in the rear end. There was

no signiﬁcant change from the Japan Championship

2022 to the Japan Championship 2023.

Figure 6 shows the principal component loadings

of the second principal component of the three com-

petitions.

From the Japan Championship 2017 to the Japan

Championship 2022, the highest factor has changed

from the BECFirst to the Second Turn. The fact

that the inﬂuence of the number of back-end turns

has increased in curling means that it is im portant

to score more than 2 points in the back end. From

Japan Championships 2 022 to Japan Ch ampionships

2023, the element w ith the highest principal compo-

nent loadings did not change in the Second Turn. The

introdu ction of the No Tick Zone Rule does not ap-

pear to h ave changed the tactics of the men’s team. It

is thought that this is because men c an throw a power-

ful shot called ”takeout” that bounce s the opponent’s

stones out of the court, and thus can break the situa-

tion where stones are concentrated in or in front of the

house.

Thus, there was no change in the men’s Japan

Championships 2022 to Japan Championships 2023.

As m entioned in section 3.1.2, the rule was estab-

lished to counteract a shot called wick in the Japan

Championships 2023. However, since no change was

observed, we can say that the wick shot is not an

important shot in the men’s compe titions. In other

words, the No Tick Zone Rule is considered to be in-

effective in the men’s competitions because the wick

does not determine the winner.

Figure 5: Contribution rate - PC1(Men).

Figure 6: Contribution rate - PC2(Men).

9.2 Women’s Load Changes

Figure 7 will be an overlay of the p rincipal com-

ponen t loading s of the ﬁrst principal component for

the Japanese Championships 20 17, 2022, and 2023

women. Here, each principal com ponent loading s are

expressed in absolute values.

The principal compon ent loadings f rom the Japan

Championship 2017 to the Japan Championship 2022

were higher in the BECSecon d(Blank End for the

Second), Steal, and FEff(Force Efﬁciency) for the rear

attackers. In addition, three factors, Second Turn,

Stolen, and LSEff(Last Stone Efﬁciency), were lower.

All of these three factors are re late d to the tactics of

the second- phase attackers. Therefore, it became im-

portant for the ﬁrst-attackers to aim for steals to gain

a scoring advantage, or to limit the opponent’s score

to on e point. The second turner should basically aim

for multiple goals, but if he/she cannot aim for mul-

tiple goals, it is important to use the tactic of blank

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

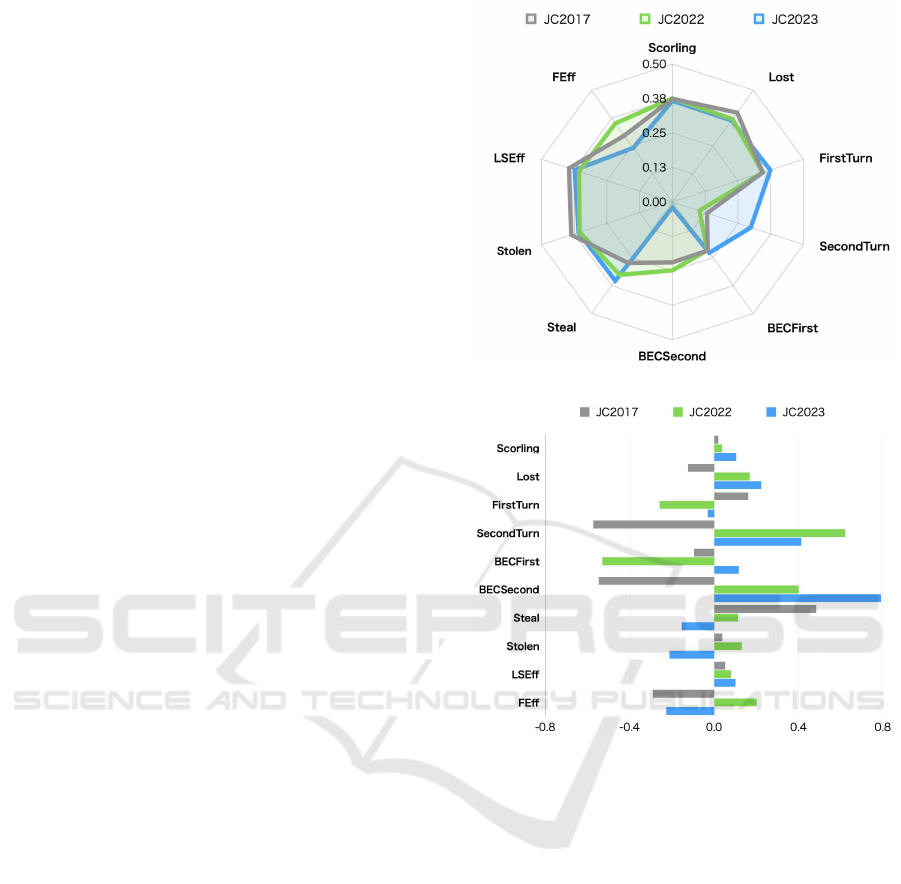
endings.

The First Turn, Second Turn , and Stea l were

higher from Japanese Championship 2022 to

Japanese Championship 2023. The BECSec-

ond(Blank End for the second attack) and FEff(Force

Efﬁciency) of the rear enders became lower. Al-

though the inﬂuence of the numbe r of rear ends

increased, the inﬂuence of the numb er of blank rear

ends decrea sed considerably, sugge stin g that the

importance of the rear ends may have decrea sed. In

addition, the higher number of steal and the lower

FEff may have made it more important to scor e points

in the ﬁrst end.

Figure8 shows the principal component loadings

of the second principal component for the Japanese

Championship 2017, 2022, and 2023 women. In the

second principal component, we focus on the ele-

ments with the highest principal component loa dings.

From the Japan Championships 2017 to the Japan

Championships 2022, the number of steal turns has

changed from the highest number of steal turns to the

Second Turn. The reason for the change from the

number of steals to the numbe r of back-end turns is

that the free guard zone rule has been revised so that

stones tend to accumulate in the house more often,

which makes it easier to score in the back-end tu rns.

From Japan Championships 2022 to Japan Cham -

pionships 2023, the factor with the highest principal

component loadings change d fr om the Second Turn to

the BECSecond(Blank En d for the second attack) .The

reason for the higher number of blank ends in the back

end is considered to b e tha t the creation of blank ends

reduces the number of back ends in which the oppo-

nent can score points. In addition, although the theory

is to aim for two or more points in the re a r end, there

are many situations in which two or more points can-

not b e scored, and it is thought that the game plan of

the players is to brand intentionally and to start the

next end in the rear end as well.

10 CONCLUSIONS

In this paper,the tactical elements obtained fro m the

analysis of opportunities to score goals in the compe-

titions with different rules were perform ed by PCA.

The change in the men’s Japan Championships

2017 to Japan Championships 2022 indicated that

scoring points by doing steal are important. There

was no signiﬁcant change from Japan Champion ships

2022 to Japan Cha mpionships 2023. We consider that

there was no change in the men’ game because they

are able to throw the takeout shot more powerfully

and thus are able to overco me the situation even in

Figure 7: Contribution rate - PC1(Women).

Figure 8: Contribution rate - PC2(Women).

a disadvantageous situation. Therefore, the No Tick

Zone Rule was considered to be a n ineffective rule in

the men’s competition.

The changes from Japan Championships 2017 to

Japan Championships 2022 for women showed the

same importance of scoring by stealing as for men.

In addition, the importance of stealing was also in-

creased from Japan Championships 2022 to Japan

Championships 2023.

From these results, it is considered that the rule

revision in curling has increased the advantage of the

ﬁrst turn. In curling, it is generally believed that the

advantage is in the second turn, but a po int scored

in the ﬁrst turn is a big advantage. Therefore, it is

concider for the losing team to turn the game around

even wh e n there is a large difference in score.

In the future, we plan to conduct a more detailed

tactical analysis by dividing tactical ele ments such as

steal and blank end of rear attack, which were shown

to be important in this study, into each end, and to

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling

discuss the tactics. In addition, we will develop an

application to provide feedback to players ba sed on

the analysis of op portunities for goals scored.

ACKNOWLEDGEMENTS

This work was supported by the “Functional Develop-

ment Project for Resilient Athlete Support” of Japan

Sports Agency.

REFERENCES

Bradley, L , J.(2009) The Sports Science of Curling. A Prac-

tical Review. Journal of Sports Science and Medicine

vol.8, pp.495-500.

Yanagi, H., Miyakoshi, K., Nakajima, Y., Yamamoto, N.

Development of Curl- ing Brush for Measuring Force

Exerted During Sweeping. Proceedings of the 30 In-

ternational Conf. on Biomechanics in Sports, pp.354-

356 (2012).

Takahashi, S. Support the Japan Women ’s Curling National

Team by a Trainer. Journal of Training Science for

Exercise and Sport 23(1): 7- 12 (in Japanese) (2011).

Masui, F., Hirata, K., Otani, H., Yanagi, H. and Ptaszynski,

M. Informatics to Support Tactics and Strategies in

Curling. Int J of Automation Technology Vol. 10,No.2,

pp.244-252 (2016).

Fujimura, A. and Sugihara, K.(2004) Quantitative Evalu-

ation of Sport Teamwork UsingGeneralized Voronoi

Diagrams. IEICE Transactions D J87- D2:818-828.

Kagawa, M. Effect of Multimedia Information on Web

Pages in Physical Training Class of University. Jour-

nal of Japan S ociety for Educational Technology 29

37-40(2006)

Otani, H., Masui, F., Hirara, K., Yanagi, H., Ptaszyn-

ski, M. Analysis of curling team strategy and tac-

tics using curling informatics. In: 4th International

Congress on Sport Sciences Research and Technology

Support(2016)

Hirata, K., Masui, F., Hiromu, O., Yanagi, H., Ptaszynski,

M. Support to strategies and tactics in curling sport

utilizing game information database - analysis of char-

acteristics of position based on shot scores. In: Pro-

ceedings of the 34th International Conf. on Biome-

chanics in Sports, P0523433 (2016)

Myeong-Hyeon Heo and Dongho Kim. The development

of a curling simulation for performance improvement

based on a physics engine. In: 6th Asia-Paciﬁc

Congress on Sports Technology (A PCST),P rocedia

Engineering 60(2013) 385-390

Duda, R. O., Hart, P. E., Stork, D . G. (2001). Pattern Clas-

siﬁcation, 2nd Edition. Wiley-Interscience.

Satomi, T., Sakabukuro, K., Yasukawa, I., Fukagawa, R.

(2009). Real-time landslide risk assessment of impor-

tant cultural heritage sites on back slopes using princi-

pal component analysis for rainfall. Journal of Japan

ChampionshipsE, Series CC, Vol. 65, No. 2, 564-578.

APPENDIX

PCA(Principal Component Analysis). The con-

cept of PCA is d escribed in section 6. In th is sec-

tion, we describe the speciﬁc calculation method of

PCA. First, n data ( x

i[j=1,2,···,m;i=1,2, ···,n]) for m

variables x

,···,x

are standardized using e quation

(1) so that th e mean and variance of all data means

are z ero and one respectively. This is done so that the

principal components do not change depending on the

unit setting of the data, making it difﬁcult to interpret

the results of the analysis.

−

√

j j

(1)

where

is the m ean of the variable x

, s

j j

is the

variance of the variable x

, the principal component

of the da ta z

is expressed as a linear expression as in

equation (2), and the variance V(z

) of this principal

component is equation (3).

= a

1 j

+ a

2 j

+ ···+ a

m j

(2)

V (z

) =

∑

i=1

−

)

= s

+ s

+ ···+ s

∑

j=1

∑

k=1

(3)

where a

are the coefﬁcients of the principal com-

ponen ts (a

= (a

1 j

, a

2 j

, ··· ,

m j

), j = 1, 2, ··· , m),X

( j = 1, 2, ··· , m) are the stan-

dardized variables in equation (1) and S

are the vari-

ances and covariances. Principal component analysis

is an analytica l m ethod to determine the coefﬁcients

of equation ( 2) such that the amount of new in-

formation obtained is maximized, which must satisfy

equation (4) as a constraint co ndition for the variance

v(z

) in equa tion (3) not to become inﬁnitely large.

+ a

+ ···+ a

= 1 (4)

The present problem, in which the ob je ctive is to

determine the coefﬁcient a

when the variance V(z

)

is maximum, using Eq. (4) and the Lagrange undeter-

mined multiplier method, is equivalent to solving the

eigenvalue problem in Eq.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

= λa;V =







b ··· s

··· s







, a =













(5)

where λ are the e igenvalues of the covariance ma-

trix V and a is the eigenvector corresponding to the

eigenvalue λ. The principal component using the

eigenvector corresponding to the largest e igenvalue

among the obtained eigenvalues λ is the ”ﬁrst prin-

cipal component”, followed by the ”second principa l

component, ···”. Then, the princ ipal component val-

ues calculated for each data using eq uation (2) are

called ”principal component scores”. The ”contribu-

tion ratio” is an indic ator of the degree to which the

ith principal component contains the original amou nt

of information, and it means the ratio of the eigenval-

ues of the ith principal component to the sum of the

eigenvalues, a nd the sum of the contribution ratios up

to the 1st i principal components is the ”cumulative

contribution rate”. [11]

Statistical Analysis of Recent Rule Revision Effects for Tactical and Strategic Elements in Curling