Optimizing CMA-ES with CMA-ES

Andr

e Thomaser

1,2 a

, Marc-Eric Vogt

1 b

, Thomas B

ack

2 c

and Anna V. Kononova

2 d

BMW Group, Knorrstraße 147, Munich, Germany

LIACS, Leiden University, Niels Bohrweg 1, Leiden, The Netherlands

Keywords:

Parameter Tuning, CMA-ES, Benchmarking, Mixed-Integer Optimization, TPE, SMAC, BBOB.

Abstract:

The performance of the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is signiﬁcantly affected

by the selection of the speciﬁc CMA-ES variant and the parameter values used. Furthermore, optimal CMA-

ES parameter conﬁgurations vary across different problem landscapes, making the task of tuning CMA-ES to

a speciﬁc optimization problem a challenging mixed-integer optimization problem. In recent years, several

advanced algorithms have been developed to address this problem, including the Sequential Model-based Al-

gorithm Conﬁguration (SMAC) and the Tree-structured Parzen Estimator (TPE).

In this study, we propose a novel approach for tuning CMA-ES by leveraging CMA-ES itself. Therefore, we

combine the modular CMA-ES implementation with the margin extension to handle mixed-integer optimiza-

tion problems. We show that CMA-ES can not only compete with SMAC and TPE but also outperform them

in terms of wall clock time.

1 INTRODUCTION

The Covariance Matrix Adaptation Evolution Strat-

egy (CMA-ES) (Hansen and Ostermeier, 1996) is a

popular algorithm used for solving complex black-

box optimization problems. It has gained signiﬁcant

attention due to its ability to handle nonlinear and

multimodal optimization problems. Over the years

several different variants have been developed, each

offering unique advantages (B

ack et al., 2013).

To achieve optimal performance with CMA-ES, it

is crucial to tune the parameters of CMA-ES and to

explore different CMA-ES variants (van Rijn et al.,

2016). However, manual parameter tuning can be la-

borious and time-consuming. As an alternative ap-

proach, automatic parameter tuning has been pro-

posed (B

ack, 1994; Grefenstette, 1986). This ap-

proach treats parameter tuning as an additional op-

timization problem besides the primary objective of

solving the original problem.

Therefore, tuning CMA-ES parameters involves

optimizing an optimization algorithm itself. The ob-

jective of such meta-optimization is to select the most

suitable set of parameter values to enhance the per-

https://orcid.org/0000-0002-6210-8784

https://orcid.org/0000-0003-3476-9240

https://orcid.org/0000-0001-6768-1478

https://orcid.org/0000-0002-4138-7024

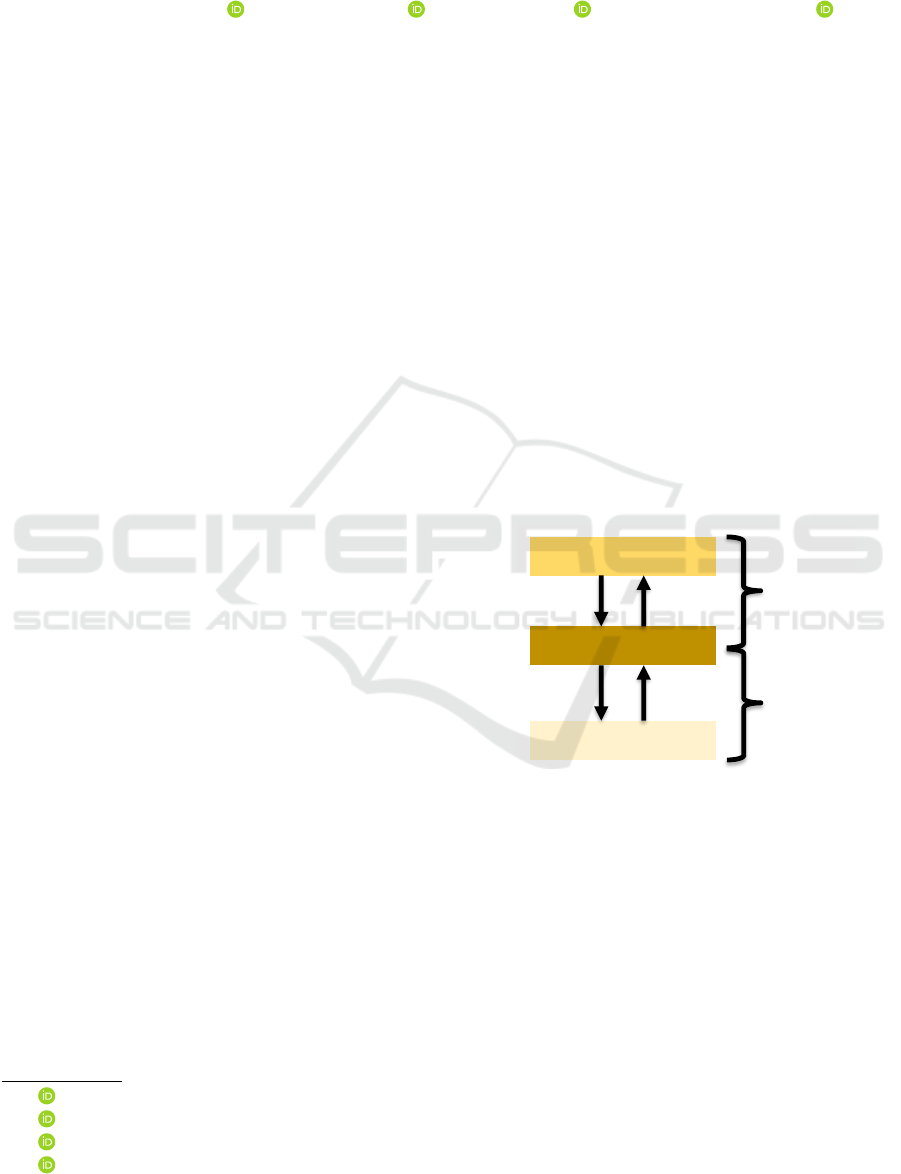
Meta-Algorithm

CMA-ES

Original Problem

problem

solving

parameter

tuning

algorithm

quality

solution

quality

optimize

Figure 1: Solving an optimization problem with CMA-ES

and parameter tuning with a meta-algorithm as two different

optimization problems (Eiben and Smit, 2011).

formance of the optimizer on the original optimiza-

tion problem. Figure 1 illustrates the relationship and

distinction between solving the original optimization

problem and tuning the parameters. While CMA-ES

optimizes the quality of solutions found (goodness

of solutions is referred to as ﬁtness) for the original

problem, a meta-algorithm is employed to optimize

the quality of the CMA-ES parameters (goodness of

performance is referred to as utility) (Eiben and Smit,

2011).

CMA-ES parameter tuning can be formulated as

a mixed-integer optimization problem where, in ad-

dition to continuous CMA-ES parameters, different

214

Thomaser, A., Vogt, M., Bäck, T. and Kononova, A.

Optimizing CMA-ES with CMA-ES.

DOI: 10.5220/0012179400003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 214-221

ISBN: 978-989-758-674-3; ISSN: 2184-3236

combinations of discrete parameter values and CMA-

ES variants can be selected to ﬁnd the optimal con-

ﬁguration. Several meta-algorithms have been devel-

oped to address such a challenge.

A popular algorithm for parameter tuning is

the Sequential Model-based Algorithm Conﬁguration

(SMAC) (Hutter et al., 2011). SMAC is a sequen-

tial model-based optimization (SMBO) approach that

combines Bayesian optimization with random for-

est regression models (Breiman, 2001). SMAC has

been successfully applied to various machine learn-

ing tasks, including algorithm conﬁguration, feature

selection, and deep neural architecture search (Feurer

et al., 2015; Lindauer et al., 2022).

Another SMBO algorithm is the Tree-structured

Parzen Estimator (TPE) (Bergstra et al., 2011). TPE

utilizes a distinct approach based on tree-structured

density estimation to efﬁciently search for optimal pa-

rameter settings. Tuning the parameters of CMA-ES

with TPE has been shown to improve the performance

of CMA-ES on a number of benchmark optimization

problems (Zhao and Li, 2018).

Recently, an extension of CMA-ES called CMA-

ES with margin (Hamano et al., 2022) has been in-

troduced. This extension enhances the capabilities of

CMA-ES to effectively handle discrete and mixed-

integer optimization problems. As a result, CMA-

ES with the margin extension can be used as a meta-

algorithm for solving the mixed-integer optimization

problem of tuning CMA-ES for speciﬁc optimization

problems.

The goal of this study is to explore the poten-

tial of CMA-ES with margin as a meta-algorithm for

tuning the parameters of CMA-ES. We conduct ex-

periments on several benchmark optimization prob-

lems and compare the performance of CMA-ES with

margin to that of SMAC, TPE, and random search.

First, we provide an overview of CMA-ES, its param-

eters, and its variants (Section 2.1). In addition, we

brieﬂy describe the margin extension, which speciﬁ-

cally addresses mixed-integer optimization problems

(Section 2.2). We then describe the experimental

setup and the software implementation employed in

our study (Section 3). Finally, we present the results

obtained from our experiments and engage in a com-

prehensive discussion of these results (Section 4).

2 CMA-ES

2.1 Parameters and Variants

The Covariance Matrix Adaptation Evolution Strat-

egy (CMA-ES) (Hansen, 2016; Hansen and Oster-

meier, 1996) is a group of iterative heuristic al-

gorithms designed to solve continuous optimization

problems with a single objective. In each genera-

tion g, a population denoted as x is generated, con-

sisting of λ offspring. These offspring are sampled

from a multivariate normal distribution characterized

by a mean value m

(g)

∈ R

, a covariance matrix C

(g)

∈

n×n

, and a standard deviation σ

(g)

∈ R

(g+1)

∼ m

(g)

+ σ

(g)

N (0,C

(g)

) ∀k = 1, ...,λ. (1)

Then, the best µ individuals are selected from the pop-

ulation to compute the new mean value m

(g+1)

with

the given weights w

(g+1)

∑

i=1

(g+1)

i:λ

, (2)

∑

= 1, w

≥ w

≥ ... ≥ w

. (3)

The covariance matrix C

(g)

is updated with the evolu-

tion path p

(g)

∈ R

(g+1)

= (1 − c

− c

∑

i=1

(g)

+ c

(g+1)

| {z }

rank-one update

∑

i=1

(g+1)

i:λ

(g+1)

i:λ

)

| {z }

rank-µ update

, (4)

(g+1)

= (1 − c

(g)

(2 − c

)µ

e f f

(g+1)

− m

(g)

, (5)

e f f

= (

∑

i=1

)

−1

, y

(g+1)

i:λ

(g+1)

i:λ

− m

(g)

, (6)

and the standard deviation σ

(g)

is updated with the

conjugate evolution path p

(g)

∈ R

and a damping pa-

rameter d

(g+1)

= σ

(g)

exp











(g+1)



N (0, I)



− 1









, (7)

(g+1)

= (1 − c

(g)

(2 − c

)µ

e f f

(g)

−

(g+1)

− m

(g)

. (8)

The optimization behavior of CMA-ES is determined

by the parameters λ, µ, c

, c

, and c

, which can be

tuned for speciﬁc functions or sets of functions (An-

dersson et al., 2015; Zhao and Li, 2018). More-

over, several variations of the CMA-ES were devel-

oped (B

ack et al., 2013). In this study, we examine the

Optimizing CMA-ES with CMA-ES

215

following variants within modular CMA-ES (de No-

bel et al., 2021; van Rijn et al., 2016): Active

Update (Jastrebski and Arnold, 2006), Elitism (van

Rijn et al., 2016), Mirrored Sampling (Brockhoff

et al., 2010), Orthogonal Sampling (Wang et al.,

2014), Threshold Convergence (Piad-Morfﬁs et al.,

2015), Weighted Recombination (Hansen and Os-

termeier, 2001), Restart with increasing population

(IPOP) (Auger and Hansen, 2005) or bi-population

(BIPOP) (Hansen, 2009), Bound Correction (Caraf-

ﬁni et al., 2019).

2.2 CMA-ES with Margin

The canonical CMA-ES is designed for continuous

problems. CMA-ES can be applied to discrete prob-

lems by rounding the continuous values from CMA-

ES to the allowed discrete values, resulting in plateaus

between the rounded values of size ρ (Hansen, 2011;

Thomaser et al., 2023a). However, its effective-

ness decreases. This limitation arises from the self-

adaption mechanism of the CMA-ES, which can

cause the variance of the mutation distribution to be-

come smaller than the granularity of the discretiza-

tion. In other words, when the mutation step is

smaller than the plateau size ρ, the optimization tends

to remain on the plateau.

To address this issue, Hamano et al. (Hamano

et al., 2022) introduced a modiﬁcation to CMA-

ES known as CMA-ES with margin (CMA-ESwM).

This approach involves incorporating a diagonal ma-

trix, denoted as A, into the mutation distribution

N (m, σ

ACA

). The purpose of this modiﬁcation is

to ensure that the marginal probabilities of the mu-

tation distribution are lower bounded, guaranteeing

a minimum probability α that the mutation steps are

larger than the plateau size ρ. The adaption of A and

m is performed in each generation.

In the proposed CMA-ES with margin, Hamano

et al. suggest using α =

λ n

as the default mar-

gin value. Experimental results on the bbob-mixint

testbed (Tu

sar et al., 2019) demonstrate that CMA-

ESwM outperforms several other methods, especially

in higher-dimensional scenarios.

3 EXPERIMENTAL SETUP

3.1 CMA-ES Performance Assessment

To optimize the performance of CMA-ES in solving

the original problem, a performance metric is needed.

Tuning the parameters of an optimization algorithm

with a ﬁxed budget will yield optimal parameters

only for that speciﬁc budget (Thomaser et al., 2023c).

Hence, to assess the effectiveness of an optimization

algorithm in terms of anytime performance, we utilize

the area under the curve (AUC) of its empirical cu-

mulative distribution function (ECDF) as a measure,

as suggested by Ye et al. (Ye et al., 2022). To com-

pute the ECDF curves, we consider 81 target values

logarithmically distributed from 10

to 10

−8

. The ob-

jective is to maximize the AUC value.

As the original optimization problems, we uti-

lize four from the black-box optimization benchmark

suite (BBOB) (Hansen et al., 2009). These functions,

namely F1, F4, F20, and F21, serve as benchmarks

for evaluating the effectiveness of CMA-ES. While

F1 and F4 have a global structure and are separa-

ble, F20 and F21 have no global structure and are

not separable. F1 is unimodal and F4, F20, F21 are

multimodal. To reduce the computational effort, we

consider the functions in two dimensions only.

In each run of the Covariance Matrix Adaptation

Evolution Strategy (CMA-ES), we allocate a maxi-

mum evaluation budget of 400 for the BBOB function

F1, and 2000 for the BBOB functions F4, F20, F21.

The reason for the smaller budget in the case of F1 is

that, unlike the other three functions, F1 is unimodal.

An optimization problem involves four instances of

the same BBOB function. We evaluate the ﬁrst four

instances of each BBOB function by performing 25

runs per instance, for a total of 100 CMA-ES runs.

This procedure is used to evaluate the effectiveness of

a CMA-ES conﬁguration by calculating the AUC.

3.2 Parameters and Meta-Algorithms

Table 1 presents an overview of the parameters and

variants of CMA-ES considered for tuning in this

study. The learning rates c

, c

, and c

are con-

tinuous, while the population size λ is an integer, and

the remaining variables are categorical. The values

considered represent a realistic problem faced by a

user who wants to ﬁnd a well performing conﬁgura-

tion of CMA-ES. Tuning these CMA-ES parameters

is a mixed-integer optimization problem.

To solve the mixed-integer parameter tuning op-

timization problem with CMA-ES itself, we use the

margin extension from (Hamano and Saito, 2022).

Furthermore, we combine the margin extension with

the modular CMA-ES (de Nobel et al., 2021; van Rijn

et al., 2016). This allows us to leverage variants such

as mirrored sampling within CMA-ESwM as a meta-

algorithm. Previous studies (Thomaser et al., 2023c;

Wang et al., 2014; Wang et al., 2019) have shown

that mirrored and orthogonal sampling generally im-

prove the exploration of CMA-ES. Increasing the ini-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

216

Table 1: Parameter space for tuning CMA-ES.

Parameter Description Variants and Parameters

Learning rate rank-one update ]0, 1]

Learning rate covariance matrix adaption ]0, 1]

Learning rate rank-µ update ]0, 1]

Learning rate step size control ]0, 1[

λ Number of children derived from parents {4,6,..,20}

Ratio of parents selected from population {0.3, 0.5, 0.7}

Initial standard deviation {0.2, 0.4, 0.6, 0.8}

Bound correction Correction if individual out of bounds {saturate, unif, COTN, toroidal, mirror}

Active update Covariance matrix update variation {on, off}

Elitism Strategy of the evolutionary algorithm {(µ, λ), (µ + λ)}

Mirrored sampling Mutations are the mirror image of another {on, off}

Orthogonal Orthogonal sampling {on, off}

Threshold Length threshold for mutation vectors {on, off}

Weights Weights for recombination {default, equal,

}

Restart Local restart of CMA-ES {IPOP, BIPOP}

tial standard deviation σ

and the population size λ

can also lead to better global performance. Therefore,

we increase the population size from 12 to 18 and the

initial standard deviation from 0.2 to 0.6 compared to

the default parameter values of modular CMA-ES.

We compare two versions of the CMA-ESwM as

meta-algorithm: one using the default values from

the modular CMA-ES, and another using a modiﬁed

CMA-ESwM with adjusted parameter values, as de-

scribed above. Both versions use saturation as the

bound correction method.

To handle categorical and integer values, a trans-

formation is required when using CMA-ESwM. To

accomplish this, we use the ordinal encoder and min-

max scaler provided by scikit-learn (Pedregosa et al.,

2011). First, integer and categorical values are ordi-

nal encoded, followed by scaling to the range [−5, 5],

which are the default values for the lower and upper

bounds within modular CMA-ES. Continuous param-

eters are only scaled to the same range of [−5, 5]. To

illustrate, the three considered values {0.3, 0.5, 0.7}

for the selection ratio µ

are ﬁrst ordinal encoded to

{0, 1, 2} and then scaled to {−5, 0, 5}.

For the purpose of comparison with the modular

CMA-ESwM, we used several other meta-algorithms,

namely SMAC3 (version 2.0.0) (Lindauer et al.,

2022), Optuna’s TPE sampler and Random sampler

(version 3.2.0) (Akiba et al., 2019), each using their

default conﬁgurations. Our evaluation budget for the

meta-algorithm was set at 3 000, and we performed

50 full parameter tuning runs on each BBOB function

for each meta-algorithm.

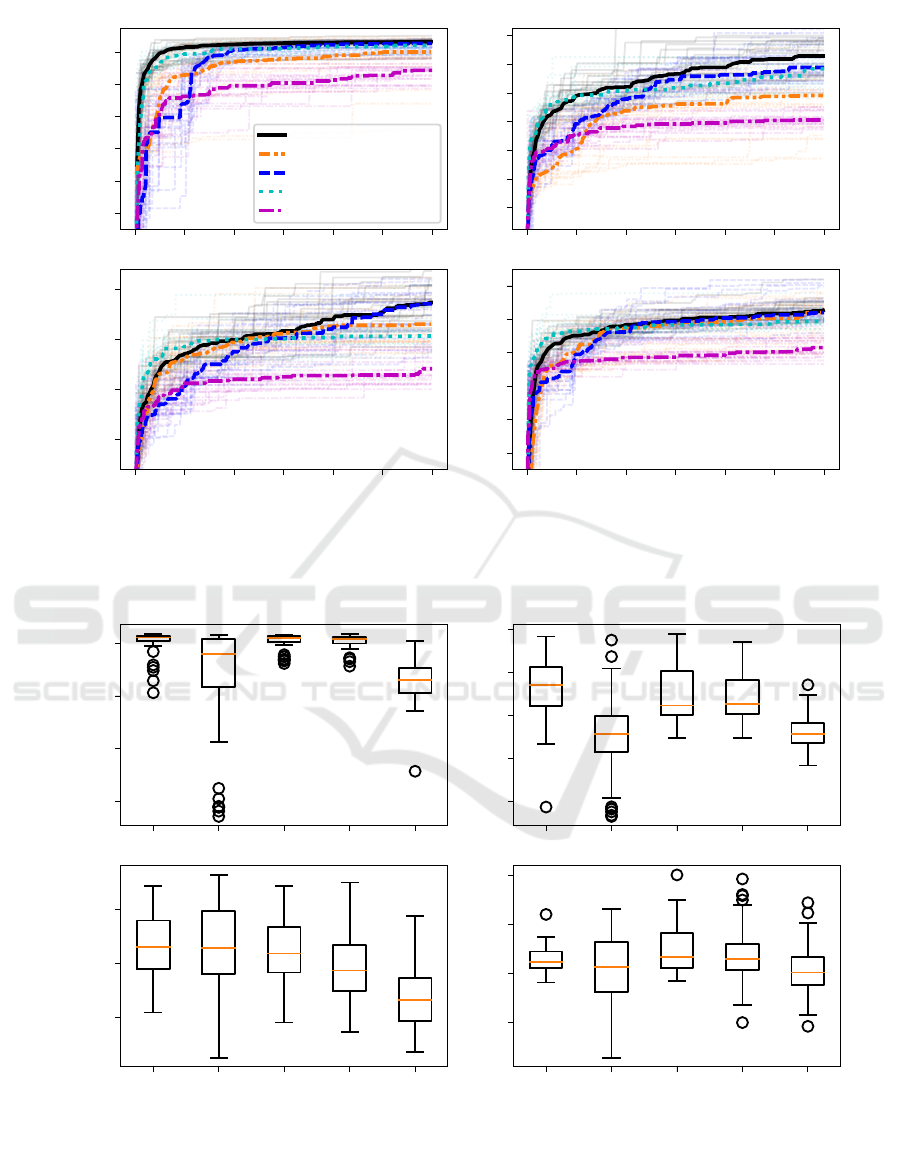
4 RESULTS

Figure 2 illustrates the average performance of CMA-

ES across 50 parameter tuning runs for each meta-

algorithm considered, on the four BBOB functions

F1, F4, F20, F21, which serve as the original opti-

mization problems. The objective is to maximize the

AUC. Each evaluation of a CMA-ES conﬁguration in-

volves 100 optimization runs on the original problem.

The results show that the majority of perfor-

mance improvements in CMA-ES parameters can be

achieved within the ﬁrst 1 000 evaluations for all four

BBOB functions. Subsequent improvements are rel-

atively small. Both the modiﬁed CMA-ESwM and

the TPE exhibit similar progressions over the eval-

uations, with TPE performing slightly better in the

early stages (up to 500 evaluations), and CMA-ESwM

mostly outperforming TPE thereafter. Around 500

evaluations, SMAC may initially appear slower in dis-

covering good solutions compared to the other algo-

rithms. However, its performance steadily improves

over time, reaching a similar performance compared

to the other meta-algorithms mentioned above. In

contrast, the random search stagnates and its progress

decreases signiﬁcantly after 500 evaluations. CMA-

ESwM with default parameters shows a worse perfor-

mance compared to the modiﬁed CMA-ESwM. This

emphasizes parameter tuning of CMA-ES, not only

for optimizing the original optimization problem but

also as a meta-algorithm for tuning itself.

To ensure a more accurate assessment of the best

conﬁguration found by a meta-algorithm, we rerun

the same conﬁgurations again 50 times for validation

and calculate the median. Figure 3 shows these vali-

dated AUC values.

Optimizing CMA-ES with CMA-ES

217

0.82

0.84

0.86

0.88

0.90

0.92

AUC

CMA-ESwM modified

CMA-ESwM default

SMAC

TPE

random

0.52

0.54

0.56

0.58

0.60

0.62

0.64

0 500 1000 1500 2000 2500 3000

Evaluations

0.65

0.70

0.75

0.80

AUC

F20

0 500 1000 1500 2000 2500 3000

Evaluations

0.84

0.86

0.88

0.90

0.92

0.94

F21

Figure 2: Median AUC values over evaluations of 50 runs (single runs transparent) for the different meta-algorithms consid-

ered for tuning CMA-ES parameters on the four 2-dimensional BBOB functions F1, F4, F20, F21.

0.86

0.88

0.90

0.92

AUC validated

0.52

0.54

0.56

0.58

0.60

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

0.62

0.64

0.66

AUC validated

F20

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

0.86

0.88

0.90

0.92

F21

Figure 3: Boxplot of the validated AUC values of the best CMA-ES conﬁgurations found by the different meta-algorithms on

each of the four BBOB functions considered. For each meta-algorithm and BBOB function, 50 parameter tuning runs were

performed. Each of the conﬁgurations found in this process is in turn validated by 50 validation runs.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

218

While CMA-ESwM with default parameters can

ﬁnd comparably good conﬁgurations, many are worse

than the solutions found by random search, especially

in the case of the two functions F1 and F4. In the me-

dian, the modiﬁed CMA-ESwM ﬁnds the best conﬁg-

uration for F1, F4, and F20. For F21 SMAC ﬁnds

the best conﬁguration, followed by TPE and the mod-

iﬁed CMA-ESwM. In summary, the modiﬁed CMA-

ESwM performs best in three out of four cases.

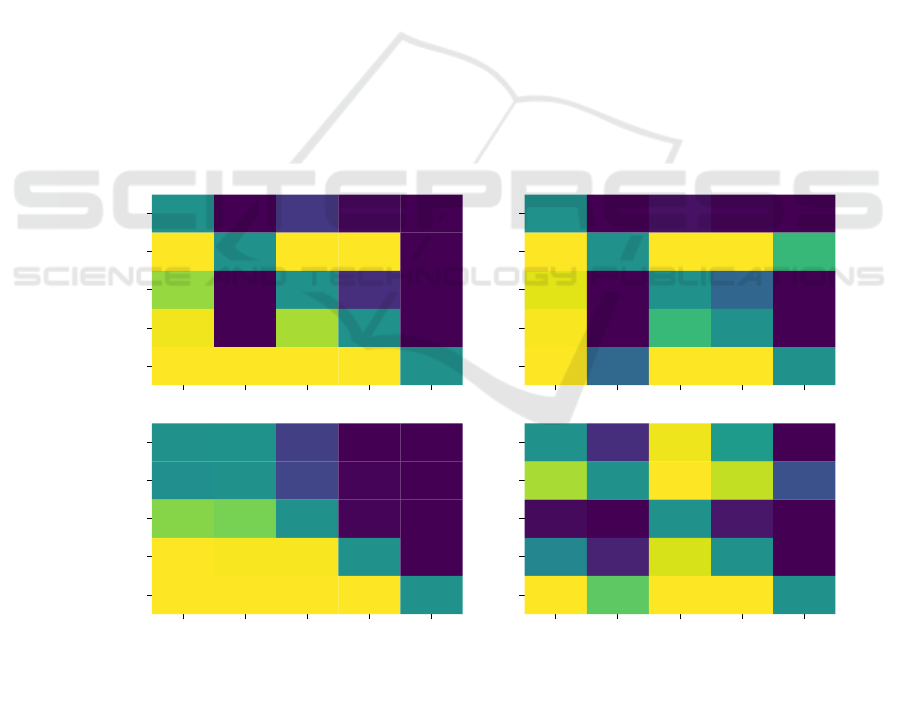
To further investigate whether the differences

in performance between the meta-algorithms are

statistically signiﬁcant, we employ the Mann-

Whitney U test (Mann and Whitney, 1947) within

SciPy (Virtanen et al., 2020) with the alternative hy-

pothesis greater. We compare the considered meta-

algorithms pairwise and for each considered function

(Figure 4). If the p-value is below 0.05, we reject

the null hypothesis in favor of the alternative hypoth-

esis, thus the performance of the algorithm (y-axis) is

greater than that of the other algorithm (x-axis).

The p-value of the modiﬁed CMA-ESwM,

SMAC, and TPE when compared with random search

is far below 0.05 for each function considered (last

column in Figure 4). Thus, based on the Mann-

Whiteney U test, our results show that the modiﬁed

CMA-ESwM, SMAC, and TPE outperform random

search as a meta-algorithm.

Moreover, regarding the Mann-Whitney U test,

the modiﬁed CMA-ESwM performs signiﬁcantly bet-

ter than TPE on F1, F4, F20, and SMAC on F4. Only

on F21 SMAC performs signiﬁcantly better than the

modiﬁed CMA-ESwM.

However, the modiﬁed CMA-ESwM, SMAC, and

TPE show similar performance but differ in their wall

clock times. On average, CMA-ESwM is the fastest

of the three. This advantage is due to its ability to

parallelize the population within a single generation,

while the others evaluate conﬁgurations sequentially.

This leads to the result that although the computa-

tional cost of evaluating a new conﬁguration within

random search is negligible, random search takes

about 50 % more time than CMA-ESwM to complete

a parameter tuning run. In contrast, both the SMAC

and TPE algorithms require about two to three times

more time than CMA-ESwM. This increased time is

due not only to their sequential evaluation procedures

but also to the additional internal computations and

model training involved in these methods, which will

not be lowered even if SMAC and TPE are imple-

mented with more parallelization.

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

0.5 1.6e-06 0.16 0.02 2.2e-15

1.0 0.5 1.0 1.0 0.00086

0.84 1.1e-05 0.5 0.13 1.2e-16

0.98 7.8e-05 0.87 0.5 6.4e-17

1.0 1.0 1.0 1.0 0.5

0.5 2.5e-10 0.046 0.01 2.3e-13

1.0 0.5 1.0 1.0 0.67

0.95 3.3e-09 0.5 0.33 1.1e-11

0.99 9.8e-09 0.67 0.5 3.2e-11

1.0 0.33 1.0 1.0 0.5

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

0.5 0.51 0.18 0.00052 1.2e-11

0.49 0.5 0.21 0.008 1.3e-07

0.82 0.79 0.5 0.01 2.1e-09

1.0 0.99 0.99 0.5 8.6e-06

1.0 1.0 1.0 1.0 0.5

F20

CMA-ESwM

modified

CMA-ESwM

default

SMAC

TPE

random

0.5 0.13 0.97 0.55 0.001

0.87 0.5 1.0 0.91 0.25

0.027 0.0034 0.5 0.061 1.6e-05

0.46 0.095 0.94 0.5 0.0039

1.0 0.75 1.0 1.0 0.5

F21

Figure 4: P-values from the Mann-Whitney U test (Mann and Whitney, 1947) with the alternative hypothesis greater when

comparing the performance of the ﬁve meta-algorithms considered pairwise with each other. The meta-algorithm on the

y-axis is compared to the meta-algorithm on the x-axis. If the p-value is below 0.05, the null hypothesis can be rejected in

favor of the alternative, thus the performance of the meta-algorithm on the y-axis is greater than the performance of the other

algorithm on the x-axis. To assess the performance of a meta-algorithm, 50 parameter tuning runs were performed.

Optimizing CMA-ES with CMA-ES

219

5 CONCLUSION

We have demonstrated signiﬁcant improvements in

the efﬁciency and effectiveness of CMA-ES by tun-

ing its parameters. To handle the mixed-integer meta-

optimization problem of parameter tuning, we used

CMA-ES with margin, which effectively handles the

discrete parameters. In addition, we combined the

margin extension with modular CMA-ES with or-

thogonal mirrored sampling activated and with in-

creased default population size and initial standard

deviation to improve global exploration. As a re-

sult, our CMA-ES conﬁguration for parameter tun-

ing competes with state-of-the-art algorithms such as

SMAC and TPE.

In terms of wall clock time, CMA-ES outperforms

SMAC and TPE due to its parallelization capability

and internal efﬁciency. This advantage further high-

lights the potential of CMA-ES in various domains.

It is worth noting that even with a simple random

search, we can ﬁnd a very good conﬁguration. Ran-

dom search is particularly advantageous in situations

where fully parallel execution is feasible.

Future research can focus on expanding the range

of original optimization problems considered and ex-

tending the study to other BBOB functions or bench-

mark sets. In addition, exploring the possibility of

tuning CMA-ES as a meta-algorithm with a third opti-

mization algorithm holds the potential for further per-

formance improvement.

The Python code to reproduce the described re-

sults has been made available on our Zenodo repos-

itory (Thomaser et al., 2023b). This repository also

contains the data of the results and additional code to

re-create the presented ﬁgures.

ACKNOWLEDGEMENTS

This paper was written as part of the project newAIDE

under the consortium leadership of BMW AG with

the partners Altair Engineering GmbH, divis intelli-

gent solutions GmbH, MSC Software GmbH, Techni-

cal University of Munich, TWT GmbH. The project is

supported by the Federal Ministry for Economic Af-

fairs and Climate Action (BMWK) on the basis of a

decision of the German Bundestag.

REFERENCES

Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama,

M. (2019). Optuna: A Next-Generation Hyperpa-

rameter Optimization Framework. In Proceedings

of the 25th ACM SIGKDD International Conference

on Knowledge Discovery & Data Mining, KDD ’19,

pages 2623–2631, New York, NY, USA. Association

for Computing Machinery.

Andersson, M., Bandaru, S., Ng, A. H., and Syberfeldt, A.

(2015). Parameter Tuned CMA-ES on the CEC’15

Expensive Problems. In 2015 IEEE Congress on Evo-

lutionary Computation (CEC), pages 1950–1957.

Auger, A. and Hansen, N. (2005). A Restart CMA Evo-

lution Strategy With Increasing Population Size. In

Proceedings of the IEEE Congress on Evolutionary

Computation, volume 2, pages 1769–1776.

ack, T. (1994). Parallel Optimization of Evolutionary Al-

gorithms. In Goos, G., Hartmanis, J., Leeuwen, J.,

Davidor, Y., Schwefel, H.-P., and M

anner, R., editors,

Parallel Problem Solving from Nature — PPSN III,

volume 866 of Lecture Notes in Computer Science,

pages 418–427. Springer Berlin Heidelberg, Berlin,

Heidelberg.

ack, T., Foussette, C., and Krause, P. (2013). Contempo-

rary Evolution Strategies. Natural Computing Series.

Springer Berlin, Heidelberg, Berlin, Heidelberg, 1st

ed. edition.

Bergstra, J., Bardenet, R., Bengio, Y., and K

egl, B. (2011).

Algorithms for Hyper-Parameter Optimization. In J.

Shawe-Taylor, R. Zemel, P. Bartlett, F. Pereira, and

K.Q. Weinberger, editors, Advances in Neural Infor-

mation Processing Systems, volume 24. Curran Asso-

ciates, Inc.

Breiman, L. (2001). Random Forests. Machine Learning,

45(1):5–32.

Brockhoff, D., Auger, A., Hansen, N., Arnold, D. V., and

Hohm, T. (2010). Mirrored Sampling and Sequential

Selection for Evolution Strategies. In Schaefer, R.,

Cotta, C., Kołodziej, J., and Rudolph, G., editors, Par-

allel Problem Solving from Nature, PPSN XI, Lecture

Notes in Computer Science, pages 11–21. Springer,

Berlin.

Carafﬁni, F., Kononova, A. V., and Corne, D. (2019). In-

feasibility and structural bias in differential evolution.

Information Sciences, 496:161–179.

de Nobel, J., Vermetten, D., Wang, H., Doerr, C., and B

ack,

T. (2021). Tuning as a Means of Assessing the Bene-

ﬁts of New Ideas in Interplay with Existing Algorith-

mic Modules. Technical report.

Eiben, A. E. and Smit, S. K. (2011). Parameter tuning for

conﬁguring and analyzing evolutionary algorithms.

Swarm and Evolutionary Computation, 1(1):19–31.

Feurer, M., Klein, A., Eggensperger, K., Springenberg, J.,

Blum, M., and Hutter, F. (2015). Efﬁcient and Ro-

bust Automated Machine Learning. In C. Cortes, N.

Lawrence, D. Lee, M. Sugiyama, and R. Garnett, edi-

tors, Advances in Neural Information Processing Sys-

tems, volume 28. Curran Associates, Inc.

Grefenstette, J. (1986). Optimization of Control Parameters

for Genetic Algorithms. IEEE Transactions on Sys-

tems, Man, and Cybernetics, 16(1):122–128.

Hamano, R. and Saito, S. (2022). CMA-ES with Margin.

Hamano, R., Saito, S., Nomura, M., and Shirakawa, S.

(2022). CMA-ES with Margin: Lower-Bounding

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

220

Marginal Probability for Mixed-Integer Black-Box

Optimization. In Proceedings of the Genetic and

Evolutionary Computation Conference, GECCO ’22,

pages 639–647, New York, NY, USA. Association for

Computing Machinery.

Hansen, N. (2009). Benchmarking a BI-Population CMA-

ES on the BBOB-2009 Function Testbed. In Pro-

ceedings of the 11th Annual Conference Compan-

ion on Genetic and Evolutionary Computation Con-

ference: Late Breaking Papers, ACM Conferences,

pages 2389–2396, New York, NY, USA. Association

for Computing Machinery.

Hansen, N. (2011). A CMA-ES for Mixed-Integer Nonlin-

ear Optimization: Research Report. Technical Report

RR-7751, INRIA.

Hansen, N. (2016). The CMA Evolution Strategy: A Tuto-

rial. Technical report.

Hansen, N., Finck, S., Ros, R., and Auger, A. (2009).

Real-Parameter Black-Box Optimization Benchmark-

ing 2009: Noiseless Functions Deﬁnitions. Technical

Report RR-6829, INRIA.

Hansen, N. and Ostermeier, A. (1996). Adapting Arbitrary

Normal Mutation Distributions in Evolution Strate-

gies: The Covariance Matrix Adaptation. In Proceed-

ings of the IEEE International Conference on Evolu-

tionary Computation, pages 312–317.

Hansen, N. and Ostermeier, A. (2001). Completely De-

randomized Self-Adaptation in Evolution Strategies.

Evolutionary Computation, 9(2):159–195.

Hutter, F., Hoos, H. H., and Leyton-Brown, K. (2011). Se-

quential Model-Based Optimization for General Al-

gorithm Conﬁguration. In Coello, C. A. C., editor,

Learning and Intelligent Optimization, volume 6683

of Lecture Notes in Computer Science, pages 507–

523. Springer Berlin Heidelberg, Berlin, Heidelberg.

Jastrebski, G. A. and Arnold, D. V. (2006). Improving

Evolution Strategies through Active Covariance Ma-

trix Adaptation. In IEEE International Conference on

Evolutionary Computation, pages 2814–2821.

Lindauer, M., Eggensperger, K., Feurer, M., Biedenkapp,

A., Deng, D., Benjamins, C., Ruhkopf, T., Sass,

R., and Hutter, F. (2022). SMAC3: A Versatile

Bayesian Optimization Package for Hyperparameter

Optimization. Journal of Machine Learning Research,

23(54):1–9.

Mann, H. B. and Whitney, D. R. (1947). On a test of

whether one of two random variables is stochastically

larger than the other. The annals of mathematical

statistics, pages 50–60.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,

Cournapeau, D., Brucher, M., Perrot, M., and Duch-

esnay,

E. (2011). Scikit-learn: Machine Learning

in Python. Journal of Machine Learning Research,

12(85):2825–2830.

Piad-Morfﬁs, A., Est

evez-Velarde, S., Boluf

e-R

ohler, A.,

Montgomery, J., and Chen, S. (2015). Evolution

Strategies with Thresheld Convergence. In 2015 IEEE

Congress on Evolutionary Computation (CEC), pages

2097–2104.

Thomaser, A., de Nobel, J., Vermetten, D., Ye, F., B

ack,

T., and Kononova, A. V. (2023a). When to be Dis-

crete: Analyzing Algorithm Performance on Dis-

cretized Continuous Problems. Technical report.

Thomaser, A., Vogt, M.-E., B

ack, T., and Kononova, A. V.

(2023b). Optimizing CMA-ES with CMA-ES - Data

and Code. https://doi.org/10.5281/zenodo.8256601.

Thomaser, A., Vogt, M.-E., Kononova, A. V., and B

ack, T.

(2023c). Transfer of Multi-objectively Tuned CMA-

ES Parameters to a Vehicle Dynamics Problem. In

Emmerich, M., Deutz, A., Wang, H., Kononova, A. V.,

Naujoks, B., Li, K., Miettinen, K., and Yevseyeva, I.,

editors, Evolutionary Multi-Criterion Optimization,

pages 546–560, Cham. Springer Nature Switzerland.

sar, T., Brockhoff, D., and Hansen, N. (2019). Mixed-

Integer Benchmark Problems for Single- and Bi-

Objective Optimization. In Proceedings of the Genetic

and Evolutionary Computation Conference, GECCO

’19, pages 718–726, New York, NY, USA. Associa-

tion for Computing Machinery.

van Rijn, S., Wang, H., van Leeuwen, M., and B

ack, T.

(2016). Evolving the structure of Evolution Strate-

gies. In 2016 IEEE Symposium Series on Computa-

tional Intelligence (SSCI), pages 1–8.

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.,

Reddy, T., Cournapeau, D., Burovski, E., Peterson, P.,

Weckesser, W., Bright, J., van der Walt, S. J., Brett,

M., Wilson, J., Millman, K. J., Mayorov, N., Nel-

son, A. R. J., Jones, E., Kern, R., Larson, E., Carey,

C. J., Polat, VanderPlas, Jake, Laxalde, D., Perk-

told, J., Cimrman, R., Henriksen, I., Quintero, E. A.,

Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pe-

dregosa, F., van Mulbregt, P., and SciPy 1.0 Contrib-

utors (2020). SciPy 1.0: Fundamental Algorithms

for Scientiﬁc Computing in Python. Nature Methods,

17:261–272.

Wang, H., Emmerich, M., and B

ack, T. (2014). Mirrored

Orthogonal Sampling with Pairwise Selection in Evo-

lution Strategies. In Proceedings of the 29th Annual

ACM Symposium on Applied Computing, SAC ’14,

pages 154–156, New York, NY, USA. Association for

Computing Machinery.

Wang, H., Emmerich, M., and B

ack, T. (2019). Mirrored

Orthogonal Sampling for Covariance Matrix Adapta-

tion Evolution Strategies. Evolutionary Computation,

27(4):699–725.

Ye, F., Doerr, C., Wang, H., and B

ack, T. (2022). Auto-

mated Conﬁguration of Genetic Algorithms by Tun-

ing for Anytime Performance. IEEE Transactions on

Evolutionary Computation, page 1.

Zhao, M. and Li, J. (2018). Tuning the hyper-parameters

of CMA-ES with tree-structured Parzen estimators.

In 2018 Tenth International Conference on Advanced

Computational Intelligence (ICACI), pages 613–618.

Optimizing CMA-ES with CMA-ES

221