Learning-Based Energy Consumption Model of Machining Processes

Using Gaussian Process Regression

Alicia Soto Bono

1,2

, Alan McGibney

1 b

, Susan Rea

1 c

and Kritchai Witheephanich

2 d

Nimbus Research Center, Munster Technological University, Cork, Ireland

Department of Electrical and Electronic Engineering, Munster Technological University, Cork, Ireland

Keywords:

Machining Processes, Digital Twin, Energy Efﬁciency, Gaussian Process Regression.

Abstract:

Currently, the global energy mix is largely dominated by the use of fossil fuels, with the industrial sector

accounting for a signiﬁcant portion of this demand. This results in a signiﬁcant carbon footprint. As such, the

manufacturing industry must become active participants in reducing their impact on the environment through

the r ealization of sustainable manufacturing practices. This study analyzes t he performance of a data-driven

model enhanced with machine learning techniques in order to build a digital twin that can update its parameters

in real-time in response to dynamic changes in t he energy consumption of a machining process. This t ype of

model is suitable for the application of a higher-level controller, such as a model predictive controller to

optimize the efﬁciency of the process operation. This paper proposes a digital twin modelling approach based

on Gaussian process regression, which updates model parameters wit h closed-loop data from the process in

real-time to retrain the model (evolving). The updating of the model online enables the model to maintain

accuracy over time despite changes in the system’s dynamics.

1 INTRODUCTION

The industrial sector accounts for more than 40% of

the world’s electricity consumption, and manufactur-

ing ﬁr ms consume nearly 50% of tha t energy (IEA,

2020). Energy efﬁciency plays an important role in

transforming factories to become more sustainable

and more environm entally friendly to address th e key

societal challenge of the d e pletion of energy resour c es

and the deterioration of the environment. However,

improving the energy efﬁciency in the manufacturing

process is a non-trivial task. This is due to the com-

plexity of ﬂexible manufacturing systems and their

power consumption dynamics.

The energy consumed by machining equipment in

discrete manufacturing processes has typically been

considered less sig niﬁcant compared to other manu-

facturing processes, e.g. the furnaces of steel indus-

tries, therefore, there is a lack of relevant research

on the energy efﬁciency and mod e ling of machining

processes despite the fact the overall impact on in-

https://orcid.org/0009-0002-7198-875X

https://orcid.org/0000-0002-0665-2005

https://orcid.org/0000-0002-4388-661X

https://orcid.org/0000-0002-0243-8917

dustrial c onsumption can be compelling (Gu e t al.,

2020). In (Moradn a zhad and Unver, 2017), it was

highlighted that improving the energy efﬁciency of

machine tools can be impactful, and more research is

required to develop methods to improve real-time en-

ergy optimiza tion beyond optimizin g time and costs.

In (Huang et al., 2023), an energy-saving con trol

strategy was developed for multi-sleep states of ma-

chine tools conside ring component priority. The re-

sults show that the control stra tegy considering c om-

ponen t priority (i.e. the order in which the com-

ponen ts of a machine tool are started up or shut

down) can obtain more stable produc tivity and a bet-

ter energy-saving effect compared to other control

strategies.

In enhancing the energy efﬁciency of machine

tools, two approaches are typically employed. Firstly,

developing machine too ls that are energy a nd

material-efﬁcient. Secondly, optimizing the machin-

ing process to conserve energy. The ﬁrst approach

needs a signiﬁcant monetary commitm e nt towards

modify ing the machine. Whereas, the second ap-

proach entails maximizing the efﬁciency of machin-

ing operations through scheduling optimiz ation and

management of both primary components and sup-

port units to minimize the usage of redundant en-

Soto Bono, A., McGibney, A., Rea, S. and Witheephanich, K.

Learning-Based Energy Consumption Model of Machining Processes Using Gaussian Process Regression.

DOI: 10.5220/0012180100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 127-134

ISBN: 978-989-758-670-5; ISSN: 2184-2809

127

ergy (Yi et al., 2020; Bermeo and Ocampo-Martinez,

2019; Quinn et al., 2022). The la tter can be carried

out by apply ing control strategies, e.g. Mod el p redic-

tive control (MPC), which has been extensively uti-

lized for industrial process optimization, resulting in

highly favourable outcomes (e.g., manufacturing sys-

tems (Lanzetti et al., 2019; Huang et al., 2023), c hem-

ical industry (Shin et al., 2020; Wu et al., 2019b),

and pharmaceutical industry (Wong et al., 2018)).

Moreover, it h as been more broadly implemented for

managing ene rgy efﬁciency (Bermeo and Ocampo-

Martinez, 2019). As a model-based control method,

MPC requires an accurate model of the controlled

system to enha nce its p e rformance. Wh e n it comes to

performance, MPC can outperform other control tech-

niques since predictions of the process permit control

actions to be calcu la te d based on future evolutions,

and it allows for preview information about references

and disturbances to be considered. Consequently, the

prediction model is a critical compon e nt of MPC (Ca-

macho, 2013).

Given the importance of an accurate mo del for

the perfo rmance of MPCs, most of the research in

learning-based MPC is focusing on improving the

model quality (Hewing et al., 2020; Narciso an d Mar-

tins, 2020). However the co mputation load required

to equate the prediction model ca n m ake the applica-

tion of the MPC in real time infeasible, e.g. compu-

tation ﬂuid dynamics (CFD) is a powerful modelling

tool, but its computation cost is large, making it pro-

hibitive for a rea l-time optimisation application ( Jeon

et al., 2019). Therefore, recent research has been fo-

cused on developing acc urate data-driven models suit-

able to be applied in real-time by a n MPC. These

methods include modeling the system’s dynamics

with machining learning (ML) technique s such as ge-

netic algorithms (GA) (e.g. (Huang et al., 2023)),

Gaussian process r egression (GPR) (e.g. (Park et al.,

2015; Maiworm et al., 2021)), decision trees, deci-

sion forests, logistic regression, support vector ma-

chine (SVM), neural network (NN) (e.g. (Shin et al.,

2020; Lanzetti et al., 2019; Wu e t al., 2019a)), and

Bayesian classiﬁers (Jordan and Mitchell, 2015).

In (Shin et al., 2020), an MPC framework using a

NN to model the system’s dynamics was developed.

The aim was to increase the speed of optimization

and accuracy of the model. The adoptio n of the NN

model instead of using the existing linearized model

enhances the operational efﬁciency o f the process in-

dustry. In (Wu et al., 2019a), a machine learning-

based pre dictive contro l system was deve loped for

nonlinear processes using an e nsemble of rec urrent

neural network (RNN) models. Their Lyapunov-MPC

formu lation employs ma c hine learning ensemble re-

gression modelling tools to improve the prediction ac-

curacy of RNN models and overall closed-loop per-

formance while parallel computing is utilized to re-

duce computation time. In (Lanzetti et al., 20 19), a

tailored RNN model for system identiﬁcation is pre-

sented. It is scalable a nd ﬂexible for handling com-

plex systems encountered in industrial applications.

The proposed framework is applied in an industrial

simulation case study, showing good performa nce in

dealing with challeng ing prac tica l conditions such as

multiple-input multiple-output (MIMO) co ntrol, non-

linearities, noise, and time delays. Which makes this

method scalable to machining pro cesses.

Degradation of mach ines and dynamic production

environments can result in variations of energy con-

sumption. In these uncertain situations, it is proposed

that optimizing the machining process using real-time

data is the most appropriate method. To achieve on-

line optimization, it is necessary to have an accurate

energy model that can cope with uncertainty relate d to

changes in machine componen ts and production pro-

cesses. Developing a new real-time predictive model

or digital twin using ML techniques can address this

challenge since it has the potential to capture inher-

ent dynamics and update parameters co ntinually dur-

ing operation . Unlike traditional system identiﬁcation

methods, most of which are suitable for ofﬂine pro-

cesses, this technology allows for real-time operation.

In (Hewing et al., 2020), the ad vantages of learning-

based MPC were explored, e. g. in c luding the ability

to ex ploit the abundance of data in a reliable m a n-

ner, particularly while taking safety constraints into

account. The proposed method addressed the auto-

mated and data-driven generation or adaptation of el-

ements of the MPC formulation such th a t the control

performance with respect to the desired clo sed-loop

system behavior is improved. The setup in which

this learning takes place can be diverse. For instance,

ofﬂine learning considers the adap ta tion of the con-

troller between different trials or episodes of a control

task, during which data are collected. In methods that

learn online, the c ontroller is adjusted during closed-

loop operation or using the data collected d uring one

task execution.

In (Park et al., 2015), energy prediction models

are developed for different subprocesses of a CNC

milling machine using a GPR model. The study in-

vestigates the effects of machining parameters on en-

ergy consumption and identiﬁes the optimum inp ut

features for the mode l of each different subprocess.

An uncertainty analysis is also presented to develop

conﬁdence boun ds for the prediction model. In ad-

dition, GPR can reﬁne the mod el online during op-

eration. GPR models are capable of efﬁcient on-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

128

line learning and can reduce the computation load

by limiting the number of training data points while

maintaining good performanc e . Gaussian pro cesses

are also ﬂexible and can handle non-linea r and non-

Gaussian systems (Maiworm et al., 2021).

Given the lack of research on the e nergy efﬁciency

of machining processes an d th e requir e ment of MPC

to have a sufﬁciently accurate model that enables real-

time op eration, this work proposes a modeling frame-

work based on GPR to capture the energy consump-

tion dynamics of machining processes. In addition,

the p roposed method is capable of online retraining

of the model (evolving), hence the accuracy of the

model is maintained even when the system’s dynam-

ics vary. M ost of the studies in this ﬁeld employ mod-

elling te c hniques such as GPR to model the system,

however, these models are built for prediction pur-

poses and are not applied in MPC applications. In

this work, a framework is provided fo r the develop-

ment of a GPR model that can be applied in MPC

applications for optimizing the energy efﬁciency of

machining processes.

2 MODELING AND EVOLVING

GAUSSIAN PROCESS

REGRESSION MODEL

In this work, a mo del using GPR to capture the sys-

tem’s energy consumption dynamics of a machining

process is built. The model is updated with new data

when changes in the physical properties of the proce ss

are detected . This enables for the capture of the un-

certainties and any variation of the system’s dynam-

ics du e to agin g or any environmental change that af-

fects the system’s dynamics. This allows the model

to improve and maintain accuracy over time. The on-

line training will b e performed using new measure-

ments obtained in c losed-loop operation. With this,

the model can be used as a control model for MPC

in order to op timize the energy consum ption and the

control perform ance can be improved over time by

utilizing the mea sured data. In wha t follows, the fun-

damentals of GPR are introduced. Then the evolving

GPR concept is described that will be applied to iter-

atively update the energy consumption model.

2.1 Gaussian Process Regression

A Gaussian process regression is a non-

parametric model with unce rtainty predic-

tions (S¨arkk¨a, 2019 ). The GP prior distribution

GP f (u) ∼ GP(m(u), k(u, u

′

)) is deﬁned by the

mean function m(u) = E[ f (u)] and the covariance

or kernel function k(u, z

′

) = cov[ f (u), f (u

′

)] =

E[( f (u) − m(u))( f (u

′

) − m(u

′

)))]. Where u is the

input called regressor and E is the expected valu e .

The mean and the covariance f unctions along with

their hyperp arameters θ deﬁne the GP. The GP is

then trained with a set of n measured input u and

output z data points deﬁned as the training dataset

D = {u, z} that will be used to infer the posterior

Gaussian distribution (Jeon et al., 2 019),

f (u|D) ∼ GP(m(u|D), σ

(u|D)). (1)

The mean function mostly used is a constant zero

prior mean m(u|θ) = 0 . The covariance fun c tion

deﬁnes the smoothne ss property of the functio ns,

which is usually selected to be the squared expo-

nential covariance function (S¨arkk¨a, 2019) . Then,

the hyper-parameters θ are determined maximizin g

the log margina l likelihood for the training data set

D = {u, z},

log(p(z|ω, θ)) = −

−1

z −

log|K|−

log(2π). (2)

One advantage of this modeling technique is that

it gives a regression mean of the p rediction along with

upper and lower error bars for the predicted values, a s

shown in Figure 1, which can be used as an estimate

of prediction uncertainty (S¨arkk¨a, 2019).

-1.5 -1 -0.5 0 0.5 1 1.5

input, x

-0.5

0.5

1.5

2.5

3.5

output, y

95% confidence intervals

Predicted

Measured

Figure 1: Ilustration of a GPR prediction.

2.2 Evolving Gaussian Process

Regression

Any change in the environmen t of the system, suc h as

humidity, temperature, noise, or aging may vary the

system’s dynamic and if the model is not updated to

capture th ose changes in the dyna mics the accuracy

of the predictions will be affected. For that reaso n,

the training dataset D = {u, z} needs to be updated so

the GP evolves with the real system (Maiworm et al.,

2021).

There are different criteria to decide if a new data

point needs to be include d in D = {u, z}. In (Mai-

worm et al., 2021), it is determined if a new data point

Learning-Based Energy Consumption Model of Machining Processes Using Gaussian Process Regression

129

is included if the prediction erro r e

and the variance

are higher than the determined thresholds ¯e and

respectively, i.e.

> ¯e (3)

. (4)

Increasing the number of data points will increase

the computation time for the prediction, which could,

at some point, make the model unfeasible for a real-

time optimization application su c h as MPC. There-

fore, there is a nee d to maintain the number of data

points n when evolving the GPR. Different metho ds

can be used to determine which data point should be

replaced with a new one, e.g.

• Erasin g the oldest data point.

• Erasin g the data point that provides less informa-

tion to the model (i.e. the one with the highest

value of accuracy when used f or prediction).

The ﬁrst method has less computational c ost,

while the second method would need to predict the

accuracy of the trainin g dataset at every time k the

model is updated ( Maiworm et al., 2021). In some

cases, the second meth od could be applied without

affecting the real-tim e performance of the model, e.g.

when the model is updated ofﬂine or if the compu-

tation time is less than the req uired prediction time-

step. In Section 5, the accuracy and computation time

of both methods is evaluated.

3 DATA ACQUISITION

This section describes the acquisition of training and

validation data. More details can be found in (Bhinge

et al., 2014). The data was used in (Park et al., 2015;

Bhinge et al., 2014; Ferguson and Park, a)

3.1 Training Data

The experiments were r un using a Mori Seiki NVD

1500 – Micro NC M illing machine with a 9.525 m m

diameter solid carbide tool to machine a 63 .5 mm x

63.5 mm x 56 mm cold ﬁnish mild steel 1018 ma-

terial. I t includes six basic c utting subprocesses: face

milling, countering, poc keting, slotting, spiraling, and

drilling, and three non-cutting subprocesses: air-cut

in x and y direction, air-cut in z-direction and rapid

motion (Bhinge et al., 2014 ).

Eighteen sample parts were machined. The face-

milling operations on the ﬁrst nine parts were carried

Database at: http://lma.berkeley.edu/raunak.html

out in the y-direction, while the r emaining nine parts

were milled in the x-direction. This ensures a better

prediction performance of the model since the data

covers both axes equally. In each part, the parameters

that affect the energy consumption the most are varied

so that every combination of them is applied for each

sample part. The spindle speed is measured in revolu-

tions per minute (RPM), the values used can be seen

in Table 1. The feed rate measured in millimeters per

minute is then obtained as the product of the spindle

speed in RPM, the chip load me a sured in millimeters

per tooth, and th e number of tool teeth (Bhin ge et al.,

2014).

3.2 Validation Data

Three test datasets were generated for validation in-

cluding six basic cutting subpro cesses: face milling,

pocketing, and drilling, and three no n-cutting sub-

processes: air-cut in x and y direction, air-cut in z-

direction, and rapid motion. In this case, th e spindle

speed (RPM) for each test data set were varied as it

can be seen in Table 1 (Bh inge et al., 2014).

Table 1: Parameters of the training and validation data.

Dataset Spindle Speed (RPM)

Tra ining {1500, 3000 , 4500}

Te st 1 {1500, 3000 , 4500}

Te st 2 {1700, 2800 , 4300}

Te st 3 {2125, 2400 , 3750}

4 GAUSSIAN PROCESS

REGRESSION BASED ENERGY

CONSUMPTION MODELS

In this section, f our different GPR-based energy con-

sumption models for machining processes are pre-

sented. The performance s are compared in Section

• Baseline mode l.

• Reduced training data set.

• Reduced training data set and evolved ofﬂine.

• Reduced training data set and evolved online.

The hyperparameters for the evolved models are

ﬁxed with the values obtained with the reduced

model, i.e . only the training dataset D = {u, z} is

modiﬁed when retraining. This means that after re-

training the model, there is no need to maximize the

log marginal likelihood again, which saves most of

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

130

the computation load o f the retrainin g process. MAT-

LAB packages: PMML (Ferguson and Park, b) and

GPML (Rasmussen and Nickisch, 20 20) were used to

generate, tr ain, optimize, store, and use for prediction.

4.1 Baseline Model

The b aseline model correspo nds to the model pro-

posed in (Park et al., 2015). Each of the 9 subpro-

cesses has a corresponding GPR model. Th e input

features or regressor s for each GPR model vary, as the

impact of input parameters o n the e nergy consump-

tion dynamics varies depending on the subprocess.

Table 2 shows w hich inputs were used for each sub-

process’s GPR m odel listed in order of importance,

i.e.

• Featur e 1 is the feed ra te (RPM).

• Featur e 2 is the spindle speed (mm/min).

• Featur e 3 is the depth of cut (mm).

• Featur e 4 is the a ctive tool axis ID. It is derived

from the length of the cut in each direction x, y,

and z.

• Featur e 5 is the cutting strategy ID. It is the

method for removing material.

Table 2: Input features of the GPR models by subprocess.

Feed Spindle speed (RPM) Input features

Cut

Facemilling {1, 2, 3, 4, 5}

Countouring {4, 1, 3, 2}

Slotting {4, 1, 2, 5}

Pocketing {4, 1, 2}

Spiraling {1, 4, 3}

Driling {1, 2, 4, 3}

No cut

Air cut in x and y {1, 2, 4}

Air cut in z {4, 1, 2}

Rapid motion {2, 4}

4.2 Reduced Training Data Set Model

In this model, the number of data points used in the

baseline model was reduced b y erasing data poin ts

from the training dataset D = {u, z}. The erased data

points were less meaningful data points for the model

e.g. the data points that we re predicted with the high-

est accuracy. Table 3 shows the difference in the num-

ber of trainin g d a ta po ints between the baseline and

the reduced models for each subprocess.

4.3 Ofﬂine Evolved Model

The reduced model is then evolved ofﬂine with data

from one of the validation datasets ofﬂine. This

Table 3: Number of tr ai ning data points of the GPR models

by subprocess.

Subpro cess Baseline model Reduced model

1 1466 733

2 425 212

3 134 67

4 168 134

5 16 8

6 18 14

7 122 120

8 140 139

9 24 24

method enables maintaining acc uracy with less c om-

putation time than the baseline model while it also en-

ables the updating of the model in order to adapt the

model to the changing dynamics of the system. Both

methods were evaluated to decide which data points

should be substituted, i.e.

• Erasing the oldest data point.

• Erasing the data point that provides less infor ma-

tion to the model.

4.4 Online Evolved Model

Our a im is to create an online learning GPR model

suitable to be applied by an MPC in real-time to op-

timize the operations of a machining proc ess. There-

fore, the threshold for substituting o ne of the train-

ing data po ints with a new one is evaluated every time

step. Both methods used f or the ofﬂine evolved mo del

to decide which data points are going to be substituted

are also benchmarked for this model.

5 RESULTS

The model has been tra ined and validated on a lap-

top machine equipped with an Intel Core i7-10610U

1.8GHz and 32GB RAM running MATLAB 2022b

64-bit with the PMML (Ferguson and Park, b) and

GPML (Rasmussen and Nickisch, 2020) packages.

Table 4 shows the accuracy of the baseline and

reduced models. Note that the accuracy o f the val-

idation is higher than the accuracy of th e training

since the training d ataset includes 9 machining sub-

processes, while the validation da ta sets only include

6 of the 9 subprocesses. It also shows that the ac-

curacy of the ba seline mo del is maintained when the

reduction of data points for training is carried out to

create the reduced model.

Table 5 shows the c omputation time for training

and the validation (prediction) processes, which are

signiﬁcantly reduced with the reduced mode l.

Learning-Based Energy Consumption Model of Machining Processes Using Gaussian Process Regression

131

Table 4: Accuracy of the baseline and reduced models.

Baseline Reduced

Dataset NMRSE(%)

Tra ining 74.0121 72.2632

Te st 1 84.4659 83.55 76

Te st 2 80.4416 79.40 65

Te st 3 68.4466 68.00 77

Table 5: Computation time of the baseline and reduced

models.

Baseline Reduced

Dataset Time (s)

Tra ining 28.27641 0.003509

Te st 1 50.34184 22.30064

Te st 2 48.66615 21.81061

Te st 3 50.06636 22.19655

Tables 6 an d 7 show that both evolved methods in

each metho d a) and b) maintain and even increase the

accuracy of the reduced model when predicting the

validation dataset. The a c curacy when predicting the

training dataset is the one ﬁxed in the reduced model.

Table 6: Accuracy of the evolved ofﬂine models.

Evolve ofﬂine

a) b)

Dataset NMRSE (%)

Tra ining 72.2632 7 2.2632

Te st 1 88.3044 88.1600

Te st 2 87.5672 86.8094

Te st 3 86.6200 86.8189

Table 7: Accuracy of the evolved online models.

Evolve online

a) b)

Dataset NMRSE (%)

Tra ining 72.2632 7 2.2632

Te st 1 86.1598 84.6490

Te st 2 85.4315 81.0116

Te st 3 76.3391 72.7208

In Ta ble 8 and 9 it can be observed that the com-

putation time for both evolving methods is similar.

The computa tional time shown in Table 5 represents

the computational time for predicting the full process,

while the c omputational time shown in Table 8 and

Table 9 represent the ave rage compu tational time for

predicting over an NC block.

Figure 2 shows the prediction s of the ba seline

model for Test 1, w hile Figures 3 and 4 show the

predictions of the evolved online model b) for Test

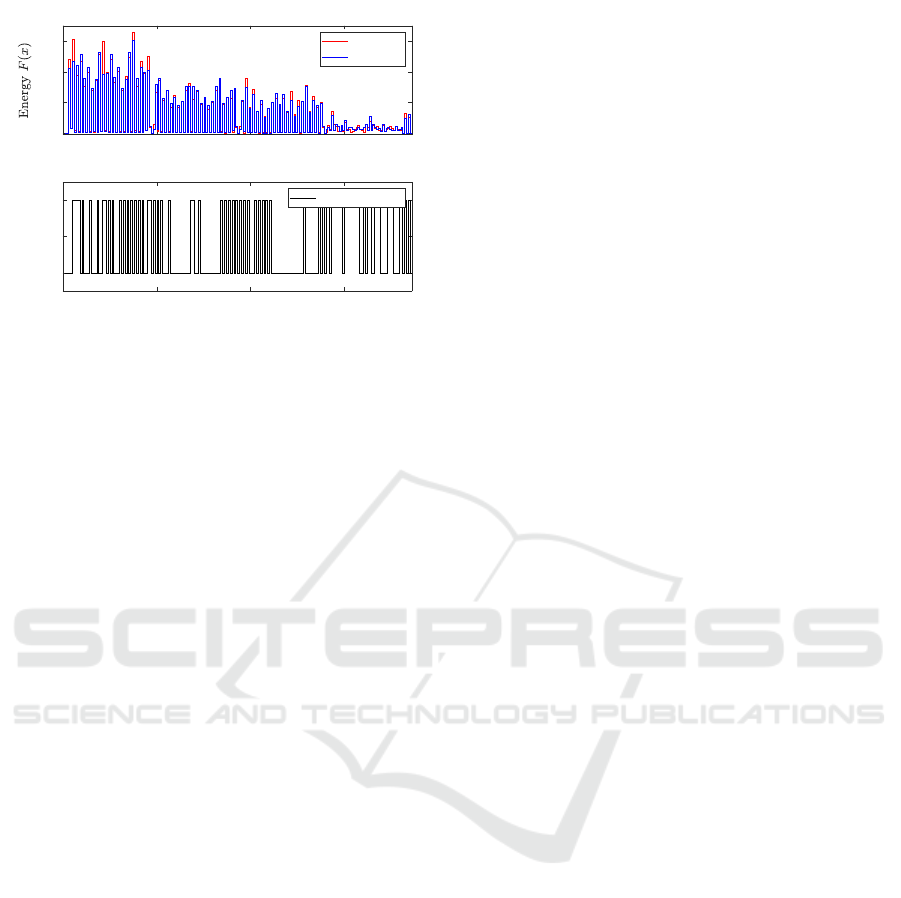
1. Figure 4 also shows at which NC block a train-

ing data point is substituted, e. i. wh en the thresh -

olds described by equations (3) and (4) are crossed.

Table 8: Computation time of the evolved ofﬂine models.

Evolve ofﬂine

a) b)

Dataset Time (s)

Tra ining 0.0033509 0 .003509

Te st 1 0.0045 0.0043

Te st 2 0.0048 0.0045

Te st 3 0.0052 0.0043

Table 9: Computation time of the evolved online models.

Evolve online

a) b)

Dataset Time (s)

Tra ining 0.003509 0.003509

Te st 1 0.00469 0.0075

Te st 2 0.00486 0.0074

Te st 3 0.00596 0.0088

86 88 90 92 94 96

NC block

100

200

300

400

Predicted

Measured

Figure 2: Measured values for Test 1 and predicted values

using the baseline model.

86 88 90 92 94 96

NC block

100

200

300

400

Predicted

Measured

Figure 3: Measured values for Test 1 and predicted values

using the evolved online model b).

For example, between NC blocks 85-95, the train-

ing data points are substituted in con secutively NC

blocks. Comparing Figures 2 and 3 it can be observed

that the pre dicted signal is c loser to the measured one

when using the evolved online model b). In Figure 4

it can be observed that between NC blocks 85-95 the

retraining of the mode l is carried out every two NC

blocks.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

132

0 50 100 150

NC block

200

400

600

Predicted

Measured

0 50 100 150

NC block

0.5

Retraining (1/0)

Figure 4: Measured values for Test 1 and predicted values

using the evolved online model b) and retraining signal.

6 CONCLUSION

The aim of this work is to build a digital twin that uses

a non-parametric regression model, i.e. Gaussian pro-

cess regression, suitable to be update d online allowing

the model to sustain its a ccuracy over time despite any

alterations that might oc cur in the system’s dynam-

ics. The performance of four different GPR models

was analysed. The baseline mo del demonstrates the

Gaussian process regression can be used to model the

energy consumption of a CNC machine. The reduced

model results demonstrate that the computation time

could be reduced when less re levant data points are

erased from the training data set while maintaining

accuracy. The ofﬂine evolved mo del results show the

reduced data po ints GP model can be retrained with

new data, so the model changes along with the real

system. Th e online evolved model demonstrate s that

the retraining of the model of the energy consumption

of a CNC machine can be done online. Both evolved

models, ofﬂine and online, have similar accuracy and

computation time, but the model evolved online will

include real-time changes in the system’s dynamics.

These results deter mine that online retraining of the

model to capture the changes in the behaviour of the

energy con sumption of a machinin g process in real

time is feasible.

A test be d is being built in order to collect new

data to analyse the performance of the evolved on-

line models. The computation time and accuracy

of the evolved online models meet the cha racter-

istics require d to build a DT–MPC framework to

model th e energy consumption of machining pro-

cesses enhanced with real-time adaptative learning of

the model and real- time optimization to reduce the en-

ergy consumption of the system. The literature review

on energy efﬁciency in machining typ ic a lly employs

alternative tec hniques for system modelling or GPR,

but does not incorp orate M PC for ene rgy efﬁciency

optimization. Thus, this study’s primary contribu-

tion is the proposed GPR model’s suitability for future

MPC applications in optimizing energy efﬁciency in

machining processes.

ACKNOWLEDGEMENTS

This research work has been supported by Science

Foundation Ireland (SFI) Co nﬁrm Centre for Smart

Manufacturin g ( CONFIRM), under Grant Number

SFI/16/RC/3918.

REFERENCES

Bermeo, M. A . and Ocampo-Martinez, C. (2019). Energy

efﬁciency improvement through mpc-based peripher-

als management for an industrial process test-bench.

IFAC-PapersOnLine, 52(13):648–653.

Bhinge, R., B iswas, N., Dornfeld, D., Park, J., Law, K. H.,

Helu, M., and Rachuri, S. (2014). An intelligent ma-

chine monitoring system for energy prediction using

a gaussian process regression. In 2014 IEEE Inter-

national Conference on Big Data (Big Data), pages

978–986. IEEE.

Camacho, Eduardo F., C. B. (2013). Model predictive con-

trol. Springer science & business media.

Ferguson, M. and Park, J. Energy consumption

prediction with gpr. https://github.com/maxkferg/

milling-energy-prediction. Online. Accessed May-

2023.

Ferguson, M. and Park, J. Gaussian process regres-

sion pmml package for matlab. https://github.com/

maxkferg/matlab-pmml. Online. Accessed May-

2023.

Gu, W., Li, Z., Chen, Z., and Li, Y. (2020). An energy-

consumption model for establishing an integrated

energy-consumption process in a machining system.

Mathematical and computer modelling of dynamical

systems, 26(6):534–561.

Hewing, L., Wabersich, K. P., Menner, M., and Zeilinger,

M. N. (2020). Learning-based model predictive con-

trol: Toward safe learning in control. Annual Re-

view of Control, Robotics, and Autonomous Systems,

3:269–296.

Huang, Z., Li, H., Cao, H., Wen, X., Ge, W., Wang, Q.,

Zhang, Q., and L i, C. (2023). Energy-saving con-

trol strategy for multi-sleep states of cnc machine tool

considering components priority. IEEE Transactions

on Industrial Electronics.

IEA, I. E. A. (2020). Key world energy stati stics 2020.

Jeon, K., Yang, S., Kang, D., N a, J., and Lee, W. B. (2019).

Development of surrogate model using cfd and deep

Learning-Based Energy Consumption Model of Machining Processes Using Gaussian Process Regression

133

neural networks to optimize gas detector layout. Ko-

rean Journal of Chemical Engineering, 36:325–332.

Jordan, M. I. and Mitchell, T. M. (2015). Machine learn-

ing: Trends, perspectives, and prospects. Science,

349(6245):255–260.

Lanzetti, N., Lian, Y. Z., Cortinovis, A., Dominguez,

L., Mercang¨oz, M., and Jones, C. (2019). Recur-

rent neural network based mpc for process i ndustries.

In 2019 18th European Control Conference (ECC),

pages 1005–1010. IEEE.

Maiworm, M., Limon, D., and Findeisen, R. (2021). Online

learning-based model predictive control with gaus-

sian process models and stability guarantees. Inter-

national Journal of Robust and Nonlinear Control,

31(18):8785–8812.

Moradnazhad, M. and Unver, H. O. (2017). Energy ef-

ﬁciency of machining operations: A review. Pro-

ceedings of the Institution of Mechanical Engi-

neers, Part B: Journal of Engineering Manufacture,

231(11):1871–1889.

Narciso, D. A. and Martins, F. (2020). Application of ma-

chine learning tools for energy efﬁciency in industry:

A review. Energy Reports, 6:1181–1199.

Park, J., Law, K. H., Bhinge, R., Biswas, N., Srinivasan, A.,

Dornfeld, D. A., Helu, M., and Rachuri, S. (2015). A

generalized data-driven energy prediction model with

uncertainty for a milling machine tool using gaus-

sian process. In International Manufacturing Science

and Engineering Conference, volume 56833, page

V002T05A010. American Society of Mechanical En-

gineers.

Quinn, W. , Cionca, V., Witheephanich, K., and Ozturk,

C. (2022). A learning factory framework: Chal-

lenges and solutions f or an irish university. IFAC-

PapersOnLine, 55(10):631–636.

Rasmussen, C. E. and Nickisch, H. (2020). Gpml mat-

lab code version 4.2. http://gaussianprocess.org/gpml/

code/matlab/doc/. Online. Accessed May-2023.

S¨arkk¨a, S. (2019). The use of gaussian processes in system

identiﬁcation. arXiv preprint arXiv:1907.06066.

Shin, Y., Smith, R., and Hwang, S. (2020). Development

of model predictive control system using an artiﬁ ci al

neural network: A case study with a distillation col-

umn. Journal of Cleaner Production, 277:124124.

Wong, W. C., Chee, E., Li, J., and Wang, X. (2018). Re-

current neural network-based model predictive control

for continuous pharmaceutical manufacturing. Math-

ematics, 6(11):242.

Wu, Z., Tran, A., Rincon, D., and Christoﬁdes, P. D.

(2019a). Machine learning-based predictive control

of nonlinear processes. part i: theory. AIChE Journal,

65(11):e16729.

Wu, Z., Tran, A., Rincon, D., and Christoﬁdes, P. D.

(2019b). Machine-learning-based predictive control

of nonlinear processes. part ii: Computational imple-

mentation. AIChE Journal, 65(11):e16734.

Yi, Q., L i, C., Ji, Q., Zhu, D., Jin, Y., and Li, L. (2020).

Design optimization of lathe spindle system for opti-

mum energy efﬁciency. Journal of Cleaner Produc-

tion, 250:119536.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

134