A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter

Optimization of a LSTM Network for Demand Forecasting of Retail

Products

Dr. Pravin Suryawanshi

, Sandesh Gaikwad

, Dr. Akansha Kumar

Akhil Patlolla

and Sai K. Jayakumar

Data Scientist, Jio Platforms Limited, Navi Mumbai, Maharashtra, India

Chief Data Scientist, Jio Platforms Limited, Hyderabad, Telangana, India

Product Manager, Jio Platforms Limited, Hyderabad, Telangana, India

Keywords:

Hyperparameter Optimization, Demand Forecasting, Genetic Algorithm, Bayesian Optimization, LSTM

Network.

Abstract:

Demand forecasting is highly inﬂuenced by the non-linearity of time series data. Deep neural networks such

as long short-term memory networks (LSTM) are considered better forecasters of such data. However, the

LSTM network’s performances are subject to hyperparameter values. This study proposes a hybrid approach

to determine the optimal set of hyperparameters of an LSTM model using Bayesian optimization and genetic

algorithm. Bayesian optimization explores the search space in the direction where the improvement over the

existing solution is likely, based on a ﬁtness function. At the same time, a genetic algorithm is an evolutionary

approach that can achieve global convergence by using selection, crossover, and mutation operators. The pro-

posed hybrid approach utilizes the strengths of both these algorithms to tune the values of the hyperparameter

of the LSTM network to minimize the forecasting error. In the dataset considered, we found that the hybrid ap-

proach reduced the forecasting error by approximately 27% compared to the Bayesian optimization approach.

Additionally, the proposed method is better than the genetic algorithm when performed independently, with a

decrease in error value by approximately 13%.

1 INTRODUCTION

The era of globalization, market competition, and

customer-centric businesses has made demand fore-

casting daunting. The accuracy of the forecast af-

fects the planning cycle of any retail business. A bet-

ter approach to forecasting can streamline the down-

stream supply chain operations and result in a bet-

ter customer experience. Recently, many predictive

approaches to forecasting have shown promising re-

sults. However, the non-linearity in demand, espe-

cially in the retail industry, multiplies the complex-

ity during predicting the target variable (Kumar et al.,

2020). Much work has been done on prescriptive

models in the areas of edge computing infrastructure

resource management (Viola et al., 2020), load fore-

casting in electricity supply (Johannesen et al., 2019),

call center arrival calls (Taylor, 2008), forecasting

of petroleum products (Sagheer and Kotb, 2019) and

others. Unlike in these scenarios, demand forecasting

in retail lacks a stable exogenous variable to guide the

forecasting process (Carbonneau et al., 2008). Thus,

it would be interesting to study and analyze the pat-

tern of demand information and minimize forecast-

ing errors while adopting advanced predictive analyt-

ics techniques. Demand forecasting for effective in-

ventory optimization falls under the purview of time-

series forecasting. Computational intelligence meth-

ods, like recurring neural network (RNN), have a spe-

cial feature of short-term memory, which utilizes the

prevailing input information to create effective future

decisions in case of time-series data (Parmezan et al.,

2019).

The prediction decisions with the memory cell

are categorized as a long short-term memory (LSTM)

network based on their strength of controlling infor-

mation for future decisions. A few issues often ob-

served in such models are variability in ﬁtting the

trend, training procedures, selection of algorithm,

and, most importantly, the selection of the optimal

set of hyperparameters. Often confused with internal

model parameters, hyperparameters are learned be-

230

Suryawanshi, P., Gaikwad, S., Kumar, A., Patlolla, A. and Jayakumar, S.

A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter Optimization of a LSTM Network for Demand Forecasting of Retail Products.

DOI: 10.5220/0012182900003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 230-237

ISBN: 978-989-758-674-3; ISSN: 2184-3236

fore the training phase of the actual time-series model.

They help in balancing the trade-off between model

accuracy and model execution by providing the best-

tuned parameters in a reasonable length of time.

As high model accuracy is vital, there is a need

to have the correct set of hyperparameters, the de-

sirable evaluation metric, the right choice of initial-

ization (with or without bias), etc., with reference to

hyperparameters. Theoretically, identifying hyperpa-

rameters has seen much advancement with the evo-

lution of different search techniques. For example,

random or grid search approaches have been tested

and proven to yield good results. With increasing net-

work structure, leading to a larger number of param-

eters and a larger search space, the performance of

such approaches has been observed to reduce (Feurer

and Hutter, 2019). It is interesting to combine meta-

heuristic approaches such as evolutionary-based ones

with BO, considering their abilities to reduce search

complexities, manage multimodal and nonlinear in-

put information, local and global searching strategies,

and achieve global optimum with fewer sets of tune-

able LSTM parameters. This makes the problem in-

teresting to study and motivates the research.

2 RELEVANT WORK

Several methods have been developed to address de-

mand forecasting challenges in retail. Most of them

rely on statistical intelligence methods. (Ramos et al.,

2015) designed a forecasting model based on state

space analysis and ARIMA (AutoRegressive Inte-

grated Moving Average) for a retail network for the

women’s footwear industry. The authors found that

state-space models outperform the ARIMA approach

in the case of out-of-sample data at the cost of high

computational efforts. It is also observed from past

research that the performance of statistical methods

such as ARIMA, moving averages, and exponen-

tial smoothing depreciates in the case of time series

with irregular and highly random features due to non-

linearity and data leakage (Abbasimehr et al., 2020).

Many studies have shown promising results consider-

ing advanced algorithms such as grid search, random

search, BO approach, etc. However, each technique

has disadvantages while training on large data sets.

In the grid search approach, the number of evalua-

tions increases exponentially with an increasing num-

ber of parameters making the grid search unproduc-

tive (Johnson, 2017). While in the random search,

due to higher variability and no intelligent decision-

making in selecting the optimal hyperparameters, the

method suffers from ﬂuctuations in the cost objec-

tive, resulting in relatively slower conversion (Kumar

et al., 2021). Furthermore, gradient-based approaches

are more likely to be trapped in a local optimum

(Frazier, 2018). Additionally, such approaches are

ineffective while handling categorical hyperparame-

ters, which is hardly the case with the BO approach

(Elsken et al., 2019).

On the contrary, the LSTM method under RNN

can create memory and forget cells to improve fore-

casting accuracy by preserving required patterns from

the past. (da Fonseca Marques, 2020) compared the

LSTM model with the seasonality-based ARIMA ap-

proach on a ﬁsh market retail network, considering

price, holidays, and whether the model features im-

proved prediction accuracy. Similar ﬁndings were ob-

served by (Abbasimehr et al., 2020) in the case of

a furniture company with a relatively stable demand

for real-time forecasting of time series data. Another

advantage of LSTM models is that they effectively

solve errors due to missing data and explore gradi-

ents using the built-in gates architecture that controls

the ﬂow of information among the cells (Cansu et al.,

2023). Often, the design of the LSTM network and

tuning of the hyperparameters is an intimidating task.

Thus, (Johnson, 2017) suggested the implementation

of hybrid approaches such as BO, evolutionary al-

gorithms, swarm-based intelligence techniques, and

others. Especially, evolutionary approaches have in-

herent qualities of not falling into the local optimal-

ity with gradient-free optimization features (Beheshti

and Shamsuddin, 2013).

Few studies mention the use of meta-heuristic

tools to create neural network infrastructure or speed

up the architecture’s performance by selecting opti-

mal tuning parameters. (Kumar et al., 2021) trained a

deep neural network model on stock market data us-

ing a genetic algorithm (GA) approach to ﬁnd the op-

timal set of network hyperparameters and data subset

selection. The main advantages of employing meta-

heuristic approaches are tuning multiple hyperparam-

eters and simultaneously providing near-optimal pre-

diction performance. Speciﬁc to demand forecasting

for retail goods, (Abbasimehr et al., 2020) designed

an LSTM network model as a forecaster and com-

pared the results with ARIMA and RNN approaches.

The authors did not use any evolutionary approaches.

Therefore, it will be interesting to study the design de-

cisions that affect the performance of the LSTM net-

work - more speciﬁcally, ﬁnding the architecture pa-

rameters of the LSTM network, identifying the hyper-

parameter tuning values, or reducing the dimension-

ality in the feature representation level of the LSTM

network.

A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter Optimization of a LSTM Network for Demand Forecasting of Retail Products

231

3 METHODOLOGY

3.1 Fundamentals of an LSTM Network

Lately, an LSTM model as a subset of RNN has been

adopted in many studies as a sequence prediction

approach considering their memory advantages and

input-output handling capabilities (Greff et al., 2016).

The advantages are evident with gates for input and

output and cell memory. Typically, an LSTM has an

internal storage system called a memory cell featured

with an internal state, different gates, and a mecha-

nism with which the internal state interacts with the

different gates in place.

Such functions are helpful to create the bounds on

the output variables with set range values generally

between 0 and 1. For every time step of the LSTM

implementation, the forget gate determines whether

to pass the current value of memory or completely

discard it. In contrast, the output gate controls the

inﬂuence of the memory cell on the output. An input

node with an activation function is often attached to

the gate. Primarily, the input gate advocates the ad-

dition of the input node’s value in the current state of

the memory cell. In our experimentation, the LSTM

architecture consists of two hidden layers, a tanh ac-

tivation function, and a single dense layer which is

trained using Adam optimizer with mean squared er-

ror as a loss function.

3.2 A Hybrid Solution Strategy

In this section, we propose a learning algorithm that

facilitates the execution of the LSTM model using a

hybrid approach based on BO and GA. Unlike pre-

viously attempted approaches of combined strategies

as in (Martinez-de Pison et al., 2019), the existing ap-

proach does not limit the number of model parameters

to ﬁnd the best features. Since most meta-heuristic

methods require an initial solution, the output from

the BO approach is fed as an initial solution to the

second stage of hyperparameter optimization. The

second stage uses GA with an initial population as ob-

tained from the BO output. With advanced operators

such as selection, crossover, and mutation, the best in-

dividual of some generations might be dropped during

iterations. To avoid these, an optional elitism strategy

is employed in the many GA-based approaches using

a simple hall-of-fame concept (Wirsansky, 2020). As

many best individuals as set by some constant integer

(i.e., the hall of fame parameter) will always be kept

in the mating pool of a population. We implement the

above concept with motivation and explanation men-

tioned by authors (Fortin et al., 2012) and (Wirsan-

sky, 2020). Such a strategy enhances the GA’s perfor-

mance by avoiding the wastage of time involved in re-

discovering the potential solution. The central idea of

the proposed hybrid strategy is depicted in Figure 1.

A mathematical description of the hyperparame-

ter optimization process is described below, with the

importance of the BO approach. Let F(h) be a given

loss function, i.e., Root Mean Square Error (RMSE).

In our case it is represented by Equation 1 and is sub-

jected to optimize over h

, h

, ··· , h

hyperparameters

and each of these hyperparameters (h

) have lower and

upper bounds [l

, u

] in a conﬁguration or hyperparam-

eter space Ω = [l

, u

] × ··· × [l

, u

F(h) =

∑

i=1

− ˆx

)

(1)

Where x

and ˆx

are the actual and forecast values

of the series in time point i, respectively.

However, computing the true objective function

is an expensive exercise. Thus, a surrogate model is

built with the acquisition function mentioned in Equa-

tion 2, which is relatively cheaper to evaluate.

∗

= argmin

h∈Ω

f (h|φ

1:i−1

) (2)

Where y is the true ﬁtness value and φ is a search

space of h and y. With every iteration, more samples

are added to the surrogate model with their respec-

tive acquisition function until a termination criterion

is reached.

The fundamental understanding of every evolu-

tionary algorithm follows the principle of the survival

of the ﬁttest individual in a search pool comprising

feasible and infeasible candidate solutions. To eval-

uate the quality of the solution, a ﬁtness measure in

terms of the objective function is employed. Often,

operators are employed in such meta-heuristics to im-

prove the candidate solution to intensify (exploita-

tion) and diversify (exploration). Some key termi-

nologies in the evolutionary algorithm are elucidated

as follows.

Selection operations are one of the fundamental

tasks in the evolutionary approach. Many parents are

selected depending on their ﬁtness strength from a set

of solution pools at each iteration. Often, this ﬁlter-

ing is performed with the help of some set criteria. In

the proposed study, we used tournament selection to

ﬁnd the best candidates, which will result in the next

generation or be a part of it (Deb and Jain, 2013).

The Crossover operator produces a diversiﬁed solu-

tion by searching different regions within the given

solution space. In contrast, the mutation operator

produces a high-quality solution by intensifying the

search within the given region of solution space. We

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

232

Figure 1: Flowchart for the proposed hybrid approach.

implemented a crossover option using simulated bi-

nary crossover and a mutation method based on poly-

nomial mutation as popularly considered in NSGA II

implementation (Deb and Jain, 2013).

4 PROBLEM DESCRIPTION,

EXPERIMENTAL SET-UP AND

RESULTS

Inventory optimization is a critical task across differ-

ent sectors of the business. Especially, fast-moving

goods pose alarming challenges in dealing with de-

mand uncertainty as it involves a huge amount of

monetary investment, time criticalities, and technol-

ogy infrastructure to manage operational challenges

and maintenance scenarios (Fildes et al., 2022). Addi-

tionally, the time series data features make forecasting

efforts more challenging. First, a high-dimensionality

problem is complex due to too many variables and

too little data information. Second, the intermittent

and promotion-driven episodes drive the random de-

mand as completely non-stationary, exhibiting vari-

able trends, i.e., the series’ frequency, mean, and vari-

ance undergo several changes over time. The prod-

uct properties and nature of the business model fur-

ther complicate the problem and may result in non-

linearity and heterogeneity (Lang et al., 2015). Build-

ing a capability of predicting highly ﬂuctuating de-

mand data would be an interesting problem to study.

However, in many situations, the results of such learn-

ing algorithms are governed by a set of hyperparam-

eters. For example, some good examples of such

top-level parameters are the number of hidden layers,

dropout rate, epoch size, batch size, learning rate, etc.

(Reimers and Gurevych, 2017). The optimal selection

of such hyperparameters improves the model’s perfor-

mance. Therefore, choosing the right set of hyperpa-

rameters and their values is a prominent question to

address before implementing the learning model.

The subsequent sections trigger the need to imple-

ment the hybrid approach to identify the optimal sets

of hyperparameters for a better LSTM network pre-

diction. We perform independent simulations for dif-

ferent approaches proposed in subsections to ﬁnd the

optimal values of the hyperparameters. It is also im-

portant to note that the experiments are performed on

an Apple M1 Pro chip with 16 GB of RAM and a ten-

core CPU. The description is further categorized into

sub-sections to explain preliminary results related to

each approach. The basic information about the non-

linearity and causality in the uni-variate forecasting

random variable is presented in Figure 2. The un-

A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter Optimization of a LSTM Network for Demand Forecasting of Retail Products

233

derlined time series demand data of retail products

consists of trends, seasonalities, and errors in terms

of residues. For example, an upward trend shows an

increase in demand values. Seasonality explains the

cyclic pattern occurring at regular intervals. In addi-

tion, a residue component is present in the time se-

ries data, which is neither systematic nor predictable

(Parmezan et al., 2019).

Figure 2: Decomposition of time series demand data.

Additional information related to the parameter

setting is as follows. Five major hyperparameters re-

lated to LSTM are considered for our experimenta-

tion. The details of which, as mentioned in the Keras

documentation (Chollet et al., 2015), is as follows:

1. Units of layer: This represents the dimensionality

of the output space and is a positive integer. We

have taken two hidden layers in the LSTM net-

work with units varying from 10 to 25.

2. Dropout: This hyperparameter decides the frac-

tion of the units to drop for the linear transfor-

mation of the inputs and takes a continuous value

between 0 and 1.

3. Batch size: This deﬁnes the number of samples

per gradient update. We took a lower and upper

bound for the batch size of 16 and 64, respectively.

4. Epochs: This decides the number of epochs to

train over the LSTM model, which is a positive

integer. Epochs are between 5 and 15 during sim-

ulation.

5. Learning rate: This hyperparameter decides how

fast the LSTM model updates its parameters. This

parameter takes a value between 0 and 1. With a

very high learning rate value, the model may not

converge, and a very low learning rate will slow

down the learning process.

GA requires a few parameters such as population

size, probabilities for crossover and mutation, maxi-

mum number of generations, and population size for

the Hall of Fame. For our experiments, we have ﬁxed

the values of these parameters with well-known stan-

dard values as described by (Fortin et al., 2012). For

example, probabilities of crossover and mutation are

taken as 0.5 each, respectively. Similarly, the crowd-

ing factor for mutation is 15, and the same is 10 for

crossover operations. Additionally, an integer value

of 2 for the Hall of Fame is considered throughout the

simulations.

4.1 BO for LSTM Network

Implementation

BO is used as a hyperparameter optimization tool in

various machine learning models and in well-known

Python libraries for building neural networks. The

methodology section fairly explains the execution of

the BO approach. This section highlights some key

computation implications related to the methodology.

The BO implementation is as per (Balandat et al.,

2019). The recorded objective (RMSE) shows a de-

clining trend with increasing execution time as the

number of iterations is increased (Figure 3).

Figure 3: Iteration vs. Mean RMSE score of BO approach

for one of the simulations.

4.2 GA with Elitism

The implementation is based on the DEAP library by

(Fortin et al., 2012). One of the major decisions on

population size (P1) and number of generations (P2)

is decided by a trial-and-error approach to understand

the implementation of the GA with elitism approach.

Different combinations of P1 and P2 are taken to

identify their best values based on fair number of ﬁt-

ness evaluations (population size multiplied by num-

ber of generations). We elucidate the behavior of the

RMSE score in Figure 4. We observed that a popu-

lation size of 20 and a number of generations of 10

has given better performance compared to other sets

of combinations. Thus, we ﬁx these values through-

out experimentation. Fixing the values of P1 and P2 is

a subjective question and depends on the dataset and

search strategy employed within the optimization al-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

234

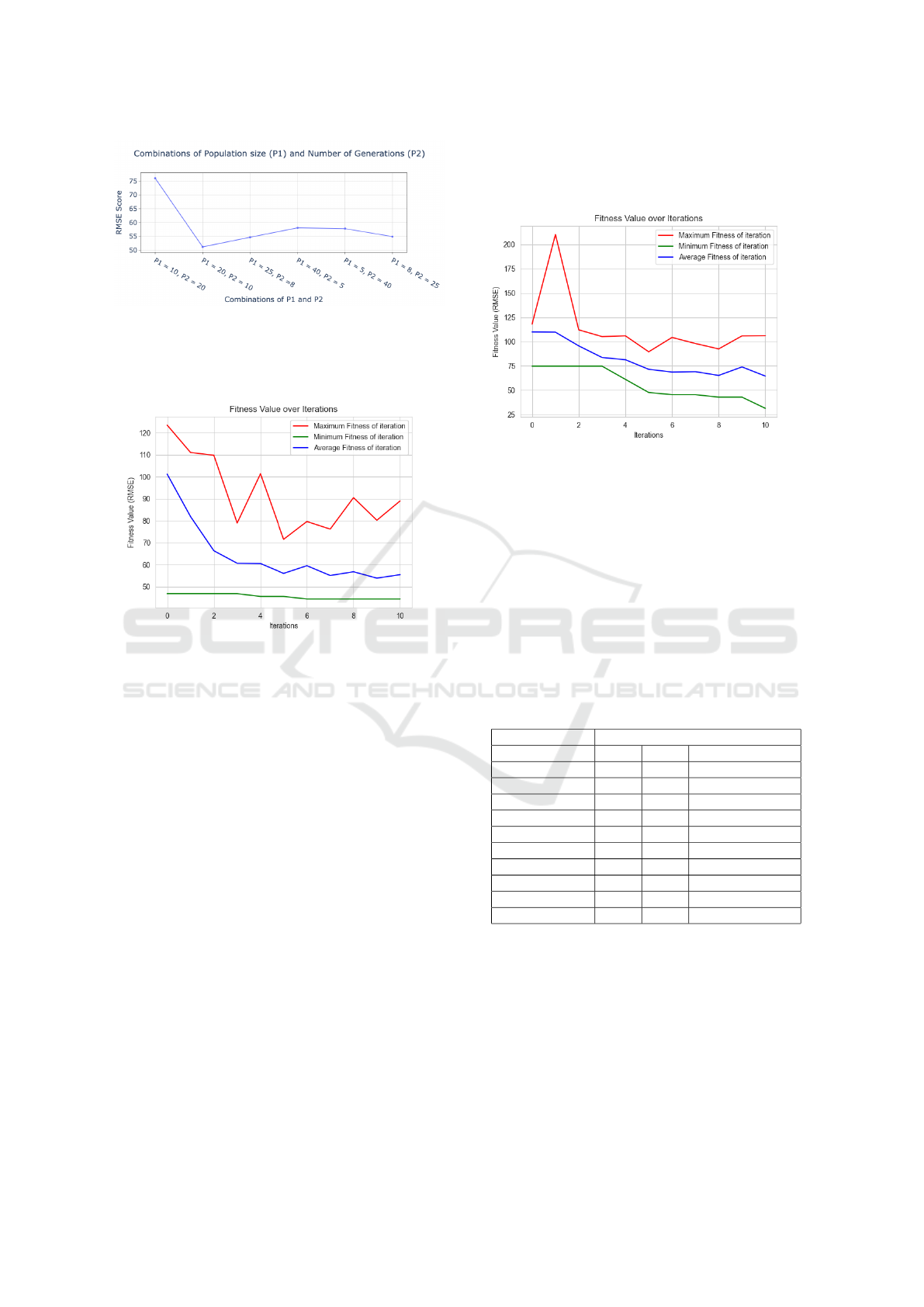
Figure 4: Trial-and-error approach for ﬁxing values of pop-

ulation size (P1) and number of iterations (P2).

gorithm. Therefore, the approach is sensitive toward

the optimal set of both these parameters.

Figure 5: Iteration vs. RMSE score of GA approach for one

of the simulations.

Figure 5 shows three series plots for maximum,

minimum, and averages of RMSE score evaluated for

the population during each iteration of the GA ap-

proach. For example, at every iteration, the algorithm

selects some set of parents out of a population pool of

20. It is observed that over the iterations, the ﬁtness

value shows a declining trend. In the instance above,

the minimum value of RMSE achieved is 46.9765.

4.3 Proposed Hybrid Strategy for

Hyperparameters Tuning

The current section mentions results related to the

combined strategy proposed in the paper. Primar-

ily, we highlight the need and advantages of adopt-

ing such approaches to model LSTM networks sub-

ject to optimal conﬁgurations of hyperparameters. It

is important to note that most of the meta-heuristics

are given an initial solution to start with. We utilize

the surrogate output from the BO to warm start the

search space for a hybrid approach. This was primar-

ily implemented with the motivation of early termi-

nation and improving the prediction strategy during

algorithm implementation. In the current simulation

experimentation, we carried out multiple sets of inde-

pendent simulations by ﬁxing the total computation

time assigned to each approach.

Figure 6: Iteration vs. RMSE score of Hybrid approach for

one of the simulations.

The Figure 6 represents one of the simulation

results for which the RMSE score achieved was

31.3041. The number of chromosomes evaluated at

every iteration during the hybrid approach might not

be equal to the number evaluated during the GA ap-

proach. Further, we performed a set of simulations to

understand the performances of each of the proposed

algorithms considering a similar execution time. The

complete simulation experiments are mentioned in

Table 1.

Table 1: Comparison of BO, GA, and hybrid approach

based on an independent set of simulations.

Simulation No. RMSE Score

BO GA Hybrid Approach

Simulation 1 49.29 43.77 30.90

Simulation 2 44.78 43.72 35.70

Simulation 3 49.45 30.04 31.30

Simulation 4 48.26 41.10 35.40

Simulation 5 51.77 54.11 40.84

Simulation 6 47.99 46.98 40.31

Simulation 7 50.50 35.95 35.90

Simulation 8 47.52 41.37 36.05

Simulation 9 45.13 42.25 36.37

Simulation 10 52.84 32.03 35.06

In most of the simulations, the hybrid approach

records a lower RMSE score, which is also high-

lighted in Figure 7. The information about hyperpa-

rameters obtained from three algorithms is mentioned

in Table 2.

Other key ﬁndings from our analysis are as fol-

lows:

• We employed GA with elitism approach. Since

meta-heuristics efﬁciently reach feasible solutions

with faster conversion, we observed an average of

A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter Optimization of a LSTM Network for Demand Forecasting of Retail Products

235

Figure 7: Boxplot of RMSE scores for BO, GA, and Hybrid approach.

Table 2: Optimal values of hyperparameters for one of the

simulations.

Hyperparameters BO GA Hybrid Approach

layer1 units 23 23 22

layer1 dropout 0.6 0.59 0.33

layer2 units 23 24 16

layer2 dropout 0.6 0.44 0.20

epochs 7 8 10

batch size 16 16 17

learning rate 0.94 0.71 0.76

160 seconds of convergence time to reach the de-

sired RMSE value after a trial-and-error simula-

tion.

• A major observation during experimentation is

that BO’s computational time is relatively higher

compared to the hybrid approach presented in the

paper. The same case is true when compared with

the GA with elitism approach.

• In the hybrid method, when the ﬁrst stage output

from BO is provided as the initial solution to the

second stage, the mean RMSE is 30.90, while the

BO approach attains a mean RMSE of 49.29 when

run for the same duration (see Table 1).

• Table 1 and Figure 7 represent independent set of

simulations for the three approaches implemented

in the proposed study. The result highlights that

the hybrid approach shows a signiﬁcant difference

in terms of RMSE score with a relatively smaller

mean and lower variability compared to BO and

GA approaches.

5 CONCLUSIONS

The proposed study conﬁgures the hyperparameters

of the LSTM network for demand forecasting of re-

tail products. The methodology can effectively set

up the LSTM network to learn patterns of the time

series data and generate the forecast. To further im-

prove forecasting accuracy and network performance,

we have incorporated a hybrid BO and GA with

elitism for hyperparameter optimization. We com-

bined the learning strengths of two well-known ap-

proaches within the optimization domain. These ob-

servations necessitate the signiﬁcance of the second

stage in the hybrid approach to conﬁguring the LSTM

network for error minimization objectives. Other

meta-heuristics approaches, such as ant colony op-

timization, particle swarm intelligence, etc., can be

explored. The hybrid strategy can be extended to hy-

perparameter optimization of machine learning objec-

tives other than retail demand forecasting algorithms

and stochastic learning methods. Although the LSTM

network acts as a benchmark model with promising

results, the optimal design of the neural network ar-

chitecture is still an appealing research direction to

explore.

REFERENCES

Abbasimehr, H., Shabani, M., and Youseﬁ, M. (2020).

An optimized model using lstm network for demand

forecasting. Computers & industrial engineering,

143:106435.

Balandat, M., Karrer, B., Jiang, D. R., Daulton, S.,

Letham, B., Wilson, A. G., and Bakshy, E. (2019).

Botorch: Programmable bayesian optimization in py-

torch. arXiv preprint arXiv:1910.06403, 117.

Beheshti, Z. and Shamsuddin, S. M. H. (2013). A review

of population-based meta-heuristic algorithms. Int. J.

Adv. Soft Comput. Appl, 5(1):1–35.

Cansu, T., Kolemen, E., Karahasan,

O., Bas, E., and Egri-

oglu, E. (2023). A new training algorithm for long

short-term memory artiﬁcial neural network based on

particle swarm optimization. Granular Computing,

pages 1–14.

Carbonneau, R., Laframboise, K., and Vahidov, R. (2008).

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

236

Application of machine learning techniques for sup-

ply chain demand forecasting. European journal of

operational research, 184(3):1140–1154.

Chollet, F. et al. (2015). Keras. https://keras.io.

da Fonseca Marques, R. A. (2020). A comparison on sta-

tistical methods and long short term memory network

forecasting the demand of fresh ﬁsh products.

Deb, K. and Jain, H. (2013). An evolutionary many-

objective optimization algorithm using reference-

point-based nondominated sorting approach, part i:

solving problems with box constraints. IEEE trans-

actions on evolutionary computation, 18(4):577–601.

Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural

architecture search: A survey. The Journal of Machine

Learning Research, 20(1):1997–2017.

Feurer, M. and Hutter, F. (2019). Hyperparameter Opti-

mization, pages 3–33. Springer International Publish-

ing, Cham.

Fildes, R., Ma, S., and Kolassa, S. (2022). Retail forecast-

ing: Research and practice. International Journal of

Forecasting, 38(4):1283–1318.

Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A. G.,

Parizeau, M., and Gagn

e, C. (2012). Deap: Evolu-

tionary algorithms made easy. The Journal of Machine

Learning Research, 13(1):2171–2175.

Frazier, P. I. (2018). A tutorial on bayesian optimization.

arXiv preprint arXiv:1807.02811.

Greff, K., Srivastava, R. K., Koutn

ık, J., Steunebrink, B. R.,

and Schmidhuber, J. (2016). Lstm: A search space

odyssey. IEEE transactions on neural networks and

learning systems, 28(10):2222–2232.

Johannesen, N. J., Kolhe, M., and Goodwin, M. (2019).

Relative evaluation of regression tools for urban area

electrical energy demand forecasting. Journal of

cleaner production, 218:555–564.

Johnson, A. (2017). Common problems in hyperparameter

optimization. Blog. sigopt. com.

Kumar, A., Shankar, R., and Aljohani, N. R. (2020). A big

data driven framework for demand-driven forecasting

with effects of marketing-mix variables. Industrial

marketing management, 90:493–507.

Kumar, P., Batra, S., and Raman, B. (2021). Deep neural

network hyper-parameter tuning through twofold ge-

netic approach. Soft Computing, 25:8747–8771.

Lang, S., Steiner, W. J., Weber, A., and Wechselberger, P.

(2015). Accommodating heterogeneity and nonlin-

earity in price effects for predicting brand sales and

proﬁts. European Journal of Operational Research,

246(1):232–241.

Martinez-de Pison, F., Gonzalez-Sendino, R., Aldama, A.,

Ferreiro-Cabello, J., and Fraile-Garcia, E. (2019). Hy-

brid methodology based on bayesian optimization and

ga-parsimony to search for parsimony models by com-

bining hyperparameter optimization and feature selec-

tion. Neurocomputing, 354:20–26.

Parmezan, A. R. S., Souza, V. M., and Batista, G. E. (2019).

Evaluation of statistical and machine learning models

for time series prediction: Identifying the state-of-the-

art and the best conditions for the use of each model.

Information sciences, 484:302–337.

Ramos, P., Santos, N., and Rebelo, R. (2015). Performance

of state space and arima models for consumer retail

sales forecasting. Robotics and computer-integrated

manufacturing, 34:151–163.

Reimers, N. and Gurevych, I. (2017). Optimal hyperpa-

rameters for deep lstm-networks for sequence labeling

tasks. arXiv preprint arXiv:1707.06799.

Sagheer, A. and Kotb, M. (2019). Time series forecasting of

petroleum production using deep lstm recurrent net-

works. Neurocomputing, 323:203–213.

Taylor, J. W. (2008). A comparison of univariate time se-

ries methods for forecasting intraday arrivals at a call

center. Management Science, 54(2):253–265.

Viola, R., Martin, A., Morgade, J., Masneri, S., Zorrilla,

M., Angueira, P., and Montalb

an, J. (2020). Predic-

tive cdn selection for video delivery based on lstm net-

work performance forecasts and cost-effective trade-

offs. IEEE Transactions on Broadcasting, 67(1):145–

158.

Wirsansky, E. (2020). Hands-on genetic algorithms with

Python: applying genetic algorithms to solve real-

world deep learning and artiﬁcial intelligence prob-

lems. Packt Publishing Ltd.

A Hybrid Bayesian-Genetic Algorithm Based Hyperparameter Optimization of a LSTM Network for Demand Forecasting of Retail Products

237