Dynamic Periodic Event-Triggered Control for Linear Systems Based on
Partial State Information
Mahmoud Abdelrahim
1,2
a
and Dhafer Almakhles
1
1
Renewable Energy Laboratory, College of Engineering, Prince Sultan University, Riyadh 11586, Saudi Arabia
2
Department of Mechatronics Engineering, Faculty of Engineering, Assiut University, Assiut 71515, Egypt
Keywords:
Periodic Event-Triggered Control, Output-Feedback, Hybrid Dynmaical Systems.
Abstract:
We are interested in the design of satabilizing event-driven controllers for linear time-invariant systems. We
assume that the plant state is partially known and the feedback signal is sent to the controller at discrete-time
instants via a digital channel and we synthesize an event-triggered controller based solely on the available plant
measurement. The event-triggering law that we construct is novel and only verified at periodic time instants,
i.e., periodic event-triggering mechanism, which i s more adapted to practical implementation. The proposed
approach ensures a global asymptotic stability property for the closed-loop system under mild conditions. The
overall model is developed as a hybrid dynamical system to truly describe the mixed continuous-time and
discrete-time dynamics. The stability is studied using appropriate Lyapunov functions. The efficiency of the
technique is illustrated on a numerical example.
1 INTRODUCTION
Event-triggered control (ETC) is an im plementation
technique in w hich the transmission instants of the
feedback measurements are generated by a state-
dependent rule instead of the traditional periodic sam-
pling approach. This allows for more efficient uti-
lization of the limited band w idth of the shar ed com-
munication channel in d ifferent do mains of applica-
tions such as networked control systems (Zhang et al.,
2017), sensors networks (Alajmi et al., 2022) , cyber
physical systems (Lu and Yang, 2020) , multi-agent
systems (Samy et al., 2022 ), (Filho et al., 2023) and
distributed control systems (Ge et al., 2017).
A significant amount of research work on E TC
is based on the continuous verification of the trig-
gering condition to decide the next transmission in-
stance, e.g., (Tabuada, 2007 ), (Abdelrahim et al.,
2013), (Wu et al., 2022), (Yang et al., 2023). How-
ever, a major challenge in this type of continuous ETC
is to prevent the accumulation of transmission in-
stants, i.e., Zeno phenomenon (Borgers and Heeme ls,
2014). Alternatively, periodic event-triggered control
(PETC) has been proposed such that the trigger ing
rule is only checked at periodic time instants, whic h
is more adapted to pra ctical implementation and au-
a
https://orcid.org/0009-0002-3940-9711
tomatically rules out Zeno behaviour (Heemels et al.,
2013b), (Postoyan et al., 2013), (Li et al., 2023),
(Wang et al., 2020), (Sun and Zeng, 2022), (Yu et al.,
2020), (Liu an d Hao, 2015), (Borgers et a l., 2018),
(Abdelrahim et al., 2015).
In this pap er, we conside r the problem of per i-
odic event-triggered control of output feedback lin-
ear time-invar iant (LTI) systems. We assume that
only an output of the plant is known and we con-
struct an appropriate periodic ETC to decide wh ether
to release a transmission at the next pe riodic instant.
The proposed periodic ETC is novel and eq uipped by
a dynamic variable, i.e., dynamic periodic ETC, to
further reduce the amount of transmissions. More-
over, the periodic sampling interval is designed based
on the approach of (Carnevale et al., 2007 ) to de-
rive the maximally allowable transmission interval
(MATI) for the case of time-triggered co ntrol. The
proposed approach is designed by e mulation where
we first ignore the effect of network and stabilize the
plant in continuous-time. Then, we consider the sam-
pling due to the network and we construct a periodic
ETC mechanism such that the closed-loop stability
is preserved. The overall system is formulated as a
hybrid d ynamical system to truly describe the mixed
continuous-time and discrete-time dynamics of the
system. Sufficient conditio ns are provided in te rms of
a linear matrix inequality (LMI) to properly identify
206
Abdelrahim, M. and Almakhles, D.
Dynamic Periodic Event-Triggered Control for Linear Systems Based on Partial State Information.
DOI: 10.5220/0012183600003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 206-213
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

the parameters of the event-trigger ing mechanism in
a systematic m anner. The stability is investigated by
using appropriate Lyapunov functions. The effective-
ness of the approach is demonstrated via numerical
simulations.
The problem of PETC synthesis has been stud-
ied in several works of the literature, see e.g., (An -
tunes et al., 2012), (Heemels et al., 2011), (Fu and Jr.,
2018), (Wei et al., 2023), (Sun et al., 2023), (Heemels
et al., 2013a), (Li et al., 2023), (Postoyan et al., 2013),
(Sun and Zeng, 2022). It is noted tha t the majority of
previous works are adapted to the case of state feed-
back control, which is not feasible in many practical
situations. The proposed approach in this paper is
adapted to the case of ou tput feedback control, which
is more challeng ing than when the fu ll state measure-
ment is available. M oreover, the setup that we con-
sider and the obtained stability prope rty are different
from existing techniqu e s of the literature.
The main contribution of this paper is summarized
below
• we construct a novel PETC for linear systems
based on partial state inf ormation;
• the sampling period is designed as the maxim ally
allowable transmission interval;
• the closed-loop system is modelled as a hybrid dy-
namical system;
• sufficient conditions are formulated in terms of an
LMI cond ition.
The rest of the paper is organised a s follows. Pre-
liminaries ar e given in Section 2 . The problem is fo r-
mally stated in Section 3. The hybrid model is given
in Section 4. We present the main results in Section
5. Numerical simulations are given in Section 6. Con-
clusions are provided in Section 7.
2 PRELIMINARIES
Let R := (−∞,∞), R
>0
:= [0,∞), N := {0, 1,2,...}
and N
>0
:= {1,2,...}. Standard notation are ddopted
in this paper.
We consider hybrid systems of the following form
(Goebel et al., 2012; Cai and Teel, 2009)
˙x = F(x) x ∈ C, x
+
∈ G(x) x ∈ D,
(1)
where x ∈ R
n
x
is the state, C is the flow set, F is the
flow map, D is th e jump set and G is the jump ma p.
Solutions to system (1) are defined on hybrid time do-
mains, see (Goebel et al., 2012), (Cai and Teel, 2009)
for mor e detail.
3 PROBLEM FORMULATION
We consider plant models with the following dy namis
˙x
p
= A
p
x
p
+ B
p
u
y = C
p
x
p
,
(2)
where x
p
∈ R
n
p
is the plant state, u ∈ R
n
u
is the
control input, y ∈ R
n
y
is the measured ou tput, and
A
p
,B
p
,C
p
,E
p
are matrices of appropriate dimensions.
The plant is stabilized by the following dynamic con-
troller
˙x
c
= A
c
x
c
+ B
c
ˆy
u = C
c
x
c
+ D
c
ˆy
(3)
where x
c
∈ R
n
c
is the controller state, ˆy ∈ R
n
y
is the
last transmitted value of y, and A
c
,B
c
,C
c
,D
c
are ma-
trices o f ap propriate dimensions. The feedback law
(3) is designed by emulation, that is we first stabi-
lize the plant (2) in continuous-time assuming perfect
communication, i.e., ˆy = y. Then, we take into ac-
count the sampling effects.
3.1 Implementation Scenario
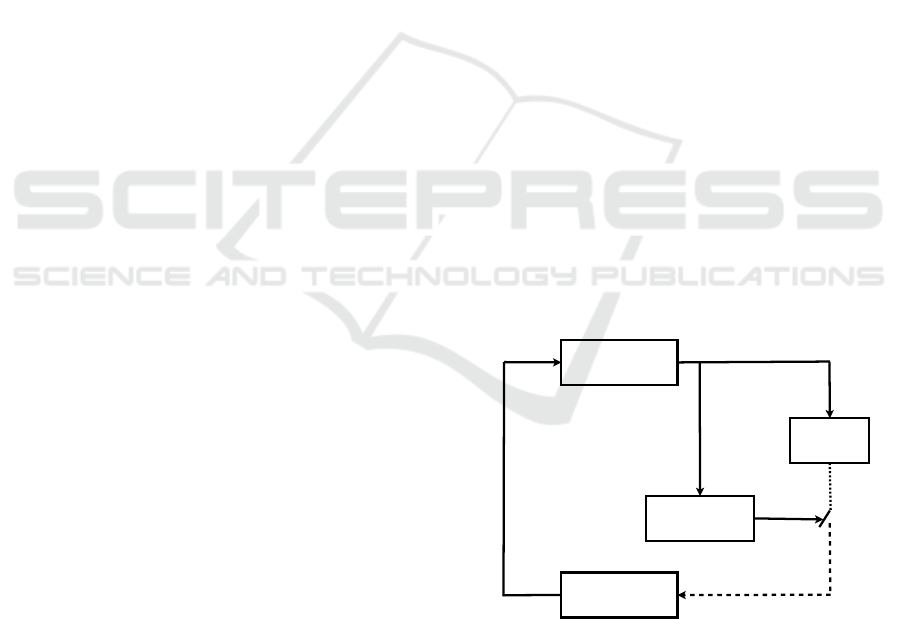
The implementa tion scenario is shown in Figure 1.
We consider the ca se where the controller is co-
located with the plant while the sensors and the c on-
troller are com municating over a shared network. We
assume that the plant state x
p
is not available for mea-
surement and only a n output y(t) can be transmitted
to the controller.
Plant
Sampler
PETC
mechanism
Controller
y(t)
y(t
s
i
)
ˆy(t
y
j
)
u(t)
Figure 1: Periodic event-triggered output feedback control.
(solid li ne) continuous-time; (dotted line) periodic instants;
(dash line) event-triggered instants.
We consider that the output y(t) is sampled at
periodic sampling times t
s
i
,i ∈ N. Then , an event-
triggering mechanism is employed to decide wether to
submit the output value y(t
s
i
), where the time instants
at which y(t
s
i
) is released are denoted by t
y
j
, j ∈ N,
Dynamic Periodic Event-Triggered Control for Linear Systems Based on Partial State Information
207

leading to the so-called pe riodic event-triggered con-
trol (PETC), and we refer by ˆy(t
y
j
) the most recent
value of y(t
s
i
) at the controller at time t
y
j
, j ∈ N, see
Figure 1. Henc e, if we define
T
s
= {t
s
i
},i ∈ N
T
y
= {t
y
j
}, j ∈ N,
(4)
where T
s
and T
y
denote the increasing sequence of
periodic time instants and transmission instants, re-
spectively. Then, it hold that T
y
⊆ T
s
.
It is important to note her e that the periodic event-
triggering mechanism is assumed to have access to
both the actual output value, i.e., y (t), and the last
transmitted value ˆy(t
k
j
), j ∈ N.
The objectives of this paper include
• Synthesis of periodic sampling interval and peri-
odic event-trigger e d controller by emulation;
• Derivation of hybrid dynamical model of the over-
all system;
• Provid ing sufficient conditions to ensure the
closed-loo p stability;
• Preventing the occurrence of Zeno behaviour.
4 HYBRID MODEL
In this section, we der ive the dynamic behaviour
of the closed-loop system and formulate it a s a hy-
brid dynamical system. We define the sampling er-
ror e
s
(t) : R
n
y
→ R
n
y
and the network induced error
e
y
(t) : R
n
y
→ R
n
y
between two transmission times as
follows, for all t ∈ [t
y
j
,t
y
j+1
)
e
s
(t) := y(t
s
i
) − y(t) ∀t ∈ [t
s
i
,t
s
i+1
),i ∈ N
e
y
(t) := ˆy(t
y
j
) − y(t
s
i
) ∀t ∈ [t
y
j
,t
y
j+1
),i, j ∈ N.
(5)
Between two periodic sampling times [t
s
i
,t
s
i+1
], the
sampled outpu t y(t
s
i
) is kept constants using ZOH.
At each periodic sampling time t
s
i
,i ∈ N, the value of
y(t
s
i
) is reset to y(t). Moreover, between two transmis-
sion instants [t
y
j
,t
y
j+1
], the last transmitted value of the
output y(t
y
j
) is kept constants using ZOH and at each
transmission instant t
y
j
, j ∈ N, e
y
(t) is reset to y(t
s
i
).
Define the total error e(t) as the difference be-
tween the last transmitted value of the output ˆy
q
(t
y
j
)
and the current output measurement y(t), that is
e(t) := ˆy(t
y
j
) − y(t) ∀t ∈ [t
y
j
,t
y
j+1
)
= e
s
(t) + e
y
(t).
(6)
Then, it holds that
˙e(t) = − ˙y = −C
p
˙x
p
t ∈ [t
y
j
,t
y
j+1
)
e(t
y
+
j
) = e
s
(t
y
+
j
) + e
y
(t
y
+
j
)
= 0.
(7)
The last property implies that the total error e(t) is re-
set to zer o at each transmission instant t
y
j
, j ∈ N since
y(t
s
i
) is updated to y(t) at each t
y
j
, j ∈ N.
Let x = (x
p
,x
c
) ∈ R
n
x
. Then, in view of (2), (3),
(6), we obtain
˙x =


A
p
+ B
p
D
c
C
p
B
p
C
c
B
c
C
p
A
c


x +


B
p
D
c
B
c


e
=: A
1
x + B
1
e
(8)
and
˙e =
h
−C
p
(A
p
+ B
p
D
c
C
p
) −C
p
B
p
C
c
i
x +
h
−C
p
B
p
D
c
i
e
=: A
2
x + B
2
e.
(9)
We define two auxiliary time variables τ
s
,τ
y
:
R
≥0
→ R
≥0
as follows
˙
τ
s
(t) = 1 t ∈ [t
s
i
,t
s
i+1
)
τ
s
(t
s
+
i
) = 0 t ∈ {t
s
i
}
i∈N
(10)
and
˙
τ
y
(t) = 1 t ∈ [t
y
j
,t
y
j+1
)
τ
y
(t
y
+
j
) = 0 t ∈ {t
y
j
}
j∈N
.
(11)
The time variable τ
s
will be used to describe the time
between two periodic sampling instants [t
s
i
,t
s
i+1
] and
it is reset to zero at each periodic instance t
s
i
,i ∈ N.
Similarly, the time variable τ
y
will be used to track the
time between two tra nsmission instants [t
y
j
,t
y
j+1
] and it
is reset to zero at each transmission instance t
y
j
, j ∈ N.
These two time variables τ
s
and τ
y
will be helpful to
construct the hybrid dynamical model of the system
as explained in the sequel.
In or der to complete the description of the over-
all system, we outline below the general structure
of th e proposed periodic event-triggering mechanism,
which will be clearly developed in the next section.
We synthesize a PETC based on a d ynamic variable
η, which has the following dynamics, see also (Gi-
rard, 2015; Dolk et al., 2017; Postoyan et al., 2015),
˙
η(t) = Ψ(y,e,η) t ∈ [t
s
i
,t
s
i+1
)
η(t
+
) = g
s
(y,e,η) t ∈ T
s
\ T
y
η(t
+
) = g
y
(y,e,η) t ∈ T
y
,
(12)
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
208

where the functions Ψ,g
s
and g
y
will be specified in
Section 5. Note that the functions Ψ,η
s
and η
y
de-
pend only on locally available information (y,e,η)
at th e event-triggering mechanism. The sequence of
transmission instants are generated by the fo llowing
mechanism
t
y
j+1
= min{t > t
y
j
| t ∈ T
s
∧ g
s
(y,e,η) 6 0}, (13)
where t
y
0
= 0.
In view of (7)-( 12) we obtain the following impul-
sive model
˙x = A
1
x + B
1
e
˙e = A
2
x + B
2
e
˙
η(t) = Ψ(y,e,η)
˙
τ
s
(t) = 1
˙
τ
y
(t) = 1















t /∈ T
s
u = C
c
x
c
+ D
c
ˆy
q
y = C
p
x
p
τ
s
(t
+
) = 0
η(t
+
) = g
s
(y,e,η)
)
t ∈ T
s
\ T
y
e(t
+
) = e
q
(t)
η(t
+
) = g
y
(y,e,η)
τ
s
(t
+
) = 0
τ
y
(t
+
) = 0











t ∈ T
y
(14)
Let ξ := (x,e,η,τ
s
,τ
y
) ∈ X be the concatenation
of the state variables, with X = R
n
x
× R
n
y
× R
>0
×
R
>0
× R
>0
. Then, we obtain the hybrid dynamica l
system
˙
ξ = F (ξ) ξ ∈ C
s
ξ
+
∈ G(ξ) ξ ∈ D
s
,
(15)
where the flow set C
s
and the jump D
s
are defined as
C
s
:=
n
ξ ∈ X : τ
s
∈ [0, T ]
o
D
s
:=
n
ξ ∈ X : τ
s
= T
o
,
(16)
where T > 0 is the periodic sampling interval and to
be designed. We also define the jump set D
y
⊂ D
s
to
identify the transmission instants as follows
D
y
:=
n
ξ ∈ X : τ
s
= T and g
s
(t) 6 0
o
. (17)
It is evident from (16) an d (1 7) that mathcalD
y
⊂ D
s
.
The flow map F (ξ) and the jump ma p G(ξ) in (15)
are given by
F (ξ) =










A
1
x + B
1
e
A
2
x + B
2
e
Ψ(y,e,η)
1
1










(18)
and
G(ξ) :=

















n
G
s
(ξ)
o
ξ ∈ D
s
n
G
y
(ξ)
o
ξ ∈ D
y
n
G
s
(ξ),G
y
(ξ)
o
ξ ∈ D
s
∩ D
y
/
0 ξ /∈ D
s
∪ D
µ
(19)
with
G
s
(ξ) :=








x
e
g
s
0
τ
y








, G
y
(ξ) :=








x
0
g
y
0
0








(20)
The system flows on C
s
when τ
s
6 T, i. e ., between
two periodic instants, oth erwise the system experi-
ences a jump. The jump map in (20) can b e inter-
preted as follows. When ξ ∈ D
s
\ D
y
, only the vari-
ables τ
s
and η are updated but no transmission is gen-
erated. When ξ ∈ D
y
, implying that the triggering
condition is violated, the variables e,η, τ
s
,τ
y
are ud-
pated.
5 MAIN RESULT
We pr e sent he re the main result. First we state the
following lemma on system (15).
Lemma 1. Consider system (15). If there exist
ε
x
,ε
y
,γ > 0 and a positive definite symmetric real ma-
trix P such that


A
T
1
P + PA
1
+ ε
x
I
n
x
+ A
T
2
A
2
+ ε
y
e
C
T
p
e
C
p
PB
1
B
T
1
P −γ
2
I
n
e


6 0,
(21)
where
e
C
p
:= [C
p
0], then the Laypunov function
candidate V (x) = x
T
Px satisfies, for a ll e ∈ R
n
e
and
almost all x ∈ R
n
x
h∇V (x),A
1
x + B
1
ei ≤ −ε
x
|x|
2
− |A
2
x|
2
− ε
y
|y|
2
+γ
2
|e|
2
.
(22)

Proof of Lemma 1.
Let V(x) = x
T
Px. Consequently, it holds that, for
all e ∈ R
n
e
and almost all x ∈ R
n
x
h∇V (x),A
1
x + B
1
ei = x
T
(A
T
1
P + PA
1
)x
+x
T
PB
1
e + e
T
B
T
1
Px.
(23)
Dynamic Periodic Event-Triggered Control for Linear Systems Based on Partial State Information
209

By post- and pre-multiplying LMI (21) respectively
by the state vector (x,e) and its transpose, we obtain
x
T
(A
T
1
P + PA
1
)x + x
T
PB
1
e + e
T
B
T
1
Px ≤ −ε
x
x
T
x
−x
T
A
T
2
A
2
x − ε
y
x
T
e
C
T
p
e
C
p
x + γ
2
e
T
e
(24)
which implies
x
T
(A
T
1
P + PA
1
)x + x
T
PB
1
e + e
T
B
T
1
Px ≤
−ε
x
|x|
2
− |A
2
x|
2
− ε
y
|
e
C
p
x|
2
+ γ
2
|e|
2
= −ε
x
|x|
2
− |A
2
x|
2
− ε
y
|y|
2
+ γ
2
|e|
2
(25)
and the con clusion of Lemma 1 holds. 
Lemma 1 establishes an L
2
-gain stability property
for the system ˙x = A
1
x + B
1
e from |e| to (|A
2
x|,|y|),
see also e.g. (Carnevale et al., 200 7; ?; Dolk et al.,
2017).
5.1 Event-Triggering Mechanism
We define W (e) := |e|, then n view of (15), it holds
that for all x ∈ R
n
x
and almost all e ∈ R
n
e
h∇W (e),A
2
x + B
2
ei 6 |A
2
x| + L|e|,
(26)
where L := |B
2
|.
The dynamics of the triggering function η in (12 )
is define d by the functions Ψ, η
s
and η
y
, which are
given by
Ψ(y,e,η) := ε
y
|y|
2
− ϑη
g
s
(y,e,η) := γ(λ −
1
λ
)|e|
2
+ η
g
y
(y,e,η) := γλ|e|
2
+ η
(27)
where λ ∈ (0, 1),
˜
λ ∈ [λ,λ
−1
),
˜
γ := γ
2
+ γ
2
˜
λ
2
+ 2γ
˜
λ
˜
L
with
˜
L := L + ν f or a ny ν > 0 and L = |B
2
|, and the
constant γ comes from L emma 1. The sampling pe-
riod T is designed as the maximally allowable trans-
mission interval (MATI) of time-triggered systems
(Carnevale et al., 2007), which leads to
T (λ,
˜
λ,γ,
˜
L) :=













1
˜
Lr
arctan

r(1−λ
˜
λ)
γ
˜
L
(λ+
˜
λ)+1+λ
˜
λ

γ >
˜
L
1
˜
L
1−λ
˜
λ
λ
˜
λ+λ+
˜
λ+1
γ =
˜
L
1
˜
Lr
arctanh

r(1−λ
˜
λ)
γ
˜
L
(λ+
˜
λ)+1+λ
˜
λ

γ <
˜
L
(28)
with r :=
r



(
γ
˜
L
)
2
− 1



. Note that when
˜
λ = λ in (28) ,
we recover the MAT I bound of time-triggered con-
trollers in (Carnevale et al., 2007). By designing the
sampling period T as the MATI bound, we opt to fur-
ther reduce the amount of the tr a nsmissions by using
the PETC mech a nism.
Remark 1. It is imp ortant to note that in view of (27),
we have that
˙
η(t) = ε
y
|y|
2
− ϑη > −ϑη. Moreover,
since η(t) is reset to g
s
(y,e,η) when g
s
(y,e,η) > 0
and η(t) is reset to g
y
(y,e,η), which is strictly pos-
itive, when g
s
(y,e,η) 6 0. Consequently, by using
the comparison principle, it hold that η(t) > 0 for all
t ∈ R
>0
. This property is crucial in establishing the
stability of the closed-loop system as will be shown
later.
5.2 Stability Result
We obtain the following result.
Theorem 1. Consider system (15) with the flow an d
the jump sets as in (16). Suppose that the LMI (21) in
Lemma 1 is satisfie d. The n, there exists a K L func-
tion β such that any solution ξ(t, j) ∈ X satisfies
|ξ(t, j)| 6 β(|ξ(0,0))|,t + j).
(29)

The proo f is omitted due to space limit. Theorem
1 implies that the closed-loo p system (15) is globally
asymptotically stable under the proposed PETC.
Remark 2. It is clear from the proposed PETM (13)
that there exists a tradeoff between the periodic sam-
pling interval T and the gen e rated amount of trans-
missions. That is, when the valu e of T is en larged , the
generated n umber of transmissions will be increased
and vice versa. This tradeoff can be adjusted by the
user to satisfy desirable performance of the PETC.
6 ILLUSTRATIVE EXAMPLE
Consider the following LTI control system
˙x
p
=


0 1
−2 −1


x
p
+


0
−1


u, y = x
p
1
˙x
c
=


0 −2
0 −3


x
c
+


0
1


ˆy
q
, u =
h
−1 −2
i
x
c
(30)
We develop the hybrid model (15) a s described in
Section 4. We check th e required conditions of
Lemma 1 a nd found that the LMI condition (21)
is feasible and we obtain the following values ε
y
=
0.7861, L = 0, γ = 3.7634. By setting λ = 0.5,
˜
λ = 0.6 and ν = 0.01 and substituting in (28), we get
T = 0.1204 and
˜
γ = 23.778. Finally, we pick ϑ = 0.01
and thus all parameters of the PETM (27) are set.
We examine the approach on MAT LAB simula-
tion with the initial conditions x
p
(0,0) = (−20, 20),
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
210

x
c
(0,0) = (10,−10 ), e(0,0) = 0, η(0,0) = 0,
τ
s
(0,0) = 0, τ
y
(0,0) = 0, µ(0,0) = 0.35, c onse-
quently, the output magnitude |y(0,0)| initially is
within the range (ℓ
in
µ(0,0), ℓ
out
µ(0,0)).
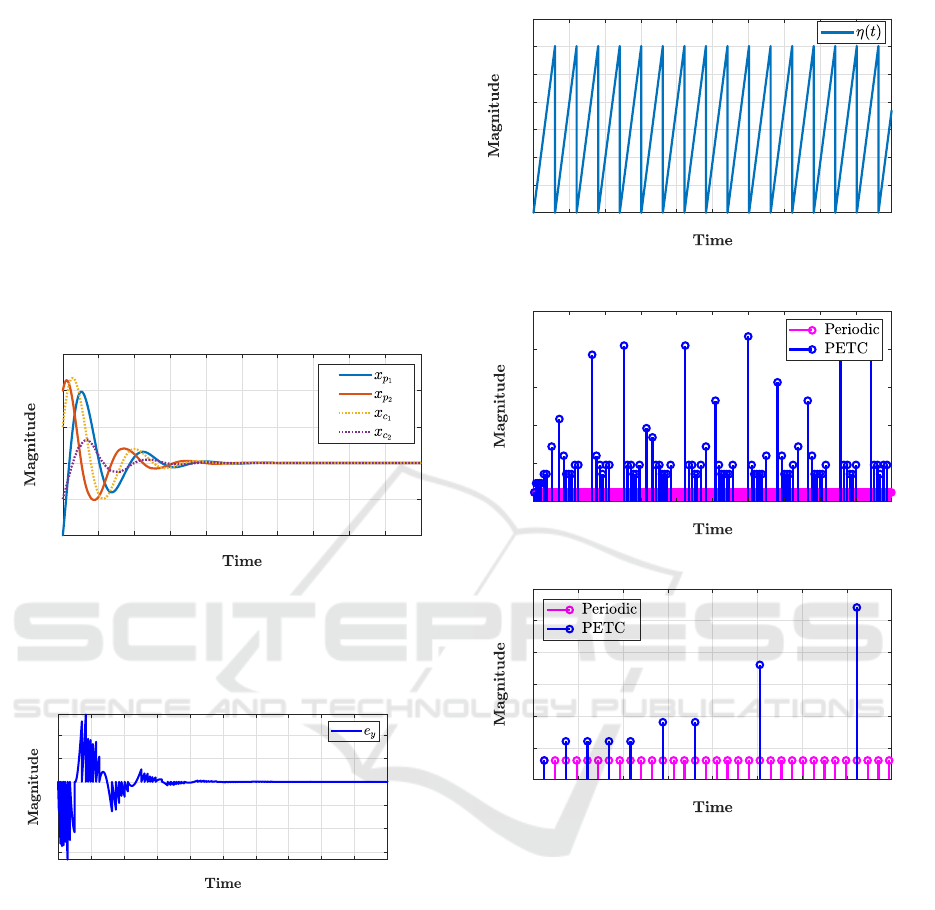
By running the simulation for 40 seconds, the
obtained minimum a nd average inter-transmission
times w e re found to be τ
min
= 0.1295 and τ
avg
=
0.4298, respectively. As expected, the minimum
inter-transmission time τ
min
is typica lly equa l to the
periodic sampling interval T , however, the average
inter-transmission tim e τ
avg
is larger than T , which
supports our analysis and justifies the benefit of the
approa c h compared to periodic sampling. The closed-
loop response is shown in the figures below.
0 5 10 15 20 25 30 35 40 45 50
-20
-10
0
10
20
30
Figure 2: State trajectories of the plant and the controller.
Figure 2 shows that the plant and the controller
states converge asymptotically to the origin as ex-
pected.
0 5 10 15 20 25 30 35 40 45 50
-6
-4
-2
0
2
4
Figure 3: Sampling induced errors.
Figure 3 shows the evolutions of samp ling
induced -errors e(t), which is reset to ze ro at eac h
transmission instant as explained.
Figure 4 shows the tra je c tory of η(t), where we
note that η(t) > 0 as stated in Remark 1.
The periodic time instants and the transmission in-
stants are shown in Figure 5. We note that the trans-
mission instants generated by the PETC is much less
than the periodic sampling instants, which suppor ts
the effectiveness of the p roposed approach.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
Figure 4: Evolution of η(t) for first 3 sec.
0
0.5
1
1.5
2
2.5
0 5 10 15 20 25 30 35 40 45 50
Figure 5: Periodic and transmission instants.
0
0.2
0.4
0.6
0.8
1
1.2
0 0.5 1 1.5 2 2.5 3 3.5 4
Figure 6: Periodic and transmission instants for fir st 4 sec.
A zoom in on th e first 4 seconds for the periodic
and the transmission instants is shown in Figure 6 to
clearly highlight the fact the event-triggering condi-
tion is only verified at periodic sampling instants and
not in contin uous-time.
7 CONCLUSION
We studied the problem of periodic event-triggered
control for linear systems based only on the output
measurement. Th e proposed solution is well adapted
to practical implementation since the event-triggering
mechanism is checked only at periodic time instants
rather than continuous- time verification. The problem
is formulated as a hybrid dynamical system to truly
describe the dynamic behaviour. By using appropri-
Dynamic Periodic Event-Triggered Control for Linear Systems Based on Partial State Information
211

ate Lyapunov function, we show that the closed-loop
stability is ensured while automatically ruling out the
Zeno phenomenon. The effectiveness of the appr oach
was proven by numerical simulation.
Future work includes extending this approach to
nonlinear plant models an d the investigation of dif-
ferent im plementation scenarios such as multi-agent
systems and distributed control architectures.
ACKNOWLEDGEMENTS
This work was supported by Princ e Sultan University.
REFERENCES
Abdelrahim, M., Postoyan, R., and Daafouz, J. (2013).
Event-triggered control of nonlinear singularly per-
turbed systems based only on the slow dynamics. In
Proceedings of the IFAC Symposium on Nonlinear
Control systems, Toulouse, France, 4–6 September,
pages 347–352.
Abdelrahim, M., Postoyan, R., Daafouz, J., and Neˇsi´c, D.
(2015). Event-triggered dynamic feedback controllers
for nonlinear systems wi th asynchronous transmis-
sions. In Proceedings of the 54th IEEE Conference
on Decision and Control, Osaka, Japan, 15–18 De-
cember, pages 5494–5499.
Alajmi, M., Nour, M., Hassine, S., Alkhonaini, M., Hamza,
M., Yaseen, I., Zamani, A., and Rizwanullah, M.
(2022). Energy aware secure cyber-physical systems
with clustered wireless sensor networks. Computers,
Materials And Continua, 72(3):5499–5513.
Antunes, D., Heemels, W., and Tabuada, P. (2012). Dy-
namic programming formulation of periodic event-
triggered control: Perf ormance guarantees and co-
design. In Proceedings of the 51st IEEE Conference
on Decision and Control, Maui, U.S.A., pages 7212–
7217.
Borgers, D. and Heemels, W. (2014). Event-separation
properties of event-triggered control systems. IEEE
Transactions on Automatic Control, 59(10):2644–
2656.
Borgers, D. P., Dolk, V. S., and Heemels, W. P. M. H.
(2018). Riccati-based design of event-triggered con-
trollers for linear systems with delays. IEEE Transac-
tions on Automatic Control, 63(1):174–188.
Cai, C. and Teel, A . (2009). Characterizations of input-to-
state stability for hybrid systems. Systems & Control
Letters, 58(1):47–53.
Carnevale, D., Teel, A., and Neˇsi´c, D. (2007). A Lyapunov
proof of an improved maximum allowable transfer in-
terval for networked control systems. IEEE Transac-
tions on Automatic Control, 52(5):892–897.
Dolk, V., Borgers, D., and Heemels, W. (2017). Output-
based and decentralized dynamic event-triggered con-
trol with guaranteed L
p
-gain performance and Zeno-
freeness. IEEE Transactions on Automatic Control,
62(1):34–49.
Filho, E., Severino, R ., Santos, P. S. D., Koubaa, A., and
Tovar, E. (2023). Cooperative vehicular platoon-
ing: a multi-dimensional survey towards enhanced
safety, security and validation. Cyber-physical Sys-
tems, pages 1–53.
Fu, A. and Jr., M. M. (2018). Decentralized periodic event-
triggered control with quantization and asynchronous
communication. Automatica, 94:294–299.
Ge, X., Yang, F., and Han, Q.-L. (2017). Distributed net-
worked control systems: A brief overview. Informa-
tion Sciences, 380:117–131.
Girard, A. (2015). Dynamic triggering mechanisms for
event-triggered control. IEEE Transactions on Auto-
matic Control, 60(7):1992–1997.
Goebel, R., Sanfelice, R., and Teel, A. (2012). Hybrid
Dynamical Systems: Modeling, Stability, and Robust-
ness. Princeton University Press: Pr inceton, NJ, USA.
Heemels, W., Donkers, M., and Teel, A. (2011). Periodic
event-triggered control based on state feedback. In
Proceedings of the IEEE Conference on Decision and
Control and European Control Conference, Orlando,
U.S.A., pages 2571–2576.
Heemels, W., Donkers, M., and Teel, A. (2013a). Model-
based periodic event-triggered control for linear sys-
tems. Automatica, 49(3):698–711.
Heemels, W., Donkers, M., and Teel, A. (2013b). Peri-
odic event-triggered control for linear systems. IEEE
Transactions on Automatic Control, 58(4):847–861.
Li, C., Zhao, X., Chen, M., Xing, W., Zhao, N., and Zong,
G. (2023). D ynamic periodic event-tr iggered control
for networked control systems under packet dropouts.
IEEE Transactions on Automation Science and Engi-
neering, pages 1–15.
Liu, C. and Hao, F. (2015). Dynamic output-feedback
control for linear systems by using event-triggered
quantisation. IET Control Theory & Applications,
9(8):1254–1263.
Lu, A.-Y. and Yang, G.-H. (2020). Observer-based control
for cyber-physical systems under denial-of-service
with a decentralized event-triggered scheme. IEEE
Transactions on Cybernetics, 50(12):4886–4895.
Postoyan, R., Anta, A., Heemels, W., Tabuada, P., and
Neˇsi´c, D. (2013). Periodic event-triggered control
for nonlinear systems. In Proceedings of the IEEE
Conference on Decision and Control, Florence, Italy,
pages 7397–7402.
Postoyan, R., Tabuada, P. , Neˇsi´c, D., and Anta, A. ( 2015).
A framework for the event-triggered stabilization of
nonlinear systems. IEEE Transactions on Automatic
Control, 60(4):982–996.
Samy, S. , Cao, Y., Ramachandran, R ., Alzabut, J., Niez-
abitowski, M., and Li m, C. (2022). Globally asymp-
totic stability and synchronization analysis of uncer-
tain multi-agent systems with multi ple time-varying
delays and impulses. International Journal of Robust
and Nonlinear Control, 32(2):737–773.
Sun, J. and Zeng, Z. (2022). Periodic event-triggered con-
trol for networked control systems with external dis-
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
212

turbance and input and output delays. IEEE Transac-
tions on Cybernetics, pages 1–9.
Sun, X., Liu, K., Wang, X. , and Teel, A. (2023). Peri-
odic Event-Triggered Control for Decentralized Lin-
ear Systems with Quantization Effects and External
Disturbances. C ontrol and Optimization Based on
Network Communication. Springer, Singapore.
Tabuada, P. (2007). Event-triggered real-time scheduling of
stabilizing control tasks. IE EE Transactions on Auto-
matic Control, 52(9):1680–1685.
Wang, W., Postoyan, R., Neˇsi´c, D., and Heemels, W. P.
M. H. (2020). Periodic event-triggered control for
nonlinear networked control systems. IEEE Transac-
tions on Automatic Control, 65(2):620–635.
Wei, X., Fu, A., and Qiao, J. (2023). Traffic models of peri-
odic event-triggered quantized control systems. Non-
linear Analysis: Hybrid Systems, 49:101370.
Wu, J., Peng, C. , Yang, H., and Wang, Y.-L . (2022). Re-
cent advances in event-triggered security control of
networked systems: a survey. International Journal
of Systems Science, 53(12):2624–2643.
Yang, Y., Fan, X., Gao, W., Yue, W., Liu, A., Geng, S., and
Wu, J. (2023). Event-triggered output feedback con-
trol for a class of nonlinear systems via disturbance
observer and adaptive dynamic programming. IEEE
Transactions on Fuzzy Systems, pages 1–13.
Yu, H., Chen, T., and Hao, F. (2020). Output-based peri-
odic event-triggered control for nonlinear plants: An
approximate-model method. IEEE Transactions on
Control of Network Systems, 7(3):1342–1354.
Zhang, D., Shibc, P., Wangd, Q., and Yu, L. (2017). Anal-
ysis and synthesis of networked control systems: A
survey of recent advances and challenges. ISA Trans-
actions, 66:376–392.
Dynamic Periodic Event-Triggered Control for Linear Systems Based on Partial State Information
213