Learning-Based Inverse Dynamic Controller for Throwing Tasks with a

Soft Robotic Arm

Diego Bianchi

1,2 a

, Michele Gabrio Antonelli

3 b

, Cecilia Laschi

4 c

Angelo Maria Sabatini

1,2 d

and Egidio Falotico

1,2 e

The BioRobotics Institute, Scuola Superiore Sant’Anna, Pontedera, Italy

Departement of Excellence in Robotics and AI, Scuola Superiore Sant’Anna, Pisa, Italy

Department of Industrial and Information Engineering and Economics, University of L’Aquila, L’Aquila, Italy

Department of Mechanical Engineering, National University of Singapore, Singapore, Singapore

Keywords:

Soft Robotics, Throwing, Open-Loop Control, Neural Network, Ballistic Task.

Abstract:

Controlling a soft robot poses a challenge due to its mechanical characteristics. Although the manufacturing

process is well-established, there are still shortcomings in their control, which often limits them to static

tasks. In this study, we aim to address some of these limitations by introducing a neural network-based

controller speciﬁcally designed for the throwing task using a soft robotic arm. Drawing inspiration from

previous research, we have devised a method for controlling the movement of the soft robotic arm during

the ballistic task. By employing a feed-forward neural network, we approximate the relationship between the

actuation pattern and the resulting landing position. This enables us to predict the input sequence that needs to

be transmitted to the robot’s actuators based on the desired landing coordinates. To validate our approach, we

conducted experiments using a 2-module soft robotic arm, which was utilized to throw four different objects

towards ten target boxes positioned beneath the robot. We considered two actuation modalities, depending

on whether the distal module was activated. The results indicate a success rate, deﬁned as the proportion

of successful trials out of the total number of throws, of up to 68% when a single module was actuated.

These ﬁndings demonstrate the potential of our proposed controller in achieving successful performance of

the throwing task using a soft robotic arm.

1 INTRODUCTION

Soft robots, often inspired by biological systems

(Laschi et al., 2016; Polygerinos et al., 2017), are con-

structed using hyper-elastic materials with a Young’s

modulus comparable to that of biological skin (Rus

and Tolley, 2015), typically ranging from 10

to 10

Pa. These robots offer several advantages over tradi-

tional robots, including the potential for low-cost and

safe human interaction due to their energy-absorbing

capabilities during collisions. Despite their unique

characteristics and wide range of potential applica-

tions, soft robots have yet to realize their full potential

(Katzschmann et al., 2018; Holland et al., 2017), pri-

https://orcid.org/0000-0001-7148-1612

https://orcid.org/0000-0001-8437-9131

https://orcid.org/0000-0001-5248-1043

https://orcid.org/0000-0003-3306-6498

https://orcid.org/0000-0001-8060-8080

marily due to sensing and control limitations.

While soft robots have been evaluated for dynamic

tasks such as trajectory tracking, there are still nu-

merous real-world dynamic tasks that remain unex-

plored (Fischer et al., 2022). In (Fischer et al., 2022),

the authors demonstrate the potential of soft robots in

various dynamic tasks, including ballistic tasks where

objects are thrown along linear trajectories. How-

ever, there is a lack of control strategies speciﬁcally

tailored for achieving ballistic tasks with soft robots,

particularly in accurately tossing an object into a user-

deﬁned target box. Therefore, the objective of our

work is to develop a control strategy to enable soft

robots to perform ballistic tasks, precisely throwing

objects into predetermined target boxes.

Despite classical robots, which are designed to

maximise the performance of an operation, soft robots

thanks to their materials are characterised by low-

cost fabrication, high deformability, and compliance.

However, this has a cost in terms of accuracy and

424

Bianchi, D., Antonelli, M., Laschi, C., Sabatini, A. and Falotico, E.

Learning-Based Inverse Dynamic Controller for Throwing Tasks with a Soft Robotic Arm.

DOI: 10.5220/0012184200003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 424-432

ISBN: 978-989-758-670-5; ISSN: 2184-2809

payload. These properties make them suitable for

delicate handling(Li et al., 2017) and operation in

unstructured environments as scenarios like assistive

robotics(Manti et al., 2016) and search and rescue

missions(Hawkes et al., 2017) can represent. How-

ever, the non-linearity of the materials combined

with the fact that soft robots show virtually inﬁnite

degrees-of-freedom, and that their properties depend

on the environment in which they work, require in-

novation in the control systems(Wang and Chortos,

2022) because it is challenging to apply directly the

conventional robotic control theory which has been

developed for rigid robots.

The main challenges that a soft robotic control

system must face are high dimension morphology and

the time-varying combined with the non-linear be-

haviour of the soft material. For these reasons, it

is really challenging to model them. Furthermore,

we need an accurate and computationally efﬁcient

representation to create a controller over the model.

However, achieving both characteristics is difﬁcult for

a soft robotic model. Indeed, with Finite Element

Analysis(Ilievski et al., 2011) (FEM) we can achieve

the biggest accuracy among the other type of models

which make some exempliﬁcative assumptions, such

as the Constant Curvature (Webster and Jones, 2010)

(CC), the Piecewise Constant Curvature(Runge and

Raatz, 2017) (PCC) and Cosserat rod models (Gaz-

zola et al., 2018) (Alessi et al., 2023).

A promising alternative is represented by Machine

Learning (ML) algorithms which could discover the

underlying structure of the data that in our case is

the model of the robot without any assumptions. ML

techniques have already been used to create static and

dynamic controllers (Laschi et al., 2023) even if there

are some limitations. Firstly, since it is a data-driven

approach to work properly it requires a (large) dataset

whose collection may be time-consuming. Then,

data might not represent the whole behaviour of the

robot but just part of it i.e., the one captured in the

dataset. In (Giorelli et al., 2013), the authors de-

veloped the earliest machine-learning controller for a

non-redundant soft robot. They demonstrated the uti-

lization of a neural network as an approximation of

the inverse kinematics of the robot.

Later, this work has been extended in

(George Thuruthel et al., 2017) to account for

redundancies based on previous works (Vannucci

et al., 2014; Vannucci et al., 2015). However,

achieving a dynamic task with a quasi-static model or

in general with a model that relies on the steady-state

assumption is impossible since its accuracy during

fast movements is limited. Due to severe limitations

in speed, throwing would not be possible with

controllers based on these models.

To overcome these limitations, model-free dy-

namic controllers have been developed. Different

open-loop strategies (Thuruthel et al., 2019), (Cen-

turelli et al., 2021) are present in the literature to con-

trol the manipulator dynamic in a trajectory tracking

task. Both works represent a model-free approach in

which recurrent neural networks are deployed to ob-

tain the model of the soft robot. Then in (Centurelli

et al., 2022) the authors designed a closed-loop con-

troller able to deal with different payloads attached

to the manipulator end-effector thanks to a deep rein-

forcement learning method. Recently, this tolerance

to external payloads has been achieved with contin-

ual learning in (Piqu

e et al., 2022), where the authors

learnt the dynamic models of the robot with differ-

ent attached weights without encountering the well-

known problem of catastrophic forgetting.

All the proposed approaches, have been devel-

oped for a speciﬁc task, the trajectory following, and

are not suitable for ballistic movements, where reach-

ing the realising point with a speciﬁed velocity de-

termines the range of the throws. Indeed, for rigid

robots, this ability has been implemented for exam-

ple (Fang et al., 2021) and (Raptopoulos et al., 2020).

Both experienced an increased work capacity and efﬁ-

ciency of a robot, especially in a weakly structured lo-

gistics sorting scene. While in (B

uchler et al., 2022),

the authors show the ballistic movement of a muscu-

lar robot, in particular, they highlight the issues as-

sociated with this fast movement on rigid robot hard-

ware components. Instead in (Zeng et al., 2019), the

authors deployed a hybrid controller to grasp an ob-

ject with an anthropomorphic robot and then toss it

at a speciﬁc target placed in front of it. The analyti-

cal model of the robot is used to make an estimation

of the control parameters once the physical problem

is solved thanks to some constraints imposed on the

movement. As stated above, this approach is difﬁ-

cult to implement with a soft robot since the dynamic

model of the robot is not always available or in gen-

eral accurate. However, lately, this task has been ex-

plored also with soft robots. The feasibility of the

ballistic task has been demonstrated by (Fischer et al.,

2022). Meanwhile, two controllers have been devel-

oped, ﬁrst in simulation and then on an real robot, for

throwing an object into a target box. These controllers

are described in (Bianchi et al., 2022) and (Bianchi

et al., 2023). The simulation-based work utilizes an

optimization process that provides the desired landing

position and predicts the actuation patterns needed to

reach it. In (Bianchi et al., 2023), the authors present

a real-time controller that employs a deep reinforce-

ment learning method.

Learning-Based Inverse Dynamic Controller for Throwing Tasks with a Soft Robotic Arm

425

In this work, we present a learning-based inverse

dynamic controller approach to performing the toss-

ing task with a soft robot. It is an open-loop con-

troller in which we trained an artiﬁcial neural network

to learn the relationship between the landing positions

and the actuation patterns necessary to reach them.

Since it is based on a single neural network, the in-

verse model of the task, the controller works in real-

time because it instantaneously predicts the actuation

pattern given a new goal position. We tested this real-

time methodology on a modular pneumatic platform

with which we tossed objects of different shapes and

weights in several directions to explore the robot’s ca-

pabilities and our controller.

2 MATERIALS AND METHODS

In this section, we will ﬁrst present an overview of the

approach we developed throughout the work. Then,

after describing the experimental setup used to test the

controller we will pass through the two main phases

that brought to its development, i.e., the dataset col-

lection and the training of the neural network on

which our controller is based.

2.1 Our Approach

Target

Predicted

actuation pattern

TRAINING

Landing positions

Actuation pattern

Inverse model of the task

Figure 1: Neural Network-based open-loop controller.

Our approach is described in Figure 1. By learning

the relationship between the landing positions and the

actuation patterns to reach them in the training phase,

our learning-based inverse dynamic controller is able

to predict the actuation pattern according to the de-

sired target position.

We deﬁned the throwing trajectories before gath-

ering the dataset to train the neural network. Inspired

by (Braun et al., 2012), we opted for a planar tra-

jectory. To enhance the dynamics of the soft robot

we choose to perform a back-swing before moving

toward the target goal. We can identify two distinct

phases in the robot’s movement: 1) the run-up phase;

and 2) the forward phase. We established that the ob-

ject should be released when the robot passes for the

lowest position of the trajectory after the back-swing.

Once collected, we used the dataset to train a feed-

forward artiﬁcial neural network, the inverse model

of the task, to approximate the relationship between

landing positions and actuation patterns, i.e., the com-

mands that we sent to the robot. Each actuation pat-

tern includes the commands responsible for the two

phases of the movement.

Once trained, we used the inverse model of the

task to perform the throws into target boxes. In this

phase, we assess the effectiveness of the approach that

is threatened by the approximation error of the neu-

ral network and the exempliﬁcations made during the

dataset collection. We conducted tests on our con-

troller using objects of various shapes and weights, as

well as different target locations.

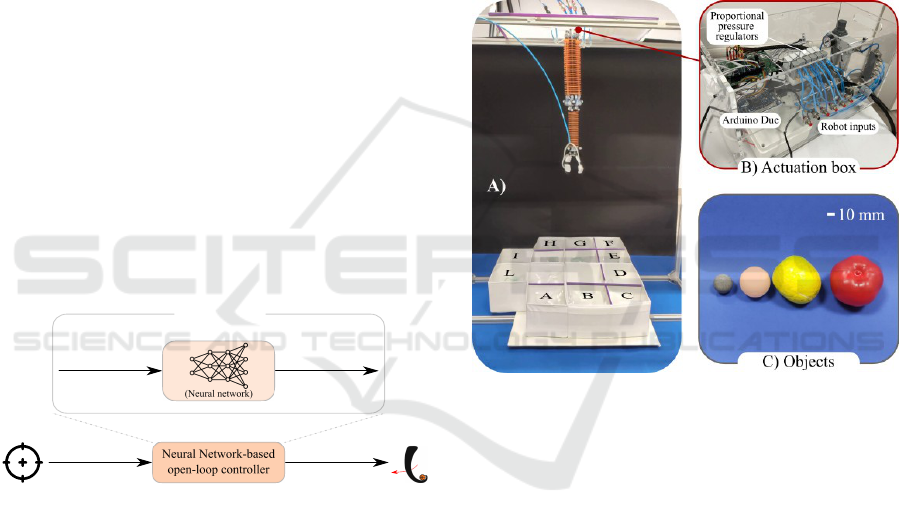
Figure 2: Experimental setup. A) The I-support robot

equipped with a pneumatic gripper is positioned over ten

designated target boxes used for the experiments. B) The

control box used to actuate the robot. C) Various objects,

including a toy lemon, a marker, and a ping-pong ball, were

thrown as part of the experiments and were also utilized in

training the neural networks.

2.2 Experimental Setup

We tested our controller on a modular robot, the I-

Support (Manti et al., 2016)(Figure 2A). Each mod-

ule presents three pairs of pneumatic McKibben-like

actuators equally spaced on a circumference and there

are several plastic disks to arrange the chambers in the

module. To inﬂate the six chamber (p

max

= 1 bar) we

used a custom actuation unit made of several pneu-

matic pressure regulators controlled with ArduinoDue

(Figure 2B).

The robot is mounted on an aluminium frame in

a vertical downward position to reduce the effect of

the gravitational force and due to weight concerns,

the two modules have different sizes. The two mod-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

426

ules are connected together, thanks to a plexiglass in-

terface, with an offset of 60 °. The ﬁxed-end of the

robot is 1000 mm distant from the ground in which

we placed the target boxes(Figure 2A). Each box is

geometrically equivalent to a square prism, whose di-

mensions are [140 ×140 ×100] mm.

In the experiments, we toss in the target boxes

with different objects (Figure 2C) whose mass and di-

mensions are shown in Table 1.

Table 1: Tossed objects. Physical characteristics of the ob-

ject used during the experiments.

Object

Characteristic

dimension [mm]

Mass [g]

Ping-pong ball 36 0.8

Lemon (toy) 62 4.8

Marker 26 3.2

Tomato (toy) 63 10.2

To hold an object during the linear trajectory

we equipped our robot with a two-ﬁnger gripper.

Each ﬁnger is made of 3D-printed surfaces joined to-

gether with thermoplastic polyurethane (TPU) cham-

bers. We characterised the gripper’s opening time. To

do that we perform ﬁfty closing-and-opening cycles

where we measure the time interval from the instant

in which the command is sent and the one in which

the distance between the two ﬁngers in ∼60 mm (ap-

proximately the dimension of the biggest object taken

into account). We assessed that the opening time of

the gripper is equal to ∼ 0.2 ±0.01 s.

To detect the position of the sections of interest we

used a vision-based motion capture system (VICON

Motion Capture Ltd) thanks to which we were able to

track the movement of the object and the robot.

2.3 Dataset collection

The ﬁrst phase of our approach is the collection of the

dataset. We decided to have a linear movement and

to divide it into two different phases: 1) Run-up; and

2) Forward, as in (Braun et al., 2012). This division

aims to increase the speed of the robot in the over-

all movement which results in an increased throwing

capacity.

To respect the counter-movement condition that

we applied to the trajectory we realised a geometri-

cal model of the throwing trajectory. Let us take as

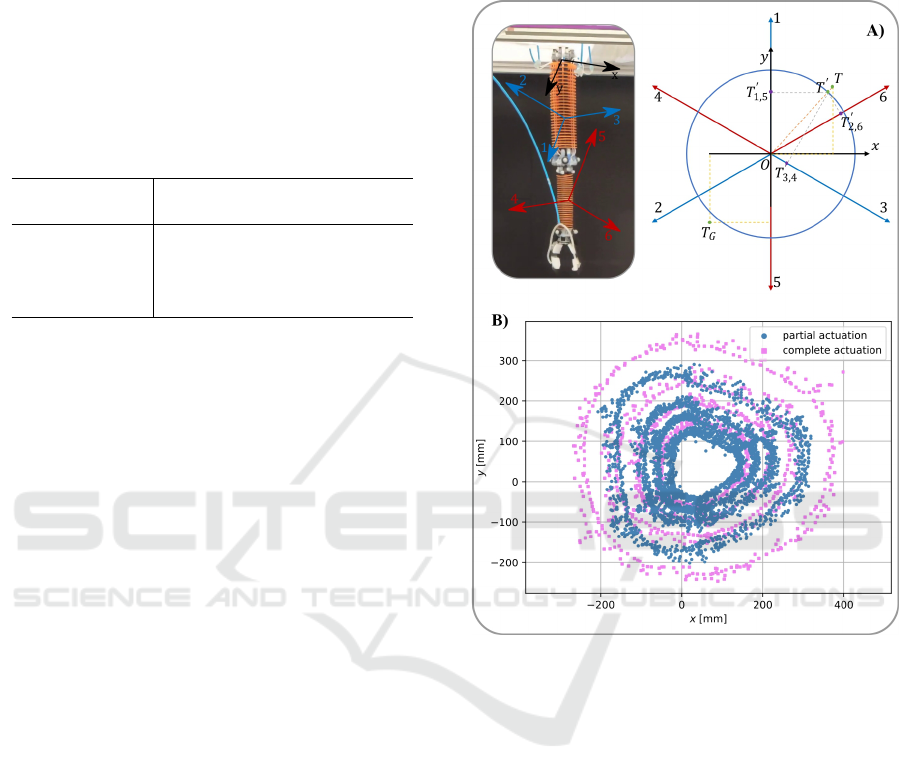
an example the model illustrated in Figure 3A. We

can identify six bending directions associated with the

different chambers of the robot (1, 2, 3 for the proxi-

mal module and 4, 5, 6 for the distal one), and let us

identify a local reference frame (xy). In relation to its

working principle, if we inﬂate chamber 1 of the soft

robot it will bend along the negative y-axis. To avoid

interference we need to prevent the simultaneous in-

ﬂation of the chamber placed in the same direction,

such as 3 and 4.

Figure 3: Training datasets. A) On the left, the identiﬁcation

of the major bending direction while on the right, the geo-

metrical model of the throwing trajectory. B) represents the

dataset used to train the neural networks for the controller in

the two actuation scenarios analysed, respectively the par-

tial and complete. These datasets have been obtained by

averaging the dataset collected with the following objects:

1) ping pong ball; 2) vicon marker; 3) lemon (toy).

By knowing the coordinates of the goal point

; y

), we can ﬁnd the throwing direction that

enables us to toss an object in that direction, which is

represented by the line that passes for this point and

the origin of the reference system. Instead, to ﬁnd

an approximative relationship between the actuations,

we ﬁrst took the desired point T

, and we identiﬁed

the objective point T (x

; y

) by taking the symmet-

ric of the goal point to the origin of the reference sys-

tem, in other words, T = (−y

; −x

). Then, we

projected the objective point on the circle of radius

equal to one centred in the centre of the reference sys-

tem. To obtain the relationships and conditions pre-

sented in Table 2, starting from the previously found

Learning-Based Inverse Dynamic Controller for Throwing Tasks with a Soft Robotic Arm

427

point T

′

; y

′

), we calculated the projection of it

on the six bending axes. The length of the projection

is proportional to the pressure we have to send to the

actuator.

Table 2: Input patterns generation. To enable the move-

ment of the I-Support robotic arm to respect the counter-

movement constraint, the actuation inputs (i.e., pressure

signals) are adjusted based on the geometric relationship.

Speciﬁcally, the point T

, representing the desired goal

point, is symmetrically reﬂected across the origin of the

axes to obtain a new point T . This new point is projected

onto the circumference of a unit radius (T

′

Dir x

′

Condition

1 0 y

′

≥ 0

′

√

′

√

′

≤ 0; y

≤ 0

′

−

√

′

−

√

′

≥ 0; y

≤ 0

′

−

√

′

−

√

′

≤ 0; y

≥ 0

5 0 y

′

≤ 0

′

√

′

√

′

≥ 0; y

≥ 0

We imposed that the ﬁrst phase has to last

run−up

= 0.50 s while the overall movement t

tra j

2.00 s. The object is manually placed between the

gripper ﬁngers and then it is released at t

e ject

= 0.97 s,

i.e., approximately the time instant in which the robot

passes through the lowest point of the trajectory after

the run-up phase. We collected more than one thou-

sand trajectories by randomly sampling the point P

in the xy plane. The overall process lasted two hours

and ﬁfteen minutes. For each trajectory, we saved the

simulated landing position and the actuation pattern

sent to the robot. To obtain the landing position co-

ordinates, starting from the positions and velocities

given by the motion tracking system we simulated the

throws with the projectile equations.

We repeated this process twice to collect the data

in the two actuation scenarios analysed in this work:

1) Partial, in which the distal module, i.e., the one

on which is attached the gripper, is passive; 2) Com-

plete, where all the six chambers are combined. In

each case we collected the dataset with three different

held objects the ping-pong ball, the marker and the

lemon (toy) and then we average them to obtain the

ﬁnal dataset. The datasets are averaged to develop

a controller that is not object-speciﬁc. The weight

of the end effector impacts the dynamics of a robot,

including its trajectories and controller performance

during throwing tasks with various objects. This ef-

fect can be ampliﬁed when combined with a size-

independent opening time. Figure 3B represents the

average dataset in the partial and complete actuation

scenario on which we trained, as shown in the next

section, the neural networks.

2.4 Neural Network Training

With the datasets represented in Figure 3B, with a

feed-forward neural network we mapped the landing

positions with the actuation pattern associated with

them, as in (1).

(τ

run−up

, τ

f orward

) = f (x

) (1)

Where the ﬁrst term is the entire actuation input com-

posed of the run-up phase and the forward one.

The model is represented by an artiﬁcial neural

network (ANN) with one hidden layer. We performed

a model selection based on the average error on the

actuation components to choose the best combination

of hyperparameters. We have changed the number of

units of the hidden layer, their activation function, and

the type of input normalisation. Default values have

been used for the different hyperparameters collected

in Table 3. In addition, to expedite the learning pro-

cess, the early stopping method has been considered.

In both cases, the input layer presents three neu-

rons, i.e., the coordinates of the landing position,

while the output layer depends on the actuation sce-

nario. Indeed, we have six units and twelve units

respectively with partial and complete actuation. In

both cases, the output layer implements the ReLU ac-

tivation function because the predictions of the ANN

are pressure values. The results of the model selection

are reported in Table 3.

3 RESULTS

To test our controllers, the robot performed throws

towards ten target boxes of objects different in size

and weight Figure 2A. We selected the box positions

to test the controller in different directions. We per-

formed our tests in two scenarios: 1) partial actuation,

in which just the module attached to the frame is actu-

ated, and 2) complete actuation, where all the cham-

bers of the bi-modular robot can be inﬂated. In our

experiments we decided to perform two types of tests:

1) quantitative ones, in which we tracked, thanks to

the motion capture system, the movement of the ob-

ject, i.e., its trajectory; and 2) qualitative tests (shown

in Figure 4), in which we recorded the movement of

the overall system to assess if the task was successful

or not. We have success if the object fell inside the

target box, with or without bouncing on the box bor-

ders. In both types of tests, we analysed the ability

of the robot to generate actuation patterns to allow the

soft robot to toss the object into the desired target. We

performed three trials for each combination of param-

eters (object type, qualitative/quantitative test, target

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

428

Table 3: Neural network training. In this table, we collected the different hyperparameters that we changed and keep ﬁxed

during the training of the inverse model of the task, in the two distinguished actuation scenarios.

Default values

learning rate 0.001 Optimiser Adam

batch’s size 16 Loss function MSE

number of epochs 4000 Training/test partition 0.90

Best combination of the changed parameters

Hyperparameter Partial Actuation Complete actuation

Number of units 64 128

Activation function ReLU tanh

Normalisation Z-score Z-score

Figure 4: An example of the qualitative experiment. A

throw toward the target box “I” with the Lemon (Toy) in

the complete actuation scenario.

position), that led to 240 throws for each actuation

modality (partial and complete). The results of the

qualitative and quantitative tests are summarised re-

spectively in Figure 5 and Figure 6. Here we have an

idea of the performance of the controllers in the two

actuation scenarios. Figure 5 is obtained by analysing

the recorded trials to check if the trials were success-

ful or not (object in/object out). We deﬁned success

rate as the ratio between the number of successful

throws and the total number of throws performed.

This index is equal to 55.83 % for the complete ac-

tuation modality and 68.33 % for the other.

The boxplots in Figure 6 illustrate the perfor-

mance of the controllers based on the quantitative

tests. These boxplots represent the distribution of er-

rors, speciﬁcally the Euclidean distance between the

desired target (the centre of the box) and the actual

landing position. The tests were conducted across

three trials for each combination of object targets.

Based on the results shown in the boxplots, the av-

erage error for the partial actuation scenario is 61.34

mm, while for the complete actuation scenario, the

average error is 80.87 mm. These values indicate the

average discrepancy between the desired and actual

landing positions, providing a quantitative measure of

the performance of the controllers.

4 DISCUSSION AND

CONCLUSION

In this work, we show that despite the lower dy-

namic and a more challenging control than traditional

robotics, a soft robot can perform a task as complex

as tossing an object inside different target boxes.

Our results show that the neural network-based

controller reaches a performance in successfully toss-

ing objects to target locations, as high as ∼56 ÷68 %

on average (depending on the actuation pattern used).

These results are highly inﬂuenced by the impossibil-

ity of the controller to generate appropriate actuation

patterns for some targets. Indeed, if we describe the

performance of the controller based on the median,

which is less sensitive to the outliers than the average,

we will obtain for the complete and partial actuation

scenario an average error of 65.69 mm and 54.44 mm

respectively.

These values are comparable to those found in

the state-of-the-art. In their publication, Bianchi et

al. (Bianchi et al., 2023) utilized a real-time open-

Learning-Based Inverse Dynamic Controller for Throwing Tasks with a Soft Robotic Arm

429

Figure 5: Qualitative results for the neural network-based controllers. The results are shown with respect to the object and

each column is proportional to the successful trials. The maximum number of throws for each target is 12, as three attempts

are made for each object.

Figure 6: Comparison between the controller in different

actuation scenarios based on the distance from the target

position, which was reconstructed by recording the falling

trajectories of the object during a toss with the Motion Cap-

ture System.

loop controller for a bi-modular robot based on a

deep reinforcement learning (RL) method. The RL-

based controller was tested in both partial and com-

plete actuation scenarios, and the authors achieved a

success rate of approximately ∼ 62 ÷63 %. Com-

pared to the current state of the art, this study presents

a controller that exhibits similar real-time characteris-

tics and comparable or slightly better performance in

certain instances. Signiﬁcantly, the inverse dynamic

method requires only a fraction of the time needed

to train the neural network compared to the training

time of the RL agent. However, the method described

in (Bianchi et al., 2023) shows the same performance

in both actuation modalities.

From Figures 5 and 6, the difference between the

performance in the two scenarios is clear. . The neu-

ral network in the complete actuation scenario has a

poor ability to generate appropriate patterns due to the

ill-posed problem. In this case, we are asking the net-

work, given three input values (the desired landing

coordinates), to predict the twelve values to perform

both the run-up and forward phases. On the contrary,

the problem is simpler in the case where the robot has

a passive module, as we will have only six values to

predict.

However, the performance of the controllers can

be improved by acting in several levels of the pro-

posed approach. Firstly, we could improve the collec-

tion of the data by trying to pass from a geometrical

model of the throwing trajectory (equations collected

in Table 2) to a model-free approach or in general a

more detailed model. Additionally, in every trial, the

object can have different initial conditions since we

manually place it which increases the variability of

our experimental data.

The gripper has a remarkable inﬂuence on the

overall experiments because it inﬂuences the initial

kinematic conditions of the object in its free-fall for-

ward target box. In our experiments, we determined

an opening time based on the biggest object that we

planned to toss and we consider that in our throwing

task speciﬁcation. However, the objects are consid-

erably different from each other, so the small objects

were released before the ideal realising instant. That

led to an increased variability of the data and a lower

accuracy of the controller.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

430

ACKNOWLEDGMENT

We acknowledge Andrea Centurelli for the help pro-

vided during the development of the proposed ap-

proach.

This work was partially supported by the Euro-

pean Union’s Horizon 2020 FET-Open program under

grant agreement no. 863212 (PROBOSCIS project).

REFERENCES

Alessi, C., Falotico, E., and Lucantonio, A. (2023). Abla-

tion study of a dynamic model for a 3d-printed pneu-

matic soft robotic arm. IEEE Access, 11:37840–

37853.

Bianchi, D., Antonelli, M., Laschi, C., and Falotico, E.

(2022). Open-loop control of a soft arm in throwing

tasks. In 19th International Conference on Informat-

ics in Control, Automation and Robotics, pages 138–

145. ISSN: 2184-2809.

Bianchi, D., Antonelli, M. G., Laschi, C., Sabatini, A. M.,

and Falotico, E. (2023). SofToss: Learning to Throw

Objects with a soft robot. IEEE Robotics and Automa-

tion Magazine.

Braun, D. J., Howard, M., and Vijayakumar, S. (2012).

Exploiting variable stiffness in explosive movement

tasks. Robotics: Science and Systems VII, 7:25–32.

uchler, D., Calandra, R., and Peters, J. (2022). Learning to

Control Highly Accelerated Ballistic Movements on

Muscular Robots. Robotics and Autonomous Systems,

page 104230.

Centurelli, A., Arleo, L., Rizzo, A., Tolu, S., Laschi, C., and

Falotico, E. (2022). Closed-loop Dynamic Control of

a Soft Manipulator using Deep Reinforcement Learn-

ing. IEEE Robotics and Automation Letters, pages 1–

1. Conference Name: IEEE Robotics and Automation

Letters.

Centurelli, A., Rizzo, A., Tolu, S., and Falotico, E. (2021).

Open-loop Model-free Dynamic Control of a Soft Ma-

nipulator for Tracking Tasks. In 2021 20th Inter-

national Conference on Advanced Robotics (ICAR),

pages 128–133.

Fang, Z., Hou, Y., and Li, J. (2021). A pick-and-throw

method for enhancing robotic sorting ability via deep

reinforcement learning. In 2021 36th Youth Academic

Annual Conference of Chinese Association of Automa-

tion (YAC), pages 479–484.

Fischer, O., Toshimitsu, Y., Kazemipour, A., and

Katzschmann, R. K. (2022). Dynamic Task Space

Control Enables Soft Manipulators to Perform Real-

World Tasks. Advanced Intelligent Systems, page

2200024.

Gazzola, M., Dudte, L. H., McCormick, A. G., and Ma-

hadevan, L. (2018). Forward and inverse problems in

the mechanics of soft ﬁlaments. Royal Society Open

Science, 5(6):171628. Publisher: Royal Society.

George Thuruthel, T., Falotico, E., Manti, M., Pratesi,

A., Cianchetti, M., and Laschi, C. (2017). Learning

closed loop kinematic controllers for continuum ma-

nipulators in unstructured environments. Soft robotics,

4(3):285–296.

Giorelli, M., Renda, F., Ferri, G., and Laschi, C. (2013). A

feed-forward neural network learning the inverse ki-

netics of a soft cable-driven manipulator moving in

three-dimensional space. In 2013 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems,

pages 5033–5039. ISSN: 2153-0866.

Hawkes, E. W., Blumenschein, L. H., Greer, J. D., and

Okamura, A. M. (2017). A soft robot that navigates

its environment through growth. Science Robotics,

2(8):eaan3028. Publisher: American Association for

the Advancement of Science.

Holland, D. P., Abah, C., Velasco-Enriquez, M., Herman,

M., Bennett, G. J., Vela, E. A., and Walsh, C. J.

(2017). The Soft Robotics Toolkit: Strategies for

Overcoming Obstacles to the Wide Dissemination of

Soft-Robotic Hardware. IEEE Robotics & Automa-

tion Magazine, 24(1):57–64. Conference Name: IEEE

Robotics & Automation Magazine.

Ilievski, F., Mazzeo, A. D., Shepherd, R. F., Chen, X.,

and Whitesides, G. M. (2011). Soft Robotics for

Chemists. Angewandte Chemie International Edition,

50(8):1890–1895.

Katzschmann, R. K., DelPreto, J., MacCurdy, R., and

Rus, D. (2018). Exploration of underwater life with

an acoustically controlled soft robotic ﬁsh. Science

Robotics, 3(16):eaar3449. Publisher: American Asso-

ciation for the Advancement of Science.

Laschi, C., Mazzolai, B., and Cianchetti, M. (2016).

Soft robotics: Technologies and systems pushing

the boundaries of robot abilities. Science Robotics,

1(1):eaah3690. Publisher: American Association for

the Advancement of Science.

Laschi, C., Thuruthel, T. G., Lida, F., Merzouki, R., and

Falotico, E. (2023). Learning-based control strategies

for soft robots: Theory, achievements, and future chal-

lenges. IEEE Control Systems, 43(3):100 – 113.

Li, S., Vogt, D. M., Rus, D., and Wood, R. J. (2017).

Fluid-driven origami-inspired artiﬁcial muscles. Pro-

ceedings of the National Academy of Sciences,

114(50):13132–13137. Publisher: Proceedings of the

National Academy of Sciences.

Manti, M., Pratesi, A., Falotico, E., Cianchetti, M., and

Laschi, C. (2016). Soft assistive robot for personal

care of elderly people. In 2016 6th IEEE International

Conference on Biomedical Robotics and Biomecha-

tronics (BioRob), pages 833–838. ISSN: 2155-1782.

Piqu

e, F., Kalidindi, H. T., Fruzzetti, L., Laschi, C., Men-

ciassi, A., and Falotico, E. (2022). Controlling

Soft Robotic Arms Using Continual Learning. IEEE

Robotics and Automation Letters, 7(2):5469–5476.

Conference Name: IEEE Robotics and Automation

Letters.

Polygerinos, P., Correll, N., Morin, S. A., Mosadegh, B.,

Onal, C. D., Petersen, K., Cianchetti, M., Tolley,

M. T., and Shepherd, R. F. (2017). Soft Robotics:

Review of Fluid-Driven Intrinsically Soft Devices;

Manufacturing, Sensing, Control, and Applications

Learning-Based Inverse Dynamic Controller for Throwing Tasks with a Soft Robotic Arm

431

in Human-Robot Interaction. Advanced Engineering

Materials, 19(12).

Raptopoulos, F., Koskinopoulou, M., and Maniadakis, M.

(2020). Robotic Pick-and-Toss Facilitates Urban

Waste Sorting *. In 2020 IEEE 16th International

Conference on Automation Science and Engineering

(CASE), pages 1149–1154. ISSN: 2161-8089.

Runge, G. and Raatz, A. (2017). A framework for the au-

tomated design and modelling of soft robotic systems.

CIRP Annals, 66(1):9–12.

Rus, D. and Tolley, M. (2015). Design, fabrication and con-

trol of soft robots. Nature, 521:467–75.

Thuruthel, T. G., Falotico, E., Renda, F., Flash, T.,

and Laschi, C. (2019). Emergence of behavior

through morphology: a case study on an octopus in-

spired manipulator. Bioinspiration & biomimetics,

14(3):034001.

Vannucci, L., Cauli, N., Falotico, E., Bernardino, A., and

Laschi, C. (2014). Adaptive visual pursuit involving

eye-head coordination and prediction of the target mo-

tion. In 2014 IEEE-RAS International Conference on

Humanoid Robots, pages 541–546.

Vannucci, L., Falotico, E., Di Lecce, N., Dario, P., and

Laschi, C. (2015). Integrating feedback and predic-

tive control in a bio-inspired model of visual pursuit

implemented on a humanoid robot. Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artiﬁcial Intelligence and Lecture Notes in Bioin-

formatics), 9222:256–267.

Wang, J. and Chortos, A. (2022). Control Strategies for

Soft Robot Systems. Advanced Intelligent Systems,

n/a(n/a):2100165.

Webster, R. J. and Jones, B. A. (2010). Design and

Kinematic Modeling of Constant Curvature Contin-

uum Robots: A Review. The International Journal

of Robotics Research, 29(13):1661–1683. Publisher:

SAGE Publications Ltd STM.

Zeng, A., Song, S., Lee, J., Rodriguez, A., and Funkhouser,

T. (2019). TossingBot: Learning to throw arbitrary ob-

jects with residual physics. Proceedings of Robotics:

Science and Systems (RSS).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

432