Approaches for Enhancing Preference Balance

in Neighbor-Based Group Recommender Systems

Le Nguyen Hoai Nam

1,2

Faculty of Information Technology, University of Science, Ho Chi Minh City, Vietnam

VietNam National University, Ho Chi Minh City, Vietnam

Keywords: Group Recommendation, Neighbor-Based Recommendation, Collaborative Filtering, Recommender System.

Abstract: The Increasing Trend of Group Activities Has Led to Changes in Recommender Systems, Shifting from

Recommending Individual Users to Recommending Groups of Users. a Group Recommender System

Consists of Two Primary Stages: Aggregating the Profiles of all Group Members to Create a Virtual User and

Providing Recommendations to This Virtual User. This Paper Focuses on the Stage of Recommending the

Virtual User. Specifically, Our Proposed Approach Aims to Recommend the Virtual User to Achieve a

Harmonious Balance Among the Diverse Preferences of Group Members by Combining the Profiles of Group

Members with that of the Virtual User. Additionally, We Integrate Textual Comments Observed from Users

to Further Enhance the Accuracy of Group Recommendations. Experiments Conducted on Three Popular

Datasets from Amazon Have Demonstrated the Effectiveness of the Proposed Approach in Terms of the F1-

Score.

1 INTRODUCTION

Nowadays, working and entertaining in groups are

becoming popular and preferred trends (Masthoff,

2015; Li et al., 2018; Nam, 2022). For example, a

family chooses a restaurant to enjoy a meal together.

Similarly, a group of friends often organizes movie

nights to experience exciting moments together,

exchange opinions, and share their feelings. There has

been a significant shift in user demands, from

individual to group. Therefore, service providers

must adapt and modify their serving methods to meet

these demands.

Recommender systems play an important role in

the decision-making process on digital platforms (Lu

et al., 2015; Villavicencio et al., 2019). In line with

the above trends, they need to provide solutions to

support group decision-making. Specifically, the

recommender systems need to predict the preferences

of groups of users instead of individual users as

before (Felfernig et al., 2018; Xiao et al., 2020). As a

result, groups will be recommended on the most

suitable items for all their members to experience

together.

There are two commonly used recommendation

approaches: model-based and neighbor-based.

Model-based recommendations focus on discovering

a concise model for predicting user preferences.

However, explaining these models presents numerous

challenges (Nam, 2021a). On the other hand,

neighbor-based recommendations rely on the

similarity of preferences between users to identify

neighbor users. Aggregating the preferences of these

neighbor users helps predict the preferences of the

active user (Lima et al., 2020).

To provide recommendations for a group of users,

it is necessary to establish a virtual user that

represents the characteristics of all the group

members (Masthoff, 2010; Nam, 2021b).

Subsequently, recommendation algorithms can be

deployed to provide recommendations for this virtual

user as if they were recommending the corresponding

group. In the context of group recommendations

based on neighbors, the contributions of this paper are

as follows:

 The accuracy of a neighbor-based group

recommendation heavily depends on the

process of determining the neighbor set of

the virtual user. For this task, this study

leverages the profiles of both the virtual user

and the group members, instead of using just

one of them as in previous studies.

306

Nam, L.

Approaches for Enhancing Preference Balance in Neighbor-Based Group Recommender Systems.

DOI: 10.5220/0012184700003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 306-314

ISBN: 978-989-758-671-2; ISSN: 2184-3228

 In certain cases, users not only provide

ratings but also write comments about items.

These textual comments help to further

clarify user preferences (Rubio et al., 2019;

Chehal et al., 2021). Therefore, we propose

an approach for integrating observed

comments into the group recommendations.

 In addition to accuracy, the implementation

methodology of an approach is also a crucial

criterion. Finally, we have designed the

implementation methodology for the

proposed approach.

The notations used in the paper are listed in Table

Table 1: The notations.

Notation Meaning

𝑢,𝑣

User

𝑖

Item

Group

𝑔

Virtual user

𝑟



*

Observed rating

𝑟



= *

Unknown rating

𝑟

,

Predicted rating

𝑠𝑖𝑚



The similarity between 𝑢and 𝑣

,

The neighbor set of user 𝑢

considering item 𝑖

𝜇



Average rating of user 𝑢

𝛼

Liking threshold

𝑘

The number of selected neighbo

2 RELATED WORKS

2.1 Group Recommendation Definition

Through surveys, users can provide ratings, such as

from 1 to 5, to express their satisfaction levels with

items (𝑟

,

∗. This data helps predict their ratings

( 𝑟

,

) for items they haven't used yet (𝑟

,

∗). In the

process of making recommendations, the system

chooses items that are predicted to be highly preferred

by the active user (Aggarwal, 2016).

However, recommending to a group of users

differs from recommending to an individual user in

the following ways. Only the items that have not been

used by all group members are considered candidate

items. For each candidate item, it is necessary to

predict the group's rating instead of an individual

user's rating (Felfernig et al., 2018; Nam, 2021b). Fig.

1 shows an example of group recommendation. In a

group G𝑢



;𝑢



, three items 𝑖



, 𝑖



, and 𝑖



will be

considered candidate items. The group's ratings for

these items will be predicted ( 𝑟

,



, 𝑟

,



, and 𝑟

,



)

to determine the recommended items for the group.

Figure 1: Group recommendation.

2.2 Group Recommendation Approach

A simple approach for predicting the rating of a group

is to individually predict the rating of each group

member. The aggregation of these predicted ratings

will then form the rating of the group (Masthoff,

2010; Felfernig et al., 2018). However, using this

approach, even minor rating prediction errors for each

group member will generate a larger error in the

group rating prediction. Moreover, it may not

adequately capture the intricate dynamics or

interactions that can arise within a group (Nam,

2021b).

Hence, it is advisable to explore approaches that

directly predict the rating of the group, rather than

relying solely on individual predictions. Specifically,

all ratings observed from the group members

(perfectly accurate preferences) can be aggregated to

create a virtual user. At this point, providing

*122∗1

243∗1∗

132***

25∗∗∗∗

𝑢



𝑢



𝑢



𝑖



𝑖



𝑖



𝑖



𝑖



Users

Items

Predict unknown ratings of the

group for candidate items

Group of users

G 𝑢



;𝑢





𝑢



Unknown

ratings

𝑟

,

∗ ∗

Observed

ratings

𝑟

,

 ∗

𝑖



Identify candidate items

Candidate items

𝑖



,𝑖



,𝑖



Predicted ratings

𝑟

,



, 𝑟

,



, 𝑟

,



Approaches for Enhancing Preference Balance in Neighbor-Based Group Recommender Systems

307

recommendations to the virtual user is essentially

equivalent to providing recommendations to the

group (Boratto and Carta, 2015; Wang et al., 2016;

Quan and Cho, 2018; Nam, 2021b)

A popular strategy for creating a virtual user of a

group is to compute a weighted average of the ratings

observed from the group members (Delic et al., 2018;

Nam, 2021b; Yalcin and Bilge, 2021). To maximize

the number of ratings aggregated in the virtual user,

many studies perform rating aggregation for an item

even if not all group members have provided a rating

for it. The availability of more aggregated ratings in

the virtual user contributes to more accurate

recommendations for the group. In the rating

aggregation process, the weighting of each group

member is related to his/her expertise, which can be

calculated based on the number of his/her observed

ratings (Ortega et al., 2016) or on his/her external

information (Villavicencio et al., 2019; Xiao et al.,

2020).

The latent factor model is a prominent approach

in model-based recommender systems. It is trained

based on observed ratings to discover compact

vectors representing users and items (Nam, 2021a).

The dot product of these two vectors helps determine

the rating of the corresponding user for the

corresponding item. The training process of the latent

factor model is essentially a low-rank approximation

of the user-item rating matrix. It becomes faster and

more accurate when integrated with various

additional data sources. For example, (Shen et al.,

2019) incorporate textual comments to provide

supplementary information about the user experience

during model training. (Khan et al., 2020) learns item

vectors from item textual descriptions and utilizes

them to improve convergence. User actions in the

system have also been demonstrated to enhance the

latent factor model (Nam, 2021a). The latent factor

model can also be applied to group recommendation,

specifically for recommending the virtual user of the

group. To predict the ratings of the virtual user, it is

necessary to capture its vector in the latent factor

model. This vector is learned by optimizing the

distance between aggregated ratings of the virtual

user and their predictions (Ortega et al., 2016; Nam,

2021b). However, this process is time-consuming,

resulting in a significant slowdown in group

recommendations.

With the compactness of the learned item and user

vectors, the latent factor model is recognized as a

highly scalable model. However, interpreting the

meaning of these vectors is extremely challenging.

This presents significant difficulties in explaining the

recommendations to users. Neighbor-based

recommendations offer greater interpretability. It

predicts unknown ratings of a user based on users

who have high similarities with him/her in the past

(Valcarce et al., 2019; Lima et al., 2020). These users

are referred to as neighbors. To be more specific, the

process of predicting the rating of user 𝑢 for item 𝑖 is

as follows:

 Calculate the similarity of preferences

between user 𝑢 and each user 𝑣 (𝑠𝑖𝑚

,

)

who has provided ratings for item 𝑖. Some

traditional similarity measures that yield

stable results are the PPC (Su and

Khoshgoftaar, 2009), Jaccard (Koutrika et

al., 2009), and MSD (Herlocker et al., 1999).

 Rank the similarity scores obtained in the

previous step to identify the top 𝑘 users most

similar to 𝑢. These users are referred to as

the neighbor set of 𝑢, denoted by N

,

 The predicted rating of 𝑢 for item 𝑖 will be

the average rating given by the neighbors for

item 𝑖.

This neighbor-based process can also be applied to

recommend to a group of users. The key concern is

proposing an approach to determine the neighbor set

of the virtual user of the group. Recently, (Nam,

2022) has proposed a similarity formula between the

virtual user 𝑔 of group G and a regular user 𝑣

(𝑠𝑖𝑚

,

 based on the similarities between each group

member 𝑢∈G and 𝑣 (𝑠𝑖𝑚

,

. The formula is as

follows:

𝑠𝑖𝑚

,

 𝑠𝑖𝑚

,



∈



(1)

3 MOTIVATIONS

In this paper, we aim to improve neighbor-based

group recommendations. The focus is on calculating

the similarity between the virtual user of the group

and a regular user, to accurately determine the

neighbor set. Although Eq. (1) has been designed to

be highly effective for this task, it relies only on the

group members, overlooking the group's virtual user.

However, the virtual user is meticulously aggregated

to represent the neutral preferences of the entire

group. Therefore, to achieve the most satisfying

group recommendations possible, in Section 4.1, we

propose a formula to calculate the similarity between

the group's virtual user and a regular user, utilizing

both the virtual user and the individual group

members.

Rating scales are often broad, corresponding to a

wide range of user preferences. Consequently, they

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

308

can unintentionally confuse users when providing

ratings. It requires more time and effort to guide users

in selecting a rating that accurately reflects their level

of satisfaction. However, accomplishing this

becomes challenging in brief and straightforward

surveys. According to (Shen et al., 2019), there are

instances where ratings completely contradict the

accompanying comments. Users may write highly

positive comments about an item but assign a low

rating on the provided scale. Based on these

arguments, we aim to combine ratings and comments

to further enhance the effectiveness of our proposed

approach. The details will be presented in Section 4.2.

4 PROPOSED APPROACHES

In this section, we propose a Neighbor-based Group

Recommendation approach, namely NGR.

Additionally, we provide its comment integration

version and implementation solutions.

4.1 NGR, a Neighbor-Based Group

Recommendation

Firstly, similar to (Ortega et al., 2016; Delic et al.,

2018; Nam, 2021b; Yalcin and Bilge, 2021), we

calculate the weighted average of ratings provided by

group members 𝑢∈G to generate the virtual user 𝑔:

𝑟

,



∑

𝑤



.𝑟

,



∈ ∧ 

,

∗

∑

𝑤

∈ ∧ 

,

∗

𝑖𝑓 ∃𝑢∈𝐺:𝑟

,

∗

∗ 𝑖𝑓 ∀𝑢∈𝐺: 𝑟

,

∗

(2)

where 𝑤



is the number of ratings provided by 𝑢.

To offer recommendations for the group, it is

essential to predict the rating of the virtual user for

each item that all group members have not yet used

(Candidate items). This process initiates by assessing

the similarity between the virtual user 𝑔 and each

user 𝑣 who has provided ratings for a candidate item

𝑖 in the past. As described in Section 3, we improve

Eq. (1) to consider both the virtual user 𝑔 and all

group members 𝑢∈G , as follows:

𝑠𝑖𝑚

,

 𝑐𝑜𝑟𝑟

,

.𝑠𝑖𝑚

,

∈

(3)

In Eq. (3), 𝑐𝑜𝑟𝑟

,

denotes the correlation between the

virtual user 𝑔 of group G and each group member 𝑢∈

G . The main objective of this component is to

emphasize that neighbors of group members with a

stronger correlation to the virtual user are more likely

to be selected as neighbors of the virtual user.

Consequently, these neighbors play a significant role

in the recommendation process for the group. In this

paper, we calculate the correlation between a group

member and the virtual user by considering the

coherence in their preferences across all items. It is

calculated based on the number of items that both

either share a liking for or share a disliking for:

𝑐𝑜𝑟𝑟

,

𝑖

𝑟

,

∗ ∧ 𝑟

,

∗

∧𝑟

,

𝛼∧𝑟

,

𝛼



𝑖

𝑟

,

∗ ∧ 𝑟

,

∗

∧𝑟

,

𝛼∧𝑟

,

𝛼



(4)

where 𝛼 is the liking threshold.

Based on the calculated similarities, a set of 𝑘

users with the highest similarity to the virtual user 𝑔

is selected, referred to as N

,

. All ratings from N

,

for item 𝑖 are then aggregated to estimate the virtual

user's rating for item 𝑖 ( 𝑟

,

), i.e., the group’s rating

for item 𝑖 ( 𝑟

,

), as follows (Aggarwal, 2016; Lima et

al., 2020):

𝑟



,

𝑟



,

𝜇





∑

𝑠𝑖𝑚

,

.𝑟

,

𝜇





∈

,

∑

𝑠𝑖𝑚

,∈

,

(5)

4.2 NGR with Integrated Textual

Comments

Like numerical ratings, textual comments also

contain information about user preferences. In this

section, we leverage user comments to improve the

accuracy of the NGR, which relies solely on ratings.

Firstly, we implement the method of (Shen et al.,

2019) to convert textual comments into numeric

ratings. This helps capture user preferences in two

ways: the ratings directly provided by the users and

the ratings inferred from the comments written by the

users. These two types of ratings complement each

other, providing a more comprehensive

understanding of user preferences. Based on these

observations, we propose two different group

recommendation approaches for combining direct

ratings and inferred ratings, named CNGR1 and

CNGR2. Specifically, CNGR1 combines direct

ratings (𝑟







 and inferred ratings (𝑟







) to

produce comprehensive ratings (𝑟







. These

comprehensive ratings are employed in the training

and prediction stages of NGR, as follows:

Approaches for Enhancing Preference Balance in Neighbor-Based Group Recommender Systems

309

𝑟









𝑟









𝑟







𝑟

,

 𝑟

,

⃪ 𝑁𝐺𝑅𝑟







(6)

In contrast to CNGR1, CNGR2 implements two

separate neighbor-based recommendations, one for

direct ratings and one for inferred ratings. Both are

then combined in the rating prediction stage, as

follows:

𝑟

,







⃪𝑁𝐺𝑅𝑟







𝑟

,







⃪𝑁𝐺𝑅𝑟







𝑟

,

 𝑟

,



𝑟

,









𝑟

,







(7)

4.3 Implementation

We have designed a solution for implementing the

proposed approach effectively in two phases: offline

and online. The goal is to predict unknown ratings

and ultimately provide recommendations for the

group as quickly as possible in the online phase. In

the offline stage, we calculate the similarity between

each pair of users based on their observed

preferences, which include the ratings directly

provided by the users and/or the ratings inferred from

the comments written by the users.

The online phase will involve a group consisting

of multiple users. In this phase, the system will

examine each item to aggregate the preferences of all

group members into a virtual user. In parallel, the

system also counts the number of items that each

group member and the virtual user like or dislike in

common. For a candidate item, the similarity between

the virtual user and each regular user who has rated

the item is calculated using Eq. (3-4). Based on the

similarities between users, which have already been

computed in the offline phase, and the correlations

between each group member and the virtual user,

which have just been calculated at the beginning of

the online phase, NGR can efficiently complete Eq.

(3-5).

5 EXPERIMENTS

5.1 Experiment Setup

In this experiment, we implemented related neighbor-

based group recommendation approaches as follows:

 SVMGR (Ghazarian and Nematbakhsh,

2015)

 DPGR (Nam, 2022) was implemented with

COPC-Hg similarity (Mu et al., 2019).

 NGR was implemented with COPC-Hg

similarity (Mu et al., 2019).

 CNGR1 was implemented with COPC-Hg

similarity (Mu et al., 2019).

 CNGR2 was implemented with COPC-Hg

similarity (Mu et al., 2019).

We divided each experimental dataset into 65%

for training and 35% for testing. To create groups for

the experiment, we randomly generated 250 groups

with 2 members and 250 groups with 3 members. The

liking threshold (𝛼) of a user is set to the average of

his/her observed ratings (Vy et al., 2023).

5.2 Datasets

The three popular datasets extracted from

Amazon (https://jmcauley.ucsd.edu/data/amazon/)

were chosen to conduct experiments:

 The Clothing and Accessories dataset comprises

278.677 reviews and ratings from 39.387 users

for 23.033 items.

 The Beauty dataset comprises 198.502 reviews

and ratings from 22.365 users for 12.101 items.

 The Tools-Home Improvement dataset

comprises 134.476 reviews and ratings from

19.856 users for 10.217 items.

5.3 Measures

The accuracy of the group recommendation

approaches is evaluated using the F1-score, which

combines precision and recall measures. Precision is

calculated based on the number of correctly

recommended items ( 𝑇∩𝐶) and the number of

recommended items (𝑇). In contrast, the recall is the

ratio of the number of correctly recommended items

(𝑇∩𝐶) to the total number of items preferred by the

group (𝐶), as follows:

𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛

𝑇∩𝐶

𝑇

𝑅𝑒𝑐𝑎𝑙𝑙

|𝑇 ∩ 𝐶|

|𝐶|

𝐹1  𝑠𝑐𝑜𝑟𝑒

2.𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛.𝑅𝑒𝑐𝑎𝑙𝑙

𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛  𝑅𝑒𝑐𝑎𝑙𝑙

(8)

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

310

Similar to many previous studies on group

recommendation (Wang et al., 2016; Ortega et al.,

2016; Nam, 2021b), we have established strict criteria

that consider an item to be preferred by a group only

when all group members express liking for it.

5.4 Experimental Results and

Discussions

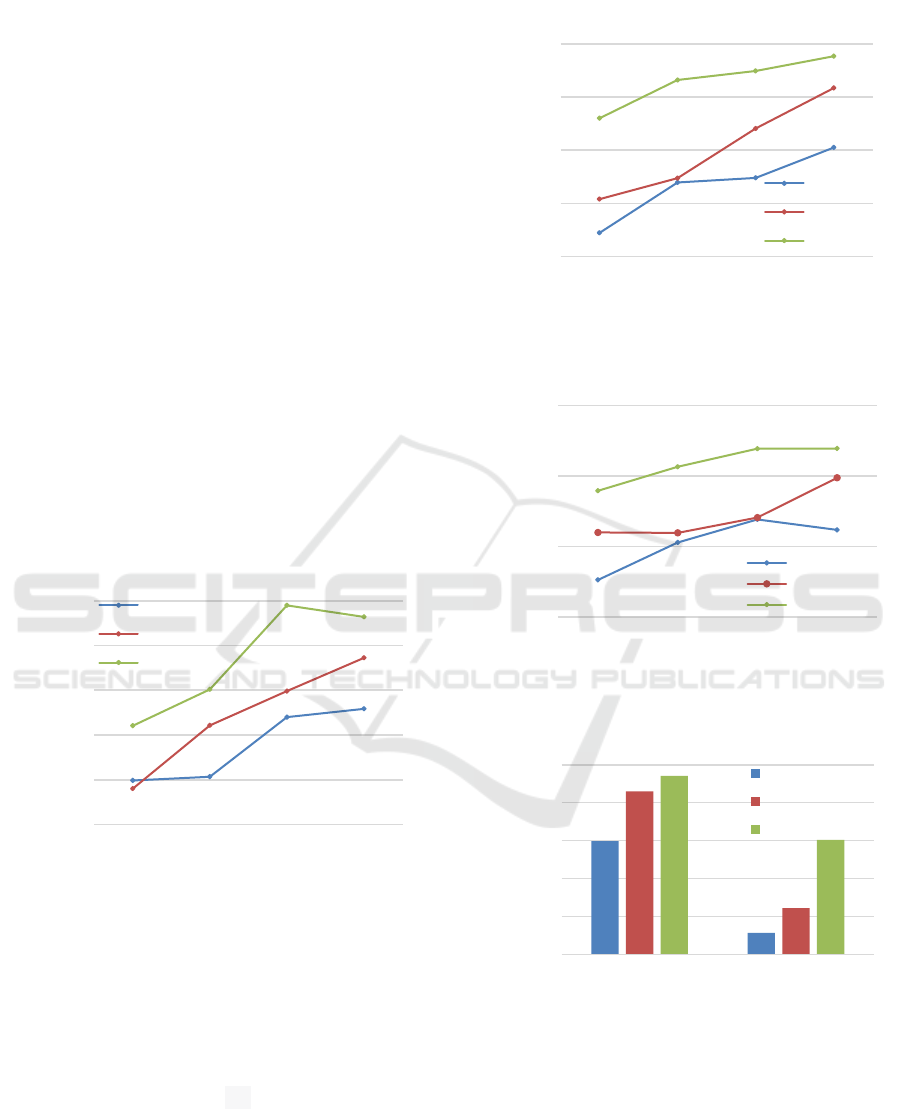
Fig. 2-4 illustrates the F1-score results of group

recommendation approaches when varying the size of

the neighbor sets. In all three experimental datasets,

our proposed approach (NGR) consistently yields

more accurate recommendation results compared to

previous approaches (SVMGR and DPGR).

Specifically, in the Tools and Home

Improvement dataset, at 50 selected neighbors, NGR

increases the F1-score by 5,1% and 6,7% compared

to DPGR and SVMGR, respectively. As shown in

Fig. 5, the improvement of NGR becomes more

evident as the group size increases from 2 to 3. As the

number of group members increases, achieving

consensus among them becomes more challenging.

At this point, the integration of virtual users into the

neighbor identification, as in the NGR, proves to be

more effective.

Figure 2: F1-score results of SVMGR, DPGR, and NGR in

the Tools and Home Improvement dataset.

In our approaches combining rating and comment

(CNGR1 and CNGR2), CNGR2 outperforms

CNGR1 in all three datasets as shown in Fig. 6-8.

However, CNGR2 requires more computation than

CNGR1 as it involves training two separate

recommendation models. Overall, integrating

comments has improved the accuracy of NGR, which

relies solely on ratings. The reason is that all three

experimental datasets contain many ratings that do

not accurately reflect user preferences. In such cases,

comments helped refine the ratings to provide a

clearer understanding of user preferences.

Figure 3: F1-score results of SVMGR, DPGR, and NGR in

the Beauty dataset.

Figure 4: F1-score results of SVMGR, DPGR, and NGR in

the Clothing and Accessories dataset.

Figure 5: F1-score results of SVMGR, DPGR, and NGR for

each group size in all experimental datasets (𝑘 =55).

40 45 50 55

F1-score

The number of selected neighbors

SVMGR

DPGR

NGR

40 45 50 55

F1-score

The number of selected neighbors

SVMGR

DPGR

NGR

40 45 50 55

F1-score

The number of selected neighbors

SVMGR

DPGR

NGR

F1-score

Group size

SVMGR

DPGR

NGR

Approaches for Enhancing Preference Balance in Neighbor-Based Group Recommender Systems

311

Figure 6: F1-score results of NGR, CNGR1, and CNGR2 in

the Tools and Home Improvement dataset.

Figure 7: F1-score results of NGR, CNGR1, and CNGR2 in

the Beauty dataset.

Figure 8: F1-score results of NGR, CNGR1, and CNGR2 in

the Clothing and Accessories dataset.

One of the important parameters in our proposed

approaches is the liking threshold used to calculate

the correlation between a group member and a virtual

user. To determine the value of this parameter, a

simple method is to fix it to the average of the rating

scale for all users (FIX). However, users have their

personalities when rating items. In other words, the

value of the liking threshold should vary for each user

(PERSONAL). Taking inspiration from (Vy et al.,

2023), we estimated the liking threshold of a user by

calculating the average of his/her observed ratings.

The experimental results in Fig. 9-11 have shown that

choosing such a liking threshold significantly

contributed to the impressive outcomes of our

approaches (NGR, CNGR1, and CNGR2).

Figure 9: F1-score results of NGR, CNGR1, and CNGR2

for each liking threshold in the Tools and Home

Improvement dataset.

Figure 10: F1-score results of NGR, CNGR1, and CNGR2

for each liking threshold in the Beauty dataset.

Figure 11: F1-score results of NGR, CNGR1, and CNGR2

for each liking threshold in the Clothing and Accessories.

5 CONCLUSIONS AND FUTURE

WORKS

To achieve a balance among all members of the

group, our approach considers not only the group

members but also a virtual user representing the

group. Furthermore, to address the issue of bias in

rating provision, we have proposed integrating user

comments into the group recommendations. The

combination of ratings and comments is performed in

two distinct stages: the training stage and the

40 45 50 55

F1-score

The number of selected neighbors

NGR

CNGR1

CNGR2

40 45 50 55

F1-score

The number of selected neighbors

NGR

CNGR1

CNGR2

40 45 50 55

F1-score

The number of selected neighbors

NGR

CNGR1

CNGR2

NGR CNGR1 CNGR2

F1-score

PERSONAL FIX

NGR CNGR1 CNGR2

F1-score

PERSONAL FIX

NGR CNGR1 CNGR2

F1-score

PERSONAL FIX

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

312

prediction stage. Finally, we efficiently implement

the proposed approach through two phases: offline

and online. The goal is to minimize the computation

time of the online phase thereby significantly

improving the user experience. One limitation of our

approach is the omission of weights for combining

ratings and comments. In the future, we aim to

accurately estimate these weights. However, the

computational cost of estimating the weights would

impose an additional burden on the offline phase.

ACKNOWLEDGEMENTS

This research is funded by the University of Science,

VNUHCM under grant number CNTT 2022-01.

REFERENCES

Aggarwal, C. C. (2016). Recommender systems (Vol. 1).

Cham: Springer International Publishing.

Boratto, L., & Carta, S. (2015). The rating prediction task

in a group recommender system that automatically

detects groups: architectures, algorithms, and

performance evaluation. Journal of Intelligent

Information Systems, 45(2), 221-245.

Chehal, D., Gupta, P., & Gulati, P. (2021). Implementation

and comparison of topic modeling techniques based on

user reviews in e-commerce recommendations. Journal

of Ambient Intelligence and Humanized Computing,

12, 5055-5070.

Delic, A., Neidhardt, J., Nguyen, T. N., & Ricci, F. (2018).

An observational user study for group recommender

systems in the tourism domain. Information

Technology & Tourism, 19, 87-116.

Felfernig, A., Boratto, L., Stettinger, M., & Tkalčič, M.

(2018). Group recommender systems: An introduction

(pp. 27-58). Cham: Springer.

Ghazarian, S., & Nematbakhsh, M. A. (2015). Enhancing

memory-based collaborative filtering for group

recommender systems. Expert systems with

applications, 42(7), 3801-3812.

Herlocker, J. L., Konstan, J. A., Borchers, A., & Riedl, J.

(1999, August). An algorithmic framework for

performing collaborative filtering. In Proceedings of

the 22nd annual international ACM SIGIR conference

on Research and development in information retrieval

(pp. 230-237).

Hernández-Rubio, M., Cantador, I., & Bellogín, A. (2019).

A comparative analysis of recommender systems based

on item aspect opinions extracted from user reviews.

User Modeling and User-Adapted Interaction, 29(2),

381-441.

Khan, Z., Iltaf, N., Afzal, H., & Abbas, H. (2020).

Enriching non-negative matrix factorization with

contextual embeddings for recommender systems.

Neurocomputing, 380, 246-258.

Koutrika, G., Bercovitz, B., & Garcia-Molina, H. (2009,

June). FlexRecs: expressing and combining flexible

recommendations. In Proceedings of the 2009 ACM

SIGMOD International Conference on Management of

data (pp. 745-758).

Li, Q., Liang, N., & Li, E. Y. (2018). Does friendship

quality matter in social commerce? An experimental

study of its effect on purchase intention. Electronic

Commerce Research, 18, 693-717.

Lima, G. R., Mello, C. E., Lyra, A., & Zimbrao, G. (2020).

Applying landmarks to enhance memory-based

collaborative filtering. Information Sciences, 513, 412-

428.

Lu, J., Wu, D., Mao, M., Wang, W., & Zhang, G. (2015).

Recommender system application developments: a

survey. Decision support systems, 74, 12-32.

Masthoff, J. (2010). Group recommender systems:

Combining individual models. In Recommender

systems handbook (pp. 677-702). Boston, MA:

Springer US.

Masthoff, J. (2015). Group recommender systems:

aggregation, satisfaction and group attributes.

recommender systems handbook, 743-776.

Nam, L. N. H. (2021a). Latent factor recommendation

models for integrating explicit and implicit preferences

in a multi-step decision-making process. Expert

Systems with Applications, 174

Nam, L. N. H. (2021b). Towards comprehensive profile

aggregation methods for group recommendation based

on the latent factor model. Expert Systems with

Applications, 185

Nam, L. N. H. (2022). Profile Aggregation-Based Group

Recommender Systems: Moving From Item Preference

Profiles to Deep Profiles. IEEE Access, 10, 6218-6245.

Ortega, F., Hernando, A., Bobadilla, J., & Kang, J. H.

(2016). Recommending items to group of users using

matrix factorization based collaborative filtering.

Information Sciences, 345, 313-324.

Quan, J. C., & Cho, S. B. (2014). A hybrid recommender

system based on AHP that awares contexts with

Bayesian networks for smart TV. In Hybrid Artificial

Intelligence Systems: 9th International Conference,

HAIS 2014, Salamanca, Spain, June 11-13, 2014.

Proceedings 9 (pp. 527-536). Springer International

Publishing.

Shen, R. P., Zhang, H. R., Yu, H., & Min, F. (2019).

Sentiment based matrix factorization with reliability for

recommendation. Expert Systems with Applications,

135, 249-258.

Su, X., & Khoshgoftaar, T. M. (2009). A survey of

collaborative filtering techniques. Advances in artificial

intelligence, 2009.

Valcarce, D., Landin, A., Parapar, J., & Barreiro, Á. (2019).

Collaborative filtering embeddings for memory-based

recommender systems. Engineering Applications of

Artificial Intelligence, 85, 347-356.

Villavicencio, C., Schiaffino, S., Diaz-Pace, J. A., &

Monteserin, A. (2019). Group recommender systems: A

Approaches for Enhancing Preference Balance in Neighbor-Based Group Recommender Systems

313

multi-agent solution. Knowledge-Based Systems, 164,

436-458.

Vy, H. & Hong, T. & Hang, V. & Pham-Nguyen, C. and

Nam, L. (2023). A Multi-Factor Approach to Measure

User Preference Similarity in Neighbor-Based

Recommender Systems. In Proceedings of the 12th

International Conference on Data Science, Technology

and Applications, pages 532-539

Wang, W., Zhang, G., & Lu, J. (2016). Member

contribution-based group recommender system.

Decision Support Systems, 87, 80-93.

Xiao, Y., Pei, Q., Yao, L., Yu, S., Bai, L., & Wang, X.

(2020). An enhanced probabilistic fairness-aware group

recommendation by incorporating social activeness.

Journal of Network and Computer Applications, 156,

102579.

Yalcin, E., & Bilge, A. (2021). Novel automatic group

identification approaches for group recommendation.

Expert Systems with Applications, 174, 114709.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

314