A Linear Regression Based-Approach to Collective Gas Source

Localization

Ronnier Frates Rohrich

1 a

, Luis Felipe Messias

1 b

, Jose Lima

2,3 c

and Andre Schneider de Oliveira

1 d

Graduate School of Electrical Engineering and Computer Science,

Universidade Tecnol

ogica Federal do Paran

a (UTFPR), Curitiba, Brazil

Research Centre in Digitalization and Intelligent Robotics (Cedri),

Polytechnic Institute of Braganc¸a (IPB), Braganc¸a, Portugal

Institute for Systems and Computer Engineering of Porto,

INESC-TEC, Porto, Portugal

Keywords:

Mobile Robot, Olfactory Robotics, Linear Regression.

Abstract:

This work addresses the problem of gas leaks and proposes a search strategy for identifying the source of

a gas leak within a virtual simulation environment. The research focuses on designing and implementing

simulation, control, and gas source search packages using swarm robotics. The simulation employs numerical

integration strategies, while the robot swarm control is based on potential ﬁelds theory. The location of the gas

source using a weighted linear regression strategy is used to estimate the gas concentration gradient, which

plays a crucial role in the optimization strategy employed. The paper presents an overview of the key concepts

employed and their relevance to different stages of the problem and highlights the main results achieved

through the chosen strategies. A signiﬁcant outcome of this work is the development of reusable software

packages applicable to various research contexts in mobile robotics.

1 INTRODUCTION

Robotic olfaction is a ﬁeld of study in mobile robotics

that aims to develop autonomous systems that can de-

tect chemical substances in the environment. Within

this perspective, two signiﬁcant problems arise: the

localization of substance sources and the mapping of

gas concentrations in the surroundings. Gas leakages

pose risks to human life and health. As a result, they

are regulated by strict standards worldwide, which

establish exposure limits for hazardous or unhealthy

work environments. Therefore, monitoring and con-

trolling exposure to such substances is paramount for

the health and well-being of workers in such condi-

tions.

Mobile monitoring offers a broader area cover-

age with fewer sensors, thereby decreasing monitor-

ing costs and enabling the surveillance of random

https://orcid.org/0000-0002-4523-8536

https://orcid.org/0000-0002-3587-0810

https://orcid.org/0000-0001-7902-1207

https://orcid.org/0000-0002-8295-366X

locations. This sensing naturally reduces the like-

lihood of not monitoring areas where hazards from

hazardous gases were not initially expected (Rohrich

et al., 2021). A monitoring system is critical in indus-

trial environments with potential exposure to harmful

gases. Using a swarm of mobile robots brings a range

of possibilities compared to static sensors, as they can

dynamically adapt to gas behavior in the environment.

This work will focus on the problem of gas source

localization in indoor environments without signiﬁ-

cant airﬂow. There will be no ﬁxed obstacles in the

environment; thus, the control system of the mobile

swarm will only focus on collision avoidance between

robots and collisions between robots and the environ-

ment’s walls.

Swarm robotics systems offer advantages over tra-

ditional approaches requiring less manual interven-

tion due to their robustness, ﬂexibility, and scalabil-

ity. Developing control techniques for robot swarm

systems provides a theoretical basis for solving vari-

ous problems, including monitoring, agriculture, and

space exploration applications (Schranz et al., 2021).

Furthermore, by providing a software solution for

Rohrich, R., Messias, L., Lima, J. and Schneider de Oliveira, A.

A Linear Regression Based-Approach to Collective Gas Source Localization.

DOI: 10.5220/0012187100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 657-664

ISBN: 978-989-758-670-5; ISSN: 2184-2809

657

such problems, it will be possible to investigate funda-

mental difﬁculties related to swarm robotics software

development. The development of mobile robotic

olfaction systems is a non-trivial problem, and ex-

cept for recent advancements, the full potential of gas

sensing by mobile robots has yet to be achieved en-

tirely (Monroy et al., 2017). Thus, this study aims

to explore the frontiers of implemented solutions and

advance toward developing new approaches.

One of the challenges encountered in such sys-

tems originates from conducting experiments in real

environments (Monroy et al., 2017). Therefore, com-

plementing previous work, a comprehensive simula-

tion and control software framework will be devel-

oped in conjunction with this study. This framework

will be applied to the gas source localization prob-

lem and will be entirely based on the Robot Oper-

ating System (ROS). Thus, the work conducted here

can serve as a foundation for investigating the disper-

sion of gas problems and other contexts where swarm

robotics may provide a potential solution.

Therefore, the approach taken in this work fo-

cuses on developing a simulation and control system

for collaborative robot swarms applied to the problem

of robotic olfaction, with the primary aim of creating

reusable software artifacts applicable to different con-

texts. The solution proposed in this work was inserted

in the real robot proposed in the work of (Rohrich

et al., 2021) as shown in Figure 1.

Figure 1: Monera robot swarm.

2 RELATED WORK

Incorporating olfactory capabilities in robots to detect

and localize chemical substances has garnered signif-

icant attention in recent research. Metal Oxide Semi-

conductor (MOX) sensors have emerged as a pop-

ular choice for gas detection due to their low cost,

ﬂexibility in production, ease of use, wide range of

detectable gases, and potential applications. For in-

stance, (Bouras et al., 2023) employed MOX sensors

on mini drones for gas detection.

(He et al., 2023) emphasized using olfactory mo-

bile quadruped robots for odor source localization in

complex environments. However, this robotic topol-

ogy presents inherent complexities. A more efﬁcient

approach to odor-based navigation involves multiple

mobile robots that communicate and make joint deci-

sions, which aligns with swarm robotics principles.

In robotic olfaction, employing robot swarms

shows promise for gas source localization. (Rohrich

et al., 2021) used a swarm of robots to search

for gas sources in real and simulated environments.

The study evaluated the method’s reliability regard-

ing odor measurement noise (sensor uncertainty) and

demonstrated its effectiveness. One of the key chal-

lenges in using robot swarms for gas source localiza-

tion is developing a control strategy that enables orga-

nized and collision-free movement of the robot group.

One viable strategy is the utilization of artiﬁcial po-

tential ﬁelds.

The notion of potential ﬁelds ﬁnds its roots in

physics, where the intricate interplay of forces char-

acterizes motion. It mirrors the gravitational pull to-

wards the desired target and the opposing repulsive

force originating from obstructions. When imple-

mented in the domain of trajectory planning for mo-

bile robots, potential ﬁelds gracefully accommodate

the presence of both static and dynamic obstacles. A

compelling demonstration of this application can be

observed in work (Wu et al., 2020), where they in-

geniously employed the bioinspired hybrid algorithm

known as BAS-APF (Antenna Search-based and Ar-

tiﬁcial Potential Field) for trajectory planning.

Potential ﬁelds, despite their advantages, possess

certain limitations. For instance, they may fail to

reach the point of interest due to local minima. Other

reported limitations include collisions with obstacles

and the inability to reach the goal when an obsta-

cle is close. Nevertheless, potential ﬁelds sufﬁce for

controlling robot swarms, avoiding collisions among

themselves and with the environment’s walls, assum-

ing the absence of additional ﬁxed or moving obsta-

cles. Once the navigation and control strategy of the

robot swarm is well-deﬁned, devising a search strat-

egy for gas sources becomes crucial.

Therefore, gradient descent, a prominent opti-

mization algorithm in neural networks, will maximize

the gas concentration the mobile sensors obtain. The

robots will move towards increasing gas concentra-

tion until they reach the source. In (Mustapha et al.,

2020), a Gradient-Based Optimization was used, but

in the previous work, various variations of gradient

descent, such as Nesterov accelerated gradient and

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

658

different asynchronous optimization algorithms, were

compared. The study demonstrated that Stochas-

tic Gradient Descent (SGD) generally converges to a

minimum but may exhibit signiﬁcantly longer conver-

gence times than other optimizers. Additionally, SGD

relies on robust initialization and may become trapped

at saddle points instead of local minima.

In this context, estimating the gas concentration

gradient around each robot will be accomplished us-

ing a local linear model. This methodology draws

inspiration from computer graphics, speciﬁcally vol-

ume rendering on unstructured meshes. In (Correa

et al., 2011) employed weighted linear regression to

estimate normal surface vectors of three-dimensional

surfaces, enhancing computational object rendering.

In (Mancinelli et al., 2018) proposed alternative gra-

dient estimation techniques on triangular meshes us-

ing an iterative gradient-based algorithm, producing

more accurate parameter estimates than stochastic

gradient (SG) algorithms based on auxiliary models.

In this study, a simpliﬁed and efﬁcient gas search

strategy employing regression is proposed.

The adoption of linear regression to estimate the

gradient primarily stems from the nature of ﬁeld sam-

pling. Traditional techniques for gradient calcula-

tion typically employ ordered sampling with ﬁxed and

predeﬁned distances. In the context of this study, ﬁeld

sampling is less ordered, with distances dependent on

the movement of the robot swarm within the environ-

ment. Thus, linear regression is justiﬁed to overcome

this characteristic of sampling.

3 COLLECTIVE OLFACTION OF

ROBOT SWARM

The study was conducted within the framework of

Robot Operating System ROS, in conjunction with

the Gas Dispersion Simulator for Mobile Robot Ol-

faction in Realistic Environments (GADEN) package,

developed by the Machine Perception and Intelligent

Robotics research group (MAPIR), aiming to achieve

realistic simulation of gas dispersion in the environ-

ment (Monroy et al., 2017). The simulation environ-

ment is depicted in Figure 2, where the virtual robots

integrated with gas sensor are represented in purple,

the simulation environment in gray, the gas source in

yellow, and the gas particles in green, providing a vi-

sual representation of the simulated scenario.

The ROS is a set of open development tools and

libraries to facilitate easier software reuse in the con-

text of robotics. The smallest software unit within a

ROS-based system is called a node. Each node per-

forms a small set of functions, and therefore, to con-

Figure 2: Simulation environment.

struct a complex system within this context, it is rec-

ommended to divide the solution into different nodes,

with each node implementing a portion of the solu-

tion.

Nodes communicate with each other through top-

ics, allowing sharing and receiving of information

within the system using the publish/subscribe model.

Each topic is associated with a speciﬁc message type:

velocity commands, actual values, vectors, and Iner-

tial Measurement Unit (IMU) data. Users can also

deﬁne new message types. A group of nodes can

be organized into packages. Each package contains

the source code for its nodes, conﬁguration ﬁles, and

node initialization ﬁles. This characteristic allows for

modifying node conﬁguration parameters without al-

tering the nodes’ source code. One of the main tools

provided by ROS is RVIZ, which enables visualiza-

tion of the critical information exchanged between

ROS topics. It includes mobile reference systems for

each robot, their positions, gas particles generated by

GADEN, IMU data, and user-deﬁned data through

Markers.

A dedicated package was developed to facilitate

the simulation of robots equipped with virtual sen-

sors. This package seamlessly integrates the mobile

robot ensemble into the simulation environment pro-

vided by GADEN and RVIZ. The visualization as-

pect is realized by utilizing Markers generated by the

simulation node. The package allows runtime con-

ﬁguration, specifying parameters such as the number

of robots, the three-dimensional ﬁle employed for vi-

sual representation, and the alert and collision radio.

The ﬂexibility of these parameters empowers users

to modify them as required, leveraging the intrinsic

adaptability of the ROS infrastructure.

Simulated sensors are instrumental in capturing

the gas concentration dynamics within the environ-

ment, and GADEN serves as the underlying frame-

work for this functionality. Speciﬁcally, the MOX

TGS2620 model was chosen for simulating the gas

sensors. Ethanol was selected as the gas of interest,

with operating conditions set at a pressure of 1 ATM

and a temperature of 298 K. The absence of solid air

A Linear Regression Based-Approach to Collective Gas Source Localization

659

currents ensures that diffusion mechanisms predomi-

nantly govern the gas dispersion.

The collective behavior of the robot swarm is or-

chestrated through a combination of gradient descent

and potential ﬁeld strategies. Gradient descent al-

lows the robots to navigate toward regions of increas-

ing gas concentration, facilitating source localization.

Concurrently, the potential ﬁeld approach aids col-

lision avoidance by considering dynamic obstacles

(robots) and ﬁxed obstacles (walls) within the envi-

ronment. Gradient calculations rely on estimating lo-

cal gas concentration functions using a planar approx-

imation. This localized model furnishes the necessary

information for effective navigation within the envi-

ronment.

4 OVERVIEW OF PROPOSED

APPROACH

The software or nodes integrated by ROS have spe-

cialized functions. This work has visualization and

simulation nodes, a control node, and a node for lin-

ear regression and gas source detection. Each node is

organized into packages containing the executable’s

source code and initialization and conﬁguration ﬁles.

The data is shared by all the robots, a central con-

troller obtains all the data, does the processing and

sends each robot its respective speeds at each step.

In this context, the visualization and simulation pack-

age will receive these speeds, simulate the behavior

of each robot and return the ﬁnal position of the robot

group. Visualization is performed using the RVIZ

tool. In the context of real robots, the communica-

tion between the central controller and each robot is

a crucial point for the good performance of the strat-

egy. The simulation environment is structured to rep-

resent essential conditions related to the dynamics of

the robots, such as the speed and acceleration limiter

implementation.

In addition to these functionalities, the color of the

robot in RVIZ is determined according to the distance

between robots. It is set as green for robots within a

safety distance (d2), yellow for an alert distance (d1),

and red to represent collisions, as depicted in Figure

3. These distances can be conﬁgured during node ini-

tialization.

4.1 Swarm Control

The control of the robot swarm is performed through

the methodology of the potential ﬁeld. The block di-

agram in Figure 4 represents this system’s topology

considering the input, process, and output variables.

Figure 3: Visualization package.

Figure 4: Block diagram of the controller.

The ﬁeld estimator calculates the components of

the potential ﬁeld at the position of the robot of in-

terestThe attraction ﬁeld is deﬁned by Equation 1, the

repulsion ﬁeld between robots is deﬁned by Equations

In this manner, the resulting ﬁeld will enable mu-

tual repulsion between each pair of robots while si-

multaneously guiding them toward the desired goal

point. The goal point serves as one of the inputs to the

controller, allowing navigation to any desired point

within the environment. This comprehensive system

enables the robots to search for the gas source safely

and collision-free.

The set of equations 1 models the attraction ﬁeld

of the robots towards the goal. Here, α represents the

angle between the robot’s and the goal positions, and

d represents the distance. The remaining constants r,

s, and beta are parameters used to adjust the robot’s

radius, attraction radius, and ﬁeld attraction constant,

respectively. These values were set to 0.20 m, 0.50 m,

and 2 m, respectively.

if d < r: (1)

= 0

if d <= s + r:

= beta ∗ (d − r) ∗ cos(α)

= beta ∗ (d − r) ∗ sin(α)

if d > s + r:

= beta ∗ s ∗ cos(α)

= beta ∗ s ∗ sin(α)

Analogously, the repulsion ﬁeld between robot i

and robot j is given by the set of equations 2. Here,

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

660

i, j

represents the angle, and d

i, j

represents the dis-

tance between robots i and j. The remaining constants

r, s, and β are parameters used to adjust the robot’s

radius, repulsion radius, and ﬁeld repulsion constant,

respectively. It was also used to the repulsion ﬁeld

between robot and the wall.

i f d < r: (2)

i, j

= 0

i, j

= 0

i f d <= s + r:

i, j

= −beta ∗ (s + r − d

i, j

) ∗ cos(α

i, j

)

i, j

= −beta ∗ (s + r − d

i, j

) ∗ sin(α

i, j

)

i f d > s + r:

i, j

= 0

i, j

= 0

Finally, the equations 3 give the vector ﬁeld’s

components.

= FG

∑

i, j

+ FPx

= FG

∑

i, j

+ FPy

(3)

The vector projection represented in Figure 5 is

given by Equation 4. The projection is performed

onto the velocity command vector in blue, in the di-

rection parallel to the robot represented by the axis x

in red in Figure 5.

Figure 5: Vector projection of the velocity vector.

The angular velocity value is calculated by a pro-

portional controller described by the equation 5.

+ v

∗ cos(arctan 2(u

) − θ

) (4)

= k

∗ (arctan 2(u

) − θ

) (5)

4.2 Estimation of Gas Source

The gas source localization algorithm is based on a lo-

cal approximation approach, which involves approxi-

mating the gas distribution function by a linear func-

tion in the vicinity of each robot within the swarm.

By utilizing this method, the gradient of the linear ap-

proximation can be effectively employed to facilitate

the implementation of a gradient descent algorithm.

At each algorithm stage, the linear regression process

is performed for each robot and the concentration gra-

dient is calculated. With the gradient, the objective

position of each robot is updated, taking each one of

them to a position of higher gas concentration. In this

way, the swarm will navigate toward the highest gas

concentration in search of the source.

As a critical component of the system, the gas

source locator considers the positions of individual

robots and the corresponding gas concentration mea-

surements obtained by each robot. All measures are

saved in the estimator’s memory so that all samples

obtained are considered in the regression. These cru-

cial inputs enable the gas source locator to effectively

estimate the location of the gas source within the envi-

ronment. The entire process is illustrated in Figure 6,

visually representing the algorithm’s functioning and

integration with the robot swarm.

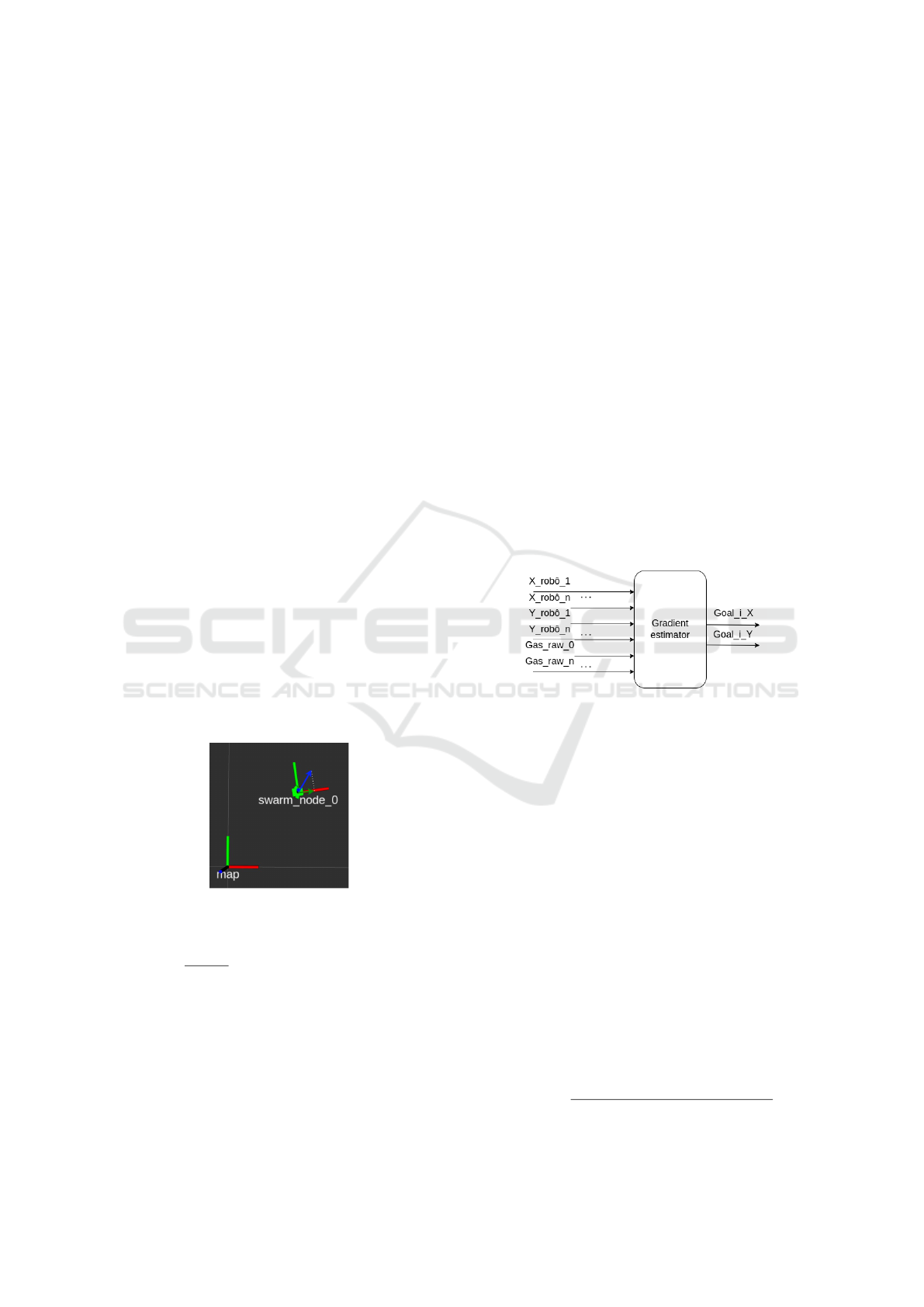
Figure 6: Block diagram of the gas source locator.

Each element of the robot swarm performs a lin-

ear regression around itself using the information col-

lected by the entire swarm. The regression locally

approximates the gas concentration according to the

model described by Equation 6.

B +







... ... ...







∇F =







GasRaw

...

GasRaw







(6)

The local model requires a different regression

with varying weights and is employed for each robot.

The regression weights are calculated according to

Equation 7, where d

i j

represents the Euclidean dis-

tance in three-dimensional space R

described by

Equation 8. The addition of the constant c in Equation

7 was used to eliminating the singularity that occurs

when d

i j

= 0.

i j

= 1/(c + d

i j

) (7)

i j

− x

)

+ (y

− y

)

+ (t

− t

)

(8)

A Linear Regression Based-Approach to Collective Gas Source Localization

661

The weights were based on the works of, (Comber

et al., 2023), and (Correa et al., 2011). Following this

strategy, ﬁeld samples collected more distant from the

robot position i and older samples will have a smaller

weight W

i j

in the regression, allowing to represent the

gas concentrations locally so that the gradient descent

strategy can be executed.

5 EVALUATION

The contributions of this work were individually ex-

perimented with to achieve control through linear re-

gression and potential ﬁelds. Thus, initially, the vi-

sualization and simulation modules were tested. Sub-

sequently, integrating these modules allowed the au-

tonomous control of the swarm to be implemented in

a gas source search algorithm.

The visualization module of the experiment con-

sists of commanding a group of robots to move from

one point to another in space and verifying if the ac-

tivation of the weight components aligns with the pa-

rameterized values. In this experiment, the robots

were commanded and positioned to observe the dy-

namic behavior of the simulation system.

Another feature implemented in the visualization

package is the limitation of acceleration and veloc-

ity. The velocity limitation experiment involves com-

manding a robot to move forward at a velocity of 100

m/s and observing the behavior of the velocity lim-

iters. The simulation package should not have un-

limited accelerations and velocities like a real robot.

Figure 7 shows a robot’s velocity and position graph

on the axis x using a velocity limitation of 1.5 m/s

and an acceleration of 1 m/s². Thus, the velocity in-

creases linearly due to the acceleration limitation until

it reaches the speed limit, as expected in the case of

robots in a real environment.

Figure 7: Speed Limitation and Acceleration Experiment.

In this experiment, it was possible to validate the

behavior of the velocity limiters and ensure that the

behavior of the swarm in subsequent experiments will

be closer to that encountered in real robots.

5.1 Collective Behavior

This experiment involves controlling ten robots to a

common target point to validate the control system.

The experiments’ evolution, as the system’s scal-

ability was increased to observe possible variations

in the system’s behavior, the position of the swarm

throughout the experiment, and the potential ﬁeld as-

sociated with the swarm’s initial position are illus-

trated by Figure 8.

Figure 8: Initial and ﬁnal positions of the experiment with

ﬁfty robots. (a) Robots. (b) Repulsion potential ﬁeld.

Thus, a swarm of 50 robots was positioned with

the coordinates x = 0m and y = 0,2m deﬁned as the

objective. With this experiment, the control system

efﬁciently coordinated the robot swarms in the se-

lected simulation environment. The above experiment

was also repeated for 18, 20, and 30 robots. In all

cases, the control system achieved coordinated move-

ment of the swarm from the initial conﬁguration to

the ﬁnal conﬁguration around the target point. In this

experiment, the target or destination point is the same

for the entire swarm to validate the controller in situa-

tions where the swarm had a high likelihood of collid-

ing with each other and making their task more chal-

lenging.

5.2 Linear Regression

In this experiment, the robots were placed in the envi-

ronment with the gas simulation. Figure 9 illustrates

the regression represented by the yellow plane per-

formed by the central robot for gas source localiza-

tion.

The blue spheres represent the data collected by

the robots and their size is proportional to the weight

of each sample in the regression. It is noticed that the

points farthest from the robot are smaller and, there-

fore, have less weight in the regression. In this way,

the robots can make a local estimate of gas concentra-

tions and go down the gradient until the stop condition

is met, which occurs when at least one sensor returns

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

662

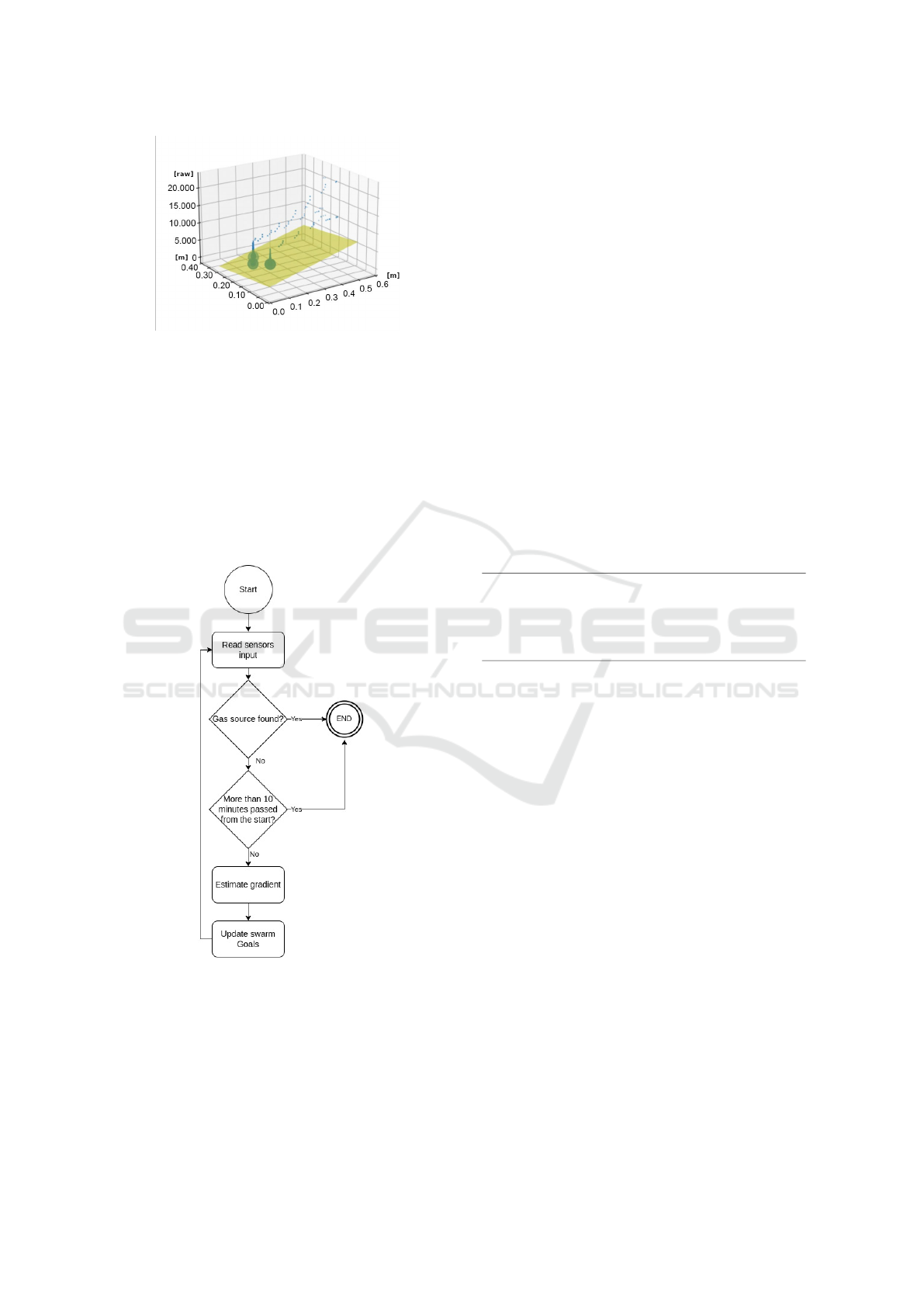
Figure 9: Gas search experiment.

a value less than 2000, indicating high gas concen-

tration, or after 10 minutes from the beginning of the

experiment.

The return of the sensor of 20000 is considered

low gas concentration, and 2000 indicates that the

sensor is very close to the source. The concentration

values returned by the sensor are dimensionless and

correspond to the RS/R0 ratio, where RS is the mea-

sured sensor resistance and R0 is the outdoor air re-

sistance. Figure 10 presents the general ﬂowchart of

the experiment.

Figure 10: Gas search ﬂowchart.

This experiment was repeated with 1 and 2 robots,

which could not ﬁnd the gas source within the 10-

minute time limit. This behavior can be explained by

analyzing the regression in Figure 10. In this case, the

plane around the robots is well-deﬁned since we have

a sampling of around three robots. In cases with only

1 or 2 robots, the plane cannot be satisfactorily esti-

mated due to the difﬁculty of deﬁning a plane with

at most three sampling points. Although this difﬁ-

culty is overcome using the previous samples stored

in the robots’ memories, the experiment using fewer

than three robots did not converge to the source within

the deﬁned 10-minute time limit.

5.3 Gas Source Search

In this experiment, the gas source search algorithm

was tested with different variations in swarm scala-

bility to obtain a performance comparison of the al-

gorithm using different numbers of robots. Initially,

the robots were positioned at random coordinates in

the environment. Subsequently, the gas source search

strategy was initiated. The system remained in op-

eration until one of the sensors returned a value be-

low 2000, corresponding to a high gas concentration.

The experiment was repeated ten times for each ﬁxed

number of robots. Table 1 contains the average values

of the obtained results.

Table 1: Results of gas search experiments.

Robots ∆ Σ Ideal X Real (%) Global/robot (m) Error abs.(m)

3 1,24% 0,0047 0,086

6 5,86% 0,0141 0,090

12 2,63% 0,0068 0,118

18 6,55% 0,0197 0,139

24 7,95% 0,0220 0,143

30 9,73% 0,0258 0,139

It can be noticed in the ﬁrst column that the ra-

tio between the actual length of the path taken by the

robots and the ideal path, the path the robots would

take if they were moving directly towards the gas

source, was above 6% in the cases of 18, 24, and 30

robots, and below 6% in the others. The average dis-

placement per robot shown in the second column is

also higher in cases 18, 24, and 30. Thus, an increase

in the algorithm’s efﬁciency can be observed for the

values of 3 and 12 robots, where the swarm cov-

ered a shorter distance than the distance they would

have traveled to the ﬁnal conﬁguration if the move-

ment were done in a straight line. The second column

shows a decrease in the system’s efﬁciency with the

increased number of robots. In the experiment with

18 robots, saturation in the system starts to occur, and

there are more robots than the environment can ac-

commodate. At this point, having more robots only

hindered the system’s performance. This observation

is also reinforced by the increase in the system’s ab-

solute error in estimating the gas source’s position.

A Linear Regression Based-Approach to Collective Gas Source Localization

663

6 CONCLUSIONS

Gas leaks are a signiﬁcant problem in homes and in-

dustrial environments. The main objective of the pre-

sented work was to develop a strategy to locate gas

leak sources using swarms of robots. The solution

presented in this work was divided into three com-

ponents: swarm simulation, swarm control, and the

gas source search algorithm. These components can

be utilized in other contexts, particularly in simu-

lated ROS and RVIZ environments, opening up fur-

ther applications and research possibilities. Through

the conducted experiments, the simulation and con-

trol strategies for robot swarms were validated. Con-

trolling up to 50 robots in a simulated environment

without collisions was possible. The gas source ex-

ploration strategy’s efﬁcacy exhibited disparate efﬁ-

ciency levels contingent upon the variability in sys-

tem scalability. The swarm trajectory closely fol-

lowed a straight line toward the source, deviating by

only 1.24% from the optimal trajectory (a straight

line) when using only three robots. Therefore, de-

ploying three robots is sufﬁcient for gas source de-

tection for the given environment size. However, in

larger environments, employing more robots may im-

prove search efﬁciency. An important ﬁnding from

the search experiment is that using three sensors for

gas sampling provides accurate gradient estimation,

enabling an efﬁcient gas source search. An alterna-

tive strategy worth exploring is using multiple sensors

attached to a single robot, achieving a similar approxi-

mation with only three gas samples without relying on

swarm coordination. Overall, the developed strategy

and software packages demonstrated their effective-

ness in successfully simulating and controlling robot

swarms and detecting gas leakage sources. Thus, the

results of this work will allow applications in different

contexts and encourage new research in related areas.

ACKNOWLEDGEMENTS

The project is supported by National Council for

Scientiﬁc and Technological Development – CNPq

(process CNPq 407984/2022-4); Fund for Scientiﬁc

and Technological Development – FNDCT; Ministry

of Science, Technology and Innovations – MCTI of

Brazil; Araucaria Foundation; and the General Super-

intendence of Science, Technology and Higher Edu-

cation (SETI).

REFERENCES

Bouras, A., Gutierrez-Galvez, A., Burgu

es, J., Bouzid, Y.,

Pardo, A., Guiatni, M., and Marco, S. (2023). Con-

centration map reconstruction for gas source location

using nano quadcopters: Metal oxide semiconductor

sensor implementation and indoor experiments vali-

dation. Measurement, 213:112638.

Comber, A., Brunsdon, C., Charlton, M., Dong, G., Har-

ris, R., Lu, B., L

u, Y., Murakami, D., Nakaya, T.,

Wang, Y., and Harris, P. (2023). A route map for

successful applications of geographically weighted re-

gression. Geogr Anal, 55(1):155–178.

Correa, C. D., Hero, R., and Ma, K.-L. (2011). A compar-

ison of gradient estimation methods for volume ren-

dering on unstructured meshes. IEEE Transactions

on Visualization and Computer Graphics, 17(3):305–

319.

He, Y., Cheng, L., Pan, Y., Li, Y., Wang, D., and Zheng,

H. (2023). Multi-sensory olfactory quadruped robot

for odor source localization*. In 2022 IEEE Inter-

national Conference on Cyborg and Bionic Systems

(CBS), pages 332–335.

Mancinelli, C., Livesu, M., and Puppo, E. (2018). Gradient

ﬁeld estimation on triangle meshes. In STAG, pages

87–96.

Monroy, J., Hernandez-Bennetts, V., Fan, H., Lilienthal, A.,

and Gonzalez-Jimenez, J. (2017). Gaden: A 3d gas

dispersion simulator for mobile robot olfaction in re-

alistic environments. Sensors, 17(7).

Mustapha, A., Mohamed, L., and Ali, K. (2020). An

overview of gradient descent algorithm optimization

in machine learning: Application in the ophthalmol-

ogy ﬁeld. In Hamlich, M., Bellatreche, L., Mondal,

A., and Ordonez, C., editors, Smart Applications and

Data Analysis, pages 349–359, Cham. Springer Inter-

national Publishing.

Rohrich, R. F., Teixeira, M. A. S., Lima, J., and De Oliveira,

A. S. (2021). Collective gas sensing in a cyber-

physical system. IEEE Sensors Journal, pages 1–1.

Schranz, M., Di Caro, G. A., Schmickl, T., Elmenreich,

W., Arvin, F., S¸ekercio

glu, A., and Sende, M. (2021).

Swarm intelligence and cyber-physical systems: Con-

cepts, challenges and future trends. Swarm and Evo-

lutionary Computation, 60:100762.

Wu, Q., Chen, Z., Wang, L., Lin, H., Jiang, Z., Li, S., and

Chen, D. (2020). Real-time dynamic path planning of

mobile robots: A novel hybrid heuristic optimization

algorithm. Sensors, 20(1).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

664