An Unsupervised Neural Network Approach for Solving the Optimal

Power Flow Problem

Alexander Svensson Marcial

and Magnus Perninge

Department of Physics and Electrical Engineering, Linnaeus University, V

axj

o, Sweden

Keywords:

AC-OPF, Unsupervised Learning, Deep Learning.

Abstract:

Optimal Power Flow is a central tool for power system operation and planning. Given the substantial rise

in intermittent power and shorter time windows in electricity markets, there’s a need for fast and efﬁcient

solutions to the Optimal Power Flow problem. With this in consideration, this paper propose an unsupervised

deep learning approach to approximate the optimal solution of Optimal Power Flow problems. Once trained,

deep learning models beneﬁt from being several orders of magnitude faster during inference compared to

conventional non-linear solvers.

1 INTRODUCTION

Optimal power ﬂow (OPF) is a fundamental tool used

in power system operation and planning. Since its

initial formulation in the 1960s (Carpentier, 1962)

OPF has been instrumental in numerous applications,

encompassing economic dispatch, securing reactive

power reserves for voltage stability (Capitanescu,

2011), generation and transmission expansion plan-

ning (Skolﬁeld and Escobedo, 2022). Furthermore,

it serves as a foundational tool for market clearing in

deregulated electricity markets.

In general, OPF is a non-convex optimization

problem that classiﬁes as NP-hard (Lavaei and Low,

2011). Its objective is to ﬁnd an optimal dispatch

∗

that minimises a speciﬁc performance metric

J(x, p

∗

),where x denotes the state of the power sys-

tem. A feasible dispatch p

∈ U ensures the power

system’s secure operation while aligning generation

with demand.

Efforts to develop efﬁcient algorithms for OPF

have led to the introduction of several approximate

methods. Most notably is the DC-OPF formula-

tion which linearizes power ﬂow constraints by ne-

glecting line resistances under the assumption that

line resistances are signiﬁcantly lower than line re-

actances, combined with the approximation of a ﬂat

voltage proﬁle and small voltage angle deviations be-

tween nodes. While the objective function is often

https://orcid.org/0000-0002-2028-9847

https://orcid.org/0000-0003-3111-4820

a smooth convex function, which enables the DC-

OPF to be effectively solved with standard solvers,

this computational efﬁciency trades off against accu-

racy. Speciﬁcally, DC-OPF tends to under perform in

heavily loaded systems and often doesn’t produce fea-

sible solutions for the original OPF-problem (Baker,

2021).To counteract these infeasibilities, DC-OPF is

generally recomputed iteratively, incorporating con-

straint adjustments (Low, 2014).

The task faced by grid operators, ensuring that en-

ergy supply meets demand, has grown considerably

more difﬁcult due to the rapid increase of intermittent

energy sources such as wind and photovoltaic sys-

tems. Unlike conventional power sources, intermit-

tent energy systems exhibit a stochastic energy pro-

duction, with an output dependent on weather condi-

tions as well as the time of the day. Consequently, to

adapt to the increased randomness of injected power,

stochastic optimization models have been proposed

in literature. Nonetheless, the underlying difﬁculties

in solving OPF remains in stochastic formulations.

This is why the proposed methods found in literature

employ the DC-OPF approximation or convex relax-

ations to reduce the computational burden,

This increase in complexity calls for more com-

putational efﬁcient algorithms, capable of solving the

OPF in short timescales (Tang et al., 2017).. Rapid

results from OPF is not only essential for real-time

grid management but also for addressing economic

dispatch problems in electricity markets with short

market time units.

In recent years, the prowess of machine learning,

214

Marcial, A. and Perninge, M.

An Unsupervised Neural Network Approach for Solving the Optimal Power Flow Problem.

DOI: 10.5220/0012187400003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 214-220

ISBN: 978-989-758-670-5; ISSN: 2184-2809

and in particular deep neural networks (DNNs) have

found a wide range of applications from the typical

classiﬁcation problem to applications in optimization

theory, aimed at curtailing the on-line computational

burden. Within the research aimed towards optimal

power ﬂow, a number of recent papers have utilized

DNNs in an effort to solve the OPF problem.

(Zhang and Zhang, 2022) does not directly pro-

vide predictions for the OPF, instead, they employ a

supervised learning approach to forecast an appropri-

ate warm-start for a conventional non-linear solver.

Similarly, (Fioretto et al., 2020) adopts a supervised

methodology, utilizing a lagrangian formulation to

enforce the constraints. Meanwhile, in (Huang et al.,

2021) while a supervised approach is presented no ef-

fort is done during training to enforce the constraints,

instead they develop a post-processing step to en-

hance the feasibility of the neural network’s predic-

tions.

This paper’s primary contribution is the introduc-

tion of an unsupervised methodology for predicting

the solutions to the OPF problem. Moreover, we de-

tail the utilization of a custom loss function, leverag-

ing the augmented lagrangian method to train the neu-

ral network towards optimal solutions. Consequently,

our approach removes the dependence of extensive

datasets of labeled data.

2 OPTIMAL POWER FLOW

In this section we describe the underlying model used

in Optimal Power Flow as well as presenting the gen-

eral AC-OPF formulation.

2.1 Power System Model

Power systems are modeled at the system level as

buses interconnected by transmission lines, with gen-

erators and loads connected to a subset of these buses.

A power system can thus be conveniently modelled as

a graph P = (N ,B), where N ⊂ N represents the set

of edges connecting the nodes. We will adhere to the

naming conventions of power systems, referring to N

as the set of nodes and B the set of transmission lines.

In modelling the power system, two equivalent for-

mulations can be used (Low, 2014): one where P is

a directed graph and the other where P is an undi-

rected graph. In this paper, we have chosen the latter

formulation; thus if (k,l) ∈ B then (l, k) ∈ B. For an

n-bus system, we assume, without loss of generality,

that N = {0,...,n − 1}. Additionally, there is a bus

∈ N which we refer to as the reference bus.

Each transmission line connecting two buses has

the admittance y

i,k

= g

i,k

+ jb

i,k

, (i,k) ∈ B. There

may also be an impedance connecting a bus to ground,

denoted by y

s,i

for i ∈ N

The power system has a set of generators, indexed

by G ⊆ N . For each i ∈ G, the associated genera-

tor can produce active power p

∈ R

and reactive

power q

∈ R. Let p

:= (p

)

i∈G

∈ R

|N |

represent

the vector of power generated in the power system.

Similarly, let q

:= (q

)

i∈G

∈ R

|N |

be the vector of

reactive power produced by the generators in the sys-

tem. Sometimes, it’s more practical to work with the

apparent power produced by the generators. In that

case, let s

:= (s

)

i∈G

∈ C

|N |

, where s

= p

+ jq

Unlike the generators, each bus can be charac-

terized by the load s

= p

+ jq

, noting that for

some i ∈ N , s

= 0 + j0. To identify the non-

zero loads, we deﬁne D

:= {i ∈ N : p

̸= 0} and

:= {i ∈ N : q

̸= 0}. Further, let p

:= (p

)

i∈D

and q

:= (q

)

i∈D

In terms of bus-related variables, let V :=

)

i∈N

∈ C

|N |

denote the voltage at each bus, where

= V

jδ

. We further deﬁne the vectors of voltage

magnitude and angles as |V | := (V

,...,V

) ∈ R

|N |

and

∠V := (δ

,...,δ

) ∈ [−π,π]

|N |

respectively. We as-

sume that δ

= 0 and that δ

, i ∈ N \{r

} is measured

with r

as reference.

Assuming that |N | = n, we deﬁne S :=

,...,s

) ∈ C

|N |

as the vector of net apparent power

injection in each node of the power system. The

nodal apparent power injection is determined using

Kirchoff’s law:

= v

∑

k:(i,k)∈B

∗

i,k

∗

− v

∗

) + |v

, i ∈ N (1)

The net apparent power injection in a node is

equivalent to the difference between the scheduled

generation s

and the scheduled load s

;



− s

i ∈ G

−s

i ∈ N \G.

(2)

Note that, if i /∈ D

∪ D

then s

= 0 + j0

Generators have both lower and upper limits in

terms of active and reactive power output. For a gen-

erator located at bus i ∈ G, the range of its active

power output is constrained to p

∈ [P

min

max

]. Sim-

ilarly the reactive power is constrained to the interval

∈ [Q

min

max

To ensure stable operation of the power system,

it’s imperative that the voltages across the buses re-

main within acceptable levels. Consequently, the

voltage magnitude for bus i ∈ N is conﬁned to the

interval [V

min

max

An Unsupervised Neural Network Approach for Solving the Optimal Power Flow Problem

215

We deﬁne the restrictions on the generators capa-

bilities and bus voltage limits to be the sets

A :=

∏

i∈G

min

max

] (3)

R :=

∏

i∈G

min

max

] (4)

V :=

∏

i∈N

min

max

] (5)

2.2 Optimization Model

In this paper, the OPF formulation we employ focuses

on economic dispatch. Speciﬁcally the objective is to

identify the operating point for generators that results

in the most cost efﬁcient production. Given a cost

function C : A → R, the OPF can be expressed as

min

C(p

) (6)

s.t. g(V, S) = 0 (7)

∈ A (8)

∈ R (9)

|V | ∈ V . (10)

While there exist various ways to formulate the cost

function given by equation (6), polynomial and piece-

wise linear approximations are frequently encoun-

tered in literature. For the purpose of this paper, we

opt for the polynomial approach. Consequently, the

cost function is expressed as:

C(p

) :=

∑

i∈G

) (11)

Note that, the speciﬁc formulation of the cost function

does not limit the applicability of this paper; the pro-

posed methodology can accommodate a diverse range

of formulations.

The power balance at each bus within the power

system is represented by equation (7) and is deﬁned

as:

(V,S) = f

(V ) − s

, i ∈ N (12)

where f

(V ) corresponds to the right-hand side of

(1)

3 DNN APPROXIMATION OF

OPTIMAL SOLUTION

3.1 Function Approximation

In this paper, we assume that the power system de-

scribed by P is static, meaning the network topol-

ogy remains unaltered. Therefore, given (p

) ∈

× D

, the objective is to determine the optimal

voltage vector V

∗

(if it exists) that solves the OPF

instance deﬁned by (p

). With this context, the

OPF can be perceived as an operator that maps a given

instance deﬁned by the loading into an optimal solu-

tion, (Zhou et al., 2020),(Falconer and Mones, 2022)

F : P

× Q

→ C

|N |

(13)

here, P

and Q

represent sets of active and reactive

loads, respectively.

For the development of the proposed approxima-

tion of the solution to the OPF, it’s advantageous to

modify the standard OPF formulation. Consider the

power ﬂow equations in (1), they can be divided into

two sets of equations,

= s

+ s

, i ∈ G (14)

0 = s

+ s

, i ∈ N \G. (15)

Combining (14) with (8)-(9) yields the inequalities

min

≤ Re(s

+ s

) ≤ P

max

(16)

min

≤ Im(s

+ s

) ≤ Q

max

(17)

Further we deﬁne the set

U(p

) := {V ∈ C

|N |

: (16),(17),(10) feasible}.

(18)

Then, given s

∈ P

× Q

and V ∈ U(s

) an operat-

ing point (p

) can be recovered from (7).

Evaluating F using conventional iterative solvers

is cumbersome. To reduce the computational burden

at inference time we therefore propose the use of a

neural network, denoted

F(p

;θ) to approximate

(13), where θ is the parameters that are learned during

training of the neural network.

A major problem is to ensure that

F(p

;θ) ∈ U(p

). Lagrangian relaxation

is a common method in conventional constrained

optimization and it has been used in training of neural

networks for constrained optimization problems. In

(Zhang and Zhang, 2022) it is used to solve super-

vised AC-OPF using a two networks for predicting

the primal and dual variables respectively. In (Pan

et al., 2020), (Pan et al., 2022) a penalty function is

used as a regularization term in the loss function for

penalizing deviations from the constraints.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

216

Figure 1: Neural network architecture.

3.2 Unsupervised Learning

To train

F(·;θ) using supervised learning, one re-

quires a substantial dataset of load samples, denoted

as D

= {(p

)}

i=1

, where (p

) ∈ P

× Q

Correspondingly, there is a set D

= {y

}

i=1

repre-

senting the ground truth, with y

= F(p

). The

neural network is then trained using some loss func-

tion, e.g. the empiric risk, as shown in (19). Reg-

ularization terms can further be incorporated to pe-

nalize any constraint violations. Equation (19) will

be revisited in subsequent sections, particularly when

comparing the supervised and unsupervised learning

methodologies.

min

∑

i=1

∥

F(x

;θ) − y

∥

(19)

Given that y

∈ U(s

), the network is trained to

imitate the true solution. Under an unsupervised

framework, the label set D

is eliminated. This means

the network need to ﬁnd an optimal θ

∗

such that

F(p

;θ

∗

) ≈ F(p

), without the guidance of

ground truth. In essence, for each sample in D

the

neural network need to predict a feasible voltage that

minimize the cost. The unsupervised training can

therefore be formulated as the constrained optimiza-

tion problem

argmin

∑

i=1

F(S

;θ))

s.t.

F(p

;θ) ∈ V (S

) ∀(p

) ∈ D

(20)

Similar to approaches used in conventional opti-

mization algorithms, (20) is in this paper relaxed to an

unconstrained optimization problem. Speciﬁcally, we

will use the Augmented Lagrangian Method (ALM)

(Bertsekas, 2016) which is a method that combines

the Lagrangian method and penalty methods. Pre-

vious works in approximating constrained optimiza-

tion problems using machine learning have reported

ALM successful. In particular, ALM has been used

in physics informed neural networks such as in (Djeu-

mou et al., 2022) (Lu et al., 2021) (Dener et al., 2020)

3.3 Neural Network Architecture

Consistent with the previous cited works of using ma-

chine learning for OPF, the neural network architec-

ture employed in this paper is a feed-forward architec-

ture, (Figure 1), as it has shown good performance in

supervised settings. For the unsupervised approach, a

single neural network is utilized. However, for the su-

pervised approach, two neural networks are deployed:

one to predict voltage magnitudes and another for

voltage angles.

As highlighted in section 3.1, the neural network’s

input comprises the load (p

) ∈ R

|N |

× R

|N |

This conﬁguration corresponds to an input layer in

the neural network with 2|N | neurons. However, it is

worth noting that since generally N \(D

∪ D

) ̸=

we can effectively reduce the neuron count in the in-

put layer to |D

| + |D

Subsequent to the input layer, there is a sequence

of hidden layers, L

, with each layer comprising n

neurons. Both the depth (number of layer) and width

(neurons per layer) of this structure are considered hy-

perparameters, that are problem speciﬁc. An increas-

ing size of N beneﬁts from an increasing number of

neurons per layer. In the speciﬁc architecture used

in this paper, all activation function within the hidden

layers are Rectiﬁer Linear Units (ReLU).

The output layer is designed with 2|N | − 1 neu-

rons. Out of these, |N | neurons are allocated for rep-

resenting the voltage magnitude V , and the remainder

serves as outputs for the voltage angle, recalling that

the bus angle of bus n

is assumed known.

One strategy to integrate a subset of the con-

straints into the architecture of the neural network

is to use appropriate activation functions on the out-

put layer of the neural network. Speciﬁcally, let

x = (x

) be the output vector of the neural net-

work, corresponding to the voltage magnitudes and

angles respectively. Then using e.g. the sigmoid

activation function we obtain the mapping σ(x) =

(σ

),σ

)) ∈ [0,1]

|N |

× [0,1]

|N |−1

. The actual

voltage magnitude and angles can then be obtained

) 7→ (V

min

)

i∈N



v,i

)(V

max

−V

min

)



i∈N

(21)

and the corresponding angles are obtained as

An Unsupervised Neural Network Approach for Solving the Optimal Power Flow Problem

217

) 7→ (δ

min

)

i∈N \{n

}



)(δ

max

− δ

min

)



i∈N \{n

}

(22)

Through this methodology, the neural network ef-

fectively enforces the voltage constraints.

3.4 Loss Function

To solve (20), ALM is used to relax the constrained

optimization problem into an unconstrained problem.

In general, ALM algorithm consists of solving a se-

quence of sub-optimization problems

∗

= argmin

(x,λ

,µ

,ρ

)

(23)

with,

(x,λ

,µ

,ρ

) = f (x) + λ

g(x) + µ

h(x)+

∥h(x)∥

∥φ(h(x))∥

(24)

Where, λ

and µ

are Lagrange multipliers and the

norms serves as penalty terms, weighted by the

penalty parameters ρ

, and φ(h(x) = max{0,h(x)}.

Then, under some mild regularity conditions it can be

shown that lim

k→∞

∗

} = x

∗

, solves the original opti-

mization problem.

In practice, each sub-problem is ﬁnitely iterated

until a stopping criteria ||∇

L|| < ε

(Bertsekas,

2016), however in the training of the neural network

we have chosen a slight different approach were we

instead use stochastic gradient descent until each sub-

optimization problem stops improving, which is cov-

ered in the next section.

3.5 Training

The load samples set, D

is divided into two disjoint

sets D

and D

out of which the former is used for

training and the latter for evaluating the performance

of the trained network.

In the spirit of ALM, the training of

F involves

solving a sequence of optimization problems. For

each outer iteration k ∈ {0,...,K − 1}, the goal is to

determine the optimal parameter θ

corresponding to

sub-optimization k. Within each outer-iteration, the

neural network is trained using the Adam optimizer

(Kingma and Ba, 2017). The training process follows

the commonly used mini-batch approach, where the

training set is randomly segmented into mini-batches

⊂ D

. Each mini-batch is used to compute the gra-

dient and subsequent weight updates for the network.

The entire dataset is processed in this fashion up to

epoch

times.

In an effort to avoid over ﬁtting and reduce train-

ing time, an early stopping mechanism with a preset

Figure 2: Neural network conﬁguration for unsupervised

learning.

patience is employed. The loss function L

is evalu-

ated after each epoch. If no improvement is recorded

for a ﬁxed number of consecutive epochs, the train-

ing of the k-th optimization problem is halted. Ad-

ditionally, adaptive learning rates are used, reducing

the learning rate if there is no observed improvement

in loss. The learning rate is reverted back to the ini-

tial learning rate in each new outer iteration. Once an

inner iteration is completed, the Lagrange multipliers

are updated in accordance with the ALM algorithm:

k+1

= λ

+ ρ

g(x

∗

)

k+1

= max{0, ρ

h(x

∗

)}

(25)

Data: Training dataset D

Result: optimal parameter θ

∗

← 0;

← ρ

init

;

for k ← 0 to K − 1 do

minimize L

(θ,λ

,µ

,ρ

) using Adam.;

k+1

← λ

+ ρ

F(S

;θ

);

k+1

← max{0, µ

+ ρ

F(S

;θ

)};

if ∥h(x)∥

∞

> η∥h

∗

∥ then

∗

← ∥h(x)∥

∞

k+1

← min{γρ

,ρ

max

}

end

Algorithm 1: Training the neural network.

4 NUMERICAL RESULTS

4.1 Hyperparameters

The proposed approach is conducted on the IEEE

300-bus system. The neural network is developed us-

ing the pyTorch library and trained on a MacBook pro

2 GHz Quad-Core Intel Core i5, 16 GB RAM.

For the supervised approach, both neural networks

feature an architecture with four hidden layers, with

a sequentially number of neurons: 1024,768,512 and

256. Meanwhile, for the unsupervised approach, the

hyperparameters with respect to hidden layers has a

network conﬁguration as illustrated in Figure 2. This

conﬁguration comprises hidden layers with neuron

counts of 2048,1024,768,512 and 256.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

218

For the training dataset, we utilize a total of |D| =

30000 samples of loads. The loads exhibit correla-

tions. The outer-loop is executed for 50 iterations,

while the inner iteration involves up to 50 epochs.

To facilitate learning, we employ an exponential de-

cay strategy for the learning rate with a decay factor

of γ = 0.9. The learning rate is decayed if the loss

does not improve for 5 consecutive epochs. We ini-

tialize the learning rate at 10

−4

. Furthermore, we set

the early stopping patience to 10 epochs, allowing for

timely termination if necessary. Regarding the ALM

algorithm, we set the initial penalty parameter, ρ

500, while the Lagrange multipliers are initialized as

zeros.

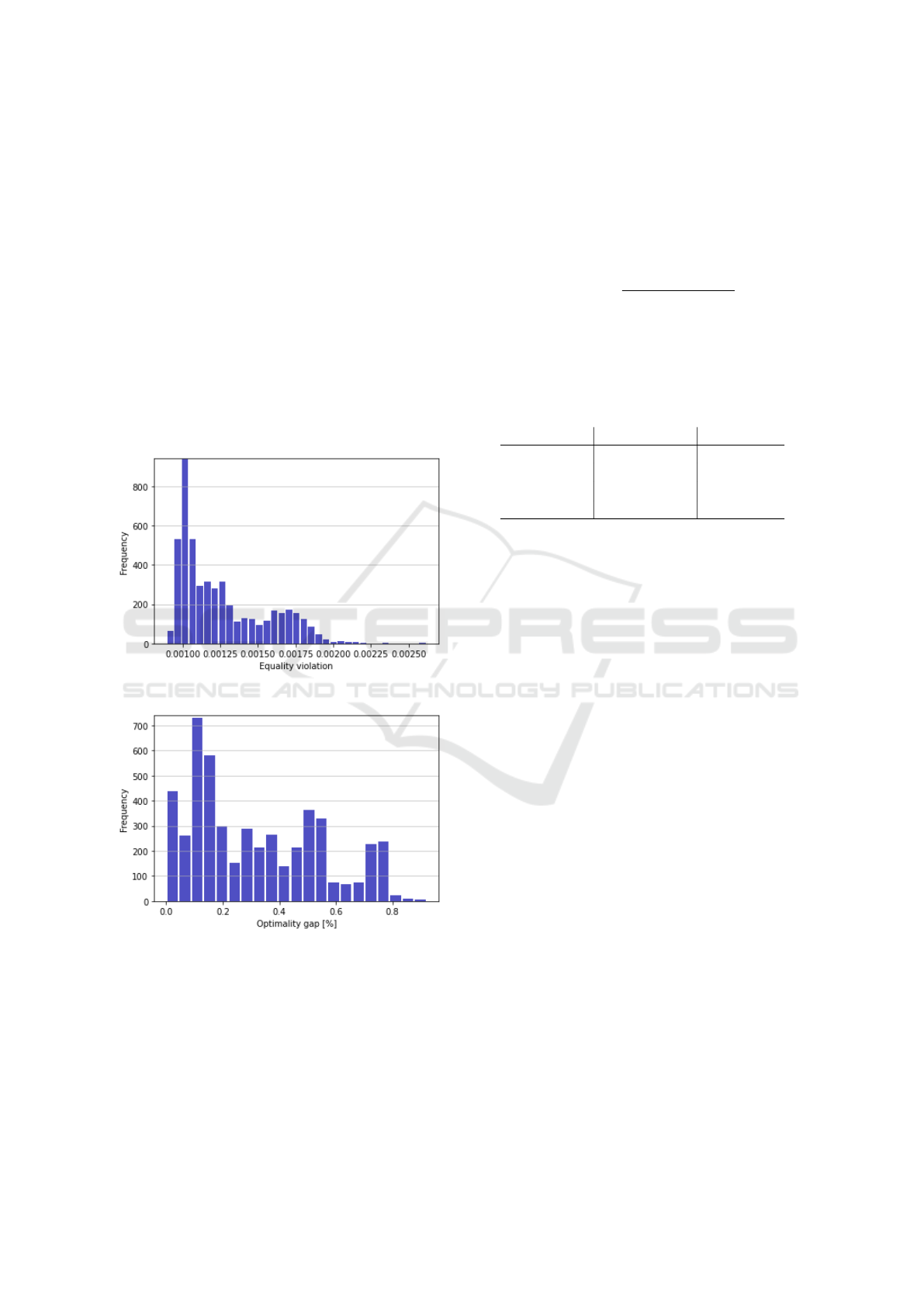
4.2 Performance

Figure 3: Mean violation of the equality constraints.

Figure 4: Optimality gap of the objective function.

The dataset D was divided into a training set D

and

a test set D

with the proportion |D

= 30000 and

| = 5000. The dataset used is labeled with the op-

timal solution retrieved from Matpower (Zimmerman

et al., 2011)(Wang et al., 2007). The unsupervised ap-

proach was trained using the Mean Squared Error as

loss function, without any regularization terms added.

The results obtained using the test set are comprehen-

sively displayed in Table 1. Histograms illustrating

the equality violation as and the optimality gap, when

using the unsupervised approach, can be seen in Fig-

ure 3-4 respectively.

Using the labeled data, the optimality gap is computed

gap

= 100

F(s

;θ

∗

) − F(s

)

F(s

)

. (26)

The values reported in Table 1 are the average across

the entire test set, except the maximum equality con-

straint violation which shows the maximum across the

entire test set.

Table 1: Result of supervised and unsupervised training.

Unsupervised Supervised

Opt.gap [%] 0.316 0.216

Eq. 1.3·10

−3

2.6·10

−3

Ineq. 6.7·10

−7

5.4·10

−6

Max eq. 0.023 0.068

5 CONCLUSION

The need for fast and accurate solutions of the Opti-

mal Power Flow problem is becoming more important

as the power systems are experiencing more unpre-

dictability in the form of intermittent power. While

training neural networks do not offer a lighter com-

putational workload compared to conventional itera-

tive non-linear solvers, they have a distinct advantage

in that they shift the computational load off-line. A

trained neural network outputs the solution in negli-

gible time. This makes neural network a promising

candidate for time sensitive applications.

Although the computational burden of supervised

learning is ofﬂine, it comes with its own challenges. It

demands a considerable amount of labeled data. This

translates to the need for a repository of OPF solutions

coming from solver like the interior-point method.

This paper primarily delved into the application

of unsupervised learning for addressing the AC-OPF

problem, without considering post-processing. A log-

ical extension to this paper would be to explore other

neural network architectures. The feed-forward archi-

tecture, as employed in this paper, might encounter

challenges when confronted with signiﬁcantly larger

power grid models. Hence it is therefore interesting

to investigate other architectures that scales well with

increasingly complex models.

An Unsupervised Neural Network Approach for Solving the Optimal Power Flow Problem

219

REFERENCES

Baker, K. (2021). Solutions of dc opf are never ac feasible.

In Proceedings of the Twelfth ACM International Con-

ference on Future Energy Systems, pages 264–268.

Bertsekas, D. (2016). Nonlinear Programming, volume 4.

Athena Scientiﬁc.

Capitanescu, F. (2011). Assessing reactive power re-

serves with respect to operating constraints and volt-

age stability. IEEE Transactions on Power Systems,

26(4):2224–2234.

Carpentier, J. (1962). Contribution to the economic dis-

patch problem. Bulletin de la Societe Francoise des

Electriciens, 3(8):431–447.

Dener, A., Miller, M. A., Churchill, R. M., Munson, T., and

Chang, C.-S. (2020). Training neural networks under

physical constraints using a stochastic augmented la-

grangian approach. arXiv preprint arXiv:2009.07330.

Djeumou, F., Neary, C., Goubault, E., Putot, S., and Topcu,

U. (2022). Neural networks with physics-informed

architectures and constraints for dynamical systems

modeling. In Learning for Dynamics and Control

Conference, pages 263–277. PMLR.

Falconer, T. and Mones, L. (2022). Leveraging power grid

topology in machine learning assisted optimal power

ﬂow.

Fioretto, F., Mak, T. W., and Van Hentenryck, P. (2020).

Predicting ac optimal power ﬂows: Combining deep

learning and lagrangian dual methods. In Proceedings

of the AAAI conference on artiﬁcial intelligence, vol-

ume 34, pages 630–637.

Huang, W., Pan, X., Chen, M., and Low, S. H. (2021).

Deepopf-v: Solving ac-opf problems efﬁciently. IEEE

Transactions on Power Systems, 37(1):800–803.

Kingma, D. P. and Ba, J. (2017). Adam: A method for

stochastic optimization.

Lavaei, J. and Low, S. H. (2011). Zero duality gap in

optimal power ﬂow problem. IEEE Transactions on

Power Systems, 27(1):92–107.

Low, S. H. (2014). Convex relaxation of optimal power

ﬂow—part i: Formulations and equivalence. IEEE

Transactions on Control of Network Systems, 1(1):15–

27.

Lu, L., Pestourie, R., Yao, W., Wang, Z., Verdugo, F.,

and Johnson, S. G. (2021). Physics-informed neu-

ral networks with hard constraints for inverse design.

SIAM Journal on Scientiﬁc Computing, 43(6):B1105–

B1132.

Pan, X., Chen, M., Zhao, T., and Low, S. H. (2022). Deep-

opf: A feasibility-optimized deep neural network ap-

proach for ac optimal power ﬂow problems.

Pan, X., Zhao, T., and Chen, M. (2020). Deepopf: Deep

neural network for dc optimal power ﬂow.

Skolﬁeld, J. K. and Escobedo, A. R. (2022). Operations

research in optimal power ﬂow: A guide to recent and

emerging methodologies and applications. European

Journal of Operational Research, 300(2):387–404.

Tang, Y., Dvijotham, K., and Low, S. (2017). Real-time op-

timal power ﬂow. IEEE Transactions on Smart Grid,

8(6):2963–2973.

Wang, H., Murillo-Sanchez, C. E., Zimmerman, R. D., and

Thomas, R. J. (2007). On computational issues of

market-based optimal power ﬂow. IEEE Transactions

on Power Systems, 22(3):1185–1193.

Zhang, L. and Zhang, B. (2022). Learning to solve the ac

optimal power ﬂow via a lagrangian approach. In 2022

North American Power Symposium (NAPS), pages 1–

6. IEEE.

Zhou, F., Anderson, J., and Low, S. H. (2020). The optimal

power ﬂow operator: Theory and computation.

Zimmerman, R. D., Murillo-S

anchez, C. E., and Thomas,

R. J. (2011). Matpower: Steady-state operations, plan-

ning, and analysis tools for power systems research

and education. IEEE Transactions on Power Systems,

26(1):12–19.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

220