Multi-Agent Pathfinding for Indoor Quadcopters: A Platform for Testing
Planning-Acting Loop
Matou
ˇ
s Kulhan and Pavel Surynek
Faculty of Information Technology, Czech Technical University in Prague,
Th
´
akurova 9, 160 00 Praha 6, Czech Republic
fi
Keywords:
Path Finding, Planning, Acting, Multiple Agents, Indoor Quadcopters, Crazyflie, MAPF, Localization,
Testing Platform.
Abstract:
We study the planning-acting loop for multi-agent path finding with continuous time (MAPF
R
). The standard
MAPF is a problem of navigating agents from their start positions to specified individual goal positions so
that agents do not collide with each other. The standard MAPF takes place in a discrete graph with agents
located in its vertices and instantaneous moves of agents across edges. MAPF
R
adds continuous elements to
MAPF via allowing agents to wait in a vertex for arbitrary length of time to avoid the collision. We focus in
this paper on executing MAPF
R
plans with a group of Crazyflies, small indoor quadcopters. We show how
to modify the existing continuous-time conflict-based search algorithm (CCBS) for MAPF
R
to produce plans
that are suitable for execution with the quadcopters. Our platform can be used for testing suitability of variants
of MAPF for execution with real agents. Our finding is that the MAPF variant with continuous time and the
related CCBS algorithm allows for extensions that can produce safe plans for quadcopters, namely cylindrical
protection zone around each quadcopter can be introduced at the planning level.
1 INTRODUCTION
Constructing planning-acting (Ghallab et al., 2016)
loops for real-life problems represents an ongoing
challenge in both artificial intelligence and robotics.
While there was a significant progress in the theory of
automated planning in recent decades (Ghallab et al.,
2004), the transfer of theoretical plans to real robotic
hardware still represents an important challenge.
Decision theoretic planning takes place in an ab-
stract environment described using logical atoms. The
state of the environment can be changes by actions
that can add or delete atoms from the state provided
precondition of the action is satisfied in the state.
The task in planning is to find a sequence of ac-
tions, a plan, that transforms the initial state to a
desired goal state. Various assumptions are adopted
to make the planning task easier such as assuming
static and deterministic environment, where each ac-
tion has a predictable outcome and it is only the
actor which changes the environment (no external
changes happen). The logical description of states
implies that decision theoretic planning is inherently
discrete. Despite the strong simplifying assumptions
and numerous advanced search and heuristic tech-
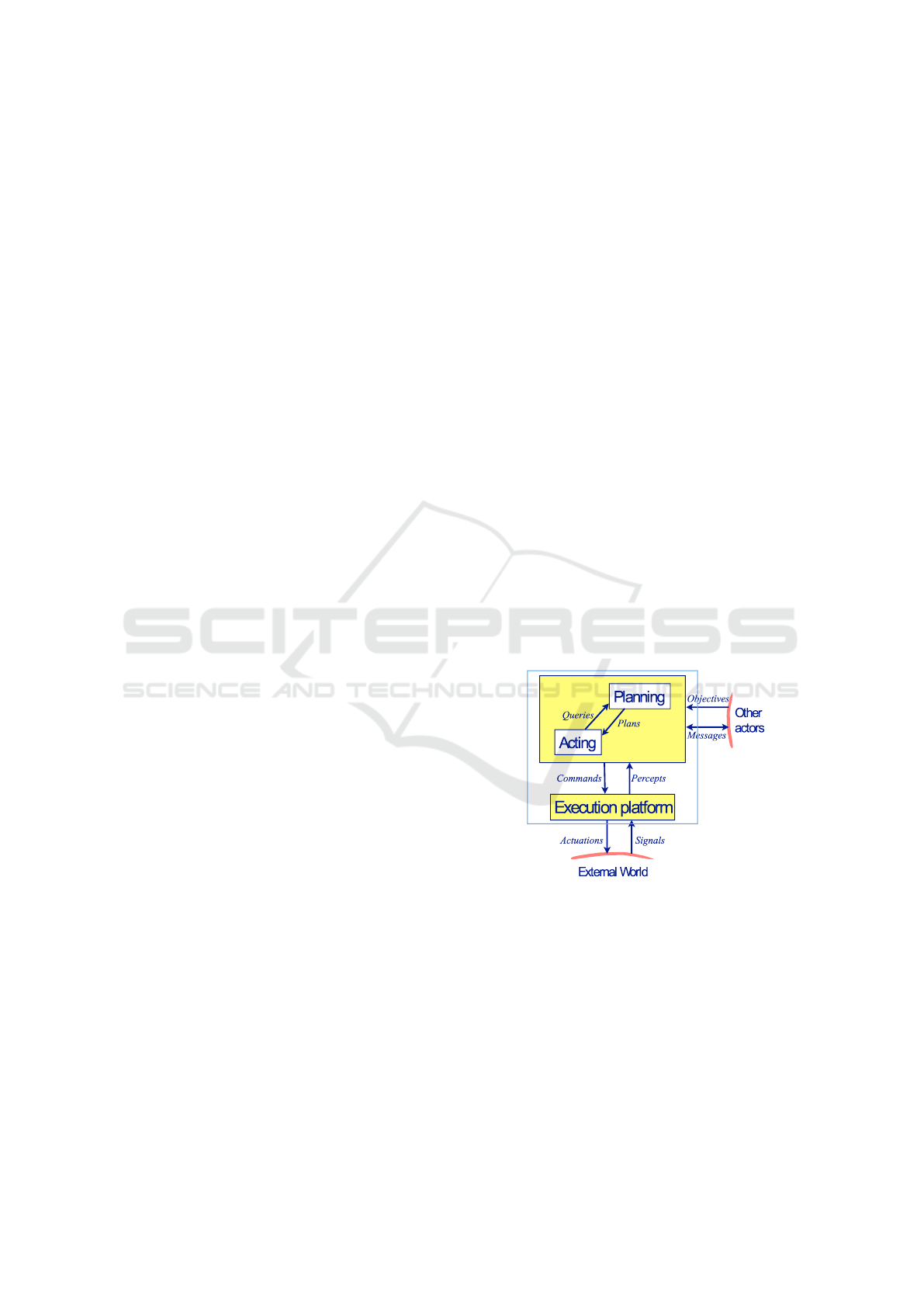
Figure 1: General scheme of planning and acting in intelli-
gent agents (Ghallab et al., 2016).
niques (Geffner, 2004; Helmert, 2006; Torralba et al.,
2017), scalability of decision theoretic planning is
still a challenge for real life scenarios (Edelkamp and
Greulich, 2018).
While assuming discrete space, time and deter-
ministic environment at the theoretical level, we can-
not adopt these assumptions when transferring plans
to real robotic hardware that is used in continu-
ous non-deterministic environments where the out-
comes of actions diverge from theoretical expecta-
Kulhan, M. and Surynek, P.
Multi-Agent Pathfinding for Indoor Quadcopters: A Platform for Testing Planning-Acting Loop.
DOI: 10.5220/0012188200003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 221-228
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
221

Figure 2: Planning and acting scheme for Crazyflie quad-
copters.
tions. Often plans need to augmented during the post-
processing phase to be executed in continuous envi-
ronments and/or a more complex schemes in which
the planning phase, the plan transformation, and ex-
ecution form a loop through which all stages interact
and respond to the current state of the environment.
We address the planning-acting loop in this paper
for the specific planning domain of multi-agent path
finding (MAPF). In multi-agent path finding (Ryan,
2008; Surynek, 2009; Wang and Botea, 2011; Sharon
et al., 2015; H
¨
onig et al., 2016) the task is to navi-
gate agents A = {a
1
,a
2
,..., a
k
} from their starting po-
sitions to individual goal positions so that agents do
not collide with each other.
This relatively homogeneous domain with lim-
ited set of actions enables deployments to physical
hardware consisting of non-trivial number of mo-
bile robots (Chud
´
y and Surynek, 2021) - agents are
uniquely mapped to mobile robot and robots execute
planned agents’ movements. Due to risk of collision
between robots, the MAPF domain offers room to
study effects of incorrect execution of actions. More-
over, real mobile robots act (move) in the continuous
environment where both space and time are contin-
uous, hence MAPF requires non-trivial treatment of
continuity during the execution phase.
The standard discrete version of MAPF takes
place in an undirected graph G = (V,E) whose ver-
tices represent positions and edges define the topol-
ogy of the environment - agents move across edges,
but no two agents can reside in the same vertex, nor
two agents can traverse an edge in opposite direc-
tions. In this discrete setting the initial configuration
of agents is defined by a simple assignment s : A → V ,
and similarly the goal configuration is defined by a
simple assignment g : A →V. The time in the standard
MAPF setting is discrete, that is, divided into discrete
time steps. The movements are instantaneous, that is
the movement of an agent from u ∈ V to v ∈ V started
at time step t in such setting means that agent disap-
pears at time step t + 1 from u and appears in v at time
step t + 1.
The abstraction adopted in MAPF via undirected
graph G brings significant simplification of the prob-
lem that allows for exhaustive search
1
and relatively
high efficiency of solving algorithms. Contemporary
techniques are capable of solving MAPF instances
with up to hundreds of agents optimally with respect
to objectives such as the makespan (Surynek, 2012)
or sum-of-costs (Sharon et al., 2013).
Recent effort in MAPF focuses on bringing the ab-
stract problem closer to real life applications. Con-
cretely a variant of MAPF that integrates continuous
aspects of the real world has been devised - MAPF
with continuous time (MAPF
R
) (Andreychuk et al.,
2022) where agents move smoothly usually along the
straight lines between the finite number of vertices
that are embedded in some metric space (continu-
ous 2D or 3D space). The instantaneous movement
of agents in no longer applied, the agent is always
present somewhere in the space. Moreover, agents
can be of any shape in MAPF
R
and the collision be-
tween agents is defined as any overlap between their
bodies. Collisions in MAPF
R
are avoided in the time
domain by allowing an agent to wait for an arbitrary
amount of time.
It is important to note that while planning-acting
loop with the standard MAPF plans in the discrete en-
vironment and plans need to be augmented for being
executed in the continuous real environment (Chud
´
y
and Surynek, 2021) this is not the case of MAPF
R
.
Solving algorithms for MAPF
R
produce plans that are
already continuous and are ready for more direct ex-
ecution with the physical robots. However the more
real plans in MAPF
R
are redeemed by the greater ef-
fort in the planning phase. Hence often intensive test-
ing to balance the difficulty of planning phase and the
accuracy of the acting phase is necessary.
1.1 Contribution
We implement the planning-acting loop as suggested
in (Ghallab et al., 2016) (Figures 1 and 2) for MAPF
R
where the planning module is represented by our
modification of the CCBS algorithm (Andreychuk
et al., 2022). The execution platform is represented by
the Crazyflie ecosystem (Bitcraze AB, 2022), consist-
ing of Crazyflies, small indoor quadcopters coupled
with localization system. Our platform can be used
to test various interconnections between the planning
1
Thanks to exhaustive search it is possible to achieve
completeness of solving algorithms, that is also unsolvabil-
ity of certain situations can be shown.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
222

and execution phase for MAPF
R
.
Three variants of MAPF
R
plan execution for
Crazyflies that we implemented within our platform
demonstrate that planning algorithms for MAPF
R
are
suitable for constructing plans that are executable by
real robotic agents. Thus we show that contempo-
rary MAPF
R
algorithms are ready for transfers into
real-life applications. In the broader perspective, our
platform can be used to test suitability of solving al-
gorithms for other variants of MAPF (Stern, 2019) for
transfer to physical hardware.
2 RELATED WORK AND
BACKGROUND
Previous attempts to bridge the theory and acting
with real robots for MAPF include the use of mobile
robots Ozobot EVO (Chud
´
y and Surynek, 2021). The
planning phase was represented by the standard dis-
crete MAPF. Hence the output plan had to be post-
processed to form continuous command sequences
before it was executed by the robots. Namely, discrete
movements between adjacent vertices u,v need to be
replaced by continuous movement along a curve con-
necting positions in 2D plane which u,v were mapped
to.
In this work, we use the MAPF
R
model and
the existing Continuous-time Conflict Based Search
(CCBS) algorithm (Andreychuk et al., 2022) that
extends the previous Conflict Based Search (CBS)
(Sharon et al., 2015) by resolving conflicts between
agents in the time domain. The original CBS uses
lazy resolution. It first plans one path per agent by
single-agent shortest path-finding algorithm ignoring
other agents.
Then the algorithm branches to resolve conflicts:
the paths calculated for each agent are verified for
conflicts. If a conflict occurs, say between agents
a
i
and a
j
in vertex v at time step t, then the CBS
algorithm resolves this conflict by introducing two
branches while in the first branch it is forbidden for
agent a
i
to visit vertex v at time step t, and in the sec-
ond branch it is forbidden for agent a
j
to visit vertex
v at time step t. Other conflicting situations such as
head-to-head collision across an edge can be resolved
similarly.
CCBS for MAPF
R
follows the same framework
as CBS (see Algorithm 1). Instead of discrete path-
finding algorithms, CCBS uses the SIPP (Phillips
and Likhachev, 2011) algorithm for single-agent path-
planning that plans w.r.t. safe time intervals assigned
to agent movement actions and allows an agent to wait
in a vertex to avoid executing a move action within the
Algorithm 1: Basic CCBS algorithm for solving MAPF
with continuous time.
1 CCBS (G = (V, E),A,s,g):
1: Root.constraints ←
/
0
2: Root.π ← {shortest temporal plan from s(a
i
) to
g(a
i
) | i = 1,2,...,k}
3: Root.µ ← max
k
i=1
µ(Root.π(a
i
))
4: OPEN ←
/
0
5: insert Root into OPEN
6: while OPEN ̸=
/
0 do
7: N ← min
µ
(OPEN)
8: remove-Min
µ
(OPEN)
9: conflicts ← validate-Plans(N.π)
10: if conflicts =
/
0 then
11: Return N.π
12: end if
13: let (a
i
,{u,v}, [t
0
,t
+
)) × (a
j
,{u
′
,v
′
},[t
′
0
,t
′
+
)) ∈
conflicts
14: for each (a, {w,z}) ∈
{(a
i
,{u,v}), (a
j
,{u
′
,v
′
})} do
15: [τ
0
,τ
+
) ← calculate-Unsafe-
Interval(a,{w,z})
16: N
′
.constraints ← N.constraints ∪
{(a,{w,z}, [τ
0
,τ
+
))}
17: N
′
.π ← update-Path(a, N.π, N
′
.constraints)
18: N
′
.µ ←
∑
k
i=1
µ(N
′
.π(a
i
))
19: insert N
′
into OPEN
20: end for
21: end while
unsafe interval that would lead to a conflict. Waiting
in vertices is possible for arbitrary amount of time, al-
ways a minimum waiting time is calculated. Hence,
after a conflict (overlap between bodies of agents)
that occurs between the movement of agent a
i
when
traversing a curve connecting positions of u and v dur-
ing the time interval [t
0
,t
+
) and agent a
j
when travers-
ing a curve connecting positions of u
′
and v
′
during
the time interval [t
′
0
,t
′
+
) (lines 9-13), the CCBS algo-
rithm determines the unsafe time interval [τ
0
,τ
+
) for
each of the agents a
i
and a
j
(line 15) during which
the agent should not commence the movement if it
wants to avoid the conflict. After branching, CCBS
searches for new paths via SIPP for agents a
i
and a
j
that avoid the calculated unsafe interval via waiting in
u or u
′
respectively. It is important to note that both
CBS and CCBS produce optimal plans with respect
to given cumulative cost
2
.
2
Often the sum-of-costs objective is used; the summa-
tion of durations of individual agents’ plans including the
waiting actions.
Multi-Agent Pathfinding for Indoor Quadcopters: A Platform for Testing Planning-Acting Loop
223

Figure 3: Crazyflie 2.1 (Bitcraze AB, 2022).
Figure 4: Loco positioning system (Bitcraze AB, 2022).
3 PLANNING AND ACTING FOR
MAPF
R
We modified the CCBS algorithm for MAPF
R
with
small quadcopters. The modified CCBS is an essen-
tial part of our platform for testing planning and act-
ing for MAPF with the quadcopters. We describe in
this sections how we implement individual compo-
nents of the planning-acting loop in intelligent agents
from Figures 1 and 2.
3.1 Planning Phase - Modification of
CCBS
We modified CCBS to support 3D grid environments.
Specifically we added collision detection mechanism
for agents moving in 3D. The shape of agents used
in the planning phase was determined by the protec-
tion zone needed for quadcopters. As the quadcopters
usually cannot fly too close to each other and must
keep relatively bigger vertical distances we model the
agents as tall cylinders. It is important to note that
in our setting the agents (cylinders) use only transla-
tional movement, that is agents do not rotate.
Thanks to absence of rotation, the collision detec-
tion between two agents (cylinders), that is the detec-
tion of overlap between their bodies, can be split in
detection of overlap between two circles correspond-
ing to the horizontal projection of the cylinders in 2D
and overlap of intervals corresponding to cylinders’
heights in 1D. The calculation of unsafe intervals af-
ter detecting a collision is done in via splitting the task
in 2D and 1D too.
Algorithm 2: BHL method for execution of MAPF
R
plan
P(a
i
) for agent a
i
.
1 BHL-Execute(P(a
i
)):
1: for each position (x,y,z,t) ∈ P(a
i
) do
2: go-to-position-HL-command(a
i
,x, y, z)
3: while current-time() < t do
4: delay()
5: end while
6: end for
3.2 Acting Hardware - Crazyflie
Ecosystem
Our planning-acting hardware component for MAPF
R
consists of Crazyflie 2.1, small indoor quadcopters
(Figure 3). Crazyflie comes with the hardware
ecosystem (Bitcraze AB, 2022):
(i) Crazyflie Family, consisting of several versions of
Crazyflie quadcopters, it is a palm sized quad-
copter weighing 27 grams supporting wireless
control over radio
(ii) Positioning systems, consisting of external types
sensors to determine the positions of Crazyflies -
our platform currently uses the Loco positioning
system (see Figure 4) based on measuring the dis-
tance to anchors, specified accuracy of 10 cm, but
our platform is open for integration of different
positioning system and
(iii) technologies for remotely controlling the
Crazyflies, this includes USB radio dongle
Crazyradio PA and cfplib, a Python library for
sending commands using the radio that interfaces
the low level hardware of Crazyflies and user
high-level programming.
3.3 Acting Software - Crazyflie Plan
Execution Module
Plan execution module is represented by our pro-
grams built on top the cfplib library. The li-
brary provides various types of commands such as
take-off, go-to specific position in 3D, move in
specific direction etc. For some commands, the
Crazyflies need need to connected with the position-
ing system. The position estimation works at the in-
terrupt level, so there is not need at the high level to
interact with the positioning system.
The basic operation of plan execution module is
to take commands from CCBS and execute them
with quadcopters using the high level commands of
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
224

Algorithm 3: BLL method for execution of MAPF
R
plan
P(a
i
) for agent a
i
.
1 BLL-Execute(P(a
i
)):
1: (x
ℓ
,y
ℓ
,z
ℓ
,t
ℓ
) ← first position of P(a
i
)
2: for each position (x,y,z,t) ∈ P(a
i
) do
3: ∆t ← t − t
ℓ
;
4: v
x
←
x−x
ℓ
∆t
; v
y
←
y−y
ℓ
∆t
; v
z
←
z−z
ℓ
∆t
5: while current-time() < t do
6: t
r
←current-time()−t
ℓ
7: x
c
← x
ℓ
+ v
x
· t
r
; y
c
← y
ℓ
+ v
y
· t
r
; z
c
← z
ℓ
+
v
z
·t
r
8: move-towards-position-LL-command(a
i
,x
c
,
y
c
, z
c
)
9: delay()
10: end while
11: x
ℓ
← x; y
ℓ
← y; z
ℓ
← z;
12: t
ℓ
← t
13: end for
Method
Error
Max. Avg.
BHL 0.644 m 0.223 m
BLL 0.662 m 0.241 m
VLL 0.601 m 0.282 m
Figure 5: Results of experiment 1.
cfplib. The more advanced plan execution modules
periodically receive the most current estimated posi-
tion from each controlled Crazyflie and sends them
individually generated flight commands based on the
flight plan generated by CCBS and in case of devia-
tion from the expected position, a command to correct
the position is generated.
We propose and compare three different meth-
ods for plan execution to demonstrate possible exper-
imentation with our platform:
• (1) BHL method - uses High Level Commander,
a firmware module, which receives abstract com-
mands containing absolute positions and leaves
the execution on Crazyflie while providing it time
according to the duration of action in plan (the
pseudo-code is shown as Algorithm 2), only few
commands are being send using this method
• (2) BLL method - uses Motion Commander pro-
viding low-level commands for moving Crazyflie
in the specific direction (see Algorithm 3) towards
the expected position of the quadcopter obtained
via linear interpolation, the difference from the
previous method is that rather many low-level
commands are send taking into account current
speed of the quadcopter
Algorithm 4: VLL method for execution of MAPF
R
plan
P(a
i
) for agent a
i
.
1 VLL-Execute(P(a
i
)):
1: (x
ℓ
,y
ℓ
,z
ℓ
,t
ℓ
) ← first position of P(a
i
)
2: for each position (x,y,z,t) ∈ P(a
i
) do
3: ∆t ← t − t
ℓ
;
4: v
x
←
x−x
ℓ
∆t
; v
y
←
y−y
ℓ
∆t
; v
z
←
z−z
ℓ
∆t
5: while current-time() < t do
6: t
r
←current-time()−t
ℓ
7: x
c
← x
ℓ
+ v
x
· t
r
; y
c
← y
ℓ
+ v
y
· t
r
; z
c
← z
ℓ
+
v
z
·t
r
8: (p
x
, p
y
, p
z
) ← current-position(a
i
)
9: v ← quadcopter-speed(a
i
)
10: size ← box-size(a
i
)
11: v
′
x
← 0; v
′
y
← 0; v
′
z
← 0;
12: for each coord ∈ {x, y, z} do
13: if p
coord
> c
coord
+ size then
14: v
′
coord
= −v
15: end if
16: if p
coord
< c
coord
− size then
17: v
′
coord
= v
18: end if
19: end for
20: move-velocity-LL-command(a
i
,v
′
x
, v
′
y
, v
′
z
)
21: delay()
22: end while
23: x
ℓ
← x; y
ℓ
← y; z
ℓ
← z;
24: t
ℓ
← t
25: end for
• (3) VLL method - augments the BLL method
with checking if the Crazyflie is inside a bound-
ing box around the desired coordinates and if not,
sends a command to move in the direction of these
coordinates (see Algorithm 3)
Generally the methods differ in how intensive con-
trol of the plan execution is being maintained and how
intensive interaction with the positioning system is
used.
4 EXPERIMENTAL EVALUATION
We performed experiments in a 2m × 2m × 2m fly-
ing area (see Figure 6) installed inside the labora-
tory equipped with 8 Loco positioning anchors, one in
each corner of the area. The position of each Crazyflie
was estimated every 10 ms.
Multiple experiments have been conducted in the
flying area, here we report a representative part of
the results, namely three scenarios in which we in-
creased the number of quadcopters. Orthogonally to
Multi-Agent Pathfinding for Indoor Quadcopters: A Platform for Testing Planning-Acting Loop
225

this, each scenario has been tested with each plan
execution method suggested in the previous section:
BHL, BLL, and VLL.
The experiments were focused on evaluating accu-
racy of accuracy w.r.t. the ideal flight plan produced
by the modified CCBS.
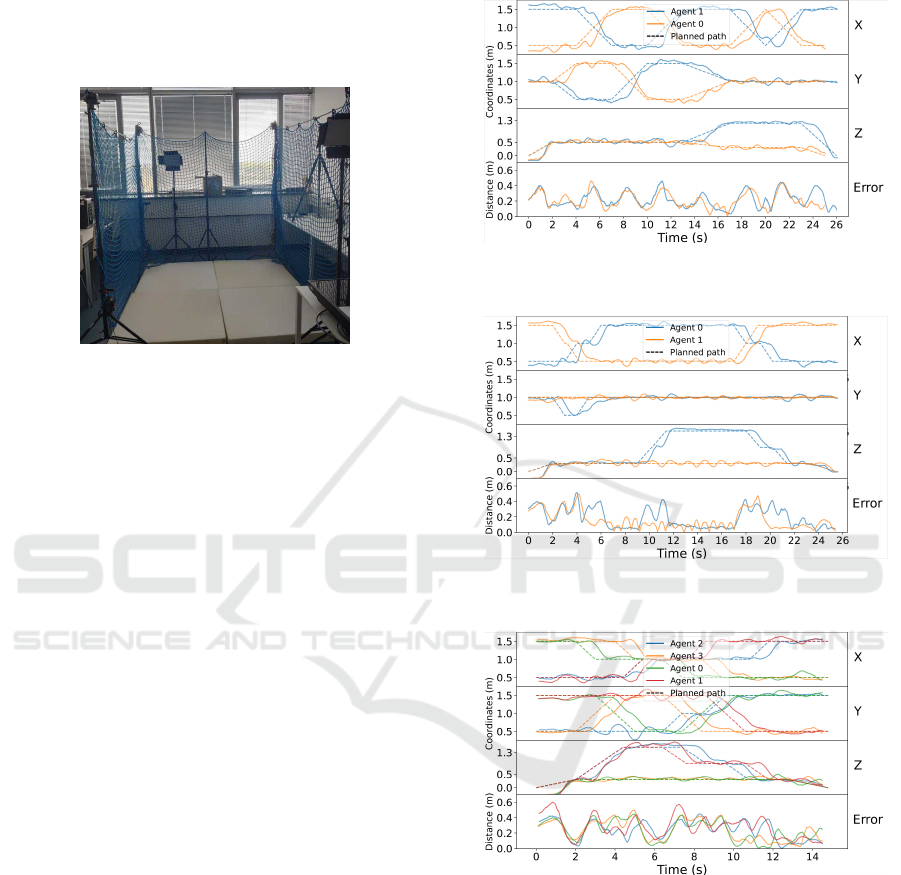
Figure 6: Laboratory flying area.
In each setup the flight plan was successfully ex-
ecuted 12 times. Aggregated results are shown in Ta-
bles 5 and 1. We report the error from the ideal plan.
It is important to note that the measurement has been
obtained from the Loco positioning system, so this is
not a measurement w.r.t. to the absolute positions of
quadcopters.
It can be observed that error from the ideal plan
ranges approximately from 0.2m to 0.3m across all
tested plan execution methods. There is also a trend
that more complex plan execution methods lead to
greater error. The explanation for worse performance
of VLL than for BHL and BLL is that calculating
speed of quadcopters from the non-smooth flight in-
troduces additional error into execution. On the other
hand, keeping the quadcopter in the bounding box
leads to smaller maximum error in VLL.
In another presentation of the results we plot er-
ror and position of the agents over time for selected
successful executions with the VLL plan execution
method. Three of these plots can be seen in Figures 7,
8, and 9. We also present error for the three reported
experiments in 3D in Figures 10, 11, and 12. In ad-
dition to this, a video recording of these experiments
can be seen on: https://youtu.be/ALWC8MkZQGI.
It can be observed that the largest error appears af-
ter the quadcopter changes the direction of its flight.
Usually before changing the direction the quadcopter
needs to stop at the position where the direction
changes which is often leads to a short oscillation
around the stop position. In can be also observed
that larger error appears during horizontal movements
while the error is less frequent during vertical move-
ments. This behavior can be explained through the
similarity of plan execution methods to proportional
controller that often exhibits similar patterns (Ang
et al., 2005).
Figure 7: Position and error over time for experiment 1 with
two agents executed by VLL.
Figure 8: Position and error over time for experiment 2 with
two agents executed by VLL.
Figure 9: Position and error over time for experiment 3 with
four agents executed by VLL.
5 CONCLUSION
Our key finding is that the proposed planning-acting
platform for MAPF
R
is capable of generating feasible
flight plans and executing them using the Crazyflie
Ecosystem with high success rate. We also demon-
strated that MAPF
R
planning algorithms are ready for
being used for real robotic agents. This shows the ma-
turity of MAPF
R
technology and feasibility of deploy-
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
226

Table 1: Selected results for various plan execution methods.
ID
Configuration Error
update type period box size speed Max. Average Median
1 BHL – – – 0,461 m 0,215 m 0,191 m
2 BHL – – – 0,644 m 0,230 m 0,205 m
3 BLL 0,05 s – – 0,580 m 0,240 m 0,244 m
4 BLL 0,05 s – – 0,544 m 0,242 m 0,242 m
5 BLL 0,1 s – – 0,520 m 0,233 m 0,243 m
6 BLL 0,1 s – – 0,382 m 0,215 m 0,224 m
7 BLL 0,2 s – – 0,591 m 0,260 m 0,256 m
8 BLL 0,2 s – – 0,662 m 0,256 m 0,257 m
9 VLL 0,1 s 0,05 m 0,3 m/s 0,601 m 0,282 m 0,284 m
10 VLL 0,1 s 0,05 m 0,3 m/s 0,587 m 0,276 m 0,272 m
11 VLL 0,2 s 0,05 m 0,3 m/s 0,594 m 0,289 m 0,304 m
12 VLL 0,2 s 0,05 m 0,3 m/s 0,533 m 0,284 m 0,295 m
Figure 10: Position and error in 3D over time for experi-
ment 1.
Figure 11: Position and error in 3D over time for experi-
ment 2.
ments of real-life MAPF
R
planning-acting systems.
The bottleneck still seems to be execution level and
the integration of execution with plans produced by
MAPF
R
planning algorithms.
Figure 12: Position and error in 3D over time for experi-
ment 3.
For future work we plan to extend our flight area.
Our current flight area can accommodate up to four
crazyflies, we expect that the number of quadcopters
can be increased in a larger area. We also plan to inte-
grate more advanced controllers into the plan execu-
tion phase such as proportional-derivative (PD) and
proportional-integral-derivative (PID) controllers.
Our execution platform can be used not only by
researchers for testing the suitability of MAPF vari-
ants for deployment on real agents but also by educa-
tors to demonstrate the difficulties of planning-acting
chain on the well understandable MAPF domain.
ACKNOWLEDGEMENTS
This research has been supported by GA
ˇ
CR - the
Czech Science Foundation, grant registration number
22-31346S.
Multi-Agent Pathfinding for Indoor Quadcopters: A Platform for Testing Planning-Acting Loop
227

REFERENCES
Andreychuk, A., Yakovlev, K. S., Surynek, P., Atzmon, D.,
and Stern, R. (2022). Multi-agent pathfinding with
continuous time. Artif. Intell., 305:103662.
Ang, K. H., Chong, G., and Li, Y. (2005). Pid control sys-
tem analysis, design, and technology. IEEE Transac-
tions on Control Systems Technology, 13(4):559–576.
Bitcraze AB (2022). System overview.
Chud
´
y, J. and Surynek, P. (2021). ESO-MAPF: bridging
discrete planning and continuous execution in multi-
agent pathfinding. In Proceedings of AAAI 2021,
pages 16014–16016. AAAI Press.
Edelkamp, S. and Greulich, C. (2018). A case study of plan-
ning for smart factories - model checking and monte
carlo search for the rescue. Int. J. Softw. Tools Technol.
Transf., 20(5):515–528.
Geffner, H. (2004). Planning graphs and knowledge compi-
lation. In Proceedings of the Fourteenth International
Conference on Automated Planning and Schedul-
ing (ICAPS 2004), June 3-7 2004, Whistler, British
Columbia, Canada, pages 52–62. AAAI.
Ghallab, M., Nau, D., and Traverso, P. (2016). Automated
Planning and Acting. Cambridge University Press.
Ghallab, M., Nau, D. S., and Traverso, P. (2004). Automated
planning - theory and practice. Elsevier.
Helmert, M. (2006). The fast downward planning system.
J. Artif. Intell. Res., 26:191–246.
H
¨
onig, W., Kumar, T. K. S., Cohen, L., Ma, H., Xu, H., Aya-
nian, N., and Koenig, S. (2016). Multi-agent path find-
ing with kinematic constraints. In Proceedings of the
Twenty-Sixth International Conference on Automated
Planning and Scheduling, ICAPS 2016, London, UK,
June 12-17, 2016, pages 477–485. AAAI Press.
Phillips, M. and Likhachev, M. (2011). SIPP: safe interval
path planning for dynamic environments. In Proceed-
ings of ICRA 2011, pages 5628–5635.
Ryan, M. R. K. (2008). Exploiting subgraph structure in
multi-robot path planning. J. Artif. Intell. Res. (JAIR),
31:497–542.
Sharon, G., Stern, R., Felner, A., and Sturtevant, N.
(2015). Conflict-based search for optimal multi-agent
pathfinding. Artif. Intell., 219:40–66.
Sharon, G., Stern, R., Goldenberg, M., and Felner, A.
(2013). The increasing cost tree search for optimal
multi-agent pathfinding. Artif. Intell., 195:470–495.
Stern, R. (2019). Multi-agent path finding - an overview. In
Artificial Intelligence - 5th RAAI Summer School, Dol-
goprudny, Russia, July 4-7, 2019, Tutorial Lectures,
volume 11866 of Lecture Notes in Computer Science,
pages 96–115. Springer.
Surynek, P. (2009). A novel approach to path planning for
multiple robots in bi-connected graphs. In Proceed-
igns of ICRA 2009, pages 3613–3619.
Surynek, P. (2012). Towards optimal cooperative path plan-
ning in hard setups through satisfiability solving. In
PRICAI 2012: Trends in Artificial Intelligence - 12th
Pacific Rim International Conference on Artificial In-
telligence, Kuching, Malaysia, September 3-7, 2012.
Proceedings, volume 7458 of Lecture Notes in Com-
puter Science, pages 564–576. Springer.
Torralba,
´
A., Alc
´
azar, V., Kissmann, P., and Edelkamp, S.
(2017). Efficient symbolic search for cost-optimal
planning. Artif. Intell., 242:52–79.
Wang, K. C. and Botea, A. (2011). MAPP: a scalable multi-
agent path planning algorithm with tractability and
completeness guarantees. J. Artif. Intell. Res., 42:55–
90.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
228