Trajectory Planning for Multiple Vehicles Using Motion Primitives: A

Moving Horizon Approach Under Uncertainty

Bahaaeldin Elsayed

and Rolf Findeisen

Systems Theory and Automatic Control, Otto von Guericke University Magdeburg, Germany

Control and Cyber-Physical Systems, Technische Universit

at Darmstadt, Germany

ﬁ

Keywords:

Model Predictive Control, Multi-Mode Operation, System Uncertainty, Mixed Integer Linear Programming,

Motion Primitives.

Abstract:

Planning motion in cluttered and uncertain environments for autonomous systems remains a daunting chal-

lenge, especially when prioritizing safety and efﬁciency. This paper introduces an innovative method of meld-

ing motion primitives with a moving horizon strategy, drawing on the principles of model predictive control.

Using motion primitives, we achieve simpliﬁed, high-level depictions of vehicle movement using various lin-

ear time-invariant models for each mode. This signiﬁcantly cuts computational complexity in the subsequent

planning stages. We integrate constraint backoff based on system uncertainties to ensure that generated tra-

jectories are robust, collision-free, and adhere to all necessary constraints. This comprehensive framework

produces optimal, safe trajectories that cater to environmental uncertainties and are suitable for real-time

applications. Our simulation outcomes robustly highlight the strengths and distinctiveness of the proposed

approach.

1 INTRODUCTION

Motion planning for autonomous vehicles operating

in cluttered environments is complex and demanding.

It involves ﬁnding an optimal trajectory for the ve-

hicle to safely navigate from its current location to

a goal point, considering the presence of static and

moving obstacles, the physical limitations of the ve-

hicle, uncertainties, and disturbance while being real-

time capable (LaValle, 2006). The problem becomes

even more challenging when multiple vehicles are in-

volved, as one vehicle’s motion can impact others’

motion, and guaranteed collision avoidance becomes

a critical concern. Therefore, there is a signiﬁcant

need to develop robust and efﬁcient motion planning

algorithms that can handle the uncertainties and com-

plexities of real-world scenarios, such as ﬂeet ad-

ministration, search and rescue operations, and agri-

culture operations in harsh conditions (Wong et al.,

2017).

Several approaches have been proposed for solv-

ing the motion planning problem for autonomous

vehicles, e.g., graph-based approaches (Stahl et al.,

2019), probabilistic planning approaches (Wang

et al., 2022), and optimization-based approaches (Ku-

lathunga and Klimchik, 2022), depend on the speciﬁc

requirements and constraints of the problem. For a

comprehensive overview, we refer to (Laumond et al.,

1998; LaValle, 2006; Goerzen et al., 2010; Latombe,

2012). While these approaches offer valuable in-

sights, they often have limitations regarding scalabil-

ity, robustness, and adaptability to changing environ-

ments. When selecting an approach, it is essential to

consider the trade-offs between accuracy and compu-

tational complexity (LaValle, 2006).

Recently, model predictive control (MPC) has

emerged as a powerful motion planning framework

involving multiple autonomous vehicles (Zuo et al.,

2020; Liu et al., 2017). The basic concept of MPC is

based on the repeated solution of optimization prob-

lems taking the system dynamics and obstacles via

constraints into account. Only the ﬁrst path segment

is applied, and then the process is repeated until the

goal is reached (Findeisen and Allg

ower, 2002; Mat-

tingley et al., 2011; Rawlings et al., 2017a). MPC

has several advantages over traditional methods, in-

cluding handling complex constraints, incorporating

multiple objectives, and adapting to changing envi-

ronments (Rawlings et al., 2017b).

However, solving the resulting optimization plan-

ning problem is often computationally challenging

(Reiter and Reiter, 2020). Therefore, often different

Elsayed, B. and Findeisen, R.

Trajectory Planning for Multiple Vehicles Using Motion Primitives: A Moving Horizon Approach Under Uncertainty.

DOI: 10.5220/0012188700003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 229-236

ISBN: 978-989-758-670-5; ISSN: 2184-2809

229

approximations and simpliﬁcations are used. How-

ever, generating a safe trajectory using a simpliﬁed

vehicle model is affected by uncertainty in the ve-

hicle’s dynamics and the environment. It may lead

to suboptimal or unsafe control sequences (Borrelli

et al., 2017). Various robust MPC approaches, such

as stochastic, robust, set-theoretic, and adaptive ap-

proaches, have been proposed to overcome these

drawbacks. However, these methods can be com-

putationally expensive, challenging to implement,

or prone to instability (Magdici and Althoff, 2016;

Rawlings et al., 2017b).

Motivated by robust predictive control, we pro-

pose an approach that combines contract-based model

predictive control (CB-MPC) (Ibrahim et al., 2020;

ogel et al., 2022) with Point-to-Point motion primi-

tives (PTP) to handle uncertainty in motion planning

while improving performance and reducing computa-

tional time complexity. The combination results in a

mixed-integer linear programming optimization prob-

lem, which generates safe, optimal, and smooth refer-

ence trajectories while avoiding obstacles even in un-

certain conditions. The simulation results show the

method’s effectiveness in maximizing vehicle perfor-

mance while handling the impact of uncertainty.

The remainder of the paper is structured as fol-

lows. Section 2 presents the problem formulation for

a single vehicle and its extension to multiple vehi-

cles. Section 3 illustrates the planning strategy and

how to integrate motion primitives in the hybrid ro-

bust receding horizon planning formulation. Section

4 presents the mathematical structure of the proposed

point-to-point motion primitives integration with a

contract-based MPC framework for real-time appli-

cations. The simulations are presented in Section 5

before concluding the paper with ﬁnal remarks in Sec-

tion 6.

2 PROBLEM FORMULATION

Motion planning for autonomous vehicles in cluttered

environments aims to ﬁnd a safe and optimal trajec-

tory to reach its goal while considering various con-

straints. Physical limitations of the vehicle, such as

maximum speed and acceleration, must be considered

to ensure safety, stability, and performance. The pres-

ence of static and moving obstacles in the environ-

ment limits the motion options and requires the mo-

tion planner to continuously update its plan to prevent

collisions. Due to the unpredictable motion of ob-

stacles, the uncertainty in the environment requires

the solution to be robust. Real-time motion plan-

ning presents a complex optimization problem as it

requires balancing conﬂicting objectives, such as task

objectives, collision avoidance, and obstacle avoid-

ance while considering the uncertainty in the envi-

ronment. This requires the solution to be computed

quickly enough to meet the real-time demands of the

vehicle’s motion. Furthermore, a new layer of com-

plexity arises when extending motion planning algo-

rithms to scenarios involving multiple vehicles navi-

gating cluttered environments. The presence of mul-

tiple vehicles increases the complexity of the opti-

mization problem. It requires the motion planner to

consider not only the avoidance of static obstacles

but also dynamic obstacles in the form of other ve-

hicles. The motion planning algorithm must handle

these complexities while satisfying the safety and sta-

bility requirements.

3 PLANNING STRATEGY

This paper addresses the challenge of devising a fea-

sible and optimal trajectory for one or more au-

tonomous vehicles (denoted as V ) to navigate from

an initial point (x

start

) to a destination (x

goal

) in a clut-

tered environment. This task involves considering un-

certainties and adhering to various constraints, includ-

ing dynamics, kinematics, and collision avoidance,

while simultaneously optimizing objectives like en-

ergy consumption and minimizing the distance to the

goal point at each time step, as illustrated in Fig. 2.

To tackle this complex problem, we propose a

robust motion planning approach that leverages a

Contract-based Model Predictive Control (CB-MPC)

framework and integrates it with the Point-to-Point

(PTP) primitives approach, as depicted in Fig. 1.

The resulting optimization problem is formulated as a

Mixed-Integer Linear Programming (MILP) problem.

MILP offers several advantages, notably its ability to

handle continuous and discrete variables. This is es-

sential for addressing challenges where discrete deci-

sions, such as mode changes due to environmental al-

terations, task objectives, or the vehicle’s capabilities,

are required (Schouwenaars et al., 2004; Schouwe-

naars, 2006).

To facilitate the understanding of the proposed ap-

proach, we will start by considering its application to

a single vehicle and present the extension to multiple

vehicles in Section 4.

3.1 Contract-Based MPC Approach

In (Ibrahim et al., 2020), a contract-based Model

Predictive Control (MPC) framework is introduced

to handle deterministic bounded uncertainty sets by

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

230

Task Objective

Optimizer

Approximated

System Dynamics

MILP Optimization Problem

On-line Moving Horizon Trajectory Planning

Low-level Controller

Autonomous System

Motion Primitives

Safety contracts

Multiple LTI Models

Environment

Obstacles

System Dynamics

Figure 1: Motion primitives integration with safety contract

receding horizon planner structure for online trajectory gen-

eration of autonomous vehicles under uncertainty.

deﬁning feasible states and controlling input sets.

This MPC framework predicts future vehicle motion

and optimizes control inputs to achieve desired per-

formance.

The contract-based approach formulates the un-

derlying optimization problem as a Mixed-Integer

Linear Programming (MILP) problem. This MILP

problem considers various constraints and accounts

for environmental uncertainty while capturing vehi-

cle capabilities through contract sets and precision-

uncertainty speciﬁcations. These contracts ensure the

satisfaction of various properties, including constraint

compliance.

By employing the contract-based approach, a

clear separation is achieved between the planning

phase and the execution of the navigation objective.

This separation enhances the overall efﬁciency and

reliability of the motion planning process (Ibrahim

et al., 2020; K

ogel et al., 2022).

To illustrate this contract-based approach, let’s

consider that linear time-invariant models represent

the dynamics of different modes for an autonomous

vehicle.

∀i ∈ {1, ... ,L}

x(k + 1) =A

x(k) + B

u(k) + ω(k), (1a)

y(k) =C

x(k), (1b)

x(k) ∈ X

, u(k) ∈ U

, (1c)

ω(k) ∈W

. (1d)

Here L is the number of modes, x(k) ∈ R

,u(k) ∈ R

are the vehicle’s states and inputs, while y(k) ∈ R

are the vehicle’s outputs (positions). A

,∀i ∈

{1,. .. ,L} are matrices of corresponding dimensions

for each mode i. Note that the dynamics are subject

to bounded uncertainties ω(k) given by:

∀i ∈ {1, ...,L}

If x(k) ∈ X

⊆ X, and u(k) ∈ U

⊆ U,

Then w(k) ∈ W

⊆ W.

We assume that X

, U

, and W

are convex compact

polytopes. The modes and uncertainty sets allow cap-

turing mode-dependent disturbances. For example, if

the vehicle moves slowly, the disturbance might be

smaller; see Fig. 2. Fast operation leads to a larger

disturbance set, e.g., capture unmodeled system dy-

namics. Note that the sets X

and/or U

can overlap

∀i ̸= j, X

∩ X

̸=

0, U

∩ U

̸=

Obstacle Avoidance with Operation Mode Depen-

dent Obstacle Enlargements:

The vehicles should navigate safely despite the dis-

turbances and model uncertainties; see Fig. 2, i.e., the

vehicle’s position y(k) should be outside the obstacle

set; see Fig. 3

y(k) /∈ O

To avoid obstacle collisions, we use safety margins

according to the ”active” operation mode W

, see

Fig. 3. This formulation provides a modular and eas-

ily constructed simple low-level velocity controller

to drive the vehicle to its ﬁnal destination while ef-

ﬁciently satisfying the constraints and rejecting exter-

nal disturbance.

Figure 2: Conservative obstacle enlargement without a fea-

sible solution or a very long solution path due to short hori-

zon.

3.2 Motion Primitives to Limit Planning

Complexity

PTP motion primitives are fundamental in au-

tonomous motion planning, facilitating real-time,

Trajectory Planning for Multiple Vehicles Using Motion Primitives: A Moving Horizon Approach Under Uncertainty

231

Figure 3: Smaller obstacle enlargement considering the

slow motion, which allows the planner to ﬁnd a feasible

solution by switching between different velocity modes.

smooth trajectory generation (LaValle, 2006; Sicil-

iano et al., 2008; Mahulea et al., 2020). They compile

a pre-computed table of feasible control inputs, adapt-

ing to the vehicle’s mode of operation for swift exe-

cution and responsive path adjustments. This reduces

computational complexity (Frazzoli, 2001). PTP mo-

tion primitives ensure continuous and seamless ve-

hicle motion (Bottasso et al., 2008; Pivtoraiko and

Kelly, 2011). These trajectories are generated by sim-

ulating the vehicle’s dynamics with various control

inputs, allowing simultaneous consideration of mul-

tiple objectives such as goal attainment, energy ef-

ﬁciency, and collision avoidance. The approach re-

mains ﬂexible and modular, requiring no alterations

to the generalized motion primitives set, while infea-

sible primitives can be excluded during optimization

(Mahulea et al., 2020) (Fig. 2).

Control inputs at each time step, u(k) ∈ U

, are

expressed as a linear combination of motion primi-

tives, P, using a binary selection variable, b

. The op-

timization problem selects the most suitable motion

primitive while respecting constraints and objectives,

where i is the index of the motion primitive:

u(k) =

∑

j=1

P (3)

Where J is the number of motion primitives, the bi-

nary variable, b

, is deﬁned such that only one mo-

tion primitive can be selected at each time step, i.e.,

∑

j=1

= 1 and b

∈ 0,1. The optimization problem

can be formulated to select the most suitable motion

primitive at each time step while considering the con-

straints and objectives of the motion planning prob-

lem.

3.3 Combining Motion Primitives and

Contract-Based MPC

The proposed method provides a more modular and

efﬁcient solution by formulating the motion planning

problem as a MILP optimization and creating a con-

tract between the high-level planner and low-level

controller. CB-MPC is a framework that uses con-

tracts, in other cases in the form of sets or constraints,

to ensure system safety while still optimizing the de-

sired performance objective. The combination of PTP

with CB-MPC provides a robust solution to the mo-

tion planning problem, as the contracts can be updated

in real-time based on the system’s current state and

the environment’s status.

4 ROBUST MILP FORMULATION

To obtain a computationally feasible optimization

problem, we consider simpliﬁed, discretized vehicle

and moving obstacle dynamics. By fusing motion

primitives and contracts, we obtain the following op-

timization problem:

minimize

{x},{u}, i



(k), u

(k)



(4a)

subject to ∀p ∈ {1,...,V },

∀k ∈ {0,...,N − 1},∀i ∈ {1,...,L},

(k + 1) = A

(k) + B

(k) + ω

(k),

(4b)

(k) = C

x(k), (4c)

(k) ∈ X

⊆ X

free,p

⊂ X

, (4d)

(k) ∈ U

mp,i

∈ U

⊆ U

, (4e)

(k) /∈ O

→ y

(k) ∈ Y

free,p

, (4f)

free,p

= Y

\ Y

obs,p

, (4g)

(k) ∈ W

⊆ W

, (4h)

(N) ∈ X

f ,i

⊆ X

free,p

, (4i)

where V is the number of the vehicles, N is the plan-

ning horizon, i represents the operation mode, and L

is the modes number. A

are the model of the

vehicle p at the mode i. The optimal solution x

∗

(k)

minimizes the path cost J, which we assume to be

given by:

J(x, u) =

∑

p=0

(||x

goal,p

− x

(N)||

∞

N−1

∑

k=0

||u

(k)||

∞

)

(5)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

232

Here ||p

(k)||

∞

penalize the control input, while the

terminal cost penalizes the distance to the goal point

goal

at the end of the planning horizon for each vehi-

cle.

4.1 Obstacle Avoidance

To simplify the problem’s complexity, we consider

that the vehicles operate in a two-dimensional space

and that the obstacles are rectangular. The position of

the obstacle is deﬁned by its lower left and upper right

corner points, denoted by (x

min

) and (x

max

respectively.

At each time step k, the position of each vehicle

must be located outside of the obstacle. The moving

object’s size is considered, and the obstacles are ac-

cordingly enlarged, reducing each vehicle to a moving

point. This approach ensures safe and efﬁcient navi-

gation for all vehicles in the same workspace while

avoiding collisions with the same obstacle. This can

be formulated as:

∀p ∈ {1,...,V },∀k ∈ {0, .. ., N − 1} :

p,k

≤ x

min

or x

p,k

≥ x

max

or y

p,k

≤ y

min

or y

p,k

≥ y

max

4.2 Collision Avoidance

When multiple vehicles are travelling to different des-

tinations, avoiding collisions between them can be ap-

proached like avoiding stationary obstacles. At each

time step, a minimum distance must be maintained

between each pair of vehicles. For example, consid-

ering the position and the velocity for any pair of ve-

hicles p and q at the k

time step as (x

p,k

) and

q,k

) respectively. Then the safety distance be-

tween them can be denoted by d

safety

for each axis as

the following:

∀k ∈ {0,...,N − 1} :∀p,q | q > p :

p,k

− x

q,k

| ≥ d

safety

p,k

− y

q,k

| ≥ d

safety

The resulting non-convex constraint can be ap-

proximated by convex polygons using the Big-M

method, introducing extra binary variables in the op-

timization problem. For further details, we refer to

(Ibrahim et al., 2019; Schouwenaars, 2006; Frazzoli,

2001).

5 SIMULATION RESULTS

To demonstrate the efﬁcacy of the proposed com-

bination of point-to-point motion primitives and a

robust contract-based receding horizon planning ap-

proach, we consider a simulation scenario in which

vehicles operate in an environment ﬁlled with obsta-

cles to reach their goal optimally. The vehicle model

has four states, x =





⊤

, where p

and p

are positions, and v

, v

are the velocities.

u(k) =





⊤

are the inputs, i.e. the accelerations

in x and y direction.

We consider a group of four homogeneous vehi-

cles, V = 4, each with its start and goal points, op-

erating simultaneously in the cluttered environment.

Each vehicle can operate in two modes, each deﬁned

by a different set of state constraints based on differ-

ent velocity bounds. Mode 1 has a velocity bound

from 0 to 1 [m/s], while Mode 2 has a velocity bound

from 1 to V

max

[m/s]. Based on the current velocity,

each vehicle is subject to bounded uncertainty, and

therefore, higher safety margins are required for op-

erating in mode 2 compared to mode 1. Addition-

ally, a safety margin is added to prevent the collision

between any two pairs of vehicles during operation,

safety

= 1 [m/s]. A ﬁnite set of motion primitives in

the input space U

= [−1,1] with sample step size

∆u = 0.1 is used.

The resulting optimization problems are formu-

lated via YALMIP (L

ofberg, 2004) and solved via

Gurobi (Optimization, 2014). To illustrate the effec-

tiveness of the proposed approach, we consider two

different scenarios. First, we assume that we have

four vehicles in the corners of the square area, and

their ﬁnal goal is to reach the opposite corner. In this

0 20 40 60 80 100

100

X [m]

Y [m]

vehicle 1

vehicle 2

vehicle 3

vehicle 4

Figure 4: Scenario 1: Trajectory Generation of the Au-

tonomous Vehicle without motion primitives with symmet-

ric paths.

Trajectory Planning for Multiple Vehicles Using Motion Primitives: A Moving Horizon Approach Under Uncertainty

233

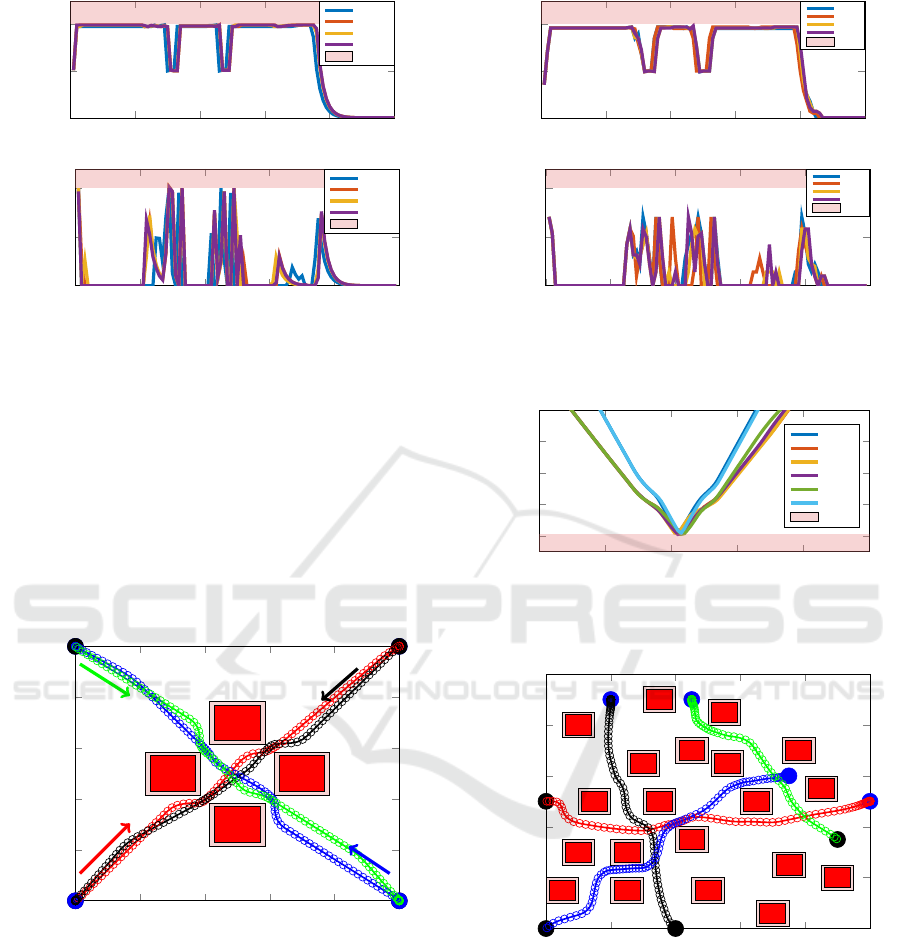
0 20 40 60 80 100

Time (sec)

Velocity (m/sec)

Constr.

0 20 40 60 80 100

0.5

Time (sec)

Acceleration (m/sec

)

Constr.

Figure 5: Scenario 1: Velocity and acceleration proﬁle with-

out motion primitives with symmetric path.

scenario, each vehicle is expected to move the same

distance while satisfying obstacle and collision avoid-

ance constraints, optimizing energy consumption, and

minimizing the distance to the goal points at each time

step. The second scenario selects arbitrary random

start and goal points in a high-density, cluttered envi-

ronment.

5.1 Results Discussions

0 20 40 60 80 100

100

X [m]

Y [m]

vehicle 1

vehicle 2

vehicle 3

vehicle 4

Figure 6: Scenario 2: with motion primitives with symmet-

ric path.

The simulation results demonstrate the capability of

the proposed approach in ﬁnding an optimal and

collision-free trajectory for the vehicle to reach its

goal.

As shown in Fig. 4,6,9, the planner can adapt to

different modes of operation, including switching to

a low-velocity mode, to handle uncertainties effec-

tively. However, it is noted that if the vehicle op-

erates at maximum velocity, the planner may not be

able to ﬁnd a feasible solution because the obstacles

0 20 40 60 80 100

Time (sec)

Velocity (m/sec)

Constr.

0 20 40 60 80 100

0.5

Time (sec)

Acceleration (m/sec

)

Constr.

Figure 7: Scenario 2: Velocity and acceleration proﬁle with

motion primitives with symmetric path.

0 20 40 60 80 100

Time (sec)

Distance [m]

v1v2

v1v3

v1v4

v2v3

v2v4

v3v4

safety

Figure 8: Scenario 2: The relative distance between any two

pairs of vehicles during operation.

0 20 40 60 80 100

100

X [m]

Y [m]

Figure 9: Scenario 3: Autonomous vehicles trajectory plan-

ning with motion primitives for arbitrary start and goal

points.

are enlarged with a large safety margin. Hence, the

proposed structure provides additional ﬂexibility and

optimizes the vehicle’s potential to achieve the task

objectives with satisfying constraints, as seen in Fig.

5,7, and 10.

Moreover, collision avoidance was effectively

maintained throughout the operation, as evidenced by

Fig 8 and 11, where the distance between any pair

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

234

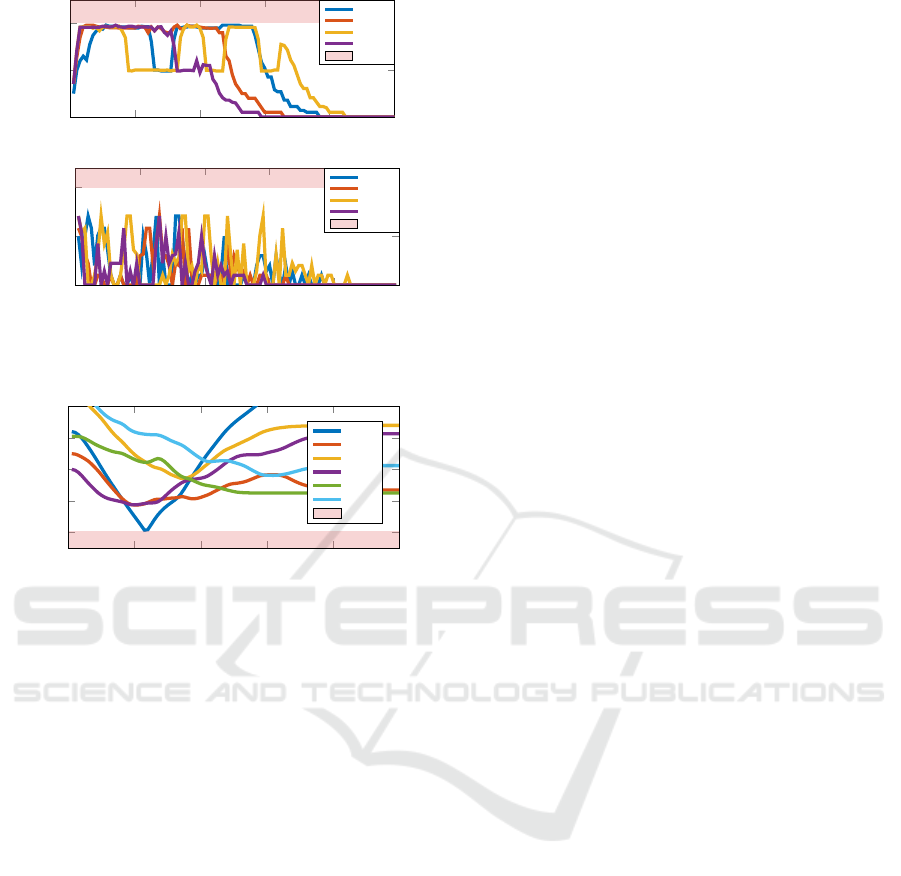
0 20 40 60 80 100

Time (sec)

Velocity (m/sec)

Constr.

0 20 40 60 80 100

0.5

Time (sec)

Acceleration (m/sec

)

Constr.

Figure 10: Scenario 3: Velocity and acceleration proﬁle

with motion primitives.

0 20 40 60 80 100

Time (sec)

Distance [m]

v1v2

v1v3

v1v4

v2v3

v2v4

v3v4

safety

Figure 11: Scenario 3: The relative distance between any

two pairs of vehicles during operation.

of vehicles remained greater than the safety margin

of the vehicle. Another aspect to consider is the im-

pact of Point-to-Point motion primitives on reducing

the computational time complexity of the problem, as

depicted in Figures 5 and 7. The proposed approach

generates smoother paths with low control effort com-

pared to other approaches without motion primitives.

6 CONCLUSION

We propose a moving horizon approach for multi-

vehicle motion planning in complex and uncertain en-

vironments. Our method combines motion primitives

with principles from model predictive control (MPC).

By employing motion primitives, we create simpli-

ﬁed representations of vehicle movement, each as-

sociated with a speciﬁc linear time-invariant model,

signiﬁcantly reducing computational complexity dur-

ing planning. We also integrate a constraint back-

off mechanism that accounts for model and exter-

nal uncertainties, ensuring the generated trajectories

are robust, collision-free, and adhere to critical con-

straints. Simulation results validate the method’s ef-

fectiveness, showcasing its ability to generate safe

and optimal trajectories for multiple vehicles in real

time.

REFERENCES

Borrelli, F., Bemporad, A., and Morari, M. (2017). Predic-

tive control for linear and hybrid systems. Cambridge

University Press.

Bottasso, C. L., Leonello, D., and Savini, B. (2008).

Path planning for autonomous vehicles by trajectory

smoothing using motion primitives. IEEE Transac-

tions on Control Systems Technology, 16(6):1152–

1168.

Findeisen, R. and Allg

ower, F. (2002). An introduction

to nonlinear model predictive control. 21st Benelux

Meeting on Systems and Control, 11:119–141.

Frazzoli, E. (2001). Robust hybrid control for autonomous

vehicle motion planning. PhD thesis, Massachusetts

Institute of Technology.

Goerzen, C., Kong, Z., and Mettler, B. (2010). A survey of

motion planning algorithms from the perspective of

autonomous uav guidance. Journal of Intelligent and

Robotic Systems, 57(1):65–100.

Ibrahim, M., K

ogel, M., Kallies, C., and Findeisen, R.

(2020). Contract-based hierarchical model predictive

control and planning for autonomous vehicle. IFAC-

PapersOnLine, 53(2):15758–15764.

Ibrahim, M., Matschek, J., Morabito, B., and Find-

eisen, R. (2019). Hierarchical model predictive con-

trol for autonomous vehicle area coverage. IFAC-

PapersOnLine, 52(12):79–84.

ogel, M., Ibrahim, M., Kallies, C., and Findeisen, R.

(2022). Safe hierarchical model predictive control

and planning for autonomous systems. arXiv preprint

arXiv:2203.14269.

Kulathunga, G. and Klimchik, A. (2022). Optimization-

based motion planning for multirotor aerial vehicles:

a review. arXiv preprint arXiv:2208.14647.

Latombe, J.-C. (2012). Robot motion planning, volume 124.

Springer.

Laumond, J.-P. et al. (1998). Robot motion planning and

control. Springer.

LaValle, S. M. (2006). Planning algorithms. Cambridge

University Press.

Liu, C., Lee, S., Varnhagen, S., and Tseng, H. E. (2017).

Path planning for autonomous vehicles using model

predictive control. In 2017 IEEE Intelligent Vehicles

Symposium (IV), pages 174–179. IEEE.

ofberg, J. (2004). YALMIP: A toolbox for modeling and

optimization in matlab. In Proceedings of the IEEE

International Conference on Robotics and Automation

(ICRA), pages 284–289. IEEE.

Magdici, S. and Althoff, M. (2016). Fail-safe motion plan-

ning of autonomous vehicles. In 2016 IEEE 19th In-

ternational Conference on Intelligent Transportation

Systems (ITSC), pages 452–458. IEEE.

Trajectory Planning for Multiple Vehicles Using Motion Primitives: A Moving Horizon Approach Under Uncertainty

235

Mahulea, C., Kloetzer, M., and Gonz

alez, R. (2020). Path

planning of cooperative mobile robots using discrete

event models. John Wiley & Sons.

Mattingley, J., Wang, Y., and Boyd, S. (2011). Reced-

ing horizon control. IEEE Control Systems Magazine,

31(3):52–65.

Optimization, G. (2014). Inc. Gurobi optimizer reference

manual, 2014. URL: http://www. gurobi. com.

Pivtoraiko, M. and Kelly, A. (2011). Kinodynamic mo-

tion planning with state lattice motion primitives. In

2011 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems, pages 2172–2179. IEEE.

Rawlings, J. B., Mayne, D. Q., and Diehl, M. (2017a).

Model predictive control: theory, computation, and

design, volume 2. Nob Hill Publishing Madison, WI.

Rawlings, J. B., Mayne, D. Q., and Diehl, M. (2017b).

Model predictive control: theory, computation, and

design, volume 2. Nob Hill Publishing Madison, WI.

Reiter, A. and Reiter, A. (2020). Path and Trajectory Plan-

ning. Springer.

Schouwenaars, T. (2006). Safe trajectory planning of au-

tonomous vehicles. PhD thesis, Massachusetts Insti-

tute of Technology.

Schouwenaars, T., Mettler, B., Feron, E., and How, J.

(2004). Hybrid model for trajectory planning of ag-

ile autonomous vehicles. Journal of Aerospace Com-

puting, Information, and Communication, 1(12):629–

651.

Siciliano, B., Khatib, O., and Kr

oger, T. (2008). Springer

handbook of robotics, volume 200. Springer.

Stahl, T., Wischnewski, A., Betz, J., and Lienkamp, M.

(2019). Multilayer graph-based trajectory planning

for race vehicles in dynamic scenarios. In 2019

IEEE Intelligent Transportation Systems Conference

(ITSC), pages 3149–3154. IEEE.

Wang, L., Yin, G., Xu, L., Dong, F., Xu, M., and

Angcheng He, Z. (2022). Motion planning frame-

work for autonomous vehicle with surrounding vehi-

cle motion prediction in highway scenarios. In 2022

6th CAA International Conference on Vehicular Con-

trol and Intelligence (CVCI), pages 1–6. IEEE.

Wong, C., Yang, E., Yan, X.-T., and Gu, D. (2017). An

overview of robotics and autonomous systems for

harsh environments. In 2017 23rd International Con-

ference on Automation and Computing (ICAC), pages

1–6. IEEE.

Zuo, Z., Yang, X., Li, Z., Wang, Y., Han, Q., Wang, L.,

and Luo, X. (2020). MPC-based cooperative control

strategy of path planning and trajectory tracking for

intelligent vehicles. IEEE Transactions on Intelligent

Vehicles, 6(3):513–522.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

236