On Switching Selection Methods to Increase Parsimony Pressure

Allan de Lima

1 a

, Samuel Carvalho

2 b

, Douglas Mota Dias

1 c

, Joseph P. Sullivan

2 d

and Conor Ryan

1 e

University of Limerick, Limerick, Ireland

Technological University of the Shannon: Midlands Midwest, Limerick, Ireland

Keywords:

Lexicase, Tournament, Bloat.

Abstract:

We proposed a novel and simple selection system that alternates between tournament and Lexicase selection to

tackle the bloat issue. In this way, we used Lexi

, an implementation of Lexicase with lexicographic parsimony

pressure, adopting the number of nodes in our solutions as size measurement. In addition, we increased the

parsimony pressure by adding a penalty, also based on the number of nodes, to the aggregated ﬁtness score.

We analysed different scenarios, including some without extra parameters, in ﬁve benchmark problems: 2-bit

Multiplier, 5-bit Parity, Car Evaluation, LED and Heart Disease. We succeeded in all of them in at least one

scenario, reducing the size signiﬁcantly while maintaining ﬁtness. Beyond error and size, we also included

results for the average number of ﬁtness cases used in each generation.

1 INTRODUCTION

Bloat is a well-known and unwanted side-effect

in evolutionary algorithms used to evolve variable-

length solutions, such as Genetic Programming

(GP) (Koza, 1992) or Grammatical Evolution

(GE) (Ryan et al., 1998). This effect consists of

a sharp growth of these solutions, not accompanied

by an analogous improvement in their respective ﬁt-

ness score (Poli et al., 2008). The immediate effect

of this issue is an increase in the computational cost

since the evaluation of bigger solutions is more time-

consuming. In addition, interpretability is hampered,

and also more complex solutions are more likely to be

overﬁtted.

The most common method to prevent bloat is to

restrict the maximum size of the solutions by deﬁn-

ing an extra parameter. This is usually the maximum

depth of the individuals generated. However, this pa-

rameter could be difﬁcult to set up, especially when

we have no clue about the size of a good solution, and

also it could constrain the search space making difﬁ-

cult the task of ﬁnding a satisfactory solution.

https://orcid.org/0000-0002-1040-1321

https://orcid.org/0000-0003-3088-4823

https://orcid.org/0000-0002-1783-6352

https://orcid.org/0000-0003-0010-3715

https://orcid.org/0000-0002-7002-5815

Other well-known methods for bloat control in-

clude parsimony pressure, the explicit punishment of

larger solutions in the selection process. The most

basic form is parametric parsimony pressure, where

the ﬁtness of a solution changes proportionally ac-

cording to its size. This proportion is usually linear,

and (Soule and Foster, 1998) presented a comprehen-

sive analysis of when this sort of parsimony pressure

can lead to successful or unsuccessful populations.

This approach adds a new parameter, the changing

factor of the ﬁtness, which can also be difﬁcult to

set up since it depends on the problem. Another op-

tion, with no extra parameters, is lexicographic parsi-

mony pressure (Luke and Panait, 2002), which prefers

smaller individuals only when the ﬁtness scores are

equal. A recently introduced variant of Lexicase,

Lexi

(de Lima et al., 2022b), applies lexicographic

parsimony pressure to Lexicase selection (Spector,

2012).

Lexi

can ﬁnd solutions as good as Lexicase selec-

tion while further reducing their size. However, we

suppose that by changing during the evolution from

that method to one which can apply parametric parsi-

mony pressure, we can reduce the size of the solutions

even more while maintaining their quality. We pro-

pose to alternate between Lexi

and tournament selec-

tion with penalised ﬁtness during the evolution. In the

period with the former, we aim to ﬁnd good solutions,

which although the lexicographic parsimony pressure

de Lima, A., Carvalho, S., Dias, D., Sullivan, J. and Ryan, C.

On Switching Selection Methods to Increase Parsimony Pressure.

DOI: 10.5220/0012188900003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 96-107

ISBN: 978-989-758-674-3; ISSN: 2184-3236

of Lexi

helps to control the bloat, the solutions are

usually bigger relative to those produced with a para-

metric method. In the periods with the latter, we in-

crease the parsimony pressure and, therefore, obtain

smaller solutions. We tried alternating using prede-

ﬁned durations for each period and also an automatic

criterion.

We addressed the 5-bit Parity and the 2-bit Multi-

plier problems. In addition, we addressed some clas-

siﬁcation problems used in recent works with Lexi-

case selection (de Lima et al., 2022b; Aenugu and

Spector, 2019): the Car Evaluation and the LED prob-

lems. We also addressed Heart Disease, a multitype

classiﬁcation problem from the UCI repository (Dua

and Graff, 2017). We used GE to evolve our solutions

due to its ﬂexibility, which facilitates the task of ad-

dressing problems with multiple outputs, but it is rea-

sonable to assume any evolutionary algorithm could

enjoy the beneﬁts of our system.

2 BACKGROUND

GE (Ryan et al., 1998; O’Neill and Ryan, 2001; Ryan

et al., 2018) is an evolutionary algorithm used to build

programs for an arbitrary language. A GE individual

is represented by a variable-length sequence of inte-

ger numbers named codons, which is mapped into a

more understandable representation following a pre-

deﬁned grammar. This mapped representation is the

actual program, which can be evaluated, and receives

a score according to its performance in a pre-deﬁned

ﬁtness function. The grammar assures the programs

are always syntactically correct and also designs the

search space for new programs.

In the evolutionary process, parents are selected

based on their ﬁtness. Then, genetic operators, such

as crossover and mutation are performed in these par-

ents to generate offspring for the following genera-

tion. Some selection methods, for example, tourna-

ment, consider the ﬁtness of an individual as a whole,

which we deﬁne as aggregated ﬁtness. A different

approach is employed by Lexicase selection (Spec-

tor, 2012), which considers the ﬁtness of each train-

ing case separately, according to the performance of

an individual in that respective training sample.

In its original proposal, the Lexicase selection pro-

cess places the whole entire population of programs in

a pool of candidates. Then, the ﬁtness of each training

case is checked in random order, one after the other,

each time eliminating from the pool those individu-

als that did not present the best ﬁtness value for the

current training case being checked. This method has

been used in many different scenarios (Helmuth et al.,

1. Initialise:

(a) Place all individuals with unique error vec-

tors in a pool of candidates

i. When individuals with the same error vec-

tor are found, place the one with the best

value regarding a pre-deﬁned tie-breaking

criterion

ii. If the tie still persists, place a random indi-

vidual within the remaining ones

(b) List all training cases in random order in

cases

2. Loop:

(a) Replace candidates with the individuals

currently in candidates, which presented

the best ﬁtness for the ﬁrst training case in

cases

(b) If a single individual remains in

candidates, return this individual

and re-run the Loop

Listing 1: Algorithm for selecting one individual with

Lexi

2016a; Aenugu and Spector, 2019; La Cava et al.,

2016), and its success is usually attributed to its ability

to maintain higher levels of diversity for individuals

than when using methods based on aggregated ﬁtness

values while still pressuring enough for the exploita-

tion of good solutions (Helmuth et al., 2015; Helmuth

et al., 2016b).

Lexi

(de Lima et al., 2022b) applied lexico-

graphic parsimony pressure to Lexicase selection,

achieving at least similar performance while reducing

the size of the solutions. Listing 1 shows the algo-

rithm for selecting a parent with Lexi

, and the key

difference between this and the original algorithm for

Lexicase selection is item 1(a)i. The listing also in-

cludes a preﬁltering step, which consists of includ-

ing in the pool of candidates only the individuals with

unique error vectors. This preﬁltering is an optional

step for any implementation of Lexicase selection but

is crucial regarding time-consuming since it avoids

useless loops when ﬁltering the pool of individuals

while not changing the results at all (Helmuth et al.,

2022; Helmuth et al., 2020).

3 PROPOSED METHOD

We propose a simple switching during the evolution

between existing selection methods to increase par-

On Switching Selection Methods to Increase Parsimony Pressure

simony pressure and decrease bloat. The motivation

is that Lexicase selection is a crucial method to im-

prove the quality of the results, but since it does not

use an aggregated value for ﬁtness, we need to apply

a simpler method, such as tournament, to implement

the more aggressive parametric parsimony pressure.

We used Lexi

instead of the original proposal

of Lexicase selection because Lexi

comes with lex-

icographic parsimony pressure, which already con-

tributes to control bloat. In this work, we break the

ties in ﬁtness with the number of nodes of the individ-

uals, but other size criteria could be considered.

To implement parametric parsimony pressure, we

increase the error score in the aggregated ﬁtness by

the number of nodes divided by 1,000,000. We use

this value for all problems, but the expected effect on

them is different. Firstly, by dividing by such a high

factor, we can assume that the penalty value will al-

ways be a low amount. In small datasets, such as,

for example, the 5-bit Parity problem, where we have

only 32 testcases, the impact of each hit in the ﬁt-

ness score is much more relevant than in big datasets.

Then, in these small datasets, we expect that the

penalty will mostly work as lexicographic parsimony

pressure.

Consider as an example two solutions for the 5-

bit Parity problem, where the ﬁrst one correctly pre-

dicts 28 testcases, and the second one 29. When using

penalised tournament, the selection of that second in-

dividual against the ﬁrst one is extremely unlikely to

happen since the difference in the number of nodes

should be in the hundreds of thousands. On the other

hand, in a problem with thousands of testcases, the

minimum value related to the difference in the num-

ber of nodes necessary to impact the selection of an

individual against one with less correctly predicted

testcases is much more likely to happen. However,

for these problems, the impact on ﬁtness, and conse-

quently in the quality of the respective individual, of

a single correctly predicted sample is much smaller.

We assessed this method in several different sce-

narios, as follows, where all periods with tournament

have the ﬁtness score penalised as stated in the previ-

ous paragraph, and all those with Lexi

break the tie

with the number of nodes.

• switch 1: We start with tournament, and then

we switch to Lexi

after 10 generations. After

the same amount of generations, we switch back

to tournament, and keep switching within these

methods every 10 generations;

• switch 2: This scenario is essentially the same as

the previous one, except that we start with Lexi

instead of tournament;

• switch 3: This scenario is almost the same as the

switch 1, but we switch every 5 generations;

• switch 4: Again, this scenario is similar to the pre-

vious ones, but we switch every generation;

• switch 5: In this scenario, we start with tourna-

ment, and switch to Lexi

, but the period for tour-

nament is one generation, while for Lexi

is 10

generations;

• switch 6: This scenario presents an automatic ap-

proach for switching. We start with tournament,

and after one generation without improving the

ﬁtness of the best individual, we switch to Lexi

Again, after one generation with no improvement,

we switch back to tournament, and keep switching

with this criteria;

• switch 7: This scenario is essentially the same as

the previous one, except that we start with Lexi

instead of tournament.

4 EXPERIMENTAL SETUP

We ran our experiments in Python 3.10.8 and

DEAP 1.3. The GE implementation used was

GRAPE (de Lima et al., 2022a), a library built on top

of the DEAP framework (De Rainville et al., 2012).

Each run was seeded with random.seed(n), where n

is an integer number in the interval [1, 30], referring

to each of the 30 runs. The whole code, as well as the

grammars used, are available in our GitHub reposi-

tory (anonymous).

In this work, we addressed two Boolean problems:

the 5-bit Parity and the 2-bit Multiplier. Moreover,

we addressed three classiﬁcation problems: the Car

Evaluation, the LED, and the Heart Disease problems.

The 5-bit Parity is a single output Boolean prob-

lem with 32 training cases, while the 2-bit Multiplier

is a multiple output problem with 16 training cases,

each with four outputs. The implementation of the

latter is motivated by (White et al., 2013), which rec-

ommends addressing Boolean problems with multiple

outputs, such as, for example, multipliers, since this

sort of problem is still not over-used as benchmark-

ing, especially because multiple output problems are

not natively addressed by GP.

The Car Evaluation problem is a four-class unbal-

anced dataset comprising six categorical features and

1727 testcases. We encoded these features into 21 bi-

nary ones using one-hot encoding. The LED prob-

lem is a ten-class dataset with seven binary features,

where each one has a probability of 10% of being in

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

error. Following this probability, we could generate

as many testcases as we want, but we used its original

approach with 500 testcases (Breiman, 1984).

Finally, the Heart Disease problem is a ﬁve-

class dataset, commonly used for binary classiﬁca-

tion (Gupta et al., 2020; Murphy et al., 2021), when

four classes, all related to the presence of heart dis-

ease, are grouped into one, while the remaining (and

predominant) class, related to the absence of heart dis-

ease, is kept unchanged. This dataset has 297 test-

cases with ﬁve continuous features and nine categor-

ical features, which we encoded into 20 binary ones

using one-hot encoding, summing up 25 features to

be used.

For the 5-bit Parity, LED and Heart Disease prob-

lems, the ﬁtness for each training case is 1 when the

output was correctly predicted and 0 otherwise. For

the 2-bit Multiplier problem, the ﬁtness is the ratio

of bits correctly predicted for each sample, and since

there are 4 bits, this ratio can assume the values 0,

0.25, 0.5, 0.75 and 1. We follow this approach to in-

troduce more ﬁtness diversity for the population and,

therefore to guide the evolution in a more resource-

ful way (Helmuth and Spector, 2013). We adopt the

same idea for the Car Evaluation problem, where we

use two bits to represent four classes, and the ﬁtness

for each training case can assume the values 0, 0.5 and

1 according to the number of bits correctly predicted.

For all problems, the aggregated ﬁtness is the average

of the scores for the training cases. This score is used

for tournament selection, while the individual ﬁtness

for each training case is used for Lexicase selection.

However, the results regarding ﬁtness reported in the

next section are the mean classiﬁcation error since,

in the end, we want to check how many testcases a

model can predict correctly, despite using other mea-

surements in the evolution.

Table 1 shows the parameters used in the exper-

iments. The population size is 1,000 for the 5-bit

Parity problem and 500 for the remaining problems.

The results reported in the next section are averaged

over 30 runs. All samples are used as training cases

for the Boolean problems since the target is to evolve

solutions that address all cases correctly. On the

other hand, the target for the remaining problems is

to evolve generalised solutions, and therefore the test

score is assessed. For these problems, we split the

datasets into 75% for training and 25% for testing.

Moreover, we make a different split for each run.

Listing 2 shows the grammars we used. The

Boolean operations are made using only universal

gates in every problem. For the 2-bit Multiplier prob-

lem, we deﬁne the multibit output with the variables

from out[3] to out[0], and then the mapping pro-

Table 1: Experimental parameters.

Parameter type Parameter value

Number of runs 30

Number of generations 200

Population size 500/1,000

Maximum depth 35

Elitism size One individual

Mutation method Codon-based integer

ﬂip (Fenton et al., 2017)

Mutation probability 0.01

Crossover method Variable one-point

(Fenton et al., 2017)

Crossover probability 0.8

Initialisation method Sensible (Ryan and

Azad, 2003)

Maximum wraps 0

Codon size 255

Tournament size 6

Lexi

criterion Number of nodes

cess generates expressions for each of them using the

production rule <e>. We also deﬁne a multibit out-

put for the Car Evaluation problem since we represent

four classes with two bits, and evolve the expressions

in the same way as the 2-bit Multiplier approach. For

the LED problem, we also included the IF function.

This function executes the IF-THEN-ELSE operation,

which is used to execute operations that return each

of the ten different outputs, deﬁned in the produc-

tion rule <o>. Finally, for the Heart Disease problem,

we also included arithmetic operations since this is a

multitype dataset. Since each individual must present

a Boolean result, these arithmetic operations should

be converted into Boolean. It is made by using the

conditional operations in the production rule <cond>,

whose results can be used as inputs in the Boolean

operations with Boolean features.

Our baseline is the scenario Lexi

, which we com-

pare to all scenarios from switch 1 to switch 7. We hy-

pothesize that we will ﬁnd similar ﬁtness, while sig-

niﬁcantly reducing the size of the solutions.

We also report results for the following scenar-

ios, but they usually presented worse results than our

baseline.

• tourn: We use tournament every generation, and

the ﬁtness score is not penalised;

• tourn/pars: We use tournament every generation,

and the ﬁtness score is penalised as stated in the

scenarios from switch 1 to switch 7;

• Lexicase: We use the original Lexicase selection

every generation.

On Switching Selection Methods to Increase Parsimony Pressure

<e> ::= and(<e>,<e>) | or(<e>,<e>)

| nand(<e>,<e>) | nor(<e>,<e>)

| x[0] | x[1] | x[2] | x[3] | x[4]

(a) 5-Bit Parity.

<multi-output> ::= out[3] = <e>;

out[2] = <e>;

out[1] = <e>;

out[0] = <e>

<op> ::= and(<e>,<e>) | or(<e>,<e>) | not(<e>)

<x> ::= x[0] | x[1] | x[2] | x[3]

(b) 2-Bit Multiplier.

<multi-output> ::= out[1] = <e>;

out[0] = <e>

<e> ::= and(<e>,<e>) | or(<e>,<e>) | not(<e>)

| <x>

<x> ::= x[0] | x[1] | x[2] | x[3] | x[4] | x[5]

| x[6] | x[7] | x[8] | x[9] | x[10]

| x[11]| x[12] | x[13] | x[14] | x[15]

| x[16] | x[17] | x[18] | x[19] | x[20]

<op> ::= and(<e>,<e>) | or(<e>,<e>)

| not(<e>) | if(<e>,<o>,<e>)

<x> ::= x[0] | x[1] | x[2] | x[3] | x[4]

| x[5] | x[6]

<o> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

(d) LED.

<e> ::= <cond> | and_(<e>,<e>) | or_(<e>,<e>)

| not_(<e>) | <bool_feat>

<cond> ::= less_than_or_equal(<op>,<op>)

| greater_than_or_equal(<op>, <op>)

<op> ::= add(<op>,<op>) | sub(<op>,<op>)

| mul(<op>,<op>) | pdiv(<op>,<op>)

| <nonbool_feat>

<bool_feat> ::= x[1] | x[4] | x[6] | x[8]

| x[9] | x[10] | x[11] | x[12]

| x[13] | x[14] | x[15] | x[16]

| x[17] | x[18] | x[19] | x[20]

| x[21] | x[22] | x[23] | x[24]

<nonbool_feat> ::= <x> | <c>

<x> ::= x[0] | x[2] | x[3] | x[5] | x[7]

<c> ::= -0.1 | -0.2 | -0.3 | -0.4 | -0.5

| -0.6 | -0.7 | -0.8 | -0.9 | -1 | 0.1

| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7

| 0.8 | 0.9 | 1

(e) Heart Disease.

Listing 2: Grammars.

100

150

200

0.1

0.2

Average best ﬁtness

tourn

tourn/pars

Lexicase

Lexi

switch 1 switch 2

switch 3 switch 4

switch 5 switch 6

switch 7

2-bit Multiplier

100

150

200

0.2

0.4

Generations

Average best ﬁtness

5-bit Parity

Figure 1: Average ﬁtness of the best individual across gen-

erations.

5 RESULTS AND DISCUSSION

Figure 1 shows the training ﬁtness throughout gener-

ations for Boolean problems, while Table 2 shows the

number of successful runs for each scenario. A run

is considered successful if it ﬁnds at least one solu-

tion that predicts all training cases correctly. As ex-

pected, the scenarios using only tournament selection

presented the worst performance.

5.1 Boolean Problems

We extensively discuss the results of the 2-bit Mul-

tiplier problem, but similar observations apply to the

5-bit Parity problem. Scenario tourn succeeded in a

small number of runs, while scenario tourn/pars did

not succeed in any, which we expect is a consequence

of parsimony pressure hampering the evolution. As

highlighted in the previous section, for a problem with

a small dataset, the penalty works as lexicographic

parsimony pressure, meaning that the smallest indi-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

100

Table 2: Number of successful runs in the 2-bit Multiplier

and 5-bit Parity problems.

Successful runs (out of 30)

2-bit Multiplier 5-bit Parity

tourn 3 0

tourn/pars 0 0

Lexicase 27 12

Lexi

29 21

Switch 1 27 9

Switch 2 29 9

Switch 3 29 10

Switch 4 30 7

Switch 5 28 13

Switch 6 30 8

Switch 7 29 8

vidual is selected only when the number of hits is the

same as the best one in the respective tournament.

Even so, this parsimony pressure, when used in ag-

gregated ﬁtness, can push the population too hard to-

wards smaller individuals hampering the evolution, as

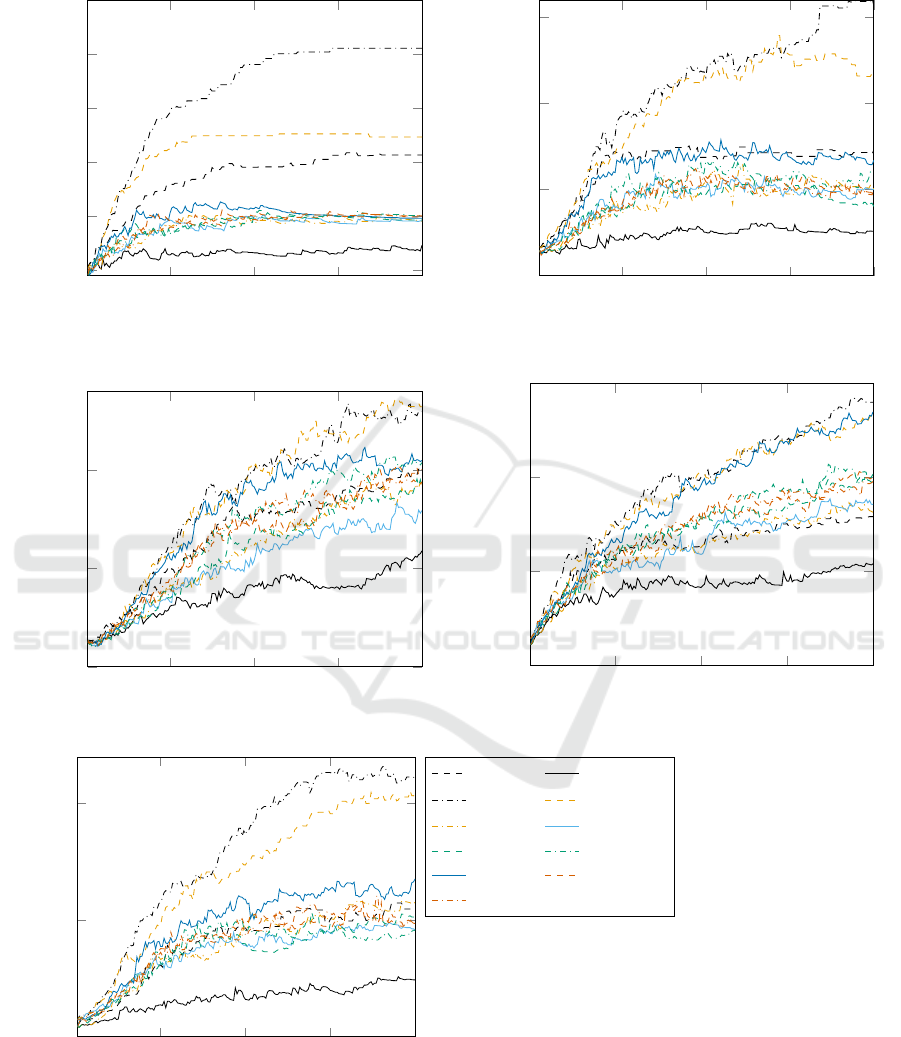
we can see in Figure 2, where the size of individuals

in scenario tourn/pars for the 2-bit Multiplier problem

is much smaller than in any other scenario.

In scenario Lexi

, where we also have lexico-

graphic parsimony pressure, the evolution was not

hampered. This is because Lexicase selection can

identify better (and oftentimes bigger) solutions, and

then when using Lexi

, the impact in the size of those

individuals is much less. For example, for the 2-

bit Multiplier problem, in Figure 1, in early gener-

ations, when the scenarios using Lexicase selection

still present a sharp decrease in error, the scenarios

using only tournament start to converge. When ex-

amining Figure 2 in this same stage of the evolution,

the size of the individuals in the scenarios using only

tournament starts to converge, while those scenarios

using Lexicase selection still present a sharp increase

in size.

Despite all scenarios using Lexicase selection pre-

senting very similar performance in Figure 1 for the

2-bit Multiplier problem, we can highlight the signiﬁ-

cant difference in size in Figure 2. Scenario Lexicase,

which used no parsimony pressure method, presented

the largest solutions, converging to an averaged num-

ber of nodes above 100. Scenario Lexi

was able to

signiﬁcantly reduce the size of the solutions, converg-

ing to a value around 65, but this is still too big when

compared to the gold solutions found with the switch-

ing approaches.

For the 2-bit Multiplier problem, where the inputs

are A1A0 and B1B0, and the output is Y3Y2Y1Y0, an

example of a set of expressions that address each bit

of the output correctly using only the operators AND,

OR and NOT is as follows.

Y3 = and(and(A1, A0), and(B1, B0));

Y2 = and(and(A1, B1), or(not(A0), not(B0)));

Y1 = or(or(and(and(A0, B1), not(A1)),

and(and(A0, B1), not(B0))),

or(and(and(A1, B0), not(A0)),

and(and(A1, B0), not(B1))));

Y0 = and(A0, B0)

The expressions were manually simpliﬁed using

the Karnaugh map, and contain a total of 46 nodes,

where each node is an operator or a bit from an input.

Scenarios from switch 1 to switch 7 were not only able

to ﬁnd solutions of this size, but converged to even

smaller values. For example, a solution found in one

run of scenario switch 1 is as follows and contains just

34 nodes.

Y3 = and(and(A1, B1), and(B0, A0));

Y2 = and(not(and(B0, A0)), and(B1, A1));

Y1 = and(not(and(and(B0, A0), and(B1, A1))),

or(and(A0, B1), and(B0, A1)));

Y0 = and(B0, A0)

In the end, scenario tourn/pars converged to the

smallest individuals so far, but we can ignore that

since their performance was very poor.

For the 5-bit Parity problem, in Figure 1, we can

see the best results were found in scenario Lexi

, fol-

lowed by scenario Lexicase, but the performance in

scenarios from switch 1 to switch 7 were very close,

while greatly reducing the size in Figure 2.

5.2 Classiﬁcation Problems

Figure 3 shows the mean classiﬁcation error in the test

set for classiﬁcation problems, and for all of them, the

baseline Lexi

presented the best results or similar val-

ues to the best one. Scenario switch 5 presented the

most similar results to the baseline for the problems

Car Evaluation and LED. However, this scenario was

not able to reduce the size signiﬁcantly for these prob-

lems, as we can see in Figure 2. Alternatively, other

scenarios, which presented similar ﬁtness, were also

able to reduce the size signiﬁcantly, notably scenarios

switch 1 and 7 for the Car Evaluation, and scenar-

ios switch 4 and 7 for the LED problem. Meanwhile,

for the Heart Disease problem, no differences were

clearly observed regarding ﬁtness, and all scenarios

signiﬁcantly reduced the number of nodes.

5.3 Average Number of Training Cases

Used

Figure 4 shows an extra analysis in this work regard-

ing the average number of cases used in the selection

On Switching Selection Methods to Increase Parsimony Pressure

101

100

150

200

100

120

Generations

Average nodes of the best ind

2-bit Multiplier

100

150

200

100

200

300

Generations

Average nodes of the best ind

5-bit Parity

100

150

200

100

Generations

Average nodes of the best ind

Car Evaluation

100

150

200

Generations

Average nodes of the best ind

LED

100

150

200

100

Generations

Average nodes of the best ind

tourn

tourn/pars

Lexicase

Lexi

switch 1 switch 2

switch 3 switch 4

switch 5 switch 6

switch 7

Heart Disease

Figure 2: Average number of nodes of the best individual across generations.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

102

Figure 3: Mean classiﬁcation error in the test set for classi-

ﬁcation problems. The scenarios are 0: tourn; 1: tourn/pars;

2: Lexicase; 3: Lexi

; 4: Switch 1; 5: Switch 2; 6: Switch

3; 7: Switch 4; 8: Switch 5; 9: Switch 6; 10: Switch 7.

process with Lexicase and Lexi

. The ﬁrst observa-

tion to highlight is that the convergence value is usu-

ally a small ratio to the number of training cases. For

the 2-bit Multiplier and 5-bit Parity problems, this is

around 70% of the training cases. For Heart Disease,

the number of training cases used converges to around

20% of the cases on average. For the LED and Car

Evaluation problems, the values are around 6% and

3.5%, respectively. The high diversity provided by

using Lexicase contributes to ﬁltering the pool faster,

and then the worst scenario, where all training cases

are used the ﬁlter the pool to select one individual, is

unlikely to happen (Helmuth et al., 2022).

Another observation is that, as expected, Lexicase

and Lexi

use a similar number of cases throughout

the evolution since there is no major difference in

their algorithms. For the 2-bit Multiplier problem, the

number of cases increases sharply for an early conver-

gence, while for the 5-bit Parity problem, that number

increases more smoothly. An explanation for this is

evident in Figure 1, where the ﬁtness throughout gen-

erations decreases faster for the 2-bit Multiplier prob-

lem. Going deeper into the ﬁtness analyses, we ob-

served that only a single training case appears really

difﬁcult to be solved for the 2-bit Multiplier problem.

This training case refers to 11 × 11, and it was the

last one to be solved in every run. Furthermore, all

the remaining training cases are solved in early gener-

ations, while that one takes longer to be solved. This

does not happen for the 5-bit Parity problem, where

we did not observe any training case being especially

more difﬁcult to be solved than the other ones.

We have a different curve for the LED problem,

which starts with a sharp increase, and then decreases

until converging. We assume that this happens due

to the structure of the generated individuals. The so-

lutions do not necessarily need to use IF clauses to

predict Classes 0 and 1 correctly, but they do need to

predict all eight remaining classes. In the ﬁrst gener-

ations, it might be difﬁcult for evolution to determine

that only predicting classes 0 and 1 correctly is not

good enough for achieving a good ﬁtness score.

6 STATISTICAL ANALYSIS

Given the different scenarios analysed in this work

and the multitude of comparisons presented on the

Results and Discussion section, a statistical analysis

was performed to investigate the signiﬁcance of these

results. The two metrics covered in this analysis were

the ﬁtness scores and individual sizes (given by the

number of nodes) throughout the multiple runs, for

each different scenario. Initially, the resulting metrics

were submitted to the Shapiro-Wilk test for normal-

ity with a p-value threshold of 0.05, where the end re-

sults for both ﬁtness and individual size were found to

be predominantly non-Gaussian for the Boolean prob-

lems, while predominantly Gaussian for the classiﬁ-

cation problems.

The various switching strategies were then com-

pared against the baseline, Lexi

, using the Student’s

T-test for the parametric cases and the Two-sided

Wilcoxon Test for the non-parametric ones. Also,

given the multiple comparisons performed, a Bon-

On Switching Selection Methods to Increase Parsimony Pressure

103

100

150

200

Generations

Average cases

2-bit Multiplier

100

150

200

Generations

Average cases

5-bit Parity

100

150

200

Generations

Average cases

Car Evaluation

100

150

200

Generations

Average cases

LED

100

150

200

Generations

Average cases

Lexicase

Lexi

Heart Disease

Figure 4: Average number of cases used in the selection process across generations.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

104

Table 3: Boolean Problems: mean and standard deviation of metrics for each approach and p-values between Lexi

selection

and each switching strategy.

Scenario

2-bit Multiplier 5-bit Parity

Fitness Size Fitness Size

Average Std Dev p-value Average Std Dev p-value Average Std Dev p-value Average Std Dev p-value

Lexiˆ2 5.21E-04 2.80E-03 - 69.37 21.61 - 1.98E-02 3.65E-02 - 235.13 122.31 -

Switch 1 1.56E-03 4.69E-03 5.24E-01 38.17 6.54 2.01E-06 5.63E-02 5.56E-02 7.02E-03 100.93 58.37 2.36E-05

Switch 2 5.21E-04 2.80E-03 1.00E+00 38.23 5.57 1.71E-06 8.02E-02 6.59E-02 2.12E-03 100.07 50.75 5.21E-06

Switch 3 5.21E-04 2.80E-03 1.00E+00 38.60 5.98 1.73E-06 5.63E-02 5.00E-02 8.93E-03 80.43 30.33 3.18E-06

Switch 4 0.00E+00 0.00E+00 7.28E-01 40.17 4.69 2.46E-06 5.10E-02 3.99E-02 6.95E-03 119.33 76.71 8.94E-04

Switch 5 1.04E-03 3.90E-03 7.51E-01 39.23 5.35 2.87E-06 4.69E-02 4.82E-02 1.78E-02 134.03 71.65 5.28E-04

Switch 6 0.00E+00 0.00E+00 7.28E-01 39.73 3.31 1.73E-06 5.00E-02 4.16E-02 1.62E-02 98.33 42.75 5.74E-06

Switch 7 5.21E-04 2.80E-03 1.00E+00 40.10 5.97 2.01E-06 6.88E-02 5.73E-02 3.61E-03 100.00 51.32 9.32E-06

Table 4: Classiﬁcation Problems: “Car Evaluation” and “Heart Disease”: mean and standard deviation of metrics for each

approach and p-values between Lexi

selection and each switching strategy.

Scenario

Car Evaluation Heart Disease

Fitness Size Fitness Size

Average Std Dev p-value Average Std Dev p-value Average Std Dev p-value Average Std Dev p-value

Lexiˆ2 1.34E-01 2.71E-02 - 132.40 54.47 - 1.92E-01 3.34E-02 - 102.83 45.32 -

Switch 1 1.55E-01 3.31E-02 1.09E-02 92.40 40.19 2.35E-03 1.89E-01 4.15E-02 7.38E-01 57.70 39.76 1.64E-04

Switch 2 1.58E-01 2.81E-02 1.69E-03 79.57 34.39 4.44E-05 1.89E-01 3.63E-02 7.18E-01 45.73 20.46 6.77E-08

Switch 3 1.58E-01 2.89E-02 2.15E-03 92.00 44.09 2.95E-03 1.96E-01 2.84E-02 5.88E-01 50.93 34.99 8.62E-06

Switch 4 1.44E-01 2.67E-02 1.80E-01 103.93 42.80 3.09E-02 2.01E-01 3.44E-02 2.84E-01 45.43 16.34 2.78E-08

Switch 5 1.33E-01 2.32E-02 8.65E-01 105.03 41.72 3.59E-02 1.98E-01 4.41E-02 5.42E-01 67.63 32.30 1.20E-03

Switch 6 1.51E-01 2.97E-02 2.45E-02 100.60 48.53 2.23E-02 1.96E-01 4.31E-02 6.62E-01 50.37 26.83 1.48E-06

Switch 7 1.48E-01 3.83E-02 1.24E-01 94.13 34.41 2.24E-03 1.87E-01 4.55E-02 6.48E-01 48.43 20.16 1.94E-07

Table 5: Classiﬁcation Problem: “LED”: mean and standard deviation of metrics for each approach and p-values between

Lexi

selection and each switching strategy.

Scenario

LED

Fitness Size

Average Std Dev p-value Average Std Dev p-value

Lexiˆ2 3.60E-01 6.24E-02 - 53.47 22.14 -

Switch 1 4.55E-01 8.18E-02 6.35E-06 32.60 16.89 1.62E-04

Switch 2 4.49E-01 7.32E-02 5.89E-06 34.30 14.67 2.65E-04

Switch 3 4.09E-01 7.50E-02 8.84E-03 40.73 15.46 1.38E-02

Switch 4 4.08E-01 7.26E-02 1.00E-02 37.93 11.34 1.37E-03

Switch 5 3.61E-01 6.11E-02 9.78E-01 54.00 17.06 9.19E-01

Switch 6 4.12E-01 5.68E-02 1.57E-03 39.37 11.81 3.70E-03

Switch 7 3.97E-01 7.81E-02 5.30E-02 39.17 16.15 6.74E-03

ferroni correction with a factor of 7 was used for a

fairer analysis. Therefore, a stricter p-value threshold

of 0.007143 was adopted for the rejection of the null

hypothesis (no difference between the metrics on the

analysed scenario and the baseline). Tables 3, 4 and 5

present the results from these analyses, where better

performance is highlighted in bold, and statistically

signiﬁcant differences are underlined for a clearer in-

terpretation. It can be seen that the use of switching

selection methods was capable of reducing the aver-

age size of the individuals in every scenario and with

statistical signiﬁcance in most of them. Regarding

ﬁtness scores, there is no clear trend for statistical

signiﬁcance, but for every problem, there is at least

one scenario where ﬁtness was not signiﬁcantly af-

fected, while the size of individuals was signiﬁcantly

reduced.

7 CONCLUSIONS

In this work, we proposed a simple selection method

that alternates between tournament and Lexicase se-

lection, aiming to reduce the bloat issue. We achieved

this by applying lexicographic parsimony pressure to

Lexicase, and also a penalty to the aggregated ﬁt-

ness score. In both cases, the parsimony pressure was

given by the number of nodes in the solutions.

We examined several different scenarios and

utilised ﬁve benchmark problems. On all problems,

at least one scenario was able to reduce the size sig-

niﬁcantly, while maintaining similar performance to

Lexi

. Our most successful scenario, Scenario switch

7, where we switch automatically starting with Lexi

was successful on all problems. Moreover, we did not

need to set up an extra parameter, since in this sce-

On Switching Selection Methods to Increase Parsimony Pressure

105

nario, we used an automatic criterion for switching.

In future work, we plan to try different combina-

tions for scenarios using nodes, depth, critical path,

etc. In addition, we intend to use different mea-

surements for size, based on complexity, for exam-

ple deﬁning different weights according to the type of

node.

REFERENCES

Aenugu, S. and Spector, L. (2019). Lexicase selection in

Learning Classiﬁer Systems. In Proceedings of the

Genetic and Evolutionary Computation Conference,

pages 356–364. arXiv:1907.04736 [cs].

Breiman, L. (1984). Classiﬁcation and regression trees.

CRC press, Boca Raton, Florida.

de Lima, A., Carvalho, S., Dias, D. M., Naredo, E., Sulli-

van, J. P., and Ryan, C. (2022a). Grape: Grammatical

algorithms in python for evolution. Signals, 3(3):642–

663.

de Lima, A., Carvalho, S., Dias, D. M., Naredo, E., Sul-

livan, J. P., and Ryan, C. (2022b). Lexi2: Lexicase

selection with lexicographic parsimony pressure. In

Proceedings of the Genetic and Evolutionary Compu-

tation Conference, GECCO ’22, page 929–937, New

York, NY, USA. Association for Computing Machin-

ery.

De Rainville, F.-M., Fortin, F.-A., Gardner, M.-A., Parizeau,

M., and Gagne, C. (2012). DEAP: a python frame-

work for evolutionary algorithms. In Wagner, S. and

Affenzeller, M., editors, GECCO 2012 Evolutionary

Computation Software Systems (EvoSoft), pages 85–

92, Philadelphia, Pennsylvania, USA. ACM.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Fenton, M., McDermott, J., Fagan, D., Forstenlechner, S.,

Hemberg, E., and O’Neill, M. (2017). PonyGE2:

Grammatical evolution in python. In Proceedings

of the Genetic and Evolutionary Computation Con-

ference Companion, GECCO ’17, pages 1194–1201,

Berlin, Germany. ACM.

Gupta, A., Kumar, L., Jain, R., and Nagrath, P. (2020).

Heart Disease Prediction Using Classiﬁcation (Naive

Bayes), pages 561–573. Springer Singapore.

Helmuth, T., Lengler, J., and La Cava, W. (2022). Popula-

tion Diversity Leads to Short Running Times of Lex-

icase Selection. In Rudolph, G., Kononova, A. V.,

Aguirre, H., Kerschke, P., Ochoa, G., and Tu

sar, T.,

editors, Parallel Problem Solving from Nature – PPSN

XVII, Lecture Notes in Computer Science, pages 485–

498, Cham. Springer International Publishing.

Helmuth, T., Mcphee, N., and Spector, L. (2016a). Lexicase

Selection for Program Synthesis: A Diversity Anal-

ysis. In Genetic Programming Theory and Practice

XIII, pages 151–167. Springer.

Helmuth, T., McPhee, N. F., and Spector, L. (2016b). Ef-

fects of Lexicase and Tournament Selection on Diver-

sity Recovery and Maintenance. In Proceedings of the

2016 on Genetic and Evolutionary Computation Con-

ference Companion, GECCO ’16 Companion, pages

983–990, New York, NY, USA. Association for Com-

puting Machinery.

Helmuth, T., Pantridge, E., and Spector, L. (2020).

On the importance of specialists for lexicase selec-

tion. Genetic Programming and Evolvable Machines,

21(3):349–373.

Helmuth, T. and Spector, L. (2013). Evolving a digi-

tal multiplier with the pushgp genetic programming

system. In Proceedings of the 15th annual confer-

ence companion on Genetic and evolutionary com-

putation, GECCO ’13 Companion, pages 1627–1634,

New York, NY, USA. Association for Computing Ma-

chinery.

Helmuth, T., Spector, L., and Matheson, J. (2015). Solv-

ing Uncompromising Problems With Lexicase Selec-

tion. IEEE Transactions on Evolutionary Computa-

tion, 19(5):630–643. Conference Name: IEEE Trans-

actions on Evolutionary Computation.

Koza, J. R. (1992). Genetic Programming - On the Pro-

gramming of Computers by Means of Natural Selec-

tion. Complex adaptive systems. MIT Press.

La Cava, W., Spector, L., and Danai, K. (2016). Epsilon-

Lexicase Selection for Regression. In Proceedings

of the Genetic and Evolutionary Computation Confer-

ence 2016, GECCO ’16, pages 741–748, New York,

NY, USA. Association for Computing Machinery.

Luke, S. and Panait, L. (2002). Lexicographic parsi-

mony pressure. In Proceedings of the 4th Annual

Conference on Genetic and Evolutionary Computa-

tion, GECCO’02, pages 829–836, San Francisco, CA,

USA. Morgan Kaufmann Publishers Inc.

Murphy, A., Murphy, G., Amaral, J., MotaDias, D., Naredo,

E., and Ryan, C. (2021). Towards Incorporating Hu-

man Knowledge in Fuzzy Pattern Tree Evolution. In

Hu, T., Lourenc¸o, N., and Medvet, E., editors, Ge-

netic Programming, Lecture Notes in Computer Sci-

ence, pages 66–81, Cham. Springer International Pub-

lishing.

O’Neill, M. and Ryan, C. (2001). Grammatical evolu-

tion. IEEE Transactions on Evolutionary Computa-

tion, 5(4):349–358. Conference Name: IEEE Trans-

actions on Evolutionary Computation.

Poli, R., Langdon, W. B., and McPhee, N. F. (2008).

A ﬁeld guide to genetic programming. Pub-

lished via http://lulu.com and freely available at

http://www.gp-field-guide.org.uk, UK. (With

contributions by J. R. Koza).

Ryan, C. and Azad, R. M. A. (2003). Sensible initialisa-

tion in grammatical evolution. In Barry, A. M., editor,

GECCO 2003: Proceedings of the Bird of a Feather

Workshops, Genetic and Evolutionary Computation

Conference, pages 142–145, Chigaco. AAAI.

Ryan, C., Collins, J., and O’Neill, M. (1998). Grammati-

cal evolution: Evolving programs for an arbitrary lan-

guage. In Lecture Notes in Computer Science, pages

83–96, Berlin, Heidelberg. Springer.

Ryan, C., O’Neill, M., and Collins, J. J., editors (2018).

Handbook of Grammatical Evolution. Springer.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

106

Soule, T. and Foster, J. A. (1998). Effects of Code Growth

and Parsimony Pressure on Populations in Genetic

Programming. Evolutionary Computation, 6(4):293–

309.

Spector, L. (2012). Assessment of problem modality by

differential performance of lexicase selection in ge-

netic programming: a preliminary report. In Pro-

ceedings of the 14th annual conference companion on

Genetic and evolutionary computation, GECCO ’12,

pages 401–408, New York, NY, USA. Association for

Computing Machinery.

White, D. R., McDermott, J., Castelli, M., Manzoni, L.,

Goldman, B. W., Kronberger, G., Ja

skowski, W.,

O’Reilly, U.-M., and Luke, S. (2013). Better GP

benchmarks: community survey results and propos-

als. Genetic Programming and Evolvable Machines,

14(1):3–29.

On Switching Selection Methods to Increase Parsimony Pressure

107