Enhancing Explainable Matrix Factorization with Tags for Multi-Style

Explanations

Olurotimi Seton

1 a

, Pegah Sagheb Haghighi

, Mohammed Alshammari

2 b

and Olfa Nasraoui

Knowledge Discovery and Web Mining Lab, Computer Science and Engineering Dept, University of Louisville, U.S.A.

Department of Computer Science, Faculty of Computing and Information Technology,

Northern Border University Arar, Saudi Arabia

Keywords:

Matrix Factorization, Model Explainability, User Generated Tags.

Abstract:

Black-box AI models tend to be more accurate but less transparent and scrutable than white-box models.

This poses a limitation for recommender systems that rely on black-box models, such as Matrix Factorization

(MF). Explainable Matrix Factorization (EMF) models are “explainable” extensions of Matrix Factorization,

a state of the art technique widely used due to its ﬂexibility in learning from sparse data and accuracy. EMF

can incorporate explanations derived, by design, from user or item neighborhood graphs, among others, into

the model training process, thereby making their recommendations explainable. So far, an EMF model can

learn a model that produces only one explanation style, and this in turn limits the number of recommendations

with computable explanation scores. In this paper, we propose a framework for EMFs with multiple styles

of explanation, based on ratings and tags, by incorporating EMF algorithms that use scores derived from tag-

centric graphs to connect rating neighborhood-based EMF techniques to tag-based explanations. We used

precalculated explainability scores that have been previously validated in user studies that evaluated user

satisfaction with each style individually. Our evaluation experiments show that our proposed methods provide

accurate recommendations while providing multiple explanation styles, without sacriﬁcing the accuracy of the

recommendations.

1 INTRODUCTION

Recommender systems (RSs) have become an in-

creasingly crucial part of the online experience; they

help users ﬁlter information and choices down from a

space with an almost endless combination of choices.

The backbone of modern RS are Machine Learning

(ML) algorithms that have become increasingly accu-

rate at predicting users’ preferences from data. As

they became more and more accurate, ML models

have also become increasingly difﬁcult to explain.

ML models whose path to making a decision can-

not be explained are called black-box models. These

models can be highly accurate but cannot explain their

predictions. However, a variety of users could beneﬁt

from explanations. These users range from shoppers

on e-commerce sites to regulatory agencies whose job

includes ensuring compliance with rules and regula-

tions (Arrieta et al., 2020). This gap between the pre-

diction power and the explainability of ML models

https://orcid.org/0009-0007-4298-4756

https://orcid.org/0000-0002-5859-7490

has motivated the rise of Explainable Artiﬁcial In-

telligence (XAI), which can be deﬁned as “a model

that produces details or reasons that make its func-

tioning or reasoning clear or easy to understand for

its target audience” (Arrieta et al., 2020). We use

this deﬁnition in this paper, with the target users be-

ing the end users who need explanations to understand

how their choices were selected for them by a recom-

mendation engine. This paper focuses on the scope

of RS ML models that are based on Matrix Factor-

ization (MF) (Koren et al., 2009), a family of state-

of-the-art black box models. The input to MF is a

two-dimensional rating matrix (R) that holds the rat-

ings given by a set of users U to a set of items I,

such that r

∈ R

|U|×|I|

, where r

is the rating given

by a user u to item i with a value within a speciﬁed

range. The rating matrix is generally very sparse be-

cause users cannot rate every item in the typically

very large set of items I. Although RSs have tradi-

tionally been evaluated based on the accuracy of their

predictions, accuracy is no longer considered sufﬁ-

cient as the only metric of evaluation (McNee et al.,

Seton, O., Haghighi, P., Alshammari, M. and Nasraoui, O.

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations.

DOI: 10.5220/0012189900003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 75-85

ISBN: 978-989-758-671-2; ISSN: 2184-3228

2006), since explanations are becoming increasingly

essential to help users understand why certain items

were recommended to them. In fact, explanations can

help humans gain more insight into a model’s recom-

mendations to allow them to make more informed de-

cisions and could even help identify biases and detect

errors in the model (Herlocker et al., 2000). There are

a variety of explainable AI methods for RS. Post hoc

methods generate post hoc explanations (Lundberg

and Lee, 2017)(Ribeiro et al., 2016) that are com-

puted after the ML model has already been learned,

typically by learning a surrogate white-box model,

and then trying to explain the predictions of the orig-

inal black box ML model using the importance of the

characteristic (Ribeiro et al., 2016) or contributions

(Lundberg and Lee, 2017) to an output prediction

score, or using a set of rules that are learned post ML

model construction (Peake and Wang, 2018). In con-

trast to post hoc methods, Explainable Matrix Factor-

ization (EMF) methods, such as (Abdollahi and Nas-

raoui, 2016)(Abdollahi and Nasraoui, 2017)(Alsham-

mari et al., 2018)(Alshammari et al., 2019), aim to

explain the black-box model from within (i.e., while

learning the model itself), by optimizing a modiﬁed

loss function that is augmented by an explainabil-

ity penalty term) rather than after building a post

hoc model. This paper extends the EMF approach

(Abdollahi and Nasraoui, 2016) by integrating user-

generated tags into the model learning process and

using these tags as an additional source of explana-

tions, thus expanding the explanations from a single

style (neighborhood style) to multiple styles (includ-

ing neighborhood style and tag style). Though this

paper focuses on tags as the second source of expla-

nations, our approach can be extended to use other

sources of explanation, therefore providing users with

multiple forms of explanation.

2 RESEARCH QUESTIONS AND

HYPOTHESES

Our research focuses on the effect of adding tag-based

information to EMF models on predictive accuracy

and explainability. Previous work by (Abdollahi and

Nasraoui, 2016)(Abdollahi, 2017) showed that EMF

methods outperform MF (Koren et al., 2009) in terms

of accuracy and had the added beneﬁt of making rec-

ommendations that were considered explainable. (Al-

shammari et al., 2018) also showed that adding se-

mantic information to EMF models did not negatively

affect the accuracy of the model and also provided

semantic-based explanations. (Vig et al., 2009) intro-

duced tag-based deﬁnitions to quantify the relation-

ship between items and tags (tag relevance) and the

relationship between users and tags (tag preference).

This work combines both approaches with the aim of

improving the accuracy and explainability of recom-

mendations. Our proposed approach also has the ben-

eﬁt of providing multiple explanations for some user-

item pairs in instances where a strong tag association

exists among the three entities (user, item, tag).

Therefore, in this research, we explore the follow-

ing question:

Does adding tag-based information affect the perfor-

mance of Explainable Matrix Factorization (EMF)

(Abdollahi and Nasraoui, 2016) algorithms in terms

of accuracy and explainability?

In order to answer this question, we attempt to an-

swer the following research questions.

RQ1: Does integrating tag-based information im-

prove the accuracy of recommendations generated by

EMF (Abdollahi and Nasraoui, 2016)?

RQ2: Does integrating tag-based information im-

prove the explainability of recommendations gener-

ated by EMF (Abdollahi and Nasraoui, 2016)?

3 RELATED WORK

The early work of Herlocker et al. (Herlocker

et al., 2000)(Herlocker et al., 2004) proposed the

Neighborhood-rating Style Explanation (NSE) for

Collaborative Filtering (CF) recommender systems, a

visual post hoc explanation based on displaying the

aggregate ratings on the recommended item, that have

been provided by users with similar preferences to

the target user. Later, Bilgic and Mooney (Bilgic

and Mooney, 2005) proposed the Inﬂuence Style Ex-

planation (ISE), a visual post hoc explanation based

on how the target user has rated items that are sim-

ilar (in terms of their rating patterns) to the recom-

mended item. The work on explainability for rec-

ommender systems has continued with (McNee et al.,

2006) making the case for the need for recommender

systems that can go beyond being accurate at predict-

ing users’ preferences while stating the need for ex-

planations for recommendations. Later work by Nava

Tintarev and Judith Mashtoff (Tintarev and Masthoff,

2007)(Tintarev and Masthoff, 2015) dichotomized the

different aims of explanations in recommender sys-

tems, including transparency (knowing how the sys-

tem works), scrutability (ability to tell that the system

is wrong), trustworthiness (increasing the conﬁdence

in the system), effectiveness (helping users make

good decisions), persuasiveness (convincing users to

try or purchase an item), efﬁciency (aiding the user

in their decision making) and satisfaction (increasing

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

the ease of use of the system). Later work by Vig. et

al. expanded the NSE and ISE explanation styles (Vig

et al., 2009) by proposing using Tagsplanations, a vi-

sual post hoc explanation based on tags. They deﬁned

tag preference as the quantiﬁcation of the relationship

between users and tags and deﬁned tag relevance as

the relationship between items and tags. These rela-

tionships were quantiﬁed on the basis of the correla-

tion between tag usage with the item and tag prefer-

ences of the users. However, NSE, ISE and tagsplana-

tions are post hoc explanations, meaning that they are

generated after the fact and therefore, by deﬁnition,

cannot give true insight into how the recommendation

may have been generated. More recently, post hoc

methods started being criticized (Rudin, 2019) (Ghas-

semi et al., 2021) for inherently falling short of the

ability to provide genuine transparency, hence limit-

ing the users’ ability to trust and scrutinize a predic-

tive system.

Within the context of model-based Collaborative

Filtering (CF) recommender systems, Matrix Factor-

ization (MF) is a group of techniques that learn to rep-

resent users and items using vectors of features which

are learned from the ratings given by users to items

with which they have interacted in such a way that a

strong association between latent factors of the user

and the item will result in a recommendation (Ricci

et al., 2012). (Koren et al., 2009) showed that MF-

based recommender system models have high predic-

tive accuracy and are robust enough to handle even

extremely sparse data. An extension of MF, Joint

MF (JMF) (Ge et al., 2012), improved MF’s accu-

racy by merging data sources including user ratings,

group behavior, demographic information, and item

features, e.g., genres and actor details in the movie

domain. As a result, JMF improved MF’s accuracy

by enriching the training data and increased user trust

by providing these user and item features as post hoc

explanations.

In contrast to post hoc approaches, Explain-

able Matrix Factorization (EMF) methods (Abdollahi

and Nasraoui, 2016)(Abdollahi and Nasraoui, 2017)

added an explainability constraint to the objective

function of MF, as shown in Eq. 1, thus directly af-

fecting the optimization of the ML model, while it is

being learned and not after the fact. The objective of

EMF methods encodes a preference (via adding to the

MF loss a soft constraint explainability penalty term)

to bring users and items that are considered explain-

able to these users closer to each other in the latent

space, and to do so during the model learning pro-

cess. This explainability penalty term is the last term

shown in (1). This proximity tends to promote the

predicted ratings for items that are explainable to a

user, and this in turn pushes them higher in the top

n-recommendation list. EMF attempts to solve for

the latent factor vectors of the user and item p

and

, respectively, by solving the following optimization

problem.

= argmin J =

∑

u,i∈R

− p

)

(kp

+ kq

) +

− q

u,i

(1)

EMF uses an explainability graph to model the rela-

tionship between users and the items considered ex-

plainable to these users, with the explainability score

estimating the strength of the explanation of a partic-

ular explainable item to a given user. (Abdollahi and

Nasraoui, 2016)(Abdollahi and Nasraoui, 2017) pro-

posed two ways to estimate the explainability scores

between users and items: the user-based explain-

ability and the item-based explainability scores, W

which are shown in equations 2 and 3, respectively.

These explainability scores have the added beneﬁt of

making the model more transparent and can be used to

generate visual or text-based explanations to explain

recommendations to users. User-based explainability

is computed using

user−based

(

(u)|

i f

(u)|

> θ

0, otherwise.

(2)

(u) is the set of neighbors of user u who rated item i

and N

(u) represents the list of k nearest neighbors of

user u. θ

is a an explainability threshold for consider-

ing item i as an explainable item to user u. Item-based

explainability is computed using

item−based

(

(i)|

i f

(i)|

> θ

0, otherwise

(3)

(i) is the set of similar items to item i previously

rated by user u and N

(i) represents the list of k near-

est neighbors of i. θ

is a threshold for consider-

ing item i as an explainable item to user u. In later

work, (Alshammari et al., 2018) proposed building a

new explainability graph using semantic Knowledge

Graphs and showed that the corresponding semantic

aware EMF provided explanations using easily rec-

ognizable attributes of items such as actors and direc-

tors in the movie domain, and authors and publishers

in the book domain.

4 PROPOSED METHODS

User-generated tags are a rich source of informa-

tion that can be used to improve the recommenda-

tion model. Inspired by (Vig et al., 2009), we pro-

pose novel tag-based explainability graphs that can be

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations

used in tag-based explanation style methods. Finally,

we propose tag-boosted multi-style methods that in-

tegrate tagging information into explainable matrix

factorization methods to provide multiple explanation

styles for recommended items. Note that the precal-

culated explainability scores utilized by EMF meth-

ods have been validated in previous work (Abdollahi

and Nasraoui, 2016) that conducted user studies and

found a higher subjective perception of transparency

among user-item pairs for items that have higher ob-

jective user-based and item-based neighborhood style

explanation scores. Our proposed tag-based explain-

ability scores are justiﬁed by previous user studies of

(Vig et al., 2009) that validated the user’s satisfaction

with preference-based and relevance-based tag-based

explanations which are the main inspiration and basis

for our tag-based explainability scores. Unlike previ-

ous works that compute the tag relevance and tag pref-

erence post hoc, our tag-based explainable method-

ology calculates these tag-based explainability scores

directly from the data, before the model is learned,

and then uses them as part of the soft constraint or

regularization mechanism, to guide the model learn-

ing. By learning models that are directly dependent

on explanations, our proposed methods are by deﬁni-

tion more transparent than post hoc methods that learn

surrogate models after the fact, which can be dissoci-

ated from the explanations.

4.1 Tag-Based Explainability Graphs

Tag-based explainability graphs are matrices that hold

the explainability score for each user for every item

available for the recommendation task. The explain-

ability score is calculated by extracting the user’s

propensity for certain tags (tag preference) and the

relevance of tags to an item (tag relevance). We used

three types of relationships to construct three explain-

ability graphs. The ﬁrst graph is a user-based graph

that describes the relationship between all users and

all available tags. The second graph is an item-based

graph that describes the relationship between all items

and all available graphs. The third graph is a combi-

nation of the aforementioned two graphs, and it repre-

sents the relationship between users and items based

on each user’s preference towards each item’s relevant

tags. The combination is obtained by using the prod-

uct of the user- and item-based graphs. In this work,

we estimate the tag relevance and tag preference using

the deﬁnitions given by (Vig et al., 2009). Therefore,

three different tag-aware graphs are constructed using

user-generated tags, as follows, where T is the set of

all tags, U is the set of users, I is the set of items.

1. Tag preference graph (T

pre f

) is a bipartite graph,

pre f

= (U, T , E

pre f

2. Tag relevance graph (T

rel

) is a bipartite graph,

rel

= (I, T , E

rel

3. User-item tag-based explainability graph (T

) is

a bipartite graph, T

= (U, I, E

The edge sets E

pre f

rel

and E

are weighted edges

with weights calculated as described in Sec. 4.1.1,

4.1.2, 4.1.3 respectively. Figure 1 depicts the rela-

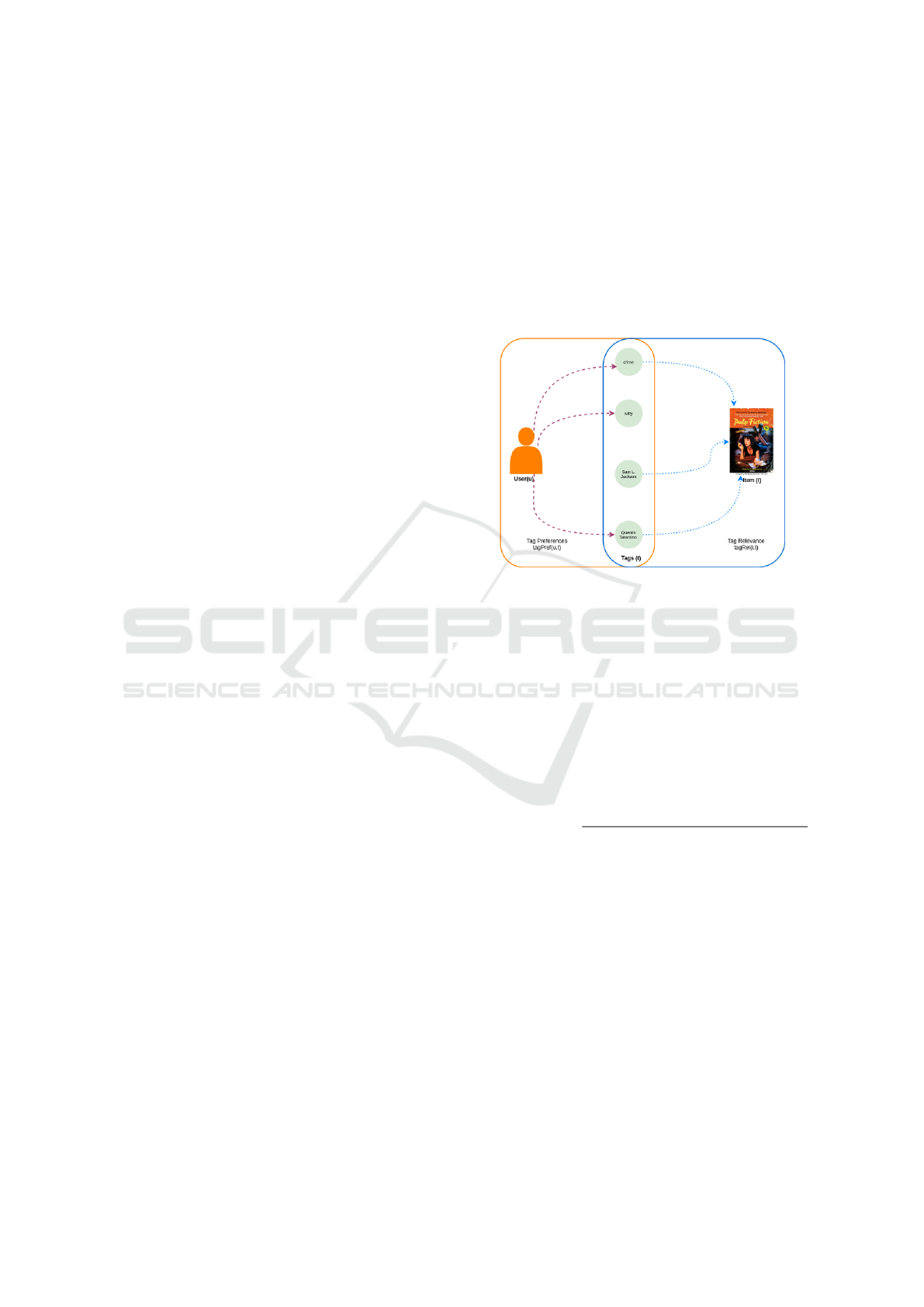
tionship between these three graphs.

Figure 1: Tag-based Explanability Graph for explaining the

recommended movie, Pulp Fiction, to a sample user, ob-

tained by combining the tag preferences (orange) and the

tag relevance (blue).

4.1.1 Tag Preference Graph (User-Tag

Relationship)

A user’s tag preference is computed using a weighted

average of the user’s rating of items tagged with that

tag. Tag preference is denoted as tagPref and the tag

preference of user u for tag t is calculated as follows:

tagPre f (u,t) =



∑

i∈I

×tagShare(t,i)



+ ¯r

× k



∑

i∈I

tagShare(t,i)



+ k

(4)

Where tagShare(t, i) is deﬁned as “the number of

times the tag t has been applied to the item i, divided

by the number of times any tag has been applied to i“

(Vig et al., 2009). I

is the set of items rated by user u,

¯r

is the average rating of user u across all items, r

is user u’s rating for item i. Finally, k is a smoothing

constant that accounts for users who have not rated

any item or rated too few items tagged with tag t.

4.1.2 Tag Relevance Graph (Item-Tag

Relationship)

A tag’s relevance to an item, denoted as tagRel, can be

calculated using the correlation between users’ pref-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

erences for the tag and their preference for the rec-

ommended item. The correlation function used is the

Pearson correlation, and tagRel is given by

tagRel(t, i) =

(

ϕ(X,Y ) i f t has been applied to i

0 otherwise

(5)

where X is the set of ratings for item i by all users

in U

(set of users who have applied tag t to item i).

This set of ratings is then adjusted by each user’s av-

erage rating to accommodate personal preferences. Y

is deﬁned as the set of inferred preference values for

the tag t for all users in U

, adjusted by the average

rating of each user. Therefore, X = {r

: u ∈ U

} and

Y = {tagPre f (u,t) : u ∈ U

4.1.3 User-Item Tag-Based Explainability Graph

The tag-based explainability score for a user

u for item i (Figure 1) is calculated as the

dot product of the edge weights of tagPref

graph, E

pre f

and the tagRel graph, E

rel

, where

pre f

= (tagPre f (u, 1), ...,tagPre f (u,|T |) and

rel

= (tagRel(i, 1), ...,tagRel(i, |T |).

u,i

(

pre f

rel

i f

pre f

rel

> θ

0 otherwise

(6)

Where θ

is a tag-based explainability threshold.

4.2 Tag-Assisted Explainable Matrix

Factorization (TA-EMF)

The neighborhood technique, used by (Abdollahi and

Nasraoui, 2016)(Abdollahi, 2017)(Alshammari et al.,

2018)(Alshammari, 2019), is built on the premise that

items liked by other users who are similar to the target

user will likely also be liked by the target user. The

semantic technique is based on estimating a user’s in-

terest in an item by estimating the user’s interest in

features of the item such as the actors and directors in

a movie or author and publisher of a book. The expla-

nation scores in these methods can be used to build

an explainability matrix for each pair of user-items.

This matrix is then used in the process of learning the

latent space vectors for both the users and the items.

In this section, we propose a method that is driven by

the User-Item tag-based (T

) explainability matrix

presented in Sec. 4.1.3.

The objective function minimized by our method

uses tag-based explainability scores instead of

neighborhood-based or semantic-based explainability

scores, and the optimization problem is given by

= argmin J

TA−EMF

∑

u,i∈R

− p

)

(kp

+ kq

) +

− q

u,i

(7)

The ﬁrst two terms of Eq. 7 come from MF (Koren

et al., 2009) and represent the error after reconstruc-

tion using the latent vectors and a regularization term

to avoid overﬁtting, respectively. β is a regularization

coefﬁcient that controls the smoothness of the regu-

larization term. The third term adds the contribution

of the explainability scores to the matrix factorization

model as in (Abdollahi and Nasraoui, 2017)(Alsham-

mari et al., 2018). γ is a smoothing coefﬁcient that

controls the contribution of the explainability term to

the learned parameters p

and q

We use Stochastic Gradient Descent to update p

and q iteratively until the convergence of J

TA−EMF

The gradient of J

TA−EMF

with respect to p

∂J

TA−EMF

∂p

= −2 (r

u,i

− p

+βp

−γ(p

−q

u,i

(8)

The gradient of J

TA−EMF

with respect to q

∂J

TA−EMF

∂q

= −2(r

u,i

− p

+βq

+γ(p

−q

u,i

(9)

Using the gradients, we derive the following up-

date rules that use learning parameters α.

(t+1)

← p

(t)

+ α(2(r

u,i

− p

(t)

)

(t)

− βp

(t)

−γ(p

(t)

− q

(t)

u,i

)

(t+1)

← q

(t)

+ α(2(r

u,i

− p

(t)

)

(t)

− βq

(t)

+γ(p

(t)

− q

(t)

u,i

)

(10)

Although rooted in MF (Koren et al., 2009) and EMF

(Abdollahi and Nasraoui, 2017), our method differs

from MF (Koren et al., 2009) because the explana-

tions are generated simultaneously with recommenda-

tions. Our method differs from other EMF methods

(Abdollahi and Nasraoui, 2017)(Alshammari et al.,

2018) because we use tag-based information to cal-

culate the explainability scores.

4.3 Tag-Boosted Multi-Style

Explainable Matrix Factorization

In this section, we propose models that minimize

novel objective functions that are inspired by MF (Ko-

ren et al., 2009) boosted MF, (Nguyen and Zhu, 2013)

and EMF (Abdollahi and Nasraoui, 2017).

We propose two new methods that incorporate

EMF and tag-boosted methods in one approach (Se-

ton et al., 2021). The intuition here is that since tags

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations

provide useful information, incorporating the user’s

preference of a tag or the tag relevance of a tag for

an item may lead to improved performance. This ap-

proach will allow recommendations to be presented

to users using two widely accepted and previously

validated explanation styles (Vig et al., 2009)(Abdol-

lahi and Nasraoui, 2016) (Abdollahi, 2017) (Abdol-

lahi and Nasraoui, 2017) (see Tables 4 and 5 for ex-

amples).

4.3.1 Preferred Tag-Boosted Multi-Style EMF

(PrefTag)

The PrefTag approach integrates only the tags that a

user has shown some preference for into the matrix

factorization model. This method is user-centered and

only considers the contribution of the tags, previously

used by a user, for an item. Our proposed method uses

both the ISE-based EMF explainability graph (Ab-

dollahi and Nasraoui, 2017) and the user preference

square matrix (S

pre f

) in the process of building latent

space vectors for users and items. The optimization

problem is given by

= argmin J

Pre f Tag

∑

u,i∈R



− p

)

(kp

+ kq

) +

− q

∑

v∈S

pre f



pre f

u,v

− p





(11)

where

pre f

(u,v) = cosineSim(u, v) =

pre f

The ﬁrst three terms in Eq. 11 are similar to the

Explainable Matrix Factorization (EMF) objective

function (Abdollahi and Nasraoui, 2017). r

repre-

sents the rating given to item i by the user u. p

and q

represent the low-dimensional latent factor

vectors of users and items, respectively. This ver-

sion of EMF uses the ISE-based explainability graph

item−based

u,i

) to represent the item-based explainabil-

ity scores given by Eq. 3. Our contribution is the

addition of the fourth term to obtain a tag-boosted

approach to integrate the information from the tags.

pre f

is a user × user similarity matrix that holds the

similarity between every pair of users. For a target

user u, we get the subset of users S

pre f

such that

v ∈ S

pre f

and u, v have used the same set of tags for

any item i. p

and p

are the latent factor vectors of

users u and v, respectively. γ is the tag-boosted term

that weights the contribution of the new term. Finally,

pre f

is the vector of preference weights given by user

u to all tags. We use Stochastic Gradient Descent to

optimize the objective function in Eq. 11.

The gradient of J

Pre f Tag

with respect to p

∂J

Pre f Tag

∂p

= −2(r

− p

+ βp

+ λ(p

− q

+γ(S

pre f

u,v

− p

The gradient of J

Pre f Tag

with respect to q

∂J

Pre f Tag

∂q

= −2(r

− p

+ βq

− λ(p

− q

Using the gradients, the formulation of the update

rules is

(t+1)

← p

(t)

+ α



2(r

− p

(t)

(t)T

(t)

− βp

(t)

−

λ(p

(t)

− q

(t)

+ γ(S

pre f

u,v

− p

(t)

(t)T

(t)



(t+1)

← q

(t)

+ α



2(r

− p

(t)

(t)T

(t)

− βq

(t)

+λ(p

(t)

− q

(t)



(12)

4.3.2 Relevant Tag-Boosted Multi-Style EMF

(RelTag)

The RelTag method utilizes the user-based explain-

ability graph for EMF and item-centered tag simi-

larity for the tag-boosted term. However, the tags

we integrate into this model are obtained from the

Tag-Relevance vectors

rel

for item i (deﬁned in Sec.

4.1.3) and the similarity matrix S

rel

that holds the sim-

ilarity between every pair of items. For a target item

i, we ﬁnd the subset of items S

rel

such that j ∈ S

rel

;

and i and j have been tagged with the same tags. The

optimization problem is given by

= argmin J

RelTag

∑

u,i∈R



u,i

− p

)

(kp

+ kq

)

− q

u,i

∑

j∈S

rel



rel

i, j

− q





(13)

where q

and q

are the latent factor vectors of items

i and j, respectively; γ is the tag-boosted term coef-

ﬁcient that weights the contribution of the new term,

and

rel

(i, j) = cosineSim(i, j) =

rel

The gradient of J

RelTag

with respect to p

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

∂J

RelTag

∂p

= −2(r

u,i

− p

+ βp

+ λ(p

− q

u,i

The gradient of J

RelTag

with respect to q

∂J

RelTag

∂q

= −2(r

u,i

− p

+ βq

− λ(p

− q

u,i

+γ(S

rel

i, j

− q

Using the gradients, the formulation of the update

rules will be

(t+1)

← p

(t)

+ α



2(r

u,i

− p

(t)

(t)T

(t)

− βp

(t)

−λ(p

(t)

− q

(t)

u,i



(t+1)

← q

(t)

+ α



2(r

u,i

− p

(t)

(t)T

(t)

− βq

(t)

+λ(p

(t)

− q

(t)

u,i

+ γ(S

rel

i, j

− q

(t)

(t)T

(t)



(14)

5 EXPERIMENTAL EVALUATION

We use the HetRec

MovieLens dataset. The data

consist of 2,113 users, 10,197 movies, 13,222 tags,

and 855,598 ratings. We chose this data set due to

the availability of tag data and due to its size which

made it suitable for a proof of concept. Similarly

to previous work on tag data in the literature, such

as (Vig et al., 2009), we applied some ﬁlters to the

data to reduce the sparsity of the data set and in-

crease the strength of tag-based relationships between

users and movies. We selected users who had rated at

least 50 unique movies and used at least 10 unique

tags. Furthermore, we selected movies that have been

rated by at least 50 unique users and tagged with at

least 10 unique tags. After applying these ﬁlters, the

data consisted of 264 users, 1239 movies, 5293 tags,

and 21,214 ratings. Although these ﬁlters further re-

duced the data set and identiﬁed users and movies

with high tag association, which might not be the case

in real-world applications, we used these experiments

as proof of concept that integrating tag-based expla-

nations and tag-relationships can improve the perfor-

mance of EMF algorithms. Other explanation styles

that are not tag-based could be used with our proposed

methods. Users’ ratings were normalized to [0,1]

using linear scaling. The evaluated models’ hyper-

parameters were tuned to their optimal values using

5-fold cross-validation. The experiments were run 10

times, and the averages are reported. The data was

https://grouplens.org/datasets/hetrec-2011/

divided into training and testing sets, with 90 % al-

located to the training set and 10 % of each user’s

ratings allocated to the testing set. We compared our

methods with three baseline methods which are con-

sidered to be in the same family: basic MF (Koren

et al., 2009), user-based EMF (EMF

) (Abdollahi

and Nasraoui, 2016), and item-based EMF (EMF

)

(Abdollahi and Nasraoui, 2016).

First, we evaluated the predictive accuracy of the

methods and hence the error rate using the Root Mean

Square Error (RMSE) given by

RMSE =

|T |

∑

(u,i∈T )

− ˆr

)

, (15)

where T represents the total number of predictions,

ˆr

is the predicted rating of item i for user u, and r

is the actual rating given by user u to item i.

Table 1: RMSE vs. number of latent factors (K). E

, Pref,

and Rel denote our proposed methods, TA-EMF, PrefTag,

and RelTag, respectively. Bold denotes the best results (sig-

niﬁcant at p-value < .05).

RMSE

K MF E

Pref Rel

5 0.147 0.142 0.146 0.146 0.154 0.152

10 0.134 0.132 0.133 0.133 0.172 0.131

20 0.154 0.141 0.149 0.156 0.165 0.141

50 0.164 0.170 0.168 0.303 0.323 0.163

5.1 Preferred Tag-Boosted Multi-Style

EMF (PrefTag)

We carried out signiﬁcance tests (one-tailed t-test) to

compare the RMSE of our methods with the base-

line methods at K = 50, from 10 experiments whose

means were reported, using 5 relevant common tags

to build the RelTag model. The tests showed that

our method outperformed EMF

and EMF

signif-

icantly with p-value < .05.

We further compute NDCG@N since RMSE only

measures the reconstruction or rating estimation error,

whereas evaluating recommendation quality places

a higher emphasis on the ordering of the recom-

mended items, especially in the top N recommenda-

tions (which is indicated by the symbol @N in the

ranking based metric below). Ranking quality is cap-

tured by the Normalized Discounted Cumulative Gain

(NDCG) (J

arvelin and Kek

ainen, 2017) shown in

Eq. 16.

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations

DCG@N =

∑

i=1

rel

log

i+1

IDCG =

∑

|REL

i=1

rel

−1

log

(i+1)

NDCG@N =

DCG@N

IDCG

(16)

where rel

is the predicted normalized rating of an

item at position i and REL

is the list of relevant

items, ordered by relevance, in the recommended list,

up to position p.

Table 2: NDCG@10 vs. number of latent factors (K). E

Pref, and Rel denote our proposed methods, TA-EMF, Pref-

Tag, and RelTag, respectively. Bold denotes the best results

(signiﬁcant at p-value < .05).

NDCG@10

K MF E

Pref Rel

5 0.857 0.848 0.854 0.855 0.861 0.877

10 0.852 0.860 0.859 0.858 0.847 0.877

20 0.822 0.844 0.852 0.850 0.848 0.848

50 0.847 0.849 0.847 0.849 0.848 0.877

We obtain high values for NDCG@10 in our ex-

periments and this might be attributed to the ﬁlters

used to select users and movies with high tag associ-

ations.

We also carried out signiﬁcance tests to compare

NDCG@10 of the compared methods at K = 50 using

3 common relevant tags to build the RelTag model.

These tests showed that our method signiﬁcantly out-

performed the baseline methods with the p value <

.05.

Since our approach aims to improve the recom-

mendation of explainable items, we also evaluated

all approaches using the explainability metrics, Mean

Explainability Precision (MEP) and Mean Explain-

ability Recall (MER) (Abdollahi and Nasraoui, 2016).

MEP =

|U |

∑

u∈U

|R ∩ E|

|R|

, (17)

MER =

|U |

∑

u∈U

|R ∩ E|

|E|

, (18)

where U represents the set of users, while R is the set

of recommended items, and E denotes the set of ex-

plainable items. When using the user-based explain-

ability graph (W ) for EMF, an item i is considered ex-

plainable to user u, when the pre-computed explain-

ability score W

, shown in Eq.2, is greater than the

explainability threshold θ

. Similarly, item i is con-

sidered explainable to user u for item-based EMF and

tag-assisted EMF if the pre-computed explainability

scores, denoted as E

and T

and shown in Eq.3 and

Eq.6 respectively, are greater than θ

and θ

respec-

tively.

MEP computes the proportion of simultaneously

recommended and explainable items to the total num-

ber of recommended items across all users. Similarly,

MER calculates the proportion of simultaneously rec-

ommended and explainable items to the total number

of explainable items, averaged across all the users.

The ﬁrst graph is the user-based explainability graph

that is based on users with preferences similar (based

on their ratings) to the target user (Abdollahi and Nas-

raoui, 2016)(Abdollahi, 2017) and is deﬁned in Eq.

2. The second graph is the item-based explainabil-

ity graph, which is based on items that are similar (in

terms of how they were rated) to the recommended

item and that have been previously rated by the user.

This graph is deﬁned in Eq. 3. The third graph is

the tag-based explainability graph T

that we con-

structed using Eq. 6.

Figure 2: MEP@10 vs. explainability score threshold (θ

)

for User-based Neighborhood Explainability Graph.

Figures 2 and 5 show the results when compar-

ing all methods using the user-based explainability

graph W . Figures 2 and 5 show that RelTag outper-

forms baseline methods for all values of θ

. This in-

dicates that the method works well when the explain-

ability constraint is low, and also performs well even

when the constraints are increased for items to be con-

sidered explainable. We performed signiﬁcance tests

to compare our methods with the baseline methods,

for both metrics using W , and the tests showed that

RelTag signiﬁcantly outperformed the baseline meth-

ods with p-value < .05. Similarly, Figures 3 and 6

show the results when comparing all methods using

the item-based explainability graph E. Figures 3 and

6 show that PrefTag outperforms baseline methods for

all values of θ

. The signiﬁcance test showed that

PrefTag outperformed the baseline methods signiﬁ-

cantly with p-value < .05.

Figure 4 shows that EMF

performed best when

evaluating MEP@10 using the tag-based explainabil-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

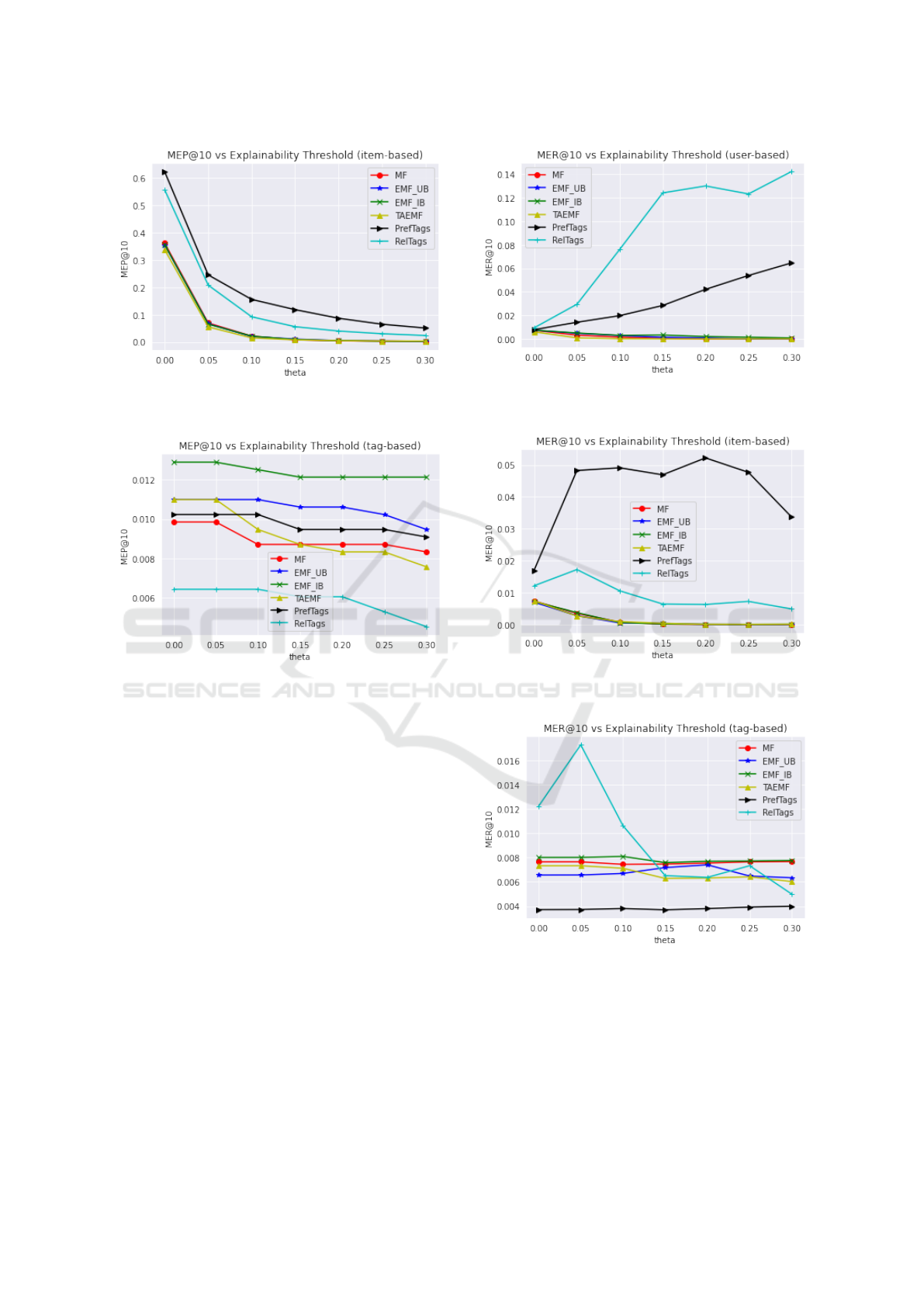
Figure 3: MEP@10 vs. explainability score threshold (θ

)

for Item-based Neighborhood Explainability Graph.

Figure 4: MEP@10 vs. explainability score threshold (θ

)

for Tag-based Explainability Graph.

ity graph, T

; while Figure 7 shows that RelTag

outperformed the baseline methods for lower values

of θ

. This indicates that when the explainability

constraint is loose, using the tag-based explainability

graph, RelTag recommends items that can be consid-

ered explainable using the tags.

We ﬁnally answer the research questions we posed

at the start based on our experimental results.

RQ1: Does integrating tag-based information im-

prove the accuracy of recommendations generated by

EMF (Abdollahi and Nasraoui, 2016)?

Our results in Table 2 and signiﬁcance tests to

compare NDCG@10 at K = 50 using 3 common rele-

vant tags to build the RelTag model, showed that our

method signiﬁcantly outperformed both MF and EMF

(p < .05). Hence the answer to RQ1 is afﬁrmative.

RQ2: Does integrating tag-based information im-

prove the explainability of recommendations gener-

ated by EMF (Abdollahi and Nasraoui, 2016)?

Our results in Figures 2 - 7 and signiﬁcance tests

to compare MEP values showed that RelTag signif-

icantly outperformed both MF as well as EMF for

Figure 5: MER@10 vs. explainability score threshold (θ

)

for User-based Neighborhood Explainability Graph.

Figure 6: MER@10 vs. explainability score threshold (θ

)

for Item-based Neighborhood Explainability Graph.

Figure 7: MER@10 vs. explainability score threshold (θ

)

for Tag-based Explainability Graph.

most of the explainability graph styles used in com-

puting the explainability metrics (p < .05). Hence the

answer to RQ2 is afﬁrmative although it is expected

to vary if a different explainability style is used for the

metrics, as expected.

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations

6 EXAMPLES

Table 3 shows the top-3 rated movies for a sample

user from the data. The results of the proposed Tag-

boosted Multi-style EMF methods, RelTag and Pref-

Tag, are shown in Tables 4 and 5, respectively.

Table 3: Top-3 rated movies for a sample user.

Top-3 rated movies

Clean and Sober

Strangers on a train

Indiana Jones and the Temple of Doom

Table 4: Output of Relevant Tag-boosted Multi-style EMF

for a Sample User.

Top-3 Recom-

mended Movies

Neighbor-rating

Style Explanation

Tag-based Expla-

nation

Rupan Sansei 2 similar users rated

this movie as 5 stars

Forrest Gump 1 similar user rated

this movie as 5 stars

vietnam, oscar (best

picture), classic

The Lion King 3 similar users rated

this movie as 4 stars

Table 5: Output of Preferred Tag-boosted Multi-style EMF

for a Sample User.

Top-3 Recom-

mended Movies

Inﬂuence Style Ex-

planation

Tag-based Expla-

nation

Iris You rated 2 similar

movies as 4 stars

Le Fabuleux Destin

Poulain

You rated 1 similar

movie as 3 stars

Pulp Fiction You rated 3 similar

movies as 4 stars

quentin tarantino,

hit-men, comedy

Tables 4 and 5 show the advantage of using multi-

ple explanation styles. The tag-based explanations are

not available for every recommended item; however,

when present, tag-based explanations provide use-

ful information about the recommended movie. The

ISE and NSE styles provide explanations to the user

about the Collaborative Filtering rationale for why the

movie was recommended; but the tag-based explana-

tion tells the user about the possible content of the rec-

ommended movie. For example, in Table 5, the ISE

explanation tells the user about movies that are simi-

lar to the recommended movie ”Pulp Fiction”, but the

tag-based explanation gives some insight into what

the user might ﬁnd interesting about the movie with

a tag that describes the director, “quentin tarantino”,

another that describes the genre of the movie, “com-

edy”; and ﬁnally, a tag that describes an important

part of the plot of the movie “hitmen”.

7 CONCLUSION

MF is a powerful model-based Collaborative Filter-

ing technique commonly used in recommender sys-

tems due to its accuracy and robustness in handling

extremely sparse data. However, MF is limited by the

opaqueness of the recommendation process, making

it difﬁcult to understand how the recommendations

were generated. Explainable MF (EMF) addressed

this limitation by adding an explainability constraint

to MF, which projects items that are considered to

be explainable to the user, closer to that user’s pro-

jection in the latent feature space. A limitation of

current EMF methods is their inability to use more

than one explanation style to explain recommenda-

tions to users. We addressed this limitation by in-

troducing tag-based explainability graphs that were

used to boost the performance of the EMF meth-

ods while improving both their accuracy and trans-

parency. Our proposed methods leverage tag-based

explainability graphs to build EMF models that are

capable of explaining recommendations using more

than one explanation style. Experimental results show

that our proposed methods outperformed the base-

line approaches in terms of error rate, recommenda-

tion relevance, and explainability metrics, especially

when placing more constraints on items that must be

considered explainable. In the future, we plan to ex-

pand our explanation methods by using other EMF

methods, perform more comprehensive experiments

in other domains, and compare our methods with

other baseline methods. Furthermore, we intend to

conduct a user study to validate the usefulness of the

explanations provided by our methods.

ACKNOWLEDGEMENTS

This work was partially supported by NSF-

EPSCoR–RII Track-1:Kentucky Advanced Man-

ufacturing Partnership for Enhanced Robotics

and Structures (Award IIP#1849213) and by NSF

DRL-2026584.

REFERENCES

Abdollahi, B. (2017). Accurate and justiﬁable: new algo-

rithms for explainable recommendations.

Abdollahi, B. and Nasraoui, O. (2016). Explainable matrix

factorization for collaborative ﬁltering. In Proceed-

ings of the 25th International Conference Companion

on World Wide Web, pages 5–6.

Abdollahi, B. and Nasraoui, O. (2017). Using explainability

for constrained matrix factorization. In Proceedings of

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

the Eleventh ACM Conference on Recommender Sys-

tems, pages 79–83.

Alshammari, M., Nasraoui, O., and Abdollahi, B. (2018).

A semantically aware explainable recommender sys-

tem using asymmetric matrix factorization. In KDIR,

pages 266–271.

Alshammari, M., Nasraoui, O., and Sanders, S. (2019).

Mining semantic knowledge graphs to add explain-

ability to black box recommender systems. IEEE Ac-

cess, 7:110563–110579.

Alshammari, M. S. (2019). An explainable recommender

system based on semantically-aware matrix factoriza-

tion.

Arrieta, A. B., D

ıaz-Rodr

ıguez, N., Del Ser, J., Bennetot,

A., Tabik, S., Barbado, A., Garc

ıa, S., Gil-L

opez, S.,

Molina, D., Benjamins, R., et al. (2020). Explainable

artiﬁcial intelligence (xai): Concepts, taxonomies, op-

portunities and challenges toward responsible ai. In-

formation fusion, 58:82–115.

Bilgic, M. and Mooney, R. J. (2005). Explaining recom-

mendations: Satisfaction vs. promotion. In Beyond

Personalization Workshop, IUI, volume 5, page 153.

Ge, L., Gao, J., Yu, X., Fan, W., and Zhang, A. (2012). Es-

timating local information trustworthiness via multi-

source joint matrix factorization. In 2012 IEEE 12th

International Conference on Data Mining, pages 876–

881. IEEE.

Ghassemi, M., Oakden-Rayner, L., and Beam, A. L. (2021).

The false hope of current approaches to explainable

artiﬁcial intelligence in health care. The Lancet Digi-

tal Health, 3(11):e745–e750.

Herlocker, J. L., Konstan, J. A., and Riedl, J. (2000). Ex-

plaining collaborative ﬁltering recommendations. In

Proceedings of the 2000 ACM conference on Com-

puter supported cooperative work, pages 241–250.

Herlocker, J. L., Konstan, J. A., Terveen, L. G., and Riedl,

J. T. (2004). Evaluating collaborative ﬁltering recom-

mender systems. ACM Transactions on Information

Systems (TOIS), 22(1):5–53.

arvelin, K. and Kek

ainen, J. (2017). Ir evaluation meth-

ods for retrieving highly relevant documents. In ACM

SIGIR Forum, volume 51, pages 243–250. ACM New

York, NY, USA.

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factor-

ization techniques for recommender systems. Com-

puter, 42(8):30–37.

Lundberg, S. M. and Lee, S.-I. (2017). A uniﬁed approach

to interpreting model predictions. In Advances in neu-

ral information processing systems, pages 4765–4774.

McNee, S. M., Riedl, J., and Konstan, J. A. (2006). Being

accurate is not enough: how accuracy metrics have

hurt recommender systems. In CHI’06 extended ab-

stracts on Human factors in computing systems, pages

1097–1101.

Nguyen, J. and Zhu, M. (2013). Content-boosted matrix

factorization techniques for recommender systems.

Statistical Analysis and Data Mining: The ASA Data

Science Journal, 6(4):286–301.

Peake, G. and Wang, J. (2018). Explanation mining: Post

hoc interpretability of latent factor models for rec-

ommendation systems. In Proceedings of the 24th

ACM SIGKDD International Conference on Knowl-

edge Discovery & Data Mining, pages 2060–2069.

Ribeiro, M. T., Singh, S., and Guestrin, C. (2016). Model-

agnostic interpretability of machine learning. arXiv

preprint arXiv:1606.05386.

Ricci, G., de Gemmis, M., and Semeraro, G. (2012). Matrix

and tensor factorization techniques applied to recom-

mender systems: a survey. Matrix, 1(01).

Rudin, C. (2019). Stop explaining black box machine learn-

ing models for high stakes decisions and use inter-

pretable models instead. Nature machine intelligence,

1(5):206–215.

Seton, O., Haghighi, P. S., Alshammari, M., and Nasraoui,

O. (2021). Tag-boosted explainable matrix factoriza-

tion methods for multi-style explanations.

Tintarev, N. and Masthoff, J. (2007). A survey of explana-

tions in recommender systems. In 2007 IEEE 23rd in-

ternational conference on data engineering workshop,

pages 801–810. IEEE.

Tintarev, N. and Masthoff, J. (2015). Explaining recom-

mendations: Design and evaluation. In Recommender

systems handbook, pages 353–382. Springer.

Vig, J., Sen, S., and Riedl, J. (2009). Tagsplanations: ex-

plaining recommendations using tags. In Proceed-

ings of the 14th international conference on Intelligent

user interfaces, pages 47–56.

Enhancing Explainable Matrix Factorization with Tags for Multi-Style Explanations