Joint-Based Robotic Impedance Control Transformations: An

Experimental Study

Carlos Saldarriaga

1 a

, Jos

e J. Pati

1 b

, Carlos G. Helguero

1 c

and Imin Kao

2 d

Facultad de Ingenier

ıa en Mec

anica y Ciencias de la Producci

on, Escuela Superior Polit

ecnica del Litoral, ESPOL,

Campus Gustavo Galindo Km 30.5 V

ıa Perimetral, P.O. Box 09-01-5863, Guayaquil, Ecuador

Department of Mechanical Engineering, Stony Brook University, Stony Brook, NY, U.S.A.

Keywords:

Impedance, Robotics, Control, Damping.

Abstract:

We present an experimental study in this paper to illustrate the effect of the Cartesian damping matrix on mod-

ulating the dynamic response of a robotic manipulator in impedance control. We ﬁrst derive the transformation

of the matrices of impedance control between the Cartesian and joint spaces using differential mathematics.

Through experiments conducted on a redundant Franka Panda robot, it is demonstrated that the coupling term

between damping and stiffness in impedance control derived from theoretical analysis, when transforming

between the Cartesian and joint spaces, is important in stabilizing the dynamic response of the joints. We

apply a methodology to modulate the dynamic response of a robot performing impedance control that allows

us to study and select diagonal and off-diagonal elements of the Cartesian damping matrix according to the

damping ratios and natural frequencies of the system in the modal space. In addition, we explain and show that

an arbitrary selection of damping is counter-productive for robots to perform tasks under impedance control,

and may lead to instability and out-of-range torques at the joints of the robotic manipulator.

1 INTRODUCTION

The main goal of impedance control at the task space

level, and all its variations is to obtain a desired com-

pliant behavior between the robot and its environment

(Hogan, 1985; Khatib, 1987; Villani and De Schut-

ter, 2008). In this type of controller, a mass-spring-

damper relationship between task forces, f, and the

errors of position and velocity of the end effector is

used. There are basically two ways of implement-

ing Cartesian impedance control (without inertia re-

shaping). One is by obtaining the interaction forces

from the errors directly in the Cartesian space and

then transform the forces into joint torques by equa-

tion (4). The other is by joint-based impedance con-

trol, where all the parameters are either given in the

joint space or mapped from the Cartesian into the

joint space, and the joint torques can be obtained di-

rectly in the joint space. A joint-based impedance

control in combination with a closed-form solution

https://orcid.org/0000-0001-9014-681X

https://orcid.org/0000-0002-3740-352X

https://orcid.org/0000-0002-6992-0572

https://orcid.org/0000-0003-1658-9166

of the multidimensional mechanical impedance sys-

tem based on theory of mechanical vibrations (Sal-

darriaga et al., 2022a) allow us to analyze and syn-

thesize the dynamics of the robot in a proper manner.

Recent work on mechanisms using physical variable

mechanical impedance elements (Vanderborght et al.,

2013; Memar and Esfahani, 2018), have encouraged

and given more relevance to the joint space analy-

sis of robotic systems, making them more computa-

tionally efﬁcient (Yu et al., 2019; Laffranchi et al.,

2014). However, the main problem of this joint space

analysis is the correct spatial transformation between

Cartesian and joint spaces.

Although there is plenty of work on handling and

design of non-diagonal stiffness matrices (Caccavale

et al., 1999; Caccavale et al., 1998), and non-diagonal

dominant inertia matrices for robotic impedance con-

trol (Pollayil et al., 2023), to the best of our knowl-

edge, there is no work on off-diagonal elements for

damping matrices.

Our methodology also allows us to select the el-

ements of both stiffness and damping matrices, so

that a desired dynamic behavior of the robot can be

obtained. This tool can also be used to select off-

diagonal values in the damping matrices to further im-

158

Saldarriaga, C., Patiño, J., Helguero, C. and Kao, I.

Joint-Based Robotic Impedance Control Transformations: An Experimental Study.

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 158-165

ISBN: 978-989-758-670-5; ISSN: 2184-2809

prove the damping ratios of the system in the modal

space. The main advantages of our methodology in-

clude: (1) it can be used without losing generality;

and (2) no assumptions of symmetry property of the

involved matrices are made. This method is particu-

larly useful for redundant manipulators.

A spatial transformation of both stiffness and

damping was derived mathematically in (Saldarriaga

et al., 2022b), which showed that damping in the

Cartesian space is actually involved in the compu-

tation of stiffness in the joint space, along with the

term from the conservative congruence transforma-

tion (Chen and Kao, 2000). An experimental study is

proposed in this paper to show how this coupling term

between stiffness and damping in the spatial trans-

formation equation is important and can be beneﬁcial

and stabilizing in Cartesian impedance control tasks.

This paper is structured as follows: all the dy-

namics preliminaries and general control equations

are presented in Section 2. After that, the mapping

equations for stiffness and damping parameters are

derived in Section 3. The dynamic response mod-

ulation methodology is explained in Section 4. The

experimental results are presented in Section 5, with

discussions and conclusion in Sections 6 and 7, re-

spectively.

2 IMPEDANCE CONTROL

The equation of motion of an n-DoF (degree of free-

dom) manipulator is given by

M(q)

q(t) + G(q,

q(t) + v(q) = τ

+ τ

ext

(1)

here the vector q contains the n joint variables, M is

the mass matrix, G is the matrix that contains the gy-

roscopic terms, v is the vector that compensates for

gravity, and τ

ext

is the vector with the external torque

values. To obtain a multi dimensional mass-damper-

spring behavior we choose the motor torques τ

[−K

q(t)−C

q(t)+v(q)+G(q,

q(t)], the system

in equation (1) becomes

M(q)

q(t) + C

q(t) + K

q(t) = τ

ext

(2)

where C

and K

are the damping and stiffness ma-

trices, respectively. The task space impedance control

is performed according to the equation:

(q)

x(t) + C

x(t) + K

x(t) = f (3)

where K

, C

, and M

are the stiffness, damping,

and mass matrices in the Cartesian space, correspond-

ingly, and f stands for the force in the Cartesian space.

A very common implementation of impedance

control is by imposing predeﬁned stiffness and damp-

ing elements in the Cartesian space, then obtaining the

required joint torques based on the errors from posi-

tion and velocity with respect to the desired values,

and applying these torques by the kineto-static rela-

tionship

τ = J

f (4)

added with the compensation of gravity and gyro-

scopic terms, similar as in (Ott, 2008; Kao and Sal-

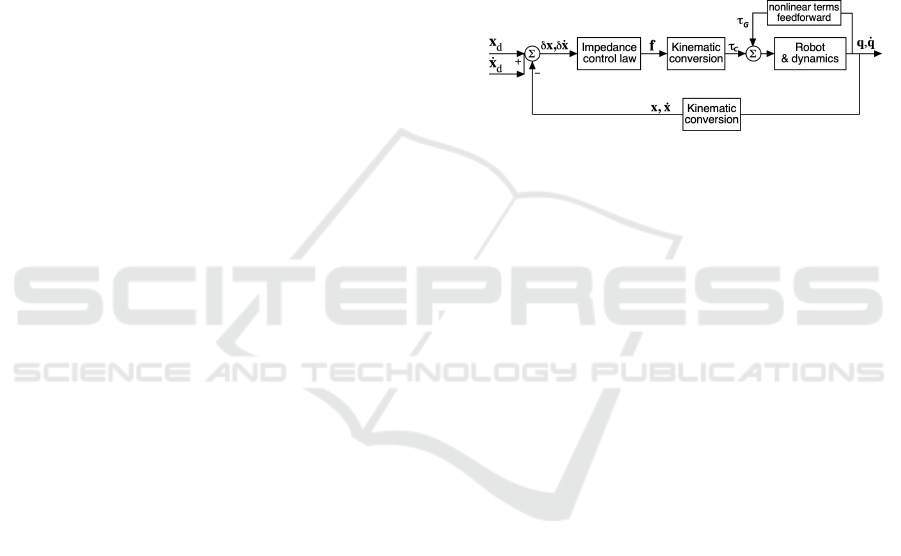
darriaga, 2023) and illustrated in Figure 1, where:

= J

(x −x

) + C

(

x −

)]

τ = τ

+ τ

and τ

is the compensation of gravity and nonlinear

terms.

Figure 1: Block diagram of the Cartesian impedance con-

troller.

The “Impedance control law” block in Figure 1

implements Equation (3) with the Cartesian force as

the output. After the kinematic conversion block, the

torque from impedance control law becomes τ

. The

nonlinear terms of the dynamic equation of motion

are canceled by using a feedforward term τ

, which

is obtained from Equation (1), based on the current

robot conﬁguration.

On the other hand, one can also implement

impedance control based directly on the joint space

(joint-based impedance control). In this case, instead

of obtaining and controlling f in Cartesian space and

then transforming to torques via equation (4), the

desired positions and its derivatives as well as the

impedance parameters are given or computed directly

in the joint space. An analysis and controller based

on the joint space was needed in order to perform

modal analysis of the redundant robot, where stiffness

and damping become singular, and the only way to

deal with this type of systems is by separating out the

zero-potential energy (ZP) and non-zero-potential en-

ergy (NZP) modes of motion, using our methodology.

This analysis allows us to obtain the torques directly

in the joint space of the robot without losing gener-

ality. This analysis carried out in the joint space lets

modulate the dynamic response of the robot through

the impedance parameters directly at the joint level of

the robot. The torque, τ

, in this case is now

= K

(q −q

) + C

(

q −

) (5)

Joint-Based Robotic Impedance Control Transformations: An Experimental Study

159

3 MAPPING BETWEEN THE

CARTESIAN AND JOINT

SPACES

In this section, we present the derivation of the map-

ping of stiffness and damping matrices from the

Cartesian space to the joint space for joint-based

impedance control (Saldarriaga et al., 2022b). A gen-

eralized deﬁnition of stiffness and damping can be

written as follows:

K =

∂f

∂x

(6)

C =

∂f

∂

(7)

where f denotes the force. From the generalization of

a manipulator Jacobian matrix, we obtain

δx = J δq (8)

Taking derivative of (8) with respect to time through

the chain rule, we obtain as follows

(δx) = J

(δq) +

Jδq (9)

From equations (6), (7) and (4) with a combined stiff-

ness and damping control law, we can write the fol-

lowing equations

δf = K

δx + C

(δx) (10)

δτ

τ = K

δq + C

(δq) (11)

δτ

τ = δJ

f + J

δf (12)

Substitute equations (10) and (11) into (12) to render

δτ

τ = δJ

f + J



δx + C

(δx)



(13)

δq +C

(δq) = δJ

f +J

δx +J

(δx)

(14)

Substituting equations (8) and (9) into (14), we obtain

δq + C

(δq) = δJ

f + J

Jδq

+ J



(δq) +

Jδq



(15)

δq + C

(δq) = δJ

f + J

Jδq

+ J

(δq) + J

Jδq

(16)

Since we know that J is a function of q but not

q, we

can rearrange δJ

f and get

δq =



∂J

∂q

 

∂J

∂q



...



∂J

∂q



δq (17)

This K

term represents the changes in geometry un-

der the presence of external forces (Chen and Kao,

2000).

From equation (16), we can obtain the joint stiff-

ness and damping matrices (K

, C

) by prescribed

matrices in the Cartesian space (K

, C

)

= J

J + K

+ K

(18)

= J

J (19)

where K

= J

J, it represents the changes in ge-

ometry due to the apparent velocity created, which

generates an apparent stiffness matrix due to the

damping matrix in impedance control. Mathemati-

cally, this term comes from the δq part of the equa-

tions, and contains the derivative of J with respect to

time. For the rest of the paper, we refer to the ﬁrst

term on the right hand side of the equal sign in equa-

tion (18), J

J, as the ‘classical’ or ‘incomplete’

transformation of stiffness.

Equations (18) and (19) describe the complete

mapping of stiffness and damping of impedance con-

trol from the Cartesian space to the joint space, mak-

ing equations (2) and (3) equivalent to each other. The

matrices in the Cartesian space can be obtained with

prescribed matrices in the joint space:





∗

−K

∗

(20)





∗

(21)

The superscript ‘*’ in equations (20) and (21) repre-

sents the generalized inverse of the manipulator Ja-

cobian J, which is not square in case of redundancy

(n > m) (Siciliano et al., 2010). Equations (18)-(21)

form the “complete” mapping of impedance control

between Cartesian and joint space. A convenient,

derivative-free way of obtaining the extra terms in the

stiffness transformation is by the screw-based Jaco-

bian J (Muller, 2014).

4 DYNAMIC RESPONSE

MODULATION THROUGH THE

USE OF DAMPING

A very common way to select the damping parame-

ters of impedance control is by a trial-and-error prac-

tice, with endless possibilities. In addition to being

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

160

cumbersome and a blind guess practice, this trial-

and-error process can lead to undesired level of joint

torques and highly unstable and dangerous systems.

Furthermore, the trial-and-error process ignores the

inﬂuence of the values of one damping parameter of

the damping matrix on the others and the overall re-

sponse. Instead, we propose to analyze the control

criteria of the system in a modal space (Meirovitch,

2001) to regulate the dynamic response. As shown

in (Saldarriaga et al., 2022a), once the system in equa-

tion (2) becomes positive deﬁnite (after the redundant

ZP mode(s) is removed), the solution of dynamic re-

sponse in the joint space is derived by using the linear

system theory, with the following linear system equa-

tion

z(t) = A z(t)+Bτ

ext

(t) (22)

where

A =



0 I

−M

−1

−M

−1



, B =



−1



(23)

The solution of equation (22) assumes the following

form

z(t) =



q(t)



= Xe

Λt

z(0)

Λτ

Bτ

ext

(t −τ)dτ (24)

where X and Y are the right and left eigenvectors of

the matrix A, and Λ

Λ is a diagonal matrix with all the

eigenvalues of A.

The details of the methodology for one redundant

DoF can be found in (Saldarriaga et al., 2022a). We

can obtain every damping ratio ζ

, corresponding to

every eigenvalue (mode) of the A matrix, and we

can improve them in a theoretically sound system-

atic manner by selecting proper elements of stiffness

and damping. By performing a parameter study of

each element of the damping matrix, we can analyze

and determine the elements (diagonal or off-diagonal)

that have most effect on the dynamic response and

speciﬁcally on which modes. Thus, we can choose

stiffness and damping parameters to modulate the dy-

namic response in a deterministic manner, without

any assumptions or trial and error.

5 EXPERIMENTS

For a given starting conﬁguration q

[0;−π/4; 0;−3π/4; 0;π/2; π/4]rad of the Panda

robot, a circular path is commanded at the end-

effector level (m = 6) for 13 seconds at a constant

speed for several cycles with a speciﬁed set of Carte-

sian stiffness and damping parameters, K

and C

respectively, using joint-based impedance control.

This circle is in the XY Cartesian space, as shown

in Fig 2. At each iteration the inverse kinematics

function of the Panda controller obtains a desired

robot joint conﬁguration based on the intended path,

as the robot moves along this plane. The Jacobian

matrix J also changes, which has an impact on the

joint stiffness and damping matrices K

and C

respectively, with the prescribed K

and C

in the

Cartesian space, as shown in equations (18) and (19).

Figure 2: 7 DoF Panda robot used in the experiments.

For these experiments, given that no external

forces are being applied (other than the torques gener-

ated by the robot joints itself), we are going to neglect

the computation of the K

term in equation (18), and

will focus on the importance of the K

term on both

the stiffness transformation and the intended robotic

task in the Cartesian space in two different situations:

(1) arbitrary or trial-and-error damping, and (2) di-

agonal proper damping. From a higher perspective,

impedance control is a trade-off or compromise be-

tween force control and position control, we chose to

test it by tracing a prescribed trajectory, to some ex-

tent similar to position control without external forces

maintaining a mechanical compliance level.

The chosen Cartesian stiffness

matrix for the robotic task was

=diag(3000,5000, 12000,100,150,100) in

SI units for both position and orientation.

Joint-Based Robotic Impedance Control Transformations: An Experimental Study

161

5.1 Arbitrary Damping Matrix

Another common practice to select a set of damping

parameters in a robotic system performing impedance

control is to assume a diagonal mass matrix M and

impose C

= 2

√

(similar to the impedance ex-

ample code provided by the manufacturer). As we

can see in the Appendix, the mass matrix is far from

being diagonal. For this case, the Panda robot became

highly unstable once we used this arbitrary damping

matrix C

. Torques and velocities in the joints can

become out of range with bifurcation, the actuators

cannot keep up with the controller. The robot can

crash with no data being collected.

0 2 4 6 8 10 12

-50

x(mm)

0 2 4 6 8 10 12

y(mm)

0 2 4 6 8 10 12

z(mm)

class only

class + Kb

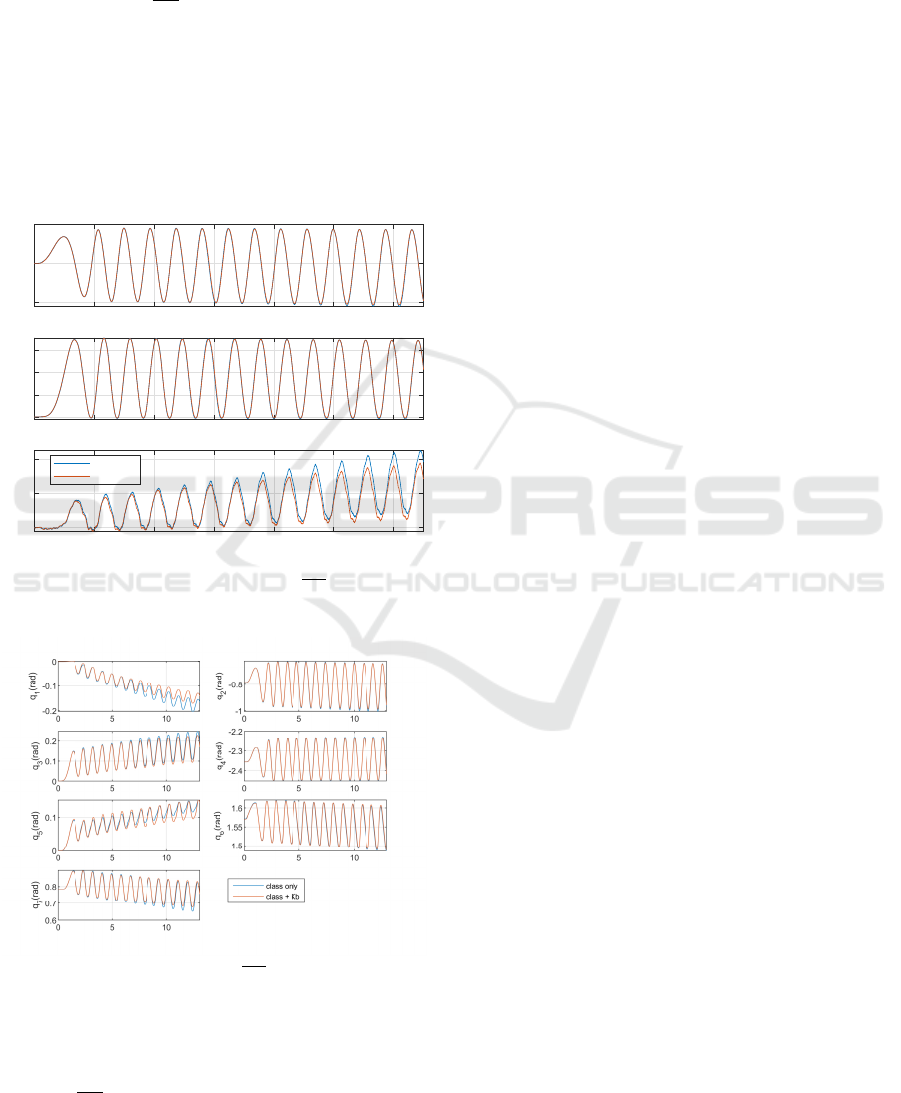
Figure 3: Results in the Cartesian space using an arbitrary

choice of damping matrix with C

√

. Comparison

between the classical (in blue) and equation (18) with K

term (in red).

Figure 4: Results of joint angles using an arbitrary choice

of damping matrix with C

√

. Comparison between

the classical (in blue) and equation (18) with K

term (in

red).

Another arbitrary damping matrix was chosen

with half of the values of the previous choice with

√

. The experimental results of the Carte-

sian positions are plotted in Figure 3 for multiple cy-

cles. Since the displacement is intended in the XY

plane, the displacement in the Z direction should be

very small, but this is clearly not the case, and gets

worse over time. The joint angles are plotted in Fig-

ure 4. The joint angles are drifting with multiple

cycles of movement, and signiﬁcantly affecting the

Cartesian positions. The addition of K

using equa-

tion (18) helps in reducing or stabilizing the response

but it is not ideal due to the selection of this arbitrary

damping matrix.

5.2 Appropriately Chosen Damping

Matrix

As explained in Section 4, the diagonal damping pa-

rameters are chosen keeping in mind the effect that

each element has on each of the damping ratios and

natural frequencies in the modal space once the re-

dundancy of the robot or ZP mode (Saldarriaga et al.,

2022a) is taken care of, without imposing high val-

ues of damping matrix that lead to over-damped or

very slow motions. After a parameter study of the

elements of C

, the chosen diagonal damping ma-

trix was C

=diag(20,30, 40,12,22,0.75) in SI units

for both position and orientation. This set of stiffness

and damping matrices generates the following damp-

ing ratios and natural frequencies in the modal space:

ζ =







0.089

0.20

0.26

0.68







; ω







49.1

15.0

31.8

−

179







rad/s

the overdamped pairs correspond to the overdamped

roots, where ζ ≥ 1.

From Figures 5 and 6 we can see how the response

of the robot is improved; especially, there is signif-

icantly less drift at the joints when the K

term is

included. In addition, more acceptable movement in

the Z direction is found with K

term. However, the

damping ratio of mode 1-2 is still low and might yield

better results when increased.

6 DISCUSSIONS

Equations (18) and (19), derived mathematically to

provide a transformation of stiffness and damping

matrices of impedance control between the Cartesian

and joint spaces, enable us to correctly compute the

stiffness and damping matrices in the joint space. As

shown in the experiments in Section 5, the classical

incomplete transformation leads to torque errors that

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

162

0 2 4 6 8 10 12

-50

x(mm)

0 2 4 6 8 10 12

y(mm)

0 2 4 6 8 10 12

z(mm)

class only

class + Kb

Figure 5: Results in the Cartesian space using an appro-

priately chosen diagonal damping matrix C

. Comparison

between the classical (in blue) and equation (18) with K

term (in red).

Figure 6: Results of joint angles using an appropriately

chosen diagonal damping matrix. Comparison between the

classical (in blue) and equation (18) with K

term (in red).

have a negative impact on a robotic impedance task.

On the other hand, including the coupling term K

the transformation equation yields a better dynamic

response, which quickly settles down after a transition

period. In comparison, the classical or incomplete

transformation leads to a joint response that drifts in-

deﬁnitely.

Based on the fundamental differential mathemat-

ics and the use of the chain rule, we derived the

transformation equation (18) for stiffness including a

term that involves the damping matrix in the Carte-

sian space and the derivative of the Jacobian matrix. It

showed up in the stiffness because of the apparent ve-

locity due to the change in Jacobian, which creates an

equivalent term of apparent damping in stiffness. This

apparent velocity due to the change in Jacobian is not

an actual physical velocity; hence, it does not gener-

ate a dissipative effect, and the conservative property

of stiffness is maintained.

Equations (22) to (24) are used to obtain the dy-

namic response of the system under impedance con-

trol. The methodology employed to select the indi-

vidual elements of the damping matrix enables us to

modulate the dynamic response, provided by equa-

tion (24), by changing the damping ratios in the modal

space of the system matrix A in equation (23) (Saldar-

riaga et al., 2022a). It is very important to maintain

stability by ensuring that none of the eigenvalues of

the modal space are in the right-half part of the com-

plex plane.

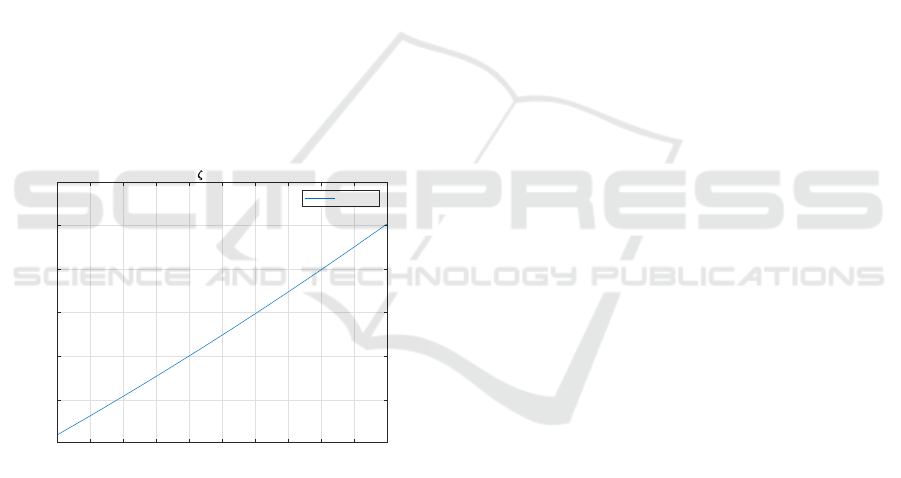
Employing the parameter study, we found that

also the off-diagonal elements can be used to increase

even more the intended damping ratio. For example,

looking at Subsection 5.2, the damping ratio corre-

sponding to mode 1-2 increases when increasing the

element (3,5) of the damping matrix C

, as shown in

Figure 7.

If we choose the element (3,5) of the Cartesian damp-

ing matrix C

to be 55, we obtain the following damp-

ing ratios and natural frequencies in the modal space:

ζ =







0.1037

0.20

0.26

0.68







; ω







51.6

15.1

31.8

−

179







rad/s

In case of working with non-symmetric matrices,

either C

or K

, or both, we need to make sure that

the positive-deﬁniteness is always maintained. For

any K

matrix, the condition: y

> 0 must be

held for all y

∈ ℜ

n×1

(Strang, 2009) to ensure a pos-

itive deﬁnite K

matrix. Note that when imposing cer-

tain off-diagonal values in C

, this condition may not

be satisﬁed and a more careful selection of parame-

ters needs to be done, which can also be accounted

for when generating the sets of parameter study using

our methodology.

Positive-deﬁniteness is a property that has not

been extensively studied on Non-symmetric matri-

ces, similar to the one in the case of element (3,5)

of the damping matrix. It is known that obtaining

positive eigenvalues is a sure consequence of deal-

ing with positive deﬁnite real matrices. That is pre-

cisely a characteristic of the non-diagonal matrix cho-

sen in the experimental work, the eigenvalues of the

reduced damping matrix are all positive (λ

λ=[1.316

7.289 8.514 14.65 23.18 8515248]), which brings the

stability and consistency needed for the system. This

can only be accounted for by using our methodology.

We also saw how the Cartesian stiffness val-

ues, especially in X and Y (3000 and 5000, which

were chosen for illustration and generalization pur-

poses only), affect the actual displacement of the end-

Joint-Based Robotic Impedance Control Transformations: An Experimental Study

163

effector, regardless of the intended circular path for

the impedance task.

As counterintuitive as it may sound, using higher

damping parameters does not necessarily mean that

the resulting damping ratios become higher as well.

This is clearly one of the main advantages of using the

proposed methodology to determine exactly which el-

ement needs to be increased to modulate the damping

behavior of the system.

One of the assumptions made in the analysis and

implementation is that the changes in the Jacobian

matrix J are relatively small, which to some extent

and for the experiments performed here it might work

relatively ﬁne, but once the displacements become

larger, as expected from theory, the damping matrix

can no longer be kept constant for a given task. The

feature of an analytically obtained, time and conﬁgu-

ration dependent damping matrix tackling this limita-

tion is part of our current work.

The apparent stiffness term, K

in the stiffness

transformation equation (18), involving the damping

matrix has a stabilizing effect in the response of the

robot performing impedance control, as it contains in-

formation on how the Jacobian matrix with conﬁgu-

ration changes over time.

0 10 20 30 40 50 60 70 80 90 100

0.095

0.1

0.105

0.11

0.115

Damping ratio

(Cc(3,5))

mode 1-2

Figure 7: Parameter study of the (3,5) element of C

Damping ratio in the modal space as a function of the el-

ement (3,5) of the Cartesian damping matrix C

In the present study we have found an unexpected

drift in the experimental results for the Z direction,

which given the relatively large stiffness value in that

Cartesian direction, should not be there. We saw that

the drift is larger and more evident in the cases that do

not consider the coupling term, further investigation

and considerations must be given to this result, and it

is also part of our future work.

7 CONCLUSION

In this paper, we derived the equations to transform

stiffness and damping matrices in impedance control

between the Cartesian and joint spaces and show ex-

perimentally the effectiveness of the proposed theory,

in comparison with the incomplete classic transfor-

mation. We also demonstrated that the stiffness ma-

trix term, K

, derived mathematically due to the ap-

parent velocity from the change in Jacobian matrix

in manipulation under impedance control, is very im-

portant and has a stabilizing effect in manipulation

and motion for the robotic manipulator. In addition,

the solution methodology based on the linear system

theory allows us to modulate the dynamic response

of the system by increasing the damping ratios in

the modal space, through the change of symmetric

and non-symmetric elements of the damping matrix

in impedance control.

REFERENCES

Caccavale, F., Siciliano, B., and Luigi, V. (1998).

Quaternion-based impedance with nondiagonal stiff-

ness for robot manipulators. volume 1, pages 468 –

472 vol.1.

Caccavale, F., Siciliano, B., and Villani, L. (1999). Robot

impedance control with nondiagonal stiffness. IEEE

Transactions on Automatic Control, 44(10):1943–

1946.

Chen, S.-F. and Kao, I. (2000). Conservative congruence

transformation for joint and cartesian stiffness matri-

ces of robotic hands and ﬁngers. The International

Journal of Robotics Research, 19(9):835–847.

Hogan, N. (1985). Impedance control: An approach to ma-

nipulation: part i - theory, part ii - implementation,

part iii - applications. Journ. of Dyn. Systems, Mea-

surement and Control, 107(1):1–24.

Kao, I. and Saldarriaga, C. (2023). Manipulation(to be pub-

lished). In Siciliano, B., editor, Springer Handbook of

Robotics, MOOCS. Springer, Berlin, Heidelberg.

Khatib, O. (1987). A uniﬁed approach for motion and force

control of robot manipulators: The operational space

formulation. IEEE Journal on Robotics and Automa-

tion, 3(1):43–53.

Laffranchi, M., Chen, L., Kashiri, N., Lee, J., Tsagarakis,

N., and Caldwell, D. (2014). Development and control

of a series elastic actuator equipped with a semi active

friction damper for human friendly robots. Robotics

and Autonomous Systems, 62(12):1827 – 1836.

Meirovitch, L. (2001). Fundamentals of Vibrations.

McGraw-Hill.

Memar, A. H. and Esfahani, E. T. (2018). A variable stiff-

ness gripper with antagonistic magnetic springs for

enhancing manipulation. In Robotics: Science and

Systems.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

164

Muller, A. (2014). Higher derivatives of the kinematic map-

ping and some applications. Mechanism and Machine

Theory, 76:70 – 85.

Ott, C. (2008). Cartesian Impedance Control of Redundant

and Flexible-Joint Robots. Springer Publishing Com-

pany, Incorporated, 1 edition.

Pollayil, M. J., Angelini, F., Xin, G., Mistry, M., Vijayaku-

mar, S., Bicchi, A., and Garabini, M. (2023). Choos-

ing stiffness and damping for optimal impedance plan-

ning. IEEE Transactions on Robotics, 39(2):1281–

1300.

Saldarriaga, C., Chakraborty, N., and Kao, I. (2022a).

Damping selection for cartesian impedance control

with dynamic response modulation. IEEE Transac-

tions on Robotics, 38(3):1915–1924.

Saldarriaga, C., Chakraborty, N., and Kao, I. (2022b). Joint

space stiffness and damping for cartesian and null

space impedance control of redundant robotic manip-

ulators. In Asfour, T., Yoshida, E., Park, J., Chris-

tensen, H., and Khatib, O., editors, Robotics Research,

pages 410–426, Cham. Springer International Pub-

lishing.

Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.

(2010). Robotics: Modelling, Planning and Control.

Advanced Textbooks in Control and Signal Process-

ing. Springer London.

Strang, G. (2009). Introduction to Linear Algebra.

Wellesley-Cambridge Press, fourth edition.

Vanderborght, B., Albu-Schaeffer, A., Bicchi, A., Burdet,

E., Caldwell, D., Carloni, R., Catalano, M., Eiberger,

O., Friedl, W., Ganesh, G., Garabini, M., Grebenstein,

M., Grioli, G., Haddadin, S., Hoppner, H., Jafari, A.,

Laffranchi, M., Lefeber, D., Petit, F., Stramigioli, S.,

Tsagarakis, N., Damme, M. V., Ham, R. V., Visser,

L., and Wolf, S. (2013). Variable impedance actua-

tors: A review. Robotics and Autonomous Systems,

61(12):1601 – 1614.

Villani, L. and De Schutter, J. (2008). Force control. In

Siciliano, B. and Khatib, O., editors, Springer Hand-

book of Robotics, pages 161–185. Springer, Berlin,

Heidelberg.

Yu, J., Zhao, Y., Chen, G., Gu, Y., Wang, C., and Huang,

S. (2019). Realizing controllable physical interaction

based on an electromagnetic variable stiffness joint.

Journal of Mechanisms and Robotics, 11(5):054501.

APPENDIX

The Jacobian and mass inertia matrices of the Panda

robot at the starting conﬁguration used for the analy-

ses were:

J(q) =







−0.0002 0.1525 −0.0001 0.1293 0 0.2106 0

0.3066 0 0.3247 0.0001 0.2104 −0.0001 0

0 −0.3066 −0.0002 0.4717 0.0001 0.0875 0

0 0.0001 −0.7070 0 1 0 −0.0025

0 1 0.0001 −1 0 −1 0.0007

1 0 0.7072 0.0001 −0.003 −0.0007 −1







M(q) =







0.5031 −0.006 0.4756 −0.0024 0.0527 −0.0005 −0.0028

−0.006 1.5460 −0.0225 −0.6848 −0.0078 −0.0335 −0.0009

0.4756 −0.0225 0.9674 −0.0146 0.0615 0.0007 −0.0034

−0.0024 −0.6848 −0.0146 0.9442 0.0208 0.1187 0.0012

0.0527 −0.0078 0.0615 0.0208 0.0229 −0.0015 0.0021

−0.0005 −0.0335 0.0007 0.1187 −0.0015 0.0444 0.0013

−0.0028 −0.0009 −0.0034 0.0012 0.0021 0.0013 0.003







Joint-Based Robotic Impedance Control Transformations: An Experimental Study

165