A PLF-CACC Design with Robustness to Communication Delays
Khadir Lakhdar Besseghieur, Abdelkrim Nemra and Fethi Demim
Laboratoire Guidage et Navigation, Ecole Militaire Polytechnique (EMP), Algiers, Algeria
Keywords:
CACC, PLF, Communication Delays.
Abstract:
In this paper, a new controller that makes a platoon of vehicles robust to large delays and loss of communication
is proposed. The constant time headway spacing policy is adopted for the separations while the vehicles are
allowed to exchange data according to the PLF communication pattern. Based on the SMC technique, the
designed controller draw the platoon towards achieving the following and the string stability objectives. Semi
strict L
2
string stability is proved to be achieved in this two-vehicle look ahead strategy with the propose
controller. Simulation are run in order to confirm the theoretical findings and to assess the effectiveness of the
proposed controller. The performances in terms of string stability and robustness against delays are compared
to a baseline PLF-CACC from the literature.
1 INTRODUCTION
Cooperative autonomous vehicles, also known as
CAVs are becoming more and more prevalent in to-
day’s world. These vehicles use advanced technol-
ogy to drive themselves without human intervention.
One of the main benefits of CAVs is their ability
to communicate with each other and with infrastruc-
ture. This allows them to work together and avoid
accidents, reducing traffic congestion and improving
overall safety on the road. The development of effec-
tive control systems for cooperative autonomous ve-
hicles is an important area of research, which involves
designing algorithms and decision-making processes
that enable multiple vehicles to work together in a co-
ordinated manner towards a common goal. Cooper-
ative adaptive cruise control (CACC) is an advanced
form of cruise control that enables multiple vehicles
to travel in a platoon, or convoy, while maintaining
a desired separation from each other. Unlike tradi-
tional cruise control, CACC uses communication be-
tween vehicles to coordinate their movements and ad-
just their speed and distance based on the actions of
surrounding vehicles. Therefore, the communication
topology is a key aspect in the design of the driving
strategy of the platoon.
Typical types of information flow topologies in-
clude predecessor following (PF), predecessor-leader
following (PLF) and bidirectional (BD), among
which PLF is the most prevailing CACC topology
(Cui et al., 2021). Under this topology, an ego-vehicle
takes in information, such as location, speed, and con-
trol input values from its predecessor and the leader.
The PLF controller is more robust than PF since in the
latter the vehicles respond only to their predecessors
(Dey et al., 2015; Seiler et al., 2004).
Another key aspect is the selected spacing policy
for the CACC system. It refers to the desired steady
state spacing between two consecutive vehicles dur-
ing vehicle following (Wu et al., 2020). The spacing
policies can be classified into two major categories:
constant spacing policy and variable spacing policies.
The most typical variable spacing policy is the con-
stant time gap (CTG) (Wu et al., 2020). The pre-
vailing definition of the time gap denotes the period
during which the rear bumper of the preceding vehi-
cle and the front bumper of the ego vehicle pass a
fixed position on the road. CTG is the strategy that
fits the best the behaviour humans driver have when
car-following, for this reason it is the most adopted
spacing policy by commercially available CACC sys-
tems (Flores, 2018).
When designing a CACC system, the control law
is another major concern which is our focus in this
work. The latter regulates the error between desired
and real spacing to drive the platoon towards achiev-
ing the desired inter-vehicles distances which are ob-
tained according to the adopted spacing policy. In
addition, the controller must ensure the string stabil-
ity of the designed CACC system. The latter is said
to be string stable if the disturbances are not ampli-
fied when propagating downstream along the vehi-
444
Besseghieur, K., Nemra, A. and Demim, F.
A PLF-CACC Design with Robustness to Communication Delays.
DOI: 10.5220/0012190500003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 444-452
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

cle string. Along this direction, prevailing control
laws in literature were proposed. Linear controllers
in (Naus et al., 2010; Xing et al., 2018) and in (Xing
et al., 2019) are designed. Although the string sta-
bility is simple to analyse, linear controllers present
some limitations when it comes to satisfy state and
input constraints. Optimal controllers solve an opti-
mization problem to determine the control input for
each vehicle of the platoon (Jin and Orosz, 2016;
Dunbar and Caveney, 2011). Although they pos-
sess the capacity to handle state and input constraints,
optimization-based controllers present a high compu-
tation burden. Both LQR and H
∞
-based controllers
that guarantee string stability were synthesized re-
spectively in (Zhang et al., 2020a) and (Ploeg et al.,
2013a) to drive the CACC system while minimizing
a cost function. When the considered vehicle model
is nonlinear or the adopted spacing policy is based on
a variable time gap, nonlinear controllers are adopted
as in (Besselink and Johansson, 2017) and (Liu et al.,
2001). One drawback of these controllers is the fact
that the string stability analysis is much more com-
plex.
In the control design, CACC systems which are
designed without considering communication delay
are likely to show poor performance in the real world
under extreme communication delay and packet loss
scenarios (Liu et al., 2001), (Lei et al., 2011). In
(Ploeg et al., 2013b), L
p
string stability of the pla-
toon system is introduced and investigated under ho-
mogenous communication delay. It is shown that the
L
∞
string stability is compromised and to ensure L
2
string stability of the system with a delay of 300 ms,
the time gap is required to be as high as 1 s. In (Zhang
et al., 2020b), authors proposed a semi-constant time
gap (Semi-CTG) spacing policy that leads along with
a linear controller to fully compensate heterogeneous
communication delays. Under predecessor follower
(PF) topology, linear controllers are employed and
it is proved that the minimum time gap guarantee-
ing string stability equals the communication delay of
the system. Under the same information flow pattern,
the research in (Zhang et al., 2020a) adopts a space
domain approach to design an optimal control-based
CACC system. Both local and string stability are
proven and robustness against communication fail-
ure is improved comparing to the state-of-the-art con-
trollers proposed in (Ploeg et al., 2013a) and (Naus
et al., 2010).
Communication delay and packet loss have rarely
been addressed under PLF information flow topology.
In (Zhang et al., 2020b), a semi-constant spacing pol-
icy is proposed to deal with communication and sens-
ing delays. However, the authors did not take into
consideration a constant time headway spacing pol-
icy. In (Fernandes and Nunes, 2012), strategies to
mitigate communication delays are proposed under
the PLF communication topology while considering a
CS spacing policy again. In (Milan
´
es et al., 2013), the
authors considered a CTH spacing policy and the pro-
posed controller is based on the PLF topology. How-
ever, the string stability analysis needs to be more de-
tailed and the communication delays are not consid-
ered.
In our work, we propose a new controller that
deals with communication delays under the CTH
spacing policy and the PLF information flow topol-
ogy. The proposed controller ensures the local and
the string stability of the platoon and its capacity to
deal with communication delays is shown. In order to
assess the effectiveness of the proposed controller, we
compare the performances with the work in (Milan
´
es
et al., 2013) which is set as a baseline.
The rest of this paper is organized as follows. Sec-
tion 2 presents the robot modelling and problem for-
mulation. In Section 3, the nominal controller is ex-
posed and its robustness against delays is analysed.
Section 4 proposes a new PLF-CACC controller and
details its local and string stability. Section 5 includes
simulations where the performance of the proposed
system is assessed.
2 PROBLEM FORMULATION
Vehicle leader
Vehicle i-1 Vehicle i
Wireless communication V2V
li
dp,i
dl,i
ui
ui-1
ul
ql
Figure 1: PLF platooning system.
In this section, the kinematic model of the vehicle is
presented. The platoon modelling is exposed and the
control problem is formulated under the PLF com-
munication topology. To facilitate further discussion,
definitions and notations are introduced here. As
shown in Figure 1, the leader vehicle is indexed as
l, the preceding vehicle is indexed as i–1 and the ego
vehicle indexed as i. l
i
, q
i
, v
i
and u
i
denote the length,
position, velocity, and control input of vehicle i, re-
spectively. In our work, the string is assumed to be
homogeneous .i.e. all vehicles of the platoon are iden-
tical. The following model is adopted (Milan
´
es et al.,
2013):
G(p) =
k
p
2
+ 2θw
n
p + w
2
n
(1)
with k, θ, w
n
defined in Table 1.
A PLF-CACC Design with Robustness to Communication Delays
445

Table 1: Vehicle model parameters.
k θ w
n
0.156 0.661 0.396
The main objective, under the CTH spacing pol-
icy and the PLF communication topology, is to reg-
ulate the subject vehicle’s longitudinal motion to fol-
low its predecessor and its leader with constant time
gaps. The desired spacing between the ego vehicle
and its predecessor, is formulated as:
d
rp,i
(t) = r
i
+ h v
i
(t) (2)
Whereas, the desired spacing from the leader of the
platoon is:
d
rl,i
(t) = r
i
+ h
l
v
i
(t) (3)
Where r
i
, h and h
l
denote the standstill distance, the
desired time gaps to the predecessor and to the leader,
respectively. This formulation leads to spacing error
with respect to the preceding vehicle and the lead ve-
hicle, respectively, as:
e
p,i
(t) = d
p,i
(t) − d
rp,i
(t)
= (q
i−1
(t) − q
i
(t) − l
i
) − r
i
− h v
i
(t)
(4)
e
l,i
(t) = d
l,i
(t) − d
rl,i
(t)
= (q
l
(t) − q
i
(t) −
i
∑
j=1
l
j
) − r
i
− h
l
v
i
(t)
(5)
Without loss of generality, r
i
= l
i
= 0 is assumed in
the remainder of this paper. Formulating the spacing
error e
i
(t) in the Laplace domain yields:
e
p,i
(p) = q
i−1
(p) − H(p) q
i
(p) (6)
e
l,i
(p) = q
l
(p) − H
l
(p) q
i
(p) (7)
with the spacing policy transfer functions H(p) and
H
l
(p) defined as
H(p) = h p + 1 (8)
H
l
(p) = h
l
p + 1 (9)
The vehicle following objective is achieved when the
inter-vehicle distance errors as defined in Equations
(4) and (5) converge to zero. To achieve this, it is as-
sumed in our work that the inter-vehicle spacing, the
speed of the subject vehicle and the predecessor, and
the acceleration of the subject vehicle are assumed to
be detected by on-board sensors, including radar or
camera, speedometer, and accelerometer. While, un-
der the adopted PLF communication pattern, the ac-
celerations, control inputs of both the predecessor and
the leader and the position of the latter are collected
by the V2V communication system and transmitted to
the ego vehicle.
As shown earlier, it is of great importance to take
into consideration heterogeneous communication and
Table 2: Controller parameters (Milan
´
es et al., 2013).
k
1
k
2
k
3
k
4
0.45 0.25 0.15 0.1
+
−
K
p
(p)
+
+
+
K
l
(p)
+
−
G(p)
H(p)
H
l
(p)
e
p,i
e
l,i
q
i
q
i−1
q
l
u
i−1
Figure 2: Nominal controller diagram.
sensor delays and in the control design. We de-
note by τ
x,i
, the subject vehicle’s on board sensor
delay to obtain the preceding vehicle’s acceleration,
speed and position; τ
u,i
, the delay of the vehicle-to-
vehicle (V2V) communication to obtain the predeces-
sor’s commands; all the information about the lead
vehicle are obtained by V2V communication delayed
by τ
l,i
.
3 NOMINAL CONTROLLER
In this section, the controller developed in (Milan
´
es
et al., 2013), which is set as a benchmark for this
work, is briefly reviewed. As in this work, the au-
thors adopted the CTH spacing policy and the PLF
communication pattern in their strategy. We briefly
analyse the controller design, its string stability and
its robustness against delays.
3.1 Control Laws
In (Milan
´
es et al., 2013), the gap regulation controller
is composed of three main terms: two feedback-
feedforward PD controllers that represent time-gap
error regulation with respect to the preceding and the
leading vehicles and the third term represents the pre-
ceding vehicle control inputs which is used as a feed-
forward term. The following control law was pro-
posed:
u
i
(t) = e
p,i
k
2
+e
.
p,i
k
1
+e
l,i
k
4
+e
.
l,i
k
3
+u
i−1
(t) (10)
where constants k
1
, k
2
, k
3
and k
4
are given in Table
2. The block diagram of the nominal CTH-PLF con-
troller is shown in Figure 2. K
p
(p) and K
l
(p) repre-
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
446

senting the time-gap error regulation controller for the
preceding and the leading vehicle respectively. Both
terms correspond to a classic PD controller given by
K
p
(p) = k
1
p + k
2
(11)
K
l
(p) = k
3
p + k
4
(12)
3.2 String Stability Analysis
In addition to the vehicle following objective, a crit-
ical task of platoon control is to maintain string sta-
bility. It can be defined as the system’s ability to
attenuate the effects of disturbances introduced by
downstream vehicles, in upstream direction. This al-
lows the platoon to avoid amplifications of variations
in accelerations, velocities and inter-vehicle distances
along the vehicle platoon. Different analysis methods
for string stability can be found in the literature (Feng
et al., 2019). Adopting the performance oriented ap-
proach, the string stability criterion in (Milan
´
es et al.,
2013) is chosen as the transfer function from the posi-
tions of the ego to the preceding vehicle, respectively.
Γ
i
(p) =
q
i
(p)
q
i−1
(p)
(13)
According to (Ploeg et al., 2013b), a vehicle platoon
is string stable if:
||Γ
i
(p)||
H
∞
= sup
||q
i
(t)||
L
2
||q
i−1
(t)||
L
2
≤ 1 , ∀i ≥ 1 (14)
where ||.||
H
∞
and ||.||
L
2
refer to the H
∞
and L
2
norms,
respectively.
On the other hand, while ignoring the communi-
cation delays and considering the fact that q
0
= 0, it
is shown in (Milan
´
es et al., 2013) that the obtained
transfer function from the ego-vehicle to the preced-
ing one is as follows:
||Γ
i
(p)||
H
∞
=
1 + G(p)K
p
(p)
1 + G(p)(K
p
(p)H(p) + K
l
(p)H
l
(p))
(15)
The magnitude of the transfer function defined above
is analysed through its Bode diagram. In (Milan
´
es
et al., 2013), it is shown that the magnitude is main-
tained below the unity. However, many parameters of
the considered transfer function are not precised. It
is known that in the two-vehicle look-ahead topology,
the desired time-gap h
l
depends on the position of the
ego vehicle in the platoon which implies that the func-
tion H
l
(p) and thus the transfer function Γ
i
(p) are not
constants for all vehicles in the platoon (Ploeg et al.,
2013a). Nevertheless, the position of the studied ego
vehicle is not precised in (Milan
´
es et al., 2013). In
the presented Bode diagram, the authors did not men-
tion which time-gap h
p
was employed in the string
10
-2
10
-1
10
0
10
1
10
2
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
Magnitude (dB)
Bode Diagram
Frequency (rad/s)
0.6 0.8 1
-0.5
0
0.5
Figure 3: String stability analysis.
stability analysis. In order to maintain the string sta-
bility, the employed PD controllers gains were tuned,
as shown in Table 2.
Figure 3 shows the frequency response magnitude
of the ego vehicle with the same controllers param-
eters provided in Table 2 We consider a platoon of
three vehicles with a leader, a predecessor and the
subject vehicle. The desired time-gaps with respect to
the predecessor and the leader are set to h
p
= 0.6 and
h
l
= 1.2, respectively. Although no delays are incor-
porated, one can clearly notice that the magnitude of
the transfer function surpasses the unity and thus the
string stability of the platoon is not guaranteed while
using the controllers parameters presented in Table 2.
3.3 Effects of Delays on the String
Stability
In the controller design, it was assumed that the wire-
less communication system and on board sensors pro-
vide zero delay. The string stability of the CACC
system is analysed when affected with the commu-
nication/sensor delays τ
x,i
, τ
u,i
, τ
l,i
as defined earlier.
The new block diagram of the delayed nominal sys-
tem is shown in Figure 4. where D
x,i
(p) = e
−τ
x,i
p
,
D
u,i
(p) = e
−τ
u,i
p
and D
l,i
(p) = e
−τ
l,i
p
As mentioned earlier, communication and sen-
sors delays compromise string stability (
¨
Onc
¨
u et al.,
2011). As shown in Figure 5, a platoon of four ve-
hicles is considered. Sensors and communication de-
lays are respectively set to τ
x,i
= 0.2s, τ
u,i
= 0.5s and
τ
l,i
= 0.5s. One can clearly notice that the second and
the third followers amplify their predecessors pertur-
bations and thus the strict L
2
string stability (Ploeg
et al., 2013b) is not ensured. To this end, the objec-
tive of our work is to make the system robust against
these communication/sensor delays.
A PLF-CACC Design with Robustness to Communication Delays
447

+
−
D
x,i
(p)
D
u,i
(p)
D
l,i
(p)
K
p
(p)
+
+
+
K
l
(p)
+
−
G(p)
H(p)
H
l
(p)
e
p,i
e
l,i
q
i
q
i−1
q
l
u
i−1
Figure 4: Nominal controller diagram with communication
delays
0 5 10 15 20 25 30 35 40 45 50
0
2
4
6
8
10
12
Leader
Vehicle 1
Vehicle 2
Vehicle 3
14 16 18 20
10
10.2
10.4
Figure 5: Time responses of the platoon vehicles with com-
munication delays.
4 CONTROLLER DESIGN
In this section, we focus on the controller synthesis
that drives the ego vehicle towards achieving the de-
sired space with respect to its predecessor and to its
leader. We note that the control of the lead vehicle is
out of the scope of this paper. The errors dynamics
with respect to the predecessor and to the leader are
respectively formulated as


e
1,i
e
2,i
e
3,i


=


e
p,i
e
.
p,i
e
..
p,i


=


q
i−1
− q
i
− hv
i
v
i−1
− v
i
− ha
i
a
i−1
− a
i
− ha
.
i


(16)


e
4,i
e
5,i
e
6,i


=


e
l,i
e
.
l,i
e
..
l,i


=


q
l
− q
i
− hv
i
v
l
− v
i
− ha
i
a
l
− a
i
− ha
.
i


(17)
Deriving the state space representation of the system
transfer function given in Equation 1, we obtain:
e
.
3,i
= −2θw
n
e
3,i
− w
2
n
e
2,i
− hku
.
i
− ku
i
+ ku
i−1
e
.
6,i
= −2θw
n
e
6,i
− w
2
n
e
5,i
− h
l
ku
.
i
− ku
i
+ ku
l
(18)
+
−
D
x,i
(p)
D
u,i
(p)
d
p
C
p
(p)
+
C
l
(p)
+
−
D
l,i
(p)
D
l,i
(p)
d
l
K
−1
(p)
G(p)
H(p)
H
l
(p)
e
p,i
e
l,i
q
i
q
i−1
q
l
u
i−1
u
l
Figure 6: Proposed controller diagram.
An SMC surface is used in the controller design and
defined as:
S =

k
1
k
2
k
3
k
4
k
5
k
6








e
1,i
e
2,i
e
3,i
e
4,i
e
5,i
e
6,i







(19)
By setting:
˙
S = −λ S and combining Equations 4, 5,
16, 17, 18 and 19, the following control law is ob-
tained:
ρ
i
(t) = αu
.
i
(t) + βu
i
(t) (20)
ρ
i
(t) =

c
1
c
2
c
3
c
4
c
5
c
6








e
1,i
e
2,i
e
3,i
e
4,i
e
5,i
e
6,i







+ d
p
u
i−1
+ d
l
u
l
(21)
where α = hkk
3
+h
l
kk
6
, β = kk
3
+kk
6
, c
1
= λk
1
, c
2
=
k
1
− k
3
w
2
n
+ λk
2
, c
3
= k
2
− 2θw
n
k
3
+ λk
3
, c
4
=
λk
4
, c
5
= k
4
− k
6
w
2
n
+ λk
5
, c
6
= k
5
− 2θw
n
k
6
+
λk
6
, d
p
= kk
3
and d
l
= kk
6
. The block diagram of
the proposed CACC under the PLF topology is pre-
sented in Figure 6 where C
p
(p) = c
1
+ c
2
p + c
3
p
2
,
C
l
(p) = c
4
+ c
5
p + c
6
p
2
and K(p) = αp + β.
The evaluation of string stability often involves
analyzing the amplification of distance error, veloc-
ity, and/or acceleration in the upstream direction. As
a result, a platoon model is created using these state
variables. This leads to the following formulation of
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
448

a homogeneous platoon model:



q
.
i
v
.
i
a
.
i
u
.
i



=




0 1 0 0
0 0 1 0
0 −ω
2
n
−2θω
n
0
−
k
x
i
α
−
k
v
i
α
−
k
a
i
α
−
k
u
i
α







q
i
v
i
a
i
u
i



+




0 0 0 0
0 0 0 0
0 0 0 0
−
c
1
α
−
c
2
α
−
c
3
α
−
d
p
α







q
i−1
v
i−1
a
i−1
u
i−1



+




0 0 0 0
0 0 0 0
0 0 0 0
−
c
4
α
−
c
5
α
−
c
6
α
−
d
l
α







q
l
v
l
a
l
u
l



(22)
Let x
i
= (q
i
v
i
a
i
u
i
)
T
be the state vector, thus the fol-
lowing state representation is obtained:
x
.
i
= A
i
x
i
+ A
p
x
i−1
+ A
l
x
l
(23)
We note that A
i
is not constant since it depends on
the parameter h
l
which depends on the position of the
vehicle in the platoon. A
p
and A
l
are constant for all
the vehicles of index i ≥ 1.
In the control structure shown in Figure 6, the
Laplace function of the vehicle i position reads:
q
i
(p) =
GC
p
D
x,i
+ D
u,i
K + G(H
l
C
l
+ HC
p
)
q
i−1
(p)
+
GC
l
D
l,i
+ D
l,i
K + G(H
l
C
l
+ HC
p
)
q
l
(p)
= Θ
i,i−1
(p)q
i
(p) + Θ
i,l
(p)q
l
(p)
(24)
In (Milan
´
es et al., 2013), the string stability is anal-
ysed through the magnitude of the transfer function
from the the ego vehicle position q
i
to the predeces-
sor position q
i−1
without taking into account that it
is dependent on the index i. As defined in (Ploeg
et al., 2013a), the semi strictly L
2
string stability of
the platoon is considered in this work. It has been in-
troduced to support the string stability analysis in the
multi-vehicle look-ahead scheme. The semi strict L
2
string stability analysis is based on the transfer func-
tion from the ego vehicle position to the leader vehicle
position which is given as:
Φ
i
(p) =
q
i
(p)
q
l
(p)
=
i−1
∑
k=1
[(Π
i−1
j=k
Θ
j+1, j
(p))Θ
k,l
(p)] (25)
Since K and H
l
depend on the vehicle’s index in the
platoon i, the semi strict string stability of the platoon
is analyzed through multiple transfer functions Φ
i
(p).
As illustrated in Figure 7, showing the gain
|Φ
i
(p)| for various values of i. No delays are con-
sidered, the desired time gap is set to h = 0.8s and the
Table 3: Proposed controller parameters.
k
1
k
2
k
3
k
4
k
5
k
6
λ
10 1 0.05 10 1 0.01 100
10
-2
10
-1
10
0
10
1
10
2
10
3
10
4
-50
-45
-40
-35
-30
-25
-20
-15
-10
-5
0
Magnitude (dB)
Bode Diagram
Frequency (rad/s)
Figure 7: String stability analysis.
controller parameters are given in Table 3. It can be
noticed that the magnitudes of all the transfer func-
tions are below the unity which confirms the semi
strict L
2
string stability of the platoon.
10
-2
10
-1
10
0
10
1
10
2
10
3
10
4
-45
-40
-35
-30
-25
-20
-15
-10
-5
0
5
Magnitude (dB)
Bode Diagram
Frequency (rad/s)
Figure 8: String stability analysis with communication de-
lays.
Figure 8 shows that the semi strict L
2
string sta-
bility is still achieved under the following commu-
nication/sensors delays: τ
x,i
= 0.2s, τ
u,i
= 0.4s and
τ
l,i
= 0.5s. This confirms the robustness of the pro-
posed controller against delays.
5 SIMULATION RESULTS
Simulations are performed using the proposed con-
troller on a CACC string comprising of ten vehicles
to verify the validity of the theoretical findings. In or-
der to assess the robustness of the proposed controller
against delays, two scenarios are considered: platoon
control without and with communication/sensor de-
lays. Based on these scenarios, two sets of simula-
tions are carried out where the following settings are
made for the experiments : A string of 20 vehicles is
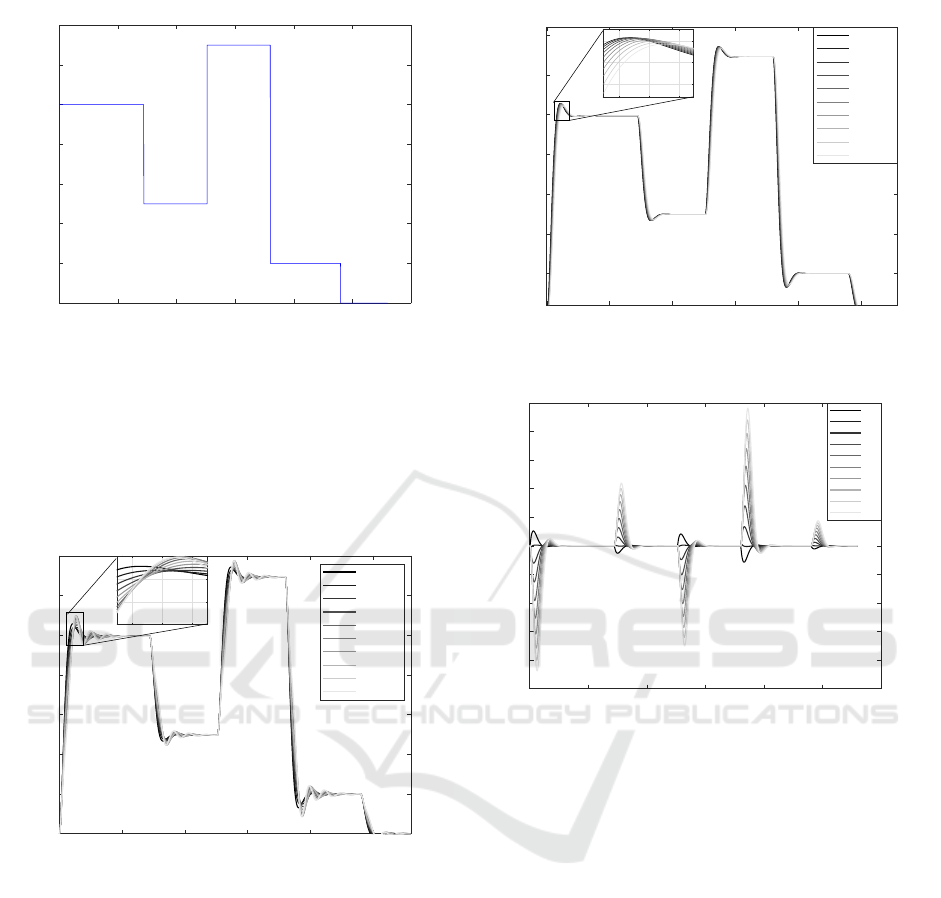
simulated with the desired speed profile of the lead
vehicle is set as depicted in Figure 9. This leads to
variable desired spacings between vehicles since in
A PLF-CACC Design with Robustness to Communication Delays
449

0 50 100 150 200 250 300
0
2
4
6
8
10
12
14
Figure 9: Desired speed for the lead vehicle.
the adopted CTH spacing policy, the desired distance
varies with the ego vehicle’s speed. In both scenarios,
the simulation horizon is: 280s and all the vehicles
initially are located at the origin with no initial speeds.
The controller parameters for both scenarios are set as
precised in Table 3 so as the semi strict string stability
of the platoon is ensured.
0 50 100 150 200 250
0
2
4
6
8
10
12
14
Vehicle1
Vehicle2
Vehicle3
Vehicle4
Vehicle5
Vehicle6
Vehicle7
Vehicle8
Vehicle9
Vehicle10
10 12 14
8
9
10
11
Figure 10: Time responses of the vehicles equipped with
the nominal controller.
In the first scenario, no communication delays are
taken into consideration and the desired time gap is
set to 0.2s which is considered a relatively short time
gap. Figure 10 depicts the time responses of the first
ten vehicles of the platoon where the nominal con-
troller in (Milan
´
es et al., 2013) is adopted. It shows
that the perturbations are amplified downstream the
platoon direction which indicates the string instabil-
ity of the platoon. With the same desired time gap,
Figure 11 presents the time responses of the first ten
vehicles of the platoon equipped with the proposed
controller. In this case, it is shown that the amplitudes
are not amplified along the downstream direction of
the platoon which confirms the theoretical findings
concerning the semi strict L
2
string stability. The lo-
0 50 100 150 200 250
2
4
6
8
10
12
14
Vehicle1
Vehicle2
Vehicle3
Vehicle4
Vehicle5
Vehicle6
Vehicle7
Vehicle8
Vehicle9
Vehicle10
10 12 14
9.5
10
10.5
Figure 11: Time responses of the vehicles equipped with
the proposed controller.
0 50 100 150 200 250 300
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
Figure 12: Distance errors of the vehicles equipped with the
nominal controller.
cal stability of the platoon is illustrated in Figure 12,
where the vehicles errors converge to zero which indi-
cates that the vehicle following objective is achieved
and the desired spaces are maintained.
In the second scenario, the desired time gap is con-
sidered to be h = 0.6 with communication and sensors
delays set to be: τ
x,i
= 0.2s, τ
u,i
= 0.5s and τ
l,i
= 0.5s.
Figures 13 and 14 show the performance of both the
nominal and proposed controller in dealing with the
delays. Clearly, the latter presents robustness against
delays and the semi strict L
2
string stability is ensured.
While, the baseline CACC shows that the delays have
compromised its string stability.
6 CONCLUSION
Robustness against communication and sensors de-
lays in order to maintain the string stability of the
CACC equipped platoons is the object of study in this
paper. The considered CACC scheme is based on the
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
450

0 50 100 150 200 250
0
2
4
6
8
10
12
14
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
10 15 20
6
8
10
Figure 13: Time responses of the vehicles equipped with
the nominal controller.
0 50 100 150 200 250
0
2
4
6
8
10
12
14
Vehicle1
Vehicle2
Vehicle3
Vehicle4
Vehicle5
Vehicle6
Vehicle7
Vehicle8
Vehicle9
Vehicle10
Vehicle11
Vehicle12
Vehicle13
Vehicle14
Vehicle15
Vehicle16
Vehicle17
Vehicle18
Vehicle19
Vehicle20
Figure 14: Time responses of the vehicles equipped with
the proposed controller.
PLF communication topology and the CTH spacing
policy is adopted in this work. A new controller is
proposed and is proved to ensure the semi strict L
2
strict stability of the platoon. A nominal controller is
briefly reviewed and set as a baseline for this work.
In order to confirm the theoretical results, simulations
are carried out and the proposed controller shows bet-
ter performance than the nominal controller in terms
of string stability and robustness against communica-
tion and sensors delays. Future works include exten-
sive analyse of the proposed controller in terms of as-
sessing the traffic flow performance and a comparison
to the PF CACC controllers needs to be carried out.
REFERENCES
Besselink, B. and Johansson, K. H. (2017). String stability
and a delay-based spacing policy for vehicle platoons
subject to disturbances. IEEE Transactions on Auto-
matic Control, 62(9):4376–4391.
Cui, L., Chen, Z., Wang, A., Hu, J., and Park, B. B. (2021).
Development of a robust cooperative adaptive cruise
control with dynamic topology. IEEE Transactions on
Intelligent Transportation Systems, 23(5):4279–4290.
Dey, K. C., Yan, L., Wang, X., Wang, Y., Shen, H.,
Chowdhury, M., Yu, L., Qiu, C., and Soundararaj, V.
(2015). A review of communication, driver charac-
teristics, and controls aspects of cooperative adaptive
cruise control (cacc). IEEE Transactions on Intelli-
gent Transportation Systems, 17(2):491–509.
Dunbar, W. B. and Caveney, D. S. (2011). Distributed re-
ceding horizon control of vehicle platoons: Stability
and string stability. IEEE Transactions on Automatic
Control, 57(3):620–633.
Feng, S., Zhang, Y., Li, S. E., Cao, Z., Liu, H. X., and Li, L.
(2019). String stability for vehicular platoon control:
Definitions and analysis methods. Annual Reviews in
Control, 47:81–97.
Fernandes, P. and Nunes, U. (2012). Platooning with
ivc-enabled autonomous vehicles: Strategies to miti-
gate communication delays, improve safety and traffic
flow. IEEE Transactions on Intelligent Transportation
Systems, 13(1):91–106.
Flores, C. (2018). Architecture de contr
ˆ
ole pour le car-
following adaptatif et coop
´
eratif. PhD thesis, Paris
Sciences et Lettres (ComUE).
Jin, I. G. and Orosz, G. (2016). Optimal control of con-
nected vehicle systems with communication delay and
driver reaction time. IEEE Transactions on Intelligent
Transportation Systems, 18(8):2056–2070.
Lei, C., Van Eenennaam, E., Wolterink, W. K., Karagiannis,
G., Heijenk, G., and Ploeg, J. (2011). Impact of packet
loss on cacc string stability performance. In 2011 11th
International Conference on ITS Telecommunications,
pages 381–386. IEEE.
Liu, X., Goldsmith, A., Mahal, S. S., and Hedrick, J. K.
(2001). Effects of communication delay on string sta-
bility in vehicle platoons. In ITSC 2001. 2001 IEEE
Intelligent Transportation Systems. Proceedings (Cat.
No. 01TH8585), pages 625–630. IEEE.
Milan
´
es, V., Shladover, S. E., Spring, J., Nowakowski, C.,
Kawazoe, H., and Nakamura, M. (2013). Coopera-
tive adaptive cruise control in real traffic situations.
IEEE Transactions on intelligent transportation sys-
tems, 15(1):296–305.
Naus, G. J., Vugts, R. P., Ploeg, J., van De Molengraft,
M. J., and Steinbuch, M. (2010). String-stable cacc
design and experimental validation: A frequency-
domain approach. IEEE Transactions on vehicular
technology, 59(9):4268–4279.
¨
Onc
¨
u, S., Van De Wouw, N., and Nijmeijer, H. (2011). Co-
operative adaptive cruise control: Tradeoffs between
control and network specifications. In 2011 14th Inter-
national IEEE Conference on Intelligent Transporta-
tion Systems (ITSC), pages 2051–2056. IEEE.
Ploeg, J., Shukla, D. P., Van De Wouw, N., and Nijmeijer,
H. (2013a). Controller synthesis for string stability
of vehicle platoons. IEEE Transactions on Intelligent
Transportation Systems, 15(2):854–865.
A PLF-CACC Design with Robustness to Communication Delays
451

Ploeg, J., Van De Wouw, N., and Nijmeijer, H. (2013b).
Lp string stability of cascaded systems: Application
to vehicle platooning. IEEE Transactions on Control
Systems Technology, 22(2):786–793.
Seiler, P., Pant, A., and Hedrick, K. (2004). Disturbance
propagation in vehicle strings. IEEE Transactions on
automatic control, 49(10):1835–1842.
Wu, C., Xu, Z., Liu, Y., Fu, C., Li, K., and Hu, M. (2020).
Spacing policies for adaptive cruise control: A survey.
IEEE Access, 8:50149–50162.
Xing, H., Ploeg, J., and Nijmeijer, H. (2018). Smith predic-
tor compensating for vehicle actuator delays in coop-
erative acc systems. IEEE Transactions on Vehicular
Technology, 68(2):1106–1115.
Xing, H., Ploeg, J., and Nijmeijer, H. (2019). Compen-
sation of communication delays in a cooperative acc
system. IEEE Transactions on Vehicular Technology,
69(2):1177–1189.
Zhang, Y., Bai, Y., Wang, M., and Hu, J. (2020a). Coop-
erative adaptive cruise control with robustness against
communication delay: An approach in the space do-
main. IEEE Transactions on Intelligent Transporta-
tion Systems, 22(9):5496–5507.
Zhang, Y., Wang, M., Hu, J., and Bekiaris-Liberis, N.
(2020b). Semi-constant spacing policy for leader-
predecessor-follower platoon control via delayed
measurements synchronization. IFAC-PapersOnLine,
53(2):15096–15103.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
452