Adaptive Granulation: Data Reduction at the Database Level

Hossein Haeri

1 a

, Niket Kathiriya

2 b

, Cindy Chen

2 c

and Kshitij Jerath

1 d

Department of Mechanical Engineering, University of Massachusetts Lowell, Lowell, MA, U.S.A.

Department of Computer Science, University of Massachusetts Lowell, Lowell, MA, U.S.A.

Keywords:

Data Granulation, Data Reduction, Data Aggregation, Training Set Size Reduction.

Abstract:

In an era where data volume is growing exponentially, effective data management techniques are more crucial

than ever. Traditional methods typically manage the size of large datasets by reducing or aggregating data

using a pre-speciﬁed granularity. However, these methods often face challenges in retaining vital information

when dealing with large and complex datasets, especially when such datasets reside in databases. We propose

a novel and innovative approach called Adaptive Granulation that addresses this issue by performing data

reduction or aggregation at the database level itself. A key concern that arises in the data reduction process

is the potential trade-off between the reduction of data volume and the preservation of prediction accuracy.

This is particularly relevant in scenarios where the primary goal is to leverage the reduced dataset for predic-

tive modeling. Our method employs Allan variance, originally developed for frequency stability analysis of

atomic clocks, to dynamically adjust the granularity of data aggregation based on the inherent structure and

characteristics of the dataset. By minimizing bias across different scales, Adaptive Granulation effectively

manages trade-offs between diverse aspects of the data such as underlying patterns, noise levels, and sampling

density. This paper outlines the algorithmic strategies for implementing Adaptive Granulation at the database

level and assesses its performance through the reduction of the training set size for a downstream regression

task on a variety of real-world and synthetic datasets. The results indicate that our method can adaptively

optimize granule sizes to effectively balance data patterns, noise levels, and sample densities across the entire

data space. Adaptive Granulation thus represents a signiﬁcant advancement for efﬁcient data management and

reduction in the big data era.

1 INTRODUCTION

Data reduction methods are increasingly becoming

vital in our data-driven world. As the proliferation

of big data continues across various sectors, includ-

ing healthcare (Raghupathi and Raghupathi, 2014),

ﬁnance (Hasan et al., 2020), social media (Sahatiya,

2018), e-commerce (Akter and Wamba, 2016), traf-

ﬁc (Lv et al., 2015; Kim and Jerath, 2022) and more

(Chen et al., 2014), the sheer volume of data we gen-

erate is staggering. For example, in healthcare, pa-

tient records, wearable device outputs, and genomic

data produce immense amounts of data. Social me-

dia platforms like Facebook and Twitter generate mil-

lions of posts and interactions daily. Retail giants like

Amazon collect data about customer behavior, prefer-

https://orcid.org/0000-0002-6772-6266

https://orcid.org/0000-0002-4146-3402

https://orcid.org/0000-0002-8712-8108

https://orcid.org/0000-0001-6356-9438

ences, and purchasing habits on a massive scale. It is

estimated that we are generating more than 2.5 quin-

tillion bytes of data each day (Zicari, 2012), and this

rate is only expected to increase with advancements

in technology and increased internet accessibility. By

2025, it is projected that there will be more than 180

zettabytes of data in the world (Holst, 2021).

Utilizing such large amounts of data for inference,

as well as storing them in databases, is increasingly

becoming an untenable exercise. While big data can

provide valuable insights and aid decision-making, it

can also overwhelm our computational and memory

resources, thus hindering effective analysis. While

studies have explored the use of cloud-based and

edge-based units, training data-driven models on ex-

tensive datasets presents multiple challenges. Firstly,

we require signiﬁcant computational resources, in-

cluding substantial processing power and memory.

This potentially constrains usage by individuals or or-

ganizations with limited computational capabilities.

Haeri, H., Kathiriya, N., Chen, C. and Jerath, K.

Adaptive Granulation: Data Reduction at the Database Level.

DOI: 10.5220/0012190700003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 3: KMIS, pages 29-39

ISBN: 978-989-758-671-2; ISSN: 2184-3228

Secondly, the time to train a model can substantially

increase with larger datasets, causing potential delays

in the implementation and deployment of models that

may be critical for time-sensitive applications. Fi-

nally, while more data generally reduces overﬁtting,

if the dataset contains a high degree of noise or ir-

relevant features, models could potentially overlearn

these aspects, negatively impacting performance on

unseen data.

Therefore, data reduction methods, which seek to

reduce the volume of data while preserving its criti-

cal information, are becoming increasingly important.

These methods allow us to manage and analyze large

datasets more efﬁciently and effectively, thereby un-

locking the potential of big data while avoiding the

pitfalls of data overload. Then, data reduction is not

just a practical necessity; it is a critical step in trans-

forming raw data into meaningful insights.

To address these complexities induced by big data,

we present a novel and innovative approach to data re-

duction at the database level itself, which we term as

Adaptive Granulation (AG). Our approach provides

a systematic way to balance the competing desires to

maintain high data ﬁdelity (and hence increase model

predictive power) and to reduce the size of the data

(and hence speed up training times). Our novel ap-

proach is inspired by the concept of Allan variance,

which was originally developed to manage similar

competing interests while examining the frequency

stability of atomic clocks (Allan, 1966). As an addi-

tional advantage, this approach enables the reduction

of the database size as well, resulting in faster approx-

imate query response times. Thus, Adaptive Granula-

tion excels in the context of big data by offering an

efﬁcient and effective means to manage and process

large volumes of data for training data-driven models,

while leveraging the capabilities of the database itself.

2 RELATED WORK

Data reduction, especially in large datasets, is cru-

cial for improving the efﬁciency of data-driven mod-

els (Sandhu, 2021). Classical methods include simple

random sampling, stratiﬁed sampling (Zhang et al.,

2022), and reservoir sampling (Kim et al., 2020).

However, with the rise of big data, methods like

record-level and block-level sampling have gained

prominence (Hasanin et al., 2019). The former can

be less efﬁcient on distributed data, while the latter,

using traditional partitioning, may not always provide

representative samples (Mahmud et al., 2020). In this

work, we introduce a new block-level sampling tech-

nique optimized for enhanced performance in regres-

sion tasks.

Researchers in the ﬁeld of machine learning have

primarily approached this methodology from perspec-

tives that are speciﬁc to the machine learning al-

gorithms themselves, i.e., there exist data reduction

methods for speciﬁc applications to Support Vector

Machines (SVMs), decision trees, and neural net-

works, to name a few (Alwajidi, 2020; Mahmud et al.,

2020; ur Rehman et al., 2016). Here, we brieﬂy re-

view some of these methods from the viewpoint of

the ML algorithms.

Support Vector Machines: For SVMs, one of the

main challenges is to reduce the number of support

vectors, which determine the decision boundary and

affect the computational cost and generalization abil-

ity of the model. Several approaches have been pro-

posed to select a subset of support vectors or training

samples that can approximate the original decision

boundary with minimal loss of accuracy (Birzhandi

et al., 2022). For example, prior works have demon-

strated the use of clustering-based techniques to iden-

tify and remove non-relevant samples that are far from

the decision boundary (Koggalage and Halgamuge,

2004; Yao et al., 2013; Santana et al., 2020). Ghaf-

fari has proposed a method to divide the training set

into boundary, non-boundary, and harmful patterns,

and then select representatives of non-boundary data

and combine them with boundary patterns to form a

reduced set (Ghaffari, 2021). Other methods include

using information entropy (Zhan and Shen, 2005),

chunking (Hsieh et al., 2008), or regression (Osuna

and Girosi, 1998) to reduce the number of training

samples for SVMs. Most of these data reduction

methods rely on a fundamental characteristic of the

SVM: that learning with the SVM algorithm is de-

pendent on only a few support vectors, as compared

to the totality of available data.

Decision Trees: For decision trees, one of the main

challenges is to manage the tree size and complex-

ity, which affect the interpretability and generaliza-

tion ability of the model. Several approaches have

been proposed to prune or simplify the tree structure

after or during the tree construction process. For ex-

ample, (Oates and Jensen, 1997) studied the effects

of training set size on decision tree complexity and

showed that increasing training set size often results

in a linear increase in tree size, even when that addi-

tional complexity results in no signiﬁcant increase in

classiﬁcation accuracy. They argued that random data

reduction is a baseline against which more sophisti-

cated data reduction techniques should be compared.

Other methods include using misclassiﬁcation costs

(Bradford et al., 1998), Laplace correction (Brodley

and Friedl, 1999), or error-based pruning (Peng et al.,

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

2021) to prune decision trees.

Neural Networks: For neural networks, one of

the main challenges is to handle large-scale vision-

language pre-training tasks, which require huge

amounts of data and computational resources. Sev-

eral approaches have been proposed to reduce the data

size or complexity for such tasks. For example, (Jin-

peng Wang et al., 2023) proposed a method called

Too Large; Data Reduction for Vision-Language Pre-

Training (TL;DR), which uses a two-stage process to

select a subset of image-text pairs that are informative

and diverse for pre-training vision-language models.

They showed that their method can achieve compara-

ble or better performance than existing methods with

much fewer data and computation time.

Adaptive Granulation differs from the existing

data reduction methods in several ways. First, it is

a systematic preprocessing method that can be uti-

lized by any data-driven model, such as SVMs, de-

cision trees, or neural networks. Unlike the methods

that are tailored for speciﬁc models or tasks, Adap-

tive Granulation does not rely on any model-speciﬁc

assumptions or parameters. Second, it is a ﬂexible

method that can dynamically adjust the granularity

level based on the underlying structure and charac-

teristics of the data using Allan variance. Unlike the

methods that use a ﬁxed or uniform level of granular-

ity across the entire dataset, Adaptive Granulation can

accommodate variations in pattern complexity, noise,

and sampling density within different sections of the

dataset. Finally, our method has the additional advan-

tage that it fundamentally operates in and leverages

the database itself. This leads to a signiﬁcant sim-

pliﬁcation of data reduction, storage, and retrieval:

all precursors to subsequent machine learning steps.

These differences make Adaptive Granulation a pow-

erful and versatile data reduction method that can ef-

fectively reduce data volume while preserving crucial

information inherent in the dataset. In the next sec-

tion, we discuss the method in more detail.

3 ADAPTIVE GRANULATION

Adaptive Granulation is an innovative approach to

data reduction that aims to effectively reduce data vol-

ume while preserving crucial information inherent in

the dataset. This method is particularly useful in the

context of big data, where handling and processing

large amounts of data efﬁciently and effectively be-

comes challenging.

By dynamically adjusting the granularity level,

Adaptive Granulation aggregates data points based on

their underlying structure and characteristics (Mad-

dipatla et al., 2023; Maddipatla et al., 2021). The

granularity here refers to the level of detail or scale

at which the data is considered or analyzed. For in-

stance, in a one-dimensional temporal dataset, granu-

larity might refer to whether the data is examined on a

yearly, monthly, daily, or hourly basis. It is important

to note that the algorithm automatically determines

the optimal level of granulation (Sinanaj et al., 2022;

Haeri et al., 2021; Haeri et al., 2022).

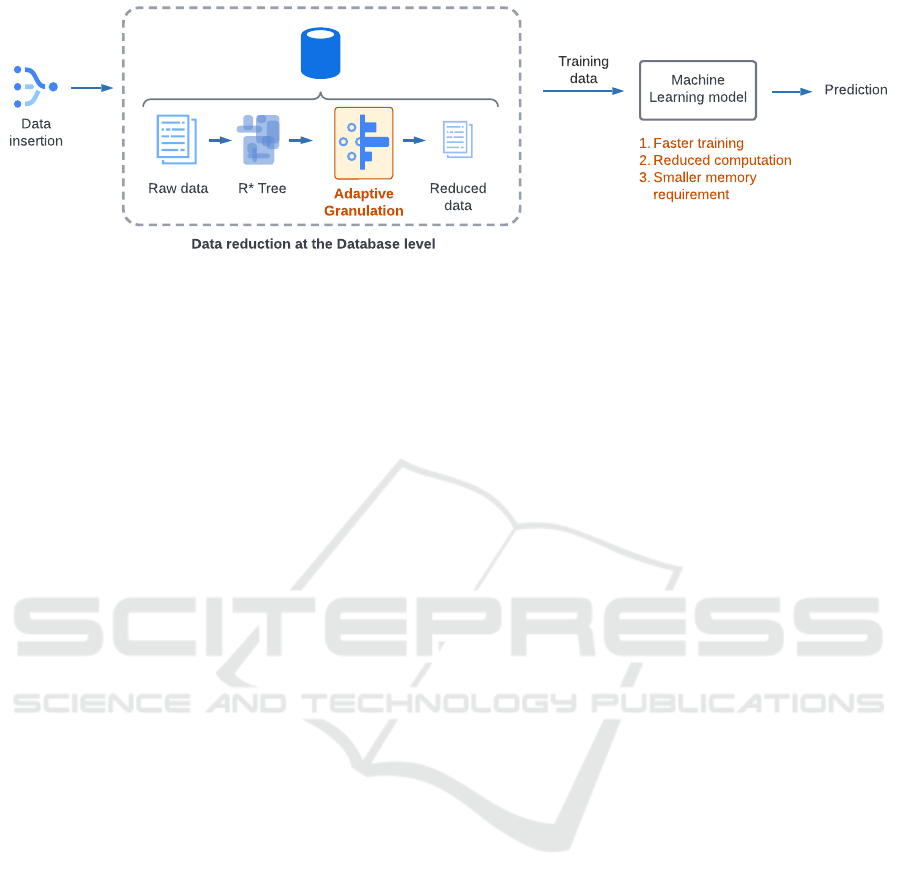
The overarching workﬂow of this study is de-

picted in Figure 1 which can be summarized as the

following. Initially, a vast assortment of data points

is incorporated as raw data into the database. These

data points subsequently serve as the foundation for

the creation of an R* tree, a spatial indexing mecha-

nism that facilitates hierarchical granulation or clus-

tering of data into nested minimum bounding rectan-

gles (MBRs). We then introduce Allan variance as

an innovative method to adaptively granulate the data

by pinpointing the optimal scale of data granularity.

This is achieved by identifying the level of granules

that exhibits the minimum Allan variance in compar-

ison to their parent and child granules, as will be dis-

cussed in Algorithm 1. The outcome of this procedure

is a series of non-nested granules that constitute a re-

duced dataset. In the ﬁnal step of our approach, the re-

duced dataset is formed by computing the centroid as

well as the average value of the target attribute. This

transformation allows us to retain the most descriptive

characteristics of the data (i.e., information that can

be effectively used for a downstream prediction task)

while signiﬁcantly reducing the volume, aiding in the

efﬁcient analysis and modeling of large datasets.

3.1 R* Tree as a Hierarchical

Clustering Data Structure

Adaptive Granulation leverages the R* tree structure

used to organize multi-dimensional large data sets.

First, data is inserted into an R* tree. This process

involves splitting and adjusting nodes in the tree to ac-

commodate the new data while maintaining the tree’s

balance and minimizing the overlapping area of the

MBRs. More details about the process of R* tree cre-

ation can be found in (Beckmann et al., 1990). The

R* tree structures data points into a nested set of Min-

imum Bounding Rectangles (MBR) where each MBR

represents a region in the multi-dimensional space

that contains one or more data points or other MBRs.

In the following discussion, we assume that x ∈ X

represents an input vector in a d

-dimensional feature

space, and y ∈ Y represent the target attribute vec-

tor in d

-dimensional space, which we are attempt-

ing to predict. Now, we begin with the large dataset

Adaptive Granulation: Data Reduction at the Database Level

Data

insertion

R* Tree

Machine

Learning model

Data reduction at the Database level

Training

data

Raw data

Adaptive

Granulation

Reduced

data

1.Faster training

2.Reduced computation

3.Smaller memory

requirement

Prediction

Figure 1: Adaptive Granulation can be deployed at the database level in order to reduce the size of training data set.

D = {(x

)} where i = {1,2,..., N} and N is the

total number of data points in the original dataset.

Next, we seek to use the Adaptive Granulation al-

gorithm to create a representative reduced data set

red

= {(

)} containing aggregated data points,

where j = {1, 2,.. .,N

red

} and N

red

denotes the total

number of data points in the reduced data set, with

the expectation that the AG algorithm will systemati-

cally lead to N

red

≪ N. We deﬁne the reduction ratio

as ζ = 1 − N

red

/N, to represent the magnitude of data

that was removed from the original dataset.

Let M be the set of all the MBRs in the R*

tree. Each MBR, m ∈ M , is identiﬁed by a tuple

min

max

, p

, ¯y

,σ

), where

• r

∈ {0, 1,2,.. .} denotes the level of the MBR in

the R* tree. In our work, level r = 0 represents the

actual data points, and the level number increases

as we move from the tree leaves towards the root.

• x

min

and x

max

are d

-dimensional vectors repre-

senting the minimum and maximum bounds of the

MBR in the multi-dimensional feature space,

• C

⊂ M is the set containing all the children of

MBR m, and the children themselves are MBRs

in the R* tree residing at level r

− 1,

• p

∈ M represents the parent of the MBR m, and

the parent is also an MBR in the R* tree residing

at level r

+ 1,

•

is a d

-dimensional vector representing the av-

erage of the target attribute vectors of the children

of the MBR m,

• σ

∈ R

is the Allan variance of the MBR m, and

is a measure of the variability within the MBR

which is discussed in the next subsection.

3.2 Using Allan Variance to Determine

the Granularity Level

The notion of Allan variance (AVAR) was ﬁrst intro-

duced by David Allan as a way to study the statistics

of frequency stability in precision oscillators such as

atomic clocks (Allan, 1966). The fundamental idea

seeks to address the phenomenon where the oscilla-

tory behavior of such systems can be noisy as well

as drift at the same time. The competition between

noise and signal makes it difﬁcult to determine the

optimal timescale that should be used to ascertain the

frequency of the atomic clock. In the context of the

current work, this can be thought of as being similar

to balancing two aspects: (a) minimizing the effects

of noise in the data reduction process, while (b) max-

imizing the ability to capture the underlying patterns

(or ‘drift’) present in the data, even as we reduce its

size. For example, if data reduction is performed via

aggregation at too small of a scale, then a signiﬁcant

amount of noise will remain in the reduced data set,

representing a missed opportunity to further reduce

the size of the dataset (Yang et al., 2021). Similarly,

if data reduction is performed via aggregation at too

large of a scale, we will manage to signiﬁcantly re-

duce the size of the data, but at the cost of poorer

predictive performance. In such scenarios, Allan vari-

ance can help us determine the optimal scale that min-

imizes the bias in the averaged signal (Jerath et al.,

2018; Haeri et al., 2021; Sinanaj, 2021; Haeri et al.,

2022), in effect providing a data reduction or aggre-

gation scale that optimally groups data points.

Thus, leveraging the principles of Allan vari-

ance, we can propose a measure of stability across

a dataset’s feature space. Prior studies have corrob-

orated the efﬁcacy of Allan variance in discerning

the ideal granule size for temporal database granu-

lation (Sinanaj et al., 2022; Sinanaj, 2021). Fur-

ther, it has been demonstrated that employing this ap-

proach facilitates optimal averaging scales for mov-

ing average estimation tasks (Haeri et al., 2022; Haeri

et al., 2020). In the present work, we build on these

foundations, charting new territory in two main direc-

tions. As an important distinction from other previ-

ous works, we extend the concept of granulation to a

multi-dimensional data environment. Equally as im-

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

portantly, we introduce an adaptive mechanism to de-

termine the granularity scale, enabling dynamic data

reduction in heterogeneous characteristics observed

across the feature space of the dataset.

The Allan variance for the MBR m can be calcu-

lated as

∑

c∈C

−

(1)

where c is a child MBR in the set C

, and

is its

average target attribute. Further, for each MBR m,

is obtained by

∑

c∈C

. (2)

In this framework, Allan variance serves as a met-

ric to assess the variability in multi-dimensional data

speciﬁc to the level of an MBR. It is important to

highlight that, in our research, σ

signiﬁes the vari-

ance of the average values from the child MBRs,

rather than the variance of individual data points

within that MBR. This variance provides insight into

the dispersion of the data points of child MBRs nested

within the MBR m. Depending on the characteristics

of the dataset, these calculations may produce differ-

ent values of the Allan variance (a) for MBRs at dif-

ferent levels r in the R* tree, but in the same general

region of the feature space, and (b) for MBRs at the

same level r, but in different regions of the feature

space. A large value of Allan variance in a speciﬁc

MBR at a speciﬁc level can be indicative of one or

more of the following phenomena:

(a) Rapid change in underlying data pattern. If the

data pattern is changing rapidly at a speciﬁc scale

and feature space region, the AVAR of the asso-

ciated MBR may be large. Using aggregated data

of this MBR as the reduced data point will lead

to a failure to capture the underlying pattern in

the dataset. This will produce smaller-sized, but

lower ﬁdelity reduced datasets.

(b) Signiﬁcant presence of noise. If the data is very

noisy at a speciﬁc scale and feature space region,

then the AVAR of the associated MBR may also

be large. Using aggregation to reduce data in

this situation will lead to capture of lot of noise

but less meaningful data patterns. This will pro-

duce higher ﬁdelity, but larger datasets without

any meaningful data reduction.

By opting for the level of granulation linked with the

minimum Allan variance, this trade-off is effectively

managed – striking a balance between data reduction

and preservation of essential information. We discuss

this further in Section 4. The overall procedure for

implementing Adaptive Granulation is depicted in Al-

gorithm 1. The algorithm begins by requiring a list

M of all the MBRs in the tree which are sorted in

ascending order according to their level, r

. In the

ﬁrst loop the Allan variance of each MBR is calcu-

lated based on Equation (1) which itself requires cal-

culating averages using Equation (2). If the MBR is

at level 0 (indicating it is a leaf node), the granulation

ﬂag is set to True; otherwise, it is set to False. This

initialization prepares the MBRs for the subsequent

steps of the algorithm. In the subsequent loop, for

each MBR in M , if every child of the current MBR

has its granulation ﬂag marked as True, and the Al-

lan variance of this MBR is smaller than that of any

of its children, the current MBR’s granulation ﬂag is

updated to True, while the ﬂags of all its children

are reset to False. This step ensures the MBR that

is selected as a granule has a variance (as deﬁned in

Equation 1) that is smaller than both its parent and

any of its children, and thus represents the optimal

granulation level. This process can also be thought

of as elevating the granulation ﬂag to a higher level,

suggesting that the target attribute exhibits less vari-

ability at a broader granulation scale. The algorithm

then concludes by returning all MBRs whose granula-

tion ﬂag is True. These selected MBRs represent the

data points that have been adaptively granulated, and

they form the reduced dataset for further analysis or

modeling tasks. According to Algorithm 1, each data

point in the R* tree will be encompassed by a singu-

lar MBR with the True granulation ﬂag. This holds

as every data point starts with a true ﬂag, and when

the algorithm opts to transfer this ﬂag to the parent-

level MBR, all its child nodes relinquish their ﬂags.

Such systematically-generated granules will provide

the best trade-off between data reduction (eliminating

noise) and data retention (keeping data patterns), irre-

spective of the eventual prediction algorithm that will

be used.

4 RESULTS AND DISCUSSION

In this section, the performance of Adaptive Granula-

tion as a data reduction method is evaluated for three

synthetic and six real-world datasets. We benchmark

the efﬁcacy of Adaptive Granulation against random

sampling—a fundamental baseline in data reduction

that, despite its simplicity, has been demonstrated to

outperform many advanced sampling methods in the

literature (Oates and Jensen, 1997; Hasanin et al.,

2019).

Our experimental setup involves comparing the

Mean Absolute Error (MAE) of various machine

Adaptive Granulation: Data Reduction at the Database Level

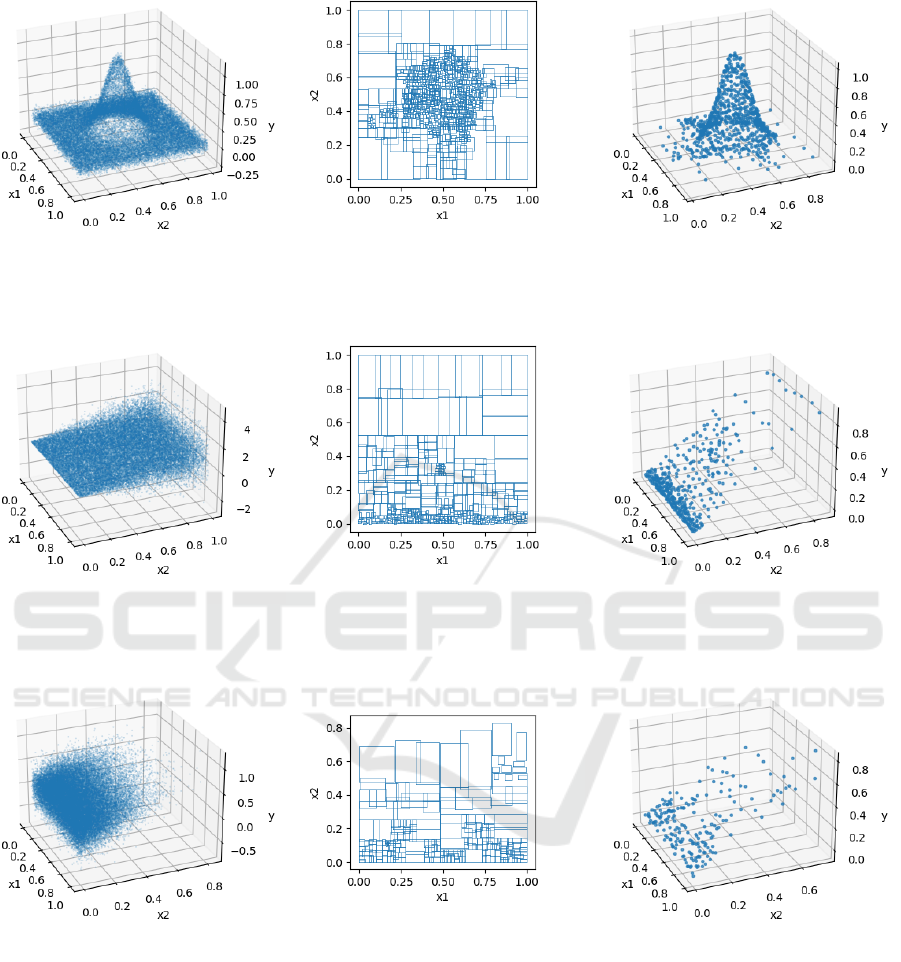
(a) (b) (c)

Figure 2: A synthetic data aggregation scenario with varying underlying pattern complexity. (a) Input data points. (b)

Generated granules using Adaptive Granulation. (c) Granule centroids (y value denotes average granule target attribute).

(a) (b) (c)

Figure 3: A synthetic data aggregation scenario with varying noise characteristics along the x

axis. (a) Input data points. (b)

Generated granules using Adaptive Granulation. (c) Granule centroids (y value denotes average granule target attribute).

(a) (b) (c)

Figure 4: A synthetic data aggregation scenario with varying data density along the x

axis. (a) Input data points. (b)

Generated granules using Adaptive Granulation. (c) Granule centroids (y value denotes average granule target attribute).

learning models. The complete dataset is initially

split into train and test datasets, with the test data

constituting 30% of the total. The Adaptive Gran-

ulation method is then applied to the training data,

using various fan-out values for the R* tree, which

represents the maximum number of children within

a single MBR. The centroids of the resulting gran-

ules serve as data points in the reduced dataset. As

a baseline comparison, an equivalent number of data

points are sampled randomly from the training data.

The evaluation process is performed 100 times for

each fan-out value, which varies from 8 to 64 with

a step size of 4. Model tuning is performed using the

RandomSearchCV function from the sklearn library,

with 100 iterations and 3-fold cross-validation.

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

Algorithm 1: Adaptive Granulation.

Require: List of all MBRs, M , in the R* tree

1: for each ordered m in M do

2: Calculate σ

according to Eq. (1) and (2)

3: end for

4: Set m.is granule to True for MBRs at level 0

and to False for all others.

5: for each ordered m in M do

6: if all children c in C

are granules, and have σ

< σ

then

7: m.is granule ← True

8: for each c in C

9: c.is granule ← False

10: end for

11: end if

12: end for

13: return MBRs in M with is granule == True

4.1 Synthetic Scenarios

Unlike conventional data reduction techniques that

apply a ﬁxed level of granularity across the entire

dataset, Adaptive Granulation is ﬂexible. It recog-

nizes that different portions of the dataset might re-

quire different levels of granularity depending on their

underlying pattern complexity, noise, and density. In

this subsection, we assess the efﬁcacy of Adaptive

Granulation through three synthetic datasets. For

these, data points are synthesized from the joint dis-

tribution f (x

,y) where x

and x

are independent

features, drawn from distributions f

and f

, respec-

tively. The target attribute, y, is produced in accor-

dance with a deterministic pattern function, supple-

mented by a stochastic noise function. In the subse-

quent sections, we outline the setup for these scenar-

ios and explore the inﬂuence of these three factors on

the determination of granule sizes.

1. Underlying Pattern Complexity: When the

complexity of the patterns in the data is high,

small granules (i.e., a ﬁner granularity) may be

needed to capture the details of these patterns.

High complexity could be due to non-linear rela-

tionships between variables, the presence of many

interacting variables, or rapidly changing patterns.

In such cases, a coarse granularity could over-

simplify the data and fail to capture these com-

plexities, resulting in the loss of crucial informa-

tion. In this experimental scenario, f

and f

are

independent uniform distributions (U(0,1)) and

the noise function is a zero mean Gaussian dis-

tribution which is consistent across both x

and

dimensions (N (0, 0.05I)). The target values y

are generated according to a squared exponential

Gaussian pattern function located at (0.5,0.5). As

shown in Figure 2, Adaptive Granulation selects

smaller granules in regions where the Gaussian

dome is rising, capturing the details of the pat-

tern. Conversely, in areas where the underlying

data pattern exhibits less variation, the Adaptive

Granulation process opts for larger granule sizes,

effectively balancing the granularity level with the

inherent complexity of the data.

2. Noise: Noise refers to random or irrelevant vari-

ation in the data. When the level of noise in

the dataset is high, it can be beneﬁcial to use

larger granules (i.e., a coarser granularity). This

is because a ﬁner granularity could risk overﬁt-

ting to the noise, leading to less accurate or less

meaningful results. By aggregating the data at a

coarser level, Adaptive Granulation can smooth

out the noise and reveal the underlying patterns

or trends in the data. Conversely, when the noise

level is low, a ﬁner granularity may be used to

capture more detailed patterns. In this scenario,

and f

are independent uniform distributions

(U(0,1)). The target attribute, y, is determined by

a linear pattern function across the x

dimension

(i.e., y = x

) and is supplemented by zero mean

Gaussian noise. This noise remains consistent

across the x

dimension but varies along the x

dimension, speciﬁcally conforming to N (0,x

As illustrated in Figure 3, Adaptive Granulation

tends towards the selection of larger granules as

the magnitude of noise escalates.

3. Sampling Density: Sampling density refers to the

number of data points in a given space. When the

sampling density is high, there are many closely

packed data points, and a ﬁner granularity may be

needed to capture the variation within this dense

space. Conversely, when the sampling density is

low, the data points are sparse and spread out, and

a coarser granularity might sufﬁce to capture the

essential characteristics of the data. By adjust-

ing the granule size based on the sampling den-

sity, Adaptive Granulation ensures that neither the

dense nor the sparse areas of the dataset are un-

der or over-represented. In this scenario, f

is a

uniform distribution (U(0,1)), however, f

is a

half-normal distribution (i.e., |N (0, 0.2 x

)|). The

target attribute, y, is determined by a linear pat-

tern function across the x

dimension (i.e., y = x

)

and is supplemented by zero mean Gaussian noise

which is consistent across both x

and x

dimen-

sions (N (0, 0.2)).

Adaptive Granulation: Data Reduction at the Database Level

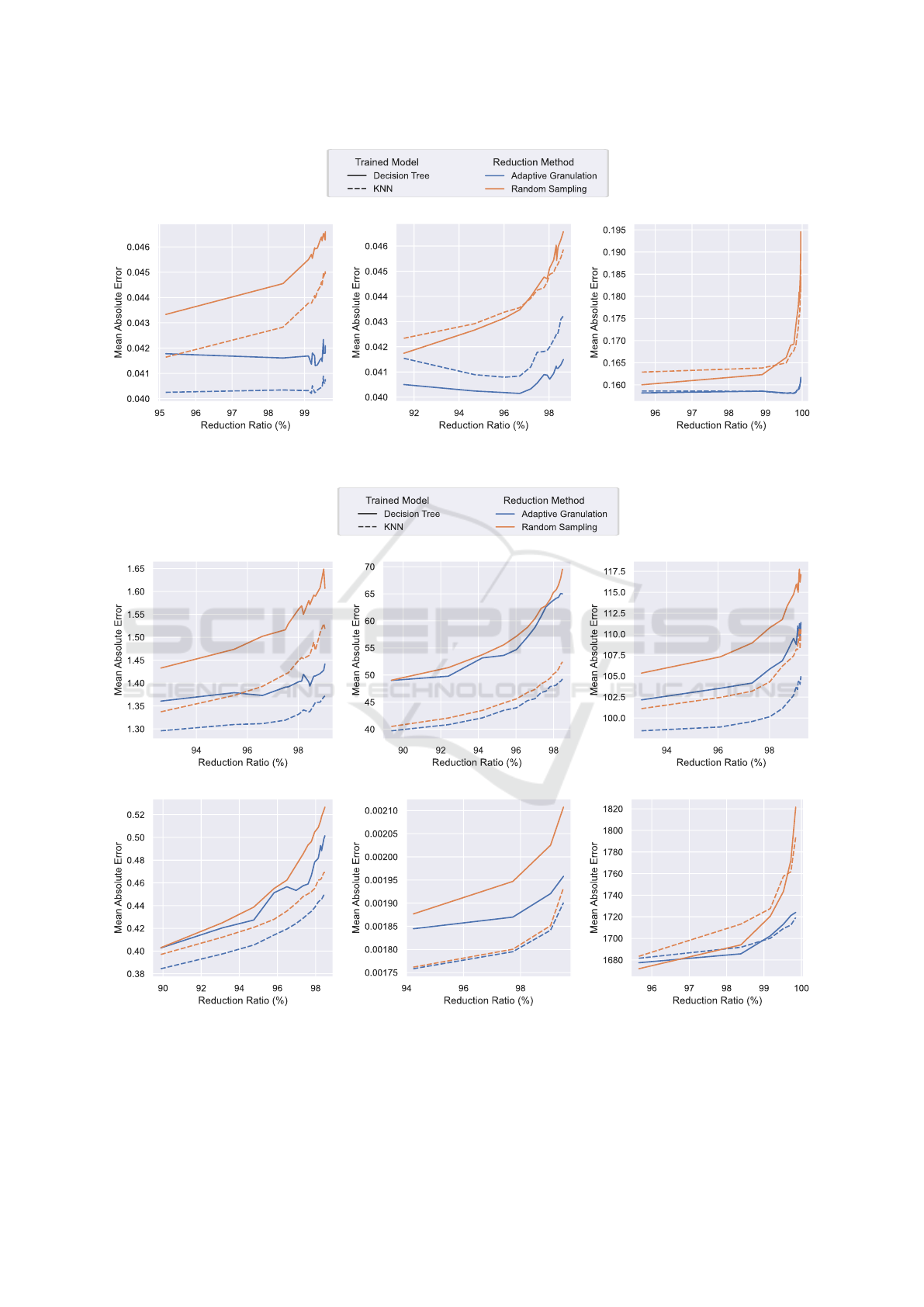
(a) Pattern varying scenario (b) Noise varying scenario (c) Density varying scenario

Figure 5: Mean Absolute Error comparison on synthetic datasets. The reported values represent the average results across

100 repeated runs.

(a) Abalone (b) Air Quality (c) Bike

(f) Metro Interstate Traffic(e) Elevators(d) California Housing

Figure 6: Mean Absolute Error comparison on real-world datasets.

4.2 Real-World Scenarios

In this subsection, we have evaluated Adaptive Gran-

ulation in six real-world datasets: (1) Abalone, en-

compassing 4,000 records (Nash et al., 1995); (2)

Air Quality, incorporating 9,000 records (Vito, 2016);

(3) Bike, containing 10,000 records (Fanaee-T and

Gama, 2014); (4) California Housing, which has

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

20,000 records (Pace and Barry, 1997); (5) Elevators,

with 16,000 records; and (6) Metro Interstate Trafﬁc

Volume, comprising 48,000 records (Hogue, 2019).

To ensure the integrity of our data prior to analy-

sis, we employ a two-pronged preprocessing strategy.

First, we eliminate any outliers using the Interquar-

tile Range (IQR) rule, whereby data points more than

1.5 times the IQR distant from the ﬁrst or third quar-

tiles are discarded. Second, we perform feature se-

lection based on the importance of each feature. The

importance is quantiﬁed by the mutual information,

calculated using the sklearn.feature selection

module. Both preprocessing steps are required since

the presence of outliers can distort the resultant gran-

ules, whereas the inclusion of non-informative fea-

tures could lead to the creation of suboptimal or ar-

bitrary granules. From the results of both synthetic

data (Figure 5) and real-world data (Figure 6), we

conclude that a model trained with Adaptive Granu-

lated data performs better than the same model trained

with randomly sampled data.

5 CONCLUDING REMARKS

In this study, we have introduced and evaluated Adap-

tive Granulation, a novel and efﬁcient data reduc-

tion technique designed to handle the growing chal-

lenges presented by the enormous volumes of data in

our digital era. In this work, we have demonstrated

that Adaptive Granulation can successfully condense

large datasets into dynamically sized granules of ag-

gregated data. The uniqueness of this method lies in

its intelligent and systematic aggregation process that

takes into consideration the noise characteristics of

the dataset, the underlying data patterns, and the data

sample density. Importantly, the use of Allan vari-

ance in the granulation process helps produce a com-

pact and less demanding dataset while preserving the

ﬁdelity of the original information. Perhaps equally

as importantly, we emphasize that Adaptive Granula-

tion can be implemented at the database level itself.

This feature offers the advantage of managing and re-

ducing data within the storage system, eliminating the

need to handle raw, unwieldy datasets directly. This

in-situ processing capability makes Adaptive Granu-

lation an attractive solution for efﬁcient data manage-

ment in data-intensive applications. However, it is

important to note that our proposed method is con-

strained to numerical values, as outlined in this pa-

per, due to the inherent inability of the averaging pro-

cess to accommodate categorical ﬁelds. Our empiri-

cal evaluation reveals that the reduced datasets gener-

ated through Adaptive Granulation are highly effec-

tive for downstream inference tasks. Speciﬁcally, our

tests have shown that models trained on these reﬁned

datasets perform comparably to those trained on ran-

domly sampled datasets, beneﬁting from a signiﬁcant

decrease in training time and resource requirements.

The capacity of Adaptive Granulation to balance the

trade-off between data size and pattern preservation,

coupled with its ease of implementation within the

database, makes it a powerful tool for handling the

complexities of Big Data. We expect this approach

to enable more efﬁcient utilization of large datasets in

training predictive models, ultimately leading to bet-

ter resource management and improved outcomes in

data-intensive domains.

ACKNOWLEDGEMENTS

This material is based upon work supported by

the National Science Foundation under Grant No.

1932138. Any opinions, ﬁndings, and conclusions or

recommendations expressed in this material are those

of the authors and do not necessarily reﬂect the views

of the National Science Foundation.

REFERENCES

Akter, S. and Wamba, S. F. (2016). Big data analytics in e-

commerce: a systematic review and agenda for future

research. Electronic Markets, 26:173–194.

Allan, D. W. (1966). Statistics of atomic frequency stan-

dards. Proceedings of the IEEE, 54(2):221–230.

Alwajidi, S. K. (2020). Hierarchical Aggregation of Mul-

tidimensional Data for Efﬁcient Data Mining. PhD

thesis, Western Michigan University.

Beckmann, N., Kriegel, H.-P., Schneider, R., and Seeger,

B. (1990). The r*-tree: An efﬁcient and robust access

method for points and rectangles. In Proceedings of

the 1990 ACM SIGMOD international conference on

Management of data, pages 322–331.

Birzhandi, P., Kim, K. T., and Youn, H. Y. (2022). Re-

duction of training data for support vector machine: a

survey. Soft Computing, 26(8):3729–3742.

Bradford, J. P., Kunz, C., Kohavi, R., Brunk, C., and Brod-

ley, C. E. (1998). Pruning decision trees with mis-

classiﬁcation costs. In Machine Learning: ECML-

98: 10th European Conference on Machine Learning

Chemnitz, Germany, April 21–23, 1998 Proceedings

10, pages 131–136. Springer.

Brodley, C. E. and Friedl, M. A. (1999). Identifying mis-

labeled training data. Journal of artiﬁcial intelligence

research, 11:131–167.

Chen, M., Mao, S., and Liu, Y. (2014). Big data: A survey.

Mobile networks and applications, 19:171–209.

Adaptive Granulation: Data Reduction at the Database Level

Fanaee-T, H. and Gama, J. (2014). Event labeling combin-

ing ensemble detectors and background knowledge.

Progress in Artiﬁcial Intelligence, 2:113–127.

Ghaffari, H. R. (2021). Speeding up the testing and train-

ing time for the support vector machines with minimal

effect on the performance. The Journal of Supercom-

puting, 77(10):11390–11409.

Haeri, H., Beal, C. E., and Jerath, K. (2020). Near-

optimal moving average estimation at characteristic

timescales: An allan variance approach. IEEE Con-

trol Systems Letters, 5(5):1531–1536.

Haeri, H., Beal, C. E., and Jerath, K. (2021). Near-

optimal moving average estimation at characteristic

timescales: An allan variance approach. IEEE Con-

trol Systems Letters, 5(5):1531–1536.

Haeri, H., Soleimani, B., and Jerath, K. (2022). Optimal

moving average estimation of noisy random walks us-

ing allan variance-informed window length. In 2022

American Control Conference (ACC), pages 1646–

1651. IEEE.

Hasan, M. M., Popp, J., and Ol

ah, J. (2020). Current land-

scape and inﬂuence of big data on ﬁnance. Journal of

Big Data, 7(1):1–17.

Hasanin, T., Khoshgoftaar, T. M., Leevy, J. L., and Bauder,

R. A. (2019). Severely imbalanced big data chal-

lenges: investigating data sampling approaches. Jour-

nal of Big Data, 6(1):1–25.

Hogue, J. (2019). Metro Interstate Trafﬁc Vol-

ume. UCI Machine Learning Repository. DOI:

https://doi.org/10.24432/C5X60B.

Holst, A. (2021). Amount of data created, consumed, and

stored 2010-2025. Technology & Telecommunications

Retrieved, pages 06–29.

Hsieh, C.-J., Chang, K.-W., Lin, C.-J., Keerthi, S. S., and

Sundararajan, S. (2008). A dual coordinate descent

method for large-scale linear svm. In Proceedings of

the 25th international conference on Machine learn-

ing, pages 408–415.

Jerath, K., Brennan, S., and Lagoa, C. (2018). Bridging the

gap between sensor noise modeling and sensor char-

acterization. Measurement, 116:350–366.

Jinpeng Wang, A., Qinghong Lin, K., Junhao Zhang, D.,

Weixian Lei, S., and Shou, M. Z. (2023). Too large;

data reduction for vision-language pre-training. arXiv

e-prints, pages arXiv–2305.

Kim, C. D., Jeong, J., and Kim, G. (2020). Imbalanced con-

tinual learning with partitioning reservoir sampling. In

Computer Vision–ECCV 2020: 16th European Con-

ference, Glasgow, UK, August 23–28, 2020, Proceed-

ings, Part XIII 16, pages 411–428. Springer.

Kim, T. and Jerath, K. (2022). Congestion-aware coop-

erative adaptive cruise control for mitigation of self-

organized trafﬁc jams. IEEE Transactions on Intelli-

gent Transportation Systems, 23(7):6621–6632.

Koggalage, R. and Halgamuge, S. (2004). Reducing the

number of training samples for fast support vector ma-

chine classiﬁcation. Neural Information Processing-

Letters and Reviews, 2(3):57–65.

Lv, Y., Duan, Y., Kang, W., Li, Z., and Wang, F.-Y. (2015).

Trafﬁc ﬂow prediction with big data: A deep learn-

ing approach. IEEE Transactions on Intelligent Trans-

portation Systems, 16(2):865–873.

Maddipatla, S. P., Haeri, H., Jerath, K., and Brennan, S.

(2021). Fast allan variance (favar) and dynamic fast

allan variance (d-favar) algorithms for both regularly

and irregularly sampled data. IFAC-PapersOnLine,

54(20):26–31.

Maddipatla, S. P., Pakala, R., Haeri, H., Chen, C., Jerath,

K., and Brennan, S. (2023). Using databases to imple-

ment algorithms: Estimation of allan variance using

b+-tree data structure. In Proc. of the Modeling, Esti-

mation, and Control Conf. 2023, Lake Tahoe, NV.

Mahmud, M. S., Huang, J. Z., Salloum, S., Emara, T. Z.,

and Sadatdiynov, K. (2020). A survey of data par-

titioning and sampling methods to support big data

analysis. Big Data Mining and Analytics, 3(2).

Nash, W., Sellers, T., Talbot, S., Cawthorn, A., and Ford, W.

(1995). Abalone. UCI Machine Learning Repository.

DOI: https://doi.org/10.24432/C55C7W.

Oates, T. and Jensen, D. (1997). The effects of training

set size on decision tree complexity. In Sixth Interna-

tional Workshop on Artiﬁcial Intelligence and Statis-

tics, pages 379–390. PMLR.

Osuna, E. and Girosi, F. (1998). Reducing the run-time

complexity of support vector machines. In Interna-

tional Conference on Pattern Recognition (submitted).

Pace, R. K. and Barry, R. (1997). Sparse spatial autoregres-

sions. Statistics & Probability Letters, 33(3):291–297.

Peng, Y., Lu, Y.-T., and Chen, Z.-G. (2021). An improved

error-based pruning algorithm of decision trees on

large data sets. In 2021 IEEE 6th International Conf.

on Big Data Analytics (ICBDA), pages 33–37. IEEE.

Raghupathi, W. and Raghupathi, V. (2014). Big data an-

alytics in healthcare: promise and potential. Health

information science and systems, 2:1–10.

Sahatiya, P. (2018). Big data analytics on social media data:

a literature review. International Research Journal of

Engineering and Technology, 5(2):189–192.

Sandhu, A. K. (2021). Big data with cloud computing: Dis-

cussions and challenges. Big Data Mining and Ana-

lytics, 5(1):32–40.

Santana, A., Inoue, S., Murakami, K., Iizaka, T., and Mat-

sui, T. (2020). Clustering-based data reduction ap-

proach to speed up svm in classiﬁcation and regres-

sion tasks. In 33rd International Conference on In-

dustrial, Engineering and Other Applications of Ap-

plied Intelligent Systems, IEA/AIE 2020, Kitakyushu,

Japan, pages 478–488. Springer.

Sinanaj, L. (2021). Allan Variance-based Granulation Tech-

nique for Large Temporal Databases. PhD thesis,

University of Massachusetts Lowell.

Sinanaj, L., Haeri, H., Maddipatla, S. P., Gao, L., Pakala,

R., Kathiriya, N., Beal, C., Brennan, S., Chen, C.,

and Jerath, K. (2022). Granulation of large temporal

databases: An allan variance approach. SN Computer

Science, 4(1):7.

ur Rehman, M. H., Liew, C. S., Abbas, A., Jayaraman, P. P.,

Wah, T. Y., and Khan, S. U. (2016). Big data reduction

methods: a survey. Data Science and Engineering,

1:265–284.

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

Vito, S. (2016). Air Quality. UCI Machine Learning Repos-

itory. DOI: https://doi.org/10.24432/C59K5F.

Yang, Z., Haeri, H., and Jerath, K. (2021). Renormalization

group approach to cellular automata-based multi-scale

modeling of trafﬁc ﬂow. In Braha, D., de Aguiar, M.

A. M., Gershenson, C., Morales, A. J., Kaufman, L.,

Naumova, E. N., Minai, A. A., and Bar-Yam, Y., ed-

itors, Unifying Themes in Complex Systems X, pages

17–27, Cham. Springer International Publishing.

Yao, Y., Liu, Y., Yu, Y., Xu, H., Lv, W., Li, Z., and Chen, X.

(2013). K-svm: An effective svm algorithm based on

k-means clustering. J. Comput., 8(10):2632–2639.

Zhan, Y. and Shen, D. (2005). Design efﬁcient support vec-

tor machine for fast classiﬁcation. Pattern Recogni-

tion, 38(1):157–161.

Zhang, D.-g., Ni, C.-h., Zhang, J., Zhang, T., Yang, P.,

Wang, J.-x., and Yan, H.-r. (2022). A novel edge com-

puting architecture based on adaptive stratiﬁed sam-

pling. Computer Communications, 183:121–135.

Zicari, R. V. (2012). Big data: Challenges and opportuni-

ties. This is Big Data.

Adaptive Granulation: Data Reduction at the Database Level