
A New Approach to Addressing Uncertainty in Information Technology
with Fuzzy Multi-Criteria Decision Analysis
Elissa Nadia Madi
1 a
, Azwa Abdul Aziz
1 b
and Binyamin Yusof
2 c
1
Faculty of Informatics and Computing, Universiti Sultan Zainal Abidin (UniSZA),
Besut Campus, Besut 22200, Terengganu, Malaysia
2
Faculty of Ocean Engineering Technology and Informatics,
Universiti Malaysia Terengganu, Kuala Nerus, Terengganu 21030, Malaysia
Keywords:
Fuzzy Number, Interval Type-2 Fuzzy Set, MCDA.
Abstract:
The problem of reasoning under uncertainty is widely recognised as significant in information technology, and
a wide range of methods has been proposed to address this problem. Uncertainty happens when imperfect
information is the only available source to solve it using quantitative methods. Therefore, there is a need
to implement a qualitative method when no numerical information is available. Linguistic uncertainties re-
lated to the qualitative part must be considered and managed wisely. Such uncertainty commonly involves
in decision-making problem which depends on human perceptions. This study explores the relationship and
difference between two variables, namely the level of uncertainty to the input and the output changes based
on multi-criteria decision analysis. There is a positive relationship between these two variables. The novel
generation interval type-2 fuzzy membership function technique is proposed based on this. It can accurately
map the decision maker’s perceptions to the fuzzy set model, reducing the potential for loss of information.
In literature, the output ranking of the system is presented as a crisp number. However, this study proposed a
new form of output in interval form based on multi-criteria decision analysis. Overall, this study provides new
insight into how we should not ignore uncertainty when it affects the input. It provides an intelligent way to
map human perceptions to the system using a fuzzy set.
1 INTRODUCTION
Life is always characterised by subjective judge-
ments, which consist of different personal opinions
that have been influenced by various factors such as
personal views, experience, background or personal
assessments of the different levels of variables of in-
terest. They are made using a mixture of qualitative
and quantitative information. Qualitative information
cannot be directly measured—for example, human
perceptions, feelings, emotions and words. However,
quantitative information can be directly measured or
computed from direct measurements such as the mean
value of temperatures and standard deviations of days.
Regardless of any information, either they are qual-
itative or quantitative, there always has uncertainty
about it and the amount of uncertainty can exist from
small to large.
a
https://orcid.org/0000-0001-5557-2231
b
https://orcid.org/0000-0002-0470-4000
c
https://orcid.org/0000-0002-3899-1474
Qualitative uncertainty can be distinguished from
quantitative uncertainty; for example, words can be
interpreted differently by different people. Therefore,
their linguistic uncertainties need to be considered
and managed wisely. Qualitative uncertainty com-
monly involves in decision-making problems as the
problem is highly dependent on human perceptions.
In this problem, for a specific context, it is highly de-
pendent on words (i.e., perceptions and words), where
words are utilised as the primary input to reach a de-
sired decision. However, words are always charac-
terised by uncertain and vague meanings, which re-
sult in increasing complexity of solving the decision-
making problem. Fuzzy sets can be considered a suc-
cessful traditional framework for dealing with uncer-
tainty. The uncertainty is presented by the degree of
membership within the range of [0,1] (i.e., certainty
degree assigned to the elements belonging to the set
or not). However, Mendel (Mendel, 2018) argued
that the fuzzy set (Type-1 fuzzy set, T1FS) is unsuit-
able for modelling words. An extension of the T1FS
Madi, E., Aziz, A. and Yusof, B.
A New Approach to Addressing Uncertainty in Information Technology with Fuzzy Multi-Criteria Decision Analysis.
DOI: 10.5220/0012191800003595
In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 387-394
ISBN: 978-989-758-674-3; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
387

set known as Type-2 fuzzy set (T2 FSs) was intro-
duced by Zadeh in 1975 (Zadeh, 1975), where in this
set, an additional dimension is associated with uncer-
tainty about the degree of membership. For example,
consider the room temperature; whether a tempera-
ture of 27 degrees Celsius belongs to this set or not
may have a degree of membership of 0.9 with a cer-
tainty of 0.5 and a membership of 0.8 with a certainty
of 0.6. Such a problem can be modelled using type-2
fuzzy sets (T2FSs). It is useful when existing uncer-
tain information determines a set’s precise and exact
membership function. In most cases, however, pro-
viding crisp numbers, for example, using the Likert
scale to assess something whether to determine the
level of certainty or measure a degree of belonging to
the set, is problematic (i.e. there could exist uncer-
tainties about them), and thus it is more meaningful
to provide intervals (Wu and Mendel, 2007). There-
fore, the type-2 fuzzy set theory provides a valuable
account of how uncertainties should be handled in
the decision-making process when uncertainty about
words is present.
Multi-criteria decision analysis problems are cat-
egorised as one of the decision-making issues which
received considerable critical attention. It is a prob-
lem which concern finding the most desirable alter-
native(s) from a set of pre-determined alternatives,
A = A
1
, A
2
, ··· , A
n
concerning the decision informa-
tion about criteria weights and criteria values pro-
vided by a group of decision-makers (DMs), DM =
DM
1
, DM
2
, · ·· , DM
m
. However, a significant prob-
lem with dealing with humans as decision-makers is
that they exhibit variation in their decision (Garibaldi
and Ozen, 2007). In order to design an intelligent
decision-making method, such variations should be
considered, especially in the initial of the system it-
self. In other words, the construction of a system
should be aimed to better resemble human reason-
ing in conjunction with using approximate informa-
tion and uncertainty to reach a decision.
In the general framework of fuzzy multi-criteria
decision analysis (MCDA), there exists a technique to
assign a linguistic label (e.g., Very Good, Very Poor,
Fair, etc.) with fuzzy membership functions (MFs)
to represent the performance of each alternative con-
cerning each criterion. For example, in one of the
techniques, known as the Fuzzy Technique for Or-
der Preference by Similarity to Ideal Solution (Fuzzy
TOPSIS) (Chen, 2000), the performance of each alter-
native is evaluated against each criterion using the nu-
merical scale, which then mapped into the fuzzy MFs
with associated parameter (Table 1). The evaluation
from the decision maker is mapped using a fuzzy set
to enhance pre-screening evaluations, where the value
Table 1: Linguistic scale for rating of alternatives in Fuzzy
TOPSIS method.
Poor (P) Fair (F) Good (G)
(0,0,5) (0,5,10) (5,10,10)
of positive rating performance, for example, ‘Good’,
can be approximated in a range of value, for example,
5 − 10.
However, the conventional FTOPSIS used Type-
1 fuzzy sets (T1FSs), characterised by precise mem-
bership functions in the range [0,1], resulting in the
uncertainty disappearing once they have been cho-
sen. In addition, humans as decision-makers exhibit
dynamic behaviour, which causes dynamic variation
in the decision-making process (Ozen and Garibaldi,
2004). Various frameworks based on fuzzy sets have
recently been suggested to model uncertainty. The
main challenge in constructing the model is the gener-
ation of the fuzzy MFs (C. Wagner, 2009; Mendel and
Wu, 2007). In the MCDA framework, this will affect
the overall ranking result at the end of the model. Ad-
ditionally, a lack of investigations has been observed
in the literature on how to construct the MFs and spec-
ify the parameter of MFs in MCDA paradigm. Thus,
in this study, a series of experiments were carried
out by introducing several different levels of small
changes (i.e., uncertainty) in the MFs associated with
the linguistic labels. The purpose of doing this is to
explore any relationship between the amount of un-
certainty (i.e., small changes level) introduced in MFs
and to observe changes in overall decision support
output. In addition, this experiment will lead towards
a proposal of a novel and direct technique to generate
Type-2 MFs for providing a better and more accurate
model of uncertainty based on MCDA technique. Ad-
ditionally, the output results remain in the same form
of information which is in a range of values (i.e., in-
terval form). This type of output result is the main dif-
ference as opposed to the standard MCDA technique,
where in the classical one, it provides output results in
a crisp rank. Thus, this novel technique is interesting
when the input and output of the information are in
the same form. Furthermore, it can minimise the po-
tential for loss of information during the process by
mapping all the information directly to fuzzy sets.
The paper is structured as follows: Section 2
briefly revises the fundamental concepts of fuzzy set
theory and the MCDA method. Section 3 presents the
experimental procedure implementing fuzzy TOPSIS
method. Section 4 provides a discussion of experi-
ment result in the comparison context. Finally, Sec-
tion 5 gives conclusions with suggestions of future
work.
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
388

2 BACKGROUND
This section reviews the background theory used in
this paper based on one of MCDA methods, namely
fuzzy TOPSIS as an application area.
2.1 Multi-Criteria Decision Analysis
(MCDA)
Over the past four decades, many MCDA methods
have been developed, and their number continues to
grow. Based on the surveys conducted by Aruldoss et
al. (Aruldoss et al., 2013), MCDA is a powerful tool
for obtaining the best choice for complex decision-
making situations. The MCDA methods have also
been successfully applied in various domains.
MCDA can be classified into two main cat-
egories:1) Multi-Objective Decision Making
(MODM); 2) Multiple-Attribute Decision Mak-
ing (MADM)(Hwang and Yoon, 1981), (Kahraman,
2008). The MODM method is suitable for the
design or planning model, whose main objective is
to achieve an optimal solution by considering the
various interactions among the given constraints.
MADM is a method that makes selections among
some elements in a set of actions with multiple,
commonly conflicting attributes. We are particularly
interested in one of MADM’s methods, namely
Fuzzy TOPSIS.
The selection of this method to be implemented
in our experiments is motivated by a few findings
provided by some studies. For example, Zanakis
(Zanakis et al., 1998) concluded that the simulation
experiment provided the result that TOPSIS has the
fewest rank reversals among other MADM methods.
Additionally, a survey conducted by (Behzadian et al.,
2012) conclude that, among numerous MADM meth-
ods developed to solve real-world decision problems,
the TOPSIS method works satisfactorily across differ-
ent application areas. More recently, Yue (Yue, 2014)
claimed that the TOPSIS method is suitable for cau-
tious (risk avoider) decision maker(s) because the de-
cision maker (s) may want to have a decision which
not only makes as much profit as possible but also
avoids as much risk as possible. Thus, in this study
fuzzy TOPSIS method (Chen, 2000) is implemented
in our experiment to observe changes in the over-
all decision support output when various uncertainty
level is introduced in the membership functions. The
reader is advised to refer to Figure 1 and (Madi et al.,
2016) for further reference on the step-wise procedure
in the fuzzy TOPSIS technique.
3 INTRODUCING UNCERTAINTY
INTO MEMBERSHIP
FUNCTIONS
3.1 Generation Type-1 Fuzzy
Membership Functions
Fuzzy sets are commonly used to represent linguis-
tic variables such as height or goodness every day.
On real-world occasions, the decision maker com-
monly faced difficulty providing assessment in a con-
clusive and precise manner. Thus, using words in-
stead of numerical values to provide assessments or
evaluations is quite natural. In the standard fuzzy
TOPSIS method, the scale is developed using TFNs.
For example, as shown in Table 1. In this study,
the evaluation given by a set of decision-makers to
the fuzzy TOPSIS model should remain fixed, and
the small changes (i.e., level of uncertainty present in
MFs) to overall decision support output would be ex-
plored. The effect of introducing small changes to the
MFs is investigated by using the type-2 fuzzy TOPSIS
method. Next, the overall experimental procedure de-
tails are explained using the following case study.
3.1.1 Case Study
The case study is provided in which the three experts
gave their opinions based on the criteria determined at
the beginning of the study. The case study consists of
a simulation of one mobile application that needs to
perform an intensive task. The experts are presented
with a list of criteria, and they need to give their opin-
ion on the decision that should be made in the offload-
ing task: whether to offload the task remotely (A
1
)
or remain local (A
2
). In a specific scenario involv-
ing the use of video editing applications on a regular
mobile phone (Samsung Galaxy S5), three experts in
Cloud Computing utilized a video-editing application
on their smartphones.
The experts, D1 and D2 are formed to conduct fur-
ther evaluation to make decision based on three crite-
ria, Battery Level (C1); Memory(C2), and Network
Signal Level (C3). The three experts evaluate these
two types of platform (i.e., local and remote) con-
cerning the three criteria C1, C2 and C3, where the
weighting vector is w = (0.2, 0.4, 0.4). The experts
use the linguistic variables scale (shown in Table 1)
to evaluate these two types of platform. Assume that
the evaluation given by experts D1 and D2 are sum-
marized in Table 2.
A New Approach to Addressing Uncertainty in Information Technology with Fuzzy Multi-Criteria Decision Analysis
389
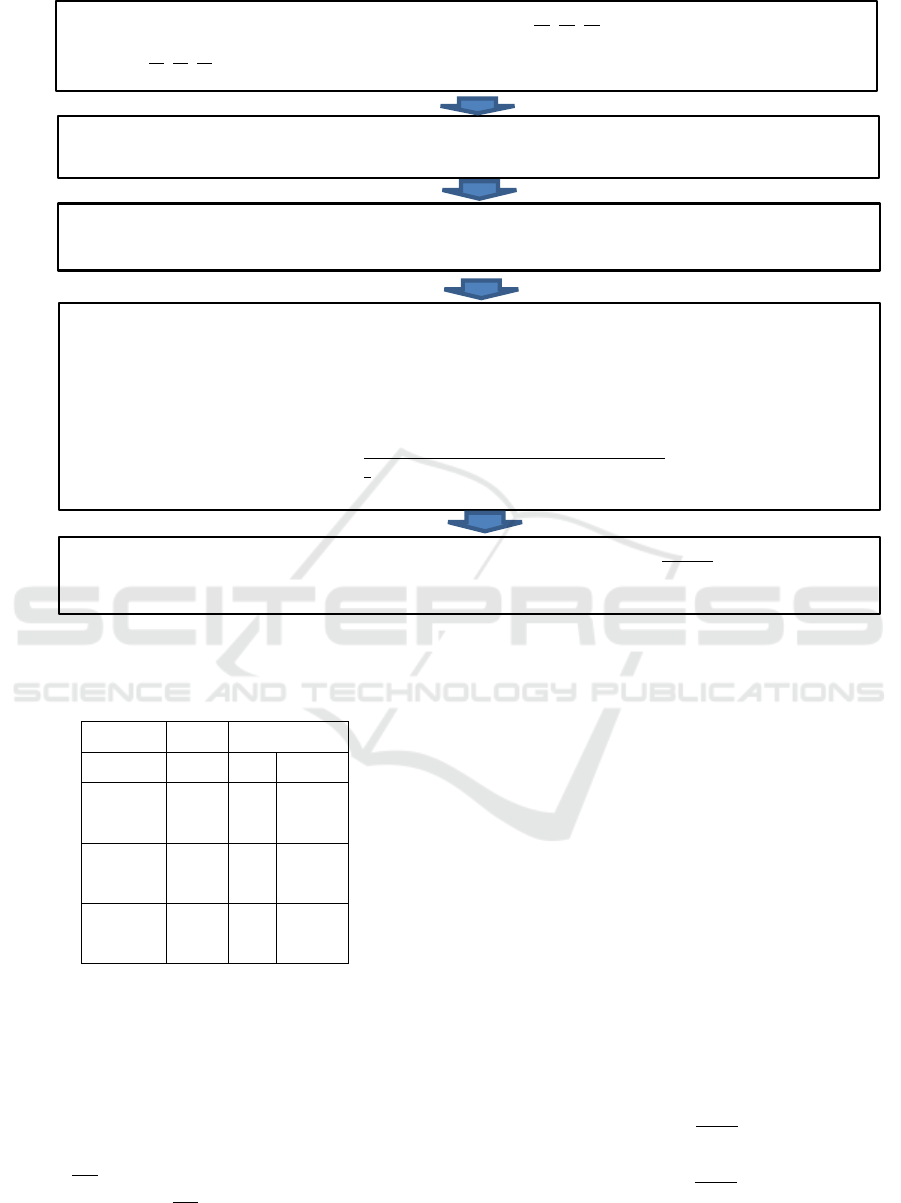
Step 2: Construct the weighted normalized decision matrix:
where
is the weight for th criterion.
Step 3 Determine the positive ideal and negative ideal solutions:
[Positive Ideal
Solution], where
[Negative Ideal Solution]; where
Step 4 Calculate separation measures for each alternative using vertex method. The separation from
positive ideal alternative:
.
The separation from the negative ideal alternative is:
; where
represent the distance between two fuzzy numbers by vertex method:
Let
and
be two triangular fuzzy numbers (TFN). Distance calculation of
these to TFN is
Step 5: Calculate the relative closeness to the ideal solution,
:
,
Select the alternative with
closest to 1.
Step 1: Construct normalized fuzzy decision matrix:
for Benefit Criteria) OR
for
(Cost Criteria; where
if and
if
Figure 1: Stepwise procedure of Fuzzy TOPSIS(Chen, 2000),(Madi et al., 2016).
Table 2: Linguistic rating of each alternative and impor-
tance weight of each criterion.
DM’s rating
Criteria Alts. D1 D2
C
1
A
1
G F
A
2
G F
C
2
A
1
G G
A
2
F P
C
3
A
1
P P
A
2
F G
3.2 Novel Method in Generation of
Interval Type-2 Fuzzy Membership
Functions (IT2 MFs)
In this section, we explained how we generate IT2
MFs using T1 MFs by introducing a series of uncer-
tainty in the MFs. Assume a T1 MFs is defined by:
µ
l
(x) =
x−b
a
+ 1, for left function which strictly in-
creasing and µ
r
(x) =
b−x
a
+1, for right function which
strictly decreasing. The generation of IT2 MFs using
T1 MFs is a symmetrical case where the value of a
is the same for both the left and right functions. For
non-symmetrical case, the properties of the function
can be summarized as follow:
• a in left side, a
l
, is not equal to a in right side,a
r
,
• a
l
< a
r
,
• If (b − a) < b, then b < (b + a)
Then, assume we introduced uncertainty with
level d to the same T1 MFs. The MF is now shifted
to IT2 MFs where the area between standard T1
MFs with upper (UMF) and lower (LMF) bound of
new MFs have now become footprint of uncertainty
(FOU).
The left, µ
l
and right, µ
r
, MFs now have two func-
tions each, where it is defined for UMF and LMF, re-
spectively. The UMF and LMF for the left side are
defined as in Eq. (1) and (2), respectively.
µ
UMF
l
(x) =
x − b
a − d
+ 1 (1)
µ
LMF
l
(x) =
x − b
a + d
+ 1 (2)
For the right side, the UMF and LMF are defined
as in Eq. (3) and (4), respectively.
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
390

0.1
0.5
0.1
0.5
0.1
0.5
0.1
0.5
Figure 2: Triangular Fuzzy membership function.
µ
UMF
r
(x) =
b − x
a + d
+ 1 (3)
µ
LMF
r
(x) =
b − x
a − d
+ 1 (4)
From these definitions (i.e., Eqs. (1) to (4), the
generation of any fuzzy MFs can be done directly
by specifying the centre for triangular MFs and the
approximate level of uncertainty (i.e., d). Next, we
demonstrate the experiment procedure by using this
novel fuzzy MF generation.
A delta series is introduced in the standard T1
MFs. The delta, δ
i
, i = 1, 2, .., m, where ∀δ
i
∈ [0, 1] are
considered as uncertainty in the decision making pro-
cess. In this experiment, we have chosen seven delta
values; δ
7
= 0.10, 0.15, 0.17, 0.20, 0.30, 0.40, 0.50,
where these values are used to shift left and right of
every MF according to Eqs. (1) to (4). We demon-
strate for the first case, δ
1
= 0.10 to be implemented
in case study.
The introduction of δ
1
= 0.10 is done by shifting
left to 0.10 and shifting right to 0.10 of standard Type-
1 MF (Figure 2).
Then, a fuzzy variable of ‘Rating’, with three lin-
guistic labels, ‘Poor’, ‘Fair’ and ‘Good’, as shown
in Figure 3, is now become an interval Type-2
fuzzy MFs (IT2 MFs), bounded with upper member-
ship function (UMF) and lower membership function
(LMF). For example, we defined UMF and LMF of
the fuzzy label ‘Poor’ as in Eqs. (5) and (6), respec-
tively.
µ
UMF
poor
(x) = 1 −
x
0.1
(5)
µ
LMF
poor
(x) = 1 +
x
0.1
(6)
Then, we can define the fuzzy label ‘Poor’
as an interval type-2 fuzzy number, Poor =
[(0, 0, 4.9), (0, 0, 5.1)], where the first element is in-
dicated of lower value and the second element is in-
dicated of upper value. The illustration of fuzzy MF
‘Poor’ is shown in Figure 3. Note that this generation
of IT2 fuzzy MF is based on the original T1 fuzzy MF
Figure 3: Interval Type-2 fuzzy variable ’Rating’.
from Table 1. The same procedure is applied to gen-
erate linguistic labels such as ‘Fair’ and ‘Good’. The
linguistic variable ‘Rating’ overall labels are now in-
terval Type-2 fuzzy MFs shown in Figure 3. Thus,
the labels in the linguistic variable ‘Rating’ can now
be rewritten as IT2 fuzzy linguistic scale as in Table
3.
Next, the same fuzzy TOPSIS procedure as Case
1 (Section 3.1.1) is applied to get the rank of the al-
ternative. However, since the IT2 fuzzy MFs bounded
by LMF and UMF, we treated the value separately,i.e.,
instead of having one single ranking value for output
results (CC
i
), in this experiment, the result is an inter-
val, which is a novel type of output. We present the
experiment result in Table 4 and Figure 4. To recall,
we used the following delta values in our experiment:
δ
7
= (0.10, 0.15, 0.17, 0.20, 0.30, 0.40, 0.50).
4 DISCUSSION
There is a significant difference in overall decision
output for the case uncertainty present. For compar-
ison purposes, we present the result of Type-1 fuzzy
TOPSIS, where in this synthetic example, the close-
ness coefficient values for both cars are 0.1971524
and 0.2005322, respectively. However, when a series
of delta (i.e., uncertainty) is introduced to the uncer-
tain spread MFs, the overall output result has a slight
difference on the output (i.e., Closeness Coefficient
value) (Table 4). One reason for having slightly dif-
ferent values on output is because only the ‘Fair’ MF
shifted to the left and the right direction, while two
other MFs, ‘Poor’ and ‘Good’, shifted to the right and
left, respectively.
Based on this, the difference among various out-
put values should be considered when implementing
any decision-making process. As this generation of
fuzzy MFs is entirely straight away, there could mini-
A New Approach to Addressing Uncertainty in Information Technology with Fuzzy Multi-Criteria Decision Analysis
391

Table 3: Linguistic scale for rating of alternatives in Interval Type-2 fuzzy TOPSIS method.
Poor (P) Fair (F) Good (G)
[(0,0,4.9),(0,0,5.1)] [(0.1,5,9.9),(-0.1,5,10.1)] [(5.1,10,10),(4.9,10,10)]
Figure 4: Case 2 result: Interval closeness coefficient, where A1 = Car 1, A2 = Car 2.
Table 4: Result: Interval Closeness Coefficient for Uncertain spread MFs.
δ = 0.10 δ = 0.15 δ = 0.20 δ = 0.25
Local [0.1971508, 0.1971569] [0.1971511,0.1971602] [0.1971521,0.1971643] [0.197154,0.197169]
Remote [0.2005143, 0.2005666] [0.2005114,0.2005901] [0.2005125,0.2006179] [0.200518,0.200650]
δ = 0.28 δ = 0.30 δ = 0.40 δ = 0.50
Local [0.197155,0.197172] [0.1971562,0.1971746] [0.1971632,0.1971878] [0.1971730,0.1972040]
Remote [0.200522,0.200671] [0.2005264,0.2006865] [0.2005556,0.2007729] [0.2005556,0.2007729]
h
2
b
b-a
b+a
h
1
Figure 5: Uncertain mean fuzzy membership function.
mize any potential of loss of information when trans-
ferring the evaluation made by decision-makers to any
decision support system. The width of the interval
output denotes the decision makers’ certainty in their
evaluation; a narrow interval is used when they are
sure where on the scale the answer lies, and a wider
one is where they are less specific. Thus, whenever
the uncertainty effect the input, it should be consid-
ered that every step in the process has that uncertainty.
Each value in the interval has a specific meaning that
we should not ignore, mainly when applied in a med-
ical context as this context commonly deals with the
life and death of humans.
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
392

−1 rating 11
0
υ
1
poor
fair
good
Figure 6: Uncertain mean fuzzy membership function.
5 CONCLUSION
In this paper, an experiment is conducted by intro-
ducing several different levels of uncertainty in the
Type-1 MFs associated with the linguistic variables.
The purpose of doing this is to explore any relation-
ship between the uncertainty introduced in MFs and
to observe changes in overall decision support out-
put. The presence of uncertainty causes output val-
ues to fluctuate. Further, this successful experiment
led towards proposing a novel and direct technique
to generate Type-2 MFs for providing a better and
more accurate uncertainty model based on the MCDA
method. This method has a few advantages as it is
a direct way of generating the MFs. Thus, it can
minimise the potential loss of information decision-
makers give. Additionally, the output results remain
in the same information form in interval-based num-
bers. This type of output result is the main difference
as opposed to the standard MCDA method, where in
the classical approach, it provides output results in a
rank of crisp number. Thus, this novel technique is
interesting when the input and output of the informa-
tion are in the same form. Each value in the interval is
considered and can support the decision maker’s de-
cision. Accurately modelling preference information
to fuzzy MFs can reduce the potential of making any
misleading decision. In future, we will explore dif-
ferent techniques and methods of ranking intervals.
We will develop our ranking algorithm based on this,
specifically focusing on various interval values.
ACKNOWLEDGEMENTS
Elissa Nadia Madi acknowledges the support by
Universiti Sultan Zainal Abidin (UniSZA) via
the university research grant, with project code
UniSZA/2022/DPU1.0/10. The authors are grateful
to anonymous reviewers for their comments.
REFERENCES
Aruldoss, M., Lakshmi, T. M., and Venkatesan, V. P. (2013).
A Survey on Multi Criteria Decision Making Methods
and Its Applications. American Journal of Informa-
tion Systems, 1(1):31–43.
Behzadian, M., Khanmohammadi Otaghsara, S., Yazdani,
M., and Ignatius, J. (2012). A state-of the-art survey
of TOPSIS applications. Expert Systems with Appli-
cations, 39(17):13051–13069.
C. Wagner, H. H. (2009). Novel methods for the design
of general type-2 fuzzy sets based on device charac-
teristics and linguistic labels survEys. In Proceedings
of the Joint 2009 International Fuzzy Systems Asso-
ciation World Congress and 2009 European Society
of Fuzzy Logic and Technology Conference. European
Society for Fuzzy Logic and Technology, pages 537–
543.
Chen, C.-T. (2000). Extensions of the TOPSIS for group
decision-making under fuzzy environment. Fuzzy Sets
and Systems, 114(1):1–9.
Garibaldi, J. M. and Ozen, T. (2007). Uncertain fuzzy rea-
soning: A case study in modelling expert decision
making. IEEE Transactions on Fuzzy Systems, 15:16–
30.
Hwang, C.-L. and Yoon, K. (1981). Multiple Attribute De-
cision Making : Methods and Application- A State of
the Art Survey. Springer Berlin Heidelberg New York,
lecture no edition.
Kahraman, C. (2008). Fuzzy Multi-Criteria Decision Mak-
ing. Springer Science+Business Media, LLC, springer
o edition.
Madi, E. N., Garibaldi, J. M., and Wagner, C. (2016).
An Exploration of Issues and Limitations in Current
Methods of TOPSIS and Fuzzy TOPSIS. In IEEE
International Conference on Fuzzy Systems (FUZZ-
IEEE), pages 2098–2105. IEEE.
Mendel, J. M. (2018). The Perceptual Computer: The Past,
Up to the Present, and Into the Future. Informatik-
Spektrum, 41(1):15–26.
Mendel, J. M. and Wu, H. (2007). Type-2 fuzzistics for
symmetric interval Type-2 fuzzy sets: Part 2, in-
verse problems. IEEE Transactions on Fuzzy Systems,
15(2):301–308.
Ozen, T. and Garibaldi, J. (2004). Effect of type-2 fuzzy
membership function shape on modelling variation in
human decision making. 2004 IEEE International
Conference on Fuzzy Systems, 2:971–976.
Wu, D. and Mendel, J. M. (2007). Uncertainty measures
for interval type-2 fuzzy sets. Information Sciences,
177(23):5378–5393.
Yue, Z. (2014). TOPSIS-based group decision-making
methodology in intuitionistic fuzzy setting. Informa-
tion Sciences, 277:141–153.
A New Approach to Addressing Uncertainty in Information Technology with Fuzzy Multi-Criteria Decision Analysis
393

Zadeh, L. (1975). The concept of a linguistic variable and
its application to approximate reasoning—Part I. In-
formation Sciences, 8:199–249.
Zanakis, S. H., Solomon, A., Wishart, N., and Dublish, S.
(1998). Multi-attribute decision making: A simulation
comparison of select methods. European Journal of
Operational Research, 107(3):507–529.
FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications
394
