Assisting Convergence Behaviour Characterisation with Unsupervised

Clustering

Helena Stegherr

∗ a

, Michael Heider

∗ b

and J

org H

ahner

∗ c

Universi

at Augsburg, Am Technologiezentrum 8, Augsburg, Germany

ﬁ

Keywords:

Metaheuristics, Behaviour Analysis, Convergence, Explainability.

Abstract:

Analysing the behaviour of metaheuristics comprehensively and thereby enhancing explainability requires

large empirical studies. However, the amount of data gathered in such experiments is often too large to be

examined and evaluated visually. This necessitates establishing more efﬁcient analysis procedures, but care has

to be taken so that these do not obscure important information. This paper examines the suitability of clustering

methods to assist in the characterisation of the behaviour of metaheuristics. The convergence behaviour is used

as an example as its empirical analysis often requires looking at convergence curve plots, which is extremely

tedious for large algorithmic datasets. We used the well-known K-Means clustering method and examined the

results for different cluster sizes. Furthermore, we evaluated the clusters with respect to the characteristics

they utilise and compared those with characteristics applied when a researcher inspects convergence curve

plots. We found that clustering is a suitable technique to assist in the analysis of convergence behaviour, as

the clusters strongly correspond to the grouping that would be done by a researcher, though the procedure

still requires background knowledge to determine an adequate number of clusters. Overall, this enables us to

inspect only few curves per cluster instead of all individual curves.

1 INTRODUCTION

Empirical studies are a common approach to com-

pare metaheuristics, to analyse their performance, and

to examine their search behaviour. However, ev-

ery empirical study requires a well-wrought, rigor-

ous design, so that the results are valid and unbi-

ased (Bartz-Beielstein et al., 2020). This goes for

selecting the algorithmic conﬁgurations, but also for

gathering the required data and applying a suitable

analysis methodology. Depending on the research

questions, this can be quite demanding, and the prob-

lem is exacerbated when the number of algorithmic

conﬁgurations to be examined grows.

Especially when the goal is the analysis of algo-

rithmic behaviour, large scale empirical studies are

quite common (see e.g. (Vermetten et al., 2022b)),

which can be based on typical benchmarking exper-

iments or on specialised experiment designs (Bartz-

Beielstein et al., 2020). These analyses are important

to not only understand how a metaheuristic achieves

https://orcid.org/0000-0001-7871-7309

https://orcid.org/0000-0003-3140-1993

https://orcid.org/0000-0003-0107-264X

∗

Authors contributed equally to this paper.

its performance, but also to derive more general in-

sights into its workings and explain which part of its

conﬁguration, i.e. which operators or hyperparame-

ters, is responsible for a certain behaviour. In such

studies, often lots of data is collected, in terms of dif-

ferent conﬁgurations and several runs, as well as the

information that is gathered during the search (e.g.

the current best value, but also the objective values

of other solutions or the solutions itself). Utilising

all data in a comprehensive analysis can advance the

explainability of the search process (Bacardit et al.,

2022), e.g. by the creation of behavioural proﬁles of

metaheuristics and their operators. These can then be

used to help non-experts to conﬁgure an algorithm for

the problem at hand, based on the provided knowl-

edge of the behaviour under speciﬁc circumstances.

However, the amount of information, and there-

fore also the amount of data, that needs to be anal-

ysed and presented for this is extremely large. Specif-

ically, data that is often analysed based on some kind

of visualisation becomes a problem. While visualisa-

tions are often easily interpretable, it becomes difﬁ-

cult when trying to compare more than a few dozen

algorithms based on visual information. Large stud-

ies, however, easily produce data of thousands or even

108

Stegherr, H., Heider, M. and Hähner, J.

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering.

DOI: 10.5220/0012202100003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 108-118

ISBN: 978-989-758-674-3; ISSN: 2184-3236

tens of thousands different algorithmic conﬁgurations

(see e.g. (van Stein et al., 2021; Vermetten et al.,

2022a)). Even when several conﬁgurations can be

combined in the visualisation of speciﬁc behavioural

characteristics, analysing them is not feasible by hu-

mans. An effective way around this is to break the

visualisations down to numbers. This can be done

utilising summarising metrics, or by looking at spe-

ciﬁc measures that indicate differences between the

conﬁgurations. Again, however, this can easily get

out of hand, when many different measures need to

be compared for analysing one speciﬁc behavioural

characteristic in depth. Furthermore, it is not always

clear up front which of these measures are the most

important to make any distinction, leading to either a

high number of preliminary studies or including un-

necessary measures in the analysis.

To alleviate these problems, we want to deter-

mine the suitability of another approach, utilising

machine learning (ML) to summarise, differentiate,

and—ultimately—explain algorithmic conﬁgurations

by their behavioural characteristics. There are many

ML techniques that could be supportive in facilitat-

ing the analysis of behavioural characteristics under

consideration of conﬁguration-speciﬁc peculiarities.

Especially unsupervised ML approaches are of inter-

est here, as these do not require data labelling, which

would again constitute a large additional effort and

defeats the purpose of not having to check all in-

dividual curves. Within unsupervised learning, the

use of traditional clustering algorithms is the logi-

cal ﬁrst step. Utilising machine learning techniques

to assist in behavioural analysis is not yet common.

There are, however, some statistical approaches that

can be employed, e.g. for examining exploration and

exploitation behaviour (Eftimov and Koro

sec, 2019).

Also, there are general as well as specialised frame-

works and statistical tools that can assist in such cases,

e.g. (Bartz-Beielstein et al., 2017; Eftimov et al.,

2020; Wang et al., 2022; Vermetten et al., 2022b).

ML is used for evaluating metaheuristics in general,

for example for predicting their performance using

regression models (Eftimov et al., 2021) or for algo-

rithm selection (see e.g. (Tanabe, 2022)). It has to be

considered that ML-assisted behaviour characterisa-

tion may not be able to provide a full picture of all de-

tails that differentiate algorithms. However, it should

at least vastly facilitate getting an initial overview.

Cases of interest, where the ML-assisted analysis is

not comprehensive enough, can still be analysed in-

dividually by looking at speciﬁc metrics, measures

or visualisations, but the data-related overhead is re-

duced drastically.

As a proof of concept and to ﬁnd the strengths,

weaknesses and prerequisites of the clustering ap-

proach, we focus—for now—on the convergence be-

haviour of metaheuristics. We assume there to be a

distinct number of “types of convergence curves” that

are largely similar to each other. While this number

might not exactly be known, we can infer some sen-

sible numbers based on expert knowledge and let the

algorithm sort the data accordingly. After construct-

ing such clusters of similar curves, practitioners can

pick a few individuals from the respective clusters for

analysis, thereby reducing the number of curves that

need initial manual checking by (multiple) orders of

magnitude.

In the following, we examine K-Means—an un-

supervised clustering algorithm—in the context of a

smaller example of behavioural analysis to determine

its applicability and restrictions. Therefore, we look

at the convergence behaviour of metaheuristics (note

that the focus is on solving real-parameter minimisa-

tion problems). We give an introduction to the charac-

teristics of convergence behaviour that are important

to distinguish different algorithmic approaches (Sec-

tion 2). Then, different conﬁgurations of K-Means

to assist in analysis based on these considerations

are presented and evaluated (Section 3), with a focus

on relating the results to our expectations. Finally,

we discuss other potential ML approaches and subse-

quent analyses that can allow to draw further conclu-

sions.

2 CONVERGENCE BEHAVIOUR

AND CHARACTERISTICS

The behaviour of metaheuristics during the search

process depends on the algorithmic conﬁguration as

well as the optimisation problem. While the con-

ﬁguration determines the general strategy the algo-

rithm uses to traverse the search space, the optimi-

sation problem itself can inﬂuence the algorithm if

objective function values are utilised in its internal

decisions. A detailed analysis of the algorithmic be-

haviour can help to identify which factors constitute

to the respective behaviour, and explain the search

process. Furthermore, this information can be used

to determine which conﬁguration might be appropri-

ate for an unknown problem. The overall algorith-

mic behaviour can be divided into subgroups that

can be examined independently, e.g. convergence-,

performance-, exploration-, or exploitation-related

behaviour. For each of these subgroups, it is required

to look at several characteristics to examine the be-

haviour in enough detail to relate it to features of the

algorithmic conﬁguration.

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering

109

This section explores the typical characteristics re-

lated to the convergence behaviour of an algorithm.

They are summarised in a way we expect that re-

searchers would look at them when analysing empir-

ical data to compare different metaheuristics. Fur-

thermore, these characteristics provide a hypothetical

foundation for Section 3 to interpret the results of the

machine learning techniques.

Typical convergence metrics, measures and plots

and their interpretations are summarised in (He and

Lin, 2016; Chen and He, 2021; Halim et al., 2020)

and statistical convergence criteria, i.e. ones that de-

termine if the algorithm has converged, can be found

in (Campelo, 2015). While they relate to the charac-

teristics of convergence behaviour, there are, to our

knowledge, no speciﬁc publications on that topic,

and no general guidelines on how to identify such

characteristics. There is, however, an approach that

uses characteristics of the convergence curve to im-

prove the algorithm, though not to understand the be-

haviour (Azad, 2019).

For a rough inspection of differences in conver-

gence behaviour, common metrics and measures are

used. These include the convergence rate, average

convergence rate and the point where the algorithm is

converged to 5% of the optimum (He and Lin, 2016;

Chen and He, 2021; Halim et al., 2020). While these

mostly utilise the objective value, other convergence

measures are based on the diversity of the population,

e.g. (Bosman and Engelbrecht, 2014). Additionally,

search trajectory networks offer more detailed visual-

isations and metrics for convergence analysis (Ochoa

et al., 2021).

Differences in convergence behaviour are often

examined in detail by comparing the plotted conver-

gence curves of the algorithmic runs. These curves

allow for two levels of detail: purely considering the

visual shape of the plotted curve, and extracting sev-

eral points of interest to compare the respective val-

ues. While in benchmarking studies, empirical cumu-

lative distribution functions (ECDFs) are the typical

visualisation (Hansen et al., 2016), in specialised ex-

periments, which are still common and useful in be-

haviour analysis and which are the focus of this work,

convergence is visualised by plotting the best objec-

tive value

per time step.

The curve types can give a general overview on

distinct convergence behaviour but without consider-

ing the scale, i.e. the range of objective function val-

ues during the run. Figure 1 presents convergence

curve types typically encountered when plotting the

best objective function value per time step. Note that

The ﬁtness of the best individual in population-based

methods.

these are only examples for the general curve form

and the ﬁnal objective value is not represented mean-

ingfully, i.e. the y-axis can be any scale.

The curves can be categorised in several main

types, with smaller distinctions within those types.

The main categories can be labelled as follows:

Normal: Fast at the beginning, with decreasing im-

provement over time.

Fast: Converged within ﬁrst few steps.

Linear: Almost linear convergence until ﬁnal value

is reached. (1 additional variation)

Fast to Slow: Initially fast, then rate of improve-

ment decreases, sometimes with a visible point of

change. (1 additional variation)

Slow to Fast: Initially slow, then rate of improve-

ment increases, sometimes with a visible point of

change. (1 additional variation)

Steps: Alternation between faster and slower

episodes. (2 additional variations)

Suboptimal: Converges to any other value. (all of

the above: 10 additional variations)

None: Almost no improvement. (2 additional varia-

tions)

Presumably, not all types are equally common, at

least in typical thought-through experiments. Espe-

cially the None type should not occur at all when

the experiment includes rigorously conﬁgured algo-

rithms. It can, however, be present when the goal is to

inspect different conﬁgurations and the resulting be-

haviour in relation to the performance, no matter if

it is good or bad. We expect one of the most com-

mon curve type to be the Normal one, which shows a

gradually decreasing rate of improvement of the ob-

jective function value. The Fast type should be fre-

quent when problems with low modality are consid-

ered, and Suboptimal should be common for prob-

lems with many local minima or plateaus in their ﬁt-

ness landscape. The other four types are presumably

the most interesting ones when analysing the algorith-

mic behaviour, as they either—for the Linear type—

show a constant improvement step size, or have dis-

tinct points in the search process where changes in the

convergence behaviour occur. Determining the fac-

tors of the algorithmic conﬁguration or of the problem

landscape responsible for this behaviour might pro-

vide valuable insights.

As stated above, the categorisation of the curve

type as a convergence behaviour characteristic is not

sufﬁcient for a detailed convergence behaviour anal-

ysis. Therefore, some common measures of the con-

vergence process are usually considered as additional

characteristics. Some of them are:

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

110

Normal Fast Linear Fast to Slow Slow to Fast Steps Suboptimal None

Variations

Main Types

Figure 1: Examples of different expected convergence curve types and some of their common variations.

Final Value: Final value to which the algorithm con-

verges to (optimum or other value).

50% Objective: When has the objective function

value reached 50% of its initial value?

75% Objective: When has the objective function

value reached 75% of its initial value?

90% Objective: When has the objective function

value reached 95% of its initial value?

50% Budget: What is the objective function value

after 50% of the given budget?

75% Budget: What is the objective function value

after 75% of the given budget?

95% Budget: What is the objective function value

after 95% of the given budget?

Number of Steps: How many “steps” are there in

the convergence curve?

Which additional measures are of interest strongly

depends on the research question and the curve type.

Therefore, there can be additional ones to those men-

tioned above. For example, when initialisation strate-

gies are taken into the overall consideration, the start-

ing point in terms of the initial best objective function

value

is of interest. Conversely, there can also be

fewer measures of interest if a more coarse grained

analysis is sufﬁcient. It is important to note that these

measures alone do also not show the whole picture

when empirically analysing convergence behaviour.

The curve types provide additional information, mak-

ing it necessary to use both, at least to some extent.

Regardless, multi-faceted and detailed analyses en-

hance a user’s (or researcher’s) understanding of the

optimiser, improving the explainability further.

The initial elitists’ objective function value.

3 CLUSTERING CONVERGENCE

CURVE DATA

As Section 2 illustrates, there are lots of character-

istics that need to be considered when analysing the

convergence behaviour—though the exact number de-

pends on the speciﬁc research goal. For larger exper-

iments, i.e. often multiple thousand algorithmic con-

ﬁgurations and the resulting data, it is not feasible to

look at each plot and measure individually. There are

several approaches on how to facilitate the analysis

of such experiments. We focus on utilising unsuper-

vised ML techniques, particularly clustering methods,

to group the data, and through that the different al-

gorithmic conﬁgurations, based on their convergence

behaviour characteristics.

Utilising clustering techniques to aid in conver-

gence behaviour analysis necessitates that they pro-

vide results that are comparable to those that re-

searchers would get when performing the analysis

themselves. Therefore, this section provides a de-

tailed examination of the process required to appro-

priately employ clustering for this case and of the re-

sulting information and its practicality. We focus par-

ticularly on discussing the necessary prior knowledge

and the advantages, disadvantages and short-comings

of the approach. Furthermore, a short overview on

subsequent and alternative strategies is provided.

We have three assumptions the clustering ap-

proach should verify to be considered applicable:

1. The clusters reﬂect the convergence curves.

2. The similarities within a cluster and the differ-

ences between clusters can be related to the char-

acteristics a researcher would look for.

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering

111

3. There should be differences in the allocation of

examples per cluster—even for a higher num-

ber of clusters—as not all curve types should be

equally common.

3.1 Data Gathering

To adequately evaluate clustering for convergence be-

haviour analysis, a representative dataset of algorith-

mic runs is required. Representative, in this case,

means including at least the most common differ-

ent convergence curve types and show differences in

the measures presented in the previous section. Fur-

thermore, enough examples need to be present in the

dataset.

We used a genetic algorithm to generate the

data, implemented in the MAHF software frame-

work (Stegherr et al., 2023), with tournament se-

lection, uniform crossover, Gaussian mutation and

elitism. We varied the hyperparameters, utilising

common values as well as values that provoke runs

not converging to the global optimum. Five typi-

cal benchmark functions were optimised, with two

settings for their respective dimensions, generating a

total of 11500 conﬁgurations, which were run once

each. The best objective function value was logged

every ten iterations for a total of 5000 iterations. The

ﬁnal data examples then contain a sequence of 500

objective values, i.e. the current best objective func-

tion value within the population for each logged iter-

ation. Note that we only want to test the capabilities

of the clustering methods. In this case, the number of

runs per conﬁguration does not matter as we aim to

produce a diverse set of curves rather than meaning-

ful insights about this particular (and probably rather

well known) GA which is easier with different con-

ﬁgurations than multiple runs of the same conﬁgura-

tion. Furthermore, while budgeting in terms of func-

tion evaluations is a more appropriate approach than

having a ﬁxed number of iterations, it does not mat-

ter here as the goal is to provide different convergence

plots not ﬁnd the best objective function values. How-

ever, we want to stress that for speciﬁc hyperparam-

eter/operator/algorithm behaviour analyses, multiple

runs and function evaluation–based budgeting should

be part of a good workﬂow (Bartz-Beielstein et al.,

2020).

3.2 Clustering Based on Convergence

Curve Information

After conducting a set of experiments, a practitioner

that wants to understand the behaviour of chosen al-

gorithmic conﬁgurations (i.e. hyperparameters, oper-

ators or general structure of the metaheuristic) should

not only evaluate based on the achieved objective

function value, but also based on the path that was

taken towards that value. This can be easily visualised

by plotting the best value at each time step which

always follows a monotone function. While these

curves can be analysed manually following the con-

siderations presented in Section 2, more comprehen-

sive tests often create too many convergence curves

for manual analysis. However, many of those curves

show similar patterns.

We propose the use of unsupervised ML to cluster

those curves. These techniques do not require labels,

which would be very labour-intensive to acquire, but

rather ﬁnd patterns in the data to correlate similar data

points. In particular, we examine the well-known K-

Means algorithm

. K-Means separates data into spec-

iﬁed numbers of clusters minimizing the in-cluster

variance. It exhibits good runtime scaling to large

sample sizes—which is particularly useful for large-

scale behavioural analyses on a variety of problems—

and has the advantage of being able to sort newly

generated data into the existing clusters, which can

be quite interesting when performing continued anal-

yses.

For the implementation in this paper we normalise

our curves individually, i.e. the value of the ﬁrst eli-

tist is set to 1 and the value of the reachable optimum

is set to 0 with everything in-between scaled accord-

ingly. Note that this can be adapted when the opti-

mum is unknown, using the minimum any algorith-

mic conﬁguration has found for a speciﬁc test func-

tion. Given the stochastic nature of the K-Means op-

timiser, we report the clusters of the minimal reached

inertia after 10 consecutive runs which is the standard

workﬂow with this algorithm.

In contrast to many other clustering techniques,

K-Means also allows us to predeﬁne the number of

clusters we expect based on expert knowledge com-

mon among researchers and is rather insensitive to

hyperparameters, which we expect to be very valuable

for those that rarely use ML-techniques (and even for

those that do). However, we do not expect the abil-

ity of our proposed approach to differ considerably

from other clustering techniques, e.g. DBSCAN or

OPTICS, should they be conﬁgured appropriately.

From our prior knowledge we know that:

1. we need at least six clusters based on the conver-

gence curves, based on their similarity (combin-

ing Normal, Fast, and Fast to Slow, and Subopti-

mal and None),

We use the implementation in the Python package

scikit-learn

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

112

(a) 6 clusters. (b) 8 clusters. (c) 16 clusters.

(d) 25 clusters. (e) 32 clusters. (f) 64 clusters.

Figure 2: Frequency of examples per cluster for different Ks.

2. we want to try eight clusters, one for each main

type,

3. we might want to test 25 clusters, one for each

possible curve,

4. we should also try some value in between, per-

haps: 16,

5. fewer than 32 clusters could still be a bit too few

so we should also run that, and,

6. ﬁnally, we want to, additionally, test 64 clusters,

one for each main curve type and for the different

measures.

Based on these considerations, we performed K-

Means clustering with K ∈ {6, 8, 16, 25, 32, 64}. The

respective distributions of curves into these clusters

can be found in Figure 2. We ﬁnd that, for all sizes,

a large number of runs can be clustered together, e.g.

the curves of cluster 1 for K = 8 are all converging

very fast towards a good objective value. Note that

the order of clusters is arbitrary. A number of inter-

esting examples of clusters and misclustering can be

found in the Figures 3 to 8 and they are discussed in

Section 3.3.

3.3 Discussion

In order to determine the usefulness of clustering

for analysing the convergence behaviour according to

speciﬁc characteristics, the results from the cluster-

ing approaches have to be examined in the context of

the aims of the analysis. We assumed that clustering

might be useful to group different algorithmic conﬁg-

urations by their convergence behaviour, which would

ease the in-depth analysis of these conﬁgurations as

only the distinct clusters rather than all curves would

need to be analysed in detail. Furthermore, we ex-

pected the clustering methods to utilise similar char-

acteristics as a researcher would (see Section 2). Fi-

nally, we surmised that some convergence curve types

should be more common than others, possibly not

only in the dataset used in this approach but in gen-

eral (e.g. a metaheuristic should perform any search,

so the None type should only result from extremely

unsuitable conﬁgurations).

In general, clustering can be used for that pur-

pose. However, there are considerations that have to

be made up front. For K-Means clustering, as em-

ployed in this work, the number of clusters has to be

speciﬁed up front. Therefore, either expert knowl-

edge is required to estimate the expected number of

clusters, or the number has to be determined by trial-

and-error. Additionally, the number of clusters also

depends on the research question. In this case, we

wanted the clustering to reﬂect the grouping we would

get when analysing all convergence curves visually,

while keeping in mind the convergence curve charac-

teristics. By looking at examples from the clusters,

we found that for 6, 8, and 16 clusters, the differenti-

ation is not ﬁne-grained enough as we could still ﬁnd

convergence curves within the same cluster that we

would identify as clearly different (see Figures 3, 4

and 5). For 25 clusters, there were still some slight

differences (cf. Figure 6), while for 32 clusters, there

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering

113

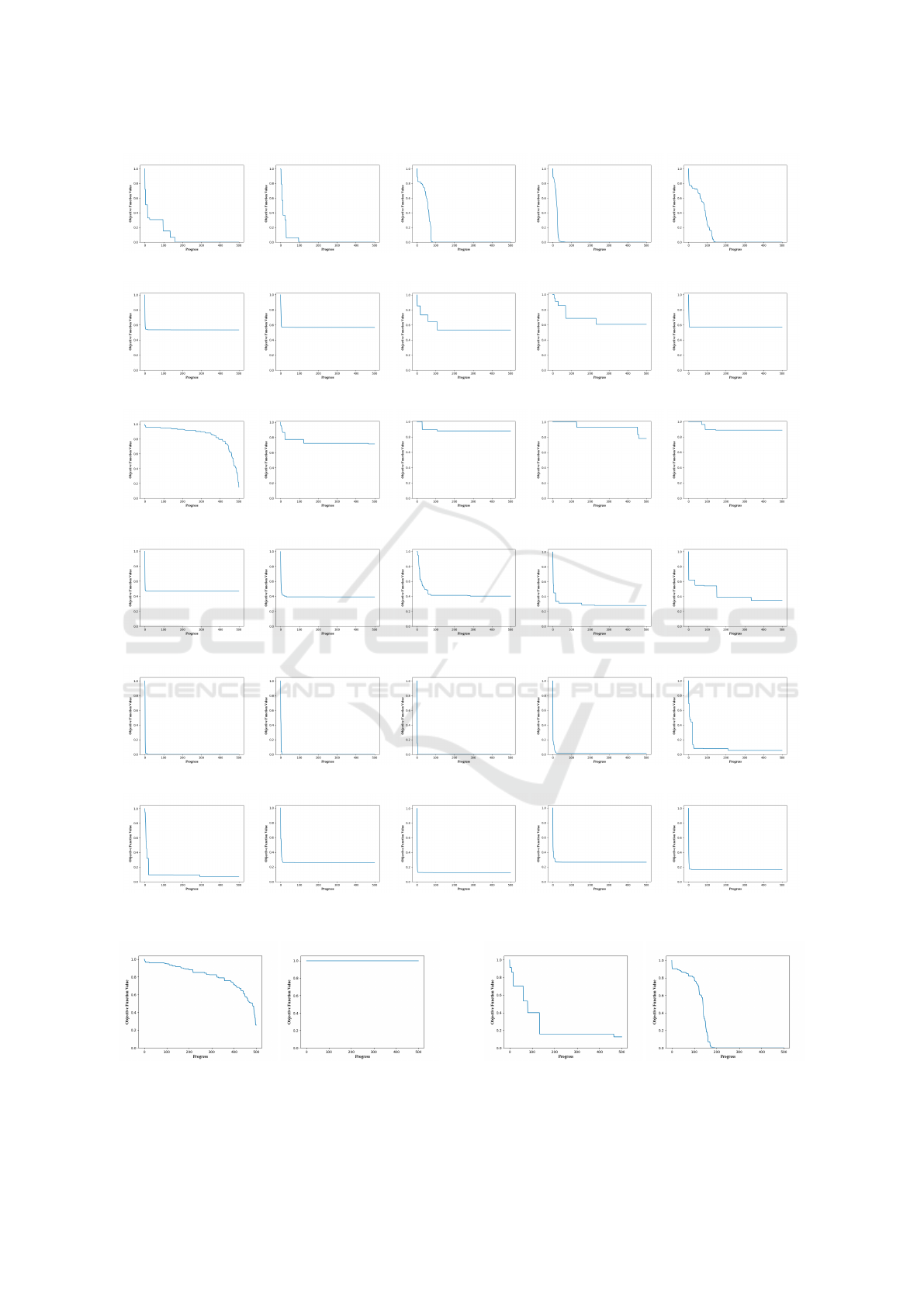
(a) Cluster 0.

(b) Cluster 1.

(d) Cluster 3.

(e) Cluster 4.

(f) Cluster 5.

Figure 3: Five randomly selected example curves per cluster for K=6.

Figure 4: Clearly different curves within cluster 5 for K = 8. Figure 5: Different curves within cluster 10 for K = 16.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

114

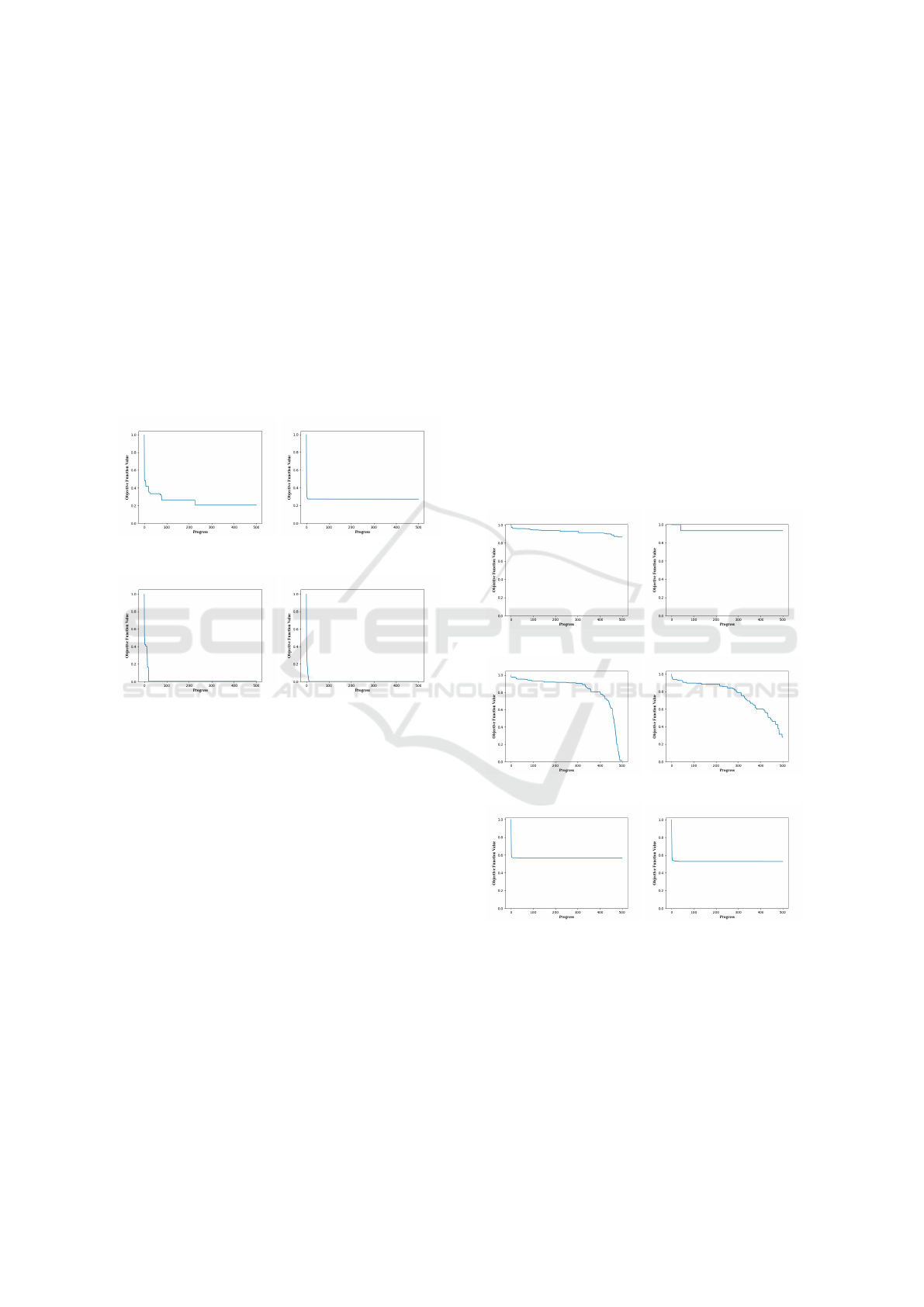
were convergence curves which seem similar but are

located in different clusters (see Figure 7). Depend-

ing on the goal of the analysis, both might still be

adequate, or any value in between. More clusters do

not seem to be useful, as even here differences within

a cluster can still be found, but more and more clus-

ters are too similar (see Figure 8). Most likely, dis-

similar curves in the same cluster are the result of the

convex decision boundaries introduced by K-Means.

However, we can assume that some curves that fall on

that border are clustered in one while others cluster

into another group. Having similar clusters is clearly

a result of K being too high and therefore introducing

new centroids that are subsequently slicing groups of

closely related curves in part.

Figure 6: Slightly differing curves within cluster 18 for K =

25.

Figure 7: Similar curves split into clusters 11 and 12 for

K = 32.

The distinction between the clusters can be related

to the characteristics described in Section 2, at least

in large parts. This is encouraging, as for a compre-

hensive analysis of the convergence behaviour, an ap-

propriate interpretability of the clusters is necessary.

For example, the cluster in Figure 3b corresponds

obviously to the Suboptimal curve type and the en-

tailed examples are additionally grouped by their ﬁ-

nal value. The cluster in Figure 3e corresponds to

Fast convergence with an (almost) optimal ﬁnal value,

while that in Figure 3a mixes Normal, Steps and Slow

to Fast, but its examples always reach the best pos-

sible ﬁnal value. When grouping into more clusters,

the differentiation is also based on more nuances in

the characteristics.

In terms of examples per cluster (see Figure 2),

we see that some clusters encompass more than oth-

ers. For a number of 6 clusters, the most examples

are grouped in cluster 4. This corresponds to Fast

or at least really good Normal convergence curves

(see Figure 3e), as was expected with not too difﬁ-

cult optimisation problems. For all K, this still stays

the same, i.e. the clusters with the highest number of

examples depict slightly different variations of Fast

type curves. Conversely, the clusters with the lowest

allocation correspond to the badly performing algo-

rithmic conﬁgurations which exhibit the None or an

extreme case of the Suboptimal curve type.

Overall, clustering can be used as a mean to facil-

itate the analysis of convergence behaviour on the ba-

sis of comprehensible characteristics and acts accord-

ing to our expectations. It summarises similar con-

vergence curves into the same cluster, enabling prac-

titioners to proceed with further (visual or computa-

tional) analyses per cluster instead of per conﬁgura-

tion, saving time and providing a ﬁrst step to correlate

similar behaviour to distinct conﬁgurations. However,

it should be noted that it is not without ﬂaws and espe-

cially not without putting in some effort, either to ﬁnd

a suitable conﬁguration or to verify that the results are

adequate for the research goal.

(a) Examples within cluster 11 show differences.

(b) Examples within cluster 18 show differences.

Figure 8: Some examples for K = 64.

3.4 Different Strategies and Subsequent

Approaches

In this paper, we relied on a traditional—and compar-

atively simple—clustering algorithm. However, we

want to raise to attention the power of modern deep

learning algorithms. In particular, we propose the use

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering

115

of autoencoder-based architectures for future analy-

ses. An autoencoder is a type of neural network that

features a so called latent space of much smaller di-

mensionality than the original inputs (dimensionality

reduction techniques in general have been used a few

times within recent years, e.g. for population dynam-

ics visualisation (Walter et al., 2022)). The network

is trained to output the input data without any loss

of information, however, by choosing a smaller la-

tent space, it is forced to learn a compression (hence

the name encoder) and a decompression function of

the data. We expect the autoencoder to be able to

compress the curves into very few (3-7) real-valued

features. These features can then be clustered simi-

larly to the current technique but, moreover, they can

be used to describe the curves and maybe these fea-

tures can even be related to how a human domain

expert would describe the convergence process, e.g.

“this curve is very steep”, but with a hard quantiﬁca-

tion that allows ordering and many more advantages

of speciﬁc numbers.

The exact design of the autoencoder is a topic

of future investigation but we assume that a tempo-

ral convolution (TCN)–based setup could be advan-

tageous over long short-term memory (LSTM)–based

or, especially, fully connected feed forward networks

(cf. the results of e.g. (Bai et al., 2018)) . Holstad

et al. (Holstad et al., 2020) found architectures us-

ing LSTM layers able to compress real-world mea-

surement curves similar to some of our found clus-

ters into only three features and reasoned about the

underlying physical processes based on that. In our

case, LSTMs might not be an ideal choice as they

tend to prioritise recent timesteps over long past ones

for their feature generation. However, some conver-

gences curves are most interesting in the beginning,

while some runs converge only late in the optimisa-

tion process (cf. Figure 3). While the use of (the en-

coding parts of) transformer networks (Vaswani et al.,

2017) could be discussed, we expect this to be unnec-

essarily complex for the task at hand. Although, the

self-attention mechanism might yield some insights

into why certain parts of a curve are of interest.

While for the current purpose K-Means seems to

be a sufﬁcient algorithm, we will test a variety of au-

toencoders in the near future as the potential advan-

tages towards greater understanding and easier anal-

ysis of operators and metaheuristics in general seem

intriguing.

Of course, other approaches can be used to group

by a speciﬁc behaviour according to predeﬁned char-

acteristics would. One would be to implement a rea-

sonable set of hard-coded rules directly, based on the

respective requirements of the research goal. While,

when done right, this approach will provide the best

results, it requires extensive expert knowledge and a

lot of time. Furthermore, if the research goal changes

or is adapted, it might be necessary to manually adapt

the procedure, requiring further knowledge of the new

circumstances. Alternative strategies to perform or

facilitate behavioural analyses of metaheuristics by

reducing the amount of (visual) information that has

to be examined include classic statistical approaches

such as factor analysis or combined metrics. Both can

be applied on their own, but also after the clustering

approach, which provides the advantage of a mean-

ingful preprocessing of the algorithmic data. Factor

analysis is aimed at ﬁnding the factors (e.g. hyperpa-

rameters or operators) or their combinations that in-

ﬂuence the criterion under investigation the most (see

e.g. (Bang-Jensen et al., 2007)). However, they are

data and computation heavy and require extensive ex-

amination of measures when the number of factors is

high. Combined metrics, on the other hand, can be

employed to summarise different measures and met-

rics (e.g. those mentioned in Section 2) into one sin-

gle value, thus reducing the amount of information

that needs to be investigated in detail (cf. e.g. (Song

et al., 2013; Chignell et al., 2015)). Their disadvan-

tage is the loss of information that can occur when not

properly devised, and it may be still required to take a

closer look at the individual measures.

4 CONCLUSION

This paper examined the applicability of unsuper-

vised machine learning techniques, particularly clus-

tering, to facilitate the analysis of the convergence be-

haviour of different algorithmic conﬁgurations. This

is especially useful when performing large empirical

studies, with several thousand conﬁgurations, where

a visual analysis of all measures and plots is infeasi-

ble. We found that clustering techniques can be suc-

cessfully applied to alleviate this problem and that

the characteristics used for clustering even relate to

those a researcher would consider. However, some

prior knowledge is still required, especially when de-

termining the number of clusters that should be used

and when analysing if the clustering performs as in-

tended. Overall, as the scale of empirical studies in

the ﬁeld of metaheuristics is growing and more com-

plex relationships between conﬁgurations and algo-

rithmic behaviour are of interest, it is worth exploring

clustering, for which we demonstrated its applicabil-

ity and advantages, and unsupervised machine learn-

ing in general, as well as to conceptualise other suit-

able approaches.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

116

ACKNOWLEDGEMENTS

This work was partially funded by the Deutsche

Forschungsgemeinschaft (DFG). It was also partially

funded by the Bavarian Ministry of Economic Affairs,

Regional Development and Energy.

REFERENCES

Azad, S. K. (2019). Monitored convergence curve: a new

framework for metaheuristic structural optimization

algorithms. Structural and Multidisciplinary Opti-

mization, 60(2):481–499.

Bacardit, J., Brownlee, A. E. I., Cagnoni, S., Iacca, G., Mc-

Call, J., and Walker, D. (2022). The intersection of

evolutionary computation and explainable AI. In Pro-

ceedings of the Genetic and Evolutionary Computa-

tion Conference Companion. ACM.

Bai, S., Kolter, J. Z., and Koltun, V. (2018). An empiri-

cal evaluation of generic convolutional and recurrent

networks for sequence modeling.

Bang-Jensen, J., Chiarandini, M., Goegebeur, Y., and

Jørgensen, B. (2007). Mixed models for the analysis

of local search components. In Engineering Stochas-

tic Local Search Algorithms. Designing, Implement-

ing and Analyzing Effective Heuristics, pages 91–105.

Springer Berlin Heidelberg.

Bartz-Beielstein, T., Doerr, C., Berg, D. v. d., Bossek, J.,

Chandrasekaran, S., Eftimov, T., Fischbach, A., Ker-

schke, P., La Cava, W., Lopez-Ibanez, M., Malan,

K. M., Moore, J. H., Naujoks, B., Orzechowski, P.,

Volz, V., Wagner, M., and Weise, T. (2020). Bench-

marking in Optimization: Best Practice and Open Is-

sues.

Bartz-Beielstein, T., Zaefferer, M., and Rehbach, F. (2017).

In a Nutshell - The Sequential Parameter Optimization

Toolbox.

Bosman, P. and Engelbrecht, A. P. (2014). Diversity rate

of change measurement for particle swarm optimisers.

In Lecture Notes in Computer Science, pages 86–97.

Springer International Publishing.

Campelo, F. (2015). Towards statistical convergence cri-

teria for mutation-based evolutionary algorithms. In

2015 Latin America Congress on Computational In-

telligence (LA-CCI). IEEE.

Chen, Y. and He, J. (2021). Average convergence rate of

evolutionary algorithms in continuous optimization.

Information Sciences, 562:200–219.

Chignell, M., Tong, T., Mizobuchi, S., Delange, T., Ho, W.,

and Walmsley, W. (2015). Combining multiple mea-

sures into a single ﬁgure of merit. Procedia Computer

Science, 69:36–43.

Eftimov, T., Jankovic, A., Popovski, G., Doerr, C., and

Koro

sec, P. (2021). Personalizing performance regres-

sion models to black-box optimization problems. In

Proceedings of the Genetic and Evolutionary Compu-

tation Conference. ACM.

Eftimov, T. and Koro

sec, P. (2019). A novel statistical ap-

proach for comparing meta-heuristic stochastic opti-

mization algorithms according to the distribution of

solutions in the search space. Information Sciences,

489:255–273.

Eftimov, T., Petelin, G., and Koro

sec, P. (2020). DSCTool:

A web-service-based framework for statistical com-

parison of stochastic optimization algorithms. Applied

Soft Computing, 87:105977.

Halim, A. H., Ismail, I., and Das, S. (2020). Performance

assessment of the metaheuristic optimization algo-

rithms: an exhaustive review. Artiﬁcial Intelligence

Review, 54(3):2323–2409.

Hansen, N., Auger, A., Brockhoff, D., Tu

sar, D., and Tu

sar,

T. (2016). COCO: Performance Assessment.

He, J. and Lin, G. (2016). Average convergence rate of

evolutionary algorithms. IEEE Transactions on Evo-

lutionary Computation, 20(2):316–321.

Holstad, T. S., Ræder, T. M., Evans, D. M., Sm

abr

aten,

D. R., Krohns, S., Schaab, J., Yan, Z., Bourret, E.,

van Helvoort, A. T. J., Grande, T., Selbach, S. M.,

Agar, J. C., and Meier, D. (2020). Application of a

long short-term memory for deconvoluting conduc-

tance contributions at charged ferroelectric domain

walls. npj Computational Materials, 6(1).

Ochoa, G., Malan, K. M., and Blum, C. (2021). Search tra-

jectory networks: A tool for analysing and visualising

the behaviour of metaheuristics. Applied Soft Com-

puting, 109:107492.

Song, M.-K., Lin, F.-C., Ward, S. E., and Fine, J. P. (2013).

Composite variables. Nursing Research, 62(1):45–49.

Stegherr, H., Luley, L., Wurth, J., Heider, M., and H

ahner,

J. (2023). A framework for modular construction and

evaluation of metaheuristics. Technical Report 2023-

01, Fakult

at f

ur Angewandte Informatik.

Tanabe, R. (2022). Benchmarking feature-based algorithm

selection systems for black-box numerical optimiza-

tion. IEEE Transactions on Evolutionary Computa-

tion, 26(6):1321–1335.

van Stein, B., Carafﬁni, F., and Kononova, A. V. (2021).

Emergence of structural bias in differential evolution.

In Proceedings of the Genetic and Evolutionary Com-

putation Conference Companion. ACM.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, L. u., and Polosukhin,

I. (2017). Attention is all you need. In Guyon,

I., Luxburg, U. V., Bengio, S., Wallach, H., Fer-

gus, R., Vishwanathan, S., and Garnett, R., editors,

Advances in Neural Information Processing Systems,

volume 30. Curran Associates, Inc.

Vermetten, D., Carafﬁni, F., van Stein, B., and Kononova,

A. V. (2022a). Using structural bias to analyse the

behaviour of modular CMA-ES. In Proceedings of

the Genetic and Evolutionary Computation Confer-

ence Companion. ACM.

Vermetten, D., van Stein, B., Carafﬁni, F., Minku, L. L.,

and Kononova, A. V. (2022b). BIAS: A toolbox for

benchmarking structural bias in the continuous do-

main. IEEE Transactions on Evolutionary Computa-

tion, 26(6):1380–1393.

Assisting Convergence Behaviour Characterisation with Unsupervised Clustering

117

Walter, M. J., Walker, D. J., and Craven, M. J. (2022). Vi-

sualizing population dynamics to examine algorithm

performance. IEEE Transactions on Evolutionary

Computation, 26(6):1501–1510.

Wang, H., Vermetten, D., Ye, F., Doerr, C., and B

ack, T.

(2022). IOHanalyzer: Detailed performance analy-

ses for iterative optimization heuristics. ACM Trans-

actions on Evolutionary Learning and Optimization,

2(1):1–29.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

118