Neural-Network for Position Estimation of a Cable-Suspended Payload

Using Inertial Quadrotor Sensing

Julien Mellet

, Jonathan Cacace

, Fabio Ruggiero

and Vincenzo Lippiello

PRISMA Lab, Department of Electrical Engineering and Information Technology, University of Naples Federico II,

Via Claudio 21, 80125, Naples, Italy

Keywords:

Neural Network, State Estimation, Quadrotor, Cable Suspended Payload.

Abstract:

This paper considers a standard quadrotor drone with a cable-suspended payload and minimal sensor conﬁg-

uration. A neural network estimator is proposed to perform accurate real-time payload position estimation. A

novel proprioceptive feedback measurement method is proposed, and a neural network has been trained with

domain randomization. The network shows accurate zero-shot estimation, even with excitations never seen

by the system before. This preliminary work has been tested in a simulated environment and aims to show

that only onboard inertial sensing is enough to achieve the sought task. The presented work may open new

applications for drone transportation in real environments subject to several perturbations.

1 INTRODUCTION

For aerial vehicles, there is a weight obsession such

that, especially for transportation tasks, each saved

gram on the platform is a gram for the payload (An-

derson and Gaston, 2013). Thanks to its simplicity,

a cable-suspended payload under an aerial vehicle re-

mains an elegant way to move any object through the

air (see Fig. 1). Compared to a mechatronic arm,

this system is lightweight and easy to install, uti-

lizing a single passive cable ﬁxation point. (Suarez

et al., 2020). Despite new aerial platforms like om-

nidirectional drones, quadrotors have demonstrated a

decade-long reliability (Bodie et al., 2019). A quadro-

tor with suspended load is comparable to helicopters

achieving object transport but with a difference in

agility and sensory system (Wendel et al., 2006). Nev-

ertheless, research tends to increase ﬂight accuracy by

embedding as many sensors as possible at the expense

of lightness and agility (Lanegger et al., 2 06), (Panet-

sos et al., 2022).

This preliminary study presents an approach that

simpliﬁes suspended payload position estimation in a

standard quadrotor, eliminating the need for extero-

ceptive sensor processing. Hence, only internal state

https://orcid.org/0009-0007-8386-0012

https://orcid.org/0000-0002-1639-5655

https://orcid.org/0000-0001-7539-9157

https://orcid.org/0000-0002-6089-2333

Figure 1: Pick and place tasks of the cable-suspended sys-

tem. In the ﬁrst frame, the drone reaches the package. The

grasp of the payload is done in the second frame. From

frame three to six, the load is transported. The last frame

shows the packet’s release, which is dropped into its target

location.

conﬁguration at a high temporal rate is employed in-

stead of cameras or any position sensor. Such sys-

tems are robust to environmental variations. The dis-

turbances induced by the payload on the system are

used to let a specially trained network ﬁnd a corre-

lation with the payload position. To the best of the

authors’ knowledge, no prior work achieved such ac-

curacy in estimating suspended payload position in

minimal aerial transportation setups.

1.1 Related Works

Conventional approaches to cable-suspended pay-

load transportation use external sensors such as cam-

Mellet, J., Cacace, J., Ruggiero, F. and Lippiello, V.

Neural-Network for Position Estimation of a Cable-Suspended Payload Using Inertial Quadrotor Sensing.

DOI: 10.5220/0012204100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 80-87

ISBN: 978-989-758-670-5; ISSN: 2184-2809

era (Tang et al., 2018), (Guo and Leang, 2020). Get-

ting a direct measurement of the payload position is

a reasonable option. Even with a relatively low mea-

surement rate compared to the low-level controller, it

allows making aggressive ﬂights (Tang et al., 2018).

However, cameras suffer from several problems like

brightness (close to shadow), ﬂickering (while ﬂying

over the sea), or fogging (in a humid area), making

their use standalone unsafe for reliable industrial ap-

plications. The issue has also been revealed by (Lee

and Kim, 2017), where the proposed solution con-

sists of adding force sensors to the system. Equiva-

lent sensing solutions have been adopted by (Lv et al.,

2021), with the addition of a universal joint between

the drone and the cable for the second one. Recently,

(Panetsos et al., 2022) used four different sensors to

get accurate cable state estimation, while (Outeiro

et al., 2023) proposed an adaptive geometric control

method with asymptotic tracking stability.

A similar approach to ours is described by (Kauf-

mann et al., 2020) and (Ciofﬁ et al., 2022) to perform

agile maneuvers. The use of internal sensing in those

papers is called sensorimotor, but for the uniﬁcation

of the terms in robotics, we will call it proprioception,

like it has been done in (Lee et al., 2020). Even if we

do not have access to direct measurement of the motor

speed, the PWM (Pulse-Width Modulation) command

gives a fair proportional estimation. A neural network

(NN) is implemented to control the drone. In partic-

ular, the work done by (Ciofﬁ et al., 2022) learns in-

ertial odometry and gets accurate position estimation

without using any visual perception. However, the

positioning tracking has been done with previously

known trajectories. In contrast, for safety reasons, we

implemented a neural network trained by supervised

learning on the estimation stage of the tethered pay-

load controller.

One of the most advanced research on payload

state estimation using quadrotor proprioception is for

parameter estimation (Prka

cin et al., 2020). Re-

cently, such a work has been improved by (Prka

cin

et al., 2021) with the implementation of an extended

Kalman ﬁlter (EKF). However, estimation of load pa-

rameters remains challenging with the employed fast

Fourier transform technique, getting only off-line re-

sults. Unfortunately, even if the research looks in an

interesting direction with a minimal drone setup, real-

time performance has not been reached. Real-world

experiments showed poor results in tracking the an-

gles of the payload. The system is non-linear, and

the IMU is noisy while drones ﬂy at high velocity.

This makes classical EKF implementation unusable

for real ﬂights application. To tackle real-time, we use

the concept of a neural observer (Chen et al., 2018)

with a recurrent NN to access indirectly measured

data (Habtom and Litz, 1997).

1.2 Contribution

In this paper, we prove the feasibility of real-time

position estimation of a cable-suspended end-effector

using only inertia sensors onboard a standard quadro-

tor. Contrary to the classic EKF approach, our method

does not need to deﬁne any parameter a priori. We

used a supervised learned network, making the posi-

tion estimation of the suspended load for a standard

quadrotor attitude controller. The neural estimator is

trained in a simulated environment, with domain ran-

domization, and runs the software controller in the

loop. We reached zero-shot generalization of the net-

work for load position estimation. After being trained

on our dataset, the network has the capability to pre-

dict previously unseen perturbations, in particular, di-

rect injection of energy into the end-effector. This

shows the consistency of the estimator implementa-

tion, as well as its generalization capabilities.

2 MATERIALS AND METHODS

Making payload pose estimation is not a trivial task,

and the classical ﬁlter approach showed accuracy lim-

itations (Prka

cin et al., 2021). In this section, we ﬁrst

deﬁne our model, which is needed for the simulation,

and implement an attitude controller. Then, we focus

on data processing to measure our features to train

the network. Finally, to smooth the training, we grad-

ually increase the measurement domain exploration

with progressively more sophisticated trajectories.

2.1 Model

For the quadrotor, we consider the dynamic model

with the Euler angles (Ollero and Siciliano, 2019).

Here we use FLU (Front-Left-Up) convention to de-

ﬁne the body frame B with axes {x, y, z}, and the

world frame W with axes {x

, y

, z

}. We deﬁne the

drone position and its attitude as p

= [x

, y

, z

]

⊤

∈

and η

= [φ

, θ

, ψ

]

⊤

∈ R

, respectively, with

their time derivatives ˙p

and

. The attitude can also

be deﬁned with R

∈ SO(3), the rotation matrix from

B to W , the special orthogonal group of dimension

three, from which the roll-pitch-yaw angles φ

, θ

and ψ

, respectively, can be extracted. These give the

linear and angular accelerations of the base as,

¨p

= g e

, (1)

Neural-Network for Position Estimation of a Cable-Suspended Payload Using Inertial Quadrotor Sensing

Payload

position

controller

Payload

attitude

controller

Quadrotor

attitude

controller

Plant

quadrotor &

payload

Neural

estimator

𝜼

𝒃

, 𝝎

𝒃

𝒇

𝒖

, 𝝉

𝒖

𝑻

, 𝜼

𝒃,𝒅

𝒑

𝒍

, 𝒑

𝒍

𝒒

𝒍

, 𝒒

𝒍

𝒒

𝒍,𝒅

𝒑

𝒃

, 𝜼

𝒃

, 𝝎

𝒑

𝒍,𝒅

, 𝒑

𝒍,𝒅

Figure 2: Control layout architecture with neural network state estimation.

Figure 3: Schematic representation of the quadrotor (in

blue) with the cable-suspended payload (in red). The terms

, l

∈ R, with l

>> l

are the support length and the cable

length, respectively. Besides, ω

∈ R, i = 1, . .. , 4 are the ro-

tation speed of the motors, while θ

, θ

∈ R are the angles

of the cable with respect to the drone.

= M(η

)

−1

(−C(η

) + Q

⊤

(η

)τ

), (2)

where g ∈ R is the gravity, m ∈ R is the drone

mass, and e

= [0, 0, 1]

⊤

. Moreover, M(η

) =

Q(η

)

⊤

Q(η

) ∈ R

3×3

is the symmetric and posi-

tive deﬁnite (provided that θ ̸= ±

) mass matrix, I

∈

3×3

is the drone inertia matrix, and Q(η

) ∈ R

3×3

is the transformation matrix such that ω

= Q(η

)

where ω

∈ R

is the angular velocity of the B with

respect to the W expressed in B. Finally, C(η

) =

⊤

(η

)S(Q(η

)

Q(η

)+Q

⊤

(η

)

⊤

Q(η

) ∈ R

is the Coriolis matrix, with S(·) ∈ R

3×3

the skew-

symmetric operator, τ

= [τ

, τ

]

⊤

∈ R

is the

torque control vector, and u

∈ R

is the total thrust.

The physical control inputs to the system, that is

the propeller velocities ω

∈ R, with i = 1, . . . , 4 (see

Fig. 3), can be retrieved from the torques and the total

thrust through the allocation matrix as follows,



















0 lc

0 −lc

−lc

0 lc

−c



















, (3)

where c

, c

∈ R

are the thrust constant and drag

factor, respectively.

For the suspended-cable, several models were pro-

posed in the literature, such as ﬁnite element approx-

imation (Goodarzi et al., 2014), elastic rope (Kotaru

et al., 2017), or a rigid bar (Tang et al., 2018). The

last model has been chosen for ease of simulation.

It represents the most interesting case for transporta-

tion. Details of the model are presented by (Sreenath

et al., 2013) and explained in Fig. 3. Recall that

the quadrotor is a differentially ﬂat system (Rathi-

nam et al., 1995), while the quadrotor with a cable-

suspended payload is a differentially ﬂat hybrid sys-

tem (Tang et al., 2018; Sreenath et al., 2013). Hence,

all state and input variables are deﬁned through non-

linear equations involving ﬂat variables and their re-

spective derivatives.

The load is considered as a point mass, the mass

of the cable is neglected, and the cable is considered

rigid. The variables are deﬁned in Fig. 3. The position

of the quadrotor in W can be retrieved from the load

position as

= q

− l

, (4)

where q

∈ R

is the load position in W and p

∈ S

with S

the manifold of unit vectors in R

, is the unit

vector pointing the load from the quadrotor’s center

of mass.

2.2 Control

The controller presented by (Sreenath et al., 2013)

and applied by (Tang et al., 2018) is here brieﬂy

reported. The state and input are deﬁned as, x =

⊤

, ˙p

⊤

, p

⊤

, ˙p

⊤

, ω

⊤

]

⊤

and u = [ f

⊤

, τ

⊤

]

⊤

, re-

spectively.

First, deﬁne the low level quadrotor attitude con-

troller as,

= −K

− K

+ S(ω

−I

(S(ω

⊤

b,d

− R

⊤

b,d

(5)

where K

, K

∈ R

3×3

are diagonal gain matrices,

⊤

b,d

− R

⊤

b,d

)

∨

∈ R

is the quadrotor at-

titude error, e

= ω

− R

⊤

b,d

∈ R

is the an-

gular velocity error, (·)

∨

is the vee operator mapping

a skew-symmetric matrix into the vector that gener-

ated it, R

b,d

∈ SO(3) is the desired quadrotor rotation

matrix, ω

b,d

∈ R

is the desired angular velocity ex-

pressed in the desired body frame.

The desired R

b,d

and ω

b,d

are retrieved from the

position controller as explained by (Tang et al., 2018).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

Features Recurrent Net MLP Labels

IMU

(accelerometer + gyroscope)

𝒑

𝒃

Control Input

(thrust + attitude)

Motors Speed

𝜼

𝒃

𝝎

𝒖

𝑻

𝜼

𝒃,𝒅

1×14

8×256

⁝

1×128 1×64

⁝



𝟐



𝟏

1×2



𝟏

𝑥



𝑦



𝑧



𝑝





𝟐

𝑦



𝑧



𝑥



𝑝





𝟏

Cable

Angles

Figure 4: Neural network architecture. The NN keeps the history of the past data at the same rate. All features are processed

through a recurrent neural network layer. Then data are processed with a fully connected multi-layer perception before getting

the two angles of the cable.

The thrust input results from,

= u

, (6)

where,

= K

+ K

˙p

+ K

dt, (7)

with K

, K

˙p

, K

∈ R

some diagonal and positive def-

inite gain matrices, e

= S(p

)

l,d

the error function

with p

l,d

∈ R

the desired load position in W , and

˙p

= ˙p

− S(S(p

l,d

) ˙p

l,d

the time derivative. Then,

the desired quadrotor attitude is,

b,d





S(b)c

∥S(b)c∥



S(b)c

∥S(b)c∥

, c



, (8)

with ∥ · ∥ the Euclidean norm, b =

∥u

∥

∈ R, and

c = [cos(ψ

), sin(ψ

), 0]

⊤

∈ R

Finally the payload position controller is deﬁned

as,

l,d

= K

+ K

˙q

+ K

q,i

dt, (9)

with K

, K

˙q

, K

q,i

∈ R

some diagonal and positive def-

inite gain matrices, e

= q

− q

l,d

∈ R

the error func-

tion, and e

˙q

= ˙q

− ˙q

l,d

∈ R

its time derivative.

The controller implementation is presented in

Fig. 2 and the NN estimator is explained in the next

section.

2.3 Neural Estimation

Through all the data provided by the IMU, the mag-

netometer has been found to add too much noise and

randomness to the result. Then, only the accelerome-

ter and the gyroscope are used.

Compared to (Kaufmann et al., 2020), we found

that sampling measurements with synchronization of

all the features were getting accurate results. Normal-

ization is done with min-max normalization. Assum-

ing X ∈ R a scalar, we use the unit-based normaliza-

tion,

norm

X −X

min

max

− X

min

. (10)

To avoid any overshoot on measurements X

meas

∈ R,

boundaries limits are ﬁxed with saturation values such

that,

meas

∈ [X

min

, X

max

]. (11)

The main network architecture Fig. 4 remains con-

densed, with relatively few hidden layers. Keeping

the network as small as possible is to implement it on

a small computational unit and reduce the processing

latency. It has three incoming features branches with

the IMU ( ¨p

) ∈ R

the motor speeds ω ∈ R

, and

the control inputs (u

, η

b,d

) ∈ R

. There is a total of

fourteen scalar input features [ ¨p

, ω, u

, η

b,d

] pre-

processed as mentioned above.

For a later comparison study, we want to com-

pare different promising NNs, namely, a time convo-

lutional network (TCN) and two recurrent neural net-

works (RNN). For both cases, networks are trained on

a history of N time past steps to the current measure-

ment that are deﬁned later. Even if TCN proved its

efﬁciency in neural estimation for drones (Kaufmann

et al., 2020; Ciofﬁ et al., 2022), RNN looks to be a

more appropriate option. These layers take advan-

tage of processing sequential data to make the predic-

tion. In this study, we used Long Short-Term Mem-

ory (Hochreiter and Schmidhuber, 1997) (LSTM)

hidden neurons that have also been used by (Perin-

gal et al., 2022; Jung et al., 2022). We can notice that

simple RNN and gated recurrent unit (GRU) have also

been tested during this research, but the results were

similar to LSTM with poorer prediction accuracy. For

this reason, LSTM is the chosen recurrent net archi-

tecture.

The recurrent network trained with N = 15 times-

tamps of the past proprioceptive measurements fol-

lows. Even if the eight past measures were used

by (Kaufmann et al., 2020), we got better perfor-

mance with ﬁfteen. Then, two fully connected layers

of MLPs give the cable angles (θ

, θ

). We use differ-

entiation to obtain the angular velocity ˙p

needed for

the controller in Fig. 2.

Neural-Network for Position Estimation of a Cable-Suspended Payload Using Inertial Quadrotor Sensing

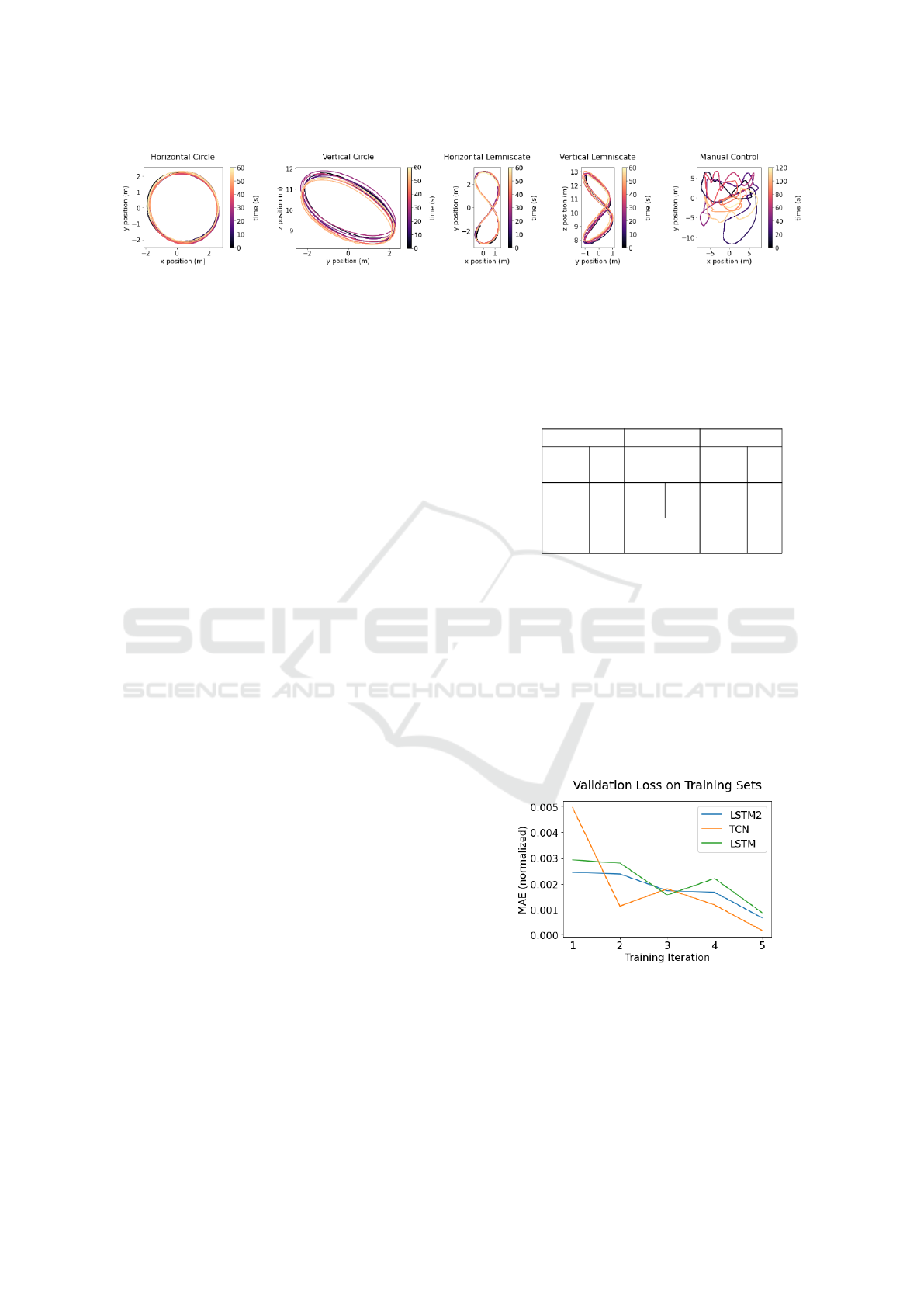
Figure 5: Sample trajectories used to train networks. From left to right, with trajectories getting more complex through the

training: 1 min horizontal circle trajectory; 1 min vertical circle trajectory; 1 min horizontal lemniscate trajectory; 1 min

vertical lemniscate trajectory; 2 min of manual control.

2.4 Training

Compared to (Lee et al., 2020), (Faust et al., 2017)

that substantially used reinforcement learning to train

their networks, we used supervised learning. How-

ever, we kept the principle of accelerating the train-

ing with a given policy. Thus, we proposed to begin

the training with simple trajectories, letting the loss

converge smoothly. Then, we complicated the trajec-

tories to ﬁnish with erratic movements. Here, only

state estimation is performed by the network. The ad-

vantage of virtual training, is to have an inﬁnite ﬂight

time with variable parameters. The payload position

controller is fed with circular, lemniscate, and random

manual trajectories (see Fig. 5).

We trained the NN estimator through ten datasets

with the ﬁve different trajectories, depicted in Fig. 5,

and two different payloads of 200 g and 800 g. The

sum of the datasets gives a total of 140.10

times-

tamped measurements for 50 min ﬂight time. We split

each trajectory dataset in two, with 20% for validation

and the remaining 80% for training.

To predict the load position, p

, a time window

of size 16 has been used. Thanks to the 15 past mea-

sured features, the 16

label is predicted. Because the

regressive network has to keep consistency through

time, no data shufﬂe was made. Nevertheless, each

data set was split up into batches of size 256. Trying

different batch sizes, it turned out this last was a good

trade-off. For the simulation, we used Gazebo, a sim-

ulator with a physic engine (Smith, 2008). The pro-

pellers’ drag, lift coefﬁcients and IMU characteristics

are simulated through the internal plugin. We simu-

late our quadcopter with a stick with a two-degree-

of-freedom (DoF) universal joint, presented in Fig. 3.

Compared to real ﬂights, the simulator does not pro-

vide any aerodynamic effects. As a result, the pay-

load is static under the drone while hovering. We then

propose to make domain randomization through the

excitation of the end-effector. It consists in applying

a relatively small bounded random force on the end-

effector. In our case, we selected a maximum force of

0.2 N. It is now about comparing the network’s per-

formances.

Table 1: Architectures of the three networks that are com-

pared for the study. LSTM2 with two recurrent layers and

an MLP before the output. TCN with a convolutional layer

followed by an MLP. LSTM embedding a unique recurrent

layer and two MLPs.

LSTM2 TCN LSTM

Hidden

layer 1

LSTM 256 Conv LSTM 256

Hidden

layer 2

LSTM 128 MLP 128 MLP 128

Hidden

layer 3

MLP 64 X MLP 64

2.5 Networks Comparisons

The ﬁrst set of experiments compares the accuracy in

the prediction of three promising neural architectures.

Table 1 compares the architectures of the three net-

works used for the research. with two recurrent layers

and an MLP before the output. TCN with a convo-

lutional layer followed by an MLP. LSTM embeds a

unique recurrent layer and two MLPs. Then, the train-

ing through the different trajectories is presented in

Fig. 6.

Figure 6: Validation loss after training on each trajectory

dataset. From left to right, 1 corresponds to the horizontal

circle, 2 corresponds to the vertical circle, 3 corresponds

to the horizontal lemniscate, 4 corresponds to the vertical

lemniscate, and 5 corresponds to manual control.

One can notice that the validation loss decreases

after each trajectory train. This points out the im-

provement of the estimation prediction with more and

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

more sophisticated trajectories. Nevertheless, even if

TCN showed a better accuracy on the validation set,

RNN performs better with the test set (see Fig. 7).

Figure 7: Mean absolute error of LSTM2, TCN, and LSTM

after being trained on the different datasets.

The better performance of TCN in Fig. 7 is notice-

able on the validation set, while LSTM is more accu-

rate on the test set. LSTM2 and even more LSTM has

thus a generalization capability. Both temporal con-

volution and recurrent networks result in the same or-

der of magnitude, thanks to temporal measurements.

The following section uses only LSTM to under-

stand what implies the change in payload mass on the

NN estimator.

3 APPLICATIONS

NN estimation takes a certain time to process. We

made an inference model of our network to accelerate

pose estimation during the experiments. We improved

the pose estimation processing from a mean response

time of 4.10

−2

s to an instant estimation of 10

−4

without losing accuracy.

3.1 Response to External Perturbations

Because the weight of the payload directly impacts

drone perturbation, and by implication the inertial

sensor measurements, we want to understand how the

weight impacts pose estimation of the end-effector.

To measure the accuracy of prediction, we have per-

turbed the load on the single x-axis with 40 N for the

200 g load (see Fig. 8) and with 100 N for the 800 g

load (see Fig. 9).

For both plots, with light-weight (see Fig. 8) and

heavy payload (Fig. 9), we notice that the estimation

follows the ground truth through time with a drop in

accuracy at the perturbation. Moreover, no perturba-

tion is measured on θ

, the non-perturbed axis, show-

ing the independence of each angle estimation.

Another critical point is the noise reduction in

payload state estimation with a heavier load. This

phenomenon should be explained for two reasons:

ﬁrstly, because the heavier load, with greater iner-

tia, have slower dynamics, which is easier to predict;

secondly, because the perturbation of the largest mass

has more effect on the system and disturbance can be

measured with higher intensity by the inertial unit.

Figure 8: Cable orientation estimation for a 200 g load and

40 N force excitation. The mean absolute error (MAE)

between ground-truth in green and estimated angle in red,

has been measured at 0.05326 rad. Perturbation is done at

t = 126 s.

Figure 9: Cable orientation estimation for a 800 g load and

100 N force excitation. The mean absolute error (MAE)

between ground-truth in green and estimated angle in red,

has been measured at 0.01772 rad. Perturbation is done at

t = 155 s.

3.2 Use Case Example

The proposed estimator was then applied in a pick-

and-place scenario. The idea is to understand the esti-

mation performance without training the network for

this speciﬁc application. The drone picks up a 600 g

package and transports it to a basket at the target lo-

cation. Figure 1 presents the environment in which

the system is used. The drone ﬂies at a relatively slow

speed, keeping the near-hovering assumption.

Compared to the system subjected to simple dis-

turbances (see Figs. 8-9), we can notice a more sig-

niﬁcant mean absolute error (MAE) during the entire

task in Fig. 10. The same comments as previously can

Neural-Network for Position Estimation of a Cable-Suspended Payload Using Inertial Quadrotor Sensing

Figure 10: Cable orientation estimation during a pick and

place task. The payload is grasped at t = 580 s, and released

at t = 1310 s. The mean absolute error (MAE) between

ground-truth in green and estimated angle in red, has been

measured at 0.08365 rad.

be made, on the inﬂuence of weight on estimation.

For θ

, MAE is more signiﬁcant with the unloaded

end-effector, while precision increases with the pay-

load transported. An estimation bias has to be noticed

for θ

during the carriage. Likewise, the grasping ac-

tion being similar to a prompt perturbation, the same

result is observed as above, with a drop in accuracy.

In contrast to the grab, the release is smoother, and

the accuracy of the estimate changes from a lower to

a higher MAE.

4 CONCLUSION AND FUTURE

WORK

This preliminary study demonstrates that inertial

measurements are sufﬁcient for estimating payload

position in cable-suspended drone systems, enabling

their integration into the controller. Moreover, in-

direct neural pose estimation has been proven ac-

curate in performing stable transportation tasks near

hovering. The hardware complexity has thus de-

creased. This estimator suits cable-suspended under-

water transport, free from sun reﬂection ﬂickering on

water waves.

Future work will focus on transferring the NN

from simulation to reality thanks to domain random-

ization presented in this paper. The core idea is to test

the neural estimator in challenging-to-simulate envi-

ronments. On the other hand, we would like to take

advantage of this estimator to perform aggressive ma-

neuvers implementing model predictive control.

ACKNOWLEDGEMENTS

The research leading to these results has been sup-

ported by the AERIAL-CORE project (Horizon 2020

Grant Agreement No. 871479) and by the AERO-

TRAIN Project, European Union’s Horizon 2020

Research and Innovation Program under the Marie

Skłodowska-Curie Grant Agreement 953454. The au-

thors are solely responsible for its content.

REFERENCES

Anderson, K. and Gaston, K. J. (2013). Lightweight un-

manned aerial vehicles will revolutionize spatial ecol-

ogy. Frontiers in Ecology and the Environment,

11(3):138–146.

Bodie, K., Brunner, M., Pantic, M., Walser, S., Pfndler,

P., Angst, U., Siegwart, R., and Nieto, J. (2019).

An Omnidirectional Aerial Manipulation Platform for

Contact-Based Inspection. In Robotics: Science and

Systems XV. Robotics: Science and Systems Founda-

tion.

Chen, B., Zhang, H., Liu, X., and Lin, C. (2018). Neural

Observer and Adaptive Neural Control Design for a

Class of Nonlinear Systems. IEEE Transactions on

Neural Networks and Learning Systems, 29(9):4261–

4271.

Ciofﬁ, G., Bauersfeld, L., Kaufmann, E., and Scara-

muzza, D. (2022). Learned Inertial Odometry for Au-

tonomous Drone Racing.

Faust, A., Palunko, I., Cruz, P., Fierro, R., and Tapia,

L. (2017). Automated aerial suspended cargo de-

livery through reinforcement learning. Artiﬁcial In-

telligence, 247:381–398. Special Issue on AI and

Robotics.

Goodarzi, F. A., Lee, D., and Lee, T. (2014). Geometric

stabilization of a quadrotor UAV with a payload con-

nected by ﬂexible cable. In 2014 American Control

Conference, pages 4925–4930.

Guo, D. and Leang, K. K. (2020). Image-Based Estimation,

Planning, and Control of a Cable-Suspended Payload

for Package Delivery. IEEE Robotics and Automation

Letters, 5(2):2698–2705.

Habtom, R. and Litz, L. (1997). Estimation of unmea-

sured inputs using recurrent neural networks and the

extended Kalman ﬁlter. In Proceedings of Interna-

tional Conference on Neural Networks (ICNN’97),

volume 4, pages 2067–2071 vol.4.

Hochreiter, S. and Schmidhuber, J. (1997). Long Short-

Term Memory. Neural Comput., 9(8):1735–1780.

Jung, J., You, S., Kim, D., and Park, J. (2022). Vari-

able Stiffness Control via External Torque Estimation

Using LSTM. In 2022 International Conference on

Robotics and Automation (ICRA), pages 8325–8330.

Kaufmann, E., Loquercio, A., Ranftl, R., M

uller, M.,

Koltun, V., and Scaramuzza, D. (2020). Deep Drone

Acrobatics.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

Kotaru, P., Wu, G., and Sreenath, K. (2017). Dynamics

and control of a quadrotor with a payload suspended

through an elastic cable. In 2017 American Control

Conference (ACC), pages 3906–3913.

Lanegger, C., Ruggia, M., Tognon, M., Ott, L., and Sieg-

wart, R. (2022-06). Aerial layouting: Design and con-

trol of a compliant and actuated end-effector for pre-

cise in-ﬂight marking on ceilings. In Proceedings of

Robotics: Science and System XVIII, page p073, s.l.

Robotics Science & Systems Foundation.

Lee, J., Hwangbo, J., Wellhausen, L., Koltun, V., and Hut-

ter, M. (2020). Learning quadrupedal locomotion over

challenging terrain. Science Robotics, 5(47).

Lee, S. J. and Kim, H. J. (2017). Autonomous swing-angle

estimation for stable slung-load ﬂight of multi-rotor

UAVs. In 2017 IEEE International Conference on

Robotics and Automation (ICRA), pages 4576–4581.

Lv, Z.-Y., Li, S., Wu, Y., and Wang, Q.-G. (2021). Adap-

tive Control for a Quadrotor Transporting a Cable-

Suspended Payload With Unknown Mass in the Pres-

ence of Rotor Downwash. IEEE Transactions on Ve-

hicular Technology, 70(9):8505–8518.

Ollero, A. and Siciliano, B. (2019). Aerial Robotic Manip-

ulation. Springer.

Outeiro, P., Cardeira, C., and Oliveira, P. (2023). Con-

trol architecture for a quadrotor transporting a cable-

suspended load of uncertain mass. Drones, 7(3).

Panetsos, F., Karras, G. C., Aspragkathos, S. N., and Kyri-

akopoulos, K. J. (2022). Precise Position Control of a

Multi-rotor UAV with a Cable-suspended Mechanism

During Water Sampling. In 2022 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS), pages 1780–1786.

Peringal, A., Chehadeh, M., Azzam, R., Hamandi, M.,

Boiko, I., and Zweiri, Y. (2022). Design of Dynamics

Invariant LSTM for Touch Based Human–UAV Inter-

action Detection. IEEE Access, 10:116045–116058.

Prka

cin, V., Palunko, I., and Petrovi

c, I. (2021). Ex-

tended Kalman ﬁlter for payload state estimation uti-

lizing aircraft inertial sensing. In 2021 Aerial Robotic

Systems Physically Interacting with the Environment

(AIRPHARO), pages 1–6.

Prka

cin, V., Palunko, I., and Petrovi

c, I. (2020). State and

parameter estimation of suspended load using quadro-

tor onboard sensors. In 2020 International Conference

on Unmanned Aircraft Systems (ICUAS), pages 958–

967.

Rathinam, M., Murray, R. M., and Sluis, W. M. (1995). Dif-

ferential Flatness of Mechanical Control Systems: A

Catalog of Prototype Systems.

Smith, R. (2008). Open Dynamics Engine.

http://www.ode.org/.

Sreenath, K., Lee, T., and Kumar, V. (2013). Geometric

control and differential ﬂatness of a quadrotor UAV

with a cable-suspended load. In 52nd IEEE Confer-

ence on Decision and Control, pages 2269–2274.

Suarez, A., Vega, V. M., Fernandez, M., Heredia, G.,

and Ollero, A. (2020). Benchmarks for Aerial Ma-

nipulation. IEEE Robotics and Automation Letters,

5(2):2650–2657.

Tang, S., W

uest, V., and Kumar, V. (2018). Aggres-

sive Flight With Suspended Payloads Using Vision-

Based Control. IEEE Robotics and Automation Let-

ters, 3(2):1152–1159.

Wendel, J., Meister, O., Schlaile, C., and Trommer, G. F.

(2006). An integrated GPS/MEMS-IMU navigation

system for an autonomous helicopter. Aerospace Sci-

ence and Technology, 10(6):527–533.

Neural-Network for Position Estimation of a Cable-Suspended Payload Using Inertial Quadrotor Sensing