Challenges of ELA-Guided Function Evolution Using Genetic

Programming

Fu Xing Long

1 a

, Diederick Vermetten

2 b

, Anna V. Kononova

2 c

, Roman Kalkreuth

3 d

Kaifeng Yang

4 e

, Thomas B

ack

2 f

and Niki van Stein

2 g

BMW Group, Knorrstraße 147, Munich, Germany

LIACS, Leiden University, Niels Bohrweg 1, Leiden, The Netherlands

Computer Lab of Paris 6, Sorbonne Universit

e, Paris, France

University of Applied Sciences Upper Austria, Softwarepark 11, 4232, Hagenberg, Austria

Keywords:

Function Generator, Genetic Programming, Exploratory Landscape Analysis, Instance Spaces.

Abstract:

Within the optimization community, the question of how to generate new optimization problems has been

gaining traction in recent years. Within topics such as instance space analysis (ISA), the generation of new

problems can provide new benchmarks which are not yet explored in existing research. Beyond that, this

function generation can also be exploited for solving expensive real-world optimization problems. By gen-

erating fast-to-evaluate functions with similar optimization properties to the target problems, we can create a

test set for algorithm selection and conﬁguration purposes. However, the generation of functions with speciﬁc

target properties remains challenging. While features exist to capture low-level landscape properties, they

might not always capture the intended high-level features. We show that it is challenging to ﬁnd satisfying

functions through a genetic programming (GP) approach guided by the exploratory landscape analysis (ELA)

properties. Our results suggest that careful considerations of the weighting of ELA properties, as well as the

distance measure used, might be required to evolve functions that are sufﬁciently representative to the target

landscape.

1 INTRODUCTION

Benchmark problems play a key role in our abil-

ity to efﬁciently evaluate and compare the perfor-

mance of optimization algorithms. Well-constructed

benchmark suites provide researchers the opportunity

to gauge the different strengths and weaknesses of

a wide variety of optimization algorithms (Hansen

et al., 2010). Following this, carefully handcrafted

sets of problems, such as the black-box optimization

benchmarking (BBOB) suite (Hansen et al., 2009),

have become increasingly popular (Bartz-Beielstein

et al., 2020). Beyond benchmarking purposes, the

https://orcid.org/0000-0003-4550-5777

https://orcid.org/0000-0003-3040-7162

https://orcid.org/0000-0002-4138-7024

https://orcid.org/0000-0003-1449-5131

https://orcid.org/0000-0002-3353-3298

https://orcid.org/0000-0001-6768-1478

https://orcid.org/0000-0002-0013-7969

BBOB suite has been intensively used in the research

ﬁeld of algorithm selection problem (ASP) (Rice,

1976), with the focus on identifying computational

and time-efﬁcient algorithms for a particular prob-

lem instance. Recently, this has been associated

with the optimization landscape properties of prob-

lem instances, where the landscape properties are ex-

ploited to predict the performance of optimization al-

gorithms, e.g., using machine learning models (Ker-

schke and Trautmann, 2019a).

One inherent limitation of these hand-crafted

benchmark suites, however, lies in the fact that they

can never cover the full instance space. For instance,

it has been shown that real-world automotive problem

instances are insufﬁciently represented by the BBOB

functions in terms of landscape properties (Long

et al., 2022). Consequently, there is a growing trend

in understanding the coverage of problem classes by

existing benchmark sets, and in the creation of new

benchmarks to ﬁll the gaps (Smith-Miles and Mu

noz,

Long, F., Vermetten, D., Kononova, A., Kalkreuth, R., Yang, K., Bäck, T. and van Stein, N.

Challenges of ELA-Guided Function Evolution Using Genetic Programming.

DOI: 10.5220/0012206200003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 119-130

ISBN: 978-989-758-674-3; ISSN: 2184-3236

119

2023; Mu

noz and Smith-Miles, 2020). In this re-

search area, or commonly known as instance space

analysis (ISA), a feature-based representation of the

problem instances are used to identify functions that

are lacking and should be newly created. This is often

combined with a performance-oriented view of sev-

eral optimization algorithms, leading to the creation

of new functions, where the beneﬁts of one algorithm

over the others can clearly be observed.

The most common approach to generating new

benchmark problems is through the use of genetic

programming (GP) (Mu

noz and Smith-Miles, 2020).

Since GP has a long history in the domain of symbolic

regression (SR), it is a natural choice for the creation

of optimization problems. Essentially, GP is guided

towards a target feature vector in a poorly-covered

part of the instance space. These features can be gen-

erated, for example, using the exploratory landscape

analysis (ELA) (Mersmann et al., 2011), which aims

to capture low-level information about the problem

landscape using a limited number of function evalu-

ations.

While this GP-based approach to function genera-

tion has shown considerable promise in ISA, it can

also be used to create a set of representative func-

tions for algorithm selection and hyperparameter tun-

ing purposes. This is especially useful for real-world

optimization problems with expensive function evalu-

ation, e.g., requiring simulator runs. Indeed, previous

work has shown that benchmark problems with simi-

lar characteristics as real-world problems can be use-

ful to tune optimization algorithms, leading to perfor-

mance beneﬁts on the original problems (Thomaser

et al., 2023). Therefore, the ability to generate a set of

problems with similar optimization properties would

be of signiﬁcant practical importance.

In this work, we focus on investigating how a

GP guided by ELA features can be utilized to gener-

ate problems which are similar to known benchmark

functions. This illustrates the challenges which still

need to be overcome to efﬁciently generate sets of

feature-based surrogate problems. In particular, our

contributions are as follows:

1. We adapt the random function generator (RFG)

from (Tian et al., 2020) into a GP approach and

investigate the impact this has on the distribution

of ELA features of the generated problems.

2. We investigate the impact of the used distance

measure between ELA feature vectors. Our re-

sults suggest that the Wasserstein distance metric

and equal treatment of all features might not be

desirable.

2 RELATED WORK

2.1 Black-Box Optimization

Benchmarking

The BBOB family of problem suites are some of the

most well-known sets of problems for benchmark-

ing optimization heuristic algorithms (Hansen et al.,

2010), particularly the original continuous, noiseless,

single-objective suite, which is often referred to as

the BBOB (Hansen et al., 2009). To facilitate the

benchmarking purposes, the BBOB suite has been in-

tegrated as part of the comparing continuous optimiz-

ers (COCO) platform (Hansen et al., 2021) and it-

erative optimization heuristics proﬁler tool (IOHPro-

ﬁler) (Doerr et al., 2018), where the statistics of al-

gorithm performances stored can be easily retrieved.

Due to its popularity, the BBOB suite has also become

a common testbed for automated algorithm selection

and conﬁguration techniques, even though the suite

was never designed with this in mind.

Altogether, the aforementioned original BBOB

suite consists of 24 functions from ﬁve problem

classes based on their global properties. While the

BBOB functions were originally designed for un-

constrained optimization, in practice however, they

are usually considered within the search domain of

[−5,5]

with their global optimum located within

[−4,4]

. Beyond the fact that they can be scaled to

arbitrary dimensionality d, the BBOB functions have

the advantage that different variants or problem in-

stances can be easily generated through a transforma-

tion of the search domain and objective values. This

transformation mechanism is internally integrated in

BBOB and controlled by a unique identiﬁer, or also

called IID.

2.2 Exploratory Landscape Analysis

In landscape-aware ASP, the landscape properties of

problem instances are associated with the perfor-

mance of optimization algorithms. For this, the most

common way is by characterizing the landscape char-

acteristics or high-level properties of a problem in-

stance, such as its global structure, multi-modality

and separability (Mersmann et al., 2010). Nonethe-

less, an accurate characterization of these high-level

properties is challenging without expert knowledge.

To facilitate the landscape characterization, ELA has

been introduced to capture the low-level properties

of a problem instance, e.g., y-distribution, level set

and meta-model (Mersmann et al., 2011). It has been

shown that these ELA features are sufﬁciently expres-

sive in accurately classifying the BBOB functions ac-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

120

cording to their corresponding problem classes (Re-

nau et al., 2021) and also informative for algorithm

selection purposes (Mu

noz et al., 2015; Kerschke

et al., 2019).

In the ELA, landscape features are computed pri-

marily using a design of experiment (DoE) of some

sample points X = {x

,...,x

} evaluated on an ob-

jective function h, i.e., h: R

→ R, with x

∈ R

, n

represents sample size, and d represents function di-

mensionality. In this work, we compute the ELA fea-

tures using the pflacco package (Prager and Traut-

mann, 2023b), which was developed based on the

flacco package (Kerschke and Trautmann, 2019b).

With more than 300 ELA features that can be com-

puted, we consider only the ELA features that can

be cheaply computed without additional re-sampling,

similar to the work in (Long et al., 2022), and dis-

regard the ELA features that only concern the DoE

samples (altogether four of the principal component

analysis features).

While we are fully aware that the ELA features are

highly sensitive to sample size (Mu

noz et al., 2022)

and sampling strategy (

Skvorc et al., 2021a), these

aspects are beyond the scope of this work. Through-

out this work, we consider the Sobol’ sampling tech-

nique (Sobol’, 1967) based on the results in (Renau

et al., 2020).

2.3 Instance Space Analysis

In general, ISA is a methodology of benchmarking

algorithms and assessing their strengths and weak-

nesses based on clusters of problem instances (Smith-

Miles and Mu

noz, 2023). The instance space refers

to the set of all possible problem instances that can

be used to evaluate the performance of such an op-

timization algorithm. The fundamental idea behind

ISA is to model the relationship between the struc-

tural properties of a given problem instance and the

performance of a set of algorithms. Through this ap-

proach, footprints can be constructed for each algo-

rithm, which are essentially regions in the instance

space where statistically signiﬁcant performance im-

provements can be inferred.

In our proposed approach, a similar concept is

utilized, namely to ﬁnd such problem instances that

resemble speciﬁc expensive real-world problems, to

allow the comparison and benchmarking of vari-

ous algorithms on a highly speciﬁc instance space.

This differs from other related works, such as the

Melbourne algorithm test instance library with data

analytics (MATILDA) software (Smith-Miles and

noz, 2023), because while other works try to cre-

ate a space-covering of instances for a general bench-

marking purpose and comparison of algorithms, we

aim to generate highly specialised benchmarks sets

that are fast-to-evaluate and representative for expen-

sive real-world black box problems. Generating such

domain-speciﬁc benchmarks would allow us to search

and optimize speciﬁc algorithm conﬁgurations that

are better applicable to a speciﬁc problem domain.

Furthermore, it also allows a better understanding of

the expensive black-box problem through the analysis

of different optimization landscapes that represent the

found instance space.

2.4 Genetic Programming

Principally, GP can be considered as a search heuris-

tic for computer program synthesis that is inspired

by neo-Darwinian evolution (Koza, 1989). As pro-

posed by Koza, GP traditionally uses trees as pro-

gram representation. A typical application of GP is to

solve optimization problems that can be formulated

as: argmin

f (t),t ∈ T , where t = (t

,··· ,t

) repre-

sents a decision vector (also known as individual or

solution candidate) in evolutionary algorithms (EAs).

Similar to other EAs, GP evolves a population of solu-

tion candidates by following the principle of the sur-

vival of the ﬁttest and utilizing biologically-inspired

operators. The feature distinguishing GP from other

EAs is the variable-length representation for t, instead

of a ﬁxed-length representation.

Throughout the years, GP has been widely used

to solve regression problems by searching through a

space of mathematical expressions. In fact, GP-based

SR (Tackett, 1995) is popular as an interpretable al-

ternative to black-box regression methods, where GP

is used to search for an explicit mathematical expres-

sion for a given dataset. By producing a mathematical

expression that can be easily understood by humans,

SR has proven to be a valuable tool in engineering

applications, where it is important to comprehend the

relationship between different decision variables.

While GP-based SR was mainly used as a surro-

gate model to either quantify the relationship between

different decision variables or replace expensive op-

timization problems in previous work (e.g., in engi-

neering), we focus on utilizing canonical GP (Tian

et al., 2020) to create functions with speciﬁc target

ELA features in this work.

2.5 Generating Black-Box Optimization

Problems

Apart from the expertly designed benchmarking test

suites, Tian et al. introduced a SR approach in gen-

Challenges of ELA-Guided Function Evolution Using Genetic Programming

121

erating continuous black-box optimization problems

(Tian et al., 2020). In their work, a function gener-

ator was proposed to generate problem instances of

different complexity in the form of tree representa-

tions that serve as training samples for a recommen-

dation model. More speciﬁcally, the function gener-

ator constructs a tree representation by randomly se-

lecting mathematical operands and operators from a

predeﬁned pool, where each operand and operator has

a speciﬁc probability of being selected. In this way,

any arbitrary number of functions can be quickly gen-

erated. To improve the functional complexity that can

be generated, such as noise, multi-modal landscape

and complex linkage between variables, a difﬁculty

injection operation was included to modify the tree

representation. Furthermore, a tree-cleaning opera-

tion was considered to simplify the tree representation

by eliminating redundant operators. In the remainder

of this paper, we refer to this function generator as

random function generator (RFG).

In fact, functions generated by the RFG in-

deed have landscape characteristics different from the

BBOB test suite and complement the coverage of

BBOB functions in the instance space (

Skvorc et al.,

2021b). Furthermore, it has been shown that, as far as

landscape characteristics are concerned, some func-

tions generated by the RFG belong to the same prob-

lem class as several automotive crashworthiness opti-

mization problem instances (Long et al., 2022).

In addition to GP and RFG approaches, a recent

paper proposed to make use of afﬁne combinations of

BBOB functions and showed that these new functions

can help ﬁll empty spots in the instance space (Diet-

rich and Mersmann, 2022). Essentially, a new func-

tion is constructed via a convex combination of two

selected BBOB functions, using a weighting factor

to control the interpolation. Extensions of this work

have generalized the approach to afﬁne combinations

of more functions (not limited to only two functions)

and shown their potential for the analysis of auto-

mated algorithm selection methods (Vermetten et al.,

2023b; Vermetten et al., 2023a).

3 METHODOLOGY

In brief, we develop our GP-based function generator

(we simply refer this as GP in the remainder of this

paper) based on the RFG and canonical GP approach.

Precisely, we consider the mathematical operands and

operators similar to those used in the RFG with slight

modiﬁcations, as summarized in Table 1. Follow-

ing this, the GP search space consists of the terminal

space S (operands) and function space F (operators),

i.e., T = S ∪ F . Unlike typical GP-based SR method,

where each design variable x

is separately treated (as

terminal), we consider a tree-based math expression,

that is, a vector-based input t = (t

,··· ,t

), to facili-

tate a comparison with the RFG (Azzali et al., 2019).

Regarding the GP aspect, we consider the canoni-

cal GP and the distributed evolutionary algorithms in

Python (DEAP) package (Fortin et al., 2012). The de-

scriptions of our GP function generator are as follows.

Data. A set DoE samples X and the ELA features

of the target functions are used as input for the GP

pipeline.

Objective Function. In the GP-system, our opti-

mization target is to minimize the differences be-

tween the ELA features of an individual and the tar-

get function. Before the ELA feature computation,

we normalize the objective values (by min-max scal-

ing) to remove inherent bias as proposed in (Prager

and Trautmann, 2023a). Furthermore, we normalize

the ELA features (by min-max scaling) before the dis-

tance computation, to ensure that all ELA features

are within a similar scale range. For this, we con-

sider the minimum and maximum values from a set

of BBOB functions (24 BBOB functions, 5 instances

each). Based on the same set of BBOB functions, we

identify and ﬁlter out ELA features that are highly

correlated in a similar fashion to the work in (Long

et al., 2022), resulting in a total of 27 remaining fea-

tures.

Infeasible Solutions. An individual is considered

to be infeasible, if any of the four following condi-

tions is fulﬁlled:

1. Error when converting the tree representation to

an executable Python expression,

2. Bad objective values, e.g., inﬁnity, missing or sin-

gle constant value,

3. Error in ELA computation, e.g., due to equal ﬁt-

ness in all samples, and

4. Invalid distance, caused by missing value in ELA

feature.

All infeasible trees are penalized with a large ﬁtness

of 10000.

Initialize Population. In the ﬁrst generation, we

initialize the initial population (of a population size

of 50 for computational reasons) using random sam-

pling, with the tree depth is limited between 3 and

12. Similar to the RFG, we assigned each operand

and operator a probability of being selected (Table 1).

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

122

Table 1: List of notations and their meaning, syntax, protection rules (if any) and probability of being selected for the GP

sampling (only during the ﬁrst generation).

Notation Meaning Syntax Remark/Protection Probability

Operands (S )

x Decision vector (x

,.. .,x

) 0.6250

a A real constant a U(1,10) 0.3125

rand A random number rand U(1,1.1) 0.0625

Operators (F )

add Addition a + x 0.1655

sub Subtraction a − x 0.1655

mul Multiplication a · x 0.1098

div Division a/x Return 1, if

≤ 10

−20

0.1098

neg Negative −x 0.0219

rec Reciproval 1/x Return 1, if

≤ 10

−20

0.0219

multen Multiplying by ten 10x 0.0219

square Square x

0.0549

sqrt Square root

0.0549

abs Absolute value

0.0219

exp Exponent e

0.0219

log Logarithm ln

Return 1, if

≤ 10

−20

0.0329

sin Sine sin(2πx) 0.0329

cos Cosine cos(2πx) 0.0329

round Rounded value

0.0329

sum Sum of vector

∑

i=1

0.0329

mean Mean of vector

∑

i=1

0.0329

cum Cumulative sum of vector (

∑

i=1

,.. .,

∑

i=1

) 0.0109

prod Product of vector

∏

i=1

0.0109

max Maximum value of vector max

i=1,...,d

0.0109

Whenever an infeasible tree is generated, we will do

re-sampling, meaning that this infeasible tree will be

replaced by generating a new tree. As such, we ensure

that the initial population is free from infeasible trees

(due to errors 1 and 2).

Mating Selection and Variation. We consider the

tournament selection with tournaments of size 5, sub-

tree crossover with a crossover probability of 0.5, and

subtree mutation with a mutation probability of 0.1.

Other remaining hyperparameters are set to default

settings. While hyperparameter tuning could poten-

tially improve our results further, we decide to leave

it for future work.

Result. An optimal individual as solution of the GP

runs.

4 EXPERIMENTAL SETUP

In this work, we test our pipeline based on all 24

BBOB functions (one by one) of three different di-

mensionalities d = 2, 5 and 10 (or simply 2d, 5d and

10d).

We consider a DoE size of 150d samples and the

search domain [−5,5]

To reliably capture the landscape characteristics,

we compute ELA features in a bootstrapping manner

(using only 80% of the DoE samples and 5 repetitions

with different random seeds). As for the optimization

objective or individual ﬁtness in the GP system, we

consider minimizing the average Wasserstein distance

between the ELA features of the ﬁrst ﬁve BBOB in-

stances and the evaluated individual (5 bootstrapped

samples for each feature, for each instance). Due to

computational limits, we perform only one run for

each target function in each dimensionality.

Reproducibility. The codes (used to generate, pro-

cess and visualize the experiments), raw data and

more ﬁgures have been made available in a Zenodo

repository (Long et al., 2023).

Challenges of ELA-Guided Function Evolution Using Genetic Programming

123

0 200 400 600 800 1000 1200 1400

Fitness evaluations

0.0

0.1

0.2

0.3

0.4

0.5

Wasserstein distance

Figure 1: GP convergence for target F1 (sphere), in 2d, with

the ﬁtness evalutions on the x-axis and the Wasserstein dis-

tance on the y-axis.

5 RESULTS

5.1 Performance of GP

We start by analysing the functions generated during

the GP runs with a 2d BBOB function as their target.

In Figure 1, we show the convergence trajectory of

a single run on F1. From this ﬁgure, we clearly see

that GP manages to improve over the initial popula-

tion (ﬁrst 50 evaluations), as time goes on. Note that,

while it has a budget of 50 generations of 50 individ-

uals each, the combination of a crossover rate of 0.5

with a mutation rate of 0.1 means that there is a prob-

ability of 0.45 that a selected individual is not modi-

ﬁed in any way, and just copied to the next generation

without being evaluated. Additionally, Figure 1 does

not include the infeasible solutions, which make up

2% of all evaluations in this run.

To give some context to the ﬁtness values shown in

Figure 1, we compare functions generated via our GP

approach with functions generated by the RFG (see

Section 2.5). For this purpose, we generate 1000 fea-

sible functions (using the RFG) for each dimension-

ality and measure their Wasserstein distance to each

of the 24 target BBOB functions. Then, we com-

pare these distances to those of the functions gener-

ated during our GP runs (∼ 1400 functions) to the

corresponding target problem. This is visualized in

Figure 2, from which we see that the lower end (i.e.,

generated functions with low distance to target func-

tions) of the GP distribution is almost always better

than that of the RFG, with some exceptions, e.g., F12

(Bent Cigar) in 10d.

For these GP runs, we can also visualize the re-

sulting function landscapes to identify how much they

resemble the target BBOB function. This is shown in

Figure 3 for F1 (sphere) in 2d, where the 5 BBOB in-

stances are plotted in the ﬁrst row, followed by 45 GP-

generated functions. These functions are selected by

sorting their ﬁtness values and taking a linear spacing

in the rank values between the best and worst func-

tions, to show a range of generated functions of vary-

ing quality. From visual inspection, we notice that

even the best functions (with the smallest Wasserstein

distance) do not quite visually represent a sphere as

we might have expected.

In a similar fashion, we can create the same visu-

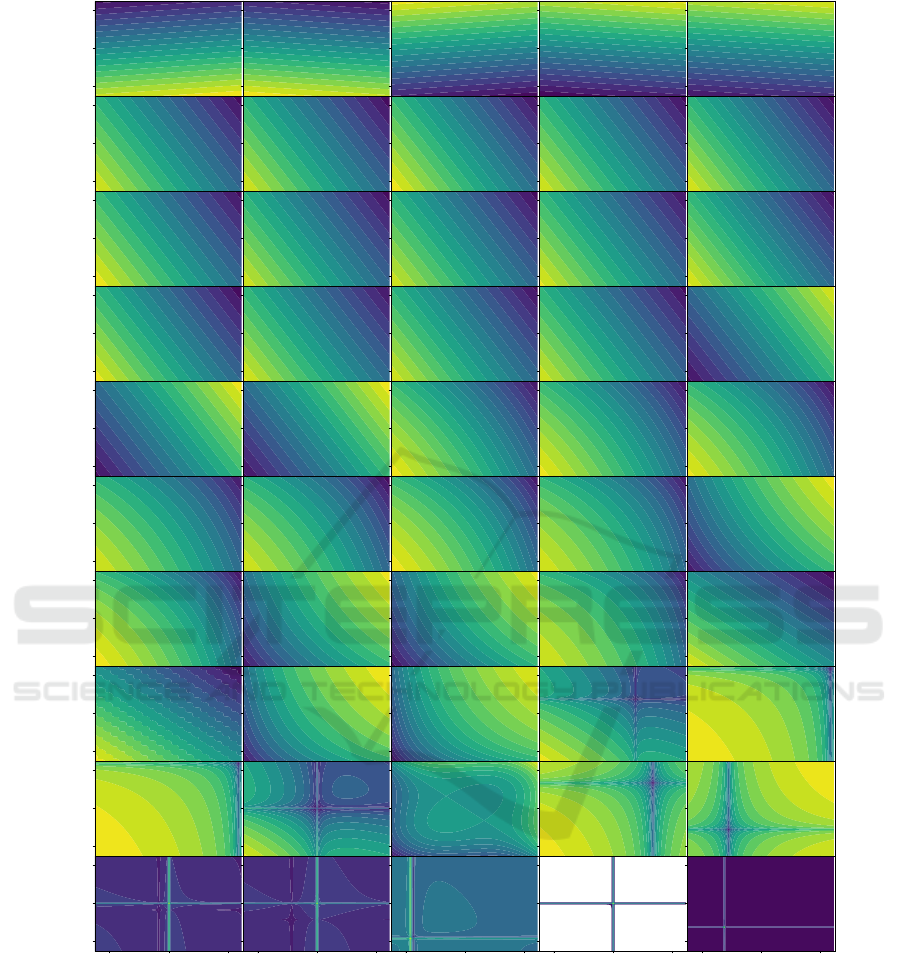
alization for other functions, e.g., F5 (linear slope), as

shown in Figure 4, where we observe a much closer

matching between the target and generated functions.

It is, however, interesting to note that some gener-

ated functions, e.g., row 7 column 5 (which repre-

sents function

), appear visually similar to the

target, but nonetheless have a relatively large ﬁtness

value. This raises the question of whether the dis-

tance to the target distribution in ELA space (using

the Wasserstein distance) really captures the intuitive

global properties of the linear slope problem.

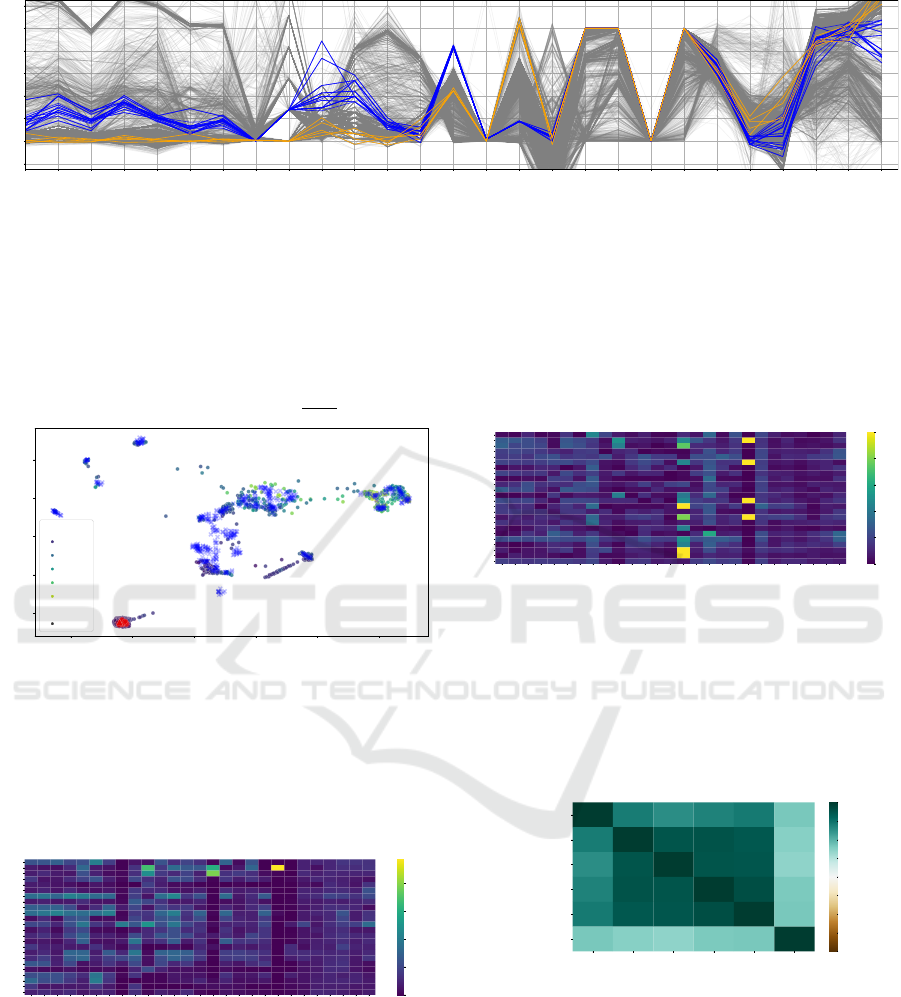
5.2 Investigating the ELA Space

To understand why the distance between this lin-

ear slope and the target function is relatively large,

we need to look at the individual ELA features.

This can be done through a parallel coordinate plot,

as shown in Figure 5. From this ﬁgure, we can

see that mostly the ela meta.lin simple.coef.min and

ela meta.lin simple.coef.max are different between

the target function and generated function

, in-

dicating that the steepness of the function might be

different. However, for the linear slope function, this

should not have a large impact as the global properties

are mostly preserved. This shows that different ELA

features are crucial for different types of target func-

tions. One direction to mitigate such problems might

be to analyse the spread of ELA feature values over

a large set of instances for each BBOB function (see

discussion around Figure 7 below).

To better understand the similarities between

functions, we visualize the ELA space ﬁlled by the

newly GP-generated functions relative to the existing

BBOB problems, by utilizing the uniform manifold

approximation mapping (UMAP) (McInnes et al.,

2018) method. For this, we ﬁrst create the map-

ping using only the feature representations from the

24 BBOB problems (all ﬁve bootstrapped repetitions

on each instance). Next, we apply this ﬁxed map on

the GP-generated functions (from one run of the GP).

The resulting plot for the target function F5 (linear

slope) is shown in Figure 6, where we see that most

GP-generated functions are indeed clustered together

around the target.

5.3 Distances in Feature Space

Our suspicion for why the distances in ELA space

do not directly seem to correlate to our visual un-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

124

fid

0.0

0.1

0.2

0.3

0.4

Wasserstein Distance

fid

0.0

0.1

0.2

0.3

0.4

Wasserstein Distance

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Function ID

0.0

0.1

0.2

0.3

0.4

Wasserstein Distance

RFG

Figure 2: Distribution of ﬁtness values (Wasserstein distance) of the set of functions from the RFG and the GP runs with

the speciﬁed BBOB target functions (horizontal axis). Rows correspond to dimensionalities: 2d, 5d and 10d (from top to

bottom).

derstanding of high-level properties might be that all

ELA features are weighted equally. This means that

even features, which are more sensitive to small de-

viations, can have the same impact as features that

might be considered crucial to characterize a function

e.g., a linear slope. To gain insight into which features

might be more important for a given function, we an-

alyze the relative standard deviation of each ELA fea-

ture within instances of the same BBOB function and

visualized the results in Figure 7.

While Figure 7 shows us the variance of each

ELA feature within the target functions, it is im-

portant to relate this to the deviations observed in

the GP-generated functions. Following this, we look

at the average standard deviation of each ELA fea-

ture across all functions sampled during a single GP

run and compute the absolute difference to the val-

ues seen on the corresponding BBOB function tar-

get. The resulting differences are shown in Fig-

ure 8, where we can see that some features, such

as ela meta.lin simple.coef.max by min, are signiﬁ-

cantly more variable in the GP-generated functions

than in BBOB. This indicates that these ELA fea-

tures might be very important for the distance mea-

surement.

In our GP experiments, we consider the average

Wasserstein distance to determine the ﬁtness value.

This choice was made, since each ELA feature can

be considered as a random variable, for which a sta-

tistical distance measure would be appropriate. Al-

ternatively, we could make use of a regular distance

measure, based on the mean values of these ELA

feature distributions. To determine the impact the

choice of distance measure might have, we consider

the Kendall-tau correlation between a set of six met-

rics on the pairwise distances between the BBOB in-

stances, consisting of the Canberra, cosine, correla-

tion, Euclidean, cityblock and Wasserstein distance,

as visualized in Figure 9.

From Figure 9, we can see that the correlations,

while clearly positive, are not perfect. This is espe-

cially the case when comparing the statistical distance

(Wasserstein) against the vector-based distances. To

gauge which distance metric might be preferable, we

then compare the distances between instances of the

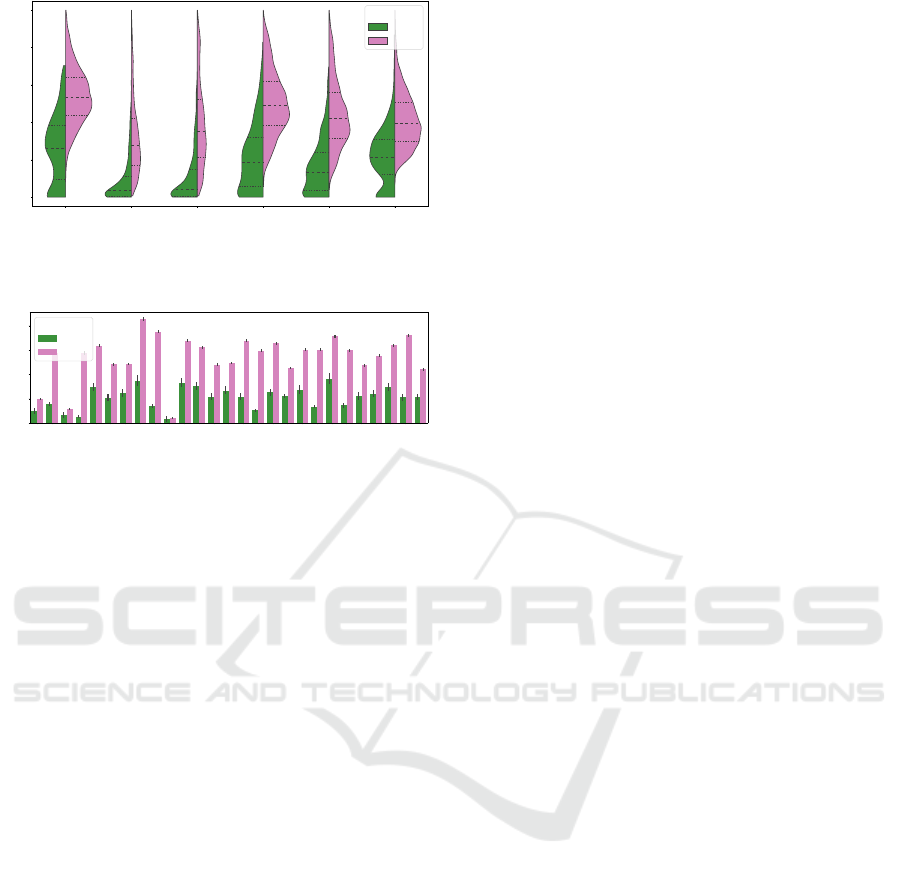
same function to the distances between instances of

different functions, as is done in Figure 10. Based on

this comparison, we notice that the Wasserstein dis-

tance surprisingly has the lowest distinguishing power

(unlike our initial intuition), while the cosine and

correlation distances show a clear trend of assigning

lower distances to same-function instances.

To further identify potential ways to modify

the distance measures, we compare the differences

in individual ELA features between same-function

and different-function instances. From the results

shown in Figure 11, we see that some features, e.g.,

ela meta.quad simple.cond, show very limited differ-

Challenges of ELA-Guided Function Evolution Using Genetic Programming

125

−4

0.12 0.12 0.12 0.12 0.12

−4

0.12 0.12 0.13 0.13 0.13

−4

0.13 0.13 0.13 0.14 0.14

−4

0.14 0.14 0.15 0.15 0.15

−4

0.16 0.16 0.16 0.16 0.17

−4

0.17 0.17 0.17 0.18 0.19

−4

0.19 0.20 0.20 0.21 0.21

−4

0.22 0.23 0.24 0.25 0.26

−4 0 4

−4

0.27

−4 0 4

0.28

−4 0 4

0.30

−4 0 4

0.32

−4 0 4

0.34

Figure 3: Grid of functions generated by the GP procedure with target function F1 (sphere) in 2d, of which 5 instances are

plotted in the ﬁrst row. The rows below are GP-generated problems selected by ranking their Wasserstein distance to the target

feature vector (indicated by the value in each subﬁgure) and taking a linear spacing in this ranking from the best (top left) to

the worst (bottom right).

ences when comparing instances of the same function

relative to different function instances. As such, it is

likely that these features contribute very little to any

distance measure, and might be potentially removed

to improve the stability, as reducing the vector dimen-

sionality can make the distances more reliable.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have shown that GP can be guided

by ELA features to ﬁnd problems with similar high-

level characteristics as a set of target problems. How-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

126

−4

0.16 0.16 0.16 0.16 0.16

−4

0.16 0.16 0.16 0.16 0.16

−4

0.16 0.16 0.16 0.16 0.16

−4

0.17 0.17 0.17 0.17 0.17

−4

0.17 0.17 0.18 0.18 0.18

−4

0.18 0.18 0.18 0.18 0.19

−4

0.19 0.19 0.19 0.20 0.21

−4

0.21 0.24 0.26 0.27 0.32

−4 0 4

−4

0.33

−4 0 4

0.37

−4 0 4

0.39

−4 0 4

0.47

−4 0 4

0.52

Figure 4: Grid of functions generated by the GP procedure with target function F5 (linear slope) in 2d, of which 5 instances

are plotted in the ﬁrst row. The rows below are GP-generated problems selected by ranking their Wasserstein distance to the

target feature vector (indicated by the value in each subﬁgure) and taking a linear spacing in this ranking from the best (top

left) to the worst (bottom right).

ever, through this process, we highlight several po-

tential pitfalls with this approach, illustrated by the

fact that we could not accurately recreate a simple

sphere problem. Although our results are based on a

very limited set of experiments, they reveal that equal

weighting of all landscape features on the distance

measure leads to difﬁculties in focusing on the more

visual high-level features.

By comparing the differences in ELA features on

the BBOB problems both between instances of the

same function and instances of different functions, we

show that a feature selection mechanism should be in-

tegrated to make the ﬁtness values more stable. Ad-

ditionally, a weighting scheme based on feature im-

Challenges of ELA-Guided Function Evolution Using Genetic Programming

127

disp.diff_mean_02

disp.diff_mean_05

disp.diff_median_05

disp.ratio_mean_10

disp.ratio_mean_25

disp.ratio_median_02

disp.ratio_median_10

ela_distr.kurtosis

ela_distr.number_of_peaks

ela_level.lda_qda_10

ela_level.mmce_lda_10

ela_level.mmce_lda_25

ela_level.mmce_qda_10

ela_meta.lin_simple.coef.max

ela_meta.lin_simple.coef.max_by_min

ela_meta.lin_simple.coef.min

ela_meta.lin_simple.intercept

ela_meta.lin_w_interact.adj_r2

ela_meta.quad_simple.adj_r2

ela_meta.quad_simple.cond

ela_meta.quad_w_interact.adj_r2

ic.h_max

ic.m0

nbc.dist_ratio.coeff_var

nbc.nn_nb.cor

nbc.nn_nb.mean_ratio

nbc.nn_nb.sd_ratio

−0.2

0.0

0.2

0.4

0.6

0.8

1.0

1.2

Figure 5: Parallel coordinate plot of the ELA features (one line for each bootstrapped DoE) for the GP-generated functions

and target function F5 (linear slope) in 2d, of which 5 instances are plotted in blue. The orange lines highlight an example of

GP-generated function, corresponding to

, which has a Wasserstein distance of 0.19 to the target.

−10 −5 0 5 10 15

−10

−5

dist

5.0

7.5

10.0

12.5

15.0

kind

Figure 6: UMAP projection of the GP-generated functions

with the target function F5 (linear slope) in 2d ELA space.

The mapping is based on BBOB instances only, which are

highlighted in blue crosses. The target F5 is highlighted in

red, with the mean feature vector across the ﬁve instances

indicated as a red triangle. The dots correspond to the

GP-generated problems, where the colour is the cityblock

or Manhattan distance to the target vector (here, coloring

based on Wasserstein distance is challenging).

disp.diff_mean_02

disp.diff_mean_05

disp.diff_median_05

disp.ratio_mean_10

disp.ratio_mean_25

disp.ratio_median_02

disp.ratio_median_10

ela_distr.kurtosis

ela_distr.number_of_peaks

ela_level.lda_qda_10

ela_level.mmce_lda_10

ela_level.mmce_lda_25

ela_level.mmce_qda_10

ela_meta.lin_simple.coef.max

ela_meta.lin_simple.coef.max_by_min

ela_meta.lin_simple.coef.min

ela_meta.lin_simple.intercept

ela_meta.lin_w_interact.adj_r2

ela_meta.quad_simple.adj_r2

ela_meta.quad_simple.cond

ela_meta.quad_w_interact.adj_r2

ic.h_max

ic.m0

nbc.dist_ratio.coeff_var

nbc.nn_nb.cor

nbc.nn_nb.mean_ratio

nbc.nn_nb.sd_ratio

Function ID

0.0

0.2

0.4

0.6

0.8

Figure 7: Relative standard deviation (of the normalized

values) of each ELA feature for each BBOB function.

Lighter color represents a larger deviation.

portances might be used to, in combination with a

distance metric, more rigorously guide the GP search

disp.diff_mean_02

disp.diff_mean_05

disp.diff_median_05

disp.ratio_mean_10

disp.ratio_mean_25

disp.ratio_median_02

disp.ratio_median_10

ela_distr.kurtosis

ela_distr.number_of_peaks

ela_level.lda_qda_10

ela_level.mmce_lda_10

ela_level.mmce_lda_25

ela_level.mmce_qda_10

ela_meta.lin_simple.coef.max

ela_meta.lin_simple.coef.max_by_min

ela_meta.lin_simple.coef.min

ela_meta.lin_simple.intercept

ela_meta.lin_w_interact.adj_r2

ela_meta.quad_simple.adj_r2

ela_meta.quad_simple.cond

ela_meta.quad_w_interact.adj_r2

ic.h_max

ic.m0

nbc.dist_ratio.coeff_var

nbc.nn_nb.cor

nbc.nn_nb.mean_ratio

nbc.nn_nb.sd_ratio

Function ID

0.0

0.2

0.4

0.6

0.8

1.0

Figure 8: Absolute difference in relative standard deviation

(of the normalized values) of each ELA feature for each

BBOB function to the functions generated by the GP run

with the respective target. Lighter color represents a larger

deviation.

canberra

cosine

correlation

euclidean

cityblock

wasserstein

canberra

cosine

correlation

euclidean

cityblock

wasserstein

1 0.71 0.64 0.68 0.71 0.42

0.71 1 0.88 0.88 0.86 0.38

0.64 0.88 1 0.88 0.87 0.35

0.68 0.88 0.88 1 0.91 0.41

0.71 0.86 0.87 0.91 1 0.42

0.42 0.38 0.35 0.41 0.42 1

−1.00

−0.75

−0.50

−0.25

0.00

0.25

0.50

0.75

1.00

Figure 9: Kendall-tau correlation between six distance mea-

sures on the BBOB instances.

towards relevant function characteristics. Further re-

search into ELA and other feature-free approaches

are also important to improve the used approach, e.g.,

models such as DoE2Vec (van Stein et al., 2023) are

a starting point in this direction.

Another aspect that should be considered is the

speciﬁc setting of the GP itself. In this work, we

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

128

canberra cosine correlation euclidean cityblock wasserstein

Metric

0.0

0.2

0.4

0.6

0.8

1.0

Normalized Distance

version

inner

outer

Figure 10: Distribution of normalized distances between

BBOB instances of the same problem (inner) and instances

of different problems (outer).

disp.diff_mean_02

disp.diff_mean_05

disp.diff_median_05

disp.ratio_mean_10

disp.ratio_mean_25

disp.ratio_median_02

disp.ratio_median_10

ela_distr.kurtosis

ela_distr.number_of_peaks

ela_level.lda_qda_10

ela_level.mmce_lda_10

ela_level.mmce_lda_25

ela_level.mmce_qda_10

ela_meta.lin_simple.coef.max

ela_meta.lin_simple.coef.max_by_min

ela_meta.lin_simple.coef.min

ela_meta.lin_simple.intercept

ela_meta.lin_w_interact.adj_r2

ela_meta.quad_simple.adj_r2

ela_meta.quad_simple.cond

ela_meta.quad_w_interact.adj_r2

ic.h_max

ic.m0

nbc.dist_ratio.coeff_var

nbc.nn_nb.cor

nbc.nn_nb.mean_ratio

nbc.nn_nb.sd_ratio

0.0

0.1

0.2

0.3

0.4

Relative difference

version

inner

outer

Figure 11: Relative difference (between normalized values)

of each of the used ELA features, between BBOB instances

of the same problem (inner) and instances of different prob-

lems (outer).

made use of default hyperparameter settings with a

relatively small population size for computational rea-

sons. This might, however, limit the ability of GP to

ﬁnd diverse solutions, leading to premature conver-

gence (Schweim et al., 2021). Care should also be

taken to include a more rigorous tree-cleaning opera-

tion, similar to (Tian et al., 2020), to simplify the re-

sulting expressions and prevent infeasible trees from

being generated.

In the future, the generation of functions with spe-

ciﬁc landscape properties has signiﬁcant potential to

help address real-world problems. By generating a di-

verse set of problems with similar features to a com-

plex target problem, we can create a test set for al-

gorithm selection and conﬁguration pipelines. This

has clear beneﬁts over training on a conventional sur-

rogate, since we can avoid overﬁtting by considering

diversiﬁed sets of problems.

ACKNOWLEDGEMENTS

The contribution of this paper was written as part

of the joint project newAIDE under the consortium

leadership of BMW AG with the partners Altair En-

gineering GmbH, divis intelligent solutions GmbH,

MSC Software GmbH, Technical University of Mu-

nich, TWT GmbH. The project is supported by the

Federal Ministry for Economic Affairs and Climate

Action (BMWK) on the basis of a decision by the

German Bundestag.

This work was performed using the ALICE com-

pute resources provided by Leiden University.

REFERENCES

Azzali, I., Vanneschi, L., Silva, S., Bakurov, I., and Gia-

cobini, M. (2019). A vectorial approach to genetic

programming. In European Conference on Genetic

Programming, pages 213–227. Springer.

Bartz-Beielstein, T., Doerr, C., Berg, D. v. d., Bossek,

J., Chandrasekaran, S., Eftimov, T., Fischbach, A.,

Kerschke, P., La Cava, W., Lopez-Ibanez, M., et al.

(2020). Benchmarking in optimization: Best practice

and open issues. arXiv preprint arXiv:2007.03488.

Dietrich, K. and Mersmann, O. (2022). Increasing the diver-

sity of benchmark function sets through afﬁne recom-

bination. In Parallel Problem Solving from Nature–

PPSN XVII: 17th International Conference, PPSN

2022, Dortmund, Germany, September 10–14, 2022,

Proceedings, Part I, pages 590–602. Springer.

Doerr, C., Wang, H., Ye, F., van Rijn, S., and B

ack, T.

(2018). IOHproﬁler: A Benchmarking and Proﬁling

Tool for Iterative Optimization Heuristics. arXiv e-

prints:1810.05281.

Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A., Parizeau,

M., and Gagn

e, C. (2012). DEAP: Evolutionary algo-

rithms made easy. Journal of Machine Learning Re-

search, 13:2171–2175.

Hansen, N., Auger, A., Ros, R., Finck, S., and Po

ık, P.

(2010). Comparing results of 31 algorithms from

the black-box optimization benchmarking bbob-2009.

In Proceedings of the 12th Annual Conference Com-

panion on Genetic and Evolutionary Computation,

GECCO ’10, page 1689–1696. ACM.

Hansen, N., Auger, A., Ros, R., Mersmann, O., Tu

sar, T.,

and Brockhoff, D. (2021). Coco: a platform for com-

paring continuous optimizers in a black-box setting.

Optimization Methods and Software, 36(1):114–144.

Hansen, N., Finck, S., Ros, R., and Auger, A. (2009).

Real-Parameter Black-Box Optimization Benchmark-

ing 2009: Noiseless Functions Deﬁnitions. Research

Report RR-6829, INRIA.

Kerschke, P., Hoos, H. H., Neumann, F., and Trautmann, H.

(2019). Automated algorithm selection: Survey and

perspectives. Evolutionary computation, 27(1):3–45.

Kerschke, P. and Trautmann, H. (2019a). Automated

algorithm selection on continuous black-box prob-

lems by combining exploratory landscape analysis

and machine learning. Evolutionary Computation,

27(1):99–127.

Kerschke, P. and Trautmann, H. (2019b). Comprehen-

sive Feature-Based Landscape Analysis of Continuous

Challenges of ELA-Guided Function Evolution Using Genetic Programming

129

and Constrained Optimization Problems Using the R-

Package Flacco, pages 93–123. Studies in Classiﬁ-

cation, Data Analysis, and Knowledge Organization.

Springer International Publishing.

Koza, J. R. (1989). Hierarchical genetic algorithms oper-

ating on populations of computer programs. In Srid-

haran, N. S., editor, Proceedings of the Eleventh In-

ternational Joint Conference on Artiﬁcial Intelligence

IJCAI-89, volume 1, pages 768–774. Morgan Kauf-

mann.

Long, F. X., van Stein, B., Frenzel, M., Krause, P., Gitterle,

M., and B

ack, T. (2022). Learning the characteris-

tics of engineering optimization problems with appli-

cations in automotive crash. In Proceedings of the

Genetic and Evolutionary Computation Conference,

pages 1227–1236.

Long, F. X., Vermetten, D., Kononova, A. V., Kalkreuth,

R., Yang, K., B

ack, T., and van Stein, N. (2023).

Reproducibility ﬁles and additional ﬁgures. https:

//doi.org/10.5281/zenodo.7896138.

McInnes, L., Healy, J., Saul, N., and Grossberger, L. (2018).

Umap: Uniform manifold approximation and projec-

tion. The Journal of Open Source Software, 3(29):861.

Mersmann, O., Bischl, B., Trautmann, H., Preuss, M.,

Weihs, C., and Rudolph, G. (2011). Exploratory land-

scape analysis. In Proceedings of the 13th Annual

Conference on Genetic and Evolutionary Computa-

tion, GECCO ’11, page 829–836. ACM.

Mersmann, O., Preuss, M., and Trautmann, H. (2010).

Benchmarking evolutionary algorithms: Towards ex-

ploratory landscape analysis. In Schaefer, R., Cotta,

C., Kołodziej, J., and Rudolph, G., editors, Parallel

Problem Solving from Nature, PPSN XI, pages 73–82.

Springer Berlin Heidelberg.

noz, M. A., Kirley, M., and Smith-Miles, K. (2022).

Analyzing randomness effects on the reliability of

exploratory landscape analysis. Natural Computing,

21(2):131–154.

noz, M. A. and Smith-Miles, K. (2020). Generating new

space-ﬁlling test instances for continuous black-box

optimization. Evolutionary computation, 28(3):379–

404.

noz, M. A., Sun, Y., Kirley, M., and Halgamuge, S. K.

(2015). Algorithm selection for black-box continu-

ous optimization problems: A survey on methods and

challenges. Information Sciences, 317:224–245.

Prager, R. P. and Trautmann, H. (2023a). Nullifying the

inherent bias of non-invariant exploratory landscape

analysis features. In Applications of Evolutionary

Computation: 26th European Conference, EvoAppli-

cations 2023, Held as Part of EvoStar 2023, Brno,

Czech Republic, April 12–14, 2023, Proceedings,

pages 411–425. Springer.

Prager, R. P. and Trautmann, H. (2023b). Pﬂacco: Feature-

Based Landscape Analysis of Continuous and Con-

strained Optimization Problems in Python. Evolution-

ary Computation, pages 1–25.

Renau, Q., Doerr, C., Dreo, J., and Doerr, B. (2020). Ex-

ploratory landscape analysis is strongly sensitive to

the sampling strategy. In B

ack, T., Preuss, M., Deutz,

A., Wang, H., Doerr, C., Emmerich, M., and Traut-

mann, H., editors, Parallel Problem Solving from Na-

ture – PPSN XVI, pages 139–153. Springer Interna-

tional Publishing.

Renau, Q., Dr

eo, J., Doerr, C., and Doerr, B. (2021).

Towards explainable exploratory landscape analysis:

extreme feature selection for classifying bbob func-

tions. In Applications of Evolutionary Computa-

tion: 24th International Conference, EvoApplica-

tions 2021, Held as Part of EvoStar 2021, Virtual

Event, April 7–9, 2021, Proceedings 24, pages 17–33.

Springer.

Rice, J. R. (1976). The algorithm selection problem. vol-

ume 15 of Advances in Computers, pages 65–118. El-

sevier.

Schweim, D., Wittenberg, D., and Rothlauf, F. (2021). On

sampling error in genetic programming. Natural Com-

puting, pages 1–14.

Smith-Miles, K. and Mu

noz, M. A. (2023). Instance space

analysis for algorithm testing: Methodology and soft-

ware tools. ACM Computing Surveys, 55(12):1–31.

Sobol’, I. M. (1967). On the distribution of points in

a cube and the approximate evaluation of integrals.

USSR Computational Mathematics and Mathematical

Physics, 7(4):86–112.

Tackett, W. A. (1995). Mining the genetic program. IEEE

Expert, 10(3):28–38.

Thomaser, A., Vogt, M.-E., Kononova, A. V., and B

ack,

T. (2023). Transfer of multi-objectively tuned cma-es

parameters to a vehicle dynamics problem. In Evo-

lutionary Multi-Criterion Optimization: 12th Interna-

tional Conference, EMO 2023, Leiden, The Nether-

lands, March 20–24, 2023, Proceedings, pages 546–

560. Springer.

Tian, Y., Peng, S., Zhang, X., Rodemann, T., Tan, K. C., and

Jin, Y. (2020). A recommender system for metaheuris-

tic algorithms for continuous optimization based on

deep recurrent neural networks. IEEE Transactions

on Artiﬁcial Intelligence, 1(1):5–18.

van Stein, B., Long, F. X., Frenzel, M., Krause, P., Gitterle,

M., and B

ack, T. (2023). Doe2vec: Deep-learning

based features for exploratory landscape analysis.

Vermetten, D., Ye, F., B

ack, T., and Doerr, C. (2023a). MA-

BBOB: Many-afﬁne combinations of BBOB func-

tions for evaluating AutoML approaches in noiseless

numerical black-box optimization contexts. AutoML

2023.

Vermetten, D., Ye, F., and Doerr, C. (2023b). Using afﬁne

combinations of BBOB problems for performance as-

sessment. CoRR, abs/2303.04573.

Skvorc, U., Eftimov, T., and Koro

sec, P. (2021a). The ef-

fect of sampling methods on the invariance to func-

tion transformations when using exploratory land-

scape analysis. In 2021 IEEE Congress on Evolution-

ary Computation (CEC), pages 1139–1146.

Skvorc, U., Eftimov, T., and Koro

sec, P. (2021b). A

Complementarity Analysis of the COCO Benchmark

Problems and Artiﬁcially Generated Problems, page

215–216. ACM.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

130