Utility of Univariate Forecasting for Workload Metrics Predictions in

Enterprise Applications

Andrey Kharitonov, Roheet Rajendran, Hendrik M

uller and Klaus Turowski

Faculty of Computer Science, Otto von Guericke University, Magdeburg, Germany

Keywords:

Commercial-Off-The-Shelf Enterprise Applications, Capacity Management, Univariate Forecasting.

Abstract:

Modern enterprise IT systems are complex solutions that require careful planning of computational capacities

and placement, especially in the cloud environments where the total cost of ownership directly depends on

provisioned resources. The decision process on infrastructure transformation or capacity sizing of existing IT

landscapes can be supported by collecting and analyzing the workload data of the running systems. However,

the scope and length of this data are limited, as its collection is often an expensive and lengthy process.

Therefore, within this work, we empirically evaluate multiple techniques for extending the workload data

by employing various univariate time series forecasting algorithms. We analyze a use case of SAP-based

enterprise applications and rely on real-world workload data collected from various running SAP system

landscapes. Our analysis demonstrates that XGBoost is best suited for univariate forecasting SAP-speciﬁc

key performance indicators for both stationary and trending time series. However, the shape of the workload

proﬁle has a high degree of inﬂuence on the results of the forecasting. Enterprise applications’ workload data

that represent regular day-to-day operations without irregular events is a prerequisite for accurate forecasting.

1 INTRODUCTION

Modern enterprise applications (EA) are essential for

the operations of many organizations. These appli-

cations are often complex IT landscapes consisting

of various systems. These can require considerable

computational capacities to operate. The availability

of these capacities ensures that the dependent busi-

ness processes run without disruptions or downtimes.

However, there are costs associated with the acquisi-

tion and running of the IT infrastructure that ensure

the availability of the required computation capacity.

Estimation of these costs can be done based on the

hardware utilization metrics (Li and Scheibli, 2010)

as well as based on EA components capacity require-

ments (Brogi et al., 2019).

Correct sizing of the infrastructure of EAs in the

cloud can also be challenging and also require ac-

curate performance estimation (Evangelinou et al.,

2018). In fact, making decisions on the capacities se-

lection in the cloud environments can be especially

difﬁcult, as such a decision process must ﬁnd the

balance between satisfying the capacity requirements

and the costs of such infrastructure while navigating

through the complexities of the cloud pricing models

(Wu et al., 2019), where capacities can be selected to

ﬁt speciﬁc workload exactly.

Accurate estimation of the running costs for both

hosted (on-premises) EAs, as well as the ones that

are placed in the cloud, requires the estimation of

the required capacities and their consumption. In

the case of the hardware refresh or infrastructure siz-

ing selection scenarios for existing EAs, this can be

achieved by measuring and recording the EAs work-

load proﬁles (M

uller et al., 2021). Recorded historical

data representing utilization metrics for various EAs

within the IT landscape can reveal speciﬁc workload

proﬁles that represent the EA’s computational capac-

ity utilization within speciﬁc time frames.

However, simply collecting the data might be in-

sufﬁcient for informed decision-making. When this

data is collected from an already existing IT land-

scape, it will always represent only the past. This

is not always ideal, while the cost planning horizon

lies in the future and may be subject to possible ﬂuc-

tuations (e.g., electricity costs, public cloud provider

pricing). Furthermore, the system’s workload proﬁle

is not necessarily static. Instead, the workload may

contain a trend that can be revealed through analysis

or prediction based on the existing data. Prediction of

the future workload patterns of EA within the horizon

of planning can also be used to assist the stakeholders

Kharitonov, A., Rajendran, R., Müller, H. and Turowski, K.

Utility of Univariate Forecasting for Workload Metrics Predictions in Enterprise Applications.

DOI: 10.5220/0012206600003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 3: KMIS, pages 231-240

ISBN: 978-989-758-671-2; ISSN: 2184-3228

231

in workload placement decision-making.

Furthermore, it is difﬁcult to continuously collect

workload data from a complex enterprise IT land-

scape. That means that in many cases, the data sam-

ples characterizing EA’s workload proﬁles will be of a

limited length and might not always be suitable for an

informed decision-making process due to imperfec-

tion or the sporadic nature of the workload within the

period of measurement. It is important to be able to

understand if any given sample of data is representa-

tive and, in fact, suitable for deriving knowledge from

it to make informed decisions.

Therefore, within this work, we strive to evaluate

the utility of univariate forecasting algorithms for pre-

dicting key IT capacity utilization metrics of standard

enterprise IT applications. We apply a few selected

state-of-the-art time series forecasting algorithms to

the workload metrics data collected from real-world

EAs and compare the accuracy of predictions between

these algorithms.

The quantity and quality of data are crucial for the

decision-making process for selecting placement and

provisioning resources for EAs (M

uller et al., 2021).

We rely on univariate time series forecasting tech-

niques to extend the dataset and determine if the spe-

ciﬁc data samples can be used for accessing the future

behavior of the EAs these represent. The hypothesis

is that if we can reliably predict the future behavior

of the system based on historical data, we can rely

on this data as the basis for a data-driven decision-

making process with a high degree of conﬁdence and

IT landscape understanding.

2 RELATED WORK

(Masdari and Khoshnevis, 2020) provides a compre-

hensive summary of different methods of forecasting

for workload prediction in cloud computing. They

also highlight reactive and proactive methods. Re-

active methods refer to approaches that respond to

changes in workload after they occur. These meth-

ods cannot handle sudden bursts of workload and may

result in service-level agreement violations. On the

other hand, proactive methods predict future work-

loads by recognizing possible resource usage patterns

and provisioning resources accordingly. This ap-

proach can help prevent performance degradation and

reduce idle resources, leading to improved proﬁtabil-

ity for cloud service providers. The applied datasets

included various types of data, such as historical us-

age patterns, network trafﬁc data, application logs,

and performance metrics from cloud computing en-

vironments. The work relies on datasets of recorded

workload from Google Cloud and AuverGrid infras-

tructure hosts in terms of CPU and memory consump-

tion.

(Nisar and Ahmed, 2020) propose the use of an

autoregressive integrated moving average (ARIMA)

model for workload forecasting in a data center en-

vironment. The authors utilize ARIMA to fore-

cast application resource utilization that is to occur

within the next ten minutes, and this forecast is per-

formed every ten seconds. This method of forecast-

ing is applied to ensure sufﬁcient but cost-efﬁcient

resource provisioning within the cloud. The authors

empirically demonstrate the sufﬁcient accuracy of this

method within a simulated environment. Within the

proposed by the authors use case, ARIMA outper-

forms such models as the moving average, autore-

gressive model, and autoregressive moving average

(ARMA). However, it is noted that sufﬁcient accuracy

is only achievable when the time series is stationary.

Speciﬁcally within the ﬁeld of enterprise applica-

tion capacity planning, (Herbst et al., 2013) proposes

a self-adaptive approach that selects suitable methods

based on feedback cycles, and shows through exper-

iments and case studies that this approach provides

continuous and reliable forecast results at run-time

with signiﬁcantly reduced errors compared to static

methods. The approaches include moving average,

ARIMA, seasonal ARIMA (SARIMA), exponential

smoothing state space model with Box-Cox trans-

formation, and ARMA errors (ETS/ARMA). MASE

(Mean Absolute Scaled Error) is used to evaluate the

accuracy of time series forecasting models, which

takes into account the scale of the data being fore-

casted. The authors, however, do not evaluate ma-

chine learning (ML) approaches.

The self-adaptive approach proposed by the au-

thors is a method for selecting suitable forecasting

methods based on feedback cycles. It uses a deci-

sion tree to select an appropriate forecasting algo-

rithm based on the user’s general objectives and then

applies direct feedback cycles to adjust the parameters

of this algorithm dynamically at runtime. This allows

it to adapt to changes in workload patterns and im-

prove forecast accuracy continuously. The approach

provides continuous and reliable forecast results with

signiﬁcantly reduced errors compared to static meth-

ods, as shown through experiments and case studies

based on real-world workload traces.

3 BACKGROUND

We begin this section by introducing in subsection 3.1

the forecasting algorithms that are used within this

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

232

work. Additionally, in subsection 3.2, we discuss the

speciﬁc metrics that were used for evaluating the re-

sults of the forecast.

3.1 Forecasting Algorithms

Forecasting algorithms employed within this work

can be put into three categories: statistical, classical

ML, and ML based on deep neural networks. The last

one is also often referred to as deep learning.

The ﬁrst category of the algorithms relies on

statistical analysis methods to identify patterns and

trends in the data. Auto-regressive integrated moving

average (ARIMA) (Siami-Namini et al., 2018) stands

out as the main linear model for time series anal-

ysis. It combines elements of autoregressive (AR),

moving average (MA), and linear regression (LR).

By analyzing the autocorrelation and partial autocor-

relation functions, optimal coefﬁcients can be deter-

mined. The Error Trend Season (ETS) (Hyndman

et al., 2002) model, also known as the exponential

time series model, is another notable statistical model.

This model considers four components: level, trend,

seasonality and error. Each of these components cap-

tures the underlying mean or reference value, the di-

rection and rate of overall change, repeated patterns

or cycles, and random ﬂuctuations. The ETS model

is particularly useful when data follow an exponential

pattern of growth or decay over time. BATS (Liv-

era et al., 2011) is a statistical model for time series

analysis. It uses Box-Cox transformations to stabi-

lize variance, ARMA errors to capture autocorrela-

tion, trend components to represent long-term sys-

tematic change, and seasonal components to explain

recurring patterns and periods in the data.

In addition to traditional statistical models,

machine learning techniques such as XGBoost

(XGB)(Chen and Guestrin, 2016) and FBProphet

(FBP)(Taylor and Letham, 2018) have attracted con-

siderable attention of researchers in time series fore-

casting. XGBoost is based on tree-based ensembles

and gradient tree boosting, and uses multiple deci-

sion trees to predict output based on given features.

It enables efﬁcient processing of large datasets by

minimizing regular targets to balance accuracy and

complexity. On the other hand, FBProphet, an open-

source forecasting tool developed by Meta (earlier

known as Facebook), focuses on accurate sales fore-

casting. FBProphet uses modular or linear regres-

sion curves for trends, Fourier series-based season-

ality, and additive regression models that enable the

automatic detection of change points.

Deep learning methods, speciﬁcally long short-

term memory (LSTM) (Hochreiter and Schmidhuber,

1997) networks are also of interest in time series fore-

casting (Siami-Namini et al., 2018): RNNs have in-

ternal states that return to the input and capture the

temporal dependence of sequential data and LSTM

networks, a variant of the RNN, effectively address

the challenge of capturing long dependencies by us-

ing gates that selectively allow or block the ﬂow of

information. These deep learning methods generally

perform well at learning complex data representations

without the need for manual feature design and are

well-suited for handling complex interdependencies

between variables in time series forecasting.

K-nearest neighbor (KNN) is a simple regression

model that can also be applied to time series forecast-

ing (Mart

ınez et al., 2019; Tang et al., 2018). It is a

machine learning approach that predicts/forecasts val-

ues based on the proximity to the training instances.

In addition, we also present an ensemble-based

model which combines both FBProphet and XGBoost

with an equal weighting scheme. The selection of the

algorithms for the ensemble is based on the early eval-

uation performed within this work.

3.2 Metrics

For evaluating the accuracy of the forecasting, we

rely on a classical metric typically used to evaluate

forecasting models: root mean square error (RMSE)

(Armstrong and Collopy, 1992). Additionally, we

make the use of the mean absolute scaled error

(MASE) metric, which is indicated in the literature

(Hyndman and Koehler, 2006) as easily interpretable

and proposed as a standard forecasting accuracy met-

ric.

MASE measures a difference between forecasted

values compared to those obtained from naive fore-

casts (e.g., using historical averages) and scales this

difference by an estimate of its variability or uncer-

tainty. A value less than 1 indicates that the model

performs better than a naive forecast, while values

greater than 1 indicate worse performance. MASE

is not a scale-dependent metric. That means that the

results of forecasting evaluation can easily be com-

pared across different unrelated datasets where the

predicated value has different minimum and maxi-

mum scales observed. That is speciﬁcally the case

within the use case dataset of this paper, discussed

later in subsection 4.1.

Unlike MASE, RMSE values directly depend on

the scale of the data. While in certain cases (Chai and

Draxler, 2014) RMSE is a preferable representation

of the forecasting evaluation results, it is not suitable

for all evaluation scenarios due to the original data

scale dependency. The result of the accuracy metric

Utility of Univariate Forecasting for Workload Metrics Predictions in Enterprise Applications

233

presents the average magnitude of the forecasting er-

ror. Therefore, a direct comparison of RMSE between

unrelated time series requires understanding the dif-

ference between the upper and lower value ranges

within the time series values. It is, however, still a

useful metric that allows us to measure the exact mag-

nitude of a forecasting error to determine how reason-

able the forecast is, and it can still be used to measure

average algorithm performance across a large number

of datasets.

We employ both of the aforementioned metrics

in the evaluation of our forecasting results. In both

cases, the lower metric values indicate higher accu-

racy of the prediction.

4 EXPERIMENTAL SETUP

We rely on Cross-industry standard process for data

mining (CRISP-DM) (Chapman et al., 2000) for con-

structing the forecasting models of our data. This

methodology involves an interactive process of data

understanding, preparation, and machine learning

model training.

4.1 Data Collection and Understanding

The foundation of this work is the time series data that

represents the workload measurement taken in run-

ning real-world enterprise IT landscapes with a spe-

ciﬁc use case of SAP-based landscapes. This work-

load data contains the overall information about the

SAP-based IT landscape, such as the number of sys-

tems, as well as available hardware capacities (e.g.,

main memory, CPU, storage, network communica-

tion) and their utilization. Within our work, we eval-

uate multiple samples of such measurements, each

of which contains workload information from differ-

ent real-world SAP landscapes that contain multiple

SAP systems. Speciﬁcally, we analyze 60 indepen-

dent SAP IT landscapes, which constitute 446 inde-

pendent SAP systems of various types.

The total length of each sample depends on the to-

tal duration of the workload measurement and ranges

from three weeks to three months. The average work-

load measurement length is 36 days. The solution

employed to collect the workload data of the running

SAP systems relies on the speciﬁc monitoring pro-

gramming interfaces offered by SAP and does not in-

troduce any additional utilization overhead or impede

the running SAP systems.

In addition to the generic hardware utilization

metrics, an SAP-speciﬁc hardware-agnostic perfor-

mance metric is present in this data: SAP Applica-

tion Performance Standard (SAPS). This value is de-

termined based on the SAP Sales and Distribution

benchmark (Marquard and G

otz, 2008) and serves as

one of SAP systems’ main capacity and performance

metrics. This metric is typically used in the capacity

sizing and placement decision process of SAP sys-

tems. Speciﬁc SAPS values are available online

not

only for various hardware products but also for certi-

ﬁed SAP cloud offerings.

SAPS is a central performance metric of compu-

tational resources for SAP systems. Accurate assess-

ment and prediction of SAPS values based on the ex-

isting workload data can assist in the process of plan-

ning the capacities for SAP systems during hardware

refresh cycles as well as cloud transformation.

4.2 Data Preparation

The collected workload data is cleaned of any tech-

nically invalid records that may have occurred during

the workload performance logging process. Further-

more, the collected data is further aggregated into a

time series with a time step length of one hour.

The presence of outliers, or non-repeated anoma-

lous events, in the time series data used as a basis for

forecasting negatively affects the result produced by

typical statistical models (Ledolter, 1989) as well as

machine learning models (Cerna et al., 2020).

Within our data, outliers signify non-repeated rare

events that can not be used as the basis for capac-

ity management and planning. Such events include

but are not limited to unexpected server failures or

power loss, temporary unplanned system unavailabil-

ity, and networking issues. Therefore, during the pre-

processing stage of our data, we remove these outliers

through an ML-based technique named isolation for-

est (IF) (Liu et al., 2008). It is shown (M

uller et al.,

2021) that IF is applicable in the context of enterprise

IT applications’ workload analysis and performs well

in comparison with selected other state-of-the-art ML

techniques.

When an outlier is discovered, the corresponding

time frame in the series is marked as anomalous. The

typical length of the anomalous time frames is one

hour, or a single time step in our time series. The

value found in the anomalous time frame is then re-

placed with a mean value calculated for this speciﬁc

hour across the entire time series. During the prelim-

inary evaluation, we observed an overall increase in

forecasting quality across most of the data samples

used with the selected forecasting models.

SAP benchmark glossary https://www.sap.com/about/

benchmark.html. [Accessed on 2023-09-17]

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

234

Since the typical length of the time series samples

used for forecasting in this work does not exceed three

months, the use of the whole timestamp is often coun-

terproductive as years and speciﬁc months are not re-

peated. We split the timestamp into separate compo-

nents (i.e., year, month, day of the week, an hour in

24-hour notation) and use only the day of the week

and the hour as features determining the time of the

occurrence. Furthermore, we encode both as integer

values.

4.3 Modelling and Evaluation

For the purposes of evaluation, we use the data dis-

cussed in section 4 with the statistical and machine

learning algorithms discussed in subsection 3.1. We

split the given dataset into two parts: training and

testing. Speciﬁcally, 75% of the dataset is used for

training and 25% for testing. The training portion of

the data is used for the initial ﬁtting of the algorithm.

The testing part is used for evaluating the quality of

the prediction by comparing the algorithm’s predicted

values with the real test values and measuring the dif-

ference using the metrics discussed in subsection 3.2.

We perform forecasting for every SAP system in

a given IT landscape separately. Essentially, every

dataset contains time series describing the workload

proﬁle of only a single SAP system. Furthermore, we

take only the portion of the time series that contains

the data for the speciﬁc metric of the speciﬁc system.

In other words, for forecasting, we concentrate on the

use-case-speciﬁc key metric of our data: SAPS.

4.4 Model Parameters

Within the iterative evaluation process applied within

this work, we have determined a set of hyperparame-

ters that yielded the best from the observed forecast-

ing results within our evaluation setup. These hyper-

parameter values were applied to obtain the ﬁnal re-

sults, which are discussed in section 5. Important to

note that in this section, we list only the hyperparam-

eter values that differ from their defaults for the re-

spective algorithms.

There are only three parameters in ARIMA algo-

rithms, and all must be selected. Within our exper-

imental setup, we set the number of autoregressive

terms and the degree of differencing to 1, while the

size of the moving average window was set to 2.

The objective function is an important hyperpa-

rameter in XGboost, the selection of which directly

depends on the problem that is being solved as the al-

gorithm strives to reduce the loss of the objective. In

our case, we rely on the Tweedie regression objective.

The learning rate is set to 0.1 and L1 regularization

parameter to 0.1 to prevent overﬁtting.

Similarly to the objective function in XGBoost,

the selection of a distance function in KNN is an im-

portant parameter that must be selected appropriately

for the data. We rely on Manhattan distance (Mart

ınez

et al., 2019). The optimal neighbors are found to be

nine.

The choice of the error term, trend component,

and seasonal component is crucial to the ETS model.

In our case, we set the error term to ”add” to represent

additive error and the trend component to ”None” to

represent no trend. In addition, we speciﬁed a sea-

sonal period of 1 hour (sp = 1) to capture the hourly

seasonality.

For BATS, the seasonal period (sp) was set to 12

to indicate a seasonality of 12 hours. In addition,

we enabled the use of the Box-Cox transformation

(use box cox = True) to handle potential nonlineari-

ties in the data. However, based on the characteris-

tics of the data, the trend component was excluded

(use Trend = False).

Based on the parameter tuning for FBProphet, we

set the seasonality mode to ”additive” to capture the

additive seasonality patterns in the data. In addi-

tion, we adjusted (holiday prior scale), which con-

trols for the ﬂexibility of the holiday component, to

0.1. We also speciﬁed the number of change points

(n chanepoints) to 20 to capture potential changes in

trend. In addition, the add country holidays parame-

ter was used to include country holidays for Germany.

In the LSTM (Long Short Term Memory) model,

ﬁnding the optimal hyperparameters is a time-

consuming process, especially when extensive cross-

validation is required. To streamline this process, one

approach is to use the predeﬁned architecture pro-

posed in (Gupta and Dinesh, 2017).

5 EVALUATION

In the following subsection 5.1, we present the nu-

merical comparison results for the selected forecast-

ing algorithms discussed in section 3. Following that,

in subsection 5.2, we discuss the applicability of se-

lected three methods to determining the suitability of

data before executing forecasting.

5.1 Forecasting

First of all, we compare the performance of the se-

lected algorithms across multiple datasets, irrespec-

tive of the time series suitability for forecasting.

Within this selection, we have about an equal number

Utility of Univariate Forecasting for Workload Metrics Predictions in Enterprise Applications

235

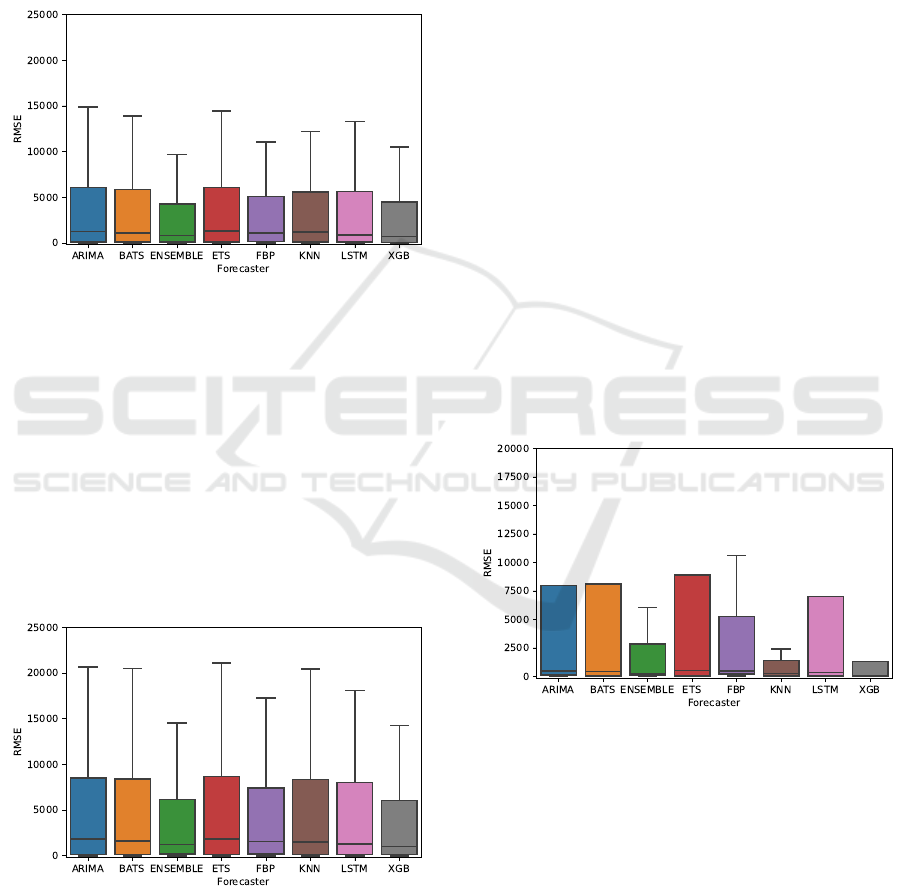
of highly regular datasets, that repeated day-to-day

business operations, and, therefore, should be better

suitable for prediction, and another half consists of

more sporadic time series.

As can be seen in Figure 1, XGBoost and Ensem-

ble performed best overall with stationary time series,

where no trend is observed. These algorithms are fol-

lowed directly by FBProphet, which is also included

in the ensemble.

Figure 1: RMSE in stationary datasets.

In order to validate the general suitability of the

selected model to trending data, we artiﬁcially inject

a trend of 50% uniform growth over the whole length

of every dataset. The results of the forecasting based

on the trending data are presented in Figure 2. It is

easy to see that the overall forecasting accuracy is re-

duced for all models. However, similarly to the results

with no induced trend, XGBoost and the considered

ensemble remain the best-performing models overall.

Among the rest of the considered algorithms, LSTM

has displayed a slightly better ability to capture the

trend.

Figure 2: RMSE in treding datasets.

During the forecasting accuracy analysis of the se-

lected algorithms, we observed that certain recorded

workload proﬁles of EAs produce better results than

others. As we previously mentioned in subsection 4.2,

outliers are removed from the data. Therefore, single

events such as system server outages can not inﬂuence

the forecasting results.

However, further analysis of the recorded work-

load metrics of the considered enterprise applications,

SAP, reveals the connection between the company’s

business operations proﬁle and the forecasting results.

Speciﬁcally, the enterprise application workload pro-

ﬁles that reﬂect regular day-to-day operations outside

of seasonal inﬂuences (e.g., holidays, extreme but rare

weather condition changes, etc.) result in a high de-

gree of prediction accuracy.

In contrast, EAs workload measurements taken

within the periods where the company’s operations

were rather sporadic, the prediction accuracy is low.

In other words, the more regular the recorded work-

load proﬁle is, the better prediction quality is to be

expected.

To better illustrate this dependency between data

and low or high-accuracy forecasting, we separate the

results based on the selected accuracy metrics. The

results for the datasets, which describe a highly reg-

ular workload, and low RMSE, are presented in Fig-

ure 3 for RMSE and in Figure 4 for MASE. It is easy

to see that XGboost, in this case, outperforms all other

algorithms with a signiﬁcant margin and results in the

highest accuracy. XGBoost is followed by KNN and

ensemble based forecasting algorithms.

Figure 3: Higher accuracy (stationary): RMSE.

If we look at the same metrics, RMSE in Fig-

ure 5 and MASE in Figure 6 for the datasets group

with observed more sporadic workload proﬁles, it is

clear that the overall quality of prediction is lower

across all models. Especially the dramatic reduction

of performance we observe for XGBoost and KNN-

based forecasters. The ensemble is a more robust so-

lution for forecasting and, on average, didn’t experi-

ence the same dramatic reduction of accuracy. LSTM

performed better in these conditions, but the overall

quality of the prediction was poor.

When we analyze the selected algorithm’s ability

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

236

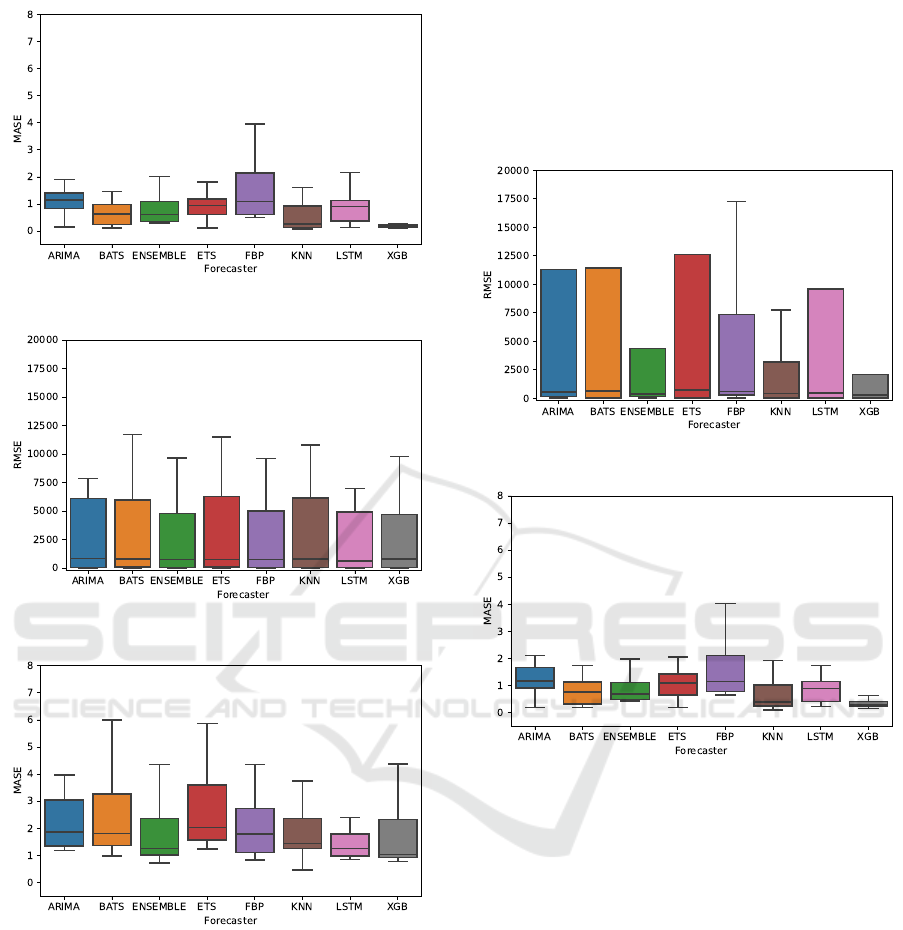
Figure 4: Higher accuracy (stationary): MASE.

Figure 5: Lower accuracy (stationary): RMSE.

Figure 6: Lower accuracy (stationary): MASE.

to capture the artiﬁcially injected uniform trend, we

do not observe a direct correlation between the work-

load proﬁle time series stability and the accuracy of

the forecast. In Table 1, we summarize the percentage

of accuracy reduction between stationary and trending

datasets for all considered algorithms. Datasets with

observed high accuracy of forecast and low accuracy

of forecast are designated in the table as two groups:

A and B, respectively.

In algorithms ﬁtted with trending data, we observe

a varying degree of accuracy reduction. Within the

group of the datasets that originally produced highly

accurate results, group A as designated in the table,

XGBoost experiences the highest accuracy lost. This

can also be easily observed in Figure 7 and Figure 8.

It is similar to the performance reduction of the KNN-

based forecaster. The least affected algorithms, in this

case, are FBProphet, ARIMA, ETS, and ensemble.

Figure 7: Higher accuracy (trending): RMSE.

Figure 8: Higher accuracy (trending): MASE.

Interestingly, when we look at the datasets that

have sporadic workloads, designated as group B in

Table 1, we observe a much lower degree of accuracy

loss. However, it is important to note, that while the

reduction in accuracy for these datasets seems lower,

it doesn’t mean that the selected algorithms are ca-

pable of capturing the trends within these datasets

better. It is rather an indication that a uniform, syn-

thetic modiﬁcation of sporadic time series might lead

to inducing artiﬁcial stability of the values within the

dataset. If we look at the exact RMSE and MASE

values for these datasets in Figure 9 and Figure 10,

respectively, we see that the actual evaluation metric

results, of course, remain poor.

As seen from our evaluation, recorded workload

metric time series stability is crucial for obtaining ac-

curate forecasting results. XGboost is clearly outper-

forming all other considered algorithms in stationary

datasets, but in trending datasets, the accuracy can de-

viate considerably. We also observe that LSTM and

Utility of Univariate Forecasting for Workload Metrics Predictions in Enterprise Applications

237

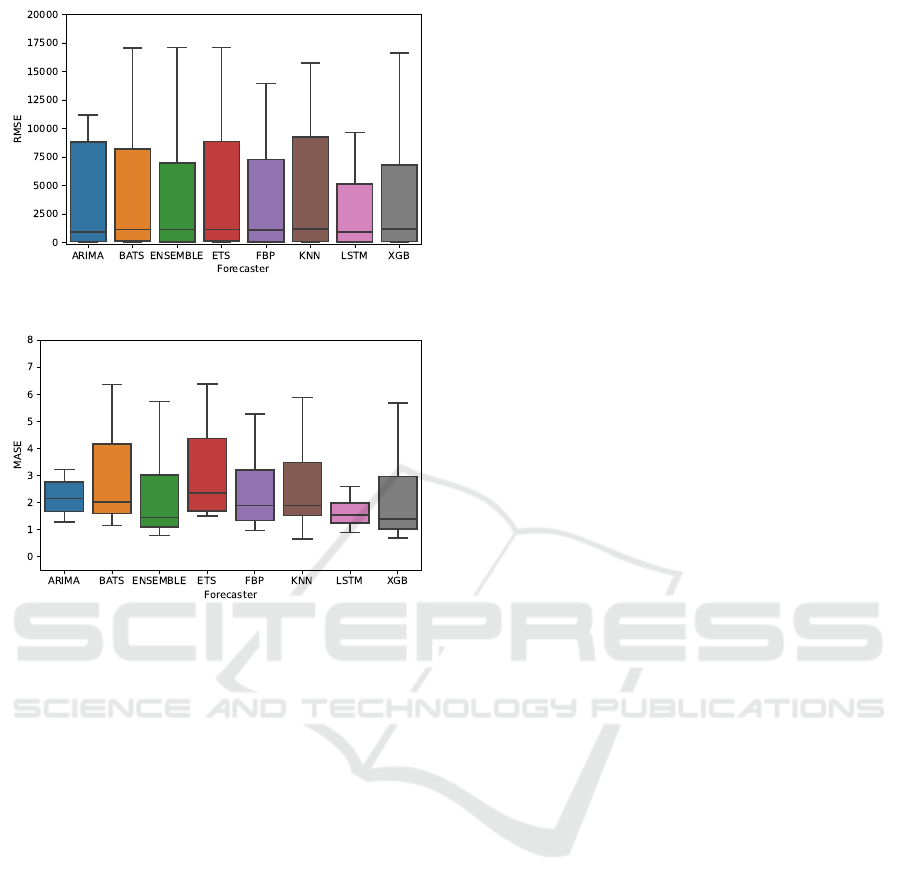
Figure 9: Lower accuracy (trending): RMSE.

Figure 10: Lower accuracy (trending): MASE.

FBProphet are less affected by trending time series in

comparison to the other evaluated algorithms.

5.2 Data Suitability Assessment

As mentioned in subsection 5.1, within the evalua-

tion, we have observed that there is a difference even

within the same context of univariate forecasting of

EAs workload metrics. Certain recorded workload

proﬁles of the EAs were better suitable for forecasting

than the others. While it is possible to distinguish the

quality of prediction based on the prediction accuracy

evaluation using metrics discussed in subsection 3.2,

the actual prediction should be performed ﬁrst.

However, some models require more time than

others to be trained and to produce the result. This

fact might result in the unnecessary use of computa-

tional resources in performing forecasting based on

the data that is badly suitable for the task.

In an attempt to tackle this challenge, we have

evaluated three computationally simple approaches

for attempting to derive a measurement of the suit-

ability of data for forecasting before any forecasting

(training) is done at all. We attempt to differentiate

the data samples based on the expected forecast accu-

racy: high or low.

First, we approach the problem in a naive way.

In this method, for the required forecast horizon, we

simply predict the average value of the required time

stamp hour using the training data. By comparing

the predictions with the actual values, we assess the

model’s performance. To determine if the data is well

suitable for forecasting, we set a threshold based on

the RMSE and MASE. If the metric is above this

threshold, then the model is expected to result in a

low-accuracy forecast. It’s important to note that the

threshold of RMSE is dependent on the scale of the

data values within the individual samples and can’t

be universally determined.

The second considered method is the assessment

of the variability using a classic statistical metric

called the coefﬁcient of variation (CV ). It’s a simple

calculation CV = σ/µ, where σ is a standard devia-

tion of the values within the selected hour, and µ is

the mean. This metric can be used to assess the sta-

bility of the data. A higher coefﬁcient of variation in-

dicates a more unstable time series. To conclude if the

data is suitable for forecasting, a threshold is required.

Within our experimental setup, we set a threshold of

CV ≤ 1.35. If the value is below this threshold, the

model will likely perform well.

Lastly, we try to determine if peaks within the time

series are repeated often. In this method, we exam-

ine the relationship between the lagged values, shift-

ing time series within itself and comparing peaks in a

speciﬁed lag period to the actuals to evaluate the ﬁt-

ness of the data. We calculate the differences between

the N-lagged values (user-deﬁned parameter) and its

original value. We ﬁnally compute the average of the

N-lagged average differences to obtain a single quan-

tiﬁed value. This method helps us understand better

how signiﬁcant the impact of past observations has

on the forecast values. Like the previous methods,

this approach also requires a threshold to classify the

suitability of the data.

To compare the three aforementioned approaches,

we select 40 data samples, that were previously used

in forecasting using XGBoost, and label these as a

high-quality forecast or low-quality according to the

evaluation metrics used within this work, discussed

in subsection 3.2. Then we apply all three methods

mentioned in this section and present the comparison

between the real labels and data evaluation in the form

of confusion matrices.

As seen in Table 2, the application of the naive

forecast method did not yield conclusive results as 21

samples were misclassiﬁed for MASE and RMSE.

The application of CV resulted in 29 data samples

being misclassiﬁed, which is depicted in Table 3. The

performance is signiﬁcantly lower than that of naive

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

238

Table 1: Accuracy decrease in percentage with trending time series.

Group ARIMA BATS ENSEMBLE ETS FBP KNN LSTM XGB

Avg. Difference in MASE A 9.85 32.12 19.86 18.61 11.31 53.91 13.00 88.98

Avg. Difference in RMSE A 33.04 50.47 46.13 43.97 33.95 78.81 33.49 108.88

Avg. Difference in MASE B 19.67 20.30 27.05 15.67 17.83 31.72 21.32 39.41

Avg. Difference in RMSE B 43.84 41.81 43.69 41.13 42.49 50.88 41.73 46.22

Table 2: Quality prediction: naive forecast (Left:MASE &

Right:RMSE).

Predicted

High Low

True

High 13 7

Low 14 6

Predicted

High Low

8 12

9 11

Table 3: Quality prediction: coefﬁcient of variation.

Predicted

High Low

True

High 8 12

Low 17 3

forecasting.

Table 4: Quality prediction: N-lag.

Predicted

High Low

True

High 9 11

Low 8 12

Finally, in Table 4, we present the results of

data samples’ suitability for forecasting prediction by

measuring if value peaks are repeated uniformly. In

this approach, 21 samples were misclassiﬁed, which

puts this approach on the same level as naive forecast-

ing.

As seen from these results, the assessment of the

data quality for forecasting using the three approaches

mentioned in this section is not feasible. None of

the results are conclusive. Therefore, these simplistic

methods can not be applied as a substitute for fore-

casting as a method of assessing data suitability in

decision-making for placement or sizing of enterprise

applications.

6 CONCLUSION

Within this work, we explore the utility of univari-

ate forecasting for predicting workload metrics in en-

terprise applications with a speciﬁc use case of SAP

IT landscapes. The availability and proper manage-

ment of the computational capacity play a critical role

in ensuring optimal performance as well as uninter-

rupted business operations. By accurately forecasting

workload metrics, organizations can effectively allo-

cate resources and make informed decisions regarding

capacity planning. The ﬁndings presented in this pa-

per highlight the possibility of using univariate fore-

casting techniques as a valuable tool to predict work-

load patterns and optimize resource allocation in en-

terprise applications.

Within our empirical evaluation, we have ob-

served a high degree of dependency between the ac-

curacy of the forecasting and the regularity of the ana-

lyzed enterprise application workload proﬁles. Work-

load proﬁles that are characterized by stable, day-to-

day business operations are more suitable for univari-

ate forecasting than workload proﬁles recorded dur-

ing periods of sporadic business activity.

The results of our evaluation indicate that, on

average, XGBoost outperformed the other forecast-

ers (i.e., ARIMA, BATS, ETS, FBProphet, KNN,

LSTM), indicating its effectiveness as a powerful ap-

proach for enterprise applications workload forecast-

ing. It is closely followed by a KNN-based forecaster

and an ensemble that combines FBProphet and XG-

Boost. These algorithms are able to handle both sta-

tionary and uniformly trending time series when the

time series follows a regular workload pattern.

The stability of the workload proﬁle time series,

which is used for forecasting, plays a crucial role in

the resulting accuracy. However, this accuracy can

only be measured after the prediction is already done

using metrics such as RMSE or MASE. This can be

time-consuming, especially if the forecasting is per-

formed for individual systems in large IT landscapes.

To tackle this challenge, we attempted to apply

three simple approaches to determine data suitability

for forecasting. Speciﬁcally, we used the coefﬁcient

of correlation, naive forecasting approach, and shift-

ing time series in order to ﬁnd if workload peaks are

repeated across the given time series. These methods

have not yielded satisfactory results and should not be

used as a substitute for forecasting.

REFERENCES

Armstrong, J. and Collopy, F. (1992). Error measures

for generalizing about forecasting methods: Empiri-

cal comparisons. International Journal of Forecast-

ing, 8(1):69–80.

Utility of Univariate Forecasting for Workload Metrics Predictions in Enterprise Applications

239

Brogi, A., Corradini, A., and Soldani, J. (2019). Estimat-

ing costs of multi-component enterprise applications.

Formal Aspects of Computing, 31(4):421–451.

Cerna, S., Guyeux, C., Arcolezi, H. H., Couturier, R., and

Royer, G. (2020). A comparison of lstm and xgboost

for predicting ﬁremen interventions. In Rocha,

A.,

Adeli, H., Reis, L. P., Costanzo, S., Orovic, I., and

Moreira, F., editors, Trends and Innovations in In-

formation Systems and Technologies, pages 424–434,

Cham. Springer International Publishing.

Chai, T. and Draxler, R. R. (2014). Root mean square er-

ror (rmse) or mean absolute error (mae)? – arguments

against avoiding rmse in the literature. Geoscientiﬁc

Model Development, 7(3):1247–1250.

Chapman, P., Clinton, J., Kerber, R., Khabaza, T., Reinartz,

T., Shearer, C., and Wirth, R. (2000). Crisp-dm

1.0 step-by-step data mining guide. resreport, The

CRISP-DM consortium.

Chen, T. and Guestrin, C. (2016). Xgboost: A scalable

tree boosting system. In Proceedings of the 22nd

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, KDD ’16, page

785–794, New York, NY, USA. Association for Com-

puting Machinery.

Evangelinou, A., Ciavotta, M., Ardagna, D., Kopaneli, A.,

Kousiouris, G., and Varvarigou, T. (2018). Enterprise

applications cloud rightsizing through a joint bench-

marking and optimization approach. Future Genera-

tion Computer Systems, 78:102–114.

Gupta, S. and Dinesh, D. A. (2017). Resource usage pre-

diction of cloud workloads using deep bidirectional

long short term memory networks. In 2017 IEEE

International Conference on Advanced Networks and

Telecommunications Systems (ANTS), pages 1–6.

Herbst, N. R., Huber, N., Kounev, S., and Amrehn, E.

(2013). Self-adaptive workload classiﬁcation and

forecasting for proactive resource provisioning. In

Proceedings of the 4th ACM/SPEC International Con-

ference on Performance Engineering, pages 187–198.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural Computation, 9(8):1735–1780.

Hyndman, R. J. and Koehler, A. B. (2006). Another look at

measures of forecast accuracy. International Journal

of Forecasting, 22(4):679–688.

Hyndman, R. J., Koehler, A. B., Snyder, R. D., and Grose,

S. (2002). A state space framework for automatic fore-

casting using exponential smoothing methods. Inter-

national Journal of Forecasting, 18(3):439–454.

Ledolter, J. (1989). The effect of additive outliers on the

forecasts from arima models. International Journal of

Forecasting, 5(2):231–240.

Li, H. and Scheibli, D. (2010). On cost modeling for hosted

enterprise applications. In Cloud Computing, pages

261–269. Springer Berlin Heidelberg.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation

forest. In 2008 Eighth IEEE International Conference

on Data Mining, pages 413–422.

Livera, A. M. D., Hyndman, R. J., and Snyder, R. D.

(2011). Forecasting time series with complex seasonal

patterns using exponential smoothing. Journal of

the American Statistical Association, 106(496):1513–

1527.

Marquard, U. and G

otz, C. (2008). Sap standard application

benchmarks - it benchmarks with a business focus. In

Kounev, S., Gorton, I., and Sachs, K., editors, Perfor-

mance Evaluation: Metrics, Models and Benchmarks,

pages 4–8, Berlin, Heidelberg. Springer Berlin Hei-

delberg.

Mart

ınez, F., Fr

ıas, M. P., P

erez, M. D., and Rivera, A. J.

(2019). A methodology for applying k-nearest neigh-

bor to time series forecasting. Artiﬁcial Intelligence

Review, 52(3):2019–2037.

Masdari, M. and Khoshnevis, A. (2020). A survey and

classiﬁcation of the workload forecasting methods in

cloud computing. Cluster Computing, 23(4):2399–

2424.

uller, H., Kharitonov, A., Nahhas, A., Bosse, S., and Tur-

owski, K. (2021). Addressing it capacity management

concerns using machine learning techniques. SN Com-

puter Science, 3(1):26.

Nisar, F. and Ahmed, B. (2020). Resource utilization in

data center by applying arima approach. In Bajwa,

I. S., Sibalija, T., and Jawawi, D. N. A., editors, Intel-

ligent Technologies and Applications, pages 752–761,

Singapore. Springer Singapore.

Siami-Namini, S., Tavakoli, N., and Siami Namin, A.

(2018). A comparison of arima and lstm in fore-

casting time series. In 2018 17th IEEE International

Conference on Machine Learning and Applications

(ICMLA), pages 1394–1401.

Tang, L., Pan, H., and Yao, Y. (2018). K-nearest neigh-

bor regression with principal component analysis for

ﬁnancial time series prediction. In Proceedings of the

2018 International Conference on Computing and Ar-

tiﬁcial Intelligence, ICCAI 2018, page 127–131, New

York, NY, USA. Association for Computing Machin-

ery.

Taylor, S. J. and Letham, B. (2018). Forecasting at scale.

The American Statistician, 72(1):37–45.

Wu, C., Buyya, R., and Ramamohanarao, K. (2019).

Cloud pricing models: Taxonomy, survey, and inter-

disciplinary challenges. ACM Computing Surveys,

52(6):1–36.

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

240