Position/Velocity Aided Leveling Loop: Continuous-Discrete Time State
Multiplicative-Noise Filter Case
Irina Avital
1
, Isaac Yaesh
1
and Adrian-Mihail Stoica
2 a
1
Elbit Systems, Land and IMI Division, Ramat Ha Sharon, Israel
2
University POLITEHNICA of Bucharest, Romania
Keywords:
Leveling Loop, Kalman Filtering, Multiplicative Noise, Systems With Finite Jumps.
Abstract:
The problem of leveling using a low cost Inertial Measurement Unit (IMU) is considered, where the IMU mea-
surements are corrupted with white noise. In such a case the state equations are subject to state-multiplicative
noise. To cope with this noise, a state-Multiplicative Kalman Filter (MKF) is applied. The state compo-
nents for the Kalman filter implementation include the Body Position Vector (BPV), the Body Velocity Vector
(BVV), which is just the Ground Velocities Vector (GVV), projected onto the body axes and the three direction
cosines related to the roll and pitch angles. The BVB is assumed to be measured using a Doppler Velocity
Log (DVL) device which consists of four antennas measuring the Doppler effect. Similarly, it is assumed that
the corresponding BPV can be measured, for instance, using the received signal power at those four antennas.
The paper includes numerical simulations and implementation aspects related to the sampled data nature of
the estimation problem.
1 INTRODUCTION
Strap Down Inertial Navigation Systems (SDINS) re-
quire initialization of position, velocity and attitude.
When the platform on which the SDINS is station-
ary, the roll and pitch of the SDINS may be measured
directly from the accelerometers readings. When the
platform moves and no transfer alignment is possi-
ble (e.g. no accurate reference INS is available), one
may resort to the leveling loop approach providing
so called coarse alignment, where the roll and pitch
angles are estimated utilizing velocity measurements
(see e.g. (Xu, 2017) and (Tal, 2017)) and accelerom-
eters and rate sensors provided by an Inertial Mea-
surement Unit (IMU). The present paper deals with
the case where the IMU is a low cost one, provid-
ing measurements corrupted with white noise. In
such a case (see also (Yaesh, 2013)) the state equa-
tions are subject to state-multiplicative noise, mak-
ing related estimation problems readily tractable, us-
ing a state-multiplicative Kalman Filter (MKF), see
(Stoica, 2009). The state vector components for the
Kalman filter implementation include the Body Posi-
tion Vector (BPV), the Body Velocity Vector (BVV),
which is just the Ground Velocities Vector (GVV),
a
https://orcid.org/0000-0001-5369-8615
projected onto the body axes and the three direction
cosines related to the roll and pitch angles. In the
present paper, the BVB is assumed to be measured us-
ing say a Doppler Velocity Log (DVL) device which
consists of four antennas measuring the Doppler ef-
fect. Similarly, the BPV is measured from the four
corresponding range (i.e. received power) measure-
ments. We deal with the special case of a low range
navigation mission, allowing a simple Cartesian for-
mulation of equations of motion, where both Earth
rotation and curvature are neglected. The resulting
equations of motion are then linear equations of the
states, simplifying both dealing with real time calcu-
lation of the transition matrix and exact modeling of
the above mentioned multiplicative noise effect. It is
well known in the inertial navigation community that
navigation initialization with ’large’ attitude-errors
usually results in error divergence. In contrast, since
in our case the states include the directions cosines
and not just errors of the attitude angles (i.e. the rota-
tion from true to calculated Local Level Local North),
the leveling loop we consider, can deal with large ini-
tialization errors for both roll and pitch angles. In the
present paper it is shown that when the IMU measure-
ment noises are taken into account, a stochastic model
with state-dependent noisy terms for the equations of
motion is naturally obtained. Two specific Kalman fil-
Avital, I., Yaesh, I. and Stoica, A.
Position/Velocity Aided Leveling Loop: Continuous-Discrete Time State Multiplicative-Noise Filter Case.
DOI: 10.5220/0012208200003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 485-488
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
485

ters for systems corrupted with state-dependent (mul-
tiplicative) noises are presented. The first one is a
discrete-time filter used in the case when measure-
ments with high acquisition rate are available. The
second one is a continuous-discrete Kalman filter hav-
ing the representation of a system with finite jumps
and it is used when the measurements have low ac-
quisition rate.
2 PROBLEM STATEMENT
We consider the following equations of motion:
dρ(t)
dt
= −ω(t) ×ρ(t) + v(t)
dv(t)
dt
= −ω(t) ×v(t) + a(t) + gc(t)
dc(t)
dt
= −ω(t) ×c(t)
(1)
where ρ and v are, respectively, the position and
velocity vectors, g is the gravity constant, a =
[a
x
,a
y
,a
z
]
T
is the sensed accelerations vector, ω =
[p,q,r]
T
is the rates vector in body axes and c =
[c
1
,c
2
,c
3
]
T
is the vector of the third row in the di-
rect cosine matrix (DCM) of Earth to body trans-
formation, namely, c
1
= −sin(θ), c
2
= sin(φ)cos(θ),
c
3
= cos(φ)cos(θ).
Note that the above equations are written in the
true variables. Since the components of ω, a pro-
vided by the IMU are corrupted with noise, we re-
write the state equation in terms of the Inertial Nav-
igation states affected by these noise signals. To this
end, we denote the state vector integrated by the INS
scheme and the IMU measurements as
x = [ρ
T
m
,v
T
m
,c
T
m
]
T
(2)
and
ω
m
= [p
m
,q
m
,r
m
]
T
,a
m
= [a
x,m,
a
y,m
,a
z,m
]
T
. (3)
The state equations are then given by the follow-
ing It
ˆ
o type stochastic differential equation (Jazwin-
ski,1970)
dx(t) = (A
0
x(t) + Bu(t))dt +
∑
3
ℓ=1
A
ℓ
x(t)dξ
ℓ
(t) + B
w
dw(t)
(4)
where w(t) represents the accelerometers noise and
u(t) is the acceleration. Indeed, taking into account
that p
m
(t) = p(t) + εξ
1
(t), q
m
(t) = q(t) + εξ
2
(t) and
r
m
(t) = r(t) + εξ
3
(t) where ε is the noise level, the
system (1) may be written in the form (4) where
A
0
(t) =


−Ω
0
(t) I
3
0
0 −Ω
0
(t) gI
3
0 0 −Ω
0
(t)


,
B = B
w
=


0
I
3
0


,
with the cross product matrix Ω
0
(t) having the ex-
pression
Ω
0
(t) =


0 −r
m
(t) q
m
(t)
r
m
(t) 0 −p
m
(t)
−q
m
(t) p
m
(t) 0


.
The coefficients of the state-dependent noise terms
have the following expressions
A
ℓ
=


−Ω
ℓ
0 0
0 −Ω
ℓ
0
0 0 −Ω
ℓ


, ℓ = 1, 2,3
where
Ω
1
=


0 0 0
0 0 −ε
0 ε 0


,Ω
2
=


0 0 ε
0 0 0
−ε 0 0


,
Ω
3
=


0 −ε 0
ε 0 0
0 0 0


.
Our aim is to estimate the direction cosines vector
c
m
from noisy measurements of the body frame posi-
tion and velocity vectors ρ
m
and v
m
respectively. We
next formulate this problem as a state-multiplicative
Kalman filtering problem.
3 DISCRETE MULTIPLICATIVE
KALMAN FILTER
Discrete time model for the above state equation can
be approximately written as
x(i + 1) = (F
0
+
3
∑
ℓ=1
F
ℓ
ξ
ℓ
(i))x(i) + Gu(i) + G
w
w(i),
(5)
i = 0,1, ... , where we added w to represent the mea-
surement noise in the accelerations vector and where,
for small enough sampling time h > 0, F
0
= e
A
0
h
,
F
i
= A
i
√
h,i = 1,2,3, G
w
= B
√
h and G = Bh. The
measurement equation is written as
y(i) = Hx(i)+ v(i),i = 0,1,. .. (6)
with H = [I
3
0
3
0
3
]. In the above equations ξ(i) and
v(i) are white noise sequences of zero mean and re-
spectively with Q, R covariances, independent of each
other. The MKF for this system is (Stoica, 2009) :
ˆx(i + 1) = F
0
ˆx(i) + Gu(i) + L(i)(y(i) −H ˆx(i)), i = 0,1,...
(7)
where
L(i) = F
0
X(i)H
T
(R + HX (i)H
T
)
−1
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
486

and where the Kalman gain L(i) is computed using the
following coupled Riccati and Lyapunov type equa-
tions
X(i + 1) =
∑
3
ℓ=0
F
ℓ
Y (i)F
T
ℓ
−F
0
X(i)H
T
×(R + HX (i)H
T
)
−1
HX(i)F
T
0
+G
w
QG
T
w
Y (i + 1) =
∑
3
ℓ=0
F
ℓ
Y (i)F
T
ℓ
+ G
w
QG
T
w
(8)
where X(i) := E(e(i)e
T
(i)
T
),e(i) := x(i) − ˆx(i) and
Y (i) := E(x(i)x
T
(i)), i = 0, 1.. .. Note that the sig-
nal y −H ˆx is known as the innovation signal and is
of zero mean and covariance of HXH
T
+ R. This ap-
proximate formulation is useful when the sampling
rate of IMU and Doppler measurements are identi-
cal. In practice, the IMU measurements are available
at a higher rate than the Doppler measurements. To
this end we represent this situation as a continuous-
discrete time problem (i.e. continuous with jumps)
where the INS-like equation mechanization is approx-
imated, due to its high rate, by a continuous-time
equation.
4 CONTINUOUS-DISCRETE
MULTIPLICATIVE KALMAN
FILTER
In this case, the state equation of (5) is replaced by the
continuous time It
ˆ
o type stochastic differential equa-
tion of (4) whereas the measurement equation of (6)
now reads
y(ih) = Hx(ih)+ v(i), i = 0, 1,. .. (9)
with H = [0
3
I
3
0
3
]. The continuous-discrete MKF for
this system is (Dragan, 2012):
˙
ˆx(t) = A
0
(t) ˆx(t) + Bu(t), t ̸= ih
ˆx(ih
+
) = ˆx(ih) + L(ih)(y(ih) −H ˆx(ih)), i = 0,1,...
(10)
where the Kalman gain L(ih) = X(ih)H
T
(R +
HX(ih)H
T
)
−1
is computed using the solution of the
following system of coupled Lyapunov equations
with jumps
˙
Y (t) = A
0
(t)Y (t) +Y (t)A
T
0
(t)
+A
1
Y (t)A
T
1
+ A
2
Y (t)A
T
2
+A
3
Y (t)A
T
3
+ G
w
QG
T
w
˙
X(t) = A
0
(t)X(t) + X (t)A
T
0
(t)
+A
1
Y (t)A
T
1
+ A
2
Y (t)A
T
2
+A
3
Y (t)A
T
3
+ G
w
QG
T
w
,t ̸= ih
X(ih
+
) = X(ih) −L(ih)HX(ih),i = 0,1, ...
(11)
Note that if ˆx(0) = 0 the first two equations of the
system (11) have the same initial condition, X(0) =
Y (0) = E(x(0)x
T
(0)] and, therefore, their solutions
would be identical if no measurement updates were
applied, namely, if L = 0.
An outline of the proof of the above result is given
as follows. Between the measurements, the estima-
tion error evolves according
de(t) = A
0
(t)e(t)dt +
∑
3
ℓ=1
A
ℓ
x(t)dξ
ℓ
(t)
+B
w
dw(t), t ̸= ih
(12)
therefore between the measurements X(t) =
E(e(t)e
T
(t)) and Y (t) = E(x(t)x
T
(t)) satisfy the
first two equations (11), respectively. However, the
measurement update is given by (10) and, therefore,
e(ih
+
) = (I −L(ih)H)e(ih) −Lv(i), i = 0,1, ... (13)
obtaining
X(ih
+
) = (I −L(ih)H)X(ih)(I −L(ih)H)
T
+L(ih)RL
T
(ih), i = 0, 1,. ..,
(14)
or equivalently,
X(ih
+
) = X(ih) + [L(ih) −X (ih)H
T
(R + HX H
T
)
−1
]
×(R + HX (ih)H
T
)
×[L(ih) −X (ih)H
T
(R + HX (ih)H
T
)
−1
]
T
−X(ih)H
T
(R + HX (ih)H
T
)
−1
HX(ih), i = 0, 1,.. ..
(15)
We readily see that L(ih) = X(ih)H
T
(R +
HX(ih)H
T
)
−1
minimizes the right side of (15)
and that X(ih
+
) is given by the third equation of the
system with jumps (11).
5 SIMULATION RESULTS
The continuous discrete MKF was simulated with
sampling time of 0.001 sec for the velocity updates
and of 0.1 sec for the position updates. The ac-
celerometers noise was taken to be a zero mean white
noise of 3m/ sec/
√
hour whereas the gyros noise is
50deg/
√
hour. Since the direction cosines square
sum to unity, normalization of [ ˆx
4
, ˆx
5
, ˆx
6
] has been per-
formed, following (Zanetti, 2006) after each measure-
ment update. Figure 1 depicts the results of 10 Monte
Carlo runs using the discrete-time model and filter.
The comparison is in terms of the normalized esti-
mation errors, using the 3σ predictions of the errors
using the diagonal terms in X, of the velocities and
of the direction cosines c
i
,i = 1,2,3. The errors are
well within the corresponding predicted standard de-
viations. The roll and pitch angle estimation errors of
the Monte-Carlo runs depicted in Figure 2, whereas
the first Monte-Carlo run, roll and pitch angles are re-
spectively depicted in Figure 3 and in Figure 4. The
results are satisfactory and encourage the implemen-
tation of the presented algorithm.
Position/Velocity Aided Leveling Loop: Continuous-Discrete Time State Multiplicative-Noise Filter Case
487

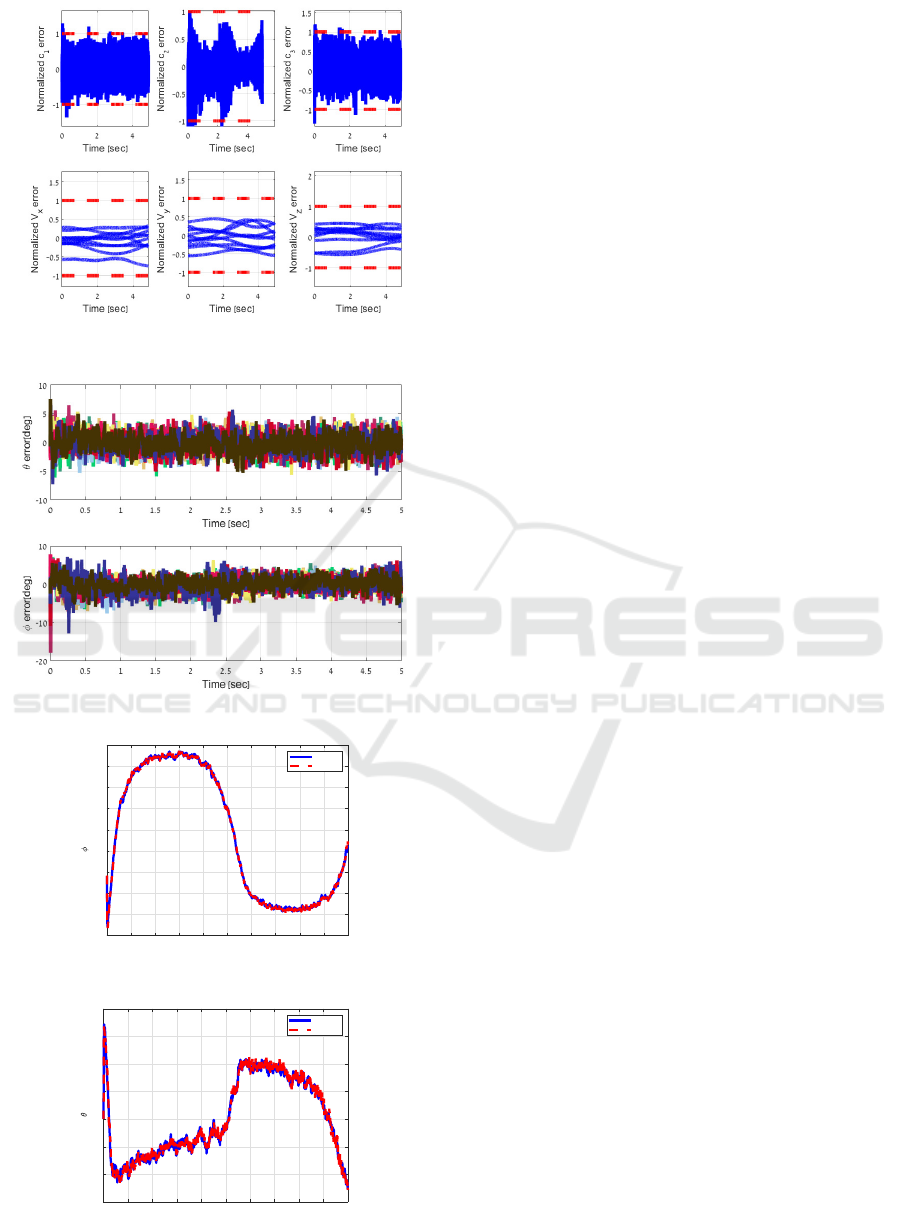
Figure 1: Continuous Discrete MKF results after 10 MC
runs.
Figure 2: Normalized Errors.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [sec]
-100
-80
-60
-40
-20
0
20
40
60
80
[deg]
True
Estimate
Figure 3: Roll angle.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [sec]
-40
-30
-20
-10
0
10
20
30
[deg]
True
Estimate
Figure 4: Pitch angle.
6 CONCLUSIONS
We considered the problem of estimating the roll and
pitch angles in order to initiate the SDINS mechaniza-
tion on a moving platform. We assumed using both
velocity and position measurements in body axes with
different sampling rates allowed by the continuous-
discrete time formulation of the state-multiplicative
noise Kalman filter we used. More rigorous normal-
ization procedure for the directions cosines within the
proposed filter, is left as topic for further research.
REFERENCES
Xiang Xu, Xiaoosu, Xu, Tao Zhang, Yao Li and Jinwu
Tung, ”A Kalman Filter for SINS Self-Alignment
Based on Vector Observation”, Sensors, Vol. 17, 2017
Asaf Tal, Itzik Klein and Reuven Katz, ”Inertial Naviga-
tion System / Doppler Velocity Log (INS/DVL) Fu-
sion with Partial DVL Measurements”, Sensors, Vol.
17, 2017
Isaac Yaesh and Adrian-Mihail Stoica, ”Levelling Design
and Loop State Multiplicative Noise Kalman Filter-
ing”, Springer special memorial volume, 2013
Adrian-Mihail Stoica, Vasile Dragan and Isaac Yaesh,
”Kalman-Type Filtering for Stochastic Systems with
State-Dependent Noise and Markovian Jumps”, Pro-
ceedings of SYSID’2009, St Malo, France
Andrew H. Jazwinski, ”Stochastic Processes and Filtering
Theory”, Academic Press, 1970
Vasile Dragan and Adrian-Mihail Stoica, ”Optimal H
2
fil-
tering for class of linear stochastic systems with sam-
pling”, Automatica, Vol. 48, pp. 2494-2501, 2012
Yaacov Bar-Shalom, X.Rong Li, Thiagalingam Kirubara-
jan, Estimation with applications to Tracking and
Navigation, 2001
Renato Zanetti, Monoranjan Majji, Robert H. Bishop and
Daniele Mortari, ”Norm constrained Kalman Filter-
ing”, Proceedings of the AIAA/AAS Astrodynamics
Specialists Conference, 2006
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
488