Comparing Ensemble and Single Classifiers Using KNN Imputation

for Incomplete Heart Disease Datasets

Ismail Moatadid

, Ibtissam Abnane

and Ali Idri

Mohammed VI Polytechnic University, Benguerir, Morocco

Ensias, Mohammed V University, Rabat, Morocco

Keywords: Ensemble Techniques, Comparative Analysis, Heart Disease Dataset.

Abstract: Heart disease remains a significant global health challenge, necessitating accurate and reliable classification

techniques for early detection and diagnosis. Choosing a suitable classifier model for a dataset containing

missing data is a pervasive issue in medical datasets, which can severely impact the performance of

classification models. In this work, we present a comparative analysis of three ensemble techniques (i.e.

Random Forest (RF), Extreme Gradient Boosting (XGB), and Bagging) and three single technique (i.e. K-

nearest neighbor (KNN), Multilayer Perceptron (MLP), and Support Vector Machine (SVM)) applied to four

heart disease medical datasets (i.e. Hungarian, Cleveland, Statlog and HeartDisease). The main objective of

this study is to compare the performance of ensemble and single classifiers in handling incomplete heart

disease datasets using KNN imputation and identify an effective approach for heart disease classification. We

found that, overall, MLP outperformed SVM and KNN across datasets. Moreover, we found that ensemble

techniques consistently outperformed the single techniques across multiple metrics and datasets. The

ensemble models consistently achieved higher accuracy, precision, recall, F1 score, and AUC values.

Therefore, for heart disease classification using KNN imputation, the ensemble techniques, particularly RF,

Bagging, and XGB, proved to be the most effective models.

1 INTRODUCTION

Heart disease continue to be a significant global

health concern, encompassing various conditions that

affect the heart and blood vessels (Felman, 2018).

Accurate and timely diagnosis of heart disease plays

a crucial role in improving patient outcomes and

optimizing treatment plans (Wrathall & Belnap,

2017). In recent years, machine learning has emerged

as a powerful approach for analyzing medical data

and facilitating precise diagnostic predictions

(Ponikowski et al., 2014).

Ensemble techniques have become valuable tools

in heart disease classification, contributing to

improved accuracy and robustness of classification

models (Asif et al., 2023). The diagnosis of heart

disease can be intricate, necessitating the use of

ensemble techniques to enhance classification

performance. Ensemble methods, such as bagging

https://orcid.org/0009-0004-8010-5570

https://orcid.org/0000-0001-5248-5757

https://orcid.org/0000-0002-4586-4158

and boosting, amalgamate predictions from multiple

individual models to effectively overcome the

limitations inherent in standalone models (Alqahtani

et al., 2022). Through this approach, ensemble

techniques address concerns regarding variance

reduction and model stability. Leveraging ensemble

techniques in heart disease classification enables

better generalization, noise and outlier resilience, and

a comprehensive understanding of heart disease

patterns, ultimately leading to more accurate

diagnoses and well-informed treatment decisions

(Shorewala, 2021).

However, one persistent challenge in medical

datasets is the presence of missing data (MD), which

can introduce bias and hinder the performance of

classification models (Ibrahim et al., 2012).

One promising approach for handling missing

data is K-Nearest Neighbors (KNN) imputation.

KNN imputation estimates missing values by

Moatadid, I., Abnane, I. and Idri, A.

Comparing Ensemble and Single Classiﬁers Using KNN Imputation for Incomplete Heart Disease Datasets.

DOI: 10.5220/0012208300003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 379-386

ISBN: 978-989-758-671-2; ISSN: 2184-3228

379

leveraging the similarities between instances and

utilizing the values of their nearest neighbors, thereby

preserving local data characteristics. However, the

specific application and performance of KNN

imputation in the context of heart disease

classification, particularly when comparing single

classifiers and ensemble classifiers, remain relatively

unexplored (Zhang, 2012).

This paper presents a comparative analysis of

three ensemble techniques (i.e. Random Forest (RF),

Extreme Gradient Boosting (XGB), and Bagging) and

three single technique (i.e. K-nearest neighbor

(KNN), Multilayer Perceptron (MLP), and Support

Vector Machine (SVM)) on four heart disease

datasets (i.e. Hungarian, Cleveland, StatLog and

HeartDisease). Our analysis focuses on evaluating

and comparing the performance of these classifiers

after applying KNN imputation to handle incomplete

heart disease datasets. The main objective is to assess

their effectiveness in accurately classifying heart

disease cases in the presence of missing data.

To conduct our analysis, we first preprocess the

heart disease dataset by employing KNN imputation

to fill in missing values. Subsequently, we train and

evaluate each classifier using the imputed dataset,

employing various performance measures such as

accuracy, precision, recall, F1-score, and area under

the receiver operating characteristic curve (AUC-

ROC). Through these evaluations, we aim to evaluate

and compare the performance of ensemble/single

techniques for heart disease classification using

incomplete datasets.

Toward this aim, two research questions were

addressed:

RQ1: What is the best single classification

technique when using KNN imputation for

heart disease classification?

RQ2: Do ensemble techniques outperform single

techniques for heart disease classification

when using KNN imputation?

The paper is structured as follows: Section 2

describes the related work, Section 3 presents k-

nearest neighbor imputation and the classification

techniques we used; Section 4 presents the four heart

disease datasets and well as the performance criteria.

Section 5 describes the experimental design. Section

6 presents and discusses the findings. Section 7

presents the threats to validity. Section 8 concludes

with a look ahead to future work.

2 BACKGROUND

This section presents k-nearest neighbor imputation

and the classification techniques we used, both

ensemble and single.

2.1 K-Nearest Neighbour Imputation

(KNNI)

Missing data refers to the absence or incompleteness

of certain information or values within a dataset. It

occurs when data points are not recorded or are

unavailable for various reasons such as data entry

errors, non-response in surveys, equipment failure, or

intentional omission. The presence of missing data

can introduce uncertainty and complicate data

analysis, potentially leading to biased or inaccurate

results if not addressed properly (Bo. et al., 1988).

Missing value imputation using the k-nearest

neighbor algorithm is efficient. It starts with

determining the k-nearest neighbors, or the records in

the dataset that are closest to the missing record in

terms of similarities, using the Euclidean distance.

In kNNI, the feature's mean value which has the

missing value among the chosen nearest neighbors is

used. The accuracy of KNNI imputation is higher

than that of mean imputation, which computes the

mean from the whole dataset rather than the k-nearest

neighbors of the missing record. However, it is costly

when dealing with huge datasets since it necessitates

searching the whole dataset for entries that are most

comparable. In addition, choosing the right k value

might be difficult (Fouad et al., 2021).

2.2 Classification Techniques

In this study we used six classification techniques.

We first start by presenting the single ML techniques

then the ensemble techniques.

2.2.1 Single Classification Techniques

K-Nearest Neighbors (KNN): K-nearest neighbors

(KNN) is a classification method that assigns a class

to a record based on its closest neighbors. It relies on

majority voting, with the choice of k determining the

neighbors to consider. KNN is a straightforward but

efficient method that works best when there is little or

no understanding of how data is distributed. The

complete training set is retained, and each query is

classified by taking into account the majority label of

its k-nearest neighbours.(Guo et al., 2004)(Imandoust

& Bolandraftar, 2013).

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

380

Multi-Layer Perceptron (MLP): Multilayer

Perceptron (MLP) is an artificial neural network

capable of representing complex relationships.

Neurons process inputs to create outputs in its input,

hidden, and output layers. MLP is learned using

backpropagation and employs nonlinear activation

functions. This training approach makes MLP useful

for a variety of applications, including classification

and regression, and enables it to handle data that is

not linearly separable. (Chlioui et al., 2020)(Amin &

Ali, 2017).

Support Vector Machine (SVM): An effective

supervised learning approach for non-linear data is

SVM. It is frequently used in many applications and

selects the best hyperplane for classifying diverse

classes. SVM is a useful technique in machine

learning with benefits including quick prediction and

precise categorization. (Chlioui et al., 2020).

2.2.2 Ensemble Classification Techniques

Random forest: Random Forest is a powerful

machine learning algorithm that combines multiple

decision trees in an ensemble.By employing random

feature selection and having lower error rates than

Adaboost, it achieves excellent accuracy. It works

well for high-dimensional classification and skewed

datasets, with accuracy depending on the strength and

correlation of each individual tree. The number of

trees, features, execution slots, and seed value are

important criteria. (Chlioui et al., 2020).

Bagging: Bagging is an ensemble classifier

technique that combines multiple independent

predictors using model averaging methods. By

repeatedly sampling the initial training dataset with

replacement, bootstrap replicates are produced. Each

replica is used in a classification iteration with a

machine learning algorithm, typically a decision tree.

In bagging, the outputs from each iteration are

merged either by taking an average or by applying a

voting principle to decide the final class labels. Equal

weights are applied to all classifiers throughout the

voting phase. (Jafarzadeh et al., 2021).

Boosting: is an ensemble learning technique

where the models are built sequentially rather than

independently. The goal of boosting is to correct the

errors made by previous predictors. In the boosting

algorithm, each individual predictor in the chain

learns to address or minimize the mistakes made by

its predecessors. It is a general supervised technique

that involves an iterative re-training procedure. This

iterative process aims to improve the overall

predictive accuracy of the ensemble by focusing on

the challenging instances that were initially

misclassified (Jafarzadeh et al., 2021).

3 DATASETS DESCRIPTION AND

PERFORMANCE CRITERIA

This section describes the dataset used as well as the

performance criteria used to evaluate the classifiers.

3.1 Datasets Description

In this study. We used four medical heart disease

datasets: Cleveland and HeartDisease datasets that

are a cardiological datasets that contain 303 samples

each, where each samples is described by 9

categorical attributes and 9 numerical attributes,

Hungarian a cardiological dataset that contain 261

samples, where each sample is described by 7

categorical attributes and 5 numerical attributes,

Statlog a general medical dataset that contain 270

samples, where each sample is described by 9

categorical attributes and 6 numerical attributes.

These data sets were chosen since they include a

variety of data (numerical and categorical), and they

are different in terms of their sources, fields, and

sizes.

3.2 Performance Criteria

In order to evaluate and compare classification

techniques, a number of classification measures have

been used in the literature. The most widely used are:

𝑎𝑐𝑐𝑢𝑟𝑎𝑐𝑦 =

𝑇𝑃 + 𝑇𝑁

𝑇𝑃

𝑇𝑁

𝐹𝑃

𝐹𝑁

(1)

𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 =

𝑇𝑃

𝐹𝑃

(2)

𝑟𝑒𝑐𝑎𝑙𝑙 =

𝑇𝑃

𝐹𝑁

(3)

𝐹1 = 2 ×

(𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑟𝑒𝑐𝑎𝑙𝑙)

(

𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 × 𝑟𝑒𝑐𝑎𝑙𝑙

)

(4)

Area Under Curve (AUC): defined as a commonly

used evaluation metric in binary classification tasks

that measures the overall performance of a model by

assessing its ability to distinguish between positive

and negative instances. It represents the area under

the receiver operating characteristic (ROC) curve,

which plots the true positive rate (sensitivity) against

the false positive rate (1 - specificity) at various

classification thresholds. The AUC score ranges

Comparing Ensemble and Single Classiﬁers Using KNN Imputation for Incomplete Heart Disease Datasets

381

from 0 to 1, where a score of 0.5 indicates random

guessing, and a score of 1 represents a perfect

classifier (Huang & Ling, 2005).

4 EXPERIMENTAL DESIGN

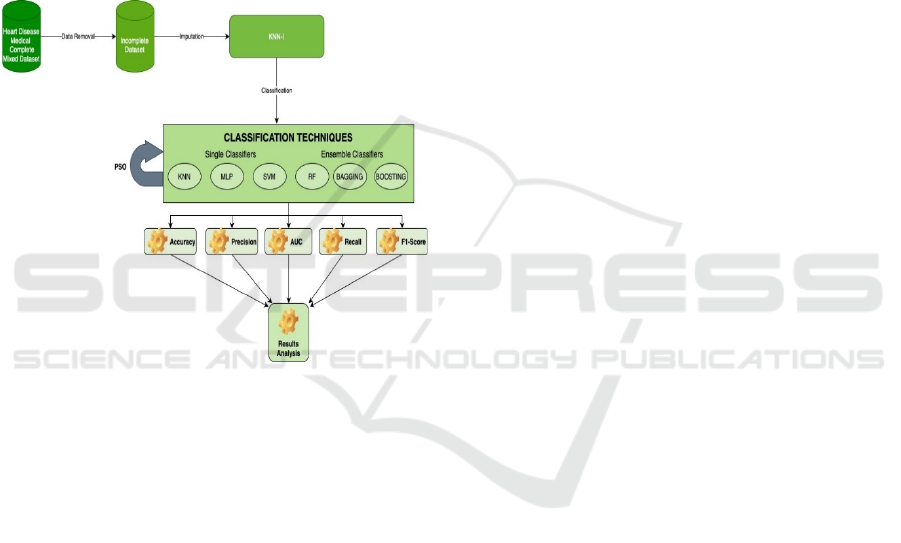
Figure 1 presents the experimental design we

followed. Data removal, Imputation, classification

and results analysis are the main components of this

process. We used four datasets with 15 % missing

data. The KNNI were then used. Utilizing accuracy,

precision, recall, F1 score and AUC, the performance

of the six classifiers approaches was evaluated.

Figure 1: Experimental Process.

4.1 Data Removal

A complete dataset is necessary for the initial step of

the empirical design. In order to obtain the

four complete data sets needed for this analysis, the

datasets were pre-processed by removing MD. Then,

we generated MD artificially using the whole

datasets.

The accuracy of imputation techniques is

negatively impacted by MD percentage, according to

the literature (Abnane & Idri, 2018)(Idri et al., 2016).

Regardless of the imputation approach employed, the

imputation accuracy increases as the MD percentage

decreases. According to the literature, analyses with

more than 10% missingness are likely biased,

whereas missingness rates of 5% or less are

insignificant (Abnane & Idri, 2018)(Dong & Peng,

2013). As a result, we fixed the MD proportion in our

empirical design at 15%. 15% of MD was arbitrarily

added to the four datasets. We currently have four

incomplete datasets.

4.2 KNN Imputation

The four incomplete datasets from Step 1 were used

to create the complete datasets in this step using

KNNI. The number of neighbors was fixed to five for

the four datasets to obtain comparable results

according to the same number of neighbors.

4.3 Single/Ensemble Classification

Techniques

The parameter settings of machine learning (ML)

algorithms, which vary from dataset to dataset, are the

key determinant of their classification accuracy.

According to the literature, tweaking the ML

technique's parameter settings is required to get

accurate results (Sharma & Shah, 2021). The choice

of parameters for the ML approaches was done using

the particle swarm optimization (PSO) approach by

getting the parameters that maximize the accuracy

according to each dataset.

Since parameter settings may have a significant

impact on the classification accuracy, the first step in

our work was to apply the PSO algorithm on the six

classification algorithms in the four datasets. The

PSO method evaluates all the possible combinations

within the ranges and then selects the configuration

of each classification technique that minimizes the

accuracy until a stopping criterion is reached (number

of iterations).

4.4 Performance Evaluation

This subsection presents the evaluation process of the

six classifiers. We first start by discussing the

accuracy results. Then, we perform the Wilcoxon test

to investigate the significance of the accuracy results.

Finally, we perform the Borda count using precision,

recall, F1-score and AUC.

4.4.1 Accuracy Results

This step evaluates and compare the accuracy results

of each classifier according to each dataset, which

will allow us to have an idea of the best classifier in

terms of accuracy.

4.4.2 Significance Testing Using Wilcoxon

In order to determine whether there is adequate

evidence that the median of two probability

distributions is located differently, this study used the

non-parametric Wilcoxon statistical test (Kafadar &

Sheskin, 1997). The significance level for each two-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

382

sided statistical test was set at α=0.05.P-values and

effect sizes are used to describe the findings. The p-

values provide information about the difference's

importance; for example, a p-value of 0.05 or less

indicates that the difference is noteworthy.

4.4.3 Borda Count

The Borda count is used to know which classifier

emerges as the preferred choice. It’s a voting method

that allows for the comparison and ranking of

alternatives based on the preferences of a group of

voters. In the context of evaluating classifiers, the

Borda count can be utilized to determine the best-

performing classifier among a set of options. Borda

count was applied using precision, recall, F1-score

and AUC (Fraenkel & Grofman, 2014).

5 RESULTS AND DISCUSSION

This section evaluates and compares the influence of

six classifiers based on both statistical and ML

metrics over 18% of MCAR missing data, imputed

through KNNI in four Heart Disease datasets.

5.1 RQ1: What Is the Best Single

Classification Technique when

Using KNN Imputation for Heart

Disease Classification

Table 1 displays the accuracy of three single classifiers

(SVM, MLP, and KNN) when using KNN imputation

on four different datasets. Table 1 shows that SVM

achieves the highest accuracy on the Cleveland (0.78)

and HeartDisease (0.79) datasets, indicating its effecti-

veness in those cases. MLP demonstrates the highest

accuracy on the Statlog dataset (0.81), showcasing its

superior performance in that scenario. On the Hungari-

an dataset, both MLP and KNN perform equally well

with an accuracy of 0.81, while KNN achieves the

lowest accuracy on the remaining datasets. Therefore,

the choice of the best classification model depends on

the specific dataset. SVM proves to be the top

performer on the Cleveland and HeartDisease datasets,

while MLP excels on the Statlog dataset.

Table 1: Accuracy of single classifiers.

Dataset

Cleveland Statlog Hungarian

Heart

Disease

Model

Svm 0.78 0.76 0.75 0.79

Mlp 0.73 0.81 0.81 0.76

Knn 0.60 0.65 0.69 0.61

The results of the statistical test using the

Wilcoxon signed-rank test further confirm the initial

comparisons made between the models SVM, MLP,

and KNN. The obtained p-values provide statistical

evidence to support the previously observed

differences in performance. The p-values of 0.05 and

0.03 for the comparisons between SVM and MLP, as

well as the p-value of 0.02 for the comparison

between SVM and KNN, align with the initial

analysis.

These p-values indicate that there is no significant

difference between SVM and MLP, reinforcing their

similar performance. Additionally, the significant p-

value of 0.02 for the comparison between SVM and

KNN supports the earlier finding that SVM

outperforms KNN. Therefore, the results of the

Wilcoxon test provide additional confirmation of the

initial observations, lending statistical support to the

conclusions drawn regarding the relative

performance of the models.

Table 2: Significance testing for single classifiers.

Model

(

)

α′

⁄

MLP KNN

Svm 0.05/0.0167 0.02/0.0167

0.03/0.0167

Furthermore, Table 3 present the the Borda count

rankings, which consider multiple performance

metrics such as precision, F1 score, recall, and AUC,

provide valuable insights into the relative

performance of the classifiers across the datasets.

MLP consistently emerges as the most favored

classifier, achieving the top rank in three out of the

four datasets. SVM also demonstrates strong

performance, securing the second rank in three

datasets. KNN, although obtaining a lower ranking in

comparison, still showcases its performance

capabilities.

Table 3: Borda count for single classifiers.

Dataset Rank Model

Cleveland 1 Mlp

2 Svm

3 Knn

Heartdisease 1 Svm

2 Mlp

3 Knn

Statlog 1 Mlp

2 Svm

3 Knn

Hungarian 1 Mlp

2 Knn

3 Svm

Comparing Ensemble and Single Classiﬁers Using KNN Imputation for Incomplete Heart Disease Datasets

383

Table 4 shows the global Borda count results

across all datasets, the MLP model achieved the

highest score indicating its superior performance

compared to the and KNN models. These findings

suggest that the MLP model consistently

outperformed the other models, demonstrating its

robustness and effectiveness. The SVM model

secured the second position, while the KNN model

obtained the lowest score. Overall, the results

highlight the MLP model as the top performer,

showcasing its potential for various tasks and

datasets.

Table 4: Global borda count rank of single classifiers.

Rank Model

1 Mlp

2 Svm

3 Knn

In conclusion, when using KNN imputation, the

evaluation of single classification techniques (SVM,

MLP, and KNN) reveals that the best technique

depends on the specific dataset. SVM demonstrates

superior performance on the Cleveland and

HeartDisease datasets, while MLP excels on the

Statlog dataset. Both MLP and KNN perform equally

well on the Hungarian dataset.

However, considering the overall performance across

multiple datasets, MLP emerges as the most favored

single classification technique. Therefore, for optimal

results when using KNN imputation, MLP is

recommended as the best single classification

technique.

5.2 RQ2: Do Ensemble Technique

Outperform Single Techniques for

Heart Disease Classification when

Using KNN Imputation?

Table 5 shows the results of ensemble/single

techniques on the four imputed heart disease datasets.

The results show that ensemble techniques generally

outperform single classifiers. In fact, Table 5 shows

that the best accuracy results are always given by an

ensemble.

From the accuracy results, it is evident that the

ensemble techniques (RF, XGB, and BAGGING)

outperform the single techniques (SVM, MLP, and

KNN) for heart disease classification when using

KNN imputation.

Table 5: Accuracy results for single and ensemble

classifiers.

Dataset

Cleveland Statlog Hungarian

Heart

Disease

Model

Svm 0.78 0.76 0.75 0.79

Mlp 0.73 0.81 0.81 0.76

Knn 0.60 0.65 0.69 0.61

Rf 0.81 0.80 0.90 0.98

Xgb 0.78 0.79 0.90 0.93

Bagging 0.81 0.83 0.90 0.90

In order to further investigate the significance of

the results, Table 6 shows the results of the statistical

test using Wilcoxon test. The results indicate the p-

values obtained from comparing each ensemble

model's performance to the single models. For

example, for the comparison between SVM and RF,

the p-values are 0.125, 0.25, and 0.125, respectively,

for RF, XGB, and BAGGING. Considering the

threshold of significance (α), which is usually set at

0.05, these p-values are all above the threshold. This

suggests that there is no significant difference

between the ensemble models (RF, XGB,

BAGGING) and the single models (SVM, MLP,

KNN) in terms of accuracy. The p-values indicate

that the differences observed between the ensemble

models and single models are not statistically

significant.

Table 6: Significance testing for single classifiers against

ensemble classifiers.

P(α) α′

⁄

Ensemble models

Rf Xgb Bagging

Single models

Svm

0.125

0.25

0.125

0.25

0.125

Mlp

Knn

Table 7 shows the Borda count rankings of

ensemble/single classifiers across all datasets. The

results demonstrate that ensemble techniques (i.e. RF,

Bagging and Boosting) were ranked in the top 3 of 3

datasets, namely: Cleveland, HeartDisease and

Hangarian. The exception was the statlog dataset;

where the first classifier was Bagging, followed by

MLP and Boosting.

In order to have a general evaluation of

ensemble/single classifiers across datasets, Table 8

presents the Borda count ranking across datasets.

Ensemble techniques were ranked first, followed by

single techniques.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

384

Table 7: Borda count for single classifiers and ensemble

classifiers.

Dataset Ran

Model

Cleveland 1 Rf

2 Bagging

4Ml

5Svm

6Knn

Heart disease 1 Rf

2 Bagging

4Svm

5Mlp

6Knn

Statlog 1 Bagging

2Ml

4Rf

5Svm

6Knn

Hungarian 1 Rf

2Ba

4Mlp

5Knn

6Svm

Table 8: Global borda count of ensemble and single

classifiers.

Ran

Model

1 Rf

2 Ba

3 X

4 Ml

5 Svm

6 Knn

6 CONCLUSIONS AND FUTURE

WORK

This study aimed to evaluate and compare the

performance of three single classifiers (KNN, MLP,

SVM) and three ensemble classifiers (RF, XGB,

Bagging) for heart disease imputed datasets using

KNNI.

RQ1: What is the best single classification

technique when using KNN imputation for heart

disease classification?

We found that when using KNN imputation, the

best single classification technique varies depending

on the dataset. SVM performs well on Cleveland and

HeartDisease datasets, while MLP excels on the

Statlog dataset. MLP and KNN show comparable

performance on the Hungarian dataset. However,

considering overall performance across multiple

datasets, MLP emerges as the preferred choice.

RQ2: Do ensemble techniques outperform single

techniques for heart disease classification when using

KNN imputation?

Ensemble techniques, including Random Forest

(RF), Bagging, and XGBoost (XGB), consistently

outperformed the single techniques (Support Vector

Machine (SVM), Multilayer Perceptron (MLP), and

k-Nearest Neighbors (KNN)) across multiple metrics

and datasets. The ensemble models consistently

achieved higher accuracy, precision, recall, F1 score,

and AUC values. Therefore, for heart disease

classification using KNN imputation, the ensemble

techniques, particularly RF, Bagging, and XGB,

proved to be the most effective models.

Overall, this study highlights the beneficial

impact of using ensemble classifiers rather than single

classifiers, improving the performance of

classification models for imputed heart disease

datasets.

Further research is warranted to explore a

comparison between a novel imputation technique

that use fuzzy logic against the KNN imputation

technique using ensemble and single classifiers on

medical datasets.

REFERENCES

Abnane, I., & Idri, A. (2018). Improved Analogy-based

Effort Estimation with Incomplete Mixed Data. 1015–

1024. https://doi.org/10.15439/2018 F95

Alqahtani, A., Alsubai, S., Sha, M., Vilcekova, L., & Javed,

T. (2022). Cardiovascular Disease Detection using

Ensemble Learning. Computational Intelligence and

Neuroscience, 2022, 1–9. https://doi.org/10.1155/20

22/5267498

Amin, M. Z., & Ali, A. (2017). Application of Multilayer

Perceptron (MLP) for Data Mining in Healthcare

Operations. Proceeding of the 3rd International

Conference …, February.

Asif, D., Bibi, M., Arif, M. S., & Mukheimer, A. (2023).

Enhancing Heart Disease Prediction through Ensemble

Learning Techniques with Hyperparameter

Optimization. Algorithms, 16(6), 308. https://doi.org/

10.3390/a16060308

Bo., N., Little, R. J. A., & Rubin, D. B. (1988). Statistical

Analysis with Missing Data. Population (French

Edition), 43(6), 1174. https://doi.org/10.2307/1533221

Chlioui, I., Abnane, I., & Idri, A. (2020). Comparing

Statistical and Machine Learning Imputation

Techniques in Breast Cancer Classification. Lecture

Notes in Computer Science (Including Subseries

Lecture Notes in Artificial Intelligence and Lecture

Comparing Ensemble and Single Classiﬁers Using KNN Imputation for Incomplete Heart Disease Datasets

385

Notes in Bioinformatics), 12252 LNCS. https://doi.org/

10.1007/978-3-030-58811-3_5

Chung, J., & Teo, J. (2023). Single classifier vs. ensemble

machine learning approaches for mental health

prediction. Brain Informatics, 10(1). https://doi.org/

10.1186/s40708-022-00180-6

Dong, Y., & Peng, C. Y. J. (2013). Principled missing data

methods for researchers. In SpringerPlus (Vol. 2, Issue

1). https://doi.org/10.1186/2193-1801-2-222

Felman, A. (2018). Everything you need to know about

heart disease. Medical News Today.

Fouad, K. M., Ismail, M. M., Azar, A. T., & Arafa, M. M.

(2021). Advanced methods for missing values

imputation based on similarity learning. PeerJ

Computer Science, 7, e619. https://doi.org/10.7717/

peerj-cs.619

Fraenkel, J., & Grofman, B. (2014). The Borda Count and

its real-world alternatives: Comparing scoring rules in

Nauru and Slovenia. Australian Journal of Political

Science, 49(2). https://doi.org/10.1080/10361146.20

14.900530

Guo, G., Wang, H., Bell, D. A., Bi, Y., Bell, D., & Greer,

K. (2004). KNN Model-Based Approach in

Classification. https://www.researchgate.net/publicati

on/2948052

Huang, J., & Ling, C. X. (2005). Using AUC and accuracy

in evaluating learning algorithms. IEEE Transactions

on Knowledge and Data Engineering, 17(3).

https://doi.org/10.1109/TKDE.2005.50

Ibrahim, J. G., Chu, H., & Chen, M. H. (2012). Missing data

in clinical studies: Issues and methods. In Journal of

Clinical Oncology (Vol. 30, Issue 26).

https://doi.org/10.1200/JCO.20 11.38.7589

Idri, A., Abnane, I., & Abran, A. (2016). Missing data

techniques in analogy-based software development

effort estimation. Journal of Systems and Software, 117.

https://doi.org/10.1016/j.jss.2 016.04.058

Imandoust, S. B., & Bolandraftar, M. (2013). Application

of K-Nearest Neighbor ( KNN ) Approach for

Predicting Economic Events : Theoretical Background.

Int. Journal of Engineering Research and Applications,

3(5).

Jafarzadeh, H., Mahdianpari, M., Gill, E.,

Mohammadimanesh, F., & Homayouni, S. (2021).

Bagging and boosting ensemble classifiers for

classification of multispectral, hyperspectral and

polSAR data: A comparative evaluation. Remote

Sensing, 13(21). https://doi.org/10.3390/rs13214 405

Kafadar, K., & Sheskin, D. J. (1997). Handbook of

Parametric and Nonparametric Statistical Procedures.

The American Statistician,

51(4). https://doi.org/10.23

07/2685909

Ponikowski, P., Anker, S. D., AlHabib, K. F., Cowie, M. R.,

Force, T. L., Hu, S., Jaarsma, T., Krum, H., Rastogi, V.,

Rohde, L. E., Samal, U. C., Shimokawa, H., Budi

Siswanto, B., Sliwa, K., & Filippatos, G. (2014). Heart

failure: preventing disease and death worldwide. In

ESC Heart Failure (Vol. 1, Issue 1).

https://doi.org/10.10 02/ehf2.12005

Sharma, T., & Shah, M. (2021). A comprehensive review

of machine learning techniques on diabetes detection.

In Visual Computing for Industry, Biomedicine, and Art

(Vol. 4, Issue 1). https://doi.org/10.1186/s42492-021-

00097-7

Shorewala, V. (2021). Early detection of coronary heart

disease using ensemble techniques. Informatics in

Medicine Unlocked, 26. https://doi.org/10.1016/j.imu.

2021.100655

Wrathall, J. A., & Belnap, T. (2017). Reducing Healthcare

Costs Through Patient Targeting: Risk Adjustment

Modeling to Predict Patients Remaining High-Cost.

EGEMs (Generating Evidence & Methods to Improve

Patient Outcomes), 5(2). https://doi.org/10.13063/23

27-9214.1279

Zhang, S. (2012). Nearest neighbor selection for iteratively

kNN imputation. Journal of Systems and Software,

85(11). https://doi.org/10.1016/ j.jss.2012.05.073

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

386