CFRLI-IDM: A Counterfactual Risk Level Inference Based Intelligence

Driver Model for Extremely Aggressive Cut-in Scenario in China

Yongqiang Li, Yang Lv, Quan Wang and Qiankun Miao

Neolix, China

Keywords:

Counterfactual Inference, Control Barrier Function, Unmanned Delivery Vehicles, Aggressive Cut-in.

Abstract:

When conducting unmanned delivery tasks on side roads in China, unmanned delivery vehicles sometimes

face a dual challenge of aggressive cut-ins and reckless followers driving closely behind them. To address

this challenge, we propose a cut-in response strategy named Counterfactual Risk Level Inference-based Intel-

ligence Driver Model (CFRLI-IDM). The CFRLI-IDM method utilizes an improved Intelligent Driver Model

(IDM) as the initial longitudinal control strategy for the ego vehicle. It then leverages counterfactual inference

to construct an optimization problem, aiming to derive a longitudinal control strategy that satisﬁes the ego

vehicle’s risk threshold constraint while maximizing compliance with the rear vehicle’s maximum acceptable

braking deceleration constraint, with minimal changes to the initial strategy. To evaluate the effectiveness

of our proposed method, we design an extremely challenging cut-in simulation scenario incorporating the

aforementioned factors and validate the algorithm within this simulated environment. Experimental results

demonstrate that our method prioritizes the safety of the ego vehicle while ensuring the safety of the rear ve-

hicle as much as possible, substantially reducing the likelihood of safety accidents occurring in such complex

scenarios.

1 INTRODUCTION

The development of e-commerce has provided vast

opportunities space for China’s unmanned delivery

business, while also posing an urgent demand for

the advancement of autonomous driving technol-

ogy. With the continuous increase in labor costs, e-

commerce giants such as JD.com, Meituan, and Al-

ibaba have begun to enter the ﬁeld of unmanned de-

livery to compete for this one trillion dollar market

(Li et al., 2020). As one of the new forces of un-

manned driving in China, Neolix has also conducted

long-term and outstanding exploration in this ﬁeld.

This article focuses on a complex scenario faced

by Neolix in its actual operation: that is, in areas

with narrow passage spaces such as urban trafﬁc aux-

iliary roads, unmanned delivery vehicles encounter

aggressive cut-in during morning and evening peak

hours. For example, the cut-in distance of the front

vehicle may be less than 0.2 meters. However, at

this time, due to trafﬁc congestion and busy roads,

unmanned delivery vehicles often have other human

drivers closely following behind them (electric vehi-

cles, tricycles, bicycles, etc.) This scenario poses a

serious challenge to the longitudinal control strategy

of unmanned delivery vehicles: if the unmanned de-

livery vehicle does not respond in a timely manner or

outputs a relatively small braking amount, it is difﬁ-

cult to cope with the possible sudden braking of the

cut-in vehicle. On the contrary, if the unmanned de-

livery vehicle responds too early (exceeding the ex-

pectations of the driver of the rear vehicle) or provides

too much braking amount, it is high likely to cause

the rear end collision due to the follower’s delayed

response.

In this scenario, the appropriate constraints is a

relatively difﬁcult problem to determine. Existing

methods may rely on precise predictions or overly

simplistic assumptions of the front vehicle, and em-

ploy certain ﬁxed constraints to construct optimiza-

tion problems, such as being at least 0.2 meters away

from the nearest vehicle in front (Bageshwar et al.,

2004; Yoon et al., 2021). This will result in a larger

braking amount output when the constraint is vio-

lated. To address this issue, we creatively propose

a dynamic constraint method, which constructs this

optimization problem based on the result of counter-

factual reasoning.

The overall idea and architecture of the method

are shown in Fig. 1. Firstly, the acceleration of an

unmanned delivery vehicle is calculated based on the

initial strategy (such as the previous version of the

Li, Y., Lv, Y., Wang, Q. and Miao, Q.

CFRLI-IDM: A Counterfactual Risk Level Inference Based Intelligence Driver Model for Extremely Aggressive Cut-in Scenario in China.

DOI: 10.5220/0012209900003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 273-280

ISBN: 978-989-758-670-5; ISSN: 2184-2809

273

Figure 1: Overall Block Diagram of the CFRLI-IDM Method: We utilize counterfactual inference to deduce the braking

intensity of the lead vehicle and the acceptable braking intensity for the following vehicle. This enables the formulation of

an optimization problem that incorporates dynamic constraints. By adopting this approach, we ensure the safety of the ego

vehicle while simultaneously the safety of the following vehicle to the greatest extent possible.

longitudinal control strategy of the unmanned deliv-

ery vehicle), and secondly, we introduce counterfac-

tual reasoning to infer the braking timing and max-

imum braking amount of the front vehicle, and then

the optimization problem based on this inference is

solved to obtain a revised output. Finally, a longitu-

dinal control strategy is obtained to ensure the safety

of the ego vehicle while ensuring the safety of the fol-

lowing vehicle as much as possible.

The proposed fusion of counterfactual inference

and an optimization based approach, has the follow-

ing advantages:

1. Considered the coping strategy when the safety

threshold of the ego vehicle is not satisﬁed

2. A counterfactual reasoning-based method for in-

ferring the braking timing and maximum braking

amount of the preceding vehicle is proposed

3. Building optimization problems based on counter-

factual reasoning rather than hand-designed ﬁxed

constraints improves the adaptability of this algo-

rithm

4. The solution to the problem can be obtained by

analytical solution, reducing the dependence on

complex optimizers

In the rest of this paper, Section 2 introduces the

RSS model and the method of SafeIDM model, Sec-

tion 3 introduces the deﬁnitions of two hypotheses

used in counterfactual reasoning and related coun-

terfactual reasoning method, Section 4 formulates

the optimization problem for our longitudinal control

strategy of the unmanned delivery vehicle, and the al-

gorithm is given in Section 5, Section 6 describes the

design of the simulation scenario and the results of

our method, and ﬁnally, Section 7 concludes the pa-

per.

2 SafeIDM MODEL

2.1 IDM Model

The IDM model is a longitudinal dynamic model pro-

posed by Martin Treiber and Arne Kesting in 2010 for

microscopic trafﬁc ﬂow simulation (Treiber and Kest-

ing, 2010). Due to its low parameter count, strong in-

terpretability and smooth acceleration output, it has

been widely used in both simulation scenario gen-

eration and real-world vehicle testing over the past

decade. The acceleration calculation formula is as fol-

lows:

IDM

(s,v,∆v) =

= a[1 −(

)

−(

∗

(v,∆v)

)

] (1)

In this formula, a

IDM

represents the acceleration

calculated based on the IDM model, s represents the

distance between the ego vehicle and the front vehi-

cle, v represents the speed of the ego vehicle, ∆v rep-

resents the speed difference between the ego vehicle

and the front vehicle, a represents the desired accel-

eration, v

represents the desired speed, s

∗

(v,∆v) =

+ vT +

v∆v

√

represents the desired safe distance,

and δ represents a parameter.

The IDM model generally works well in the ma-

jority of cases, but there are exceptions, and the ag-

gressive cut-in problem discussed in this article is one

of them. From the acceleration calculation formula

of the IDM model, it can be observed that in aggres-

sive cut-in situations, the front vehicle distance s be-

comes very small, while the desired safe distance is

related to the ego vehicle’s own speed and the param-

eter T. Once the speed is high (resulting in a larger

desired safe distance), the term−(

∗

(v,∆v)

)

outputs a

large negative value, which leads to abrupt braking of

the vehicle.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

274

To improve the IDM model, we introduce the

RSS (Responsibility-Sensitive Safety) model and use

it to calculate a more reasonable desired safe distance

(Shalev-Shwartz et al., 2017) (Shalev-Shwartz et al.,

2018).

2.2 RSS Model

Deﬁnition 1. (Safe longitudinal distance — same di-

rection) A longitudinal distance between a car c

that

drives behind another car c

, where both cars are

driving at the same direction, is safe w.r.t. a response

time ρ if for any braking of at most a

max,brake

per-

formed by c

, if c

will accelerate by at most a

max,accel

during the response time and from there on will brake

by at least a

min,brake

until a full stop then it won’t col-

lide with c

Lemma 2. Let c

be a vehicle which is be-

hind c

on the longitudinal axis. Let ρ,

max,brake

max,accel

min,brake

be as in Deﬁnition 1.

Let v

be the longitudinal velocities of the cars.

Then, the minimal safe longitudinal distance between

the front-most point of c

and the rear-most point of

is:

min



ρ +

max,accel

+ρa

max,accel

)

min,brake

−

max,brake



(2)

2.3 SafeIDM

According to the deﬁnition of the minimum longitu-

dinal safe distance in RSS, it is possible for the min-

imum safe distance d

min

to be very small when the

current front vehicle speed is high. Using this deﬁ-

nition of safe distance can greatly improve the issue

of abrupt braking caused by high speed but small cut-

in distances front vehicle in the original IDM model.

The desired following distance in SafeIDM can be de-

ﬁned as follows:

∗

= 1.1 ∗d

min

+ s

(3)

Compared to the original IDM model, the

SafeIDM model provides a more reasonable acceler-

ation output when dealing with aggressive cut-in sit-

uations. However, this does not guarantee the safety

of the vehicle since the IDM model assumes that the

acceleration output is highly smoothed (typically us-

ing a fourth-order approximation). Additionally, the

SafeIDM model does not consider the safety of the

rear vehicle. We will discuss viable methods for en-

suring safety in longitudinal safety model in Chapter

4 and provide the complete algorithm in Chapter 5.

3 COUNTERFACTUAL

INFERRENCE

The longitudinal safety distance of an unmanned de-

livery vehicle is inﬂuenced by various factors, Fig.

2. In the context of this article, inferring the maxi-

mum braking amount of the front vehicle can signiﬁ-

cantly contribute to determining an effective strategy

for the ego vehicle to adopt.To address this concern,

we present two hypotheses:

Hypothesis 1. When the front vehicle merges into

the lane occupied by the ego vehicle, it is essential

to consider the potential occurrence of accidents and

the associated liability concern. If, during the merg-

ing maneuver, the distance between the front vehicle

and the ego vehicle is too small, and the front vehicle

abruptly applies the brakes (resulting in a calculated

minimum longitudinal safety distance exceeding the

current distance), the responsibility for the ensuing

accident does not rest with the ego vehicle(as this can

be categorized as a deliberate collision).

Hypothesis 2. When following the ego vehicle, the

rear vehicle should consider the maximum braking

amount that the ego vehicle may adopt to maintain

a safe distance as much as possible. Compared with

unmanned delivery vehicles, human drivers have rich

driving experience in complex interaction scenarios,

such as aggressive cut-in scenario. Therefore, human

drivers adopt the practice of closely following due to

the presumption that, in this situation, the ego vehi-

cle does not require the implementation of excessive

braking strategies (in the vast majority of cases).

Based on Hypothesis 1, we can deduce the max-

imum braking amount that the front vehicle can uti-

lize in aggressive cut-in scenarios by solving the fol-

lowing equation in reverse, resulting in the calculated

min

exactly matching the current longitudinal dis-

tance between the ego vehicle and the front vehicle.

Similarly, based on Hypothesis 2, we can deduce

the maximum braking amount that the rear vehicle as-

sume the ego vehicle may take.

In order to not always use the worst-case assump-

tion, we propeses a graded risk strategy for the in-

ferrence of the braking amount of the front vehicle,

which means the braking behavior can be happend in

the condition of the longitudinal safety distance is sat-

isﬁed when the braking amount is in the set of [-0.5,

-1, -1.5, -2.0, -2.5, -3, -3.5, -4.0, -4.5, -5] as small as

possible(from the perspective of absolute values), if

the longitudinal distance between the ego vehicle and

the front vehicle is larger than the longitudinal safe

distance calculated by the assumption of the front ve-

hicle would brake at the maximum braking amount of

CFRLI-IDM: A Counterfactual Risk Level Inference Based Intelligence Driver Model for Extremely Aggressive Cut-in Scenario in China

275

Figure 2: Operation Scenario.

-5, the maximum braking amount of the front vehicle

would be assumpted as -5, and then the longitudinal

risk level of the ego vehicle is calculated based on this

inference result.

4 LONGITUDINAL SAFETY

MODEL

4.1 Optimization Problem

To ensure that the acceleration output of the ego ve-

hicle satisﬁes the safety constraints, we need to con-

sider the output of the SafeIDM model from previous

steps as the initial guess for the problem. Based on

counterfactual inference, we can obtain the minimum

safety distance and the acceptable risk level threshold

for the ego vehicle. Using these values, we construct

the optimization problem as follows:

argmin

∥

a −a

ini

∥

s.t. c(s,a) ≤C

(4)

Here, a

ini

represents the output of the SafeIDM

model, and c denotes the longitudinal safety signal.

We represent it as the ratio of the minimum safety

distance to the current distance. c(s,a) =

min

cur

repre-

sents the risk level that will occur at the next moment

when taking action a in the current state. d

ur repre-

sents the current distance. C represents the acceptable

risk level threshold (in this paper, we use C = 1/1.1).

The solution to this optimization problem allows us

to obtain actions that satisfy the risk level threshold

constraints while minimizing changes to the original

actions.

To solve this problem, we can approximate the

dynamic model of the longitudinal risk level using a

ﬁrst-order approximation. This allows us to transform

the optimization problem into a quadratic program-

ming problem, namely:

∗

= argmin

∥

a −a

ini

∥

s.t. c(s)+ g ∗a ≤C

(5)

4.2 Risk Level Dynamic Model

Assuming we have knowledge of the maximum brak-

ing action taken by the preceding vehicle (inferred

from counterfactual reasoning), we can calculate the

minimum safe distance required based on the RSS

model for the current state. Then, based on our def-

inition of risk, we can determine the risk level of the

ego vehicle in the current state. At this point, if we are

given the action taken by the ego vehicle and assume

that the preceding vehicle will brake with the maxi-

mum braking action inferred from counterfactual rea-

soning, we can calculate the state and the risk level

for the next moment (assuming the preceding vehicle

continues to brake with the maximum braking action).

Figure 3: The relationship among speed, acceleration, and

risk level is manifested in the following manner: when con-

sidering the velocities of the ego vehicle and the lead ve-

hicle, as well as the lead vehicle’s braking intensity, the

ego vehicle adapts its acceleration accordingly. As a con-

sequence of this adaptation, there is a linear variation in the

risk level over a brief future timeframe.

To approximate the dynamics of the risk level in

a ﬁrst-order manner, we sample within the range of

accelerations available to the ego vehicle (e.g., with

a step size of 0.1). By doing so, we can obtain the

risk level for the next moment (e.g., at a time inter-

val of 0.2 seconds). By performing linear regression

on this data, we can obtain the ﬁrst-order approxima-

tion coefﬁcient ”g” used in the previous formula. To

achieve a better linear approximation, we normalize

the changes in acceleration and the changes in the risk

levels, the result of this approximation can be seen

in Fig. 3. This involves transforming the aforemen-

tioned ﬁrst-order approximation into an incremental

representation as follows:

c(s

′

) ≈ c(s) + g(s; w)

(6)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

276

′

−c)−min(c

′

−c)

max(c

′

−c)−min(c

′

−c)

acc−min

acc

max

acc

−min

acc

∗g

(7)

When formulating the optimization problem, we

utilize reverse normalization to obtain the constraint

representation of the quadratic programming prob-

lem. This is expressed as follows:

′

= g

a−acc

min

acc

max

−acc

min

∗(max(c

′

−c) −min(c

′

−c)) + c + min(c

′

−c)

(8)

Since the current risk level at the present moment

is a constant, the maximum change in the safety signal

is typically brought about by the ego vehicle apply-

ing the maximum braking action, while the minimum

change in the safety signal is caused by the ego ve-

hicle applying the maximum acceleration. Therefore,

the aforementioned equation can be simpliﬁed as fol-

lows:

′

= g

a−acc

min

acc

max

−acc

min

∗(max(c

′

) −min(c

′

)) + min(c

′

)

(9)

4.3 Optimization Problem Solution

Since the dimensionality of actions in our problem

is one-dimensional, representing the acceleration of

an unmanned delivery vehicle, and the constraint is

a single linear constraint, this optimization problem

can be simpliﬁed to a quadratic function optimization

problem. It can be solved using an analytical solution

to obtain the global optimal solution for the problem

(Dalal et al., 2018).

Firstly, we can write down the Lagrange equation

for the optimization problem based on the constraint

and objective function. The Lagrange equation takes

the following form:

L(a,λ) =

∥

a −a

ini

∥

+ λ ∗(c(s) + g ∗a −C)

(10)

Since both the objective function and the constraint

are convex, the optimal solution to the problem must

satisfy the Karush-Kuhn-Tucker (KKT) conditions,

which are as follows:

▽

L = a

∗

−a

ini

+ λ

∗

∗g = 0

(11)

∗

∗(c + g ∗a

∗

−C) = 0

(12)

Therefore, we obtain the analytical expression for the

optimal solution. If λ=0, then a

∗

= a

ini

. Otherwise,

we have c + g ∗a

∗

−C = 0. Substituting this equation

into equation (11), we can derive:

∗

= [

g ∗a

ini

+ c(s) −C

]

(13)

We have utilized normalization to calculate g and

substituted it into the result of reverse normalization.

As a result, we obtain the ﬁnal computation:

∗

= [

ini

−acc

min

acc

max

−acc

min

∗(max(c

′

)−min(c

′

))+min(c

′

)−C

]

(14)

If λ

∗

= 0, it implies that no adjustments need to

be made to the initial output. Otherwise, the optimal

solution is given by:

∗

= a

ini

−λ

∗

(15)

Due to the analytical form of this solution, we can

conveniently modify the initial values of the SafeIDM

output to ensure that the ﬁnal output meets our accept-

able risk level, without relying on complex optimiz-

ers.

5 ALGORITHM

In this section, the complete solution for the compli-

cate cut-in scenario is proposed, this method is based

on the basic models introduced in the preceding sec-

tions and a method to identify the cut-in intention of

the front vehicle.

Firstly, we use SafeIDM model as the initial lon-

gitudinal control strategy of the unmanned delivery

vehicle and use the deﬁnition of lateral safe distance

which is also deﬁned by the RSS model to recognize

the cut-in vehilce, that is, the front vehicle will be con-

sidered as the cut-in vehilce if the lateral safe distance

between the ego vehicle and the front vehilce is not

satisﬁed, and then the cut-in coping strategy will be

activate.

Secondly, the counterfactual inference method is

used to infer the the braking timing and maximum

braking amount of the front vehicle. If the current

longitudinal risk level is higher than the longitudinal

risk threshhold that we can accept, the same counter-

factual inferrence method is used to infer the maxi-

mum braking amount that the rear vehicle can accept,

then the output acceleration of the ego vehilce will

be equal to a scaling factor less than 1.0 (in this pa-

per, 0.5 is selected) multiply the maximum accept-

able braking amount of the rear vehicle. Otherwise,

an optimization problem is constructed based on the

inference results, and the control quantity given by the

initial strategy is corrected.

We use the longitudinal safety model to correct

the output of the initial longitudinal control policy, if

the corrected output is greater than zero or the abso-

lute value of the output is smaller than the absolute

value of the acceptable maximum braking amount of

the rear vehicle, the output is directly sent to the low-

level control system. Otherwise, the second corrected

output is obtained as the acceptable maximum brak-

ing amount of the rear vehicle is used as the initial

guess of the longitudinal safety model, the samller ab-

solute value of these two outputs is sent to the control

system.

CFRLI-IDM: A Counterfactual Risk Level Inference Based Intelligence Driver Model for Extremely Aggressive Cut-in Scenario in China

277

The steps of the proposed algorithm CFRLI-IDM

can be summarized as follows.

1. Determine whether the lateral safety distance be-

tween the ego vehicle and the front vehicle meets

the requirements, if it is ture, the initial outout is

unchanged, otherwise, go to step 2.

2. Determine whether the longitudinal safety dis-

tance between the ego vehicle and the front vehi-

cle is greater than the needed longitudinal safety

distance calculated at the assumption of the front

vehicle’s maximum braking amount is -0.5, if it is

true, go to step 4, otherwise, go to step 3.

3. Obtain the acceptable maximum braking amount

of the rear vehicle using the counterfactual in-

ferrence mothod, and output 0.5 multiply this

amount.

4. Determine the maximum braking amount of the

front vehicle, and obtain the output of longitudi-

nal safety model, if the output is greater than zero

or its absolute value is smaller than the absolute

value of the acceptable maximum braking amount

of the rear vehicle, send the output to control sys-

tem, otherwise, go to step 5.

5. Use the acceptable maximum braking amount of

the rear vehicle as the initial guess as the opti-

mization control problem, and output the smaller

absolute value between this output and the output

of step 4.

6 EXPERIMENT

We consider an aggressive cut-in scenario, where the

initial speed of ego vehicle is 3m/s, the initial speed

of front vehicle is 5m/s, so the front vehicle will take

over ego vehicle and then take the cut-in action, after a

few moment, the front vehicle braking with a random

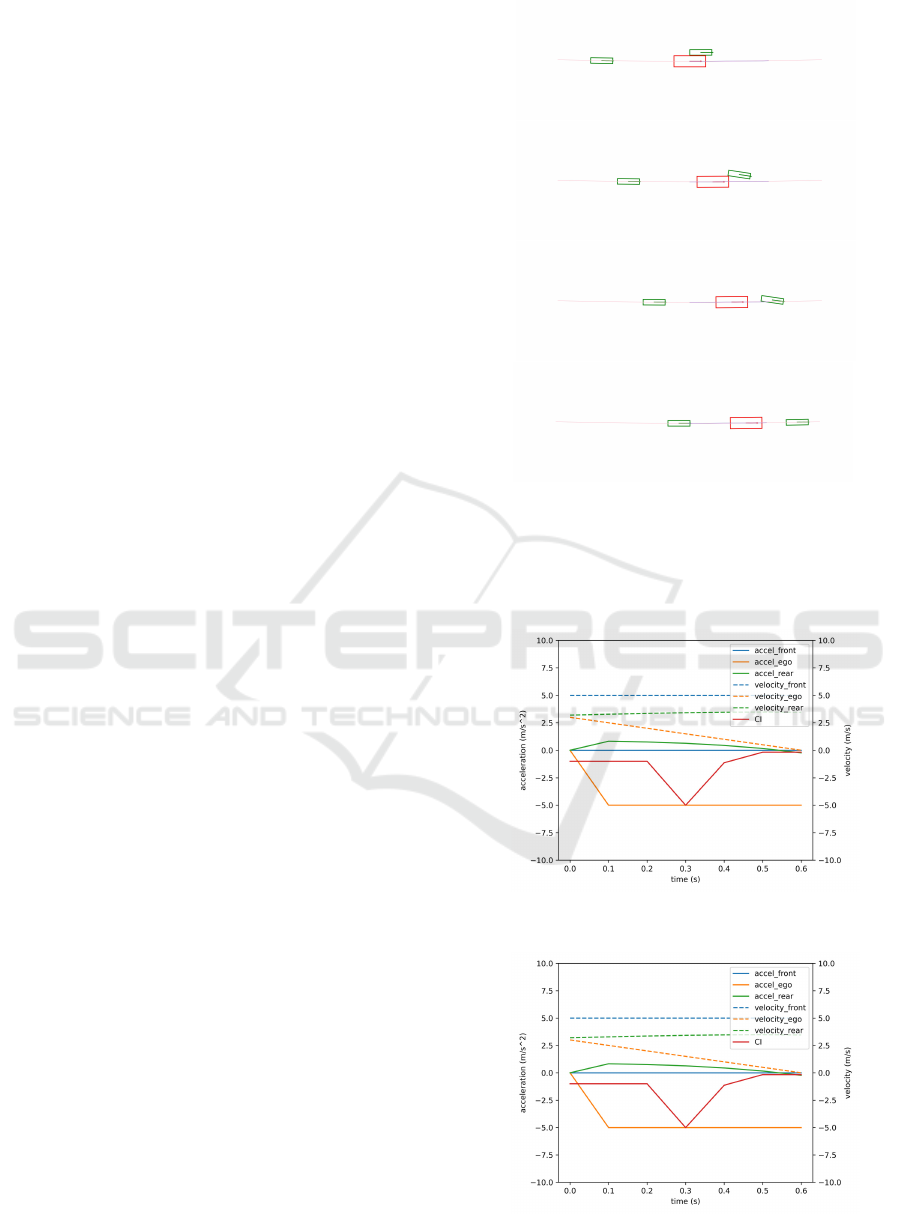
deceleration between -1 and -5, See Fig. 4.

Since the high risk in the scene is mainly related to

the acceleration output by the ego vehicle, we tested

the acceleration control amount given by different al-

gorithms (IDM, SafeIDM, longitudinal safety model,

CFRIL-IDM), as shown in Fig. 5 to Fig. 11.

It can be seen that although in the original IDM

model, we used a very small T=0.5s, when the aggres-

sive cut-in occurs, the IDM model still gives a large

amount of braking, far exceeding the rear car toler-

ance level, Fig. 5. Since then, the IDM model lacks

protection against the possible sudden braking of the

vehicle in front, so it has been in a high-risk area, Fig.

11.

SafeIDM performs better than the original IDM

when the vehicle in front has a certain cut-in distance,

Figure 4: The simulation scenario involves three vehicles,

namely the front vehicle, rear vehicle, and ego vehicle. In

this scenario, the front vehicle performs an abrupt brak-

ing action after performing a cut-in maneuver from the left

side of the ego vehicle. The ego vehicle’s longitudinal con-

trol strategy adopts the CFRLI-IDM model, while the IDM

model is utilized for the longitudinal control of the rear ve-

hicle.

Figure 5: IDM model gives very large amount of breaking

in extreme condition.

Figure 6: Both the SafeIDM and IDM models are inefﬁcient

in dealing with extreme situations.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

278

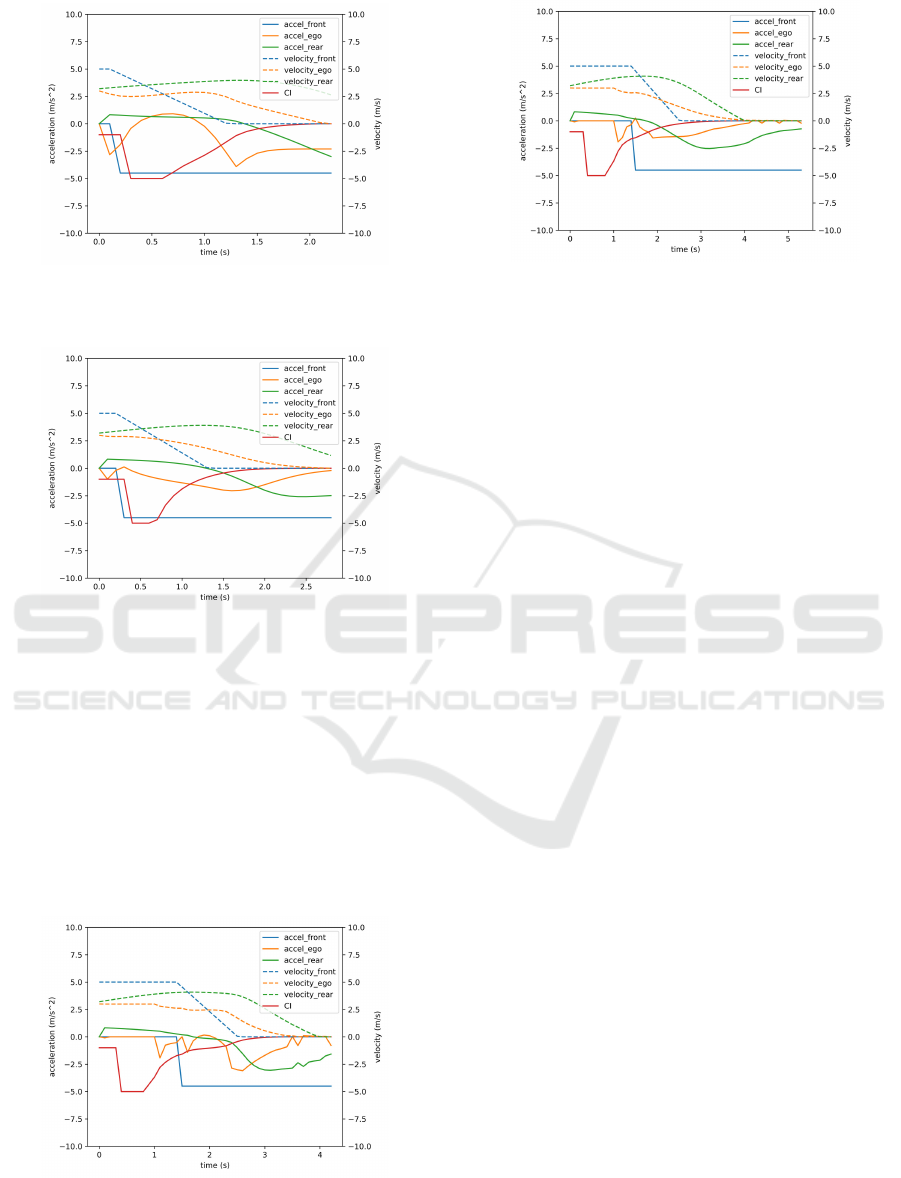
Figure 7: Under non-extreme conditions, the IDM model

produces excessive braking levels beyond the acceptable

range for the rear vehicle.

Figure 8: The SafeIDM model outperforms the IDM model

in non-extreme situations by providing smoother braking

levels for ego vehicle.

Fig. 7, Fig. 8, but it is difﬁcult for SafeIDM to give

a good solution when the vehicle in front is too ag-

gressive, such as the detection distance is less than

0.1 meters, Fig. 6.The longitudinal safety model per-

forms well when the vehicle in front cuts in, but as the

vehicle in front brakes suddenly, in order to ensure the

safety of the ego vehicle, the amount of braking given

is still beyond the tolerance of the vehicle behind, Fig.

9. In addition, due to the adoption of the worst-case

Figure 9: The longitudinal safety model outperforms the

conventional IDM model in emergency situations but lacks

sufﬁcient protection for the rear vehicle.

Figure 10: The CFRLI-IDM model effectively protects both

the ego vehicle and the rear vehicle in emergency situations.

assumption for the vehicle in front, the response was

not timely, resulting in the risk level not being con-

trolled below the threshold of its own acceptable risk

level, Fig. 11. As a comparison, the CFRIL-IDM

model has always considered the safety of the rear ve-

hicle. Compared with other models, it has the small-

est violation of the expectation of the rear vehicle, and

gradually makes the braking amount of the ego vehi-

cle consistent with the expectation of the rear vehicle,

Fig. 10. At the same time, its own risk level is gradu-

ally reduced below the risk threshold, Fig. 11.

7 CONCLUSION

We propose a coping strategy for aggressive cut-in

scenarios during rush hours in China by leveraging

counterfactual inference. This strategy aims to en-

hance the adaptability of unmanned delivery vehi-

cles operating in complex urban environments. Our

method demonstrates the successful application of

causal reasoning within unmanned delivery scenarios.

By employing causal inference, we acquire dynamic

constraints for optimizing vehicle cooperation and

signiﬁcantly reduce the likelihood of rear-end colli-

sions, a prevalent issue found in accident reports from

Waymo. While our method performs effectively in

this scenario, there is room for improvement through

data-driven approaches. These approaches can be uti-

lized to obtain a more reﬁned initial strategy or in-

corporate additional information, such as the acceler-

ation of the front-front vehicle (Pourabdollah et al.,

2017; Chen et al., 2023). Further research can ex-

plore these aspects to enhance the capabilities of our

proposed strategy.

CFRLI-IDM: A Counterfactual Risk Level Inference Based Intelligence Driver Model for Extremely Aggressive Cut-in Scenario in China

279

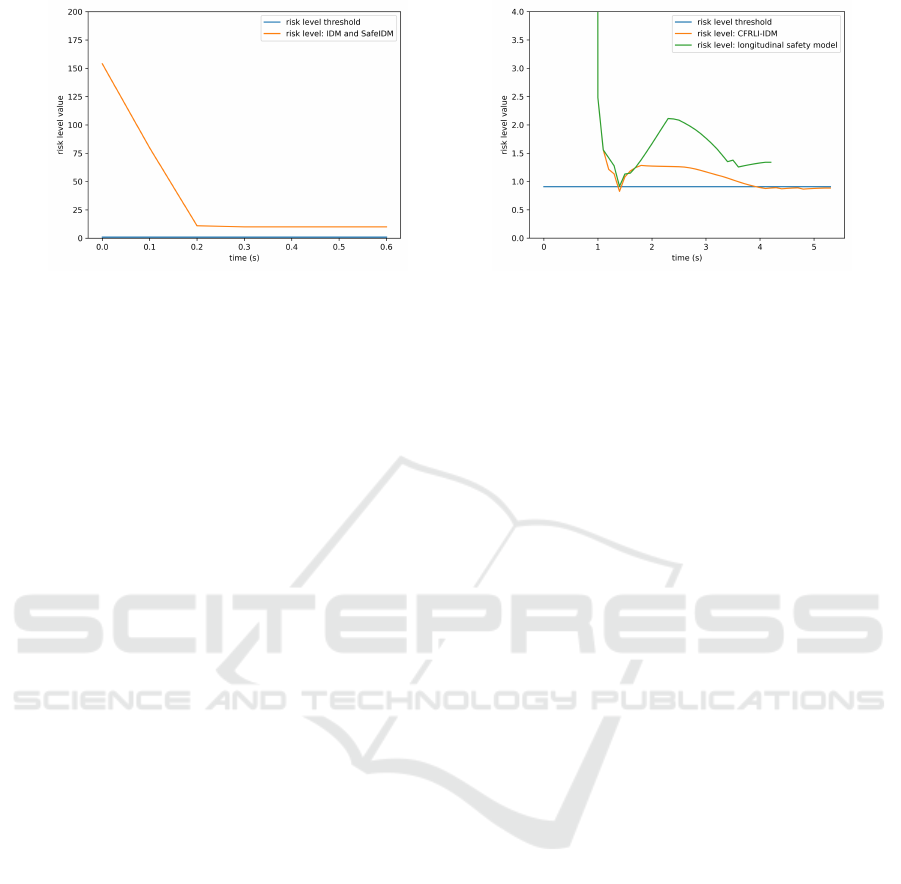
Figure 11: The IDM model and SafeIDM model cannot eliminate the risk of sudden braking from the front vehicle, while the

longitudinal safety model partially reduces the risk but does not eliminate it completely. In contrast, the CFRLI-IDM model

maintains a lower risk level during cut-in situations and gradually eliminates the risk of sudden braking from the front vehicle.

REFERENCES

Bageshwar, V. L., Garrard, W. L., and Rajamani, R. (2004).

Model predictive control of transitional maneuvers for

adaptive cruise control vehicles. IEEE Transactions

on Vehicular Technology, 53(5):1573–1585.

Chen, X., Zhu, M., Chen, K., Wang, P., Lu, H., Zhong, H.,

..., and Wang, Y. (2023). Follownet: A comprehen-

sive benchmark for car-following behavior modeling.

arXiv preprint arXiv:2306.05381.

Dalal, G., Dvijotham, K., Vecerik, M., Hester, T., Paduraru,

C., and Tassa, Y. (2018). Safe exploration in continu-

ous action spaces. arXiv preprint arXiv:1801.08757.

Li, B., Liu, S., Tang, J., Gaudiot, J. L., Zhang, L., and Kong,

Q. (2020). Autonomous last-mile delivery vehicles in

complex trafﬁc environments. Computer, 53(11):26–

35.

Pourabdollah, M., Bj

arkvik, E., F

urer, F., Lindenberg, B.,

and Burgdorf, K. (2017). Calibration and evaluation

of car following models using real-world driving data.

In In 2017 IEEE 20th International conference on

intelligent transportation systems (ITSC), pages 1–6.

IEEE.

Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2017).

On a formal model of safe and scalable self-driving

cars. arXiv preprint arXiv:1708.06374.

Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2018).

Vision zero: can roadway accidents be eliminated

without compromising trafﬁc throughput. arXiv

preprint.

Treiber, M. and Kesting, A. (2010). An open-source micro-

scopic trafﬁc simulator. IEEE Intelligent Transporta-

tion Systems Magazine, 2(3):6–13.

Yoon, Y., Kim, C., Lee, J., and Yi, K. (2021). Interaction-

aware probabilistic trajectory prediction of cut-in ve-

hicles using gaussian process for proactive control of

autonomous vehicles. IEEE Access, 9:63440–63455.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

280