Fixed-Time Tracking Control for a Class of Nonlinear Systems via

Command Filtered Backstepping

Wen-Nian Qi

1 a

and Rui-Qi Dong

2,∗

School of Mechanical Engineering and Automation, Harbin Institute of Technology (Shenzhen), Shenzhen, P.R. China

School of Mechanical Engineering, Tsinghua University, Beijing, P.R. China

Keywords:

Nonlinear Systems, Fixed-Time Stability, Command Filtered Backstepping.

Abstract:

The ﬁxed-time tracking control problem is addressed for a class of nonlinear systems. A novel command

ﬁltered backstepping control law including virtual control signals, ﬁxed-time command ﬁlters, and error com-

pensation signals is constructed. By the introduced ﬁxed-time command ﬁlters, the problem of “explosion of

complexity” caused by backstepping approach is avoided. Simultaneously, the ﬁltering errors produced by the

introduced ﬁxed-time command ﬁlters are eliminated by the designed error compensation signals. It is proven

that the resulted closed-loop tracking control system under the proposed command ﬁltered backstepping con-

trol law is ﬁxed-time stable.

1 INTRODUCTION

The control of nonlinear systems has been widely in-

vestigated, and many effective control methods, in-

cluding backstepping control (Kanellakopoulos et al.,

1991; Morawiec et al., 2020; Mazenc and Bliman,

2006), adaptive control (Tang et al., 2003), neural

network control (Wang and Huang, 2005), etc, have

been proposed. Among these control methods, the

backstepping technique is widely utilized due to its

superiority in dealing with mismatched uncertainties

and disturbances (Kanellakopoulos et al., 1991). In

recent works (Feng et al., 2020; Zhao et al., 2021;

Tong et al., 2020), the backstepping approach was

further incorporated with ﬁnite-time control, fault-

tolerant control, and adaptive control. It should be

noted that the backstepping control needs to construct

virtual control laws step by step, and the derivative of

virtual control signal in the last step is required to con-

struct the virtual control law in the current step. Ac-

cordingly, repeatedly differentiating the virtual con-

trol signals causes the problem of “explosion of com-

plexity” (Chen and Wang, 2021; Swaroop et al.,

2000), and the complexity becomes severe especially

for high-order dynamics. To address this problem, a

dynamic surface control (DSC) approach was ﬁrstly

proposed in (Swaroop et al., 2000) to avoid differenti-

https://orcid.org/0000-0002-4627-1151

∗

Corresponding author.

ating virtual control signals by introducing ﬁrst-order

ﬁlters in the backstepping design procedure. A draw-

back of DSC is that the ﬁltering errors caused by the

introduced ﬁrst-order ﬁlters are ignored. To compen-

sate the ﬁltering errors, a command ﬁltered backstep-

ping was proposed in (Farrell et al., 2009), where the

command ﬁlters were used to approximate the deriva-

tives of virtual control signals, and the compensation

mechanism were proposed to reduce the inﬂuence of

ﬁltering errors. Further, the command ﬁltered back-

stepping was united with adaptive technique or neural

network approximation method in (Dong et al., 2011;

Shen and Shi, 2015), respectively, to eliminate the in-

ﬂuence of uncertain nonlinearities.

The aforementioned command ﬁltered backstep-

ping control algorithms in (Farrell et al., 2009; Dong

et al., 2011; Shen and Shi, 2015) merely achieve

inﬁnite-time convergence property of the closed-loop

system. From the practical point of view, many en-

gineering systems are often required to achieve fast

tracking control in ﬁnite time. In view of this require-

ment, ﬁnite-time control methods combining with

command ﬁltered backstepping technique have been

developed for many nonlinear systems. Typical works

can be found in (Yu et al., 2018; Li, 2019; Fu et al.,

2020; Wang et al., 2019; Cheng et al., 2023; Wang

et al., 2021). In (Yu et al., 2018), the ﬁnite-time com-

mand ﬁltered backstepping tracking controller was

constructed for a class of nonlinear systems in strict-

feedback form. In (Li, 2019), the parametric uncer-

Qi, W. and Dong, R.

Fixed-Time Tracking Control for a Class of Nonlinear Systems via Command Filtered Backstepping.

DOI: 10.5220/0012210200003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 50-57

ISBN: 978-989-758-670-5; ISSN: 2184-2809

tainties and actuator faults were taken into considera-

tion, and the ﬁnite-time tracking control law was de-

veloped by adaptive command ﬁltered backstepping

approach. In (Fu et al., 2020), the tracking control for

uncertain switched nonlinear systems was considered,

and a neural-network based command ﬁltered back-

stepping controller was developed to achieve ﬁnite-

time convergence of the closed-loop system. It should

be pointed out that the initial conditions of the system

limit the settling time ensured by ﬁnite-time control

approaches (Guo et al., 2021). To solve the problem

of initial condition dependence, the ﬁxed-time con-

trol approach, which can guarantee that settling time

is only depended on the parameters of the closed-loop

system, have been developed for various control sys-

tems. In (Tian et al., 2017; Su and Zheng, 2019), the

ﬁxed-time control laws were constructed to stabilize

second-order systems. In (Tian et al., 2018), the back-

stepping control approach was applied for high-order

integrator systems, and the ﬁxed-time tracking control

was achieved. To our knowledge, the ﬁxed-time com-

mand ﬁltered backstepping tracking control is barely

investigated for high-order nonlinear systems.

Motivated by the aforementioned discussions, the

tracking control for a class of nonlinear systems is in-

vestigated in this paper. The control objective of this

paper is to construct a control law such that the output

of the nonlinear system can track a reference signal in

ﬁxed time. To achieve this control goal, a new ﬁxed-

time command ﬁltered backstepping control method

is proposed. Compared with most existing works, the

main contributions are presented as follows.

(1) The proposed control law is constructed by

combining ﬁxed-time control approach and command

ﬁltered backstepping technique. Compared with the

contribution in (Yu et al., 2018), in which the track-

ing error converges to a region around the origin in ﬁ-

nite time, the proposed control law in this work makes

sure that the tracking error converges to the origin in

ﬁxed time.

(2) The ﬁxed-time ﬁlter is introduced to replace

the ﬁnite-time ﬁlter in (Yu et al., 2018; Li, 2019; Fu

et al., 2020; Wang et al., 2019; Cheng et al., 2023;

Wang et al., 2021). Therefore, the output of the intro-

duced ﬁxed-time ﬁlter can estimate the derivative of

the virtual control law and the problem of “explosion

of complexity” is obviated.

(3) Compared with (Yu et al., 2018; Li, 2019; Fu

et al., 2020; Wang et al., 2019; Cheng et al., 2023;

Wang et al., 2021), novel compensation mechanism

is constructed to timely reduce the negative effect of

the ﬁltering error.

The rest of this paper is organized as follows. The

system description and preliminaries are provided in

Section 2. The control law design and stability anal-

ysis are presented in Section 3. An example is con-

ducted in Section 4 to verify the effectiveness and

advantages of the proposed control law. Finally, the

conclusion of this paper is drawn in Section 5.

Notations. Throughout this paper, R denotes the

real number, R

denotes the n dimensional real vector,

and

denotes the absolute value. For two integers

a ≤ b, I[a,b] denotes the set

{

a, a + 1, ..., b

}

. For

any scalar x ∈ R, deﬁne sig

(x) =sign(x)

where

sign(·) is the standard sign function. For any vector

x = [x

··· x

]

∈ R

∥

is the 2-norm of the vec-

tor x. Furthermore, deﬁne

sign(x) = [sign(x

) sign(x

) ·· · sign(x

)]

and

sig

(x) = [sig

) sig

) ·· · sig

)]

2 SYSTEM DESCRIPTION AND

PRELIMINARIES

Consider the following n-th order nonlinear systems

˙x

= f

(¯x

) + g

(¯x

i+1

˙x

= f

(x) + g

(x)u

y =x

(1)

where i ∈ I[1,n − 1], x = [x

·· · x

]

∈ R

is the

state vector, ¯x

= [x

·· · x

]

∈ R

; u ∈ R and y ∈ R

are the input and output of the system, respectively.

The functions f

(·) and g

(·), i ∈ I[1,n], are assumed

to be known. Denote the reference signal and its ﬁrst-

order derivatives by y

∈ R, ˙y

∈ R, respectively. Both

and ˙y

are assumed to be bounded and known.

The control objective of this paper is to construct

the control law u for system (1) such that the output

y tracks the reference signal y

in a ﬁxed time. The

following assumption on the n-th order nonlinear sys-

tems (1) is presented.

Assumption 1. For system (1), there exists an open

set Ω

⊂ R

which includes the origin and the initial

condition x (0). (1) f

(m)

(·) and g

(m)

(·) are bounded

in the closed set

Ω

for i ∈ I[1,n − 1], m ∈ I[1, n − i];

(2) f

(·) and g

(·) and their ﬁrst-order derivatives

are bounded in the closed set

Ω

In what follows, some useful deﬁnitions and lem-

mas are introduced.

Lemma 1. (Hardy et al., 1952) For x

> 0, i ∈ I[1,N]

Fixed-Time Tracking Control for a Class of Nonlinear Systems via Command Filtered Backstepping

there holds

∑

i=1

≥

∑

i=1

, if 0 < γ ≤ 1,

∑

i=1

≥ n

1−γ

∑

i=1

, if γ > 1.

Considered an autonomous system

˙x = f (x, u) , x (0), x ∈ U ⊂ R

, (2)

where f : U × R

→ R

is continuous on an open

neighborhood U of the origin x = 0. Suppose for any

initial condition x (0) ∈ U, there is a unique solution

x (t,x (0)) of system (2).

Lemma 2. (Polyakov, 2012) For the system (2), if

there is a Lyapunov function V (x) with initial value

V (x (0)), and some real numbers a > 0, b > 0, 0 <

p < 1, and q > 1, such that

V (x) ≤ −aV

−bV

, then

the origin of the system (2) is ﬁxed-time stable, and

the convergence time is bounded by

T ≤

a(1 − p)

b(q − 1)

3 CONTROL LAW DESIGN AND

STABILITY ANALYSIS

In this section, a command ﬁltered backstepping con-

trol law is constructed for the system (1) to ensure

that the output y tracks the reference signal y

in a

ﬁxed time, and the ﬁxed time stability of the closed-

loop system are analysed theoretically.

3.1 Control Law Design

Following the command ﬁltered backstepping ap-

proach, the coordinate transformation is introduced as

= y −y

, (3)

= x

−

, (4)

where i ∈ I[2,n], and

is the output of a ﬁxed-time

command ﬁlter with the virtual control law α

as the

input. The ﬁxed-time command ﬁlter is introduced as

follows.

(

=−λ

sig

(

−α

)−λ

sig

(

− α

)+φ

=−λ

sign



−



−λ

sig

2γ−1

(

−α

(5)

where i ∈ I[2,n], γ > 1, and λ

, λ

, and λ

are positive parameters. The ﬁxed time convergence

property of the signals

and ϕ

are shown in the fol-

lowing Lemma.

Lemma 3. (Basin et al., 2017) For the system (5)

with α

as the input signal, and positive parameters

, λ

, and γ > 1, the outputs

and ϕ

converge to α

and

in a ﬁxed time, respectively.

In what follows, the details of the ﬁxed-time com-

mand ﬁltered backstepping control law design are

presented in n steps.

Step 1: design of virtual control law α

. From (1)

and (3), the time derivative of z

˙z

= f

+ g

− ˙y

= f

+ g

−

− α

+ α

) − ˙y

= f

+ g

− α

+ α

) − ˙y

. (6)

When we construct virtual control law α

, a compen-

sation mechanism is needed to reduce the inﬂuence of

the ﬁltering error

− α

. The compensation signal

is proposed as

= − l

sig

(ξ

) − l

sig

(ξ

)

+ g

(

− α

) + g

, (7)

where l

> 0, l

> 0, 0 < p < 1, and q > 1 are some

designed parameters. ξ

is another compensation sig-

nal to reduce the inﬂuence of the error

− α

, and

will be designed in the next step.

Deﬁne the compensated tracking errors as

= z

− ξ

, (8)

= z

− ξ

. (9)

By using (6) and (7), the time derivative of χ

=˙z

−

(χ

+ α

) + f

− ˙y

+ l

sig

(ξ

) + l

sig

(ξ

). (10)

For the ﬁrst subsystem composed of (7) and (10),

a Lyapunov candidate function can be chosen as

. (11)

Taking the time derivative of V

yields

=χ

+ ξ

=χ

+ g

+ f

− ˙y

+ l

sig

(ξ

)

sig

(ξ

)) + ξ

(−l

sig

(ξ

)

−l

sig

(ξ

) + g

(

− α

) + g

). (12)

Then for the ﬁrst subsystem composed of (7) and (10),

a virtual control law α

can be constructed as

(−k

sig

(χ

)−k

sig

(χ

)+ ˙y

− f

), (13)

where k

> 0 and k

> 0 are some designed param-

eters.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

Substituting (13) into (12) yields

= − k

1+p

− k

1+q

+ g

+ l

sig

(ξ

) + l

sig

(ξ

) − l

1+p

− l

1+q

+ g

(

− α

)ξ

+ g

. (14)

Step i, i ∈ I[2,n − 1]: design of virtual control law

i+1

. From (1) and (4), the time derivative of z

˙z

= f

+ g

i+1

−

= f

+ g

i+1

− α

i+1

+ α

i+1

) −

. (15)

Proceeding similarly, to reduce the inﬂuence of the

ﬁltering error

i+1

−α

i+1

, the compensation signal ξ

is designed as

= − l

sig

(ξ

) − l

sig

(ξ

) + g

(

i+1

− α

i+1

)

+ g

i+1

− g

i−1

, (16)

where l

> 0 and l

> 0 are some designed param-

eters, and ξ

i+1

is another compensation signal to re-

duce the inﬂuence of the error

i+2

− α

i+2

in the next

step.

Deﬁne the compensated tracking errors as

− ξ

, (17)

i+1

− ξ

i+1

, (18)

By using (15) and (16), the time derivative of χ

i+1

+ f

−

+ l

sig

(ξ

) + l

sig

(ξ

)

+ g

i+1

+ g

i−1

. (19)

For the i-th subsystem composed of (16) and (19),

a Lyapunov candidate function can be chosen as

. (20)

From (16) and (19), the time derivative of V

is ob-

tained as

=χ



i+1

+ f

−

+ l

sig

(ξ

) + l

sig

(ξ

)

i+1

i−1

)+ξ

(−l

sig

(ξ

)−l

sig

(ξ

)

(

i+1

− α

i+1

) + g

i+1

− g

i−1

). (21)

Then the virtual control law α

i+1

can be constructed

i+1

(−k

sig

(χ

) − k

sig

(χ

)

− f

− g

i−1



, (22)

where k

> 0 and k

> 0 are some designed parame-

ters.

Substituting (22) into (21) yields

= − k

1+p

− k

1+q

− l

1+p

− l

1+q

+ l

sig

(ξ

) + l

sig

(ξ

) + g

i+1

− g

i−1

+ g

(

i+1

− α

i+1

)ξ

+ g

i+1

− g

i−1

. (23)

Step n: design of actual control law u. The time

derivative of z

˙z

= f

+ g

u −

. (24)

The compensation signal ξ

is designed as

= −l

sig

(ξ

) − l

sig

(ξ

) − g

n−1

. (25)

where l

> 0 and l

> 0 are some designed param-

eters. The compensated tracking error χ

is deﬁned

= z

− ξ

. (26)

By using (24) and (25), the time derivative of χ

u + f

−

+ l

sig

(ξ

) + l

sig

(ξ

)

+ g

n−1

. (27)

For the n-th subsystem composed of (25) and (27),

a Lyapunov candidate function can be chosen as

. (28)

Taking the time derivative of V

yields

= χ



u + f

−

+ l

sig

(ξ

) + l

sig

(ξ

)

n−1

) + ξ

(−l

sig

(ξ

) − l

sig

(ξ

)

−g

n−1

). (29)

Then the virtual control law α

i+1

can be constructed

u =



−k

sig

(χ

) − k

sig

(χ

) +

− f

− g

n−1

). (30)

where k

> 0 and k

> 0 are some designed param-

eters.

Substituting the control law u into (29), yields

=−k

1+p

−k

1+q

−l

1+p

−l

1+q

+ l

sig

(ξ

) + l

sig

(ξ

) − g

n−1

− g

n−1

. (31)

In this subsection, the virtual control laws (13)

and (22) are constructed step by step, and the ﬁxed-

time command ﬁlter (5) are provided to avoid repeat-

edly calculating the time derivative of the virtual con-

trol laws. Besides, the compensation mechanism pro-

vided by (7), (16) and (25) are provided to compen-

sate the ﬁltering errors caused by the ﬁxed-time com-

mand ﬁlter (5). Finally, the actual control law u are

constructed as in (30).

3.2 Stability Analysis

The ﬁxed-time stability of the closed-loop system can

be concluded in the following theorem.

Fixed-Time Tracking Control for a Class of Nonlinear Systems via Command Filtered Backstepping

Theorem 1. For the system (1) satisﬁes Assumption

1, if the ﬁxed-time command ﬁlter is chosen as in (5),

the virtual control laws are constructed as in (13) and

(22), and the compensation mechanism are design as

in (7), (16) and (25), then the control law can be de-

signed as in (30) such that the tracking error z

in (3)

converges to origin in a ﬁxed-time.

Proof. For the closed-loop system, a Lyapunov func-

tion candidate can be selected as

V =

∑

i=1

Then by using (14), (23), and (31), the time deriva-

tive of V is

V = −

∑

i=1



1+p

+ k

1+q



∑

i=1

sig

(ξ

)

sig

(ξ

)) −

∑

i=1



1+p

+ l

1+q



n−1

∑

i=1

(

i+1

− α

i+1

)ξ

. (32)

According to Young’s inequality(Deng and Krsti

1997), there holds

sig

(ξ

) ≤

1 + p

1+p

1 + p

1+p

sig

(ξ

) ≤

1 + q

1+q

1 + q

1+q

. (33)

Substituting (33) into (32) and properly choosing pa-

rameters k

1+p

, k

1+q

, l

1+p

, and l

1+q

, yield

V ≤ −

∑

i=1



1+p

1+q



−

∑

i=1



1+p

1+q



n−1

∑

i=1

(

i+1

− α

i+1

)ξ

(34)

where

= k

−

1+p

= k

−

1+q

= l

−

1+p

and

= l

−

1+q

. Besides, according to Lemma 3,

the ﬁltering error

i+1

− α

i+1

= 0 can be achieved in

a ﬁxed time T

by properly choosing the parameters

, λ

, and γ. Then for t ≥ max{T

}, there

holds

V ≤ −

∑

i=1



1+p



−

∑

i=1



1+q



. (35)

Denoting ϖ

= min

{

}, ϖ

= min

{

}, and

applying Lemma 1, there holds

V ≤ − ϖ

∑

i=1



+ ξ



1+p

− ϖ

1−q

∑

i=1



+ ξ



1+q

= −

1+p

−

1+q

. (36)

where

= 2

1+p

= 2

1+q

1−q

. According

to Lemma 2, inequality (36) implies that χ

= 0 and

= 0, i ∈ I[1,N], are achieved in a ﬁxed time T

which is bounded by

≤ max

{

}

(1 − p)

(q − 1)

Since z

= χ

+ ξ

, then it can be obtained that the

tracking error z

= 0 is achieved in a ﬁxed time T

Thus the proof is completed.

In this section, the ﬁxed-time tracking control law

(30) is constructed based on the virtual control laws,

ﬁxed-time ﬁlters, and compensation mechanism. The

problem of “explosion of complexity” is avoided by

the introduced ﬁxed-time ﬁlter (5). The inﬂuence of

the ﬁltering errors is reduced timely by the proposed

compensation mechanism as in (7) and (25). More-

over, it is proved in Theorem 1 that the ﬁxed-time

tracking performance of the closed-loop system is en-

sured by the proposed control law.

4 SIMULATION RESULTS

In this section, the proposed ﬁxed-time control law

will be compared with the ﬁnite-time control law

in (Yu et al., 2018) via an electromechanical sys-

tem, composed of a single-link manipulator and mo-

tor. The dynamics of electromechanical system is de-

scribed as follows.











D ¨q + B ˙q +Nsin(q) = τ

τ + Hτ = D(u) −K

˙q

y = q

(37)

where q, ˙q, and ¨q are the position, velocity, and accel-

eration of the link, respectively, τ is the motor shaft

angle, and u represent the motor torque. The parame-

ters are chosen as D = 1, B = 1, M = 0.05, H = 0.5,

N = 10, and K

= 10.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

Deﬁne x

= q, x

= ˙q, and x

= τ/D, the dynamics

(37) can be written as











˙x

= x

˙x

= −x

−

sin(x

) +

˙x

+ u

(38)

The reference signal is

= 0.5sin(t) + 0.5sin(0.5t).

The designed parameters of virtual control law,

actual control law, and compensation signals are taken

as k

= k

= 5, p = 0.6, q = 1.05, and l

= l

= 2,

i ∈ I[1, 3].

The initial condition of the system states, com-

mand ﬁlters, and compensation signals are taken as

(0) x

(0)] = [4 3 2],

[

(0) ϕ

(0)] = [0 0],i = 2,3,

[ξ

(0) ξ

(0)] = [0 0 0].

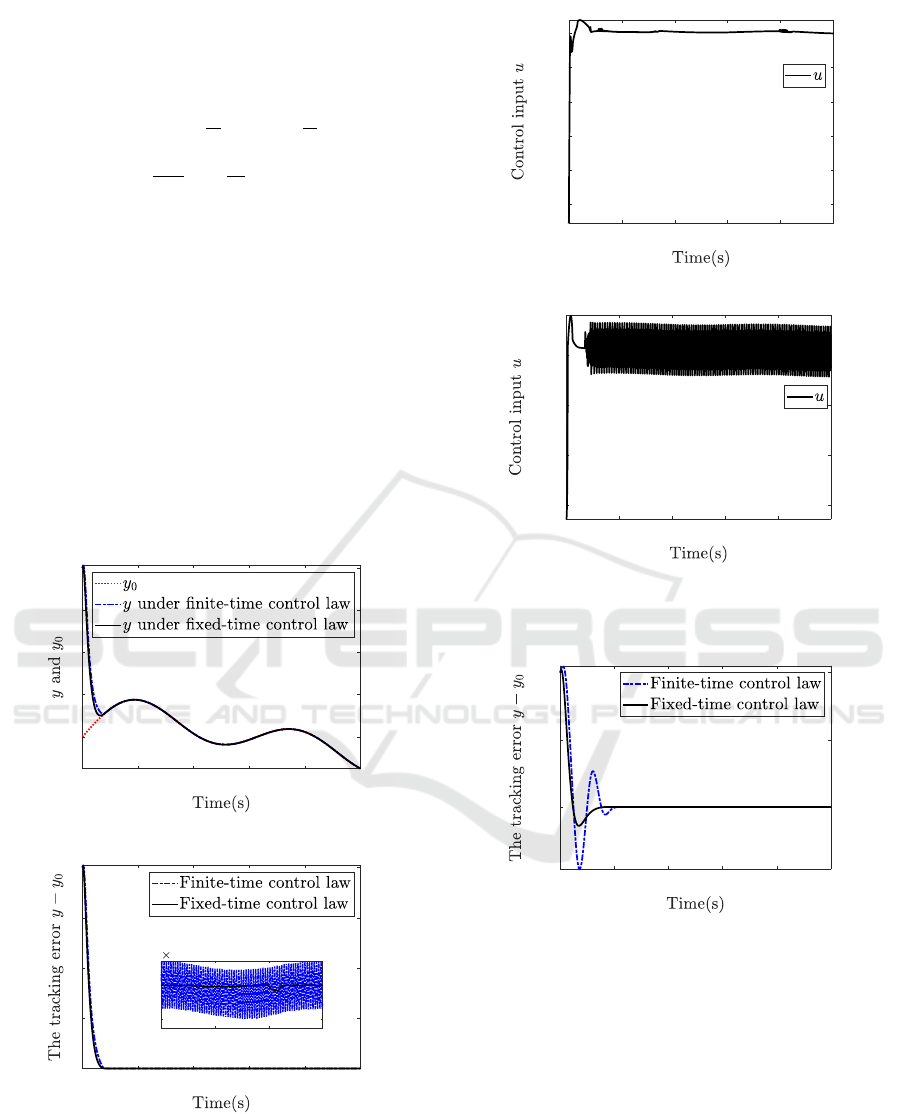
0 2 4 6 8 10

Figure 1: Trajectories of y and y

0 2 4 6 8 10

4 6 8 10

-4

-2

-4

Figure 2: Tracking error y − y

The simulation results are shown in Figures 1-3.

In Figure 1, the tracking performance under the pro-

posed ﬁxed-time command ﬁltered backstepping con-

trol law and ﬁnite-time command ﬁltered backstep-

ping control law in (Yu et al., 2018) are presented.

0 2 4 6 8 10

-500

-400

-300

-200

-100

(a) u under the ﬁxed-time control law in this paper

0 2 4 6 8 10

-300

-200

-100

(b) u under the ﬁnite-time control law in (Yu et al.,

2018)

Figure 3: Control input.

0 2 4 6 8 10

100

Figure 4: Tracking error y − y

for another condition.

Figure 2 depicts the tracking error. Figure 3 shows

the time response of input signal u. From Figure 1 and

2, it can be found that the proposed ﬁxed-time com-

mand ﬁltered backstepping control law in this work

achieves faster convergence rate and better tracking

accuracy than the ﬁnite-time command ﬁltered back-

stepping control law in (Yu et al., 2018). From Figure

3, it is observed that less chattering is suffered under

the proposed ﬁxed-time command ﬁltered backstep-

ping control law.

To better show the superiority of the proposed

ﬁxed-time control law, another initial condition

(0) x

(0)] = [100 75 50]

Fixed-Time Tracking Control for a Class of Nonlinear Systems via Command Filtered Backstepping

is chosen. The tracking errors under such condition

are depicted in Figure 4, from which we can ﬁnd

that the proposed ﬁxed-time tracking control law pos-

sesses faster time response compared with the ﬁnite-

time tracking control law in (Yu et al., 2018) when

the initial condition of the system is far away from

the target value.

5 CONCLUSION

In this paper, a novel ﬁxed-time adaptive command

ﬁltered backstepping control approach is proposed to

solve the tracking control problem for a class of non-

linear systems. According to this approach, a group of

novel virtual control laws and the actual control law

are constructed to achieve the ﬁxed-time convergence

of the closed-loop system. The ﬁxed-time differen-

tiator is introduced to approximate the time derivative

of virtual control laws in a ﬁxed time. The new com-

pensation mechanism is developed to reduce the neg-

ative effect of the ﬁltering error. By using the ﬁxed-

time stability criterion, the ﬁxed-time tracking perfor-

mance of the closed-loop system under the proposed

command ﬁltered backstepping control law is anal-

ysed, and a rigorous theoretical proof is presented.

ACKNOWLEDGEMENTS

This work was supported in part by the National Nat-

ural Science Foundation of China under Grant No.

62203255.

REFERENCES

Basin, M., Yu, P., and Shtessel, Y. (2017). Finite-and ﬁxed-

time differentiators utilising hosm techniques. IET

Control Theory & Applications, 11(8):1144–1152.

Chen, L. and Wang, Q. (2021). Finite-time adaptive neural

dynamic surface control for non-linear systems with

unknown dead zone. IET Control Theory & Applica-

tions, 15(1):40–50.

Cheng, F., Wang, H., Zong, G., Niu, B., and Zhao, X.

(2023). Adaptive ﬁnite-time command-ﬁltered con-

trol for switched nonlinear systems with input quanti-

zation and output constraints. Circuits, Systems, and

Signal Processing, 42(1):147–172.

Deng, H. and Krsti

c, M. (1997). Stochastic nonlinear

stabilization–i: A backstepping design. Systems &

Control Letters, 32(3):143–150.

Dong, W., Farrell, J. A., Polycarpou, M. M., Djapic, V.,

and Sharma, M. (2011). Command ﬁltered adaptive

backstepping. IEEE Transactions on Control Systems

Technology, 20(3):566–580.

Farrell, J. A., Polycarpou, M., Sharma, M., and Dong, W.

(2009). Command ﬁltered backstepping. IEEE Trans-

actions on Automatic Control, 54(6):1391–1395.

Feng, C., Wang, Q., Hu, C., and Zhang, S. (2020). Finite-

time backstepping control with command ﬁlter for a

class of nonlinear systems with parametric uncertain-

ties. Transactions of the Institute of Measurement and

Control, 42(12):2297–2307.

Fu, C., Wang, Q., Yu, J., and Lin, C. (2020). Neu-

ral network-based ﬁnite-time command ﬁltering con-

trol for switched nonlinear systems with backlash-like

hysteresis. IEEE Transactions on Neural Networks

and Learning Systems.

Guo, X., Ma, H., Liang, H., and Zhang, H. (2021).

Command-ﬁlter-based ﬁxed-time bipartite contain-

ment control for a class of stochastic multiagent sys-

tems. IEEE Transactions on Systems, Man, and Cy-

bernetics: Systems.

Hardy, G. H., Littlewood, J. E., P

olya, G., P

olya, G., et al.

(1952). Inequalities. Cambridge university press.

Kanellakopoulos, I., Kokotovic, P. V., and Morse, A. S.

(1991). Systematic design of adaptive controllers for

feedback linearizable systems. In 1991 American con-

trol conference, pages 649–654. IEEE.

Li, Y. (2019). Finite time command ﬁltered adaptive fault

tolerant control for a class of uncertain nonlinear sys-

tems. Automatica, 106:117–123.

Mazenc, F. and Bliman, P.-A. (2006). Backstepping design

for time-delay nonlinear systems. IEEE Transactions

on Automatic Control, 51(1):149–154.

Morawiec, M., Strankowski, P., Lewicki, A., Guzi

nski, J.,

and Wilczy

nski, F. (2020). Feedback control of mul-

tiphase induction machines with backstepping tech-

nique. IEEE Transactions on Industrial Electronics,

67(6):4305–4314.

Polyakov, A. (2012). Nonlinear feedback design for ﬁxed-

time stabilization of linear control systems. IEEE

Transactions on Automatic Control, 57(8):2106–

2110.

Shen, Q. and Shi, P. (2015). Distributed command ﬁltered

backstepping consensus tracking control of nonlinear

multiple-agent systems in strict-feedback form. Auto-

matica, 53:120–124.

Su, Y. and Zheng, C. (2019). Global ﬁxed-time output feed-

back stabilization for a class of double integrator sys-

tems. IEEE Transactions on Circuits and Systems II:

Express Briefs, 67(10):1954–1958.

Swaroop, D., Hedrick, J. K., Yip, P. P., and Gerdes, J. C.

(2000). Dynamic surface control for a class of nonlin-

ear systems. IEEE transactions on automatic control,

45(10):1893–1899.

Tang, X., Tao, G., and Joshi, S. M. (2003). Adaptive ac-

tuator failure compensation for parametric strict feed-

back systems and an aircraft application. Automatica,

39(11):1975–1982.

Tian, B., Lu, H., Zuo, Z., and Wang, H. (2018). Fixed-

time stabilization of high-order integrator systems

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

with mismatched disturbances. Nonlinear Dynamics,

94(4):2889–2899.

Tian, B., Zuo, Z., Yan, X., and Wang, H. (2017). A ﬁxed-

time output feedback control scheme for double inte-

grator systems. Automatica, 80:17–24.

Tong, S., Li, K., and Li, Y. (2020). Robust fuzzy adap-

tive ﬁnite-time control for high-order nonlinear sys-

tems with unmodeled dynamics. IEEE Transactions

on Fuzzy Systems, 29(6):1576–1589.

Wang, D. and Huang, J. (2005). Neural network-based

adaptive dynamic surface control for a class of uncer-

tain nonlinear systems in strict-feedback form. IEEE

transactions on neural networks, 16(1):195–202.

Wang, H., Kang, S., and Feng, Z. (2019). Finite-time adap-

tive fuzzy command ﬁltered backstepping control for

a class of nonlinear systems. International Journal of

Fuzzy Systems, 21:2575–2587.

Wang, K., Liu, X., and Jing, Y. (2021). Adaptive ﬁnite-time

command ﬁltered controller design for nonlinear sys-

tems with output constraints and input nonlinearities.

IEEE Transactions on Neural Networks and Learning

Systems, 33(11):6893–6904.

Yu, J., Shi, P., and Zhao, L. (2018). Finite-time command

ﬁltered backstepping control for a class of nonlinear

systems. Automatica, 92:173–180.

Zhao, D., Jiang, B., and Yang, H. (2021). Backstepping-

based decentralized fault-tolerant control of hyper-

sonic vehicles in pde-ode form. IEEE Transactions

on Automatic Control, 67(3):1210–1225.

Fixed-Time Tracking Control for a Class of Nonlinear Systems via Command Filtered Backstepping