Filter Evolution Using Cartesian Genetic Programming for Time Series

Anomaly Detection

Andreas Margraf

1 a

, Henning Cui

, Stefan Baumann

and J

org H

ahner

Fraunhofer IGCV, Am Technologiezentrum 2, 86159 Augsburg, Germany

University of Augsburg, Universit

atsstraße 2, 86159 Augsburg, Germany

Keywords:

CGP, Evolutionary Learning, Signal Processing, Condition Monitoring, Non-Destructive Testing.

Abstract:

Industrial monitoring relies on reliable and resilient systems to cope with unforeseen and changing envi-

ronmental factors. The identiﬁcation of critical conditions calls for efﬁcient feature selection and algorithm

conﬁguration for accurate classiﬁcation. Since the design process depends on experts who deﬁne parameters

and develop classiﬁcation models, it remains a time-consuming and error-prone task. In this paper, we suggest

an evolutionary learning approach to create ﬁlter pipelines for machine health and condition monitoring. We

apply a method called Cartesian Genetic Programming (CGP) to explore the search space and tune parameters

for time series segmentation problems. CGP is a nature-inspired algorithm where nodes are aligned in a two-

dimensional grid. Since programs generated by CGP are compact and short, we deem this concept efﬁcient

for ﬁlter evolution and parameter tuning to create performant classiﬁers. For better use of resources, we in-

troduce a dependency graph to allow only valid combinations of ﬁlter operators during training. Furthermore,

this novel concept is critically discussed from a efﬁciency and quality point of view as well as its effect on

classiﬁer accuracy on scarce data. Experimental results show promising results which - in combination with

the novel concept - competes with state-of-the-art classiﬁers for problems of low and medium complexity.

Finally, this paper poses research questions for future investigations and experimentation.

1 INTRODUCTION

Production environments depend on reliability and

performance of machinery throughout the workﬂow

to ensure a high level of efﬁciency, quality, and out-

put, to meet customers’ needs. Over the course of

their operational lifespan, machine elements experi-

ence degradation resulting from physical impacts and

varying external conditions. Without countermea-

sures, these effects lead to unexpected failures with

possibly catastrophic consequences for the process

built around these elements. As an intermediary, con-

dition monitoring (CM) allows production machines

to run within a deﬁned tolerance window. CM enables

engineers to closely monitor key parameters along the

processing chain and obtain an up-to-date overall pic-

ture of the state of the entire production cycle. For the

manufacturing industry, detecting oncoming machine

faults helps to reduce unplanned downtime, minimize

repair effort and even decrease replacement expenses.

Furthermore, companies can minimize costs of equip-

https://orcid.org/0000-0002-2144-0262

ment failures by planning ahead and timing procure-

ment. Hence, CM becomes an essential factor in op-

timizing operational efﬁciency. Parameters that can

be measured to monitor the production environment

comprise engine power, valve states and pressure of

steering ﬂuids, to name a few.

In this paper we will consider the following parts

in particular: valve states of a hydraulic system and

eddy current data of aluminum surface structures.

As part of CM, Digital Signal Processing (DSP)

employs signal ﬁlters to detect critical states in real-

time, enabling failure prediction and maintenance

scheduling. However, designing CM systems remains

complex due to the need for individual parameterized

ﬁlters. For this purpose, we propose an Organic Com-

puting (OC) approach, employing evolutionary learn-

ing for automated digital ﬁlter design. OC (M

uller-

Schloer and Tomforde, 2017) represents a design

paradigm using nature-inspired concepts. The evo-

lution of ﬁlters is set out to allow for predicting criti-

cal states in machine parts, using Cartesian Genetic

Programming (CGP) for feature selection and OC

principles, denoted self-x properties. More precisely,

300

Margraf, A., Cui, H., Baumann, S. and Hähner, J.

Filter Evolution Using Cartesian Genetic Programming for Time Series Anomaly Detection.

DOI: 10.5220/0012210700003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 300-307

ISBN: 978-989-758-674-3; ISSN: 2184-3236

the approach is deemed to be self-conﬁguring, self-

learning and self-optimizing, thereby employing core

principles of OC on signal processing.

As part of CM, we also consider eddy current test-

ing of carbon ﬁber reinforced plastics (Matvieieva

et al., 2018; Bardl et al., 2018) and the adaption of

signal ﬁlters for depth inspection. In this regard, CM

represents a preliminary step to anticipate production

downtime and unscheduled replacement of parts by

employing reactive, preventive and predictive main-

tenance.

1.1 Related Work

Various other works have concentrated on automating

the CM procedure. However, to the best of our knowl-

edge, the authors have not encountered any relevant

publications on ﬁlter evolution beyond those already

mentioned. Yang et al. presented a CM approach

for rolling-element bearings using envelopes (Yang,

2015). In the machine learning related ﬁelds of re-

search, Miller et al. introduced Cartesian Genetic Pro-

gramming (CGP) as a derivative of genetic program-

ming, initially to evolve electronic circuits (Miller

and Thomson, 2000). Subsequent work identiﬁed

great potential of CGP for learning Boolean functions

(Miller, 1999) or designing executable FPGA circuits

(Sekanina et al., 2011). Since then, several variants of

CGP have been proposed and employed in different

areas of application (Miller, 2019).

Glette et al. (Glette et al., 2008) presented an

overview on evolutionary hardware (EHW) for clas-

siﬁcation tasks discussing the potential for digital sig-

nal processing. Following studies were dedicated to

the classiﬁcation problem of hand prostheses move-

ments with evolutionary algorithms by Boschmann et

al. (Boschmann et al., 2009). Kaufmann et al. (Kauf-

mann et al., 2012) compared different classiﬁers for

electromyography signals using EHW. Also, Jack et

al. (Jack and Nandi, 2000) proposed a method for fea-

ture selection with GA in condition monitoring. In

a DSP related but theory based work, Hammami et

al. (Hammami et al., 2018) proposed a ﬁlter-wrapper

for feature construction using evolutionary learning.

1.2 Structure

The remainder of this paper is structured as follows:

We start by introducing the applications in Section 1

and continue by deﬁning the adaptation of CGP for

evolutionary learning of signal ﬁlters in Section 2. In

the following Section 3 we describe the experimental

setup in which we elaborate on the datasets we used

for testing our hypotheses. We then discuss the re-

sults in Section 4 and conclude with an overview of

future applications, their potential, and research goals

in Section 5.

2 APPROACH

CM is set to monitor parameters of a machine’s con-

dition, e.g., temperature, vibration, or position. The

underlying data is usually derived from analogue sen-

sors and converted to the digital domain. In order to

evaluate a machine’s state, several parts of the same

device have to be monitored at once and analyzed.

Data processing relies on either statistical approaches

(e.g., tolerance, pre-deﬁned parameters, probabilis-

tic methods) or machine learning techniques. In this

study, CM is employed to eddy current and valve sen-

sors to demonstrate how reliable classiﬁers can be de-

signed to identify critical states or make predictions

for emerging operational faults.

2.1 Design of Digital Filters

The design workﬂow for DSP pipelines can be di-

vided into six stages: (1) signal acquisition, (2) AD

conversion, (3) digital ﬁltering, (4) feature selection,

(5) dimensionality reduction and (6) classiﬁcation.

For stages 1 and 2, the system components, i.e. sen-

sors and converters as well as interfaces vary with the

technical environment. In the digital domain, though,

signal data can be represented in the time and fre-

quency domain and analyzed in different dimensions.

This paper takes only stages 3 to 6 into account. Sig-

nal and ﬁlter requirements share common character-

istics: 1) discrete vs. continuous nature, 2) multidi-

mensionality (channels, locality, intensity), 3) high-

volume data, and 4) their reproducibility. When deal-

ing with continuous signals, isolating the core fre-

quency is vital due to signal overlays from neighbor-

ing parts, resonances, and noise. Adding ﬁlter nodes,

such as low-pass or wave rectiﬁers, to the pipeline al-

lows cleaning and preparation for further processing.

Digital ﬁlters can be categorized as ﬁnite impulse re-

sponse (FIR) or inﬁnite impulse response (IIR). For

signal ﬁlter applications that meet requirements such

as noise suppression, cutoff frequency, and pass band

matching, as well as anomaly detection, we propose

an approach utilizing CGP for evolutionary ﬁlter de-

sign. The methodology renders algorithm develop-

ment self-conﬁguring and self-adaptive, as elaborated

in Section 2.2.

Filter Evolution Using Cartesian Genetic Programming for Time Series Anomaly Detection

301

2.2 Adaptation of Cartesian GP

2In general, CGP is an evolutionary algorithm that

represents programs as a directed acyclic graph

(DAG) with nodes arranged in rows and columns on a

Cartesian grid. In this section, we outline an approach

for grouping DSP ﬁlters to avoid non-executable con-

nections but allow all remaining valid combinations.

Regular CGP employs a two-dimensional grid to rep-

resent the genotype. Three general node types are

used for training: input nodes, function nodes, and

output nodes. All function nodes F are positioned on

the grid and can be connected using vertices to form

the DAG. However, not every node needs to be linked

to an output node, making them non-coding genes.

During training, a high number of nodes remain inac-

tive, which has been found to increase the probability

of evading local optima (Turner and Miller, 2015;

Cui et al., 2023), partly because it allows more neu-

tral genetic drift and favors genetic diversity. Typi-

cally, the genotype exhibits a signiﬁcant number of

non-coding genes that have no impact on the pheno-

type. This property allows for greater variation in the

underlying encoding during training. The program P

is deﬁned as follows:

P := {G, i,o, n, F f , r, c, l} (1)

In the set, G represents the genotype, while the num-

ber of inputs and outputs of each pipeline are denoted

by i and o. The grid is limited by indices r and c which

indicate the number of rows and columns, adding up

to n nodes. This constraint helps mitigate genetic

bloat. The encoding is represented as a sequence of

operator nodes as can be seen in Figure 1.

Except for the levels back parameter l, regular

CGP conﬁgurations do not impose constraints on the

order of successive operators, generating a theoreti-

cally large number of invalid solutions in early gen-

erations. In some previous studies, the possible com-

binations between operators were considerably lim-

ited, as presented by (Margraf et al., 2017). For the

sake of efﬁcient search space exploration, we suggest

to apply limitations only to prevent invalid solutions

during evolution. However, the conﬁguration should

allow any executable ﬁlter combination to preserve

the probability of identifying an optimum. Therefore,

any data that has been processed by one operator and

passed to the next must carry enough information for

reasonable ﬁltering. F consists of f functions form-

ing the search space, while l denotes the levels back

parameter. Similar to the modiﬁcations proposed by

(Margraf et al., ress) for image processing, we in-

troduce a Dependency Graph DG(T, E

) with op-

erator type set T and connections E

with operator

types T

∈ T with i = 1, . . . , n. The dependency graph

is applied to the columns and thereby deﬁnes which

columns can be associated with a column under con-

sideration. Each node in the dependency graph rep-

resents a column in the grid. To pool the node types,

we introduce a program P

, derived from P which is

deﬁned as follows:

= {F, T, G, r} (2)

The number of layers contained in the graph G

implicitly deﬁne the number of columns c, there-

fore P

does directly depend on c. The height of G

equals its number of columns c and its size, thereby:

c = |G| = height(G). Unlike earlier implementations

(Leitner et al., 2013)), the arity a of each function

varies according to its precondition, allowing to mu-

tate each parameter of a function, therefore:

a = max(#Inputs(F

)) (3)

For the evaluation of DSP ﬁlter pipelines, the ﬁt-

ness will be deﬁned as a candidate solution’s accuracy

on the training data. More precisely, for the set of la-

beled training feature vectors X = (x, l)

the ﬁtness of

an evolved ﬁlter pipeline p is deﬁned by Matthew’s

correlation coefﬁcient (MCC). MCC represents the

intersection between ground truth and prediction for

each series in the series-label pair and is established

as:

T P × T N −FP × FN

(T P + FP)(T P + FN)(T N + FP)(T N + FN)

(4)

This metric allows to accurately reﬂect the qual-

ity of binary classiﬁcations, particularly when deal-

ing with imbalanced datasets. Unlike related met-

rics, it effectively considers the ratio between positive

and negative elements, resulting in a more conclusive

evaluation. In this case, false classiﬁcation is not di-

rectly penalized.

2.3 Processing Pipeline Speciﬁcations

The training yields executable chains of operators de-

noted ‘processing pipelines’. They consist of opera-

tors and their directed connections and represent ex-

plicit components in the data ﬂow, equivalent to phe-

notypes in classical CGP. Figure 2 depicts a sample

pipeline represented as a graph with a Threshold op-

erator that outputs predictions. The left branch ap-

plies the square root of each value on input time se-

ries, while the right branch transforms the time series

with FFT and computes a Lowpass to attenuate fre-

quencies before inversing to the time domain.

DG is designed to accommodate repetitions of the

core graph. This ﬂexibility is achieved through the

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

302

Figure 1: Illustration of a CGP encoding for genotype G and phenotype P, visualizing the ﬂow of information from input

nodes through non-coding (dashed border) and active nodes to the output nodes; in the bottom row, the operator type is

depicted which follows the deﬁnition given by dependency graph DG.

Figure 2: Sample pipeline with ﬁlter operators.

conﬁguration of a hyperparameter called cycled N,

where N represents the number of repetitions of the

predeﬁned initial graph. By setting the cycled N

value, the number of columns c in the graph can be

derived in a forward manner, directly from the graph

conﬁguration. This way, DG becomes scalable by set-

ting one parameter. The extension is introduced to

steer transformation between the time and frequency

domain, as they only yield valid solutions, if a trans-

formation in one direction is reversed before connect-

ing to the output operator. The simplest solution to en-

force this rule would have been to only allow one ﬁl-

ter operation between the transformations. The same

issue occurs for forked operator pipelines that run

parallel to each other, as it is the case for ScipySqrt

in Figure 2. For each forked pipeline, a join node

TwoSignalsToSignal has to be deﬁned. In order to

allow more complex operator combinations while at

the same time setting a limitation to a potentially in-

creasing pipeline length, we introduced the parameter

cylced N that prevents genetic bloat in the original

sense of CGP.

Figure 3: Dependency Graph conﬁguration with 2 cycles.

The proposed adaptation of CGP enables the gen-

eration of ﬁlter pipelines to accurately segment sec-

tions in time series data exhibiting anomalies or de-

fects. However, for multi-class differentiation, the

pre-segmented time series data needs to be further

processed using subsequent classiﬁers. For this pur-

Filter Evolution Using Cartesian Genetic Programming for Time Series Anomaly Detection

303

pose, common state-of-the-art classiﬁcation models,

e.g. Artiﬁcial Neural Networks (ANN), k-Nearest

Neighbors (k-NN), Support Vector Machine (SVM),

Decision Trees (DT), Bayesian classiﬁers, Gaussian

mixtures or Hidden Markov Models can be applied.

This is, however, not part of this study, but we en-

courage the community to pursue future research in

this direction.

3 VALIDATION

In order to demonstrate the viability of signal ﬁlter

evolution by means of CGP, we tested the adapted al-

gorithm on real-world data from a) a lab-based eddy

current testing sensor and b) a hydraulics test stand

dataset proposed by (Helwig et al., 2015). The ﬁrst

dataset was created in our lab using an aluminum rod

and eddy current sensor. The latter presents a proof of

concept to demonstrate automated training of a CM

application with several fault scenarios for both ﬁxed

and random hydraulic load cycles.

3.1 Experimental Setup

An eddy current sensor operates based on the prin-

ciple of electromagnetic induction, where a changing

magnetic ﬁeld induces eddy currents in a conductive

material. These eddy currents generate a secondary

magnetic ﬁeld that interacts with the sensor, allowing

for the detection of conductivity, thickness or surface

defects. The sensor consists of a closed coil through

which the measured object is passed. For our experi-

ment, an aluminum rod with nuts and 8 successively

arranged grooves of different thickness was moved

through the sensor while recording the data as shown

in Figure 4. This ﬁgure plots distance (x-axis in mm)

against normalized impedance output (y-axis), show-

ing how eddy currents induced in a conductive object.

The surface variations serve as known anomalies to

trigger sharp deﬂections in the signal data. With the

aid of the defect positions marked with dashed lines

on the calibration tube. The eddy current signal de-

ﬂections can be mapped to speciﬁc test defects.

In Helwig et al.’s study, four typical faults of a hy-

draulic system were simulated and recorded as mea-

surement data. The resulting dataset contains time se-

ries data and corresponding labels, and is therefore

well-suited to benchmark classiﬁcation models. The

test setup comprises a primary working circuit and a

secondary cooling and ﬁltering circuit connected via

an oil tank. In repetitive 60-second load cycles, mea-

surement data such as pressure, ﬂow rate, and tem-

peratures are recorded at various locations in the cir-

Figure 4: Rendering of the aluminum calibration rod and

eddy current signal allocation of the surface with deﬂections

labelled as anomalies with a red overlay.

cuit while the state of four components (pump, cooler,

valve, and accumulator) is quantitatively modiﬁed.

Our proposed conﬁguration was tested on valve val-

ues because the anomalies appearing in the readings

were of the most explicit among the sensor data.

The algorithm was entirely implemented using the

signal sub-package of the SciPy python library

. This

is reﬂected in the names of some ﬁlter operators. For

the conducted experiments, we introduced variations

in key parameters, namely the scipy series length ssl,

the number of rows r, and the cycle conﬁguration of

the dependency graph DG denoted cycled

N, which

affects the number of columns c. The parameter ssl

deﬁnes the length of the series batch utilized for ﬁl-

tering in one operation that is sequentially performed.

Subsequently, we conducted the experiments us-

ing 6 distinct hyperparameter settings for N and ssl

and 4 variations of r, resulting in the generation of

144 data tuples for the hydraulic valve data. For the

eddy current dataset, only 5 variations of ssl were

applied, which returned 120 tuples. All experiment

data were collected with particular emphasis on the

MCC ﬁtness score, which ranges between 0 and 1.

We minimize the ﬁtness value, which means a ﬁtness

of 1 indicates a perfect solution. The evolved oper-

ator pipelines were compared against state-of-the-art

ﬁlters and evaluated through time series segmentation

tasks.

3.2 Comparison of Hyperparameters

The top heatmap plot in Figure 5 illustrates the MCC

ﬁtness values corresponding to various conﬁgurations

of cycled N, the number of rows r, and the series

length ssl. Similarly, the bottom plot presents the

rows r associated with each dependency graph con-

see https://scipy.org/

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

304

Figure 5: Fitness values achieved on valve data of the hy-

draulic system for parameters ssl, rows and cycled N.

ﬁguration DG, ssl, and their respective mean ﬁt-

ness values MCC. In contrast, Figure 6 depicts

the results for the eddy current measurement data.

They provide visualizations of dependencies among

the same four parameters. A range of edge cases

was tested for cycled N, including values of N ∈

{2, 5, 10, 20, 40, 60}, as well as varying numbers of

rows r ∈ {0, 50, 500, 5000}, and series lengths ssl ∈

{6k, 18k, 30k, 60k, 120k, 300k}. The intervals were

chosen to reveal potential trends while balancing

computational time and effort. Despite an initial ex-

amination not revealing a clear pattern, the obtained

results display signiﬁcant heterogeneity. In the fol-

lowing section, we will critically analyze the con-

ducted experiments.

Figure 6: Fitness values achieved on calibration rod scan

data for parameters for ssl, rows and cols.

As illustrated in Figure 6, the ﬁtness f

MCC

the eddy current ﬁlter pipelines achieves values for

MCC

> 0.5. However, despite the overall high ﬁt-

ness results observed across various hyperparameter

settings, the range still varies from 0.5 < f

MCC

< 0.8.

It is worth noting that one particular experiment en-

countered failure due to an assignment error for ssl =

150, r = 5000, N = 60. On the other hand, the sec-

ond experiment conducted on the hydraulic data test

demonstrates a more diverse range of ﬁtness values.

This wider range spans between 0.2 < f

MCC

< 1.0 for

the given set of parameters. Additionally, it is impor-

tant to mention that in this experimental setup, too,

three experiments failed due to assignment errors for

ssl = 12k, r = 50, N = {2, 5, 10}. Nevertheless, the

results allow for a thorough assessment of the param-

eters for signal ﬁltering using CGP.

4 RESULTS AND DISCUSSION

This section presents a detailed account of the ﬁnd-

ings and offers critical reﬂections on the results ob-

tained through this approach.

4.1 Evaluation of Experiments

The test rod data exhibits clear anomalies in the sig-

nal, which can be effectively analyzed using con-

cise and compact ﬁlter programs, as can be seen

in our experiments. Through the evolutionary pro-

cess of CGP, favorable ﬁtness values are consistently

achieved, generating ﬁlter pipelines that contain at

most 8 operators for both datasets. For the experi-

ments, the number of generations was set to 150 with

10 iterations. Although this experimental setup repre-

sents a straightforward and low-complexity problem,

it demonstrates the successful utilization of CGP to

evolve compact pipelines with varying hyperparame-

ters.

Upon visually examining the parameter plots, it

appears that smaller values of ssl tend to yield better

results. An analysis of the speciﬁc Pearson r corre-

lation allows for more objective insights. The cor-

relation between the mean ﬁtness and the ssl shows

a weak but measurable positive correlation, with a

Pearson r of ρ(ssl, µ

f it

) > 0.3. This indicates that,

as the series length decreases, the potential ﬁtness in-

creases. There are several potential reasons for this

effect. One possibility is that longer series introduce

higher complexity, requiring more powerful opera-

tors. However, CGP is speciﬁcally designed to han-

dle problems with lower complexity. This observa-

tion suggests that trainings should be performed with

ssl < 6000. It should be mentioned that the valve

dataset labels were transformed to binary classiﬁca-

tion (OK / NOK) although the original labels distin-

guish between 4 fault types. The class deﬁnitions

Filter Evolution Using Cartesian Genetic Programming for Time Series Anomaly Detection

305

were merged to one class to train for one pipeline.

Since several fault types appear in the label data that

substantially differ from each other potentially in-

creases the segmentation complexity.

4.2 Analysis and Interpretation

In general, the MCC ﬁtness achieved on the eddy cur-

rent dataset reached favorable MCC values indepen-

dent of the hyperparameter settings. Although the

dataset contains anomalies with a comparably large

deﬂection that is supposedly easy to ﬁlter, the ex-

periments suggest that the CGP conﬁguration allows

evolving compact and well-suited ﬁlter pipelines.

This is noteworthy because an obvious use case for

ﬁlter pipeline evolution is the preprocessing of raw

signal data before passing it to a more complex clas-

siﬁcation model.

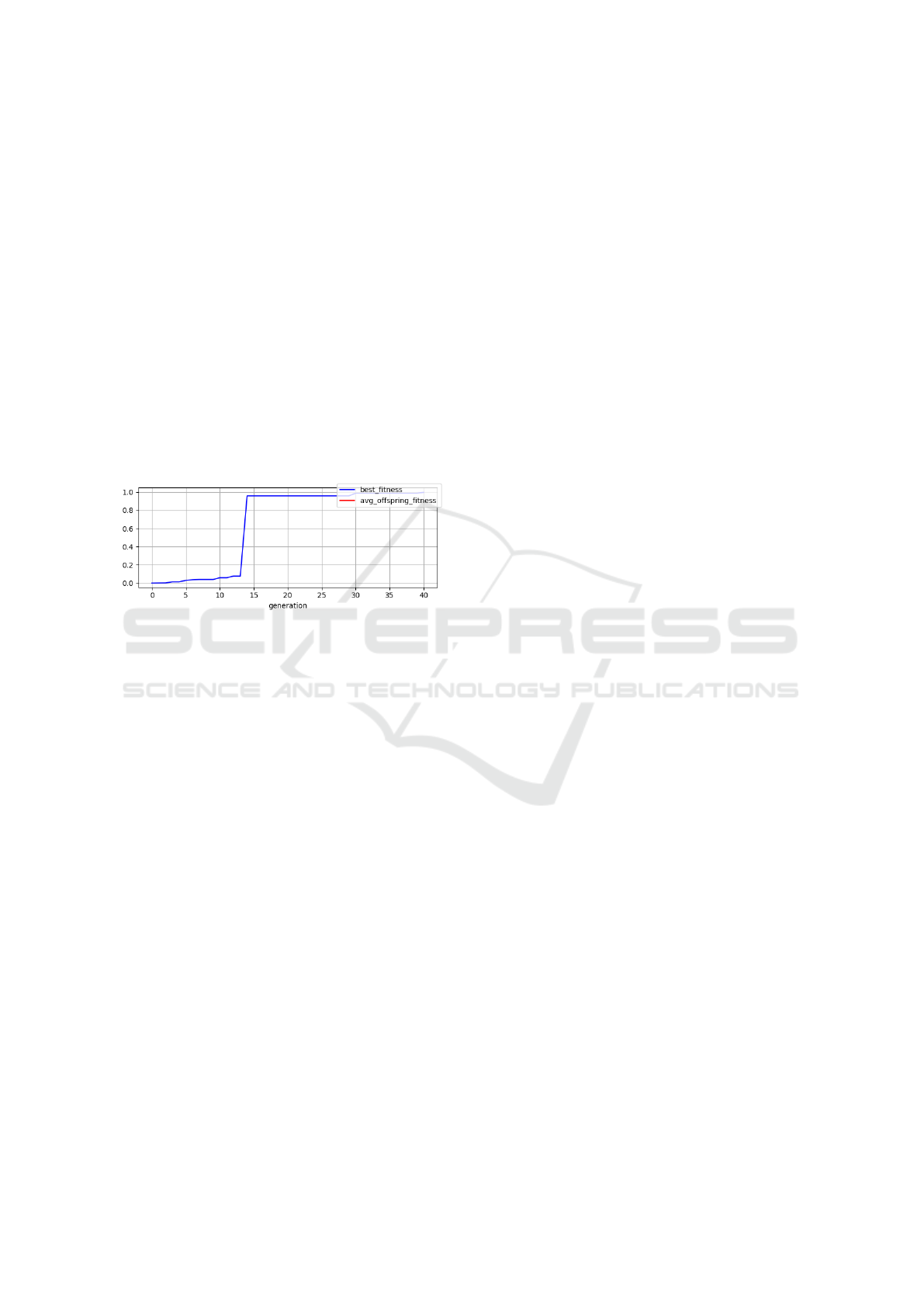
Figure 7: Fitness evolution of the best run on the hydraulic

valve dataset.

For one run on the hydraulic valve data, we ob-

served a remarkable top scorer with an f

MCC

= 0.99,

which is already considered high. As Figure 7 shows,

a signiﬁcant leap appears in the early stages of the

evolution appeared for experimental runs that yield

high ﬁtness. This pattern suggests that it would be

more efﬁcient to evaluate the evolving pipelines on

a small subset of training data initially, as improve-

ments can be achieved more efﬁciently with fewer

data points. As the generations progress, the eval-

uation set can be gradually expanded to encompass

the full-scale dataset for comprehensive assessment.

This approach would save valuable time during the

early stages. Additionally, an alternative strategy in-

volves computing similarities and analogies between

datasets, training on multiple representative datasets,

and logging the results. Once the dataset reaches

a certain size, efforts can be made to ﬁnd a suit-

able match and initiate the evolution with ‘pretrained’

pipelines to attain a higher ﬁtness state.

5 CONCLUSION

CM and PdM to hold signiﬁcant potential for enhanc-

ing efﬁciency, due to its high impact in continuously

running production systems. In environments with

tightly linked schedules that leave little room for un-

foreseen incidents, maintenance shutdowns set free a

chain of complications. The risk for economical dam-

age increases at the same rate as the probability of

failures of wear parts while it becomes even less pre-

dictable. Therefore, CM will help to keep track of ma-

chine conditions and helps to evaluate possible risks

more precisely.

5.1 Summary

We presented an evolutionary learning approach for

ﬁlter evolution to process signal and time series data

and detect anomalies or remove noise. The proposed

CGP adaptation employed on time series data from

different industrial applications show promising re-

sults for ﬁlter pipeline evolution, speciﬁcally for em-

bedded applications or preprocessing in combination

with subsequent classiﬁer models. Since data streams

from both valve and eddy current sensors were con-

verted to time series, we use a widespread data rep-

resentation that can be found throughout CM applica-

tions. Despite the popularity of ANNs, evolutionary

algorithms still exhibit a substantial advantage: the

dependency from large training sets is less severe. It

should be emphasized that other physical data will

likely enhance the success of predictive maintenance,

as suggested in this paper. Ultimately, we plan to ex-

amine the detection accuracy for different samples of

condition sensors to evaluate a wider product range.

The adaption of CGP for evolving signal ﬁlters

is regarded as an implementation encompassing both

the principles of Automated Design of Processing

Pipelines (ADPP) and Life Long Learning (Stein

et al., 2018). Since these concepts coincide with

Automated Algorithm Design (AAD) and Automated

Algorithm Conﬁguration (AAC), there will be future

effort to integrate evolutionary learning for DSP into

ADPP.

5.2 Outlook

By evolving compact ﬁlter pipelines for industrial sig-

nal data, the efﬁciency of monitoring systems is in-

creased. Research work should be continued in this

spirit by conducting experiments with smaller search

spaces. This would allow for a deeper understand-

ing of how ﬁtness evolves. Also, single operators

should be improved to target speciﬁc ﬁlter problems.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

306

However, the use of further classiﬁcation models, es-

pecially more complex machine learning algorithms,

was not examined. Employing further machine learn-

ing models to classify the preprocessed signal data

can increase the accuracy of anomaly detection and

classiﬁcation. We encourage the community to ex-

plore the potential of CGP when interacting with re-

lated ML techniques, e.g. by evolving ﬁlter programs

for data preparation and cleansing before the actual

classiﬁcation. In industrial applications, this approach

constitutes a promising concept for future OC efforts

with high potential. The adaptation of CGP allows

integrating self-optimizing signal ﬁltering in exist-

ing condition monitoring systems. This approach can

help advance the digitalization of production lines in

the manufacturing industry to enhance efﬁciency, re-

duce scrap and optimize processes.

REFERENCES

Bardl, G., Kupke, R., Heuer, H., and Cherif, C. (2018).

Eddy current testing in cfrp production. Lightweight

Design worldwide, 11:48–53.

Boschmann, A., Kaufmann, P., Platzner, M., and Winkler,

M. (2009). Towards multi-movement hand prostheses:

Combining adaptive classiﬁcation with high precision

sockets. In Proceedings of the 2nd European Confer-

ence Technically Assisted Rehabilitation. Citeseer.

Cui, H., P

atzel, D., Margraf, A., and H

ahner, J. (2023).

Weighted mutation of connections to mitigate search

space limitations in cartesian genetic programming. In

Proceedings of the 17th ACM/SIGEVO Conference on

Foundations of Genetic Algorithms, pages 50–60.

Glette, K., Torresen, J., Kaufmann, P., and Platzner, M.

(2008). A comparison of evolvable hardware archi-

tectures for classiﬁcation tasks. In International Con-

ference on Evolvable Systems, pages 22–33. Springer.

Hammami, M., Bechikh, S., Hung, C.-C., and Said, L. B.

(2018). A multi-objective hybrid ﬁlter-wrapper evo-

lutionary approach for feature construction on high-

dimensional data. In 2018 IEEE Congress on Evolu-

tionary Computation (CEC), pages 1–8. IEEE.

Helwig, N., Pignanelli, E., and Schutze, A. (2015). Condi-

tion monitoring of a complex hydraulic system using

multivariate statistics. In 2015 IEEE International In-

strumentation and Measurement Technology Confer-

ence (I2MTC) Proceedings. IEEE.

Jack, L. and Nandi, A. (2000). Genetic algorithms for fea-

ture selection in machine condition monitoring with

vibration signals. IEE Proceedings-Vision, Image and

Signal Processing, 147(3):205–212.

Kaufmann, P., Glette, K., Gruber, T., Platzner, M., Torre-

sen, J., and Sick, B. (2012). Classiﬁcation of elec-

tromyographic signals: Comparing evolvable hard-

ware to conventional classiﬁers. IEEE Transactions

on Evolutionary Computation, 17(1):46–63.

Leitner, J., Harding, S. L., and F

orster, A. (2013). Hu-

manoid learns to detect its own hands.

Margraf, A., Cui, C., Stein, A., and H

ahner, J. (2023 in

press). Evolving processing pipelines for industrial

imaging with cartesian genetic programming. In 2023

IEEE International Conference on Autonomic Com-

puting and Self-Organizing Systems (ACSOS).

Margraf, A., Stein, A., Engstler, L., Geinitz, S., and H

ahner,

J. (2017). An Evolutionary Learning Approach to

Self-conﬁguring Image Pipelines in the Context of

Carbon Fiber Fault Detection. In Proceedings of

the 16th IEEE International Conference for Machine

Learning and Applications.

Matvieieva, N., Schulze, M., Mizukami, K., Kharabet, I.,

and Heuer, H. (2018). Determination of indication

depths at high frequency eddy current testing of cfrp.

In proceedings of the 10th International Symposium

NDT in Aerospace.

Miller, J. F. (1999). An Empirical Study of the Efﬁciency

of Learning Boolean Functions Using a Cartesian Ge-

netic Programming Approach. In Proc. of 1st Annual

Conference on Genetic and Evolutionary Computa-

tion, GECCO’99, pages 1135–1142, San Francisco,

CA, USA. Morgan Kaufmann Publishers Inc.

Miller, J. F. (2019). Cartesian genetic programming: its sta-

tus and future. Genetic Programming and Evolvable

Machines, pages 1–40.

Miller, J. F. and Thomson, P. (2000). Cartesian Genetic

Programming, pages 121–132. Springer Berlin Hei-

delberg.

uller-Schloer, C. and Tomforde, S. (2017). Organic Com-

puting: Technical Systems for Survival in the Real

World. Autonomic Systems. Birkh

auser, Cham, 1st

edition.

Sekanina, L., Walker, J. A., Kaufmann, P., and Platzner, M.

(2011). Evolution of Electronic Circuits, pages 125–

179. Springer Berlin Heidelberg.

Stein, A., Margraf, A., Moroskow, J., Geinitz, S., and

Haehner, J. (2018). Toward an organic computing ap-

proach to automated design of processing pipelines. In

ARCS Workshop 2018; 31th International Conference

on Architecture of Computing Systems.

Turner, A. J. and Miller, J. F. (2015). Genetic programming

and evolvable machines, volume 16, chapter Neutral

genetic drift: an investigation using Cartesian Genetic

Programming, pages 531–558. Springer Science and

Business Media.

Yang, Z. (2015). Automatic condition monitoring of indus-

trial rolling-element bearings using motor’s vibration

and current analysis. Shock and Vibration, 2015.

Filter Evolution Using Cartesian Genetic Programming for Time Series Anomaly Detection

307