A Novel Fuzzy Geometric Naive Bayes Network for Online Skills

Assessment in Training Based on Virtual Reality

Jodavid A. Ferreira

1,2 a

, Arthur R. R. Lopes

, Liliane S. Machado

2,3 b

and Ronei M. Moraes

2,4 c

Graduate Program in Decision Models and Health, Federal University of Para

ıba, Jo

ao Pessoa, Para

ıba, Brazil

Laboratory of Technologies for Virtual Teaching and Statistics, Federal University of Para

ıba,

ao Pessoa, Para

ıba, Brazil

Departament of Informatics, Federal University of Para

ıba, Jo

ao Pessoa, Para

ıba, Brazil

Departament of Statistics, Federal University of Para

ıba, Jo

ao Pessoa, Para

ıba, Brazil

Keywords:

Fuzzy Geometric Naive Bayes, Geometric Distribution, User’s Assessment, Virtual Reality.

Abstract:

Computational intelligence-based assessment systems have been proposed for implementation in virtual reality

(VR) simulators to enhance technical proﬁciency in secure environments. Traditional training methods in

healthcare, such as live subjects, cadavers, or mannequins, have limitations in reﬂecting realistic characteristics

and deteriorate over time. Virtual reality-based assessment systems offer the advantage of check users skills

in realistic and immersive training experiences, providing feedback at the end of the training. This paper

presents a novel approach to assessment using a Single-User Assessment System (SUAS) that incorporates

a Fuzzy Geometric Naive Bayes Network. The proposed method utilizes geometric distribution to model

the fuzzy boundaries and assess the performance of gynecological examinations in a virtual reality simulator.

The study evaluates the effectiveness of the proposed SUAS by comparing it with three other assessment

methods. The results demonstrate the superior performance of the proposed method in accurately evaluating

user performance in the simulated gynecological examinations.

1 INTRODUCTION

Computational intelligence-based assessment sys-

tems have been suggested for implementation in vir-

tual reality (VR) simulators (Moraes et al., 2021),

speciﬁcally designed to enhance technical proﬁciency

of students and professionals in secure, 3D graphical

and interactive environments. In the context of health-

care, practical training is typically conducted using

live subjects, cadavers, guinea pigs or mannequins.

However, these methods deteriorate over time and fail

to fully reﬂect realistic characteristics, thereby im-

pacting the effectiveness of the training. On the other

hand, virtual reality-based assessment systems do not

deteriorate over time and constantly strive to simu-

late the situation in the most realistic manner possible

(Souza et al., 2006).

One notable beneﬁt of assessment systems is its

capacity to capture user interactions in real-time, en-

https://orcid.org/0000-0002-2131-6464

https://orcid.org/0000-0002-1182-2929

https://orcid.org/0000-0001-8436-8950

abling the assessment of user’s skills based on this

data (Moraes and Machado, 2009). Consequently, re-

ceive feedback just after the simulation becomes cru-

cial and can be utilized to generate a comprehensive

analysis of the user’s abilities or to adjust the sim-

ulation’s difﬁculty level. Earlier studies have pro-

posed the integration of both single-user assessment

systems (SUAS) and multi-user assessment systems

(MUAS) with VR simulators for training (Moraes and

Machado, 2012).

The assessment of a procedure necessitates the es-

tablishment of metric parameters and the tracking of

user interactions. It is widely recognized that VR sim-

ulators offer realistic representations (Moraes et al.,

2021). Protocols do not consider exact values for lo-

cation and movements but include linguistic descrip-

tion for them. It makes fuzzy events modeling an ap-

propriate approach for assessment purposes. Further-

more, each procedure has unique characteristics in

terms of assessment metrics and, as consequence, in-

teraction data follows speciﬁc statistical distributions.

Thus, the quality of the assessment results can be en-

hanced by achieving a more accurate ﬁt with the sta-

Ferreira, J., Lopes, A., Machado, L. and Moraes, R.

A Novel Fuzzy Geometric Naive Bayes Network for Online Skills Assessment in Training Based on Virtual Reality.

DOI: 10.5220/0012211000003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 395-401

ISBN: 978-989-758-674-3; ISSN: 2184-3236

395

tistical distribution. In the scientiﬁc literature, few

fuzzy methods based on discrete random variables

can be found. In fact, two methods based on Poisson

(Moraes and Machado, 2015) and Binomial (Moraes

and Machado, 2016) distributions were proposed by

the same authors. However, other discrete distribu-

tions can be suitable to be embedded on assessment

systems, as for instance, Geometric distribution.

SITEG 2.0 is an advanced virtual reality simula-

tor designed speciﬁcally for gynecological examina-

tion training(Moraes et al., 2020). It offers realistic

graphics and interactive tasks to enhance the learning

experience.

The simulator provides a wide range of cases, in-

cluding healthy patients, as well as patients with Her-

pes, HPV (Human Papillomavirus), and varying de-

grees of cervical cancer. As in real life, in this sim-

ulator users must visually analyse the vagina and use

a haptic device to collect material from cervix. The

haptic device acts as a spatula or cotton swab (Fig-

ure 1). This is a soft interaction and the force applied

on cervix and the amount of material are relevant to

achieve success in the procedure. To ensure effective

assessment, SITEG 2.0 incorporates an embedded as-

sessment system that monitors user interactions dur-

ing the anamnesis (patient history) and physical ex-

amination stages of the simulation.

Figure 1: SITEG 2.0 with the haptic device acting as a spat-

ula.

This paper presents a novel approach to as-

sessment using a Single-User Assessment System

(SUAS) based on a Fuzzy Geometric Naive Bayes

Network to model the number of independent attemps

of an user to successfully collect material from cervix

using a spatula and a cotton swab. This collect must

cover all region of the cervix and requires a speciﬁc

range of force during the touch. The proposed method

utilizes geometric distribution to model and assess the

performance of the gynecological examination.

The SUAS implemented in SITEG 2.0 is respon-

sible for evaluating the user’s performance during the

simulation. It provides valuable feedback and as-

sessment based on the user’s actions and interactions

within the virtual environment (Figure 2).

Figure 2: SUAS of the SITEG 2.0 simulator with the Fuzzy

Geometric Naive Bayes Network.

The theoretical framework of this SUAS is elab-

orated upon in subsequent sections, along with the

simulation results obtained using data from SITEG

2.0. Additionally, a comparative analysis of the SUAS

with two other assessment methods is presented for a

comprehensive evaluation.

The paper is structured as follows: Section 2

presents the statistical fundamentals of geometric dis-

tribution; Section 3 describes fuzzy probability in

Zadeh approach and networks based on Naive Bayes

hypothesis are described. Section 4 brings the accu-

racy measures used in this paper. The results obtained

and the discussion can be seen on Section 5. Section

6 brings conclusions of this paper.

2 STATISTICAL MODELING

2.1 Geometric Distribution

The geometric distribution ﬁnds its utility in various

ﬁelds, ranging from reliability analysis to queueing

theory, providing a mathematical framework to quan-

tify the number of independent attempts required to

achieve the ﬁrst success in a Bernoulli experiment. In

the SITEG 2.0, that distribution is suitable for model-

ing the number of trials until the successful execution

of a given task. This is a good parameter for user’s

skills assessing, since that for a well trained user, this

task should be performed with the shorter possible

number of trials.

A discrete random variable X follows a geometric

distribution X ∼ G(p) if its probability distribution

function (pdf) has the following equation (1). This

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

396

distribution is provided by one parameter, deﬁned as

p (Mendenhall et al., 2012).

f (x; p) = p(1 − p)

, (1)

where 0 < p ≤ 1 and x = 0,1,2,...

2.2 Mathematical Properties

The expectation and variance are important properties

of the geometric distribution. Thus, let X ∼ G(p), its

expectation is given by

E(X) =

1 − p

(2)

and the variance of geometric distribution is given by

V (X) =E(X

) − (E(X))

1 − p

(3)

where 0 < p ≤ 1.

2.3 Parameter Estimation

Let X

,. .. ,X

a random sample i.i.d. of a random

variable X ∼ G(p), such that p is a geometric distribu-

tion scalar parameter, with the restriction 0 < p ≤ 1.

Thus, we have that ˆp is obtained by

ˆp =

n +

∑

i=1

1 + X

, (4)

where X =

∑

i=1

/n.

3 A NEW FUZZY NAIVE BAYES

GEOMETRIC

NETWORK-BASED

ASSESSMENT METHOD

A Naive Bayes network assumes that the variables are

conditionally independent, i.e., the information about

an event is not dependent on that of other events. Ad-

ditionally, we assume geometric distribution for vari-

ables present in the training simulation. Initially, we

describe the classical Geometric Naive Bayes Net-

work and in the following the new SUAS based on

Naive Bayes Network with geometric distribution for

fuzzy events.

Thus, let x

{

,. .. ,X

}

a random vector

of data in the i-th sample with k-information (dimen-

sion/variables) obtained when training is performed

and w

, j ∈ Ω the performance class most likely to be

chosen, since the set Ω = 1,..., M where M is the to-

tal number of performance classes for the assessment

of a user in the simulator. The probability of the per-

formance class w

assuming that each variable X

conditionally independent of any other variable X

for

all t ̸= l ≤ k, is:

P(w

,..., X

) =

P(w

)

∏

t=1

P(X

) (5)

where S is a scale factor.

3.1 The Geometric Naive Bayes

Network

For better understanding, we present ﬁrst the classi-

cal Geometric Naive Bayes Network. In this case, it

is assumed for P(X

) in eq. (5) the conditional

probability using Geometric distribution. Thus, af-

ter mathematical manipulations, the eq. (5) can be

rewritten as a discriminating function g, as follows:

g(w

) = log P(w

) (6)

= log P(w

) + k log p

∑

t=1

log(1 − p

)

(7)

where p

is estimated by eq. (4).

The decision rule for the vector x

and a perfor-

mance class w

is given by:

ˆw

= arg max

j∈Ω

g(w

3.2 The Fuzzy Geometric Naive Bayes

Network

The new Bayesian Network named Fuzzy Geomet-

ric Naive Bayes Network is proposed from union of

the Zadeh’s deﬁnition of probability of fuzzy events

(Zadeh, 1968) and geometric distribution. Formally,

let (R

, B, P) a probability space, where B is σ-ﬁeld

of Borel subsets in R

and P is probability measure of

. Let F in B a fuzzy event with membership func-

tion µ

: R

−→ [0, 1], then the probability of a fuzzy

event F is deﬁned by the Lebesgue-Stieltjes integral

presented in the eq. (8).

P(F) =

F⊆R

(x)dP = E(µ

)

F⊆R

(x) f (x)dP (8)

A Novel Fuzzy Geometric Naive Bayes Network for Online Skills Assessment in Training Based on Virtual Reality

397

where f (x) is a density function of a random vari-

able X (Zadeh, 1968). Thus, let a random vector

{

,. .. ,X

}

, such that each X

, t = 1,...,k

is a fuzzy random variable with membership function

), j = 1, .. ., M, so we have:

P(w

,..., X

) =

P(w

)

∏

t=1

P(X

)µ

(9)

where S

is a scale factor.

As in the case of the Geometric Naive Bayes Net-

work, assuming that P(X

) follows a geometric

distribution, and applying some mathematical manip-

ulations, the Fuzzy Naive Bayes Geometric Network

can be described by a discriminating function g

) = log P(w

)

=log P(w

) + k log p

∑

t=1

log(1 − p

)

+ log µ

) (10)

where p

are estimated using the training data of for

each class w

, j ∈ Ω and the estimator given by the

eq. (4). When compared equation (10) to equation

(6) it is worth noting the membership function of X

for the performance class w

is modelling the fuzzy

information.

The vector x

will be assigned to the performance

class w

, according to the decision rule:

ˆw

= arg max

j∈Ω

4 ACCURACY MEASURES

In this section, the performance of the assessment

methods is measured. The accuracy (a) and Kappa

coefﬁcient (κ) are adopted as comparison criteria,

which are deﬁned as follows.

The accuracy (a) is a metric that relies on the con-

fusion matrix, depicted in Table 1. It is determined by

the following deﬁnition:

a =

∑

i= 1

∑

i= 1

∑

j =1

i j

, (11)

where

∑

i= 1

is the sum of the main diagonal terms

of the confusion matrix,

∑

i= 1

∑

j =1

i j

is the sum of

all its entries and g represents its pre-deﬁned parti-

tions.

Another assessment measure that is commonly

used is the Kappa coefﬁcient (K), as proposed by Co-

hen (Cohen, 1960). This coefﬁcient is deﬁned based

on the confusion matrix as follows:

Table 1: Confusion matrix.

Real class (c)

1 2 ·· · g

Assigned class ( ˆc)

1 n

·· · n

2 n

·· · n

g n

κ =

− P

1 − P

, (12)

where P

= N

−1

∑

i= 1

, P

= N

−2

∑

i= 1

, n

is the sum of elements at the main diagonal of the

confusion matrix, n

is the sum of its elements at ith

row, n

is the sum of its elements at ith column and

N represents the total number of decisions at the con-

fusion matrix. Variance of Kappa (σ

) was also cal-

culated. According to (Landis and Koch, 1977), the

Kappa coefﬁcient may interpreted by means of con-

cordance percentage in Table 2.

Table 2: Levels of correlation of Kappa coefﬁcient.

κ Kind of concordance

< 0.00 Poor

0.00 |— 0.20 Small

0.20 |— 0.40 Standard

0.40 |— 0.60 Moderate

0.60 |— 0.80 Good

0.80 |— 1.00 Excellent

5 RESULTS

The Fuzzy Geometric Naive Bayes Net-

work was implemented in the FuzzyClass

package ((Ferreira and Moraes, 2023)) of

the R software, available at https://cran.r-

project.org/web/packages/FuzzyClass/index.html

and used to produce the results that follows.

Two simulation studies were conducted in order to

know the performance of the new Fuzzy Geometric

Naive Bayes Network. The ﬁrst study aimed to verify

the maximum likelihood estimator presented in Sec-

tion 2, while the second study focused on generating

a dataset to assess the proposed new training assess-

ment method. Both results are presented throughout

this section.

Table 3 presents the results of parameter estima-

tion for the geometric distribution, speciﬁcally for the

parameter p. Accurate parameter estimates in statisti-

cal distributions are crucial for obtaining reliable and

precise results in analysis and inference. Appropri-

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

398

ate parameter estimation enables a correct description

and understanding of the data, as well as it also en-

ables evidence-based decision making supported by

robust statistical evidence.

In this case, four values for the parameter p were

randomly selected to cover the entire parameter space,

adhering to the constraint 0 < p ≤ 1. The values of p

used in this study were p = [0.05, 0.20,0.60, 0.95]

⊤

Additionally, the sample size was varied to assess

whether the estimation converges to the true param-

eter value with increasing sample size. In this case,

sample sizes of n = [10,30, 100,1000]

⊤

were em-

ployed.

Table 3: Performance of the estimation of parameter for the

Geometric distribution.

ˆp



MSE

ˆp



p=0.05 p=0.20

10 0.0553 0.2153

( 2.8×10

−2

) ( 2.3×10

−1

)

30 0.0523 0.2050

( 5.3×10

−3

) ( 2.5×10

−2

)

100 0.0506 0.2020

( 3.7×10

−4

) ( 4.2×10

−3

)

1000 0.0501 0.1999

(1.8×10

−5

) ( 1.7×10

−6

)

p=0.60 p=0.95

10 0.6255 0.9556

( 6.5×10

−1

) ( 3.1×10

−2

)

30 0.6110 0.9532

( 1.2×10

−1

) ( 1.0×10

−7

)

100 0.6022 0.9501

( 5.1×10

−3

) ( 1.7×10

−5

)

1000 0.6001 0.9501

(1.8×10

−6

) ( 1.0×10

−5

)

The results obtained from this simulation study re-

veal that a Monte Carlo simulation with 1,000 repli-

cations was conducted for each case. The average

value of ˆp across the 1,000 replications and the mean

squared error (MSE

ˆp

) were calculated. The results in-

dicate that as the sample size increases, the estimates

converge to the true parameter value. For instance,

when p = 0.05 and n = 10, the estimated value of ˆp

is 0.0553 with MSE

ˆp

= 2.8 × 10

−2

. However, with

n = 1000, the estimated values for ˆp and MSE

ˆp

are

0.0501 and 1.8 × 10

−5

, respectively. This behavior is

observed consistently across all other cases.

The performance assessment of the proposed

Fuzzy Naive Bayes Geometric Network in a SUAS

(Single-User Assessment System) was conducted

through a Monte Carlo simulation consisting of

1,000 replications. In each replication, a sample of

1,500 observations was generated, representing three

classes of performance that correspond to different as-

sessments of the procedure. These classes include:

Class 1, indicating that ”the procedure was performed

well”; Class 2, indicating that ”the user needs more

training”; and Class 3, indicating that ”the user needs

much more training”.

During the simulation, 70% of the sample was uti-

lized for training the new SUAS based on the Fuzzy

Geometric Naive Bayes Network, while the remain-

ing 30% was allocated for testing purposes. In Table

4, we present the estimated values of p that were used

to generate the samples for this portion of the study.

Figure 3 displays a scatter plot of the ﬁrst two

dimensions of the simulated data. In this case, the

classes are distinguished by different colors. The

Class 1 is represented by light gray, Class 2 by dark

gray, and Class 3 by black. It is worth noting the con-

centration of Classes 1 and 2 points in the lower left

corner of that scatter plot. Densities with parameters

of Table 4 can be observed in the Figure 4, according

to the geometric distribution deﬁned in equation (1).

It is evident that assessment methods with data ex-

hibiting such behavior is challenging due to the over-

lapping distributions.

The proposed network, named Fuzzy Geomet-

ric Naive Bayes (FGeomNB) was compared with

the classical Geometric Naive Bayes (GeomNB), the

Naive Bayes (NB) and the Fuzzy Naive Bayes (FNB)

networks. The results can be found in Table 5, where

the best assessment method was FGeomNB, achiev-

ing a total accuracy of 0.81 and a Kappa coefﬁcient

of 0.72. GeomNB followed closely with an accuracy

of 0.77 and a Kappa coefﬁcient of 0.67. The NB and

FNB assessment methods obtained the same accuracy

and Kappa coefﬁcients, which were 0.60 and 0.40, re-

spectively.

Table 4: Parameters used in the simulation by Monte Carlo.

Estimated Class 1 Class 2 Class 3

Parameters p p p

Dimension 1 0.01 0.50 0.90

Dimension 2 0.01 0.50 0.70

Dimension 3 0.01 0.50 0.50

In Tables 6 and 7, the confusion matrices of the

analyzed methods are found. Table 6 presents the re-

Table 5: Simulation results by Monte Carlo, where a is ac-

curacy, κ is Kappa coefﬁcient, σ

is Kappa coefﬁcient vari-

ance.

Methods a κ σ

NB 0.60 0.40 1.1×10

−3

FNB 0.60 0.40 1.1×10

−3

GeomNB 0.77 0.67 7.7×10

−4

FGeomNB 0.81 0.72 7.3×10

−4

A Novel Fuzzy Geometric Naive Bayes Network for Online Skills Assessment in Training Based on Virtual Reality

399

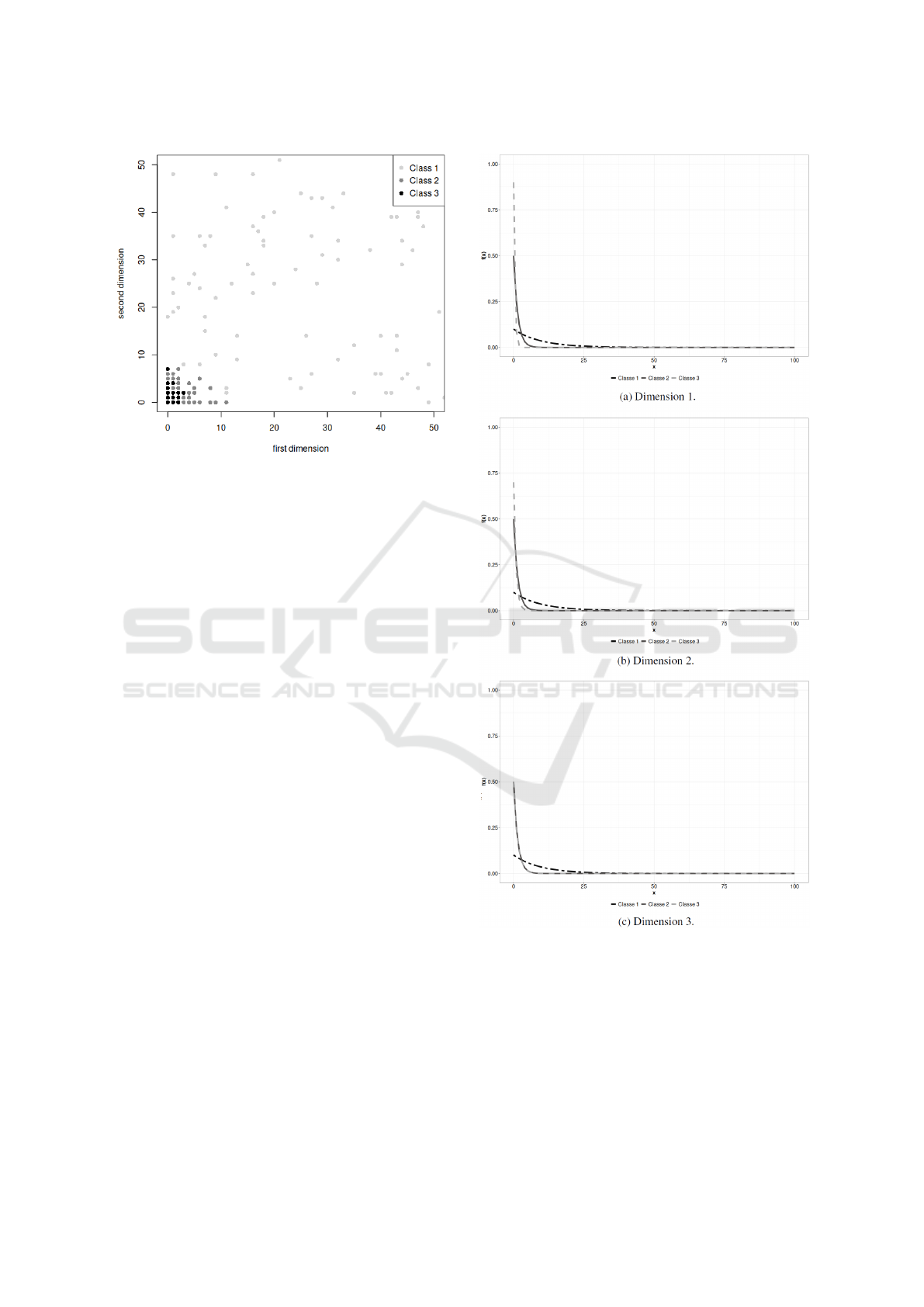
Figure 3: Scatter plot depicting the ﬁrst and second dimen-

sions of the simulated data of a Monte Carlo iteration.

sults for FGeomNB (left) and GeomNB (right). In

Table 7, can be found the results for FNB (left) and

NB (right).

The 30% of the test sample represents that out of

the 450 observations, 158 observations were selected

for class 1, 146 for class 2, and 146 for class 3. In Ta-

ble 6, can be observed that for FGeomNB, it correctly

predicted 156 out of 158 possible instances of class 1,

82 instances of class 2, and 128 instances were cor-

rectly predicted of class 3. For the GeomNB method,

it achieved higher accuracy, correctly predicting 158

out of 158 possible instances of class 1, 47 instances

of class 2, with 99 errors, and 145 instances of class

Similar interpretations can be drawn from Table

6, as they obtained the same discrimination with the

same quantities of correct predictions and errors for

each class. This may demonstrate the difﬁculty of

this method in correctly classifying data with geomet-

ric behaviors. For class 1, the NB and FNB methods

correctly predicted 152 out of 158 possible instances.

For class 2, the methods struggled to make accurate

predictions, correctly assigning only 36 out of 146

possible instances. For class 3, the methods correctly

predicted 91 out of 146 possible instances.

The FGeomNB method demonstrated superior ac-

curacy and Kappa coefﬁcient performance. However,

upon observing the results for each class in tables 6

and 7, it is evident that FGeomNB did not outper-

form GeomNB in correctly allocating observations

for classes 1 and 3. In this case, the utilization of

fuzzy information aided in correctly classifying ob-

servations in class 2, where FGeomNB correctly al-

located approximately twice instances with respect to

Figure 4: Geometric distribution by dimension (variable)

distinct by classes.

GeomNB. Therefore, the choice of the best training

method also depends on the speciﬁc interest in the op-

timal assessment of a particular training case.

Fuzzy information provided improvements in the

SUAS based on Fuzzy Geometric Naive Bayes when

compared to the SUAS based on Geometric Naive

Bayes. However, the same did not occur with SUAS

based on Fuzzy Naive Bayes when compared with the

FCTA 2023 - 15th International Conference on Fuzzy Computation Theory and Applications

400

SUAS based on Naive Bayes. In this case, both SUAS

provided the same results.

Table 6: Confusion matrix of FGeomNB (left) and Ge-

omNB (right) assessment methods.

FGeomNB GeomNB

Real class

Assigned Class Assigned Class

C1 C2 C3 C1 C2 C3

C1 156 2 0 158 0 0

C2 0 82 64 0 47 99

C3 0 18 128 0 1 145

Table 7: Confusion matrix of FNB (left) and NB (right)

assessment methods.

FNB NB

Real class

Assigned Class Assigned Class

C1 C2 C3 C1 C2 C3

C1 157 1 0 157 1 0

C2 95 10 41 95 10 41

C3 38 3 105 38 3 105

In summary, it is found that the proposed network

based on the geometric distribution achieved good

correct allocations for the data used in this study. The

network surpassed previously proposed networks in

the literature such as Naive Bayes and Fuzzy Naive

Bayes, indicating that they can serve as viable alter-

natives for assessment methods.

6 CONCLUSION

In this paper, a novel approach called the Fuzzy Geo-

metric Naive Bayes Network was introduced to han-

dle multidimensional intervals by modeling them us-

ing geometric distributions. This network served as

the foundation for SUAS speciﬁcally designed for

Virtual Reality (VR) simulators, such as SITEG 2.0.

Simulations were conducted using data that fol-

lowed a geometric distribution and compared against

Naive Bayes and Fuzzy Naive Bayes SUAS. The sim-

ulation results demonstrated that the SUAS based on

the geometric distribution has superior discrimina-

tion capabilities, outperforming the traditional Naive

Bayes and Fuzzy Naive Bayes approaches.

Moreover, the Fuzzy Geometric Naive Bayes Net-

work proposed in this study can also be effectively

utilized for datasets that involve intersections with

values close to zero.

ACKNOWLEDGEMENTS

This research is supported by the National Coun-

cil for Scientiﬁc and Technological Development -

CNPq (Grants 305914/2021-9 and 315298/2018-9)

and Fundac¸

ao de Apoio

a Pesquisa do Estado da

Para

ıba - FAPESQ-PB.

REFERENCES

Cohen, J. (1960). A coefﬁcient of agreement for nominal

scales. Educational and psychological measurement,

20(1):37–46.

Ferreira, J. A. and Moraes, R. M. (2023). Fuzzy-

class: A family of fuzzy and non-fuzzy probabilistic-

based classiﬁers. Journal of Open Source Software,

8(88):5613.

Landis, J. R. and Koch, G. G. (1977). The measurement of

observer agreement for categorical data. biometrics,

pages 159–174.

Mendenhall, W., Beaver, R. J., and Beaver, B. M. (2012).

Introduction to Probability and Statistics. Cengage

Learning, 14th edition.

Moraes, R. and Machado, L. (2009). Online training eval-

uation in virtual reality simulators using possibilistic

networks. In Proc. Safety Health and Environmental

World Congress, pages 67–71. Citeseer.

Moraes, R., Silva, I. L. A., and Machado, L. (2020). Online

skills assessment in training based on virtual reality

using a novel fuzzy triangular naive bayes network.

In Proc. FLINS, pages 446–454. World Scientiﬁc.

Moraes, R. M., Ferreira, J. A., and Machado, L. S. (2021).

A new bayesian network based on gaussian naive

bayes with fuzzy parameters for training assessment

in virtual simulators. International Journal of Fuzzy

Systems, 23(3):849–861.

Moraes, R. M. and Machado, L. S. (2012). A new architec-

ture for assessment of multiple users in collaborative

medical training environments based on virtual real-

ity. In Uncertainty Modeling in Knowledge Engineer-

ing and Decision Making, pages 1119–1124. World

Scientiﬁc.

Moraes, R. M. and Machado, L. S. (2015). A fuzzy poisson

naive bayes classiﬁer for epidemiological purposes. In

2015 7th International Joint Conference on Computa-

tional Intelligence (IJCCI), volume 2, pages 193–198.

IEEE.

Moraes, R. M. and Machado, L. S. (2016). A fuzzy bino-

mial naive bayes classiﬁer for epidemiological data.

In 2016 IEEE International Conference on Fuzzy Sys-

tems (FUZZ-IEEE), pages 745–750. IEEE.

Souza, D. F., Valdek, M. C., Moraes, R. M., and Machado,

L. S. (2006). Siteg–sistema interativo de treinamento

em exame ginecol

ogico. In VIII Symposium on Virtual

Reality SVR, volume 12.

Zadeh, L. A. (1968). Probability measures of fuzzy events.

Journal of mathematical analysis and applications,

23(2):421–427.

A Novel Fuzzy Geometric Naive Bayes Network for Online Skills Assessment in Training Based on Virtual Reality

401