Analysis of Powder Behavior Inside the Mortar During

Tableting Process

Yosuke Tachikawa

, Tetsu Kamiya

and Takanori Yamazaki

Graduate School of Science and Engineering, Graduate school of Tokyo Denki University,

Ishizaka, Hatoyama, Hiki, Saitama, 350-0394, Japan

Nagase&Co.Ltd., Tokiwabashi Tower, 2-6-4 Ote, Chiyoda, Tokyo, 100-8142, Japan

School of Science and Engineering, Tokyo Denki University, Ishizaka, Hatoyama, Hiki, Saitama, 350-0394, Japan

Keywords: Tableting, Powder Behavior, Wall Stress, Discrete Element Method.

Abstract: Tableting machines are used to make tablets from food, pharmaceutical, and other powders. It is well known

that the quality of tablets formed by tableting machines varies greatly depending on the compression

conditions, such as compression speed and compression force. Therefore, it is important to clarify the behavior

of powder inside the mortar during the compaction process. In this present research, we designed and

manufactured a thin-walled cylindrical mortar. A special strain gage was attached to the mortar to measure

the force acting on the mortar wall during tableting. Based on these results, a discrete element method (DEM)

simulation is performed, we compare and discuss the behavior of powder inside the mortar during the tableting

process.

1 INTRODUCTION

A tablet machine is a device that makes tablets from

powder by compression molding, and is widely used

in the pharmaceutical and food industries. The

advantage of using powder as tablets is the reduction

of transportation and storage costs due to the reduced

volume, which is expected to be applied not only in

the food industry but also in the materials industry

(Kamiya, 2022). Typical performance requirements

for compression molding of powders include high-

speed molding to improve productivity and high-

hardness molding to prevent tablets from

disintegrating easily (Danjo, 1998). However, the

dynamic behavior of the powder during the

compression process seems to be unclear. One of the

problems with the current product is that strength of

the top and bottom corners of the tablets are weak,

resulting in defective tablets during transportation.

In the manufacture of tablets for various kings of

pharmaceuticals, it is a major issue to optimize

tableting conditions according to the physical

properties of the various raw material powders, from

prototyping to mass production (Natsuyama, 2001).

Powder simulation is a useful solution to this issue,

and there are two major methods for this: the DSMC

and the DEM method. The DSMC method treats

particles as hard spheres. This method calculates the

time for the next collision across the system and uses

that time as a time step to translate and rotate the

particles. When particles collide, the direction of

velocity is reversed, and the velocity after repulsion

is calculated from the relative velocity before

collision and the coefficient of repulsion. The DEM

method represents a material as a collection of DEM

particles, and solve the equations of motion for the

translational and rotational motion considering the

contact force (repulsive force, frictional force),

gravity, and adhesive force (van der Waals force,

liquid bridge force) acting between particles. By

using this method, the dynamic behavior of powder

can be reproduced and predicted (Yamanoi, 2018).

The DEM method is recently gathering attention as a

simulation tool for treating with various technical

problems in the pharmaceutical, food, and lumber

processing industries using powder (Hassanpour

2010).

There are also two advantages to using the DEM

method. First, since particle collisions are considered

as soft potentials, large time steps are possible. As a

result, it can be applied to large-scale systems. The

second is applicable to high concentration systems. In

Tachikawa, Y., Kamiya, T. and Yamazaki, T.

Analysis of Powder Behavior Inside the Mortar During Tableting Process.

DOI: 10.5220/0012212000003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 297-301

ISBN: 978-989-758-670-5; ISSN: 2184-2809

297

the case of compression molding, the particles are

always in contact, so the DSMC method, which treats

them as rigid spheres, is not realistic. For the above

reasons, this paper uses the DEM method.

In our previous studies, we found that the

hardness of compression-molded tablets varied

depending on the height position and confirmed that

the hardness was lower at the top and bottom of the

tablets. From these results, it was considered that the

force applied to the powder in the mortar was not

uniform. In this present research, we designed and

manufactured a thin-walled cylindrical mortar. A

special strain gage was attached to the mortar, by

using this, the force acting on the mortar wall during

tableting was measured. Furthermore, based on the

compressive forces measured in actual tableting, the

forces acting on the powder in the mortar were

calculated by simulation using the DEM method and

we discuss the behavior of powder inside the mortar

during the tableting process.

2 EXPERIMENTAL DEVICE

2.1 Tableting Machine

Figure 1 shows the overall structure of a tableting

machine. There are two types of tableting machines:

the single-shot type and the rotary type. In this

research, the single-shot type was adopted because

the purpose of tableting is prototyping and the

tableting conditions can be changed.

The tableting machine consists of a base plate and

three plates for installing each component on an

aluminum frame, insert a long bolt into each of the

left and right hollow shafts and fix them. the upper

and lower pestles are operated by an electric cylinder

consisting of a servo motor and a ball screw. The

pestle moves 5 mm per rotation of the motor. The

specifications of the upper and lower servo motors are

rated torque 1.15 N·m, rated current 2.8 A, and

voltage AC 200 V.

2.2 Tableting Experiment

Compression molding is performed by moving the

pestle by numerical control using a host device

(PMAC made by OMRON). In this case, the upper

pestle was used as a dynamic pestle.

The experimental procedure is, first, the sample

(powder) is weighed using an electronic balance with

an accuracy of 1.9995 g to 2.0004 g and the sample

throw inside a 20 mm-diameter mortar. Next, run the

numerical control program and form a tablet. First,

the initial position of the pestle is that the lower pestle

is 10 mm into the mortar, and the upper pestle is 50

mm from the top of the mortar. The compression

procedure is divided into two parts: the lowering and

rising motions of the upper pestle. The descending

motion performs acceleration, uniform motion, and

deceleration over a distance of 61.5 mm. The speed

of uniform motion is 1 mm/s. After the descent ends,

it begins an upward motion without stopping. The

rising motion also accelerates, moves at a constant

velocity, and decelerates over a distance of 61.5 mm.

The speed of uniform motion is 50 mm/s. This

completes one tableting motion.

After compression molding, the tablet height is

measured using a laser sensor, and the tablet mass is

measured using an electronic balance. The material of

mortar is aluminum (A5052). The shape of the mortar

is thin-walled cylindrical, a diameter of 20 mm and a

wall thickness of 1 mm. A special strain gauge was

attached the mortar to measure circumferential strain.

Figure 2 is a photo of the mortar attached to strain

gauge and their locations are shown in Figure 3. The

numbers in Figure 3 are in mm.

2.3 Experimental Results

In the tableting experiment, the compression force of

the upper pestle was 1467 N, the compression force

of the lower pestle was 803 N, and the diameter of the

upper pestle was 19.9 mm, so the upper pestle

pressure was 4.72 MPa. Although not shown in the

graph, these are the measurement results of the load

cell installed at the base of the upper and lower pestles.

These results are the average of the three experiments.

Figure 1: Tabletting machine.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

298

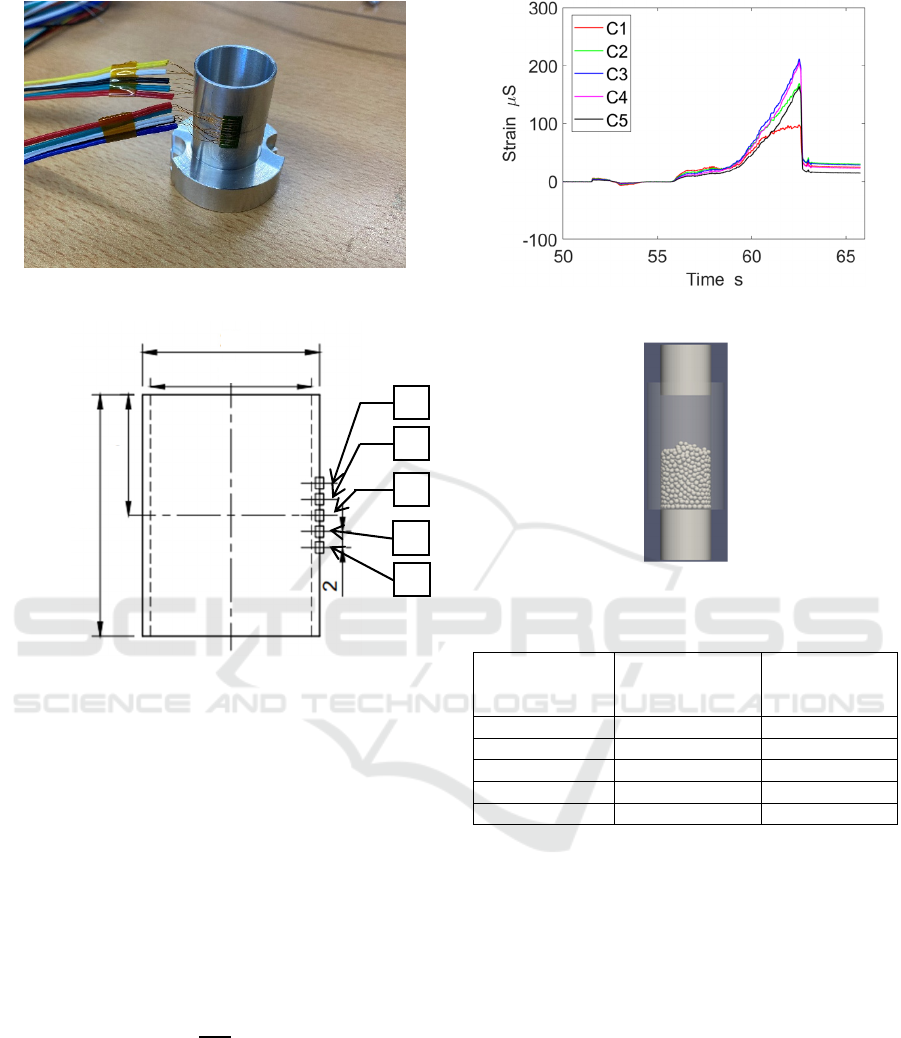
Figure 2: A mortar with a strain gauge.

Figure 3: Strain gauge position.

Figure 4 shows the measurement results of the

circumferential strain obtained in the experiment.

Using the following relational expression for a thin-

walled cylinder, The calculated internal pressure

acting on the inner wall of the mortise is shown in

Table 1. These results are the average of the three

experiments, where, 𝜎



：circumferential stress,𝑃



：

internal pressure, E ： Young's modulus, 𝜀



：

circumferential strain, r：radius of the inside of the

mortar, t：wall thickness.

𝜎



𝐸𝜀

(1)

𝜎





𝑃



𝑟

𝑡

(2)

According to Table 1, the strain in the height direction

was the largest for C3 and the smallest for C1. When

the pressure acts uniformly in a pressure vessel, the

strain generated on the wall surface is considered to

be constant, but this experiment revealed that the

force acting on the inner wall of the mortar has

adistribution. We also found that even the highest C3

value is

lower

than

the

pressure

calculated

from the

Figure 4: Circumference strain.

Figure 5: Overall structure in simulation.

Table 1: Comparison of strain and internal pressure.

Determination

of position

Circumferential

strain

μS

Internal

pressure

MPa

C1 93.9 0.639

C2 166 1.12

C3 212 1.44

C4 205 1.39

C5 164 1.11

upper pestle compressive force. It was found that the

pressure applied to the wall of mortar was about

30.5% of the pressure of the upper pestle.

3 SIMULATION

3.1 Discrete Element Method

DEM is a numerical method for predicting

mechanical dynamics such as position, velocity and

motion of individual particles. The basic principles of

DEM are as follows. (a) Forces exerted by adjacent

particles or boundaries of each particle are computed

in a single time step using the contact model. (b)

Apply Newton's second law to calculate the particle

velocity. (c) Based on the same principle, the

Analysis of Powder Behavior Inside the Mortar During Tableting Process

299

rotational momentum balance is solved to track the

rotational velocity of the particle. (d) New positions

of the particles are computed for the length of the time

step. This procedure is applied to each particle in a

single time step and repeated for each time step (Su,

2019).

3.2 DEM Simulation Condition

The conditions of the DEM simulation were as

follows. The tableting conditions were single stroke

tableting at 1 mm/s, the same as in the experiment.

The size of the mortar was set to 1/10 the diameter in

order to shorten the calculation time. In this analysis,

since we focused on equalizing the pressure applied

to the powder, although the actual compression

pressure was 4.72 MPa, the simulation compression

pressure was 3.85 MPa. As a result, both pressures are

almost equal at 4 MPa.

The particle size of the powder is assumed to be

200 μm. It should be noted that the average particle

size of the actual powder is about 200 μm, but which

is not so uniform. Figure 5 shows how the powder

was filled in the mortar used in the simulation.

3.3 DEM Simulation Result

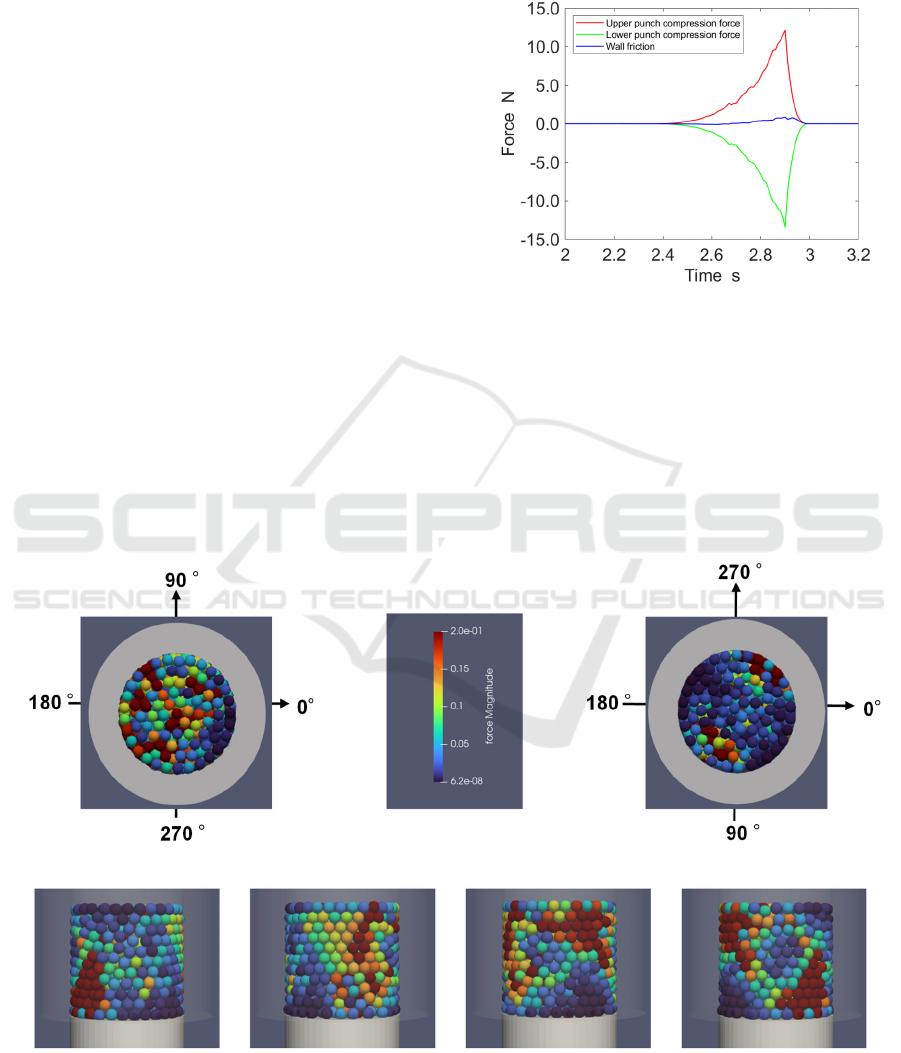
Figure 6 shows the frictional forces on the upper

pestle, lower pestle, and wall calculated from the

tableting simulation. The force acting on the pestle

and wall is calculated as the sum of the forces acting

on the particles in contact with the pestle and wall.

Figure 6: Upper and lower pestle compression force, wall

friction force.

Basically, it can be found that the upper pestle

compressive force plus the wall friction force are

equal to the lower pestle compressive force.

The forces on the particle at the instant of

maximum compression are shown in Figure 7. Where,

the results are viewed from (a) top, (b) bottom, (c) 0

degree side, (d) 90 degree side, (e) 180 degree side,

and

(f) 270 degree side, respectively. First, from

(a) Top view (b) Bottom view

Figure 7: Force on particles at maximum compression.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

300

Figure 7(a) and (b), it is clear that the force does not

reach the lower pestle in the case of upper pestle

compression, although there are variations. Therefore,

it is expected that the hardness of the upper part will

be higher. The results in Figures 7(c)-(f) also show

that there is variation in the state of the lateral surfaces.

Compared to the strain measured in the Figure 4, the

force at the upper end C5 is smaller, indicating that

the distribution is close to the condition shown in

Figure 7(c). In the future, it will be necessary to

improve the accuracy of the experiment, including the

position of strain measurement.

4 CONCLUSIONS

In this paper, the behavior of the powder inside the

mortar the tableting process is analyzed by

experiment and simulation.

In the experiment, we

measured the strain in the circumferential direction of

the mortar and found that the force acting on the

formed tablets varied in the height direction.

In the

simulation, there was validity between the analytical

results of the upper and lower pestle compressive

forces and the measured results. In the case of upper

pestle compression (upper pestle is driving pestle), it

was confirmed that the force acting on the upper part

of the tablet is large. It was confirmed that the force

from the upper punch was not fully transmitted to the

bottom of the tablet, and that not much force was

acting on it.

However, when looking at the side surface, the

force acting on the powder varied depending on the

angle. This was a new discovery. This suggests the

possibility that the hardness changes depending on

the direction in which the hardness test is performed.

In addition, we were able to confirm the

rearrangement of the powder, which was not seen in

the actual tableting process. It is necessary to pay

attention to the rearrangement of particles because it

greatly affects the quality of tablets (Furukawa, 2017).

In the future, we plan to conduct analysis using a

mortar that is more realistic, and to proceed with

verification by comparison with experiments.

REFERENCES

Kamiya, T., Hanyu, K. (2022). Hardening Mechanism of

Tablet Infant Formula -The Role that Synchrotron Light

Technology Carries Out-. in Japanese.

Danjo, K., Hiramatsu, A., Otsuka, A. (1998). Effect of

Pestle Velocity on the Compressibility and Stress

Relaxation of Particles and Granules. Powder

Engineering Journal. in Japanese.

Natsuyama, S. (2001). Particle Motion Analysis in Solid

Dosage Equipment by DEM Simulation and

Application to Equipment Development. in Japanese.

Yamanoi, M., Nakata, Y. (2018). Basics and application

examples of the Discrete Element Method. in Japanese.

Hassanpour, A., Tan, H., Bayly, A., Gopalrishnan, P., Ng,

B., Ghadiri, M., (2010). Analysis of particle motion in

a paddle mixer using Discrete Element Method (DEM).

Powder Technology.

Su B., Eun-Sol H., Min-Soo K., Seonf H., Sung-Joo H., Du

H. (2019). Application of the Discrete Element Method

for Manufacturing Process Simulation in the

Pharmaceutical Industry.

Furukawa, R., Kadota, K., Noguchi, T., Shimosaka, A.,

Shirakawa, Y. (2017). DEM Modelling of Granule

Rearrangement and Fracture Behaviours During a

Closed-Die Compaction. PharmSciTech.

Analysis of Powder Behavior Inside the Mortar During Tableting Process

301