A Novel Hybrid Approach Combining Beam Search and DeepWalk for
Community Detection in Social Networks
Aymene Berriche
2,∗
, Marwa Na
¨
ır
2,∗
, Kamel Mohammed Yamani
2,∗
, Mehdi Zakaria Adjal
2,∗
,
Sarra Bendaho
2
, Nidhal Eddine Chenni
2
, Fatima Benbouzid-Si Tayeb
1,2
and Malika Bessedik
1,2
1
Laboratoire des Methodes de Conception de Syst
`
emes (LMCS), BP 68M - 16270 Oued Smar, Alger, Algeria
2
Ecole Nationale Sup
´
erieure d’Informatique (ESI), BP 68M - 16270 Oued Smar, Alger, Algeria
Keywords:
Social Networks, Community Detection, Combinatorial Optimization Problem, Beam Search, DeepWalk,
Modularity.
Abstract:
In the era of rapidly expanding social networks, community detection within social graphs plays a pivotal
role in various applications such as targeted marketing, content recommendations, and understanding social
dynamics. Community detection problem consists of finding a strategy for detecting cohesive groups, based
on shared interests, choices, and preferences, given a social network where nodes represent users and edges
represent interactions between them. In this work, we propose a hybrid method for the community detection
problem that encompasses both traditional tree search algorithms and deep learning techniques. We begin
by introducing a beam-search algorithm with a modularity-based agglomeration function as a foundation. To
enhance its performance, we further hybridize this approach by incorporating DeepWalk embeddings into the
process and leveraging a novel similarity metric for community structure assessment. Experimentation on
both synthetic and real-world networks demonstrates the effectiveness of our method, particularly excelling in
small to medium-sized networks, outperforming widely adopted methods.
1 INTRODUCTION
The explosive growth in social media users, projected
to reach nearly six billion by 2027 (Dixon, 2023),
has highlighted the critical importance of community
detection. This task, extending beyond traditional
applications such as targeted advertising and trend
analysis, content recommendation, and online secu-
rity (Jain et al., 2020; Kumar et al., 2020; Jain et al.,
2023), now finds utility in novel domains like epi-
demiology, political science, and social psychology,
making it a central research focus in the contempo-
rary digital landscape.
Community detection, a core problem in social
network analysis, involves identifying distinct groups
of nodes within a network characterized by robust in-
terconnections. This is achieved by effectively par-
titioning network nodes into cohesive clusters with
dense internal connections while maintaining sparse
connections with nodes in other clusters.
Various approaches to addressing the community
detection problem in social networks have been pro-
∗
These authors contributed equally to this work and
share first authorship
posed, as highlighted in a recent survey of (Bara’a
et al., 2021), in which researchers formulated the is-
sue as a combinatorial optimization problem. This
formulation allows for the use of various optimiza-
tion methods, such as heuristics and meta-heuristics.
Many functions to evaluate the quality of partition-
ing in network communities have been proposed, but
Modularity emerged as one of the most well-known
and widely used measures in this field (Newman and
Girvan, 2004).
Tree-search (TS) algorithms, initially designed
for exploring search spaces to identify optimal or
near-optimal solutions, have demonstrated their effi-
cacy in solving optimization problems. Such appli-
cations include Monte Carlo optimization algorithms
for dense subgraph identification (Zhang and Chen,
2015), branch-and-bound methods for quasi-clique
detection (Mahdavi Pajouh et al., 2014), and adap-
tations for diverse problems like puzzles (Cazenave,
2012) and the Container Pre-Marshalling Problem
(CPMP) (Tanaka and Tierney, 2018). Furthermore,
TS algorithms have found utility in community de-
tection, with approaches such as efficient detection
of disjoint communities (Palsetia et al., 2014) and
454
Berriche, A., Naïr, M., Yamani, K., Adjal, M., Bendaho, S., Chenni, N., Tayeb, F. and Bessedik, M.
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks.
DOI: 10.5220/0012231500003584
In Proceedings of the 19th International Conference on Web Information Systems and Technologies (WEBIST 2023), pages 454-463
ISBN: 978-989-758-672-9; ISSN: 2184-3252
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

BBmst for real-time community detection in evolving
networks (Nath, 2022).
Lately, machine learning (ML) methods, particu-
larly graph embeddings (Perozzi et al., 2014), have
gained attention in community detection. Graph
embeddings represent graph structures in low-
dimensional vector spaces, capturing node and edge
relationships and features. Graph Convolutional Net-
works (GCNs) (Kipf and Welling, 2017; Jia et al.,
2019) have also seen extensive use in community de-
tection.
Acknowledging the effectiveness of ML methods,
their integration with tree-search (TS) algorithms has
been explored to enhance performance. As noted
by (B
¨
other et al., 2022), these efforts have yielded
mixed results, with some studies showing signif-
icant enhancements while others remain inconclu-
sive. Such approaches include ML-guided heuris-
tics for NP-hard combinatorial optimization problems
(Khalil et al., 2017), employing an ML model to guide
Beam Search in selecting promising nodes (Huber
and Raidl, 2022), and Utilizing Graph Neural Net-
works for expansion within the search space (Li et al.,
2018). However, to the best of the authors’ knowl-
edge, the hybridization of TS algorithms with ML
have not yet been explored in the context of commu-
nity detection.
In this work, our challenge not only aims to eval-
uate the effectiveness of TS algorithms in addressing
the community detection problem but also delves into
the impact of hybridizing them with ML techniques.
Our contributions can be summarized as follows:
• We introduce a beam-search algorithm with a
modularity-based agglomeration function as a
baseline of our approach.
• To further boost the performance of our algorithm,
we integrate DeepWalk embeddings into the pro-
cess. We refer to the resulting hybrid algorithm as
BeamWalk.
• We present the Compound Similarity, an new
similarity metric designed for evaluating interme-
diate solutions discovered during the execution of
BeamWalk.
The rest of the paper is organized as follows. In
Section 2, we define the problem of community de-
tection. In Section 3, we introduce Beam Search as
a fundamental method and then present an enhanced
ML-boosted variant. We outline the experiments con-
ducted to evaluate the effectiveness of our approach,
along with the obtained results and their interpretation
in Section 4. Finally, Section 5 concludes the paper
with our conclusions, and proposes potential avenues
for future research.
2 PROBLEM STATEMENT
A social network can be modeled by a graph, G =
(V, E) which includes N =
|
V
|
nodes and m =
|
E
|
edges. V is the set of nodes and E is the set of edges.
Formally V = {v
1
, . . . , v
n
} and E = e
i j
n
i, j=1
.
The problem of community detection involves
finding a strategy for detecting communities given
a network where the nodes represent users and the
edges represent connections between two users. The
similarity w
i j
between users i and j is the weight of
the edge connecting i and j (This value lies in the in-
terval [0, 1] and indicates the degree of similarity in
their interests). The result is a set of communities
C = {C
1
,C
2
, . . . ,C
K
}. A node v
i
classified in commu-
nity C
k
must satisfy the condition that its internal de-
gree within the community is greater than its external
degree. If C
k
∩C
k
′
=
/
0 for all k, k
′
, then C denotes dis-
joint communities; otherwise, overlapping communi-
ties.
3 PROPOSED APPROACH
Beam search is a TS algorithm that is widely used
in computer science and natural language process-
ing. The algorithm explores a graph by expanding
the most promising node in a limited set, reducing
the memory requirements of best-first search. Beam
search is also similar to breadth-first search (BFS)
(Sabuncuoglu and Bayiz, 1999), in that it progresses
level by level without backtracking. However, unlike
BFS, beam search only moves downward from the β
most promising nodes (rather than all nodes) at each
level, where β is referred to as the ”beam width.” The
remaining nodes are simply ignored.
In this section, we present our proposed model-
ing of the problem of community detection into a TS
problem, this will serve as the building block for the
next section where we propose a hybridization with
DeepWalk.
3.1 Proposed Beam Search Algorithm
To adapt beam search for community detection, we
begin by representing the community partition as a
list of sets, with each set denoting a distinct commu-
nity of nodes. The subsequent step entails defining
the foundational elements of the beam search algo-
rithm. This encompasses the determination of the so-
lution approach whether it be improvement-focused
or constructive in nature. Within this framework, we
must specify tree nodes, establish expansion rules,
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks
455

formulate an evaluative function for guiding our ex-
ploration, devise a scoring mechanism to estimate
solution quality, and ultimately establish the criteria
governing the termination of the search.
In what follows, we will delve into a comprehen-
sive exploration of the proposed algorithm, providing
a detailed implementation of its step-by-step process
in Algorithm 1.
• Search Strategy. We explore the solutions
space using an improvement approach; starting
with singletons as initial communities. Solutions
are expanded by considering all potential commu-
nity merges, thereby exploring every conceivable
community partition that may arise from the ini-
tial partition.
• Tree Node. We define a tree node to be a cor-
rect community partitioning for that graph, more
formally let G = (V, E) be a network graph, a tree
node is noted as C, where C = {C
1
,C
2
, . . . ,C
K
} is
denoting a set of disjoint communities, K being
the number of partitions.
• Expansion Rule. We expand a node using all
the possible community merges, the expansion
is done by merging two communities at a time.
For a node C = {C
1
,C
2
, . . . ,C
K
}, a child-node
C
′
is defined as C
′
= {C
1
,C
2
,C
′
3
. . . ,C
K−1
} where
C
′
3
= {C
i
,C
j
} 1 ≤ i, j ≤ K, i ̸= j is the resulting
community merge.
• Evaluation and Score function. Here we define
both the evaluation and score function to be the
modularity score (Newman and Girvan, 2004).
Modularity would be employed to determine the
best β communities, with their modularity values
being evaluated at each tree level. The ultimate
solution returned would be the community parti-
tioning that exhibits the highest modularity score.
• Stopping Criteria. We define the stopping crite-
ria as the measure of no improvement in terms of
modularity score, for that the difference between
the modularity score of the parent node and the
child node is measured.
Figure 1 shows an example of our beam search mod-
eling for the community detection problem.
3.2 Proposed BeamWalk Algorithm
The major problem with the proposed beam search
approach is the time complexity in the modularity
computation which is in the order of O(mn). This
makes the algorithm very slow and not suitable for
large graphs hence the need for a more convenient and
less complex metric.
...
... ... ...
5
7
4
6
Q = -0.0769
0
3
1
2
5
7
4
6
Q = -0.0769
0
3
1
2
5
7
4
6
Q = 0.0059
0
3
1
2
5
7
4
6
Q = 0.0237
0
3
1
2
5
7
4
6
Q = -0.0355
0
3
1
2
5
7
4
6
Q = -0.0858
0
3
1
2
5
7
4
6
Input Graph
0
3
1
2
Figure 1: Beam search modeling for the problem of com-
munity detection with β = 2. Q refers to modularity.
Input: G = (V, E), β, N
min
Output: S
best
beam list = [{v
i
} for v
i
∈ V ];
K : number of communities for the current
level;
while ∆Q
i
> 0 and K ≥ N
min
do
foreach node in beam list do
Generate child nodes from the current
node;
Evaluate modularity for each child
nodes ;
Save ∆Q
i
for child
i
;
Prune if ∆Q
i
< 0;
end
Select the top β nodes based on
modularity; Re-initialize beam list with
the best β nodes for next iteration;
end
Return S
best
, the best solution seen so far;
Algorithm 1: Modularity-Based Beam Search for Commu-
nity Detection.
Therefore, in this paper, we propose an approach
(Figure 2) that first maps the problem into a latent
space representation in R
d
using a graph embedding
algorithm: DeepWalk (Perozzi et al., 2014). Then, we
adapt our TS algorithm introduced before to the new
modeling by introducing a new evaluation function
based on the cosine similarity which is of the com-
plexity of O(d) where d is the learned vector dimen-
sion (usually ranges from 32-128).To further acceler-
ate the search, we initialize the algorithm with Max-
imum Independent Cliques as initial communities,
which helps accelerate the algorithm by restricting the
search space, as cliques tend to be in the same com-
munity. To estimate the minimum number of com-
munities N
min
, a heuristic estimation is performed; in
WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies
456

Input graph
Embeddings
Maximum Independent
Beam Search with compound similarity
Predicted communities
And
...
Graph Embedding
using DeepWalk
Cliques Detection
Estimation of the
number of communities
Figure 2: BeamWalk Process.
our experiments, we used the Elbow method. We also
introduce a pruning strategy to speed up the search.
Finally, a beam search is conducted on the initial set
of communities, and the output is the best commu-
nity S
best
as measured by (2), meeting the minimum
number of communities requirements.
The Beamwalk algorithm is recalled in Algorithm
2, and its main features are detailed in the sub-
sections below.
3.2.1 DeepWalk Algorithm
DeepWalk learns a latent space representation of so-
cial interactions in R
d
. The learned representation
encodes community structure so it can be easily ex-
ploited by standard classification methods. The algo-
rithm consists of three main steps (Figure 3):
1. Sampling Random Walks. In this first step, ran-
dom walks on the graph are generated. A random
walk starts from a node and traverses the graph by
randomly choosing one of its neighboring nodes
as the next step. This process is repeated for a
fixed number of steps or until a termination condi-
tion is met. By performing multiple random walks
starting from different nodes, the algorithm aims
to capture the structural information of the graph.
2. Training Skip-Gram Model. Once the random
walks are generated, the next step is to use them to
train a skip-gram model, which is a popular tech-
nique in natural language processing for learning
word embeddings. In the context of DeepWalk,
the skip-gram model is adapted to learn node em-
beddings. The skip-gram model takes a node as
input and tries to predict the nodes that are likely
to appear in its neighborhood based on the ran-
dom walks. By optimizing the skip-gram model
using the generated random walks, the algorithm
learns meaningful representations for nodes in the
graph.
3. Computing Embeddings. After training the
skip-gram model, the final step is to obtain the
embeddings for each node in the graph. The em-
beddings represent the learned low-dimensional
vector representations that capture the structural
properties of the graph. The embeddings can be
Skip-Gram
Embeddings
1 2 3 4
2 23 3
3 4 5 6
5 6 3 2
Random Walk
2
1
3
4
5
6
Input Graph
Figure 3: DeepWalk steps for learning a latent space repre-
sentation of social interactions in R
d
.
computed by extracting the learned parameters of
the skip-gram model, which contain the represen-
tations for each node.
3.2.2 Agglomeration Function
The agglomeration is performed using cosine similar-
ity, as defined by Equation (1). Cosine similarity val-
ues range from -1 to 1. In our case, we only consider
merges with positive similarity values. It’s important
to note that when measuring similarity between two
communities, the centroid of each community is con-
sidered.
Similarity(A, B) =
∑
n
i=1
A
i
B
i
q
∑
n
i=1
A
2
i
q
∑
n
i=1
B
2
i
(1)
Where A and B are the two vectors representing
node embedding.
3.2.3 Compound Similarity
The cosine similarity, as a scoring function, proves
insufficient since it exclusively considers the most
recent merge, thereby lacking the ability to provide
prior insights into the quality of past merges or the
overall performance of all branches within the parti-
tioning process. Therefore, we define a new similarity
measure that takes into account all the past merges
and can serve for comparing solutions at the same
level. This measure has proven to give very good re-
sults, better than the modularity measure. The com-
pound similarity measure is computed according to
equation 2:
Compound-Similarity(N
L
) =
L
∑
i=1
log
2
Similarity(N
i
)
(2)
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks
457

where L is the length of the branch leading to the
evaluated solution N
L
, Similarity (N
i
) is the cosine
similarity calculated for each tree node N
i
leading
to N
L
. We only consider positive merges, hence
Similarity(N
i
) ∈]0, 1].
3.2.4 Similarity Threshold
In order to avoid exploring solutions we don’t con-
sider promising, we define a similarity threshold,
where we prune any branch that would result in a
below-threshold maximum merge similarity value as
shown in Figure 4. The value of the threshold should
be defined for each graph, next we define how we es-
timate a good working value for all graphs.
Root
0.9 0.2
0.6 0.4
0.6 0.5
...
Figure 4: Pruning mechanism example, where solutions
having a similarity below threshold = 0.5 are pruned.
We estimate the threshold for each graph G =
(V, E) as the mean of N random similarity measures
sampled from the initial communities initialized as
singletons. More formally, we define it as follows:
T hreshold =
1
N
N
∑
(V
i
,V
j
)∈V
Sim (V
i
,V
j
) (3)
where N is the number of samples.
4 EXPERIMENTAL RESULTS
AND DISCUSSION
To assess the efficiency and performance of our pro-
posed algorithms, we conducted a comprehensive
set of experiments on both synthetic and real-world
networks using a personal computer running Win-
dows 10 Enterprise, equipped with Intel(R) Xeon(R),
2.30GHz, 16 Cores, and 16 GB RAM.
For the synthetic networks, we used the well-
known LFR benchmark (Lancichinetti et al., 2008).
We generate networks using a mixing parameter rang-
ing from 0.1 to 0.6 and nodes from 400 to 10k. For
real-world networks, experiments are conducted on
six widely used real-world datasets namely Zachary’s
Karate (Zachary, 1977); Dolphins Football (Girvan
and Newman, 2002); Polbooks (Lusseau et al., 2003);
Input: G = (V, E), β
Output: S
best
X = Deepwalk(G);
threshold : as defined in (3);
beam list =
MaximumIndependentCliques(G);
N
min
= Elbow(X)
1
;
K : number of communities for the current
level;
while not beam list.empty() and K > N
min
do
foreach node in beam list do
Generate child nodes from the current
node;
Evaluate the child nodes using (1) ;
Prune if Similarity(N
i
) < threshold ;
end
Select the top β nodes based on
evaluation (2);
Re-initialize beam list with the best β
nodes for next iteration;
end
Return S
best
, best solution for level N
min
based on (2);
Algorithm 2: BeamWalk for community detection.
(Rossi and Ahmed, 2015); Email ((Yin et al., 2017));
and Actor ((Tang et al., 2009)).
We adopted two widely used criteria to evaluate
the accuracy of community detection algorithms: the
normalized mutual information (NMI) (Danon et al.,
2005) to measure the similarity between the ground
truth community structure and the predicted one; and
the modularity (Newman and Girvan, 2004) to mea-
sure the quality of the uncovered community struc-
ture.
4.1 Parameters Settings
The BeamWalk approach consists of two stages: ob-
taining embeddings using Deepwalk and then apply-
ing beam search for community partitioning. The pa-
rameters being investigated are those of DeepWalk:
the length of walk sequences denoted as t, the num-
ber of walks conducted per vertex denoted as γ, the
dimensionality of the vector representation space de-
noted as d, and the window size denoted as w.
In order to assess the impact of these parameters
on the performance of the model, we carried out a
01
Note that once in a latent space, the minimum num-
ber of communities could be estimated using different tech-
niques, the one used in our implementation is the Elbow
method(Thorndike, 1953).
WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies
458

rigorous process of systematic parameter adjustment.
During this process, three parameters were kept con-
stant while the remaining parameter was systemati-
cally varied. The resulting vertex vector represen-
tations were then documented, and community de-
tection was performed to evaluate the efficacy of the
model using the NMI score. This analysis was con-
ducted on the synthetic networks, the outcomes of this
investigation are presented in Figure 5.
In Figure 5a, 5c, 5e, and 5g, we kept the walk-
ing length t, dimension d, and window size w con-
stant while altering the number of walks γ to ob-
serve the corresponding NMI score. By varying the
number of walks, we obtained an NMI curve. The
results indicate that the learning algorithm achieves
optimal community detection performance and stabi-
lizes when the number of walks γ reaches 60. Further-
more, when the window size w is set to 5, the commu-
nity detection results demonstrate a higher NMI score
compared to other window sizes. Therefore, for more
accurate community partitioning, we used a window
size of 5 and a number of walks of 60.
In graphs 5b,5d,5f and 5h, we conducted an in-
depth exploration of the influence of different vec-
tor representation dimensions and walk lengths on
the NMI score. We observed that for complex net-
works like LFR4(µ = 0.4), the NMI score stabilizes
after reaching a vector representation dimension of
128. However, for simpler networks, the optimal di-
mension size may be lower, indicating that the com-
munity detection performance benefits from higher-
dimensional vector representations up to a certain
limit, which is dependent on the complexity of the
network. Similarly, we noticed a similar trend for
walk lengths, where longer walk lengths tend to re-
sult in higher NMI scores. Furthermore, the mixing
parameter for the graphs exerts a noticeable influence
on the observed fluctuations. As the mixing parame-
ter increases, we observe a corresponding rise in fluc-
tuations, indicating a greater impact of randomness
on the community detection outcomes. Nevertheless,
our method maintains stability and delivers satisfac-
tory performance despite these fluctuations. Based on
our findings, we used a dimension size of 128 for the
vector representation, as it consistently yields favor-
able results. For achieving more accurate community
detection, we suggest using a high window size value
of 60 when the mixing parameter value is lower than
0.4. However, if the mixing parameter value exceeds
0.4, we advise utilizing a higher window size value of
80 to mitigate the effects of increased randomness.
4.2 BeamWalk Performance Analysis
Figure 6 depicts the NMI score and modularity val-
ues for real datasets. The results show that our hybrid
method gives the best NMI scores in comparison to
other approaches like SSLPA (Cordasco and Gargano,
2010) and Louvain (Blondel et al., 2008). BeamWalk
achieves a maximum NMI score of 1 in the Karate
graph and outperforms other methods in other graphs.
When it comes to more complex graphs like Actor,
our method outperforms the others. The modularity
score isn’t what our method is trying to maximize thus
we could expect other modularity-based algorithms
like Louvain to score better. In general, our method
gives modularity values relative to the quality of the
solutions found.
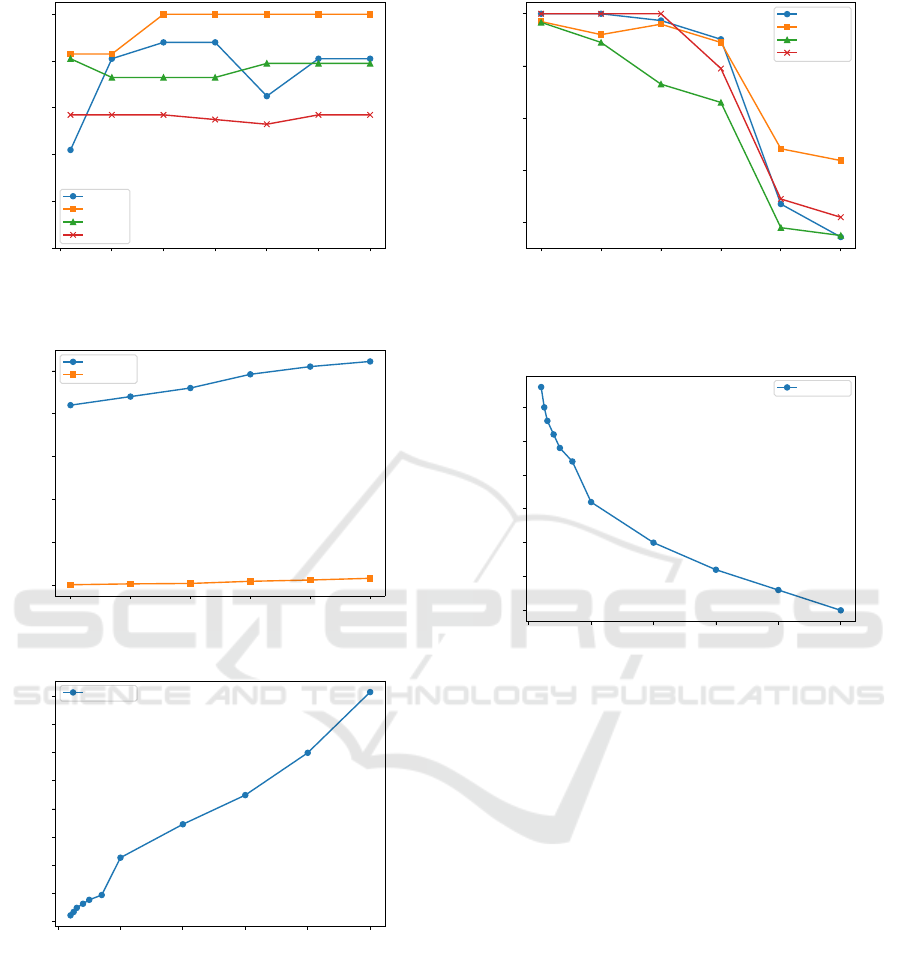
During the analysis of the resulting partitioning
quality for varying beam widths in Figure 7, a consis-
tent improvement in quality is observed as the beam
width increases. However, it is worth noting that this
improvement tends to plateau after reaching a beam
width of β = 10. It is important to acknowledge that
in certain cases, the quality may even decrease. This
behavior can be attributed to the imperfect positive re-
lationship between optimizing the NMI score and the
defined compound similarity metric used in our ap-
proach.
The increased effectiveness achieved through the
hybridization of the initial beam search can be ob-
served in Figure 8, wherein the extent of improve-
ment is positively correlated with both the size and
complexity of the network. Our experimental inves-
tigation, carried out on the LFR dataset (µ = 0.6) in
Figure 9, demonstrates the time scalability of our ap-
proach as the network size increases. Notably, the
time complexity associated with the hybridization is
relatively low due to the avoidance of intricate modu-
larity calculations and the utilization of quality prun-
ing. As a result, our method is particularly suitable
for small to medium-sized networks.
Upon comparison with the vanilla beam search
and other methods, Figure 10 illustrates the robust-
ness of the BeamWalk method, particularly complex
networks. Significantly improved results are achieved
when the value of the µ parameter surpasses 0.5. As
demonstrated in Figure 11, our method exhibits ro-
bustness when faced with an increase in the number
of nodes. Particularly, it yields highly satisfactory re-
sults for small to medium-sized networks.
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks
459

0 20 40
60
80
Walks per vertex
0.2
0.4
0.6
0.8
1.0
NMI
w=5
w=10
w=15
w=20
w=25
w=30
(a)
0
50
100
150
200
250
Representation dimension
0.92
0.93
0.94
0.95
0.96
0.97
NMI
t=20
t=40
t=60
t=80
(b)
0 20 40
60
80
Walks per vertex
0.55
0.60
0.65
0.70
0.75
0.80
0.85
0.90
NMI
w=5
w=10
w=15
w=20
w=25
w=30
(c)
0
50
100
150
200
250
Representation dimension
0.725
0.750
0.775
0.800
0.825
0.850
0.875
0.900
0.925
NMI
t=20
t=40
t=60
t=80
(d)
0 20 40
60
80
Walks per vertex
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
NMI
w=5
w=10
w=15
w=20
w=25
w=30
(e)
0
50
100
150
200
250
Representation dimension
0.65
0.70
0.75
0.80
0.85
0.90
NMI
t=20
t=40
t=60
t=80
(f)
Figure 5: NMI for different LFR benchmark networks. (a) and (b) correspond to LFR1 (µ = 0.1), (c) and (d) LFR2 (µ = 0.2);
(e) and (f) LFR3 (µ = 0.3); (g) and (h) LFR4 (µ = 0.4).
WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies
460

0 20 40
60
80
Walks per vertex
0.5
0.6
0.7
0.8
0.9
NMI
w=5
w=10
w=15
w=20
w=25
w=30
(g)
0
50
100
150
200
250
Representation dimension
0.35
0.40
0.45
0.50
0.55
0.60
0.65
NMI
t=20
t=40
t=60
t=80
(h)
Figure 5: NMI for different LFR benchmark networks. (a) and (b) correspond to LFR1 (µ = 0.1), (c) and (d) LFR2 (µ = 0.2);
(e) and (f) LFR3 (µ = 0.3); (g) and (h) LFR4 (µ = 0.4) (cont.).
Dolphins
Karate
Football Email
Actor
0.0
0.2
0.4
0.6
0.8
1.0
NMI
SSLPA
Louvain
BeamWalk
Vanilla BS
(a)
Dolphins
Karate
Football Email
Actor
0.1
0.2
0.3
0.4
0.5
0.6
0.7
modularity
SSLPA
Louvain
BeamWalk
Vanilla BS
(b)
Figure 6: NMI and modularity scores.
5 CONCLUSION
In this study, we introduced a novel hybrid approach
for community detection in social networks, which
combines a deep learning component: DeepWalk and
Beam search. To the best of our knowledge, this is
the first method that proposes to address this problem
using a tree search approach. Our proposed method
has exhibited several desirable characteristics:
• Effectiveness. The NMI scores achieved by our
method are comparable to, and in some cases sur-
pass, those of other existing approaches. This
demonstrates the effectiveness of our hybrid ap-
proach in accurately detecting community struc-
tures.
• Stability. Our method has demonstrated stability
and robustness when faced with increasing net-
work complexity. This suggests that our approach
can reliably identify communities even in highly
complex networks.
• Relatively Fast. Despite being a TS algorithm,
our method exhibits reasonable computational
time. By leveraging a good initialization, a hy-
brid approach, and an effective pruning strategy,
we have achieved reasonable timing performance.
While our study has presented promising results,
there are several unresolved issues that warrant fur-
ther investigation. One such issue is the adaptation of
our method to social networks with additional node
information. Additionally, accelerating these algo-
rithms remains a challenge. Exploring efficient ini-
tialization algorithms that provide a promising start-
ing point for the tree search, where valuable neighbor-
hoods can still be explored, could be a potential av-
enue for improvement. Furthermore, designing a dy-
namic pruning strategy that adapts the threshold dur-
ing the search based on solution acceptance and local
similarity could enhance the overall performance of
the method.
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks
461

0
5
10
15
20
25
30
β (beam width)
0.0
0.2
0.4
0.6
0.8
1.0
NMI
Dolphins
Karate
Football
Polbooks
Figure 7: Quality comparison on real-world datasets when
augmenting the beam width.
0.1 0.2 0.3 0.4
0.5 0.6
µ (mixing parameter)
0
100
200
300
400
500
Time(s)
Vanilla BS
BeamWalk
Figure 8: Time scaling for large-sized networks.
0 2000 4000
6000
8000 10000
N (Nodes number)
0
200
400
600
800
1000
1200
1400
1600
Time(s)
BeamWalk
Figure 9: Time scaling when augmenting the number of
nodes, the test was conducted on LFR Networks of µ = 0.6.
REFERENCES
Bara’a, A. A., Abbood, A. D., Hasan, A. A., Pizzuti, C., Al-
Ani, M.,
¨
Ozdemir, S., and Al-Dabbagh, R. D. (2021).
A review of heuristics and metaheuristics for commu-
nity detection in complex networks: Current usage,
emerging development and future directions. Swarm
and Evolutionary Computation, 63:100885.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-
0.1 0.2 0.3 0.4
0.5 0.6
µ (mixing parameter)
0.2
0.4
0.6
0.8
1.0
NMI
Vanilla BS
BeamWalk
SSLPA
Louvain
Figure 10: Quality comparison between other methods and
ours when augmenting the complexity of the network, the
test was conducted on LFR Networks of N = 128.
0
2000 4000
6000
8000 10000
N (Nodes number)
0.20
0.25
0.30
0.35
0.40
0.45
0.50
NMI
BeamWalk
Figure 11: Quality scaling when augmenting the number of
nodes, the test was conducted on LFR Networks of µ = 0.6.
vre, E. (2008). Fast unfolding of communities in large
networks. Journal of statistical mechanics: theory
and experiment, 2008(10):P10008.
B
¨
other, M., Kißig, O., Taraz, M., Cohen, S., Seidel, K., and
Friedrich, T. (2022). What’s wrong with deep learning
in tree search for combinatorial optimization. arXiv
preprint arXiv:2201.10494.
Cazenave, T. (2012). Monte carlo beam search. IEEE
Transactions on Computational Intelligence and AI in
games, 4(1):68–72.
Cordasco, G. and Gargano, L. (2010). Community de-
tection via semi-synchronous label propagation al-
gorithms. In 2010 IEEE international workshop
on: business applications of social network analysis
(BASNA), pages 1–8. IEEE.
Danon, L., Diaz-Guilera, A., Duch, J., and Arenas, A.
(2005). Comparing community structure identifica-
tion. Journal of statistical mechanics: Theory and ex-
periment, 2005(09):P09008.
Dixon, S. (2023). Number of worldwide social network
users 2027.
Girvan, M. and Newman, M. E. (2002). Community struc-
ture in social and biological networks. Proceedings of
the national academy of sciences, 99(12):7821–7826.
Huber, M. and Raidl, G. R. (2022). Learning beam search:
WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies
462

Utilizing machine learning to guide beam search for
solving combinatorial optimization problems. In
Machine Learning, Optimization, and Data Science,
pages 283–298, Cham. Springer International Pub-
lishing.
Jain, R., Jain, N., and Nayyar, A. (2020). Security
and privacy in social networks: data and structural
anonymity. Handbook of Computer Networks and Cy-
ber Security: Principles and Paradigms, pages 265–
293.
Jain, R., Kumar, A., Nayyar, A., Dewan, K., Garg, R., Ra-
man, S., and Ganguly, S. (2023). Explaining senti-
ment analysis results on social media texts through vi-
sualization. Multimedia Tools and Applications, pages
1–17.
Jia, Y., Zhang, Q., Zhang, W., and Wang, X. (2019). Com-
munitygan: Community detection with generative ad-
versarial nets. pages 784–794.
Khalil, E., Dai, H., Zhang, Y., Dilkina, B., and Song, L.
(2017). Learning combinatorial optimization algo-
rithms over graphs. Advances in neural information
processing systems, 30.
Kipf, T. N. and Welling, M. (2017). Semi-supervised clas-
sification with graph convolutional networks.
Kumar, A., Sangwan, S. R., and Nayyar, A. (2020). Mul-
timedia social big data: Mining. Multimedia Big
Data Computing for IoT Applications: Concepts,
Paradigms and Solutions, pages 289–321.
Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).
Benchmark graphs for testing community detection
algorithms. Physical review E, 78(4):046110.
Li, Z., Chen, Q., and Koltun, V. (2018). Combinatorial
optimization with graph convolutional networks and
guided tree search. Advances in neural information
processing systems, 31.
Lusseau, D., Schneider, K., Boisseau, O. J., Haase, P.,
Slooten, E., and Dawson, S. M. (2003). The bot-
tlenose dolphin community of doubtful sound features
a large proportion of long-lasting associations: can ge-
ographic isolation explain this unique trait? Behav-
ioral Ecology and Sociobiology, 54:396–405.
Mahdavi Pajouh, F., Miao, Z., and Balasundaram, B.
(2014). A branch-and-bound approach for maxi-
mum quasi-cliques. Annals of Operations Research,
216:145–161.
Nath, K. (2022). Local intrinsic density based com-
munity detection using branch-and-bound and mini-
mum spanning tree. Systems and Soft Computing,
4:200044.
Newman, M. E. and Girvan, M. (2004). Finding and eval-
uating community structure in networks. Physical re-
view E, 69(2):026113.
Palsetia, D., Patwary, M. M. A., Hendrix, W., Agrawal, A.,
and Choudhary, A. (2014). Clique guided community
detection. In 2014 IEEE International Conference on
Big Data (Big Data), pages 500–509. IEEE.
Perozzi, B., Al-Rfou, R., and Skiena, S. (2014). Deepwalk:
Online learning of social representations. Proceed-
ings of the ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining.
Rossi, R. A. and Ahmed, N. K. (2015). The network data
repository with interactive graph analytics and visual-
ization. In AAAI.
Sabuncuoglu, I. and Bayiz, M. (1999). Job shop scheduling
with beam search. European Journal of Operational
Research, 118(2):390–412.
Tanaka, S. and Tierney, K. (2018). Solving real-world sized
container pre-marshalling problems with an iterative
deepening branch-and-bound algorithm. European
Journal of Operational Research, 264(1):165–180.
Tang, J., Sun, J., Wang, C., and Yang, Z. (2009). Social in-
fluence analysis in large-scale networks. In Proceed-
ings of the 15th ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, pages
807–816.
Thorndike, R. L. (1953). Who belongs in the family? Psy-
chometrika, 18(4):267–276.
Yin, H., Benson, A. R., Leskovec, J., and Gleich, D. F.
(2017). Local higher-order graph clustering. In
Proceedings of the 23rd ACM SIGKDD international
conference on knowledge discovery and data mining,
pages 555–564.
Zachary, W. W. (1977). An information flow model for con-
flict and fission in small groups. Journal of anthropo-
logical research, 33(4):452–473.
Zhang, J. and Chen, Y. (2015). Monte carlo algorithms for
identifying densely connected subgraphs. Journal of
Computational and Graphical Statistics, 24(3):827–
845.
A Novel Hybrid Approach Combining Beam Search and DeepWalk for Community Detection in Social Networks
463