Breast Cancer Epidemic Model and Optimal Control

Martina Brunetti, Paolo Di Giamberardino

, Daniela Iacoviello

and Marialourdes Ingrosso

Department of Computer Control and Management Engineering Antonio Ruberi, Sapienza University of Rome, Rome, Italy

Keywords:

Modelling, Breast Cancer, Containment Strategies, Optimal Control.

Abstract:

The breast cancer represents one of the most frequent disease diagnosed worldwide; with the modern im-

provements in medicine and technology a fast detection of tumor could allow a total recovery. In this paper,

it is proposed a compartmental epidemiological model in which the female population is partitioned depend-

ing on the condition with respect to the tumor diagnosis. The model is identiﬁed referring to the population

of a region of Italy, using real data; increasing levels of control are introduced, from noninvasive prevention

to combination of surgery and chemotherapy. In the framework of optimal control, aiming at reducing the

number of severe cases and of women dead by tumor, a suitable combination of control effort is determined,

considering constraints in the containment measures. Numerical results stress the importance of prevention

that at the very beginning increases the number of discovered positive diagnosis, and, successively, signiﬁ-

cantly contains the fatal consequences of breast cancer on the population by reducing the late diagnosis.

1 INTRODUCTION

Breast cancer is the most common type of cancer di-

agnosed worldwide; accounting for nearly 12% of all

tumor cases, it is the type of cancer that causes the

highest number of deaths among the female popula-

tion, (WHO, 2023). It can be invasive or non-invasive,

(Alkabban and Ferguson, 2022) and can take various

forms depending on the particular type of breast cells

that are harmed; breast cancers are typically ductal

or lobular epithelial tumors, (Choi, 2022). Carcino-

mas, which begin in the epithelial cells that line the

body’s organs and tissues, are the most common type

of breast cancer, while adenocarcinoma, a more spe-

ciﬁc type of carcinoma that begins in cells in the ducts

or lobules, is the typical carcinoma that develops in

the breast. The most frequent forms of breast cancer

are:

• Ductal carcinoma in situ (DCIS): it is a non-

invasive or pre-invasive breast cancer also known

as intraductal carcinoma or stage 0 breast cancer.

• Invasive (inﬁltrating) ductal carcinoma (IDC): it

begins in the breast’s milk duct’s cell lining. From

there, the cancer spreads into the adjacent breast

tissues after penetrating the duct’s wall. It might

be able to metastasize to other parts of the body

https://orcid.org/0000-0002-9113-8608

https://orcid.org/0000-0003-3506-1455

through the lymph system and bloodstream.

• Invasive lobular carcinoma (ILC): it starts in the

lobules and may spread to other bodily regions.

On physical exam and imaging, ILC could be

harder than IDC to detect.

There are other forms of breast cancer less frequent

than those previously mentioned which may have a

better prognosis than the more prevalent IDC, (Amer-

ican Cancer Society, 2023). These include: Ade-

noid cystic (or adenocystic) carcinoma, Low-grade

adenosquamous carcinoma (this is a type of metaplas-

tic carcinoma), Medullary carcinoma, Mucinous (or

colloid) carcinoma, Papillary carcinoma and Tubular

carcinoma. The American Joint Committee on Can-

cer (AJCC) has developed and updated the Tumor-

Node-Metastasis (TNM) staging system for breast

cancer. The staging is determined by the size and

location of the tumor, the spread to lymph nodes or

other parts of the body, the grade of the tumor and the

presence of biomarkers, (City of Hope, 2023). There

are ﬁve general stages under the TNM system for the

breast cancer:

• Stage 0: it is known as ”carcinoma in situ”; cancer

cells are present but they haven’t spread yet.

• Stage 1: the tumor is very small and may or may

not have migrated to a neighboring lymph node. A

cancer that has spread into the surrounding area is

referred to as invasive breast cancer. In particular:

Brunetti, M., Di Giamberardino, P., Iacoviello, D. and Ingrosso, M.

Breast Cancer Epidemic Model and Optimal Control.

DOI: 10.5220/0012232000003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 195-202

ISBN: 978-989-758-670-5; ISSN: 2184-2809

195

– Stage 1A: the tumor is smaller than 0.2 mm and

has not spread to the lymph nodes.

– Stage 1B: Cancer between 0.2 mm and 2 mm is

found in the lymph nodes.

• Stage 2: compared to stage 1, the tumor is larger

and might have migrated to a few nearby lymph

nodes. In particular:

– Stage 2A: Though it can’t be detected, the tu-

mor has spread from one to three lymph nodes

(but has not spread to other parts of the body).

The tumor can be 20 mm or smaller (less than

20 mm it cannot be identiﬁed) and can spread

to one to three lymph nodes, or the tumor is be-

tween 20 mm and 50 mm and has not spread to

lymph nodes.

– Stage 2B: The tumor is between 20 mm and 50

mm and has spread to one to three lymph nodes,

or the tumor is larger than 50 mm but has not

spread to any lymph nodes.

• Stage 3: the tumor is larger than at stage 2 and/or

has spread to several lymph nodes and/or to tissue

around the breast or breast bone. In particular:

– Stage 3A: The tumor has spread from four to

nine lymph nodes or to mammary lymph nodes,

but not to other parts of the body; or the tumor

is larger than 50 mm and spread to one to three

lymph nodes.

– Stage 3B: The tumor has spread to the chest

area or caused the breast to swell, or it is in-

ﬂammatory breast cancer. It may have spread

to up to nine lymph nodes but has not spread to

other parts of the body.

– Stage 3C: This refers to any tumor that has

spread to 10 or more lymph nodes, including

those under the collarbone, but has not spread

to other parts of the body.

• Stage 4: the cancer has metastasized, or mobi-

lized, and spread to distant parts of the body, typ-

ically bones, lungs or liver. This is an advanced

stage of cancer, called metastatic breast cancer.

It is possible to have recurrence breast cancer within

the ﬁrst two or three years after treatment, but, in

some cases, it may recur also many years later, (City

of Hope, 2023).

Screening is essential since early diagnosis can

change the course of the disease by avoiding reach-

ing the metastatic form; without any form of preven-

tion, there is a risk of tumor growth and of its spread

through metastases, affecting the success of the ther-

apy and decreasing the probability of survival. Di-

agnostic tests (e.g. mammography, ultrasonography,

magnetic resonance imaging, breast self-examination,

as well as modern and more precise imaging methods)

help the early detection of tumors or lesions predis-

posing to tumors, (Kolak et al., 2017).

The problem of the containment of breast cancer

has been faced also studying the patient’s molecular

proﬁle, to predict the drug response, as in (Huang

et al., 2021). A compartmental modeling approach

is proposed in (Tang et al., 2022), where adverse re-

action on the patient heart (cardiotoxicity) is studied

in the framework of fractional calculus.

The aim of this paper is to carry out an epidemio-

logical study of the spread of breast cancer, proposing

a compartmental model able to represent, in a simpli-

ﬁed way, the population partitioned with respect to

the individuals’ conditions regarding the breast can-

cer. Male breast cancer is rare and accounts for about

1% of cancers occurring in men and about 1% of all

breast cancers worldwide, so the target population is

the female population, (Fox et al., 2022). In particu-

lar, ﬁve compartments are introduced:

• Healthy population.

• Population at stage 0, 1 and 2.

• Population at stage 3 and 4.

• Population of dead subjects from causes different

from breast cancer.

• Population of dead individuals because of breast

cancer.

The population division is inspired by the arti-

cle (Van der Broek et al., 2018), whose model sim-

ulates individual life histories from birth to death,

with and without breast cancer, in the presence and

in the absence of screening and treatment, facing the

problem of risk based screening and treatment by us-

ing MISCAN-Faia microsimulation model. The MIS-

CAN is a computer program introduced in (Habbema

et al., 2018) based on Monte Carlo simulation, yield-

ing the effect of screening on morbidity and mortality

on the population.

In this paper, after the introduction of a dynamical

model describing the evolution of the population in

the ﬁve stages, the identiﬁcation of model parameters

is obtained by using real data of the female popula-

tion of Lazio (region of Italy). Then, three contain-

ment measures are considered, corresponding to non

invasive prevention, like echografy and mammogra-

phy screening, ﬁrst level actions, corresponding to

chemotherapy, and second level actions, correspond-

ing to surgery. In the framework of optimal control

theory it is possible to propose the best resource al-

location strategy aiming at reducing the number of

population at stage 3 and 4 as well as the number of

individuals dead for breast cancer.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

196

The paper is organized as follows. In Section 2

the mathematical model is introduced and the optimal

control is determined, considering also resource con-

straints; in Section 3, ﬁrst the model parameters are

identiﬁed and successively optimal control is imple-

mented and applied. Conclusions an future develop-

ments are outlined in Section 4.

2 MATERIALS AND METHODS

In this paper, the diffusion of breast cancer is studied

at population level, considering groups of subjects ho-

mogeneous with respect to their health condition. As

already pointed out in the introduction, in the popula-

tion, beside the healthy people, only two groups of in-

dividuals with breast cancer are introduced, simplify-

ing the description of the dynamics of the population

with tumor; other two compartments of dead subjects

are considered, distinguishing between those dead as

consequence of tumor and those who died from other

causes than breast cancer. These two compartments

are useful for the identiﬁcation step.

In the following section, a compartmental model

is proposed, introducing control action aiming at re-

ducing the number of subjects affected by this pathol-

ogy. Optimal control appears to be the suitable frame-

work in which determine the best resource allocation

strategy considering limitations, both from economic

and logistic point of view.

2.1 Mathematical Model

The population is partitioned into ﬁve compartments

, i = 1, ...,5, the ﬁrst three corresponding to alive

subjects in different condition with respect to the di-

agnosis of tumor:

• X

(t) represents the number of subjects with no

diagnosis of breast cancer at time t;

• X

(t) corresponds to number of individuals that at

time t are in stage 0, 1 and 2 of the ofﬁcial classi-

ﬁcation of breast cancer patients;

• X

(t) includes the subjects that at time t are in

the more severe condition of breast cancer corre-

sponding to stages 3 and 4.

Other two compartments of removed subjects are in-

troduced, being useful in the parameters’ identiﬁca-

tion step:

• X

(t) represents the number of subjects dead at

time t for other causes than breast cancer;

• X

(t) represents the number of subjects dead at

time t due to breast cancer.

The compartments X

, X

and X

represent possi-

ble stages of human condition with respect to breast

cancer. It is assumed that, also without speciﬁc con-

trol action, it is possible for a subject to recover, and

therefore to transfer, from compartment X

, and even

from X

, to X

. Be the parameter c

the rate of new-

born individuals in X

; c

is the rate at which an in-

dividual in the X

state can receive a positive diagno-

sis of breast cancer, and therefore transfer in the X

class. If c

is very small, at least less than the aver-

age life time, it means that a subject does not receive

a positive diagnosis for life. The parameters c

and c

represent, respectively, the natural recovery from the

and X

compartments to X

; c

is the rate of tran-

sition from X

to X

, corresponding to tumour stage

aggravation. In addition to these evolution parame-

ters, the terms

4/5

, i = 1,..,3 account for the death

rates for classes X

respectively, not connected with

tumour evolution, slightly decreasing on time. The

term

4/5

is the rate of death due directly to tumour,

assumed occurring from the X

condition only. Both

death rates, due to tumor

4/5

and to natural causes

4/5

, i = 1,..,3, are modeled by a decreasing exponen-

tial analytical function, in accordance with the devel-

opment of medical technologies and the improvement

of the quality of life over the years.

Finally, Z

, i = 1,2, 3 denote the rate of possible

new incomers in the compartments X

respectively.

With these positions, and setting C

= c

4/5

, i =

1,2,3, the dynamical matrix:

(t) =





−C

−c

−C

0 c

−C

−

4/5





describes the evolution of the states X

, X

and X

absence of control actions according to the equations





(t)





= A

(t)





(t)













In addition, the evolution of the removed subjects is

given by:



(t)



= A

(t)



(t)



once the matrix

(t) =

4/5

0 0

4/5

is introduced.

The distinction between the evolution of the num-

ber of people who died from other causes than breast

Breast Cancer Epidemic Model and Optimal Control

197

cancer or as consequences of breast cancer is intro-

duced to support the identiﬁcation step, as will be

shown in Section 3.

Introducing the state vector X(t) =



(t) X

(t)



, and deﬁn-

ing the block matrix:

A(t) =



(t) 0

3×2

(t) 0

2×2



in which 0

i× j

denotes the i × j matrix with all entries

equal to zero, the system evolution, without any con-

trol action, can be described in compact form as fol-

lows:

X(t) = A(t)X(t) + Z (1)

with Z =



0 0



Three controls u

, u

and u

are introduced. u

represents non invasive actions able to identify tumor

in the ﬁrst diagnosis as well as possible worsening

of the situation; in the ﬁrst case, u

is the preven-

tion involving subjects in the X

category, still un-

aware of the possible presence of tumor. After the

regular screening, part of individuals with positive di-

agnosis are transferred in group X

and another part

in X

. Non invasive control is applied also to the pa-

tients in X

and, in case of increased severity of the

tumor revealed, they are transferred to class X

. With

i j

is indicated in compact form the product of the

percentage of subjects transferring from the compart-

ment X

under the control u

, i, j = 1, 2,3 and the rate

at which this transfer occurs; the quantity P

weight-

ing the transfer from compartment X

to X

and X

split in

and P

−

, respectively.

Other two invasive controls are added, u

(t) and

(t); they are applied when the subject begins the

treatment process and therefore they can be consid-

ered once the control u

is applied; the efﬁcacy of

these treatments u

is indicated by B

, j = 1, 2,3.

Therefore, by deﬁning the control vector U(t) =

(t) u

(t))

and the matrices:

(U ) =





−P

−

−P





(U ) =





0 B

0 −B

0 0 −B





and

G(U ) =



(t) + G

(t) 0

3x2

2x3

2x2



the dynamical system representing the possible evolu-

tion of the number of people in the ﬁve compartments

X(t) = A(t)X(t) + G(U )X(t)+ Z (2)

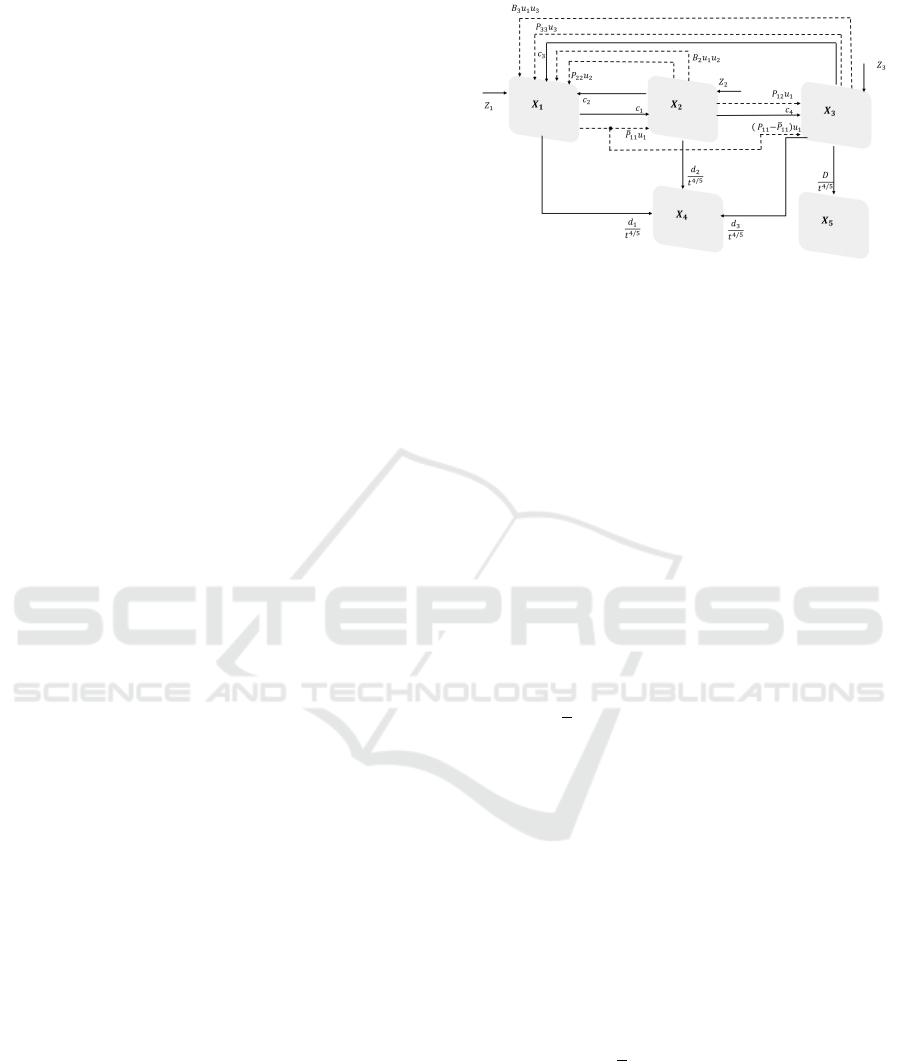
Figure 1: Block diagram of the proposed model.

In Fig.1 it is shown the proposed partition of the

female population indicating with bold arrows the

natural transition between compartments and with the

dotted ones the forced transfer due to external control

actions.

2.2 Optimal Control

Prevention is the best strategy to detect as soon as

possible breast cancer that, if identiﬁed and treated in

advance, could allow complete recover, avoiding in-

vasive treatments. In this section, by considering the

economic, cultural and logistical limitations, it will be

proposed a suitable allocation strategy in the frame-

work of optimal control theory. A cost index is intro-

duced:

J(X,U) =

(α

(t) + α

(t) +

∑

j=1

(t))d t

where α

, i = 1,2, 3 and β

, j = 1,2,3 are the weights

respectively for the states to be minimized and the

controls. The goal of this choice is to reduce the num-

ber of severe cases and of deaths due to tumor. The

controls u

are assumed bounded between 0 (no con-

trol) and 1 (maximum effect)

0 ≤ u

≤ 1 i = 1,2,3 (3)

By denoting with λ(t) =

(λ

(t) λ

(t))

the costate

function, the Hamiltonian is introduced:

H(X,U,λ) =

(α

(t) + α

(t) +

∑

j=1

(t))

+ λ

(t)

X(t) (4)

The Pontryagin principle can be applied yielding nec-

essary conditions:

(t) = minH(X,U,λ), (5)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

198

among all the admissible controls u

in [0,1], i =

1,2,3, with the λ satisfying the costate equations:

λ(t) = −

∂H

∂X



(6)

thus yielding:

(t) = −[λ

−C

− P

) + λ

)

+ λ

−

1)u

+ (λ

− λ

)

4/5

]

(t) = −[λ

+ P

+ B

)

− λ

+ P

− B

− P

)

+ λ

+ c

) + (λ

− λ

)

4/5

]

(t) = −α

− [λ

+ P

+ B

)

− −λ

+ c

4/5

+ B

)

+ (λ

− λ

)

4/5

+ λ

4/5

]

(t) = 0

(t) = −α

Being not ﬁxed the ﬁnal state, all the costate functions

are equal to zero in the ﬁxed t

. The necessary con-

dition (5) with the constraint (3) can be implemented

by using the control equation 0 =

∂H

∂u



0 =

∂H

∂u

= β

+ (λ

− λ

+ λ

− λ

+ λ

− λ

+ λ

−

+ λ

(7)

0 =

∂H

∂u

= β

+ λ

(X − 2 − X

)

+ (λ

+ λ

(8)

0 =

∂H

∂u

= β

+ (λ

− λ

+ (λ

− λ

(9)

and successively applying the saturation due to (3).

From equation (8), the control u

can be expressed as

function of u

= −

− X

)

−

+ λ

= f

) (10)

From equation (9), also the control u

can be ex-

pressed as function of u

− λ

+ P

) = f

)(11)

By substituting (10) and (11) into (7), it is possible

to solve with respect to u

, denoting by ¯u

the solu-

tion. By substituting ¯u

into f

) and f

), ¯u

and

¯u

are obtained, respectively. Taking into account the

constraint in (3), the optimal controls are:

(t) = min(max( ¯u

(t),0),1)

(t) = min(max( ¯u

(t),0),1)

(t) = min(max( ¯u

(t),0),1)

3 NUMERICAL RESULTS

To choose the parameters of mathematical model pro-

posed in (2) real data regarding the Lazio region (in

the center of Italy), are used. In the considered period,

about 1980−2020, greater attention from the institu-

tions and sensitivity of the population certainly con-

tributed to tackling the problem of breast cancer with

growing awareness, even if in discontinuous way, due,

for example, to economic/social conditions. There-

fore, the considered data are the effects of applied

policies and behaviors, such as screening campaigns,

sanitary resources, economic and social conditions.

These applied control measures are not identiﬁed and

the parameters of the proposed model are determined

trying to get the general trends and the order of am-

plitude of the considered quantities. The data are re-

trieved from ISTAT’s ”Health for All” database, (IS-

TAT, 2023), speciﬁcally:

• Female population data from 1982 to 2020;

• Female prevalence data from 1980 to 2016;

• Female number of death due to tumor from 1990

to 2018;

• Female deaths due to non-tumor-related causes

from 1990 to 2018.

It must be stressed that only in the last years, es-

pecially with COVID-19 emergency, data collection

has becoming more detailed; therefore, in this case,

also the information carried on by the trend in the an-

nual number of deaths for breast tumor is used for the

model parameters identiﬁcation and has suggested the

introduction of the compartment X

in the model. The

parameters are chosen to minimize the difference be-

tween the model output and the actual available data:

X(0) = (259 ·10

1500 4000 17500 930)

Z = (10

3 · 10

0 0)

= d

= 0.045, D = 0.055,

= 5 · 10

−4

, c

= 7.8 · 10

−4

= 2.5 · 10

−3

, c

= 0.99 (12)

Breast Cancer Epidemic Model and Optimal Control

199

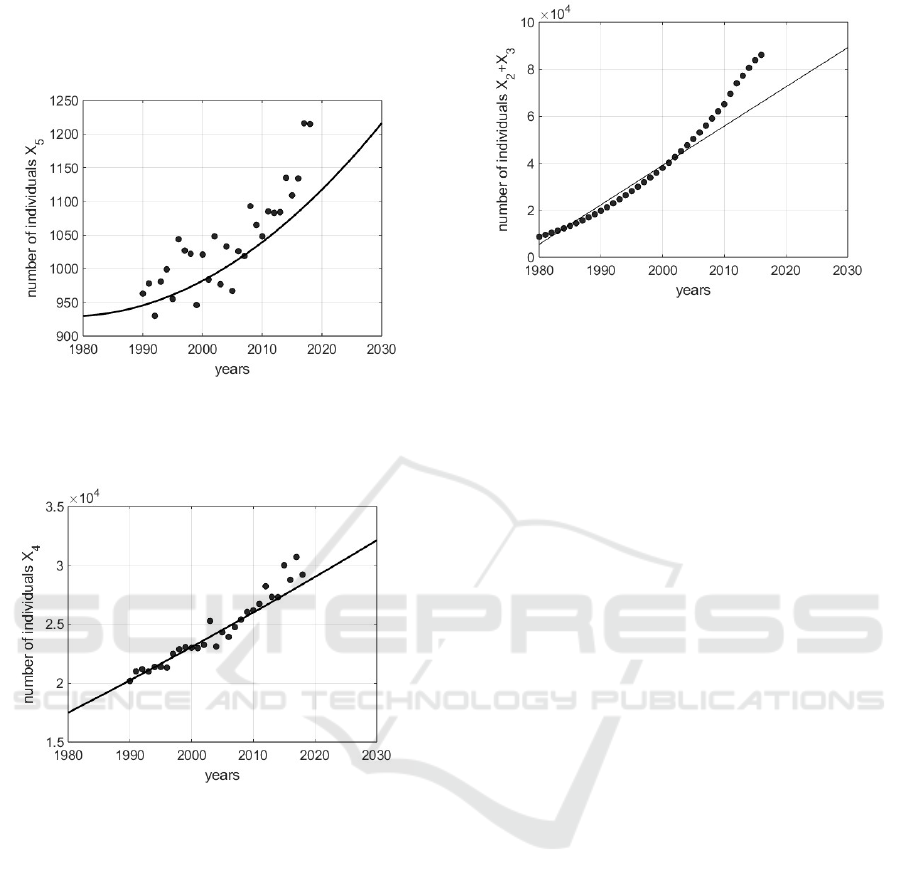
In Figs. 2 − 3 it is shown the number of dead subjects

for breast tumor and the number of dead individuals

for causes independent on tumor respectively.

Figure 2: Number of dead individuals for causes related

with breast cancer: the points are the real values referring

to the Lazio (Italy) region, whereas the continuous line is

the trend of the identiﬁed model.

Figure 3: Number of dead individuals for causes not related

with breast cancer: the points are the real values referring to

the Lazio (Italy) region, whereas the continuous line is the

trend of the identiﬁed model.

In both cases, especially up to data regarding

2013, the model states X

and X

(without the intro-

duction of control) adequately track the real data. In

the proposed model for simplicity in X

are collected

the number of cases at stages 0, 1 and 2, whereas the

more severe cases are in X

; the sum of all diagnosed

tumor real cases is compared to the sum X

, thus

showing the trends of Fig. 4, resulting acceptable up

to 2005. Again, the not uniform ﬁtting in all the con-

sidered period is due to the adoption, in this phase, of

a not controlled model, whereas in the real data the ef-

fects of some kind of control could be present. Once

the model parameters are determined to represent the

typical trends of a western region, the control actions

are introduced. As far as the parameters regarding

the effectiveness of the control actions the following

Figure 4: Number of dead individuals with a positive di-

agnosis of breast cancer, X

(t) + X

(t): the points are the

real values referring to the Lazio (Italy) region, whereas the

continuous line is the trend of the identiﬁed model.

choices are taken:

= 0.95, B

= 0.8,

= 1.5 · 10

−3

, P

= 8 · 10

−2

= 7 · 10

−4

= 0.97, P

= 10

−5

(13)

With these choices it is modeled the effectiveness

of the control in improving the number of positive di-

agnosis to start the treatments as soon as possible.

The optimal controls u

, i = 1,2,3 are obtained

by choosing for the weights in the control index the

values:

= 10

−4

, α

= 0.09,

= 300, β

= 900 (14)

The optimal control U

depends on these choices aim-

ing at decreasing the number of patients in X

and of

dead individuals in X

, allocating properly the limited

resources; the weights β

of u

and β

of u

are one

third of the corresponding value β

trying to guide the

solution to privilege controls u

and u

, rather than

more severe and invasive treatment u

. In Fig.5 it

is shown the trend of the three optimal controls u

i = 1, 2,3 when the parameters are chosen as in (3)

and (14). Note the requirement of the prevention u

in all the control period, whereas control u

is a little

bit relaxed to increase in the last ten years of control

when, on the other hand, it can be decreased the ef-

fort fo the severe treatments. The corresponding state

evolutions are shown in Fig. 6 Note that with the ap-

plication of controls the number of individuals with a

positive diagnosis in compartment X

is improved, be-

ing the effects of early diagnosis that allows the start

of effective treatments; moreover, the convenience of

the application of containment measures can be ap-

preciate both noting the reduced number of dead in-

dividuals X

and of the total number of subjects with

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

200

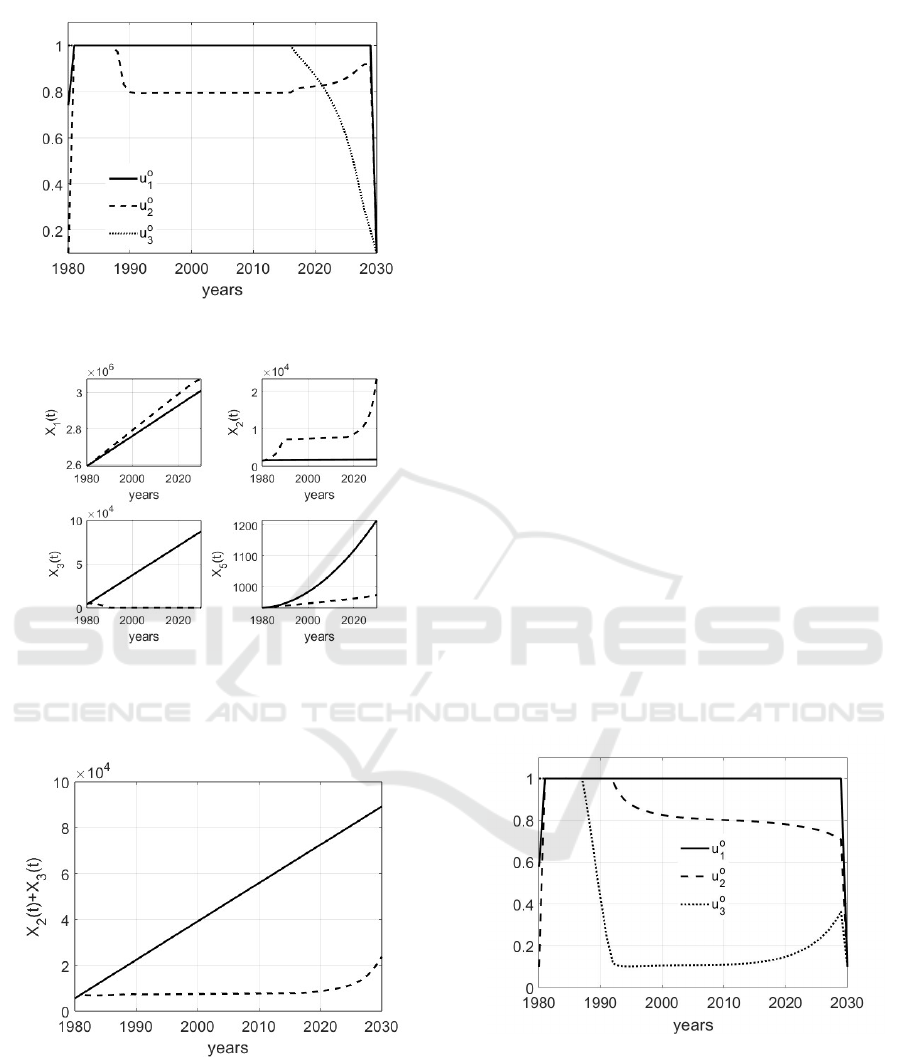
Figure 5: Trend of the optimal controls u

, i = 1,2, 3 when

the parameters are chosen as in (3) and (14).

Figure 6: Trend of the optimal states X

, X

when

the parameters are chosen as in (3) and (14); the continuos

lines represent the evolutions in absence of control, whereas

the dashed lines are the effects of the optimal controls.

Figure 7: Trend of X

(t) + X

(t) when the parameters are

chosen as in (3) and (14); the continuous line represents the

evolution in absence of control, whereas the dashed one is

the effect of the application of the optimal controls.

a positive diagnosis, as shown in Fig.7. The evolution

of X

, the number of individuals dead for reasons not

related to tumor, is not shown being, obviously, the

same, without and with control.

Different choices of the weights α

, i = 1,2 and

, j = 1,2,3 in the cost index can lead to strongly

different resource allocations and states evolution; as

a further example, it is proposed an alternative to

the choice for the weights in (14); in particular, it

is augmented the ratio between the values of the β

i = 1,2,3 and those of α

, j = 1,2:

= 10

−7

, α

= 10

−7

= β

= 1, (15)

With this choice the controls are weighed without

privileging one with respect to the other. The obtained

optimal controls u

, i = 1,2,3 are shown in Fig. 8, in

which it is evident the fundamental role of prevention

and the limited action of u

, the severe treatment.

For this simulation it is interesting to show the evolu-

tion of the sum of subjects with a positive diagnosis

of breast cancer, in Fig.8.

Note that the trend of X

(t)+X

(t) with the appli-

cation of control becomes higher up to year 2020 with

respect to the case in which no action is applied, Fig.

9; successively, the relation among these two evolu-

tions is reverted. This means that the prevention al-

lows early detection and, therefore, an increase in the

number of diagnosed individuals, but the treatments

allow successively a decrease in X

(t)+X

(t). The ef-

fectiveness of this approach is further conﬁrmed con-

sidering the trend of the number X

(t) of individuals

dead for breast cancer: the application of the optimal

control decreases this number in all the simulate con-

trol period, see Fig. 10.

Figure 8: Trend of the optimal controls u

, i = 1,2, 3 when

the parameters are chosen as in (3) and (15).

4 CONCLUSIONS

In the medical ﬁeld, thanks to the developments in the

treatment of breast cancer, even people with positive

diagnoses have a good chance of a complete recov-

ery, provided they have a timely diagnosis. However,

Breast Cancer Epidemic Model and Optimal Control

201

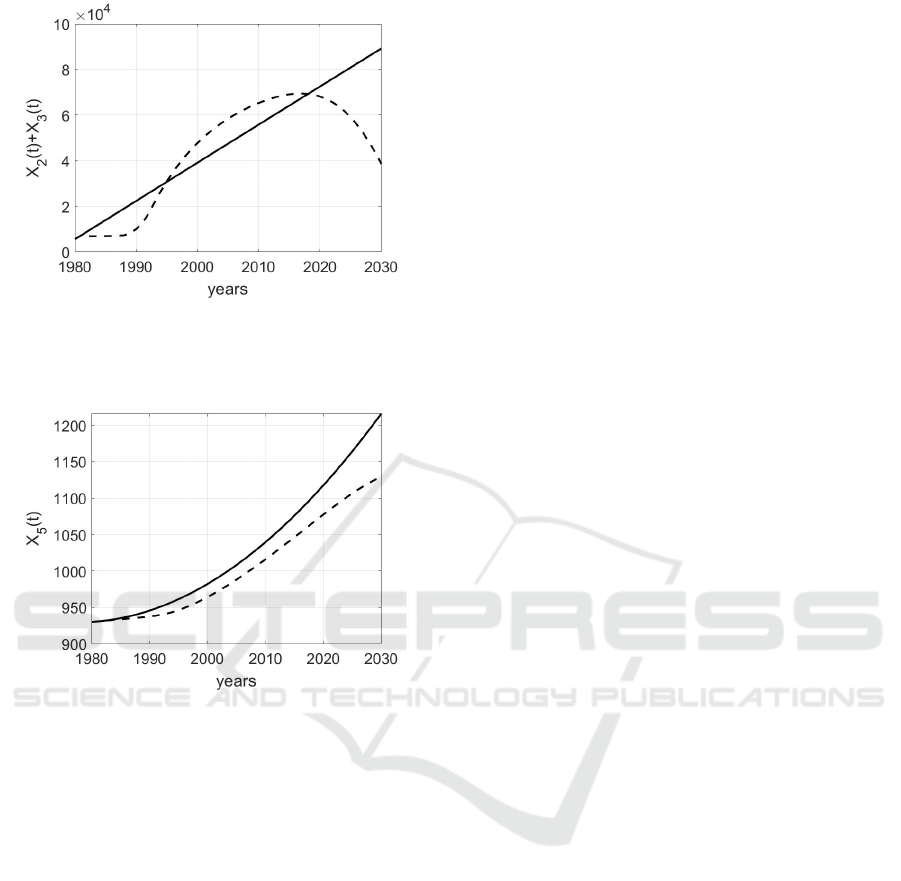
Figure 9: Trend of X

(t) + X

(t) when the parameters are

chosen as in (3) and (15); the continuous line represents the

evolution in absence of control, whereas the dashed one is

the effect of the application of the optimal controls.

Figure 10: Trend of X

(t) when the parameters are chosen

as in (3) and (15); the continuous line represents the evo-

lution in absence of control, whereas the dashed one is the

effect of the application of the optimal controls.

economic and logistical resources, combined with a

lack of awareness of the importance of prevention, do

not always allow the problem to be tackled effectively.

The introduction of an epidemiological model, iden-

tiﬁed with reference to a western population, allows,

within the optimal control theory, to plan an adequate

allocation of resources to reduce mortality and severe

cases. The novelty and advantages of such approach

may be listed as follows:

• it is proposed an epidemiological model for the

spread of breast cancer customized on a speciﬁc

population;

• the availability of such a model yields a medium-

term forecast at population level of the disease

course under different control conditions;

• the application of optimal control allows an ade-

quate allocation of limited resources.

Future developments will regard:

• a deeper model parameter identiﬁcation: this as-

pect requires the analysis of the containment mea-

sures applied starting from 1980 and therefore the

use of this information in the identiﬁcation step;

• an accurate analysis of real data to deﬁne the av-

erage effectiveness of the introduced controls, as

well as their limits in facing the breast cancer; this

aspect could allow a more accurate choice of con-

trol parameters;

• consider data regarding female populations with

different sanitary systems and habits, so to apply

the proposed control strategy;

• a deep study of over diagnosis versus the impor-

tance of prevention, so to avoid the detection of

not life-threatening and, at the same time, pre-

serve the fundamental role of screening.

REFERENCES

Alkabban, M. and Ferguson, T. (2022). Breast cancer. In

https://www.ncbi.nlm.nih.gov/books/NBK482286/.

American Cancer Society (2023). All about can-

cer. In https://www.cancer.org/cancer/types/breast-

cancer/about/types-of-breast-cancer.html.

Choi, L. (2022). Breast cancer. In https: //www.msdmanua

ls.com/professional/gynecology-and-obstetrics.

City of Hope (2023). Breast cancer stages. In

https://www.cancercenter.com/cancer-types/breast-

cancer/stages.

Fox, S., Speirs, V., and Shaban, A. (2022). Male breast

cancer: an update. In Virchows Arch.

Habbema, J., Van Oortmarssen, G., Lubbe, J., and Van der

Maas, P. (2018). The miscan simulation program for

the evaluation of screening for diseasea. In Medical

Decision Making.

Huang, S., H, P., and Lakowski, T. (2021). Predicting breast

cancer drug response using a multiple-layer cell line

drug response network model. In BMC Cancer.

ISTAT (2023). Istituto nazionale di statistica. In

https://www.istat.it/.

Kolak, A., Kaminska, M., sygit, K., Budny, A., Surdyka, D.,

Kukielka-Budny, B., and Burdan, F. (2017). Primary

and secondary prevention of breast cancer. In Annals

of Agricultural and Environmental Medicine.

Tang, T., Shah, Z., Bonyah, E., Jan, R., Shutaywi, M., and

Alreshidi, N. (2022). Modeling and analysis of breast

cancer with adverse reactions of chemotherapy treat-

ment through fractional derivative. In Computational

and Mathematical Methods in Medicine.

Van der Broek, J., Van Ravesteyn, N., Heijnsdijk, E., and

De Koning, H. (2018). Simulating the impact of risk-

based screening and treatment on breast cancer out-

comes with miscan-fadia. In Medical Decision Mak-

ing.

WHO (2023). World health organization. In

https://www.who.int/.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

202