Distributed Predictive Control for Roundabout Crossing Modelled by
Virtual Platooning
Alessandro Bozzi
1,2
a
, Simone Gra ffione
1 b
, Roberto Sacile
1 c
and Enrico Zero
1 d
1
Department of Informatics, Bioengineering, Robotics and System Engineering, University of Genova, Genova, Italy
2
Laboratory System and Materials for Mechatronics (SYMME), Universit´e Savoie Mont Blanc, Annecy, France
Keywords:
ADMM, MPC, Distributed Control, Virtual Platooning.
Abstract:
Roundabouts pose complex challenges for autonomous vehicles. Approaching and crossing them safely re-
quires a significant amount of information, much of which is typically unavailable. With autonomous vehicles
becoming increasingly prevalent on the roads, new approaches are necessary to address these upcoming is-
sues. While platoons and distributed control have been extensively studied in the past decade, roundabouts
have received less attention. This paper presents a distributed Nonlinear Model Predictive Control (NMPC)
approach using the Alternating Direction Method of Multipliers (ADMM) to utilize virtual platooning and
enhance the throughput of a roundabout wit hout requiring approaching vehicles to come to a stop. Instead, it
manages the velocity of each vehicle while maintaining a safe distance. The proposed approach is validated
through two case studies.
1 INTRODUCTION
Platoons represent a fundamental step in au tonomo us
driving to group vehicles by similar paths and in-
crease road throughput.
Concernin g autonomous driving, the additional
degree of complexity in automatin g the displacement
of multiple vehicles at once is given by the coordi-
nation that they need to provide overtime to avoid
collision and ensu re optimal behaviour for the other
agents on the road. When dealing with highway sce-
narios, many works of literature provide tec hniques
to handle one-dimensional displacement over time
(Bozzi et al., 2021) comes up with a robust algo-
rithm to optimally space and enhance safety on high-
ways, while (Bengtsson et al., 2015) proposes proto-
cols for highway platoon merge. On the other hand,
one of the main bottlene cks in autonomous driving
is represen te d by intersections. Huge efforts have to
be put into designing safe and high-p erforming algo-
rithms to handle the travelling order. Cooperative ap-
proach e s may help in improving intersection through-
put (Wei and He, 2022), even if when vehicles ap-
a
https://orcid.org/0000-0002-2436-0946
b
https://orcid.org/0000-0003-0882-586X
c
https://orcid.org/0000-0003-4086-8747
d
https://orcid.org/0000-0002-9995-1724
proach roundabout they usua lly are independent of
the others. Thus, if they happen to share the same
path after the intersection, a coordination mechanism
is needed to merge them into a platoon for consequent
road sections. Order criteria should consider both th e
distance from the insertion point and the long-term
efficiency properties that a specific formation has, as
stated in (Alam et al., 2014) (i.e. vehicles should
be ordered by bra king capacity). Control strategies
can be applied to tackle intersection c oordin a tion with
the ultimate goal of reducing the travel time of ve-
hicles inside those areas (Wang et al., 2022). How-
ever, f rom the intersection perspective, the main goal
surely remains the cho ic e of platoons’ order based on
their arrival at the intersection. Afterwards, several
works that analyse manoeuvres within a platoon may
be considered to modify the initial formation (Lam
and Katupitiya, 2013; Bozzi et al., 2022). In (Masi
et al., 2022) , virtual platoonin g is implemented to pre-
dict future situations of a roundabout b y creating oc-
cupancy intervals and making decisions to avoid col-
lisions.
The aforementioned works deal with the design
of feasible trajectories for vehicles to pursue. As a
matter of fact, to physically pro mpt input, the vehi-
cle’s dynamics should be taken into account. This is
needed to ensure more reliable beh aviour over time.
With this aim, Model Predictive Control (MPC) is ex-
Bozzi, A., Graffione, S., Sacile, R. and Zero, E.
Distributed Predictive Control for Roundabout Crossing Modelled by Virtual Platooning.
DOI: 10.5220/0012232700003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 295-301
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
295

ploited in different scenarios of autonomous driving.
For instance , (Tang et al., 2020) couples the MPC
with a kinematic model for path-trac king p urposes,
while (Gra ffione et al., 2022) uses a nonlinear MPC
(NMPC) to handle both lon gitudinal and lateral dis-
placement in the insertion a nd exit of a vehicle pla-
toon.
In contro l engineering, the Alternating Direction
Method of Multipliers (ADMM) is widely used to
guaran tee a robust, method f or solving large pro b-
lems b y iteratively solving corresponding subprob-
lems, which ensures a sort of coordination betwe e n
each agent, as implemented in (Liu et al., 2022) for
energy resources. There exists also a c onsensus-based
approa c h in which agents communicate with each
other until convergence. A recent example with multi-
robot teams can be found in (Haksar et al., 2022).
The scalability and feasibility of the ADMM have
been also tested in an urban traffic problem (Li and
De Schutter, 2021). A distributed model-free adap-
tive predictive con trol has been proposed for multi-
region urban traffic networks. The proposed method
has been tested in a real case study in China in the
traffic network of Linfe n. The simulation results show
that the distributed model proposed yields better per-
formance than the fixed-time control and centra lize d
MPC contr oller.
In the management and control of a fleet of fuel
cell ca rs, a c omparison of three different distributed
control strategies based on dual decomposition has
been shown (Alavi et al., 2019). The partial method
has the most negligible lo ss of performance when the
number of cars in the system is small.
This work proposes a dual-level controller to han-
dle the crossing of roundabouts and con sequent merg-
ing as a platoon. The high-level controller exploits the
consensus-based ADM M to coordinate independent
vehicles to form the platoon, while the decentralized
low-level MPC tries to pursue the optimal trajectory
for each element to respect the scenario pr ovided by
the other controller.
This paper is organised as follows: Section 2
presents the problem formulation and the proposed
approa c h, while Section 3 introduces the two case
studies analyzed and the results that validate the ef-
fectiveness of the work. Finally, the final rema rks are
in Section 4.
2 METHODS
This section will focus on the meth ods used to imple-
ment distributed control through virtual platooning.
2.1 Simulation Environment
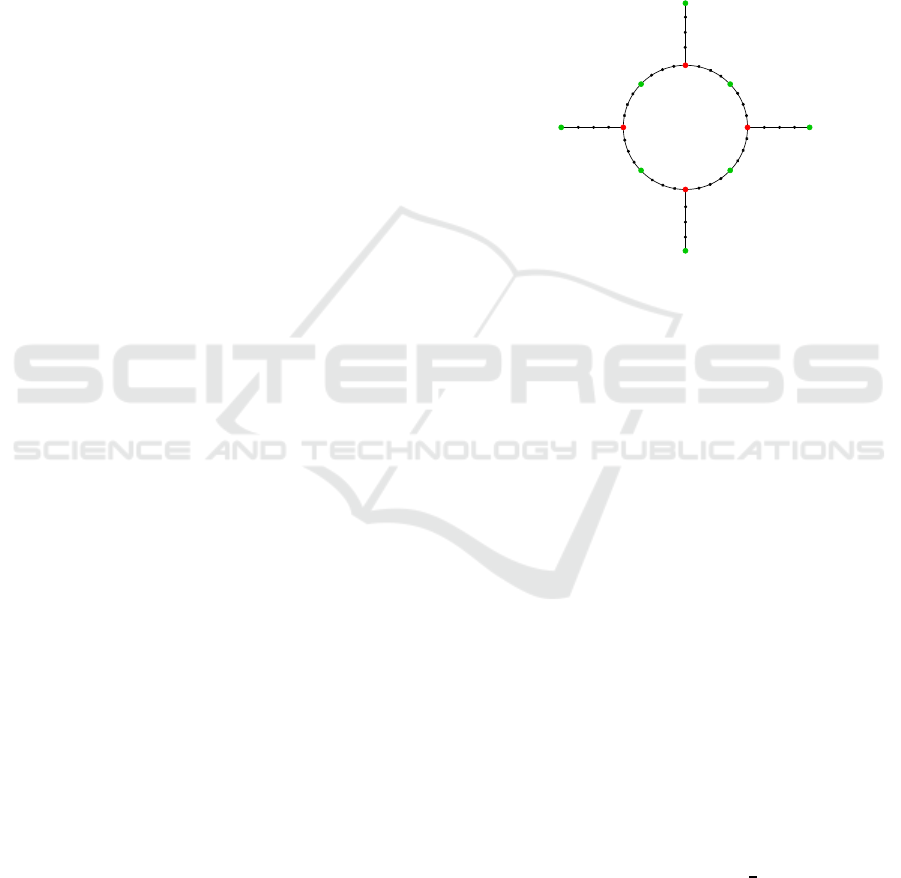
Let’s conside r a roundabout with four approach ing
and leaving roads. Each road (rou ndabout included)
has only on e lane and is described by a sequence o f
points called ”Joints” connected between each other
with an ”Arc”. Each ”Arc” is defined by a sequence of
points, derivatives, lengths and directions (approach-
ing lane, leaving lane or in a roundabout). Fig. 1
shows a roundabout used in this paper.
j
j+1
j-1
Figure 1: Roundabout example. Each big dot represents a
Joint and each line connecting the two joints is an Arc. The
smaller black dots are the points describing the Arc. The red
Joints are the ”Criti cal Joints” where a collision may occur.
Given an Arc length l and a path for each vehicle
defined by a series of Arcs, the curvilinear distance
d
i,J
between vehicle i and the ”Critical Joint” J is
d
i,J
=
∑
k∈P
i
l
k
(1)
Given N ho mogeneous autonomous vehicles, the
goal is to exploit virtual platoon ing to ma ke a cle an
passthrough of the roundabout for all vehicles. It
is also supp osed to have a centra l unit placed in the
roundabout with the sole objective of computing the
platoon order and being a communicatio n bridg e be-
tween vehicles.
2.2 Vehicle Model
The vehicle in this work is described with a seco nd-
order differential equation that considers on ly the lon -
gitudinal displacement and velocity with acceleration
as input. Thus, the discrete-time model for vehicle i
is
(
s
i
(k + 1) = s
i
(k) + ∆tV
i
(k) +
1
2
∆t
2
a
i
(k)
V
i
(k + 1) = V
i
(k) + ∆ta
i
(k)
(2)
Where k is the time instant, ∆t is th e sam ple time, s
is the longitudinal displacement, V is the longitudinal
speed and a is the longitudinal acceleration.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
296

The model (2) for vehicle i can be written in state
space form X
i
(k+1) = AX
i
(k)+BU
i
(k) where X
i
(k) is
the state vector at time k, U
i
(k) control vector at time
k and A and B are state and control matrices. How-
ever, to have a general formulation of the approach,
the following notation is chosen
˙
X
i
= f
i
(X
i
,U
i
) (3)
Which is discretized thro ugh the Euler method, r esult-
ing in
X
i
(k + 1) = X
i
(k) + ∆t f (X
i
(k),U
i
(k)) (4)
2.3 Virtual Platooning
Virtual platooning makes it possible to represent mul-
tiple vehicles inside a road in frastructure as a platoon
moving in one direction. The goal is to find an order
of vehicles such that it would be possible to ente r a
roundabout witho ut stopping.
The controller’s goal is to adjust the distance be-
tween platoon members ensuring safety during the
roundabout crossing. Various studies discuss which
technique and which informatio n sh ould be consid-
ered to make a platoon effective and stable. In this
work, each member will consider the distance from
the preceding vehicle and the leader as in (Graffione
et al., 2 022). This configuration reduces the oscil-
lation caused by a string-like formation while giv-
ing grea t results in terms o f stability and convergence
time.
A platoon can be defined as a concatenation of each
vehicle’s system as follows
X(k + 1) = (I ⊗ A)X(k) + (I ⊗ B)U(k)
(5)
Where X and U are the state and control vecto r of
the p la toon, N is the number of vehicles, I is an iden-
tity matrix of size N and the sy mbol ⊗ represents the
Kronecker product. The pr oposed algorithm (A lg. 1)
to compute the virtual platoon is supposed to be exe-
cuted by a central infrastructure in the rou ndabout and
then propagated to the involved vehicles. Fig. 2 is an
example of the application of the algorithm.
2.4 Platoon Distance Controller
The platoon obtained by the algorithm 1 needs to be
controlled to keep its formation and safety distance
while each me mber is app roaching the roundabout.
Consider N vehic les indexed as 1, 2, . . . , N where
1 is the leader and the exchange of information is
managed by a central unit pla c ed in the roundabout.
The in formation used by vehicle i is the distance be-
tween its precedin g vehicle and the leader of the pla-
toon. Thus, the proposed control model aims to min-
imize the square divergence of the longitudinal speed
foreach Time instan t do
Search for common critical joints j
among vehicles based on their path;
Check curvilinear distance d
i, j
between
each vehicle i and co mmon critical joint
j;
Find the closer critical joint J and the
correspo nding vehicle I;
Sort the distance vector d
i,J
, resulting
order is the platoon formation;
end
Algorithm 1: Virtual Platooning Algorithm.
1
2
3
4
d
1,J
d
2,J
d
3,J
d
4,J
Critical joint J
32
14
Figure 2: Example of virtual platooning. The distances of
each vehicle from the critical joint J define the order of the
virtual platoon and the initial condition for the controller.
This process is repeated every time step by a centralized an-
tenna that works also as an Access Point for all vehicles.
Each member of the virtual platoon will consider its pre-
ceding vehicle and the leader as a reference for the inter-
vehicular distance control.
of each vehicle to a reference value and the intra-
vehicular distance between each member of the pla-
toon i and its pre ceding vehicle and the leader. The
proposed approach employs a non-line a r predictive
approa c h where the model (linear or non-linear ) is
used to predict the trajectory state along a time hori-
zon to optimize the control ac tion to the predicted
state and the desired state.
The cost fu nction at time k is d e fined as follows:
J(X (k),U(k)) =
H
p
−1
∑
k=1
(
N
∑
i=2
q
1
(s
1
(k) − s
i
(k) − (i − 1)d
des
)
2
+
+q
1
(s
i
(k) − s
i−1
(k) − d
des
)
2
+
+q
2
(V
i
(k) −V
re f
)
2
)+
+r
1
a
i
(k)
2
(6)
Distributed Predictive Control for Roundabout Crossing Modelled by Virtual Platooning
297

Where H
p
is the prediction hor iz on of the controller,
q
1
, q
2
, q
3
and r
1
are weight parameters, d
des
is the
safety distance and V
re f
is the ref erence speed.
Remark 1. The reference speed of the leader is V
re f
as well. The difference from the other vehicles lies
in the fact that it does not consider the distance from
other vehicles since it is in the front of the platoon.
The minimization of the cost function defined in
(6) is m inimized every time step k, resulting in the
following Non-L inear Model Pr e dictive Control ap-
proach
minimize
X,U
J(X (k),U(k)) (7a)
subject to equation(5), (7b)
V
min
≤ V
i
(k) ≤ V
max
, (7c)
a
min
≤ a
i
(k) ≤ a
max
, (7d)
d
min
≤ s
i
(k) − s
i−1
(k) (7e)
Where for constraint (7b) k = 1, . .. , H
c
and for con-
straints (7c),(7d),(7e) k = 1, . . . , H
p
with H
c
≤ H
p
.
Value H
c
is the control horizon in which the con trol
is optimize d, which is usually between 10% and 20%
of the prediction horizon. For k > H
p
, the optimal
control action is kept constant with the last computed
value of U. To ensure safety and avo id collisions, it
has been added a minimum distance between vehi-
cles that consider the length of the vehicle. To im-
prove the efficiency and accuracy of the controller, a
Direct Multiple Shooting Method is used (Bock and
Plitt, 1984). This approac h approximates the time
horizon in a set of n sub-intervals [τ
i
.τ
i+1
]. At each
sub-interval, the initial condition of the state vector
and control are parametrized as
U(k) = V
i
f or t ∈ [t
i
,t
i+1
]
X(k
j
) = h
i
i = 0, 1, . . . , n − 1
(8)
Thus, to ensure the continuity of the solutions, two
other constraints are added to the problem, and the
cost fu nction is slightly changed:
J(t) =
n−1
∑
j=1
Z
τ
k+1
τ
k
J (X
j
(k),V
j
(k)) dτ
(9)
minimize
X,U
J(X
j
(k),V
j
) (10a)
subject to h
0
− X(0) = 0, (10b)
h
j+1
− X
j
(k
j+1
, h
j
,V
j
) = 0, (10c)
g(h
j
,V
j
) ≥ 0 (10d)
Where constraint (10b) is the initial condition con-
straint, (10c) is the continuity constraint that assur e s
that the comp uted solution is coherent among subin-
tervals, (10d ) contains all the constraints de fined by
(7c),(7d) and (7e) and other non-linear constraints if
required.
2.5 Distributed Control
In a real-case scenario, a distributed control would
be the best choice to ha ndle such a computationally
heavy problem. Thus, to design a Distributed NMPC,
a distributed control approach based on the Consensus
Alternating Direction of Multipliers is pro posed.
The Consensus ADMM is employed in scena rios
where multip le agents share a com mon objective but
simultaneou sly face con flicting interests. By defining
the common global variable ˜z and the local decision
variables x
i
, the problem is defined as follows
minimize
x
i
N
∑
i=1
f
i
(x
i
)
subject to x
i
− ˜z = 0 i = 1, . . . , N
(11)
The problem (11) is computed on each agent i and its
result consists of an optimal control u
i
(k) and a state
estimation of other age nts (depending on the a gents’
interconnection in the system). All of th ese estima-
tions are used to estimate an average state value for
each agent r e sulting in a new value of ˜z to use in the
next optimization step for each agent i. The platoon
members will agree only with th e vehicles they are in-
terested in. Thus, the ADMM algorithm is as follows
x
k+1
i
= min
x
i

f
i
(x
i
) + y
kT
i
x
i
+
ρ
2
kx
i
− ˜z
k
i
k
2
2
)

(12a)
z
k+1
= min
z
m
∑
i=1

−y
kT
i
˜z
i
+
ρ
2
kx
k+1
i
− ˜z
i
k
2
2

!
(12b)
y
k+1
i
= y
k
i
+ ρ(x
k+1
i
+ ˜z
k+1
i
) (12c)
Where equatio n (12a) is the local variable optimiza-
tion step, (12b) is the z-upda te step that results in the
average of the agents according to the age nts’ inter-
connection and finally (12c) is the dual variable up-
date. From an implementation point of view, steps
(12a) and (12c) can be dra gged out in parallel on each
agent. In stead, step (12b), requires synchronization of
the information exchange or some kind of predictio n
in case of missing data. In this paper, it is supposed
that the vehicles are syn chronized without data loss.
Further work will include this event.
In order to use the ADMM formulation (12), it
is required to define the functions f
i
(x
i
) and the set
of local variable x
i
for each agent from the central-
ized cost function (9). Local variables for the p la toon
leader are related on ly to the leader itself since it is in
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
298

front of the platoon. The second vehicle has only the
distance from the preceding vehicle which is also the
distance to the lea der. All the other vehicles will have
both distances from the leade r and the preceding ve-
hicle. According to th is reasoning, the local variables
are as follows
x
1
=
˙
X
1
, x
2
=

˙
X
1
˙
X
2

x
i
=


˙
X
1
˙
X
i−1
˙
X
i


with i = 3, . . . , N
(13)
and the f unctions f
i
(x
i
) are
f
1
(x
1
) =
H
p
∑
k=1
q
2
(V
1
−V
re f
)
2
+ r
1
a
2
1
f
i
(x
i
) =
H
p
∑
k=1
(X
i
− X
r,i
)
T
Q
i
(X
i
− X
r,i
) +U
T
i
R
i
U
i
(14)
where i = 2, . . . ,N. Thus
X
2
=


s
1
− s
2
V
1
V
2


X
r,2
=


d
des
V
re f
V
re f


U
2
=

a
1
a
2

Q
2
= diag(q
1
, q
2
, q
2
) R
2
= diag(r
1
, r
2
)
X
i
=







s
1
− s
i−1
s
1
− s
i
s
i−1
− s
i
V
1
V
2
V
3







X
r,i
=







d
des
(i − 1)d
des
d
des
V
re f
V
re f
V
re f







U
i
=


a
1
a
i−1
a
i


Q
i
= diag(q
1
I
3×3
, q
2
I
3×3
) R
i
= diag(r
1
, r
2
, r
3
)
(15)
3 RESULTS
The proposed algorithm has been tested and evalu-
ated in two different scenarios. The two case studies
are reported to show the effectiveness of the proposed
method. The case study does no t consider real-size
vehicles but Wheeled Mobile Robots (WMR) 25 cm
long a nd 18 cm wid e beca use further development in-
cludes a real-time implementation of physical steer-
ing WMR to validate the approach even in a r eal case
scenario. However, this does not invalidate the r esults
since vehicles and road sizes are simply scaled, ensur-
ing con sistency in the whole execution.
The first case study (Fig. 3) consists of three veh i-
cles, two in the r oundabout and one on an approach-
ing lane, the second one (Fig. 4) consists of five vehi-
cles, one inside the roundabout and four vehicles on
three different approaching lanes.
Numerical sim ulations have been conducted on
Matlab with a variable number o f vehicles inside and
outside the roundabout.
Figure 3a shows the initial condition of the round-
about where each vehicle ha s an initial speed of 0.1
m/s and an in te r-vehicular distance that does not re-
spect the bounds defined in Table 1.
Table 1: Main parameters used.
Param
Value Unit Description
q
1
1 Gain on platoon distances
q
2
10
Gain on state variable V
r
{1,2,3}
1 Gain on control variable a
T s 0.1 s Sampling time
H
p
10 Prediction Horizon
H
c
2 Control Horizon
d
des
0.55 m Inter-vehicular distance
d
min
0.45 m Minimum safety distance
In the first instant of the simulation, the algorithm
1 defines the order of vehicles as (1 − 3 − 2), and
then the ADMM is initialized on each one (Fig. 3a).
The estimation of other vehicles is initialized on each
agent as a zeros state. At this point, the control makes
vehicles 1 and 2 respectively accelerate and dec elerate
(as shown in the first seconds of Fig.5c) to create more
space for vehicle 3 to enter. I n the meanwhile, the ve-
locity of all vehic le s converges to the reference even if
the distances have priority for safety reasons. Figu re
3c shows th e instant when vehicle 3 enters the round -
about, alre ady at a safe distance from the other vehi-
cles, finally able to continue on its path while main-
taining the formation (Fig. 3d. The results shown in
Fig. 5 prove the co nvergence of both distance and
speed through the simulation.
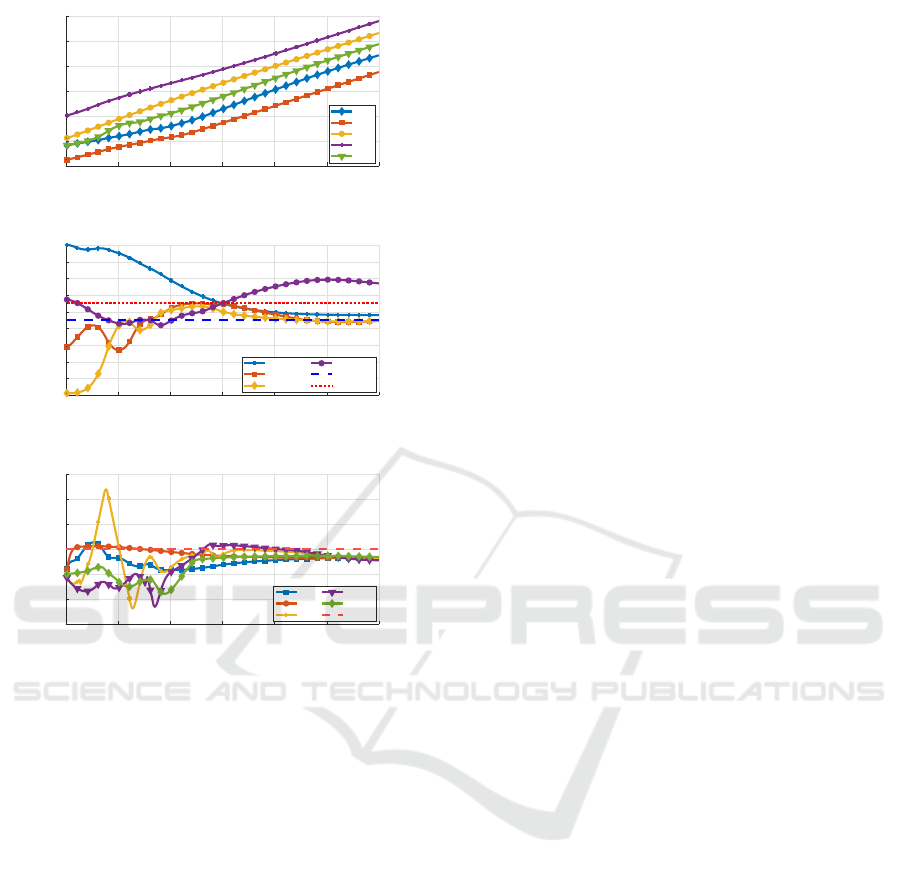
The second case study considers vehicles at an ini-
tial speed of 0.1 m/s. The comp uted platoon’s order is
(4 − 3 − 5 − 1 − 2), indicating critical inter-vehicular
distances between vehicles 1 and 5, as well as be-
tween 3 and 5. Conversely, vehicles 3 and 4 have
substantial distances to reduce to mitigate c ongestion.
Fig. 4a shows the initial position of vehicles and
6b shows in detail the initial distances. As a conse-
quence, the required control action of each agent is
stronger resulting in a slower convergence time (about
15 seconds against 10 seconds in the first case study).
Fig. 4b and Fig. 6b show that vehicles 1 and 2
slow down to increase space between 1 and 3 and let
5 enter the roundab out. Vehicle 2 slows down as a
consequence of vehicle 1 deceleration. Fig. 4 c shows
moments before vehicle 1 enters the roundabout, fol-
lowed by vehicle 5 which is placed right befo re in the
platoon order. Finally, Fig. 4d shows all vehicles in
formation and continuing the ir programmed path (ve-
hicle 4 is leaving the roundabout).
Distributed Predictive Control for Roundabout Crossing Modelled by Virtual Platooning
299

(a) Init ial condition of t he
roundabout.
(b) Vehicles 1 and 2 create
more distance to let vehi-
cle 3 enter.
(c) Vehicle 3 successfully
enters the roundabout.
(d) All three vehicles pro-
ceed along the roundabout
keeping a safe distance.
Figure 3: Fi r st case study. Two vehicles were inside the
roundabout and one on the approaching lane.
(a) Init ial condition of t he
roundabout.
(b) Vehicles create more
distance to let the vehicles
outside the roundabout en-
ter.
(c) Vehicle 3 successfully
enters the roundabout and
vehicles 1 and 5 are close
to enter.
(d) A ll vehicles success-
fully enter and proceed
along the roundabout
keeping a safe distance.
Figure 4: Second case study. Five vehicles are involved in
this scenario. Four vehicles are approaching the r oundabout
and the last one is already in it. Fig. 6b shows the distances
during the simulation. Fig. 6c shows the speeds during
simulation.
4 CONCLUSIONS
The proposed approach consists of a distributed
NMPC through ADMM exploiting virtual platooning
to let vehicles e nter a roundabout without stopping.
0 5 10 15 20 25 30
Time [s]
-1
0
1
2
3
4
5
Longitudinal Displacement [m]
WMR
1
WMR
2
WMR
3
(a)
0 5 10 15 20 25 30
Time [s]
0
0.1
0.2
0.3
0.4
0.5
0.6
Distances [m]
WMR
1
-WMR
3
WMR
3
-WMR
2
Bounds
Reference
(b)
0 5 10 15 20 25 30
Time [s]
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Velocity [m/s]
WMR
1
WMR
3
WMR
2
Reference
(c)
Figure 5: Results of the first case study. Fig. 5a shows
the longitudinal displacement of vehicles and the platoon’s
order. Fig. 5b and Fig. 5c show the distances and speeds.
Two case studies with three and five vehicles are pro-
vided to prove the effectiveness and broadly assess
the scalability of the algorithm. The results demon-
strate satisfactory performance, despite the simplic-
ity of the algo rithm used to constru ct the virtual pla-
toon. Improvements can be made by con sid ering the
initial inter-vehicular distance to ensure a smoother
response from the controller. Additionally, inc orpo-
rating ”time-to-arrival” prediction would be essential
for assessing collision risks caused by the controller’s
slow convergence.
Although the results co nsider a case study with a
limited number o f vehicles, it is crucial to anticipate
unexpected behaviors when scaling up to accommo-
date a larger number of member. Further studies will
be conducted to evaluate the effectiveness of this im-
plementation depending on the number of vehicles in -
side the roundabout.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
300

0 5 10 15 20 25 30
Time [s]
-2
-1
0
1
2
3
4
Longitudinal Displacement [m]
WMR
1
WMR
2
WMR
3
WMR
4
WMR
5
(a)
0 5 10 15 20 25 30
Time [s]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Distances [m]
WMR
4
-WMR
3
WMR
3
-WMR
5
WMR
5
-WMR
1
WMR
1
-WMR
2
Bounds
Reference
(b)
0 5 10 15 20 25 30
Time [s]
0
0.05
0.1
0.15
0.2
0.25
0.3
Velocity [m/s]
WMR
4
WMR
3
WMR
5
WMR
1
WMR
2
Reference
(c)
Figure 6: R esults of the second case study. Fig. 6a shows
the longitudinal displacement of vehicles and the platoon’s
order. Fig. 6b and Fig. 6c show the distances and speeds.
REFERENCES
Alam, A., Gattami, A., Johansson, K. H., and Tomlin, C. J.
(2014). Guaranteeing safety for heavy duty vehicle
platooning: Safe set computations and experimental
evaluations. Control Engineering Practice, 24:33–41.
Alavi, F., Van De Wouw, N., and De Schutter, B. (2019).
Power scheduling of fuel cell cars in an i slanded mode
microgrid with private driving patterns. IEEE Trans-
actions on Control Systems Technology, 28(4):1393–
1403.
Bengtsson, H. H., Chen, L., Voronov, A., and Englund,
C. (2015). Interaction protocol for highway platoon
merge. In 2015 IEEE 18th International Conference
on Intelligent Transportation Systems, pages 1971–
1976. IEEE.
Bock, H. G . and Plitt, K.- J. ( 1984). A multiple shooting
algorithm for direct solution of optimal control prob-
lems. IFAC Proceedings Volumes, 17(2):1603–1608.
Bozzi, A., Sacile, R., and Zero, E. (2022). Propor-
tional integral derivative decentralized control vs lin-
ear quadratic tracking regulator in vehicle overtaking
within a platoon.
Bozzi, A., Zero, E., Sacile, R., and B ersani, C. (2021). Real-
time robust t rajectory control for vehicle platoons: A
linear matrix inequality-based approach. In ICINCO,
pages 410–415.
Graffione, S., Bersani, C., Sacile, R., and Zero, E. (2022).
Non-linear mpc for longitudinal and lateral control
of vehicle’s platoon wit h insert and exit manoeu-
vres. In Informatics in Control, Automation and
Robotics: 17th International Conference, ICINCO
2020 Lieusaint-Paris, France, July 7–9, 2020, Revised
Selected Papers, pages 497–518. Springer.
Haksar, R. N., Shorinwa, O., Washington, P., and Schwa-
ger, M. (2022). C onsensus-based admm f or task as-
signment in multi-robot teams. In Robotics Research:
The 19th International Symposium ISRR, pages 35–
51. Springer.
Lam, S. and Katupitiya, J. (2013). Cooperative au-
tonomous platoon maneuvers on highways. In 2013
IEEE/ASME International Conference on Advanced
Intelligent Mechatronics, pages 1152–1157. IEEE.
Li, D. and De Schutter, B. (2021). Distributed model-free
adaptive predictive control for urban traffic networks.
IEEE Transactions on Control Systems Technology,
30(1):180–192.
Liu, H., Shi, Y., Wang, Z., Ran, L., L¨u, Q., and Li, H.
(2022). A distributed algorithm based on relaxed
admm for energy resources coordination. Interna-
tional Journal of Electrical Power & Energy Systems,
135:107482.
Masi, S., Xu, P., and Bonnifait, P. (2022). Roundabout
crossing with interval occupancy and virtual instances
of road users. IEEE Transactions on Intelligent Trans-
portation Systems, 23(5):4212–4224.
Tang, L., Yan, F., Zou, B., Wang, K., and Lv, C. (2020). An
improved kinematic model predictive control for high-
speed path tracking of autonomous vehicles. IEEE
Access, 8:51400–51413.
Wang, C., Wang, Y., and Peeta, S. (2022). Cooperative
roundabout control strategy for connected and au-
tonomous vehicles. Applied Sciences, 12(24):12678.
Wei , Y. and He, X. (2022). Adaptive control for reli-
able cooperative intersection crossing of connected
autonomous vehicles. International Journal of Me-
chanical System Dynamics, 2(3):278–289.
Distributed Predictive Control for Roundabout Crossing Modelled by Virtual Platooning
301