Interval Type-2 Fuzzy Control to Solve Containment Problem

of Multiple USV with Leader’s Formation Controller

Wen-Jer Chang

1

, Yann-Horng Lin

1

and Cheung-Chieh Ku

2

1

Department of Marine Engineering, National Taiwan Ocean University, Keelung, R.O.C., Taiwan

2

Department of Marine Engineering, National Kaohsiung University of Science and Technology, Kaohsiung, R.O.C.,

Taiwan

Keywords: Interval Type-2 Fuzzy Control, Containment Problem, Multiple USVs, Formation Controller.

Abstract: An interval type-2 (IT2) fuzzy controller design method is proposed in this paper to simultaneously solve the

formation and containment control problems of multi-unmanned surface vehicles (USVs) system. Via the

construction of IT2 Takagi-Sugeno Fuzzy Model (IT2T-SFM), the control problem of nonlinear multi-USVs

system can be transferred into the linear problem and the uncertain factors can be described more completely.

Based on the IT2T-SFM, the IT2 fuzzy formation and containment controller is designed by the imperfect

premise matching method to achieve the more flexible design process. When the IT2 fuzzy formation

controller is designed for the leader USVs system, some problems are occurred in the containment analysis

process. Therefore, the design concept for unknown leader’s input is extended to solve the problem. And a

technique is applied to obtain the less-conservative IT2 fuzzy controller design process for the containment

purpose. Finally, the simulation results are presented to verify the proposed design method.

1 INTRODUCTION

By virtue of the unmanned feature, the developments

of Unmanned Surface Vehicle (USV) and unmanned

aerial vehicle have rapidly grown up (Yan et al., 2010

& Ucgun et al., 2022). Especially, USV has become

an important role in the navy for every countries

because it can efficiently put people out of critical

danger in the extreme situations such as battlefields

and nuclear regions. It is witnessed that USVs can

efficiently substitute the human beings to achieve

various required tasks. In addition, USV has also been

extended to the control problem in daily-life (Manley,

2008). However, the dynamic of vessels whether the

ships maneuvered by human or USV often consist of

highly nonlinearities since the complex working

environment. These nonlinearities will make USV

difficult to perform well. In (Fossen, 1999),

researcher has established the nonlinear system to

represent dynamic behaviors of a navigating ship

more completely. And some researchers have

developed the control methods for USV with this kind

of nonlinear system (Gonzalez-Garcia et al., 2021).

Nevertheless, the complex environment and

disturbances still make mathematical models not

precise enough.

Over the past few decades, the control method

based on the multi-agent systems has attracted a lot of

attention. Benefiting from the rapid progress of

wireless transmission technology, the multi-agent

control system can be realized in various practical

applications (Jiang et al., 2019). Moreover, the

leader-following structure of multi-agent systems has

been proposed to further distinguish the tasks of each

agent (Jadbabaie et al., 2003). And the containment

control problem has been proposed when the leader

agents are more than one (Ji et al., 2008). Nowadays,

the formation control and containment control issues

are widely discussed for multi-USVs system (Zhou et

al., 2020 & Wu and Tong, 2022). Nevertheless, the

nonlinear systems are considered to develop the

control methods in these researches. Due to the

complex dynamic behaviors of a navigating USV,

directly designing a nonlinear controller is a

challenging task. Also, the controller is required to be

designed with a nontrivial process.

Using the if-then fuzzy rule, Takagi-Sugeno

Fuzzy Model (T-SFM) has been proposed to

represent nonlinear systems by many linear fuzzy

subsystems (Wang et al., 1996). Hence, the nonlinear

controller design problem is efficiently transferred

into linear problem. Over the past few decade, more

302

Chang, W., Lin, Y. and Ku, C.

Interval Type-2 Fuzzy Control to Solve Containment Problem of Multiple USV with Leader’s Formation Controller.

DOI: 10.5220/0012233700003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 302-310

ISBN: 978-989-758-670-5; ISSN: 2184-2809

and more research devoted their effort to solving the

control problem of nonlinear system using the T-SFM

(Precup et al., 2013). Moreover, some researchers

have developed the fuzzy controller design method to

improve control performances of a ship (Chang and

Hsu, 2016 & Chang et al., 2019). However, these

methods is based on the type-1 T-SFM, which isn’t

capable enough to deal with the uncertainties. It is

obvious that the dynamic behavior of a USV is much

more complex than the vehicles on the ground. In

addition, a lot of biofouling will also adhere to the

ship hull during the long-term transportation, which

generates the resistance to ship dynamics. And these

uncertain problems will become more serious in the

multi-USVs system due to the error dynamic

information continuously exchanged between USVs.

Extending the type-1 mebership function and T-SFM,

the Interval Type-2 T-SFM (IT2T-SFM) has been

developed to better describe the nonlinear systems

with uncertain factors (Bojan-Dragos et al., 2021 &

Lam et al., 2013).

In this paper, an IT2 formation and containment

fuzzy controller design method is proposed for multi-

USVs systems. Firstly, the IT2T-SFM is constructed

for nonlinear multi-USVs system based on leader-

following structure with the effect of uncertainties.

Referring to the results in (Lam et al., 2013), the IT2

fuzzy controller is designed for the IT2T-SFM using

the imperfect premise matching method to obtain the

less-conservative design process. Although the IT2

formation and containment control methods have

already been developed in (Lin et al., 2022). Some

imposed assumption is considered in the stability

analysis to achieve the containment purposes.

Extending the concept of (Li et al., 2021), the

containment analysis method is proposed without the

requirement of the assumption in this paper. However,

the analysis process will also become too

conservative by applying the method in (Li et al.,

2021). Because of the reason, the analysis method of

linear multi-agent system is extended to relax the

stability analysis process (Xi et al., 2011). Finally, the

simulation results of multi-USVs system is presented

to verify the formation and containment control

performances of the proposed design method.

2 SYSTEM DESCRIPTION AND

PROBLEM STATEMENT

In this section, a nonlinear system and IT2T-SFM are

established to describe the dynamic behaviours of

multi-USVs by combining with the uncertain factors..

According to the research for the analysis and control

problems of ship’s nonlinear dynamic behaviours

(Fossen, 1999), the constructive process of nonlinear

system for a moored tanker has been introduced based

on the ship’s parameters in (Fossen and Grovlen,

1998). Extending the nonlinear system, the nonlinear

multi-USVs system can be presented as follows.

() ()

()

() ()

()

1 3 14 4 3 15 5

x

t cosxt txt sinxt txt

ϑϑ ϑϑ ϑ

=+Δ−+Δ



(1)

() ()

()

() ()

()

2 3 24 4 3 25 5

x

t sinxt txt cosxt txt

ϑϑ ϑ ϑ ϑ

=+Δ++Δ



(2)

() ()

()

3366

1

x

ttxt

ϑϑ

=+Δ



(3)

() () () ()

4141

0.0358 0.0797 0.9215

x

txtxtut

ϑϑϑϑ

=− − −



(4)

() () () ()

() ()

5256

23

0.0208 0.0818 0.1224

0.7802 1.4811

x

txtxtxt

ut ut

ϑϑϑϑ

ϑϑ

=− − −

++



(5)

() () () ()

() ()

6256

23

0.0394 0.02254 0.2468

1.4811 7.4562

x

txtxtxt

ut ut

ϑϑϑϑ

ϑϑ

=− − −

++



(6)

where

()

1

x

t

ϑ

and

()

2

x

t

ϑ

are north and east position,

()

3

x

t

ϑ

is yaw angle,

()

4

x

t

ϑ

and

()

5

x

t

ϑ

are surge and

sway motion,

()

6

x

t

ϑ

is yaw angular velocity, and the

uncertain factors are considered as

() ()

14 36

~ttΔΔ

in

system (1)-(6). Note that the index

1, 2,...,

ϑ

=Φ+Ξ

denotes the agent number of USVs. The essential

information for the interaction topology is given in

the following definition according to graph theory.

Definition 1

For an undirected graph

Λ

, the structure of graph is

represented by nodes and edges which denote the

agents and the interaction between agents. The node

set is defined as

()

{

}

12

N n ,n ,...,n

Φ+Ξ

Λ=

and the edge

set is defined as

()

{

}

: En,nn,nN

ϑη ϑη

Λ⊆ ∈ Λ

. The

set of neighbour agents from

n

ϑ

is

() ()

()

{

}

: ZnNn,nE

ϑϑη

Λ= ∈ Λ ∈ Λ

. Then, the

adjacency matrix is defined as

()()

Rj

ϑη

Φ+Ξ × Φ+Ξ



=∈



J

. In matrix J, the element values

1j

ϑη

=

and

0j

ϑη

=

respectively denote there is and isn’t an interaction

between agent

n

ϑ

and

n

η

. The degree matrix is also

constructed with the element of J as

() ( )

{

}

1

00diag , , ,d ,...,d

Φ

Φ+ Φ+Ξ

=D  where

1

dj

ϑϑη

η

Φ+Ξ

=



and

{

}

diag 

denotes the diagonal

matrix with the item



. Therefore, the Laplacian

Interval Type-2 Fuzzy Control to Solve Containment Problem of Multiple USV with Leader’s Formation Controller

303

matrix is obtained as follows by =−LDJ to

represent the interaction relationship of all the agents.

21



=





00

L

LL

(7)

where

1

R

Ξ×Ξ

∈L denotes the interaction between

followers and

2

R

Φ×Ξ

∈L denotes the interaction from

leaders to followers. To develop the IT2 fuzzy

controller, the IT2T-SFM is constructed for nonlinear

multi-USVs system (1)-(6) as follows

Model Rule

α

: If

()

3

x

t

ϑ

is

M

α



, then

() () ()

x

txtut

ϑϑϑ

αα

=+AB



(8)

where

() () () () () () ()

T

123456

x

t xtxtxtxtxtxt

ϑ ϑϑϑϑϑϑ



=



,

() () () ()

T

123

ut ut ut ut

ϑ ϑϑϑ



=



and

1, 2, 3

α

=

. To

demonstrate the effectiveness of IT2 membership

function in the uncertain problem, the model matrices

α

A and

α

B are selected same as the type-1 T-SFM

(Chang and Hsu, 2016 & Chang et al., 2019)

according to the following operating points.

T

o

1

00 90 000

op

x

ϑ



=−



,

T

o

2

000 000

op

x

ϑ



=



,

T

o

3

0090 000

op

x

ϑ



=



.

Note that

1

A and

1

B of fuzzy rule 1 are related to

1op

x

ϑ

and so on. Considering three operating points,

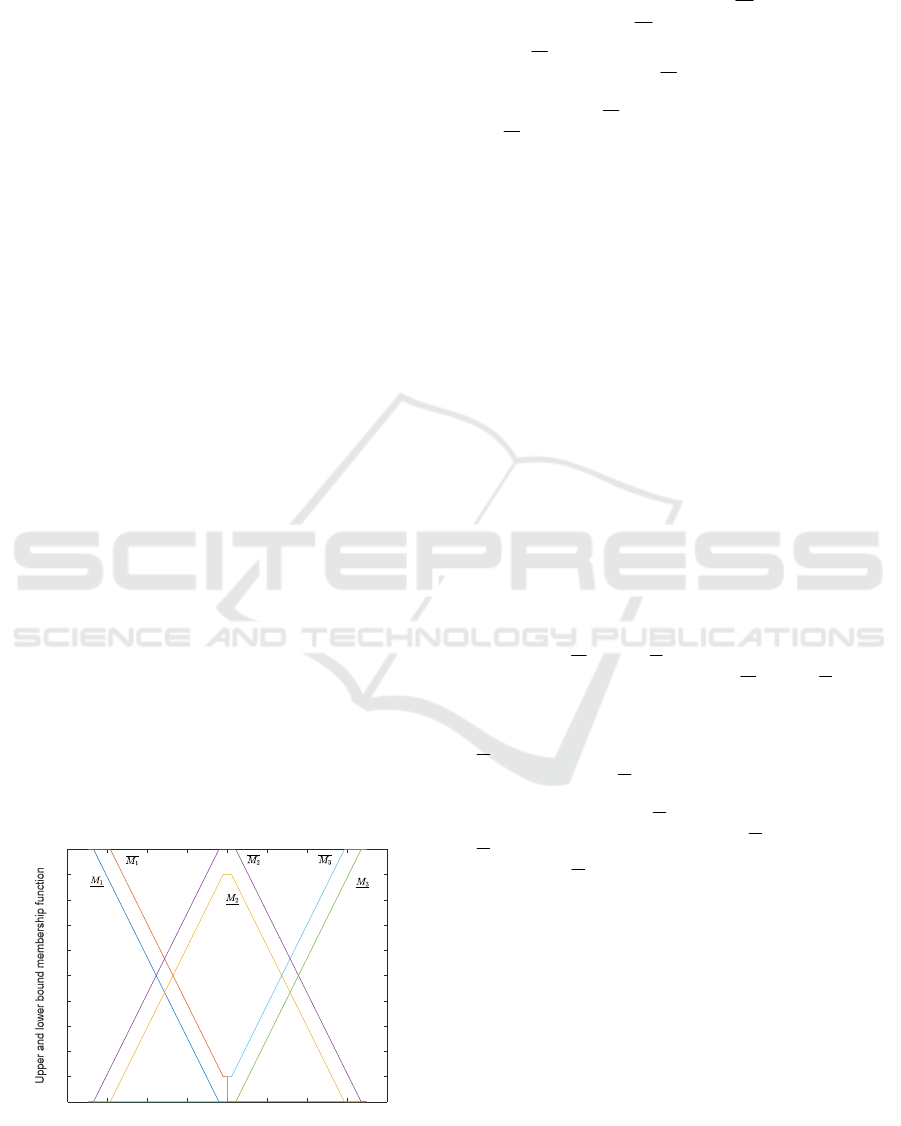
the IT2 membership function is designed in Figure 1

to more completely describe the uncertain factors.

Figure 1: IT2 membership function of IT2T-SFM.

Based on the IT2 membership function the Fig. 1, the

fired strength for IT2T-SFM (8) is obtained as

()

333

MM,M

x

txtxt

ϑϑϑ

α





=







(9)

where

()

3

M

x

t

ϑ

α

and

()

3

M

x

t

ϑ

α

denotes the upper

and lower bound membership functions which satisfy

()

33

0M M 1xt xt

ϑϑ

α

≤≤≤.

To achieve the formation purpose, the IT2T-SFM

(8) is further presented into the following form.

Model Rule

α

: If

()

3

x

t

ϑ

is

M

α



, then

() () ()

1,...,

ttutfor

xt xt ut for

ϑϑϑ

αα

ϑϑϑ

αα

ϖϖ ϑ

ϑ



=+ =Φ





=+ =Φ+Φ+Ξ





AB



(10)

where

() ()

txt

ϑϑ ϑ

ϖ

=−ℜ

denotes the translated

state vector with the desired value vector

ϑ

ℜ

for the

states of leader USVs. Then, the following overall

IT2T-SFM is inferred from the model (10) with (9).

() ()

()

() ()

{

}

3

1

Mtxttut

ϑϑϑϑ

ααα

α

ϖϖ

=

=+



AB





1, 2,...,for

ϑ

=Φ (11)

() ()

()

() ()

{

}

3

1

M

x

txtxtut

ϑϑϑϑ

ααα

α

=

=+



AB





1, 2,...,for

ϑ

=Φ+ Φ+ Φ+Ξ (12)

where

()

33333

MM M

x

t xtxt xtxt

ϑϑϑϑϑ

αα

α

=Ω+Ω



,

()

3

M0xt

ϑ

α

≥



and

()

3

1

M1xt

ϑ

α

=





. Note that

()

3

x

t

ϑ

α

Ω and

()

3

x

t

ϑ

α

Ω denote the nonlinear

functions which are unnecessary to be known. These

functions satisfy

()

33

10xt xt

ϑϑ

α

≥Ω ≥Ω ≥ and

()

33

1xt xt

ϑϑ

α

Ω+Ω=. According to (10), the IT2

fuzzy formation and containment controller can be

designed as follows.

Controller Rule

β

: If

()

3

x

t

ϑ

is

N

β



, then

() ()

() () ()

()

1,...,

N

ut t for

ut jxtxt for

ϑϑ

β

ϑϑη

βϑη

η

ϖϑ

ϑ

∈Λ



==Φ





=−=Φ+Φ+Ξ







F

K

(13)

where

N

β



denotes the IT2 fuzzy set and

β

denotes

the rule number of IT2 fuzzy controller,

β

F

and

β

K

denote the feedback gains to be designed. And the IT2

membership function of (13) is designed in Figure 2.

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

x3(t)

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

304

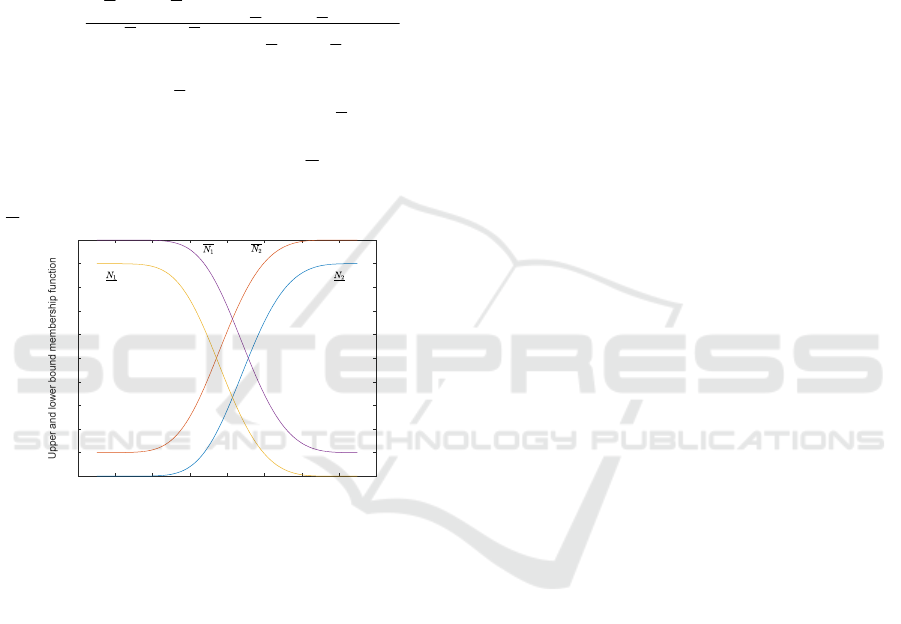
Then, the IT2 fuzzy controller (13) is referred into

overall fuzzy controller as follows.

() ()

()

{

}

2

3

1

Nut xt t

ϑϑϑ

ββ

β

ϖ

=



F



1, 2,...,for

ϑ

=Φ (14)

() ()

()

() ()

()

2

3

1

N

ut xt jxtxt

ϑϑ ϑη

ββϑη

β

η

=

∈Λ





=−









K



1, 2,...,for

ϑ

=Φ+ Φ+ Φ+Ξ (15)

where

()

{}

33 33

3

2

33 33

1

NN

N0

NN

xt xt xt xt

xt

xt xt xt xt

ϑϑ ϑϑ

β

ϑ

β

ϑϑ ϑϑ

=

+

=≥

+











,

()

2

3

1

N1xt

ϑ

β

=





,

()

3

N

x

t

ϑ

β

and

()

3

N

x

t

ϑ

β

denote the upper and lower bound membership

functions presented in Figure 2,

()

3

x

t

ϑ

β

 and

()

3

x

t

ϑ

β

 denote the predefined functions.

Figure 2: IT2 membership function of fuzzy controller.

Respectively substituting the IT2 fuzzy formation

and containment controller of (14)-(15) into the IT2T-

SFM (11)-(12), the following closed-loop IT2 fuzzy

model can be obtained.

() ()

()

{

}

32

33

11

MN

LLL L

L

txtxt t

αβ ααβ

αβ

ϖϖ

==

=⊗+



IABF





(16)

() ()

()

{}

32

33

11

12

MN

FFF

FL

F

xt xt xt

x

txt

αβ

ααβ αβ

==

=

×⊗+⊗ +⊗



IALBK LBK





(17)

where

() () ()

T

1L

tt t

ϖϖ ϖ

Φ



=





,

() () ()

T

1L

x

txt xt

Φ



=





,

() () ()

T

1F

x

txt xt

Φ+ Φ+Ξ



=





,

L

I and

F

I denote

the identity matrix with the proper dimension,

⊗ is

Kronecker product. For the containment purpose, the

containment error system is constructed as follows

() ()

()

1

12 6

FF L

et xt xt

−

=+ ⊗LL I

(18)

where

() () () ()

12F

et e t e t e t

Φ+ Φ+ Φ+Ξ





=







and

() () ()

()

N

et j xt xt

ϑϑη

ϑη

η

∈Λ

=−



for

1,...,

ϑ

=Φ+ Φ+Ξ

.

Then, the error dynamic system can be obtained as

follows via the closed-loop system (16)-(17) and (18).

() ()

()

{}

32

33

11

1

112

MN

FFF

F

L

F

et xt xt

et

αβ

ααβ α

==

−

=

×⊗+⊗ − ⊗ℜ



IALBK LLA





(19)

Referring to the design method in (Li et al., 2021),

the containment error dynamic system (19) can be

represented with the following form.

() ()

()

() ( )

{}

32

33

11

1

MN

FFF

F

FLc

et xt xt

et

αβ

ααβ α

==

=

×⊗+⊗ +⊗ℜ



IALBK IA





(20)

where

1

Lc

h

ϑ

Φ

℘

℘=

ℜ=− ℜ



for

1,...,

ϑ

=Φ+ Φ+Ξ

,

h

ϑ

℘

is the (

,

ϑ

℘

)-th element in the matrix

1

12

−

−LL

which satisfies

0h

ϑ

℘

−≥ and

1

1h

ϑ

Φ

℘

℘=

=



. Then, the

more relaxed IT2 fuzzy controller design process can

be obtained by referring to (Xi et al., 2011) as follows.

For a Laplacian matrix

1

L , the Jordan canonical form

is defined as

-1

1

=ΘΖLΖ

with the non-singular

matrix

Ζ

. And

ϑ

λ

is defined as eigenvalue of matrix

1

L whose number is related to the follower USVs.

Then, the eigenvalues are rearranged with the

relationship

{

}

{

}

{

}

12

Re Re Re

λλ λ

Φ+ Φ+ Φ+Ξ

<<<

where

{

}

R

e 

and

{

}

Im 

denotes the real and

imaginary part of

 .

Lemma 1 (Xi et al., 2011)

Considering the eigenvalue

ϑ

λ

of Laplacian matrix,

the following relation can be obtained.

If

{

}

{

}

123

0Re Im

λλ

Π+ Π+ Π <





for

1, 2,=

3, 4

is satisfied, then

{

}

{

}

123

0Re Im

ϑϑ

λλ

Π+ Π+ Π <

for

1,...,

ϑ

=Φ+ Φ+Ξ

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

x3(t)

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Interval Type-2 Fuzzy Control to Solve Containment Problem of Multiple USV with Leader’s Formation Controller

305

is also satisfied, where the eigenvalue

λ





is defined

with

{

}

1,2 1

Re j

λλκ

Φ+

=±



and

{

}

3,4

Re j

λλκ

Φ+Ξ

=±



,

κ

is defined as

{

}

max

ϑ

κλ

=

for

1,...,

ϑ

=Φ+ Φ+Ξ

.

Applying the matrix

Ζ

, the error dynamic system

(20) can be further transferred into the following form.

() ()

()

{

}

32

33

11

MN

L

c

et xt xt et

ϑϑϑϑϑ

αβ ααβ α

αβ

==

=+ℵ+ℜ



ABK A







  



(21)

where

{

}

,diag

ααα

=AAA



,

{

}

,diag

ααα

=BBB



,

()

Re e t

et

Im e t

ϑ





=







,

()

Lc

Re

Im



ℜ



ℜ=



ℜ





,

{

}

{

}

{} {}

66

Re Im

Im Re

ϑϑ

ϑ

ϑϑ

λλ



−



ℵ=





II

. Note that the error

signal

()

et

ϑ



and desired value

L

c

ℜ



are obtained

from

()

1

d

et et

−

=⊗ZI



and

()

1

L

cdLc

−

ℜ= ⊗ ℜZI



.

Therefore, an IT2 fuzzy formation and

containment controller design method is proposed in

next section with the closed-loop system (16)-(17).

3 IT2 FUZZY FORMATION AND

CONTAINMENT

CONTROLLER DESIGN

Via the IT2 fuzzy controller design with (14)-(15), the

formation and containment purposes can be achieved

with the following theorem.

Theorem 1

If there exist the positive matrices

L

Q ,

F

Q ,

L

α

β

W

,

F

α

β

W

, common symmetric matrices

L

M ,

F

M , the

matrices

L

β

G

,

F

β

T

such that the following sufficient

conditions are satisfied with the given positive scalars

1

iq

αβ

δ

,

1

iq

αβ

δ

,

ε

,

φ

, then the leader USVs can achieve

the stability and complete the formation. Additionally,

the containment is achieved for all follower USVs.

0

LF L F

,, ,

αβ αβ

>QQ W W



(22)

0

LL

αβ αβ

++>ΓW M (23)

()

111 1

32

11

0

iq iq iq L iq L L

αβ αβ αβ αβ αβ αβ

αβ

δδδ δ

==

−− + −<



ΓWMM

(24)

0

FF

αβ αβ

++>ΨW M (25)

()

111 1

32

11

0

iq iq iq F iq F F

αβ αβ αβ αβ αβ αβ

αβ

δδδ δ

==

−− + −<



ΨWMM

(26)

2

12

0

*

FF

φ



>





QQ

I



(27)

{

}

2

min

φ

(28)

where

TTT

LLL L

α

β

αα

β

α

β

α

=+ ++ΓAQBGQAGB

,

TTT

12

*

FFF FF

ϑϑ

ααβαβα α

αβ

ε





+ℵ + +ℵ +

=





−





AQ BT QA T B Q A

Ψ

I

   

  

,

L

ββ

=GFQ

,

F

ββ

=TKQ





,

1

L

−

=QP

,

1

F

−

=QP



.

proof

Because the limitation of this paper, the main

derivation related to the contribution of this paper is

provided instead of detailed proof. The stability

analysis process of closed-loop IT2 fuzzy model (16)

is similar to the general control method based on T-

SFM. Moreover, the imperfect premise matching and

related stability analysis have been completely

introduced for IT2T-SFM and fuzzy controller design

method in (Lam, Deters et al., 2013). Referring to

(Lam et al., 2013) and defining the Lyapunov

function of

() ()

()

T

11

LL

Vt t t

ϖϖ

= P

, the stability

conditions (22)-(24) can be derived. In Theorem 1,

the parameter

1

iq

αβ

δ

and

1

iq

αβ

δ

are obtained from IT2

membership function such that the more relaxed

stability analysis process than the type-1 fuzzy

control method can be proposed. It is worth notice

that the stability analysis process is only required to

be developed for leader USV 1. And the stability of

all other leader USVs is also ensured because of the

homogenous property. Therefore, the leader USVs

can be controlled to the desired position by properly

setting the desired value of states

ϑ

ℜ

.

However, the redundant item related to

ϑ

ℜ

can

be seen in error dynamic system (19) which causes

the analysis problem in IT2 fuzzy containment

controller design method. To solve the problem, the

stability analysis method can be developed as follows

by referring to (Li et al., 2021). According to the

properties of

1

12

−

−LL , whose element is nonnegative

and individual row sum is equal to 1, the error

dynamic system (19) is transferred into (20). The

detailed information can be referred to (4)-(9) in (Li,

Jabbari et al., 2021). And the system (20) is further

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

306

transferred into the Jordan canonical form (21). Then,

defining Lyapunov function

() ()

()

T

FF

Vt et et

ϑϑ

= P







where

{

}

,

F

FF

diag=PPP



and ellipsoid

() ()

()

{

}

T

2

:|

F

et et et

ϑϑ ϑ

σ

μ

≤ℑP

 



 

, the stability

conditions (25-26) for error dynamic system (21) can

be obtained as follows

() ()

(

)

T

0

FFLcLc

Vt Vt

ε

+−ℜℜ<





(29)

Referring to (Li et al., 2021), one can know that if the

condition (29) is satisfied,

σ

is an attractive invariant

set for (21). And the Problem 1 in (Li et al., 2021) for

the containment purpose is achieved with the effect

of the item related to

L

c

ℜ



. In ellipsoid, the symbol ℑ

is defined for the upper bound for the leader’s

unknown input in (Li et al., 2021). It is worth notice

that no matter the designed desired value

L

c

ℜ



or the

leader control input in this paper is definitely finite

due to the convergence of states. Obviously, if the

sufficient conditions (25)-(26) are satisfied by

Theorem 1, then the stability condition (29) is

satisfied. And the relationship

()

2

et

ϑ

φ

≤Ξℑ



can be

obtained according to the definition of ellipsoid and

condition (27) where

Ξ denote the follower numbers.

Via the minimization with condition (28), the upper

bound from

L

c

ℜ



to

()

et

ϑ



is minimized.

However, the conservative stability conditions

(25)-(28) is also caused due to the minimization of

(28) on a common positive definite condition. To

solve the problem, Lemma 1 is applied to obtain the

more relaxed stability analysis process. Regardless of

the USV’s number, the sufficient conditions (25)-(28)

is only required to be satisfied for four kinds of

eigenvalue.

4 SIMULATION OF FORMATION

AND CONTAINMENT FOR

MULTI-USVS SYSTEM

In the simulation of this section, the IT2 fuzzy

controller design method in Theorem 1 is applied to

simultaneously solve the formation and containment

control problems of multi-USVs system (1)-(6). Thus,

the control gains are obtained as follows by solving

the conditions (22)-(28) with MATLAB.

1

2

0.6703 0.3381 0.0034 2.7782 0.7549 0.0070

0.6315 1.3098 0.5664 1.3769 5.4683 0.6326

0.1243 0.2727 0.3430 0.2710 1.1520 0.2953

0.6719 0.3372 0.0034 2.7848 0.7529 0.0070

0.6297 1.3124 0.5667 1.373

−−−−−









=− −









−−−−





−−−

=− − −

F

F 0 5.4795 0.6335

0.1239 0.2732 0.3431 0.2702 1.1540 0.2955









−









−−





(30)

4

1

4

2

1.5121 0.0185 0.0013 1.7365 0.0213 0.0020

10 0.0006 0.8910 0.0271 0.0008 1.0260 0.0310

0.0188 0.1737 0.0130 0.0216 0.2001 0.0140

1.4753 0.0124 0.0017 1.6942 0.0144 0.0024

10 0.0597 0.8703 0.

−− −−









=×− − − −









−−−−





−− −−

=×− −

K

K 0265 0.0684 1.0021 0.0303

0.0302 0.1702 0.0128 0.0346 0.1960 0.0138









−−









−−





(31)

Then, the state responses of nonlinear multi-USVs

system (1)-(6) are obtained in Figures 3-8 by applying

the IT2 fuzzy controller (14)-(15) with the gains (30)-

(31).

Figure 3: State

()

1

x

t

ϑ

responses of multi-USVs system.

Figure 4: State

()

2

x

t

ϑ

responses of multi-USVs system.

0 1020304050

time

(

s

)

-5

0

5

10

15

20

25

30

3

5

x

1

(t): X position

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

0 1020304050

time

(

s

)

-20

-10

0

10

20

30

x

2

(t): Y position

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

Interval Type-2 Fuzzy Control to Solve Containment Problem of Multiple USV with Leader’s Formation Controller

307

Figure 5: State

()

3

x

t

ϑ

responses of multi-USVs system.

Figure 6: State

()

4

x

t

ϑ

responses of multi-USVs system.

Figure 7: State

()

5

x

t

ϑ

responses of multi-USVs system.

According to the simulation results in Figures 3-4,

it is seen that the X position and Y position of all

leader USVs can achieve the stability and converge to

the desired value. Following the states of leader USVs,

the states of follower USVs simultaneously complete

Figure 8: State

()

6

x

t

ϑ

responses of multi-USVs system.

Figure 9: Trajectories of multi-USVs system.

the containment task such that all the states are forced

into the interval formed by leader USVs. Moreover,

the states of follower USVs can also be forced to zero

if the states of all leader USVs are set to zero value in

Figures 5-8. Based on the results of Figures 3-4, the

trajectories of all the USVs in the nonlinear multi-

USVs system (1)-(6) are also presented in Figure 9. It

is obvious that the triangular region is successfully

formed by three leader USVs via the IT2 fuzzy

formation controller design method in this paper

without the communication between USVs. And all

follower USVs are controlled into the triangular

region. In this simulation, the effect of uncertainties

is considered as

() () ()

14 36

~0.1ttsintΔΔ=

. It is worth

notice that the good formation and containment

control performances can be obtained in Figures 3-8.

And the smooth trajectories of all USVs can be

obtained in Figure 9. Thus, it is said that the IT2 fuzzy

controller design method of Theorem 1 in this paper

is a good choice to simultaneously achieve the

0 1020304050

time

(

s

)

-6

-4

-2

0

2

4

6

8

x

3

(t): yaw angle

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

0 1020304050

time

(

s

)

-10

-8

-6

-4

-2

0

2

4

6

x

4

(t): surge

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

0 1020304050

time

(

s

)

-8

-6

-4

-2

0

2

4

x

5

(t): sway

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

0 1020304050

time

(

s

)

-15

-10

-5

0

5

10

1

5

x

6

(t): yaw angular velocity

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

-10 0 10 20 30 40

X Positio

n

-20

-10

0

10

20

30

Y position

LDR1

LDR2

LDR3

FLR4

FLR5

FLR6

FLR7

FLR8

FLR9

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

308

formation and containment purposes for a nonlinear

multi-USVs system with uncertain problem.

5 CONCLUSIONS

In this paper, an IT2 fuzzy formation and containment

controller design method is developed for the multi-

USVs system based on the IT2T-SFM. Using the

imperfect premise matching method, the IT2 fuzzy

formation and containment controller can be designed

with the different IT2 membership function from the

model. The design concept for leader’s unknown

input is successfully extended to solve the analysis

problem. And the analysis method according to the

Jordan canonical form of Laplacian matrix is applied

to obtain a more relax IT2 fuzzy controller design

process. From the simulation results, the smooth

responses to achieve the formation and containment

purposes can be obtained even under the effect of

uncertainties.

ACKNOWLEDGEMENTS

This work was supported by the National Science and

Technology Council of the Republic of China under

Contract NSTC 112-2221-E-019-057.

REFERENCES

Yan, R. J., Pang, S., Sun, H. B., & Pang, Y. J. (2010).

Development and missions of unmanned surface

vehicle. Journal of Marine Science and Application, 9,

451-457.

Ucgun, H., Okten, I., Yuzgec, U., & Kesler, M. (2022). Test

platform and graphical user interface design for vertical

take-off and landing drones. Romanian Journal of

Information Science and Technology, 25(3–4), 350-367.

Manley, J. E. (2008, September). Unmanned surface

vehicles, 15 years of development. In OCEANS 2008

(pp. 1-4). IEEE.

Fossen, T. I. (1999). Guidance and Control of Ocean

Vehicles, Wiley. New York, USA.

Gonzalez-Garcia, A., & Castañeda, H. (2021). Guidance

and control based on adaptive sliding mode strategy for

a USV subject to uncertainties. IEEE Journal of

Oceanic Engineering, 46(4), 1144-1154.

Jiang, Z., Yang, T., Zhou, L., Yuan, Y., & Feng, H. (2019).

Maritime search and rescue networking based on multi-

agent cooperative communication. Journal of

Communications and Information Networks, 4(1), 42-

53.

Jadbabaie, A., Lin, J., & Morse, A. S. (2003). Coordination

of groups of mobile autonomous agents using nearest

neighbor rules. IEEE Transactions on automatic

control, 48(6), 988-1001.

Ji, M., Ferrari-Trecate, G., Egerstedt, M., & Buffa, A.

(2008). Containment control in mobile networks. IEEE

Transactions on Automatic Control, 53(8), 1972-1975.

Zhou, W., Wang, Y., Ahn, C. K., Cheng, J., & Chen, C.

(2020). Adaptive fuzzy backstepping-based formation

control of unmanned surface vehicles with unknown

model nonlinearity and actuator saturation. IEEE

Transactions on Vehicular Technology, 69(12), 14749-

14764.

Wu, W., & Tong, S. (2022). Fixed-time adaptive fuzzy

containment dynamic surface control for nonlinear

multiagent systems. IEEE Transactions on Fuzzy

Systems, 30(12), 5237-5248.

Wang, H. O., Tanaka, K., & Griffin, M. F. (1996). An

approach to fuzzy control of nonlinear systems:

Stability and design issues. IEEE Transactions on

Fuzzy Systems, 4(1), 14-23.

Precup, R. E., Tomescu, M. L., Preitl, S., Petriu, E. M.,

Fodor, J., & Pozna, C. (2013). Stability analysis and

design of a class of MIMO fuzzy control systems.

Journal of Intelligent & Fuzzy Systems, 25(1), 145-155.

Chang, W. J., & Hsu, F. L. (2016). Sliding mode fuzzy

control for Takagi–Sugeno fuzzy systems with bilinear

consequent part subject to multiple constraints.

Information Sciences, 327, 258-271.

Chang, W. J., Lin, Y. H., Du, J., & Chang, C. M. (2019).

Fuzzy control with pole assignment and variance

constraints for continuous-time perturbed Takagi-

Sugeno fuzzy models: Application to ship steering

systems. International Journal of Control, Automation

and Systems, 17, 2677-2692.

Bojan-Dragos, C. A., Precup, R. E., Preitl, S., Roman, R.

C., Hedrea, E. L., & Szedlak-Stinean, A. I. (2021).

GWO-based optimal tuning of type-1 and type-2 fuzzy

controllers for electromagnetic actuated clutch systems.

IFAC-PapersOnLine, 54(4), 189-194.

Lam, H. K., Li, H., Deters, C., Secco, E. L., Wurdemann,

H. A., & Althoefer, K. (2013). Control design for

interval type-2 fuzzy systems under imperfect premise

matching. IEEE Transactions on Industrial Electronics

,

61(2), 956-968.

Lin, Y. H., Chang, W. J., & Ku, C. C. (2022). Solving the

Formation and Containment Control Problem of

Nonlinear Multi-Boiler Systems Based on Interval

Type-2 Takagi–Sugeno Fuzzy Models. Processes,

10(6), 1216.

Li, P., Jabbari, F., & Sun, X. M. (2021). Containment

control of multi-agent systems with input saturation and

unknown leader inputs. Automatica, 130, 109677.

Xi, J., Shi, Z., & Zhong, Y. (2011). Consensus analysis and

design for high-order linear swarm systems with time-

varying delays. Physica A: Statistical Mechanics and

its Applications, 390(23-24), 4114-4123.

Fossen, T. I., & Grovlen, A. (1998). Nonlinear output

feedback control of dynamically positioned ships using

Interval Type-2 Fuzzy Control to Solve Containment Problem of Multiple USV with Leader’s Formation Controller

309

vectorial observer backstepping. IEEE Transactions on

Control Systems Technology, 6(1), 121-128.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

310