Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance

Forecasting

George Marinos

1,2 a

, Manos Karvounis

2 b

and Ioannis N. Athanasiadis

1 c

Data Competence Center, Wageningen University & Research, Wageningen, Netherlands

Agroknow IKE, Athens, Greece

Keywords:

Survival Analysis, Threshold Exceedance, Extreme Event Forecasting.

Abstract:

This study presents a novel framework designed for predicting threshold exceedance in time series data through

the use of survival analysis techniques. Contrasting the traditional binary classiﬁcation methodologies typi-

cally applied to this problem, our approach offers a unique perspective, modeling and predicting not only

the occurrence but also the time-to-event information. This signiﬁcant differentiation furnishes an invaluable

tool for understanding and anticipating extreme events, and more importantly, it enhances decision-makers’

comprehension of temporal dynamics of such risks, enabling early intervention strategies. These facets are

especially critical in various domains where timely action is essential. The effectiveness of our methodology

has been empirically conﬁrmed using both simulated and real-world datasets, showcasing our method’s preci-

sion in forecasting threshold exceedance. An illustrative application within the food safety domain, leveraging

real-world data related to food recalls over time, further demonstrates the practical utility of our approach,

particularly in preventing and controlling high-risk hazards like salmonella. These ﬁndings underscore the

wide-ranging implications of our method, particularly in applications where understanding the temporal dy-

namics of risks is paramount.

1 INTRODUCTION

The advent of extreme event forecasting holds

tremendous signiﬁcance across multiple domains, in-

cluding ﬁnance, environmental sciences, engineering,

public health, food safety and natural disaster man-

agement. The characteristically sporadic nature of ex-

treme events, often marked by their rare occurrence

yet substantial impact, presents formidable challenges

to forecast accurately. Nevertheless, precise predic-

tions of these events are integral to mitigating po-

tential disruptions, minimizing losses, and informing

decision-making processes.

Within the domain of ﬁnance, forecasting extreme

market ﬂuctuations facilitates informed investment

decisions and risk management strategies. Environ-

mental sciences greatly beneﬁt from predictions of

extreme weather events, aiding in disaster prepared-

ness and infrastructure planning. The anticipation

of extreme loads in engineering can guide the de-

https://orcid.org/0000-0002-2220-0009

https://orcid.org/0000-0003-3750-2066

https://orcid.org/0000-0003-2764-0078

sign of resilient structures, and in public health and

food safety, accurate forecasting can bolster preven-

tive measures and surveillance systems, notably in

the context of infectious disease outbreaks or food-

related incidents like salmonella.

However, the sparsity of extreme event data, cou-

pled with their inherent uncertainty and potential non-

stationarity and nonlinear behavior, can obstruct the

path to robust forecasting models. The risk of overﬁt-

ting becomes a stark reality, with models potentially

capturing noise rather than true underlying patterns.

Furthermore, the inﬂuence of external factors, such

as climate change and socioeconomic variables, add

to the complexity, necessitating a comprehensive un-

derstanding of underlying mechanisms.

In light of these challenges, this study introduces

a novel framework leveraging survival analysis tech-

niques to model and predict not only the occurrence of

such events but, critically, the time until these events

transpire. This shift from conventional binary clas-

siﬁcation methodologies provides a novel perspec-

tive on threshold exceedance prediction, offering a

vital tool for understanding and anticipating extreme

events. Furthermore, our method enhances the com-

Marinos, G., Karvounis, M. and Athanasiadis, I.

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting.

DOI: 10.5220/0012234700003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 3: KMIS, pages 62-72

ISBN: 978-989-758-671-2; ISSN: 2184-3228

prehension of the temporal dynamics of extreme risks,

crucial for facilitating timely interventions.

We demonstrate the efﬁcacy of our approach us-

ing both simulated and real-world datasets, highlight-

ing its precision in forecasting threshold exceedance.

A practical application of our method within the con-

text of food safety underscores its utility, especially

in managing high-risk hazards. The ramiﬁcations of

this approach are far-reaching, holding promise for a

broad range of applications where understanding the

temporal dynamics of risk is crucial. This universal

framework, applicable to any univariate or multivari-

ate time series dataset, presents a promising avenue to

address the intricacies of extreme event forecasting.

2 RELATED WORK

Within this research ﬁeld, we have identiﬁed two dis-

tinct sub-areas. The ﬁrst sub-area focuses on extreme

event forecasting, where researchers aim to develop

predictive algorithms that account for the presence of

extreme events. Neural networks are often utilized

in these methods, as they exhibit sensitivity towards

predicting extreme values. However, the primary ob-

jective in this sub-area is to forecast the exact value

of the time series, leading to the evaluation of these

methods using classic regression metrics.

On the other hand, the second sub-ﬁeld, known as

exceedance threshold forecasting, also involves pre-

dicting extreme values in a time series. However, a

crucial difference lies in the approach taken. In this

sub-ﬁeld, a threshold is set, and the goal is to forecast

whether or not there will be a threshold exceedance

in the upcoming timestamps. Consequently, this can

be framed as a binary classiﬁcation problem, where

the focus shifts to predicting the occurrence or non-

occurrence of the threshold exceedance. In our work,

we contribute to the second sub-ﬁeld of exceedance

threshold forecasting.

2.1 Extreme Event Forecasting

The authors in (Abilasha et al., 2022) address the

challenge of accurately predicting extreme events in

time series forecasting by proposing the Deep eX-

treme Mixture Model (DXtreMM). This model com-

bines Gaussian and Generalized Pareto distributions

to better capture extreme points. It consists of a Vari-

ational Disentangled Auto-encoder (VD-AE) classi-

ﬁer and a Multi-Layer Perceptron (MLP) forecaster

unit. The VD-AE predicts the possibility of extreme

event occurrence, while the forecaster predicts the ex-

act extreme value. Extensive experiments on real-

world datasets demonstrate the model’s effectiveness,

comparable to existing baseline methods. The DX-

treMM model, with its novel formulation and con-

sideration of heavy-tailed data distributions, offers a

promising approach for accurate extreme event pre-

diction in time series forecasting.

This (Dai et al., 2022) paper introduces a novel

clustering algorithm, the Generalized Extreme Value

Mixture Model (GEVMM), for accurate prediction

of extreme values in scenarios with mixed distribu-

tion characteristics. The algorithm adaptively clas-

siﬁes block maximum data into clusters based on

their weights in the population, creating a GEVMM

that can forecast maximum values in a speciﬁed re-

turn period. The optimal number of clusters is de-

termined using the elbow method, along with RMSE

and R-squared, to prevent over- and under-ﬁtting. The

method is validated through theoretical examples and

applied to trafﬁc load effects on bridges using weight-

in-motion data. Results demonstrate superior perfor-

mance compared to existing methods, showcasing the

potential of the proposed approach for accurate esti-

mation of extreme values with mixed probability dis-

tributions across various ﬁelds.

The (Hill Galib et al., 2022) paper introduces

DeepExtrema, a novel framework for accurate fore-

casting of extreme values in time series data. Deep-

Extrema combines a deep neural network (DNN) with

the generalized extreme value (GEV) distribution to

forecast the block maximum value. The authors ad-

dress the challenge of preserving inter-dependent con-

straints among the GEV model parameters during

DNN initialization. The framework enables condi-

tional mean and quantile prediction of block maxima,

surpassing other baseline methods in extensive exper-

iments on real-world and synthetic data. DeepEx-

trema incorporates the GEV distribution into a deep

learning framework, capturing nonlinear dependen-

cies in time series data. The paper overcomes techni-

cal challenges such as positivity constraints and data

scarcity through reparameterization of the GEV for-

mulation and a model bias offset mechanism. Con-

tributions include the novel framework, GEV con-

straint reformulation, model bias offset mechanism,

and comprehensive experiments demonstrating Deep-

Extrema’s superiority over baselines.

2.2 Threshold Exceedance Forecasting

In their study, (Taylor and Yu, 2016) propose an

approach to manage ﬁnancial risk using exceedance

probability. They aim to predict if the returns of ﬁnan-

cial assets will surpass a certain threshold. To achieve

this, they employ a method called CARL (conditional

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting

auto-regressive logit) that utilizes logistic regression.

Building upon this (Taylor, 2017) extends CARL to

handle multiple threshold problems. This extended

model proves useful in predicting wind ramp events,

where forecasting the extreme values on both ends of

the distribution is crucial.

The (Krylova and Okhrin, 2022) study proposes a

two-stage procedure for predicting exceedances of le-

gal limits for PM10 and O3 concentrations in air pol-

lution using machine learning. Hourly pollutant con-

centrations are forecasted using the Stochastic Gradi-

ent Boosting Model, demonstrating superior perfor-

mance compared to similar studies. The forecasts are

then utilized to predict exceedances of daily limits,

achieving an average detection probability above 80%

with low false alarm probability.

The (Gong and Ordieres-Mer

e, 2016) study fo-

cuses on forecasting daily maximum ozone thresh-

old exceedances in the Hong Kong area using pre-

processing techniques and ensemble artiﬁcial intel-

ligence (AI) classiﬁers. The researchers address the

imbalance data problem by employing methods such

as over-sampling, under-sampling, and the synthetic

minority over-sampling technique. Ensemble algo-

rithms are proposed to enhance the accuracy of the

classiﬁers. Additionally, a regional data set is gen-

erated to capture ozone transportation characteristics.

The results demonstrate that the combination of pre-

processing methods and ensemble AI techniques ef-

fectively predicts ozone threshold exceedances. The

study provides insights into the relative importance

of variables for ozone pollution prediction and high-

lights the signiﬁcance of regional data. The ﬁndings

can be utilized by Hong Kong authorities to enhance

existing forecasting tools and guide future research in

selecting appropriate techniques.

The (Zhou et al., 2016) study introduces a novel

method for predicting trafﬁc load effects on bridges.

Traditionally, load effects were assumed to be identi-

cally and independently distributed, but this method

recognizes that different loading events have dif-

ferent statistical distributions. The approach uses

the peaks-over-threshold method with the generalized

Pareto distribution to model the upper tail of load

effects for each event type. The distributions are

then combined based on their weights to determine

the overall distribution. Numerical studies validate

the method’s effectiveness in predicting extreme val-

ues. The proposed method addresses the challenges

of non-identically distributed load effects and pro-

vides a mathematical formulation for analysis.

The (Kazemi et al., 2023) paper proposes a ma-

chine learning approach to predict iron threshold ex-

ceedances in drinking water distribution networks.

Using ten years of data, models were trained with

Random Forests, Support Vector Machines, and RUS-

Boost Trees algorithms. The best model achieved pre-

diction accuracies over 70% for the UK regulatory

concentration. The predicted probabilities were used

to rank relative risk and inform proactive management

decisions. The aim is to provide predictive tools for

proactive water quality management.

In (Cerqueira and Torgo, 2022) authors explore

the prediction of exceedance probability in the con-

text of signiﬁcant wave height forecasting. They pro-

pose a novel methodology that involves transforming

the univariate time series data into a supervised learn-

ing format. This is achieved by using the lag values

of the time series as input features in a standard re-

gression algorithm. Once the regression model gen-

erates predictions for the future values of the time se-

ries, the authors proceed to estimate the probability

of exceeding a predeﬁned threshold (τ). To accom-

plish this, they rely on a selected distribution, which

can be a well-known distribution such as the normal,

Gumbel, generalized Pareto, or others. The authors

calculate the (CDF) cumulative distribution function

of the chosen distribution, utilizing the predicted val-

ues as the mean and the standard deviation computed

from the training data. By applying the formula

= 1 − CDF

( ˆy

, σ

)(τ) (1)

to the predicted values, the authors obtain an es-

timate of the exceedance probability for the speci-

ﬁed threshold. This approach leverages the regression

model’s predictions ( ˆy

) and incorporates the statis-

tical properties of the chosen distribution to provide

probabilistic estimates of threshold (τ) exceedance.

The proposed methodology offers a unique perspec-

tive on exceedance probability forecasting by com-

bining regression modeling and distributional analy-

sis. By utilizing well-established distributions, this

methodology enables the estimation of exceedance

probabilities based on the predicted values of the

time series ( ˆy

) along with the standard deviation

(σ

) measured by the training set. Such an ap-

proach has the potential to improve risk assessment

and decision-making in domains such as maritime

operations, where accurate estimation of exceedance

probabilities is crucial.

2.3 Contribution

This study unveils a novel framework for estimating

the likelihood of threshold exceedance in time series

data, pivoting on the utilization of survival analysis

techniques (table 1). These techniques furnish the ca-

pacity to model and predict the time-to-event infor-

mation, namely the duration until an anticipated event

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

occurs. This is a departure from the conventional bi-

nary classiﬁcation approach habitually used to tackle

this issue, and it is precisely in this deviation that our

method’s novelty lies.

By employing survival analysis, our approach

yields not merely an occurrence probability but the

time until an event transpires, thereby transforming

the data effectively to craft a dataset optimally tai-

lored for training and forecasting. This provides an

invaluable asset for comprehending and prognosticat-

ing extreme events, enhancing decision makers’ un-

derstanding of the temporal dynamics of such risks,

thereby allowing for timely action. This feature is

particularly critical across various domains.

One of the primary merits of survival analysis is

its utility in analyzing time-to-event data, enabling a

robust examination of the temporal dynamics of out-

comes. It is distinctly beneﬁcial in scrutinizing the

duration until an anticipated event materializes or a

stipulated condition is fulﬁlled. This is particularly

pertinent in the arena of threshold exceedance fore-

casting, where understanding the temporal dynamics

holds paramount importance.

Survival analysis manifests its strength by adeptly

managing censoring, an eventuality when certain sub-

jects have not yet experienced the event of interest at

the study’s conclusion, or subjects are lost before the

event occurs. By integrating duration variables and

event indicators, survival analysis unravels the com-

plex relationship between time and the probability of

the event’s occurrence.

Furthermore, survival analysis is proﬁcient in han-

dling censored observations, a common occurrence in

threshold exceedance forecasting, where the thresh-

old may remain uncrossed at the observation period’s

conclusion. Survival analysis capably leverages data

from both observed events and censored instances,

paving the way for superior estimations and more pre-

cise forecasts.

Survival analysis’s competence extends to accom-

modating time-varying covariates, external factors, or

changing conditions that may affect the event under

consideration. By incorporating these covariates, sur-

vival analysis enables a more inclusive and dynam-

ically adaptable modeling approach in threshold ex-

ceedance forecasting.

Signiﬁcantly, survival analysis estimates the haz-

ard function, reﬂecting the instantaneous risk of the

event occurrence at any given time point. This capa-

bility is especially valuable in threshold exceedance

forecasting as it sheds light on the intricate dynamics

and patterns surrounding the event, permitting a more

reﬁned analysis that captures the ﬂuctuating risk over

time, thereby enhancing the precision of forecasts.

3 BACKGROUND

3.1 Survival Analysis Basics

Survival analysis is a statistical method used to ana-

lyze time-to-event data, where the event of interest is

the occurrence of a particular event or outcome. This

method is widely used in medical research, where the

event of interest may be the occurrence of a disease,

death, or relapse. However, survival analysis can also

be applied to other ﬁelds, including ﬁnance, engineer-

ing, and environmental science.

In survival analysis, the key concept is the sur-

vival function, denoted by S(t). The survival func-

tion (Lee and Wang, 2003) (Klein and Moeschberger,

2006) represents the probability that the time to the

event of interest is not earlier than a speciﬁed time t.

Often survival function is referred to as the survivor

function or survivorship function in problems of bio-

logical survival and as the reliability function in me-

chanical survival problems. The survival function is

represented as follows:

S(t) = P(T > t) (2)

The function above denotes an individual that sur-

vives longer than t. Survival function decreases when

the t increases. Its starting value is 1 for t = 0 which

represents that at the beginning of the observation, all

subjects survive.

Another important concept in survival analysis is

the hazard function, denoted by h(t). It is also called

the force of mortality, the instantaneous death rate or

the conditional failure rate (Dunn and Clark 2009).

The hazard function h(t) (Lee and Wang, 2003) and

(Klein and Moeschberger, 2006) does not indicate the

prospect or probability of the event of interest, but it is

the rate of event at time t as long as no event occurred

before time t. In this sense, the hazard is a measure of

risk. The hazard function is deﬁned as:

h(t) =

f (t)

S(t)

(3)

In addition to the above relations, there is another

important connection between h(t) (or H(t)) and S(t)

given by

S(t) = exp(−

h(x)dx) = exp(−H(t)) (4)

Various parametric and non-parametric statistical

techniques have been proposed over the years to esti-

mate survival and hazard functions, providing valu-

able tools for analyzing time-to-event data and in-

vestigating the impact of covariates on survival time.

Survival analysis also allows for the inclusion of co-

variates to investigate their impact on survival time.

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting

Table 1: Contribution of the proposed approach.

Contributions of Our Approach Implications for Threshold Exceedance

Forecasting

Outputs time-to-event information

Endorses survival analysis’s suitability for

capturing temporal aspects of threshold ex-

ceedance events, a unique and signiﬁcant ad-

vantage over binary classiﬁcation methods

Handles censored observations

Leverages data from both observed events and

censored instances, leading to superior estima-

tions and more precise forecasts

Accommodates time-varying

covariates

Allows a dynamically adaptable modeling ap-

proach, considering external factors or chang-

ing conditions affecting the event

Estimates the hazard function

Provides insights on the instantaneous risk of

the event at any given time point, permitting a

reﬁned analysis that captures ﬂuctuating risk,

thereby enhancing forecast accuracy

This can be done using regression models, such as the

Cox proportional hazards model, which assumes spe-

ciﬁc parametric assumptions. Additionally, machine

learning algorithms, including various regression and

classiﬁcation algorithms, can also be employed to ex-

plore the effects of covariates on the hazard function

without the need for speciﬁc assumptions. These ma-

chine learning algorithms offer ﬂexibility and versa-

tility in handling complex relationships and can pro-

vide insights into the impact of covariates on survival

time in a more data-driven manner.

In this paper, we introduce a new approach to

extreme value forecasting using survival analysis.

Speciﬁcally, we use survival analysis to model the

time until the event of interest, which in our case is

the appearance of threshold exceedance. By employ-

ing the proposed method, we can not only produce

a binary outcome indicating the chance of a thresh-

old exceedance but also retrieve valuable informa-

tion about the survival distribution (or, conversely, the

hazard distribution) of a data point. This capability

enables us to delve deeper into the dynamics of ex-

treme events and their probabilities, a critical aspect

for enhancing the safety and quality of food produc-

tion and supply chains. By gaining a comprehensive

understanding of the hazard distribution of data points

in the food production and supply chain, we can

proactively identify situations with higher risk lev-

els, allowing for targeted interventions and risk man-

agement strategies. This proactive approach not only

helps prevent potential extreme events but also aids in

minimizing the impact of adverse incidents, such as

food recalls, which can have severe consequences on

public health, consumer conﬁdence, and industry rep-

utation. The proposed methodology adopts a compre-

hensive two-phase approach to estimate the time until

the next extreme event in a time series. Each phase

consists of several well-deﬁned steps, which are visu-

ally depicted in 2 and 4. Phase 1 involves the prepro-

cessing of the time series data. This preparatory stage

comprises multiple crucial steps, including data trans-

formation and formatting, to ensure that the data are

suitable for survival analysis. By carefully handling

the data in this phase, we lay the foundation for accu-

rate and meaningful insights into extreme event fore-

casting. Phase 2 focuses on applying survival analysis

techniques to model the time-to-extreme-event data.

Within this phase, various steps are performed, build-

ing upon the outcomes of Phase 1. These steps may

include utilizing survival analysis models such as ran-

dom survival forests, estimating the hazard function,

and making predictions on the time until the next ex-

treme event. By systematically conducting these anal-

yses, we can extract valuable information about the

survival distribution (or, conversely, the hazard distri-

bution) of data points, enhancing our understanding

of extreme event dynamics and their associated prob-

abilities.

We demonstrate the effectiveness of our approach

through a series of simulations and real-world case

studies in the food sector, highlighting the potential

of survival analysis in extreme value forecasting

4 PROBLEM FORMULATION

In our research work, we focus on the problem of uti-

lizing lag values of a univariate time series dataset to

predict whether the future timestamp’s value will ex-

ceed a certain threshold. A univariate time series, de-

noted as Y , represents a temporal sequence of values

, y

, . . . , y

}, where each y

∈ Y ⊂ R represents the

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

value at time i, and n is the length of the time series.

The objective of our research is to develop a model

that leverages the relationship between past observa-

tions and future outcomes. Speciﬁcally, we consider

the most recent q known values of the time series

as lagged predictors. Let X

= {y

i−1

, y

i−2

, . . . , y

i−q

}

represent the lagged predictors for the i-th observa-

tion, where X

∈ X ⊂ R

denotes the corresponding

embedding vector. The difference with conventional

timeseries forecasting is that we are not aim to pre-

dict y

∈ Y ⊂ R, but instead the probability this value

to be bigger than the predeﬁned threshold denoted as

follows:

• The probability of exceeding a predeﬁned thresh-

old τ in a given instant i, denoted as p

, represents

the likelihood that the value of a time series will

surpass that threshold. This probability is cap-

tured by a binary target variable b

, which can be

deﬁned as follows: b

takes the value 1 if the value

of the time series is greater than or equal to the

threshold τ, and 0 otherwise.

(

1 if y

≥ τ,

0 otherwise.

Given the lagged predictors X

, the objective is to

build a forecasting model, denoted as f , that estimates

whether or not a future value y

will exceed a prede-

ﬁned threshold. Thus, the model can be represented

as y

= f (X

, Z

), where Z

represents any additional

covariates or factors known at the i-th instance that

may inﬂuence the outcome. The same applies also to

our formulation so it can be used either for univariate

or multivariate timeseries data.

By developing an accurate forecasting model us-

ing lag values, we aim to provide insights into the

occurrence of threshold exceedance in future times-

tamps, enabling proactive decision-making and risk

management strategies.

5 PROPOSED METHODOLOGY

The proposed methodology aims to estimate the time

until an extreme value occurrence in a time series us-

ing survival analysis techniques. To achieve this goal,

we ﬁrst transform the univariate time series to a super-

vised dataset with the binary event indicator and the

duration variables which are needed for the survival

dataset, where the event of interest is the occurrence

of a threshold exceedance, and the survival time is

the time counted until the threshold exceedance. Fi-

nally, we apply a range of survival analysis methods

to model the survival dataset and make predictions.

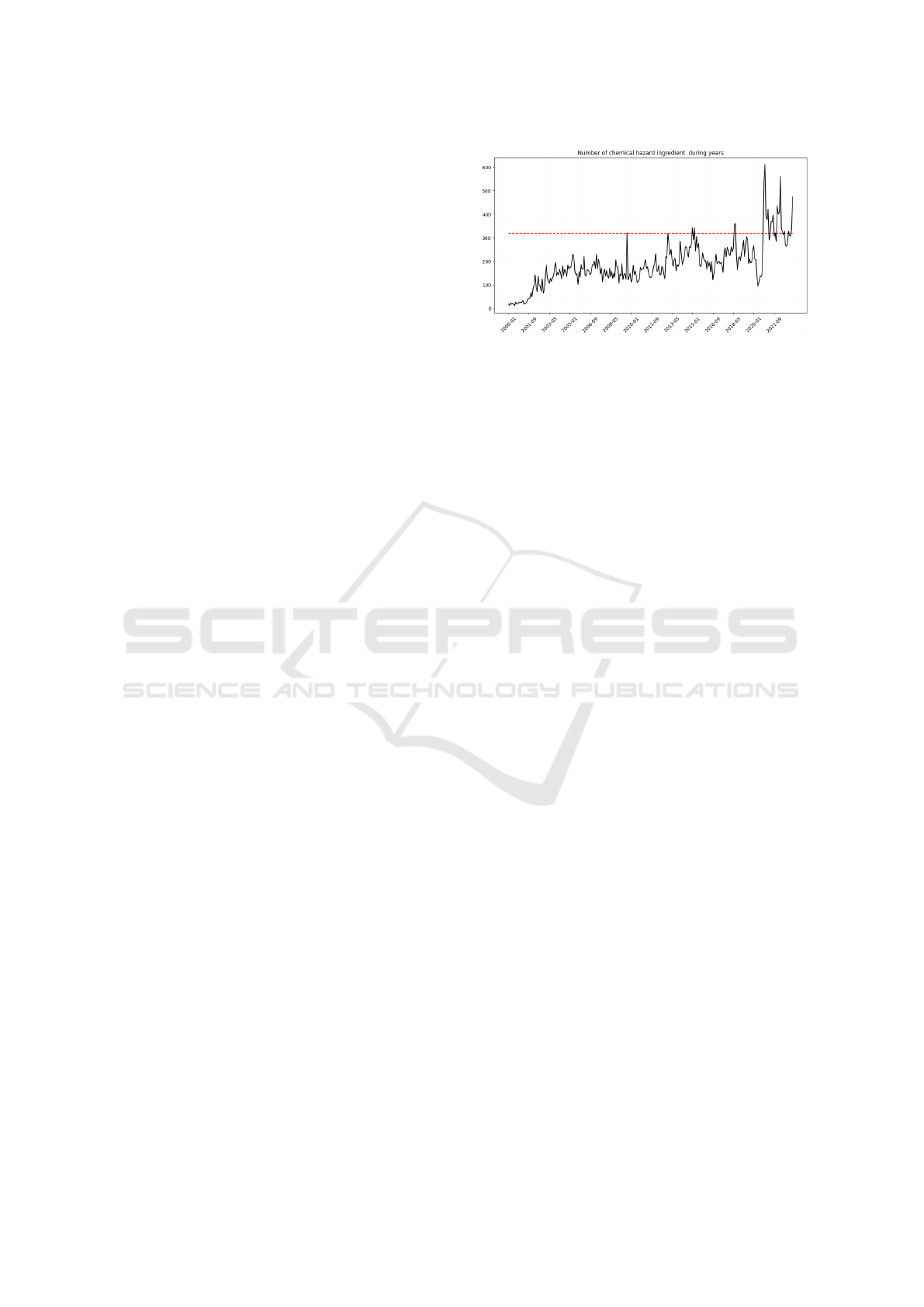
Figure 1: Real-world data showcase.

The proposed methodology can be applied to vari-

ous time series datasets to identify the time until the

next extreme event and provide insights for decision-

making in various domains.

The rest of this section is divided into two main

parts. The ﬁrst one aims to describe the pre-

processing steps that we follow and the second one

is the post-processing pipeline until we reach the pre-

diction outcome.

5.1 Pre-Processing Steps

In order to perform survival analysis on our time se-

ries for threshold exceedance forecasting, it is imper-

ative to undertake a data transformation process to

align the data with the requisite format. The format

for survival analysis comprises three essential compo-

nents. Firstly, the data predictors which, in our case,

correspond to the lagged values of the univariate time

series conﬁned within the predetermined time win-

dow. Secondly, the binary event indicator, and lastly,

the duration variable. This entails the generation of a

binary event indicator as well as a duration variable

for each observation within the series.

Having as a starting point the time-series dataset

which can be either univariate or multivariate the ﬁrst

action in the pre-processing pipeline in our methodol-

ogy is the re-framing (step 2 in ﬁgure 2) of the time-

series dataset into a supervised form using the X vec-

tor of lagged values X

= {y

i−1

, y

i−2

, . . . , y

i−q

} as pre-

dictor variables as deﬁned in the problem formulation

section and the b

as the variable we want to predict.

The number of lag values is adjustable and is denoted

by the user.

Right after, as is demonstrated in the second

step of 2 is the identiﬁcation of extraordinary occur-

rences within each individual time series. As pre-

viously indicated, owing to the adaptable nature of

our approach, the threshold can be established ei-

ther through manual determination by the user or by

heeding the guidance of a domain expert. Neverthe-

less, in our empirical investigations, we present out-

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting

Figure 2: Phase 1: Pre-processing Steps.

Figure 3: Schematic representation of the proposed method

showcasing the sequential transformation of time-series

dataset to survival analysis-ready dataset which consist of

N data points (D.P).

comes employing a uniform procedure introduced in

the scholarly work of (Cerqueira and Torgo, 2022)

which is predicated upon a data-centric technique re-

lying on the n-th percentile, speciﬁcally the 95th per-

centile, of the training dataset that is accessible.

The third step as it is shown in ﬁgure 2 as well as

in the algorithm 1 is the calculation of the duration

variable which plays a critical role in our methodol-

ogy. The computation of the duration variable is exe-

cuted through the utilization of a sliding window tech-

nique as depicted in 3, where the parameters deﬁn-

ing the window, including the number of lag values,

are determined by the user. For each individual data

point within the series, there exists a corresponding

start date and end date. Notably, the start date re-

mains constant until an observed data point exhibits

an extreme event in its most recent value. In such

cases, the start date transitions to the date associated

with that speciﬁc data point, while the end date re-

mains the concluding date of the respective sliding

window. By incorporating these three fundamental

components, our methodology facilitates the analysis

of survival patterns, enabling a comprehensive explo-

ration of the impact of extreme events on the duration

of the time series.

Following the transformation, we apply survival

analysis algorithms to the dataset, akin to conven-

tional machine learning. The data is split into train-

ing and test sets, and various algorithms are evalu-

ated. Survival analysis excels in modeling time-to-

event data, especially when events are rare or cen-

sored. In our proposed methodology, we explore

non-parametric methods like Decision Survival Trees,

RandomSurvival Forest, Survival SVM, and neural

network-based models such as DeepSurv.

Our methodology is conﬁgurable, allowing users

to experiment with different methods and tailor their

analysis. For instance, the selection of extreme events

can be customized based on domain knowledge. The

user has the ﬂexibility to experiment with different

numbers of the lagged values, different percentiles

to determine the threshold at which values are con-

sidered extreme, various survival analysis algorithms,

and even different train and test sizes. This allows

for customization in deﬁning the criteria for extreme

values within the dataset.

5.2 Post-Processing Steps

The objective of this study is to predict whether or not

a threshold exceedance will occur in the next times-

tamp, necessitating the conversion of survival analy-

sis results into binary output. Our approach encom-

passes two alternatives, each described in detail be-

low.

In the ﬁrst alternative, we construct a survival

analysis model and we predict the survival distribu-

tion for each data point. Subsequently, we extract the

mean probability from the distribution, signifying the

sharpness of the probability distribution. The intu-

ition behind this is the idea that the greater the sur-

vival probability of the data point the most probable

that we will not have a threshold exceedance in the

future timestamp. To transform this output into a bi-

nary outcome, analogous to a probability prediction

of a binary classiﬁer, we employ a threshold-based ap-

proach. By comparing the mean probability against a

pre-deﬁned threshold which is regularly at 0.5 like in

the conventional classiﬁcation tasks, we assign a bi-

nary label indicating exceedance or non-exceedance

of the threshold.

The second alternative in the proposed methodol-

ogy involves utilizing the survival analysis model to

predict the risk associated with each data point. In-

spired by the concept presented in Cerqueira et al.

(Cerqueira and Torgo, 2022), we employ the trained

survival model to estimate the survival risk for each

data point. Subsequently, in order to obtain a binary

outcome indicating the occurrence or absence of a

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

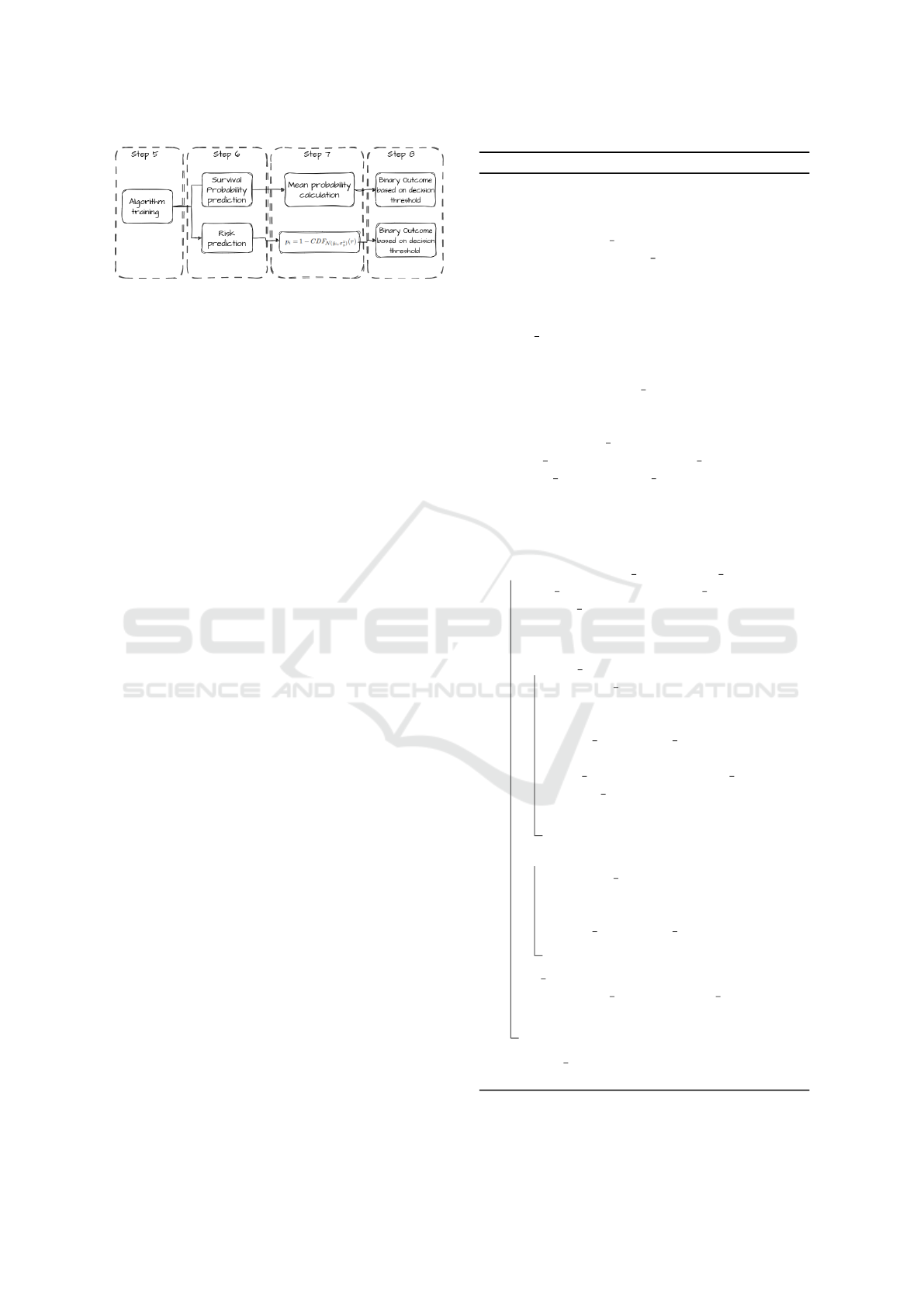
Figure 4: Phase 2: Post-processing Steps.

threshold exceedance in the future, we apply the for-

mula used in Cerqueira et al. (Cerqueira and Torgo,

2022), which is given by:

= 1 − CDF

( ˆy

, σ

)(τ) (5)

The above function is utilized to transform the sur-

vival risk into a binary outcome. Leveraging a well-

known distribution, such as the Normal distribution,

where the predicted survival risk ( ˆy

) is set as the

mean of the distribution for each data point and the

standard deviation (σ

) is computed from the train-

ing set, we can predict whether the survival risk will

exceed a speciﬁc threshold (τ) for each data point.

This transformation enhances the practicality and in-

terpretability of the survival analysis results, facil-

itating informed decision-making in the context of

threshold exceedance predictions.

As previously elucidated, within the context of

time series reframing, a speciﬁc time window is des-

ignated, allowing for systematic traversal along the

temporal axis. Subsequently, the binary event indica-

tor is assigned a value of 1 when an extreme value

manifests itself at the conclusion of the aforemen-

tioned time window.

Conversely, if an extreme value fails to materialize

at the conclusion of the time window, the binary event

indicator assumes a value of 0. Pertinent to note is

that data points exhibiting an extreme value at the ter-

mination of the time window are deemed uncensored,

while those lacking an extreme value are classiﬁed as

censored.

6 EXPERIMENTS

In order to assess the performance of our framework,

we rigorously evaluate it using multiple real-world

and synthetic datasets. This evaluation process serves

to validate the effectiveness and robustness of our pro-

posed approach.

By conducting extensive evaluations on both real

and synthetic datasets, we ensure the thorough exam-

ination of our framework’s capabilities and provide

evidence of its efﬁcacy in exceeding threshold fore-

casting.

Algorithm 1: Duration variable calculation.

Input : DataFrame d f with time series

column, date column, and binary

column denoting extreme events,

window size

Output: DataFrame d f new with lag columns,

real value column, extreme event

column, start date column, stop date

column, duration column

start date ← d f [0] ; // set the start

date to the first date in the time

series

lags ← df[i:i+window size].shift(n) ;

// create lag variables from time

series within the window for n in

range(window size)

target value ← d f [i + window size +

out put steps −1][time series] ; // get the

real value

threshold ← [threshold value] ; // set the

threshold value

for i ← 0 to

[len(d f ) − window size −out put steps] do

stop date ← d f [i + window size +

out put steps −1][date] ; // set the

stop date to the end of the time

window

if target value > threshold then

threshold exceedance ← 1 ; // set

threshold exceedance to 1

duration ←

(stop date − start date).days ;

// calculate the duration

start date ← d f [i + window size +

out put steps −1][date] ; // set the

start date to the date where

the extreme event occurred

else

threshold exceedance ← 0 ; // set

threshold exceedance to 0

duration ←

(stop date − start date).days ;

// calculate the duration

df new ←

[lags,target value,threshold exceedance,

start, stop, duration] ; // add the new

row to the output DataFrame

return df new ; // return the new

DataFrame

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting

6.1 Simulated Data

The data used in this research paper were simulated

using random seeds for reproducibility. The data were

generated using a covariance matrix and multivariate

normal distribution, with mean values set to zero for

all series. Some random extreme values were added to

each series. Additionally, trends and seasonality were

added. The data were decomposed into the trend, sea-

sonality, and residual components. The trend, season-

ality, and residual components were added to the data,

and negative values were set to zero.

6.2 Real Data

In this study, data on food incidents caused by sys-

temic factors led to massive food recalls across the

globe. A web crawler was used to systematically

search for ofﬁcial announcements from authorities

in different countries. The collected data were then

stored in a database. Named entity extraction was

performed using a deep learning algorithm to extract

relevant information from the texts, such as hazard

types and food product types. A team of food experts

curated the data, removing any erroneous data points

and ensuring accurate extraction of hazards and prod-

ucts. The curated data were analyzed to identify pat-

terns and trends in food incidents across regions and

food categories. Time stamps of the incidents were

also recorded to project the absolute number of inci-

dents over time. The use of a web crawler and data

curation process ensured comprehensive and reliable

data for analysis.

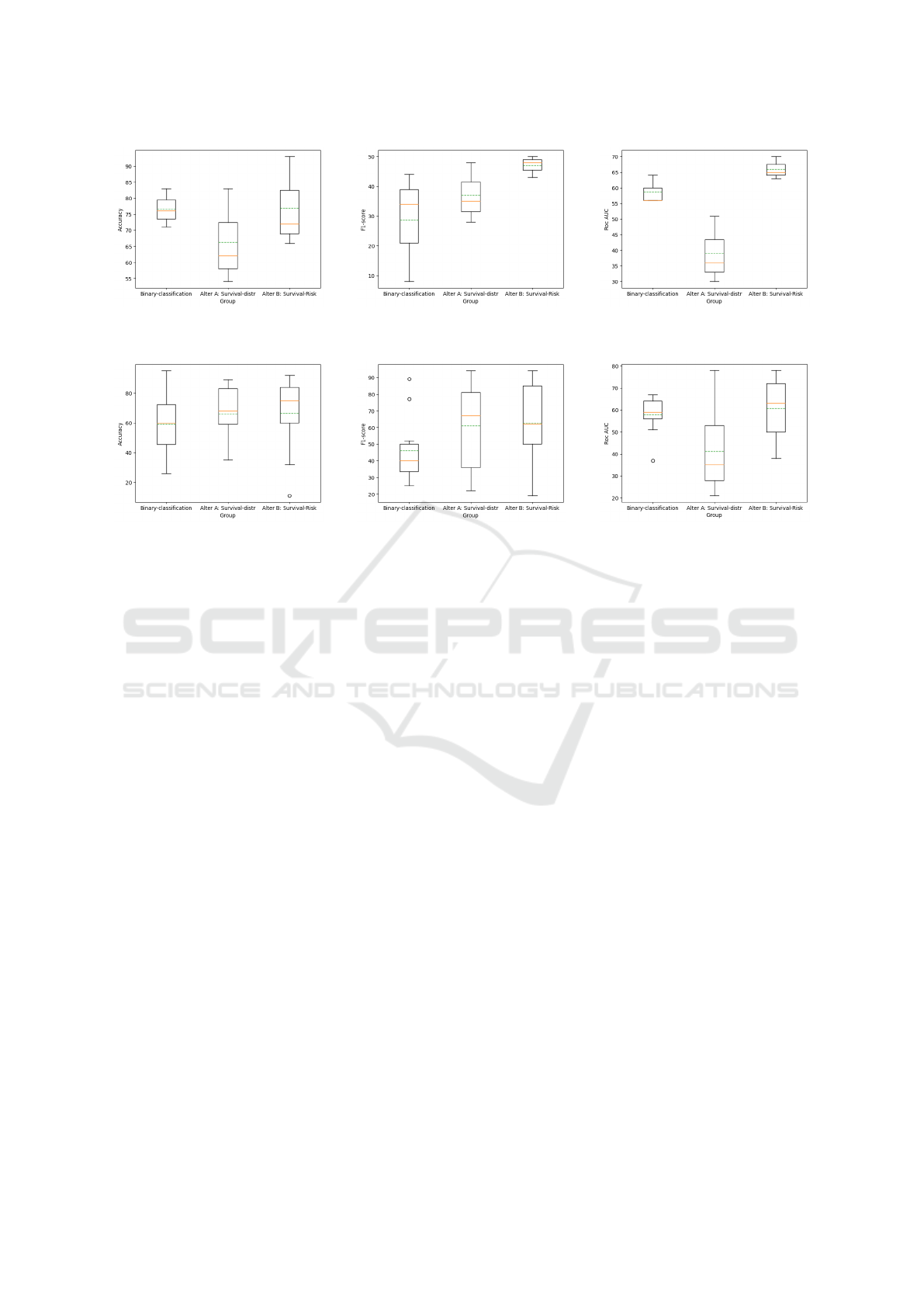
6.3 Results

In this section, we present the results of our experi-

ments, which are visually depicted in table 2 and in

ﬁgure 5. Our objective is to compare the performance

of our proposed method with a baseline approach

encompassing the common core approach which is

mentioned in the related work which is the binary

classiﬁcation. This comparison is based on several

evaluation metrics, including accuracy, F1-score, and

ROC curve. The experiments were conducted on di-

verse datasets, encompassing both real-world time se-

ries which consist of food incidents from public an-

nouncements as well as synthetic datasets. Through

the analysis of boxplots, it becomes evident that our

approach yields improved results compared to the

baseline approach across the aforementioned metrics.

The observed performance enhancements underscore

the effectiveness of our method in addressing various

real-world and synthetic data scenarios.

Table 2: Classiﬁcation Results.

Dataset Approach

Mean Performance Measures

Accuracy Precision Recall F1-score Auc-score

Real

Binary clas. 59% 67% 48% 46% 58%

S.A. Alter A 66% 50% 91% 61% 41%

S.A. Alter B 67% 54% 88% 63% 61%

Synthetic

Binary clas. 77% 51% 20% 25% 62%

S.A. Alter A 57% 25% 74% 35% 43%

S.A. Alter B 77% 54% 49% 44% 67%

6.4 Discussion

In this study, we have embarked on a journey towards

redeﬁning the way we approach the challenging task

of threshold exceedance forecasting in time series

data. By departing from the conventional binary clas-

siﬁcation methods, our novel framework leverages the

power of survival analysis techniques, thus ushering

in a fresh perspective in this domain.

The essence of our approach lies in its ability not

only to predict the occurrence of events but also to un-

ravel the temporal dimension by estimating the time

until an event takes place. This fundamental depar-

ture from the binary classiﬁcation paradigm provides

us with a unique advantage. By shifting our focus to

understanding the duration until an anticipated event

materializes, we transform our data into a more in-

formative and tailored dataset, ripe for training and

forecasting.

The implications of this paradigm shift are far-

reaching and of immense value across diverse do-

mains. For decision-makers, our framework offers a

deeper comprehension of the temporal dynamics of

extreme events. Armed with insights into when these

events are likely to occur, timely actions can be taken

to mitigate risks and enhance preparedness.

Survival analysis, as a central component of our

framework, brings several advantages to the table.

First and foremost, it excels in the analysis of time-to-

event data, enabling a robust examination of the tem-

poral dynamics of outcomes. This strength is particu-

larly pertinent in the context of threshold exceedance

forecasting, where understanding when an event is

likely to occur is of paramount importance.

One of the key strengths of survival analysis is its

adept handling of censoring, a common occurrence in

our domain. By seamlessly integrating duration vari-

ables and event indicators, survival analysis unravels

the intricate relationship between time and the prob-

ability of event occurrence. This capability is pivotal

in scenarios where certain subjects have not yet expe-

rienced the event of interest at the conclusion of the

study, or when subjects are lost before the event un-

folds.

Moreover, survival analysis excels in accommo-

dating censored observations, a frequent scenario in

threshold exceedance forecasting. Here, the threshold

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems

(a) Accuracy metrics boxplot for the

synthetic datasets.

(b) F1-score metrics boxplot for the

synthetic datasets.

(d) Accuracy metrics boxplot for the

real-world datasets.

(e) F1-score metrics boxplot for the

real-world datasets.

(f) Roc-auc metrics boxplot for the

real-world datasets.

Figure 5: Metrics observed from the application of our approach to real-world and synthetic datasets.

may remain uncrossed at the end of the observation

period. Survival analysis ingeniously leverages data

from both observed events and censored instances,

enabling more accurate estimations and precise fore-

casts.

While our novel framework brings fresh perspec-

tives to threshold exceedance forecasting, it’s impor-

tant to acknowledge certain limitations that are in-

herent to this domain. One of the primary chal-

lenges we face is the issue of imbalanced data. In

scenarios where extreme events, our positive cases,

are relatively rare compared to non-extreme events,

our dataset becomes inherently skewed. This imbal-

ance can pose a signiﬁcant challenge, as the frame-

work’s performance may be affected. The scarcity

of positive cases can lead to decreased performance

metrics, making it challenging to achieve the same

level of accuracy and precision as in more balanced

datasets. Addressing this limitation is a critical area

of future research, and we recognize the need for in-

novative techniques to handle imbalanced data effec-

tively. Strategies such as oversampling, undersam-

pling, or the use of specialized algorithms tailored for

imbalanced datasets are avenues worth exploring to

mitigate this limitation and further enhance the frame-

work’s robustness.

In addition to our innovative framework, it is es-

sential to highlight potential directions for future re-

search that can build upon the foundation laid in this

study. A primary challenge that warrants further ex-

ploration is the issue of imbalanced data, particularly

when dealing with rare extreme events. As men-

tioned, data imbalance can affect the performance of

the framework. To address this limitation, future work

could delve deeper into advanced techniques for han-

dling imbalanced datasets. Strategies such as cost-

sensitive learning, synthetic data generation, or en-

semble methods tailored for imbalanced scenarios can

be investigated to improve the framework’s resilience

in such situations. Furthermore, expanding the frame-

work to accommodate additional sources of temporal

information, such as external factors or dynamic co-

variates, represents another promising avenue for fu-

ture research. By incorporating these elements, we

can enhance the adaptability and predictive power of

the framework, making it even more valuable for vari-

ous applications. In summary, while this study marks

a signiﬁcant milestone, there is ample room for fur-

ther innovation and reﬁnement to unlock the full po-

tential of threshold exceedance forecasting in time se-

ries data.

7 CONCLUSION

In conclusion, our innovative framework, anchored by

survival analysis, brings a profound transformation to

threshold exceedance forecasting. By delving into the

Survival Analysis as a Risk Stratiﬁcation Tool for Threshold Exceedance Forecasting

temporal intricacies and unveiling the instantaneous

risk through hazard function estimation, our approach

enhances precision and timeliness in forecasting ex-

treme events. This paradigm shift is not only a pio-

neering step but also a potential game-changer in how

we comprehend and act upon extreme events. It of-

fers resilience in the face of censoring, adaptability to

changing conditions, and the promise of more effec-

tive risk mitigation. The ability to understand when

events are likely to occur, regardless of data imbal-

ance, empowers decision-makers across diverse do-

mains, making our framework an invaluable asset in

the realm of temporal risk assessment.

ACKNOWLEDGEMENTS

The research presented in this paper has been sup-

ported with funding from the European Union’s Hori-

zon Europe programme under the Extreme Food Risk

Analytics (EFRA) project with grant agreement No

101093026.

REFERENCES

Abilasha, S., Bhadra, S., Dadarkar, A. Z., and Deepak, P.

(2022). Deep extreme mixture model for time series

forecasting. In 31st ACM International Conference

on Information and Knowledge Management: CIKM

2022.

Cerqueira, V. and Torgo, L. (2022). Exceedance probability

forecasting via regression for signiﬁcant wave height

forecasting. arXiv preprint arXiv:2206.09821.

Dai, B., Xia, Y., and Li, Q. (2022). An extreme value predic-

tion method based on clustering algorithm. Reliability

Engineering & System Safety, 222:108442.

Gong, B. and Ordieres-Mer

e, J. (2016). Prediction of

daily maximum ozone threshold exceedances by pre-

processing and ensemble artiﬁcial intelligence tech-

niques: Case study of hong kong. Environmental mod-

elling & software, 84:290–303.

Hill Galib, A., McDonald, A., Wilson, T., Luo, L., and

Tan, P.-N. (2022). Deepextrema: A deep learning

approach for forecasting block maxima in time series

data. arXiv e-prints, pages arXiv–2205.

Kazemi, E., Kyritsakas, G., Husband, S., Flavell, K.,

Speight, V., and Boxall, J. (2023). Predicting iron ex-

ceedance risk in drinking water distribution systems

using machine learning. In IOP Conference Series:

Earth and Environmental Science, volume 1136, page

012047. IOP Publishing.

Klein, J. P. and Moeschberger, M. L. (2006). Survival

analysis: techniques for censored and truncated data.

Springer Science & Business Media.

Krylova, M. and Okhrin, Y. (2022). Managing air quality:

Predicting exceedances of legal limits for pm10 and o

3 concentration using machine learning methods. En-

vironmetrics, 33(2):e2707.

Lee, E. T. and Wang, J. (2003). Statistical methods for sur-

vival data analysis, volume 476. John Wiley & Sons.

Taylor, J. W. (2017). Probabilistic forecasting of wind

power ramp events using autoregressive logit mod-

els. European Journal of Operational Research,

259(2):703–712.

Taylor, J. W. and Yu, K. (2016). Using auto-regressive

logit models to forecast the exceedance probabil-

ity for ﬁnancial risk management. Journal of the

Royal Statistical Society Series A: Statistics in Soci-

ety, 179(4):1069–1092.

Zhou, X.-Y., Schmidt, F., Toutlemonde, F., and Jacob, B.

(2016). A mixture peaks over threshold approach for

predicting extreme bridge trafﬁc load effects. Proba-

bilistic Engineering Mechanics, 43:121–131.

KMIS 2023 - 15th International Conference on Knowledge Management and Information Systems