Comprehensive Φ-Bonacci Index for Walking Ability Assessment in

Paroxysmal Positional Vertigo: Role of Rehabilitation

Nicol´o Colistra

1,∗

, Luca Pietrosanti

, Mohamed El Aray shi

, Sara Maurantonio

Beatrice Francavilla

, Piergiorgio Gia comini

and Cristiano Maria Verrelli

Department of Electronic Engineering, University of Rome Tor Vergata, Via del Politecnico 1, 00133 Rome, Italy

Division of Ot olaryngology, University Hospital of Rome Tor Vergata, Viale Oxford 81, 00133 Rome, Italy

Keywords:

Gait Analysis, Walking Gait, Asymmetry, Self-Similarity, Golden Rat io, Benign Paroxysmal Positi onal

Vertigo.

Abstract:

Very recent research directions have been devoted t o providing a theoretical foundation to the experimental

evidence that human movements, such as walking, are able to induce time-harmonic motor patterns. The re-

sulting ﬁndings have shown that such harmonic structures are characterized by the golden ratio occurring as

the ratio of the durations of the walking gait sub-phases that compose generalized F ibonacci sequences. A

new comprehensive gait index, named Φ-bonacci gait number, and a new related experimental conjecture –

concerning the position of the foot relative to the tibia – have been concurrently proposed to capture the most

reliable and objective (quantitive) outcome measures (and their distortions in pathological subjects) of recur-

sivity, asymmetry, consistency, and self-similari ty (harmonicity) of the gait cycle. This paper provides, for

the ﬁrst time, experimental results on healthy and pathological gaits – related to benign paroxysmal positional

vertigo (BPPV) – that fully support the aforementioned theoretical derivations.

1 INTRODUCTION

Starting from the evidence that foot off reliably occurs

at 60% to 62% of a physio logical gait at a comf ortable

speed, it has been shown by (Iosa et al., 2013) that in

(symmetrical and recursive) walking of healthy sub-

jects – being described by fo ur time intervals –, but

not in pathological ones, the ratio between consec-

utive durations of swing and double support phases

is close to the go lden ratio φ value at a comfort-

able speed of 4 km/h (Cavagna and Margaria, 19 66).

Such an irrational number φ = (1 +

√

5)/2 ≈ 1.618

(φ

−1

= φ −1), which is related to Euclid’s pr oblem

of cutting in a self-proportional way a given straight

segment, captures self-similarity (harmon ic ) features

in symmetric walking of healthy subjects (Iosa et al.,

2019), and a reduction of the smooth, gracefu l, and

melodic ﬂow of movement in the altered gait of pa-

tients (Iosa et al., 2016) (see the related discussions in

(Verrelli et al., 2 021; Marino et al., 2020)). Further-

more, human walking naturally includes asymmetr ic

and non-recursive components, especially in patho-

logical cases, so at least eight (in place of four) time

intervals have to be considered for left and right lower

∗

Corresponding author.

limbs, namely doub le support, swing, stance, and gait

cycle (Dugan and Bhat, 2005). This has been actu-

ally don e in (Verrelli et al., 2021), where the dura-

tions of those eight time intervals have bee n demon-

strated to concern a newly deﬁned composite gait cy-

cle, which involves two speciﬁc couple of overlapping

(left and right) gait cycles. Indeed , the dynamics-

on-graph concepts- and generalized ﬁnite-length Fi-

bonacci sequences- based ana lysis presented in (Ver-

relli et al., 2021) has generalized the one in (Iosa et al.,

2013)

, as much as the new quantitative index of (Ver-

relli et al., 2021) – namely, the Φ-bonacci gait num-

ber – has constituted the most straightforward gen-

eralization of the gait ratio in (Iosa et al., 2013) to

the case in which non-{symmetric & recursive}com-

ponen ts of walking (including the concep t of dou-

ble support consistency) oc cur. Furthermore, differ-

ently from the ar ea of the Synchronicity Rectangle

in ( Marino et al., 2020), such a new index takes its

minimum zero-value just when the strongest version

of self-similarity, namely the enforced adjoint sym-

Differently from (Marino et al., 2020), no complex

tools from linear algebra, associating special φ-dependent

subspaces with a common temporal model for human walk-

ing gaits, are employed.

Colistra, N., Pietrosanti, L., El Arayshi, M., Maurantonio, S., Francavilla, B., Giacomini, P. and Verrelli, C.

Comprehensive Φ-Bonacci Index for Walking Ability Assessment in Paroxysmal Positional Vertigo: Role of Rehabilitation.

DOI: 10.5220/0012237100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 203-210

ISBN: 978-989-758-670-5; ISSN: 2184-2809

203

metric self-similarity, o c curs. It is able to unveil hid-

den time-harmonic and self-similar structures along

the new direc tion toward a fractal human walking de-

composition. The a bove index

, has also innovatively

involved a term relying on a new experimental con-

jecture that relies on the position of the foot relative

to the tibia while op ening new a nalysis and diagno-

sis perspectives on the internal a nalysis of the do u-

ble support phase. The resulting theoretical approach

thus moves along the direction of using temporal gait

analyses to complement, in c linical or general per-

formance evaluations the classical gait analyses in-

cluding motion analysis, dynam ic electromyography,

force plate recordings, e nergy cost measurements or

energetics, measurement of stride characteristics.

Now, even though the Φ-bonacci gait number is

able to comprehensively capture the m ost reliable and

objective (quantitive) outco me measures of recursiv-

ity, asymmetry, consistency, and self-similarity (har-

monicity) of the gait cycle, however, up to this stage,

only two different simpliﬁed versions of such an in-

dex have been tested: i) in (El Ar a yshi et al., 2022),

concerning the distinction between patients affected

by Ataxia Telangiectasia and th eir healthy counter-

parts, no internal analysis of the double support phase

has be en performed; in (Verrelli et al., 2021), con-

cerning patients with highly a symmetric deﬁcits (such

as patients with hemiparetic stroke and patients with

an alteration in gait ratio not always being acco m-

panied by motor asymmetries [such as patients with

quite symmetric symptoms due to Parkinson’s Dis-

ease]), data concerning the adjoint gaits are neglected.

In this paper, we thus illustrate, for the ﬁrst time

in the literature, not only the effectiveness of th e com-

plete version of the aforementioned index in discrim-

inating healthy subjects from pathological ones, but

also its responsiveness in quantifying patients’ im-

provements coming from rehabilitation. To this aim,

we have recruited a cohort of patients with BPPV,

i.e., a peripheral vestibular disorder leading to b al-

ance difﬁculties and increased fall risks (Zhang et al.,

2021). Such BPPV patients suffer from transient ver-

tigo and nystagmus, leading to balance impairm e nts

and incre a sed fall risk , so their treatment typically in-

volves a canalith reposition maneuver, practiced by

expert physicians, and requires, at least, two weeks

to have an appreciable effect. These featu res promote

them as g ood candida te s to be tested, before and after

the repositioning maneuver, in order to show that the

Φ-bonacci gait number, in its complete version, repre-

sents a mea ningful index, capable of explicitly quan-

Even though it can be naturally extended to even as-

sess gait index variability along past walking gaits, this is

how ever out of the focus of this paper.

tifying and detecting the recovery level and improve-

ments due to rehabilitation. Experimen ta l results con-

ﬁrm such a conjecture.

2 MATERIALS AND METHODS

This section r ecalls the concept of com posite gait cy-

cle and the notions of recursivity, harmonicity, sym-

metry, and double support consistency as d eﬁned in

(Verrelli et al., 2021 ). It also reports the mathemat-

ical expression of the Φ-bonacci ga it numbe r, in its

complete and simpliﬁed versions. Methods are then

described, along with the experimental setup and the

data acquisition modality. Finally, the main features

of the participants are introduced and the results com-

ing from the statistical analysis are reported.

2.1 Φ-Bonacci Sequence-Based Indices

Consider a walking gait (Iosa et al., 2013; Verrelli et

al., 2021) and let: GC stand for gait cycle; HS stand

for heel-strike; T O stand for toe-off; r and l stand for

right and left, respectively; ad j stand for adjoint; ST

stand for stance; SW stand for swing; DS stand for

double support. In Figure 1, a comprehensive mode l

of the composite gait cycle in (Verrelli et al., 2021),

which involves two speciﬁc couples of overlap ping

gait cycles, namely the left and right gait cycles (GCl

and GCr) and the adjoint right a nd left gait cycles

(GCr

ad j

and GCl

ad j

), is shown. For the sake of clar-

ity, STr, STl, SWr, and SWl represent the right and

left stance phase durations and the right and left swing

phase d urations, respec tively. Moreover, the dura-

tions DSr and DSl of the r ight and left double support

phase satisfy DSr = DSx + DSy, DSl = DSy + DSz,

with DSx, DSy, DSz being graphically deﬁn e d in Fig-

ure 1. Accordingly, the equal partition of the double

support sub-phases, i.e., DSx = DSy (and DSw = DSy,

DSy = DSz in Figure 1) involves the concept of dou-

ble support consistency. The same duration s for the

adjoint right and left gait cycles, denoted by STradj,

STladj, SWradj, SWladj, DSradj, and DSladj, are re-

ported in Figure 1. Now, Verrelli et al. (2021) have

innovatively c haracterized the aforementione d com-

posite gait cycle by means of a new mathematical and

meaningful index, namely the Φ-bonacci gait number,

which relies, in its self-similar kernel, on generalized

ﬁnite-length Fibona cci sequences, exploiting the ro le

of the golden ratio φ. Spe ciﬁcally, the complete ver-

sion of such an ind ex, here called Y

and r eported in

(10) of (Verrelli et al., 2021), has relied on a new ex-

perimental conjecture concerning an extended fractal

walking decomposition paying attention to the posi-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

204

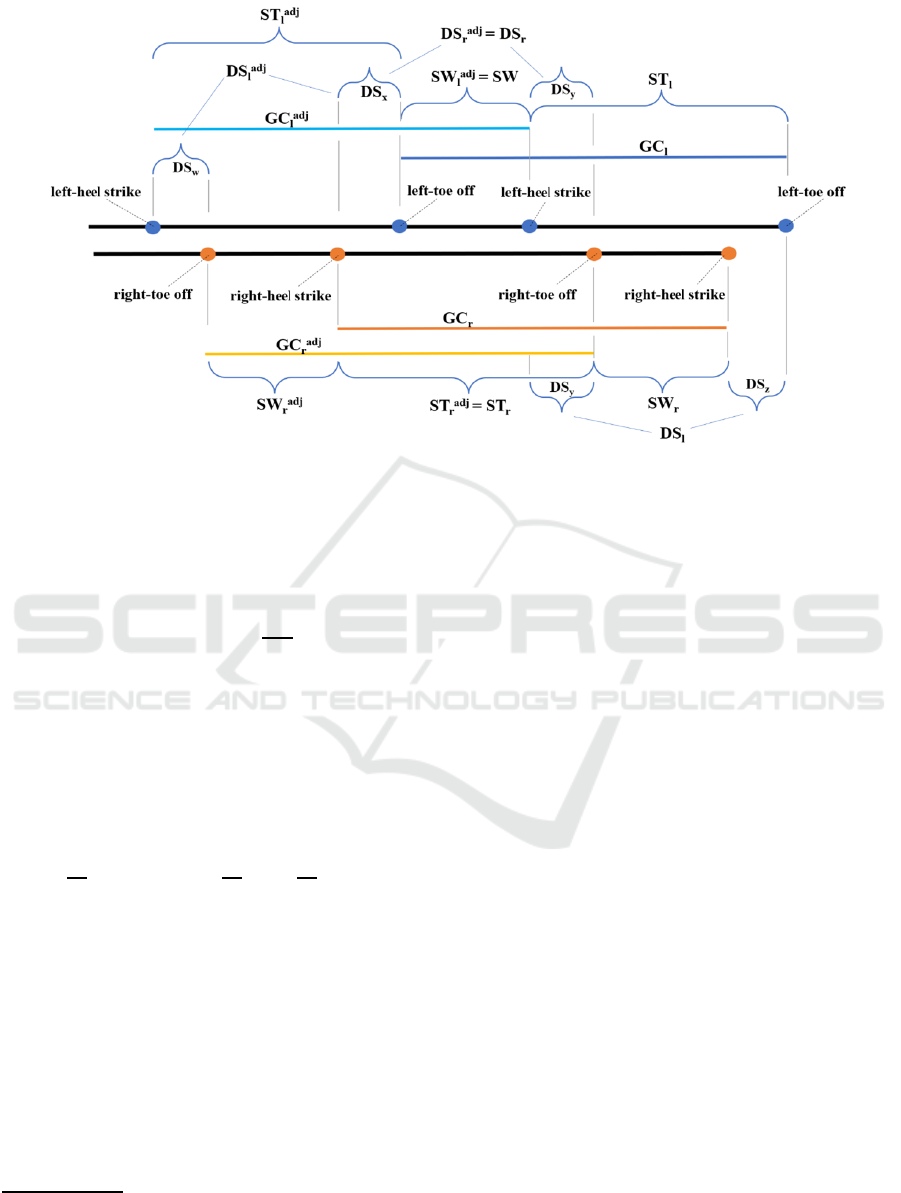
Figure 1: Composite gait cycle: right and left gait cycles and adjoint right and left gait cycles.

tion of the f oot relative to the tibia. It turns out to

constitute the most n atural generalization, to the non-

{symmetric & recursive} walking case, of the cor-

respond ing gait ratio |SW/DS − φ| deﬁned in (Iosa

et al., 2013; Iosa et al., 20 16) for symmetric walk-

ing, while it simply incorporates a weighted modi-

ﬁcation of the index = |∆SW|/SW in (Bła˙zkiewicz

et al., 2014), evaluated at both the g a it and the ad-

joint gait. The corresponding two simpliﬁed versions,

here called s1-Φ-bonacci gait number Y

[s1] and s2-

Φ-bonacci gait number Y

[s2], have appeared in (6)

of El Arayshi et al. (2022) and in (11) of Verrelli et

al. (2021) , respectively. They are reported in Table I,

where λ, δ, µ

adj

, λ

adj

, ν

conj

are positive weights

and

the normalized quantity is given by:



−ξ







−1



−ξ



(1)

in terms of positive reals ξ

, ξ

(where n generi-

cally stands for numerator, d stands for denominator,

v stands for value), whereas the p ositive real numbers

, z

denote the time distance s the correspon d-

ing left or right heel-strikes and toe-off instants of the

three time instants re presenting the three instants of

minimum angular p ositions (with negative signs) of

the (left and right) fe et relative to the tibias (with a 90

degrees-angle between foot and tibia being p lotted at

0-degrees).

Values close to 0 for the ab ove complete or sim-

pliﬁed indices describ e different levels of recursivity,

Such weights play the role of gains. They can be freely

chosen by the user, in accordance wi th the speciﬁc analysis

requirements.

self-similarity (harmonicity), swing symmetry, and

double supp ort consistency, depending on the level of

terms neglected in the index computation. Values far

from 0 typically refer to pathological gaits.

Remark 2.1. The conjecture used in the above in-

dices (see (Verrelli et al., 2021)) extends the ideas

underlying a fractal approach to the double support

sub-phases within the gait. It is inspired by the exper-

imental results reported in (Novacheck, 1998) show-

ing that physiological symmetric walking is not only

characterized by a stan ce duration being close to 62%

of gait cycle duration, a swing d uration being close

to 38% of gait cycle duration, a double support du-

ration being consequently c lose to 24% of gait cy-

cle duration, but also by an in sta nt of minimum an-

gular position (with negative sign ) of the foot rel-

ative to the tibia (with a 90 degree s-angle between

foot and tibia be ing plotted at 0-degrees) occurring at

about 7% of gait cycle du ration in each doub le sup-

port sub-phase (with 5% as percentage for the com-

plementary interval duration). It may thus be inter-

estingly recognized that the structure of a Fibonac ci

sequence (with ﬁxed point φ) appears in the sequence:

5 × 2 = 10 (1/φ

≈ 9.018); 7 × 2 = 14 (1/φ

≈

14.591); 24 (1/φ

≈ 23 .608); 3 8 (1/φ

≈ 38.19 8);

62(1/φ ≈ 61 .804); 100.

2.2 Subjects, Data Acquisition, and

Experimental Protocol

Patients affected by BPPV (n = 7, age = 55.6 ±5 .3)

were asked to perform 20-meters-walking tests in a

Comprehensive Φ-Bonacci Index for Walking Ability Assessment in Paroxysmal Positional Vertigo: Role of Rehabilitation

205

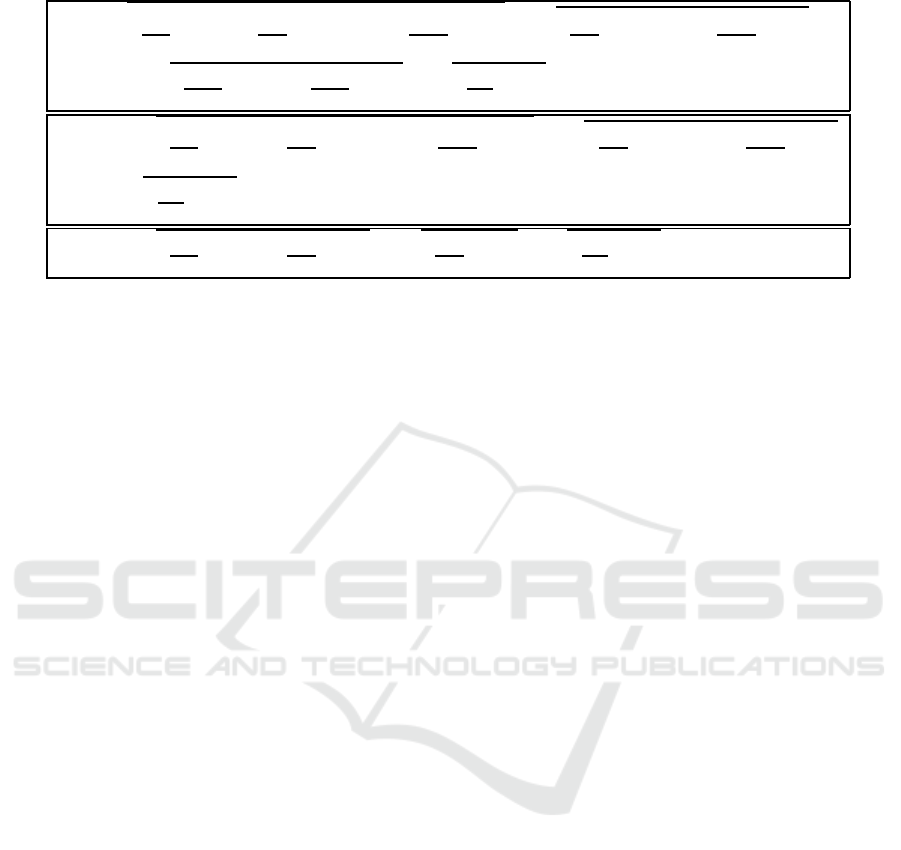
Table 1: Mathematical expressions for the Φ-bonacci gait number and its simpliﬁed versions.



−φ





−φ



+ µ

adj



adj

−φ



+ λ



−1



+ λ

adj



adj

−1



+ν

conj



−φ





−φ



+ δ



−1



[s1] =



−φ





−φ



+ µ

adj



adj

−φ



+ λ



−1



+ λ

adj



adj

−1



+δ



−1



[s2] =



−φ





−φ



+ λ



−1



+ δ



−1



hallway, at the ir c omfortable speed, before and af-

ter the canalith repositioning maneuver. For com-

parison, age-matched healthy control subje cts (HCS)

(n = 6, age = 59.4 ±7.3) were asked to perform, at

their co mfortable speed, a single 20-meter-walking

test. HCS we re asked about their history of dizziness,

lightheade dness, balance problem s, and other symp-

toms similar to the ones exhibited by the BPPV pa-

tients in the past six months. All the subjects were

required to wear th e wearable sensors of the motion

capture system Movit System G1 (Captiks, Rome,

Italy) for movement capture and analysis (see (El

Arayshi et al., 2022)). The Movit System G1 provides

accelerometer, gyroscope, magnetometer, quaternion,

and barometer synced data and is composed of 13-

DOF wireless light-weight wearable small iner tial de-

vices and an USB wirele ss receiver (Costantini et al.,

2018, Ricci et al., 2019b, Ricci et al., 2019a). The

Motion Studio & Motion Analy zer software, to be

used in conjunction with the aforementioned data ac-

quisition system, is then respectively used to collect

the movement da ta from each sensor and fuse/process

sensors data to generate the .csv ﬁles of the c onsec-

utive time instants of the HS and T O for the left and

right foot, in addition to the an a tomical angles, which

are used to obtain information on the position of the

foot (left and right) relative to the tibia.

2.3 Data and Statistical Analysis

The temporal gait parameters, obtained from Motio n

Analyzer from the r aw senso rs data fusion and pro-

cessing operations, were loaded on a custom-made

MATLAB (The Mathworks, Natick, MA, USA) algo-

rithm that recognizes the time instants of HS and TO

for the left and right foot belo nging to the (left an d

right) gait cycle and the adjoint gait cycle subphases

and involved in the computatio n of the Φ-bona c ci gait

number (all th e weights therein were set equal to 1).

The developed MATLAB algorithm automatically al-

lows for the computation of the values of Y

, Y

[s1],

and Y

[s2] corresponding to all the composite gait cy-

cles detected in the full walking event for each sub-

ject. To reduce the effect of measurement errors of

the sensors and possible transient behaviors of the

gait, the algorithm just considered the composite gait

cycles belonging to the middle of the walking event,

along with the immediately previous and subsequent

gait cycles. Statistical analyses an d data visualization

were performed using GraphPad Prism Software Ver-

sion 9. The reported results involve the average of

the in dices computed over the three gait cycles be-

longing to the middle of the walking event for each

subject. Since data do not follow a normal distribu-

tion (evaluated by the Kolmogorov- Smirn ov normal-

ity test), a non-parametric Mann-Whitney U test was

used to ﬁnd differences between the mean values of

each pair of samples. Statistical analyses were con-

sidered signiﬁcant in all cases when the p-values were

less than 0.05. Moreover, for the evaluation of the in -

dices as diagno stic test receivers, operating character-

istic curve (ROC) analyses [Wilson/Brown method]

were performed; index accuracy was measured by the

area under the ROC curve (AUC). If the AUC value

was greater than 0.5, the test was considered signiﬁ-

cant. We considered the Youden in dex with likelihood

ratio LR= Sensitivity / (1 - Speciﬁcity) > 2 as a crite-

rion for ch oosing the optimal threshold value for the

ROC curve, na mely the thresh old value c for which

the quantity Sensitivity + Speciﬁcity - 1, evaluated at

c, is the largest one.

3 RESULTS AND DISCUSSION

Up to now, studies have shown how gait phases are a

reliable and valid measure for the assessment of sub-

jects’ walking ability. In addition, gait phase changes

have been reported in patients affected by several neu-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

206

Figure 2: Φ-bonacci gait number Y

and its simpliﬁed versions Y

[s1], Y

[s2], computed for each subject (n = 7, each row)

with BPPV before and after the patient treatment and evaluated at three subsequent stages (i −1,i,i + 1) [i = gait cycle in the

middle of the walking event ( bold values)].

Figure 3: Φ-bonacci gait number Y

and its simpliﬁed versions Y

[s1], Y

[s2], computed for each healthy subject (n = 5, each

row) and evaluated at three subsequent stages (i −1,i,i + 1) [i = gait cycle in t he middle of the walking event (bold values)].

rodegenerative diseases or disorders after rehabilita-

tive interventions (Jonsdottir et al., 2 020; Leone et al.,

2018). In lig ht of those ﬁndings, we were encouraged

to investigate the capability of the new indices r e-

ported in the previous section to be successfully used

in clinical settings and thus, to exhibit responsiveness

to (even small) changes coming fro m rehabilitation

(see (Verrelli e t al., 2021 ) fo r a comparison with clas-

sical indice s such as Mean Gait Ratio MGR and Sym-

metry Index SI).

The values of Y

, Y

[s1], Y

[s2] – computed for

each HCS and each BPPV patient before and after the

canalith repo sitioning maneuver and evaluated at the

gait cycle (i) in the middle of the walking event and

at the immediately previous (i −1) and subsequent

one (i + 1) – appear in the tables belonging to Figures

2 and 3. Figures 4 and 5 report the corresponding

mean ± SD. They assess a certain level of stability of

the measurement, for both th e HCS and the patients.

For the ﬁrst time in the literature, data of Figure 6-8

illustrate h ow the Y

[largely better than its simpliﬁed

versions Y

[s1], Y

[s2]] is able to distinguish healthy

subjects from pathological ones better than the

correspo nding simpliﬁed indices. In particular, the

ROC analysis and the AUC being obtained using

observed in BPPV patients and controls shows

that such a comprehensive index – when used as a

diagnostic test – displays a great accuracy (in terms of

sensitivity & speciﬁcity, as well a s of p-value, AUC

and Likelihoo d Ratio) in distinguishing between

BPPV patients and healthy subjects: ROC curve

related to Y

for the evaluation of the index as a

Comprehensive Φ-Bonacci Index for Walking Ability Assessment in Paroxysmal Positional Vertigo: Role of Rehabilitation

207

Figure 4: Mean ± SD of Φ-bonacci gait number Y

and its simpliﬁed versions Y

[s1], Y

[s2], for data appearing in Figure 2.

Figure 5: Mean ± SD of Φ-bonacci gait number Y

and its simpliﬁed versions Y

[s1], Y

[s2], for data appearing in Figure 3.

diagnostic te st. AUC=1.000; 95% conﬁdence inter-

val AUC=[1.000, 1.000 0]; p-value AUC =0 .0045;

cut-off value ROC=0.5577; Sensitivity at cut-off

value=100%; 95% CI=[64.57%,100.0%]; Speciﬁcity

at cut-off value=80%, 95% CI=[37.55%,98.97%];

Likelihood Ratio (LR)=5.00. Such accura te results

are not achieved when the simpliﬁed versio ns of

index Y

are used, instead (see Figur e s 7 a nd 8).

Quantiﬁcation o f the recovery level of each BPPV

patient after the c analith repositioning maneuver can

be taken from Figure 4. Speciﬁcally, Y

, Y

[s1],

and Y

[s2] values show a reduction for each patient

in post-treatment c ondition, highlighting a different

recovery level of healthy harm onic and symmetric

components among the patients and thus, point out

the in dices ab ility to dete ct and quantify individual

improvements due to rehabilitation. In particular,

the perc entage-variation ((post.treatment.value −

pre.treatment.value)/pre.treatment.value) ∗ 100%

for Y

of each patien t reads: Patient 1: -78%, Patient

2: - 55%, Patient 3: -50%, Patient 4: -8 6%, Patient 5:

-61%, Patient 6 : -39%, Patient 7: - 63%.

4 CONCLUSIONS

The experimen ta l results on healthy and pathological

gaits related to BPPV of Section 3 illustrate how the

new comprehensive Φ-bonacci gait number of Table I

(better than its simp liﬁed versions) is able to capture

the most reliable and o bjective (quantitive) outcome

measures of recursivity, asymmetry, consistency, and

self-similarity ( harmonicity) of the g a it cycle (and

their distortions in pathological subjects), as well as

of r ehabilitation- based recovery effects.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

208

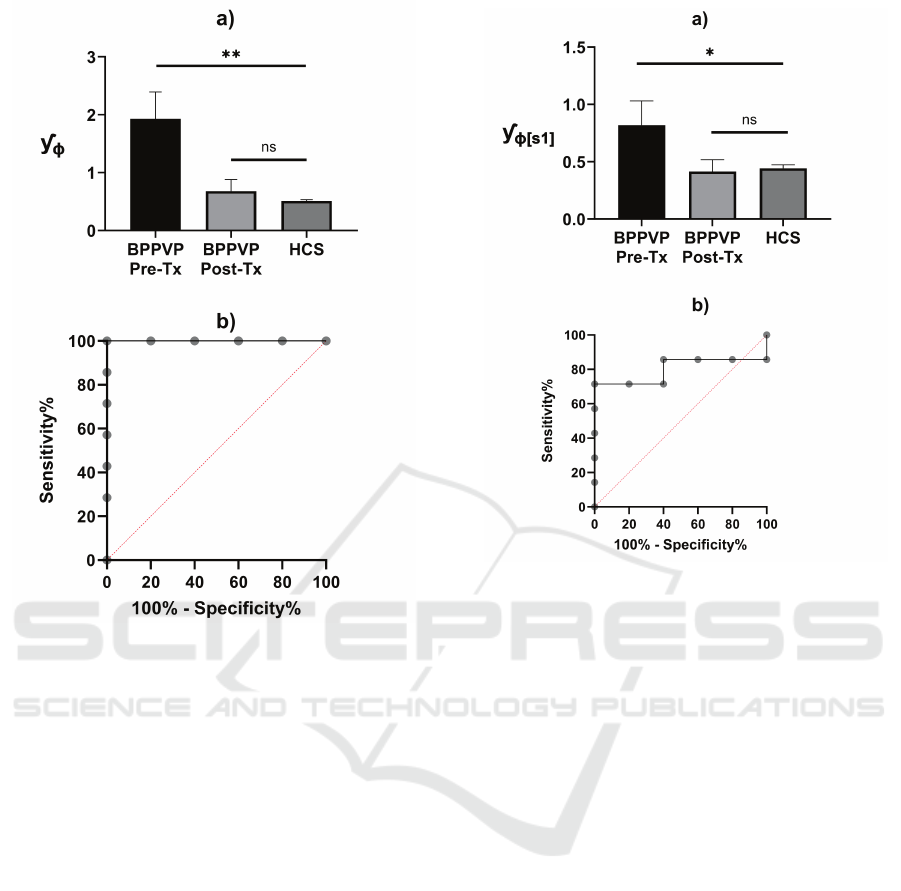
Figure 6: (a) mean ± SEM of the average Y

values

computed for BPPV patients (before and after the treat-

ment) and healthy controls subjects (HCS): n = 7 (BPPV

patients), n = 5 (HCS) . p-values are calculated using

the Mann-Whitney U test, ∗∗ : p < 0.01, ns: not signiﬁ-

cant. b) ROC curve related to Y

for the evaluation of

the index as a diagnostic test. AUC=1.000; 95% con-

ﬁdence interval AUC =[1.000, 1.0000]; p-value AUC =

0.0045; cut-off value ROC=0.5577; Sensitivity at cut-off

value=100%; 95% CI=[64.57%,100.0%]; Speciﬁcity at cut-

off value=80%, 95% CI=[37.55%, 98.97%]; Li kelihood Ra-

tio (LR)=5.00.

ACKNOWLEDGEMENTS

The authors are indeb te d to Prof. G. Saggio for pro-

viding us with the Movit System.

REFERENCES

Bła˙zkiewicz, M., Wiszomirska, I., and Wit , A. (2014).

Comparison of four methods of calculating the sym-

metry of spatial-temporal parameters of gait. A ct a of

Bioengineering and Biomechanics, 16(8):29–35.

Cavagna, G. and Margaria, R. (1966). Mechanics of walk-

ing. Journal of applied physiology, 21(1):271–278.

Costantini, G., Casali, D., Paolizzo, F., Alessandrini, M.,

Micarelli, A., Viziano, A., and Saggio, G. (2018). To-

Figure 7: (a) mean ± SEM of the average Y

[s1] values

computed for BPPV patients (before and after the treat-

ment) and healthy controls subjects (HCS): n = 7 (BPPV

patients), n = 5 (HCS). p-values are calculated using the

Mann-Whitney U test, ∗ : p ∈ (0.01,0.05), ns: not sig-

niﬁcant. b) ROC curve related to Y

[s1] for the eval-

uation of the index as a diagnostic test. AUC=0.8000;

95% conﬁdence interval AUC=[0.5244, 1.0000]; p-value

AUC=0.0882; cut-off value ROC=0.5577; Sensitivity at

cut-off value=71.43%; 95% CI=[35.89%,94.92%]; Speci-

ﬁcity at cut-off value=80.00%; 95% CI=[37.55%,98.97%];

Likelihood Ratio (LR)=3.571.

wards the enhancement of body standing balance re-

covery by means of a wireless audio-biofeedback sys-

tem. Medical engineering & physics, 54:74–81.

Dugan, S. and Bhat, K. (2005). Bi omechanics and analysis

of running gait. Physical Medicine and Rehabilitation

Clinics, 16(3):603–621.

El Arayshi, M., Verrelli, C., Saggio, G., Iosa, M., Gentile,

A., Chessa, L., R uggieri, M., and Polizzi, A. (2022).

Performance index for in home assessment of motion

abilities in ataxia telangiectasia: A pilot study. Ap-

plied Sciences, 12(8):4093.

Iosa, M., De Bartolo, D., Morone, G., Bofﬁ, T., Mammu-

cari, E., Vannozzi, G., Bini, F., Marinozzi, F., An-

tonucci, G., and Paolucci, S. (2019). Gait phase pro-

portions in different locomotion tasks: The pivot role

of golden ratio. Neuroscience Letters, 699:127–133.

Iosa, M., Fusco, A., Marchetti, F., Morone, G., Caltagirone,

C., Paolucci, S., and Peppe, A. (2013). The golden

ratio of gait harmony: R epetitive proportions of repet-

itive gait phases. BioMed research international,

2013.

Comprehensive Φ-Bonacci Index for Walking Ability Assessment in Paroxysmal Positional Vertigo: Role of Rehabilitation

209

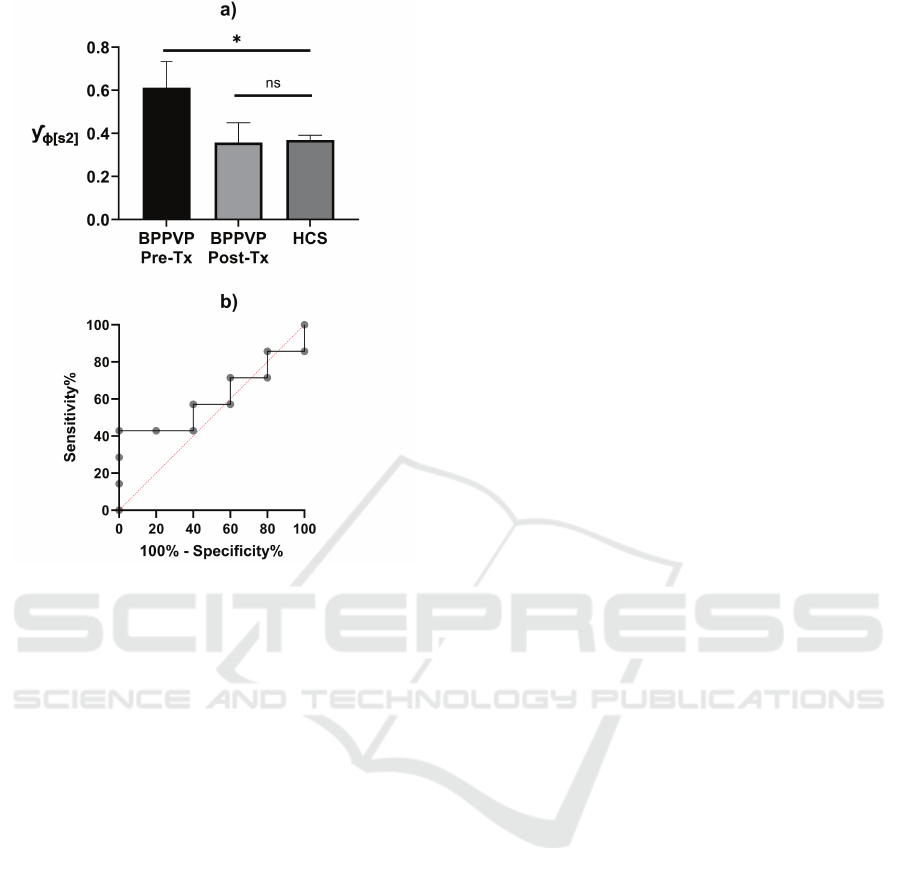
Figure 8: (a) mean ± SEM of the average Y

[s2] val-

ues computed for BPPV patients (before and after the

treatment) and healthy controls subjects (HC S): n =

7 (BPPV patients), n = 5 (HCS). p-values are calcu-

lated using t he Mann-Whitney U test, ∗ : p ∈ (0.01,0.05),

ns: not signiﬁcant. b) ROC curve related to Y

[s2]

for the evaluation of the index as a diagnostic test.

AUC=0.5492; 95% conﬁdence interval AUC=0.6000;

95% conﬁdence interval AUC=[0.2686, 0.9314]; p-value

AUC=0.5698; cut-off value ROC=0.5577; Sensitivity at

cut-off value=42.86%; 95% CI=[15.82%,74.95%]; Speci-

ﬁcity at cut-off value=80.00%; 95%CI=[37.55%,98.97%];

Likelihood Ratio (LR)=2.143.

Iosa, M., Morone, G., Fusco, A., Marchetti, F., Caltagirone,

C., Paolucci, S., and Peppe, A. (2016). Loss of fractal

gait harmony in parkinson’s disease. Clinical Neuro-

physiology, 127(2):1540–1546.

Jonsdottir, J., Lencioni, T., Gervasoni, E., Crippa, A., Anas-

tasi, D., Carpinella, I., Rovaris, M., Cattaneo, D., and

Ferrarin, M. (2020). Improved gait of persons with

multiple sclerosis after rehabilitation: effects on lower

limb muscle synergies, push-off, and toe-clearance.

Frontiers in Neurology, 11:668.

Leone, C., Kalron, A., Smedal, T., Normann, B., Wens, I.,

Eijnde, B., and Feys, P. (2018). Effects of rehabilita-

tion on gait pattern at usual and fast speeds depend on

walking impairment level in multiple sclerosis. Inter-

national Journal of MS Care, 20(5):199–209.

Marino, R., Verrelli, C., and Gnucci, M. (2020). Syn-

chronicity rectangle for temporal gait analysis: Ap-

plication to parkinson’s disease. JBiomedical Signal

Processing and Control, 62.

Novacheck, T. (1998). The biomechanics of running. Gait

and Posture, 7:77–95.

Ricci, M., Di Lazzaro, G., Pisani, A., Mercuri, N., Gian-

nini, F., and Saggio, G. (2019a). Assessment of motor

impairments in early untreated parkinson’s disease pa-

tients: the wearable electronics impact. I EEE journal

of biomedical and health informatics, 24(1):120–130.

Ricci, M., Terribili, M., Giannini, F., Errico, V., Pallotti,

A., Galasso, C., Tomasello, L., Sias, S., and S aggio,

G. (2019b). Wearable-based electronics to objectively

support diagnosis of motor impairments in school-

aged children. Journal of biomechanics, 83:243–252.

Verrelli, C., Iosa, M., Roselli, P., Pisani, A., Giannini,

F., and Saggio, G. (2021). Generalized ﬁ nit e-length

ﬁbonacci sequences in healthy and pathological hu-

man walking: Comprehensively assessing recursiv-

ity, asymmetry, consistency, self-similarity, and vari-

ability of gaits. Frontiers in Human Neuroscience,

15:649533.

Zhang, Y., Wang, H., Yao, Y., Liu, J., Sun, X., and Gu,

D. ( 2021). Walking stability in patients with be-

nign paroxysmal positional vertigo: An objective as-

sessment using wearable accelerometers and machine

learning. Journal of neuroengineering and rehabili-

tation, 18:1–9.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

210