Intelligent Agents with Graph Mining for Link Prediction over Neo4j

Michalis Nikolaou

, Georgios Drakopoulos

2 a

, Phivos Mylonas

3 b

and Spyros Sioutas

1 c

Computer Engineering and Informatics Department, University of Patras, Patras, Greece

Department of Informatics, Ionian Univerity, Kerkyra, Greece

Informatics and Computer Engineering Department, University of West Attica, Athens, Greece

Keywords:

Intelligent Agents, Network Structural Integrity, Connectivity Patterns, Link Prediction, Graph Mining, Neo4j.

Abstract:

Intelligent agents (IAs) are highly autonomous software applications designed for performing tasks in a broad

spectrum of virtual environments by circulating freely around them, possibly in numerous copies, and taking

actions as needed, therefore increasing human digital awareness. Consequently, IAs are indispensable for large

scale digital infrastructure across ﬁelds so diverse as logistics and long supply chains, smart cities, enterprise

and Industry 4.0 settings, and Web services. In order to achieve their objectives, frequently IAs rely on

machine learning algorithms. One such prime example, which lies in the general direction of evaluating the

network structure integrity, is link prediction, which depending on the context may denote growth potential or

a malfunction. IAs employing machine learning algorithms and local structural graph attributes pertaining to

connectivity patterns are presented. Their performance is evaluated with metrics including the F1 score and

the ROC curve on a benchmark dataset of scientiﬁc citations provided by Neo4j containing ground truth.

1 INTRODUCTION

Intelligent agents (IAs) are advanced and ﬂexible au-

tonomous piece of software tailored for pursuing mul-

tiple and potntially conﬂicting objectives whose rank-

ing may change over time while operating in an evolv-

ing environment which may not be fully known (Li

et al., 2022a). In this sense IAs are invaluable for sup-

porting digital awareness extending the human pre-

scient ability with regards to digital infrastructure.

In order for IAs to be effective in their respec-

tive missions, they are frequently augmented with

machine learning (ML) capabilities. For instance, it

would make sense to use ML to enhance communi-

cation reliability in an industrial or a smart city con-

text as communication channels are in practice con-

stanctly subject to various sources of noise depending

on the operational setting. This holds especially true

in distributed systems where wired links are corrupted

by white Gaussian noise, while mobile links are prone

to lognormal noise, shadowing, or even intersymbol

interference (ISI) from any nearby links.

This has been further enhanced with the advent of

https://orcid.org/0000-0002-0975-1877

https://orcid.org/0000-0002-6916-3129

https://orcid.org/0000-0003-1825-5565

graph signal processing (GSP), a ﬁeld which has re-

cently garnered intense interdisciplinary research at-

tention as it allows for established ML techniques to

be applied on a graph mining setting. IAs can bene-

ﬁt from GSP since most of the infrastructure, whether

digital or physical, they routinely operate on is or at

least can be represented by a graph. Common exam-

ples include long supply chains, power and water net-

works, and computer networks.

The primary research objective of this conference

paper is the development of an IA capable of perform-

ing link prediction based on a wide array of ML algo-

rithms running on local attributes such as the Adamic-

Adar index and the resource allocation metric. Since

numerous local decisions are critical for the emer-

gence of global patterns in scale free graphs, the effect

of the former can be evaluated on a macroscopic scale

through metrics like the F1 score and the receiver op-

erating characteristic (ROC). This work differentiates

itself from existing approaches by heavily focusing

on graph locality properties. The benchmark dataset

is represented in a Neo4j database and in fact it was

taken directly from the Neo4j developer site

The remaining of this work is structured as fol-

lows. In section 2 the recent scientiﬁc literature re-

https://neo4j.com/developer/graph-data-science/link-

prediction/graph-data-science-library/

504

Nikolaou, M., Drakopoulos, G., Mylonas, P. and Sioutas, S.

Intelligent Agents with Graph Mining for Link Prediction over Neo4j.

DOI: 10.5220/0012238100003584

In Proceedings of the 19th International Conference on Web Information Systems and Technologies (WEBIST 2023), pages 504-511

ISBN: 978-989-758-672-9; ISSN: 2184-3252

garding IAs, GSP, and graph mining strategies is

brieﬂy overviewed. In section 3 the IA architecture

and its functionality are explained. The results ob-

tained by the proposed methodology are analysed in

section 4. Future research directions are given in sec-

tion 5. Bold capital letters denote matrices, small

boldface vectors, and small plain scalars. Function

parameters come with a semicolon after their argu-

ments. Technical acronyms are explained the ﬁrst

time they are encountered in the text. Finally, nota-

tion is summarized in table 1.

2 PREVIOUS WORK

A major part of IA functionality (Moussawi et al.,

2023) is the interaction with their environment (Chi-

atti et al., 2022), especially for enhancing human dig-

ital awareness (Riedl, 2019). IA design elements in-

ﬂuence among others user acceptance (Elshan et al.,

2022), seamless integration with various ML algo-

rithms (Kaswan et al., 2022), presentation to the ﬁ-

nal user (Narumi et al., 2022), coordination with

other IAs (Neﬂa et al., 2022), and Web mining op-

timization (Yoon et al., 2022). IA applications in-

clude strategically searching LinkedIn for trusted can-

didates (Drakopoulos et al., 2020c), monitoring long

food supply chains (Pirsa et al., 2022), and digital

health (Chen et al., 2022). ML algorithms which have

been used by IAs are shown in table 2.

GSP is an emerging ﬁeld where graphs are two-

dimensional signals from an irregular domain (Or-

tega, 2022) which can be combined with graph neu-

ral networks (GNNs) (Li et al., 2022a) or other ML

techniques (Shi and Moura, 2022) to extract knowl-

edge from graphs. Applications include cultural con-

tent recommendation based on affective attributes

(Drakopoulos et al., 2022), collaborative ﬁltering (Liu

et al., 2023), the smart decompression of long graph

sequences (Drakopoulos et al., 2021a), graph recon-

struction with Sobolev smoothness (Giraldo et al.,

2022), GNNs for evaluating the affective coherence

of fuzzy (Drakopoulos et al., 2021b) and ordinary

(Drakopoulos et al., 2020a) Twitter graphs, transfer

learning between graphs (Ruiz et al., 2023), aprox-

imating directed graphs with undirected ones using

matrix polar factorization (Drakopoulos et al., 2021c),

ensemble learning (Shang et al., 2022), intelligent

fault diagnosis (Li et al., 2022b), probabilistic ap-

proximation of topological correlation (Drakopoulos

and Kafeza, 2020), multiscale learning (Zhao et al.,

2022), wide learning of massive graphs (Gao et al.,

2022), and community discovery on Twitter based on

multiple criteria (Drakopoulos et al., 2020b).

Graph mining is a broad ﬁeld (Dong et al., 2023)

encompassing quite diverse research such as opin-

ion mining (Lin et al., 2022), enhanced ontolo-

gies (Drakopoulos et al., 2017), parallel graph pro-

cessing (Dai et al., 2022), face recognition (Bedre

and Prasanna, 2022), heuristic community discovery

(Drakopoulos and Mylonas, 2022), and ﬁnding inter-

related requirements in software architectures from

large texts (Singh, 2022).

3 INTELLIGENT AGENT DESIGN

The conceptual architecture of an IA is shown at ﬁg-

ure 1. Notice how any IA can interact besides the

digital realm also with its physical environment by

accepting input, even incomplete or fuzzy depending

on the operational context, through a broad array of

available heterogeneous sensors depending on its con-

ﬁguration such as light, atmospheric pressure, humid-

ity, acceleration, and electromagnetic ﬁeld sensor to

name only a few. Therefore IAs can bridge the gap

between the physical and the digital realms.

According to the original Russel-Norvig classiﬁ-

cation there are the following types of IAs:

• Simple Reﬂex Agents: They react to external

stimuli but do not take into consideration any his-

tory.

• Model Based Reﬂex Agents: They live in par-

tially observable environments and have state his-

tory.

• Goal Based Agents: They select among a set of

desirable goal states and make a course of actions.

• Utility Based Agents: They can quantify how de-

sirable a given state is and choose between them.

• Learning Agents: They adapt and can dynami-

cally select actions leading to a desired goal.

The proposed IA clearly belongs to the ﬁfth and

most general level of the above taxonomy. In semi-

supervised and unsupervised learning settings the

concept of state is paramount, since it codiﬁes the

knowledge IA has for the environment and its past

interactions with it. Maintaining such information is

vital for an IA operating in the Web since the latter

is stateless by dsign. The state vector s as shown in

equation (1) is a column vector containing p state

variables which essentially reﬂect the conﬁguration

of the proposed IA and they control its actions. In

this particular context, the p variables are the at-

tributes collected for each vertex shown later in this

section, suggesting thus that the IA trajectory and ac-

Intelligent Agents with Graph Mining for Link Prediction over Neo4j

505

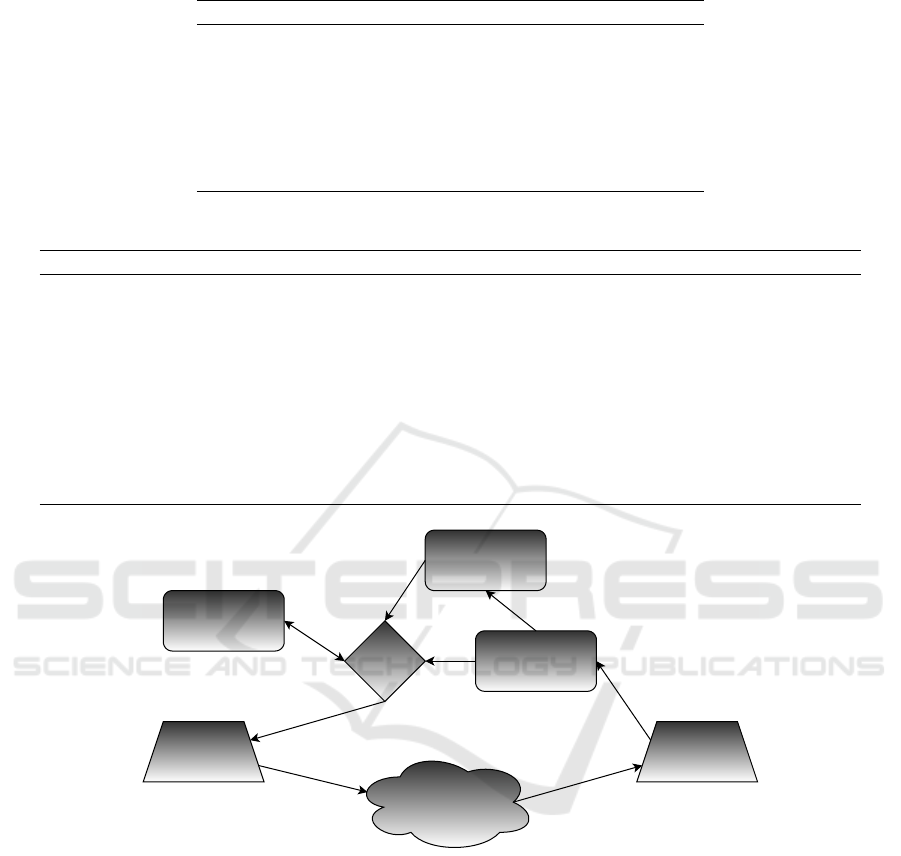
Table 1: Notation of this work.

Symbol Meaning First in

△

= Deﬁnition or equality by deﬁnition Eq. (1)

{

, . . . , s

}

Set with elements s

, . . . , s

Eq. (2)

Set cardinality functional Eq. (2)

(u, v) Undirected edge between u and v Algo. 1

deg(u) Degree of vertex u Eq. (7)

Γ(u) Neighborhood of vertex u Eq. (6)

prob

{

Ω

}

Probability of event Ω occurring Eq. (14)

Table 2: Neural network architectures.

Model Unsupervised Supervised Software

Autoencoder Yes No keras, H2O

Convolutional Deep Belief Network Yes Yes tensorﬂow, keras, H2O

Convolutional Neural Network Yes Yes tensorﬂow, fastai

Deep belief network Yes Yes theano, pytorch, tensorﬂow

Deep Boltzmann machine No Yes boltzmann-machines, pydbm

Denoising autoencoder Yes No tensorﬂow, keras

Long short-term memory No Yes keras, lasagne, BigDL, Caffee

Multilayer perception No Yes keras, sklearn, tensorﬂow

Recurrent neural network No Yes keras

Restricted Boltzmann machine Yes Yes pydbm, pylearn2, theanoLM

Current state

estimation

Environment

Actuators

Decision

Sensors

Decision history

State history

Figure 1: IA architecture.

tions along a given graph rely on vector embeddings.

△



. . . h



(1)

The strategy of the proposed IA is outlined in sec-

tion 1. Its main loop ensures that each vertex is vis-

ited exactly once and that the local attribute vector is

taken into account. In many IA problems vertex visit

strategy is critical, but here a single visit sufﬁces.

The predetermined set of actions can be repre-

sented as a set I

as in (2). Notice that in general

depending on the current vertex and the agent state

not every action from the set I

may be applicable or

even available. However, here only two actions are

available, namely collect vertex attributes and decide

whether a latent edge exists between the local edge

and one of its non-neighboring vertices.

△

{

, . . . , a

}

= n (2)

For each action of (2) there is an associated posi-

tive cost, which in general depends on the functional

parameters of the IA and the environment, as well as

a related reward. In general both can depend on time,

but here this is omitted. Action costs and rewards are

represented also by two sets as in (3). Observe that I

, and I

have the same cardinality.

△

{

, . . . , c

}

and I

△

{

, . . . , r

}

(3)

WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies

506

Data: Input graph and IA parameters

Data: Set of termination conditions τ

Result: The predicted edges marked as such

start from a random vertex;

while τ is not satisﬁed do

collect local attributes of u;

foreach not connected vertex v do

collect local attributes of v;

create joint attributes of u and v;

if ML ﬁnds a latent (u, v) then

connect u and v with (u, v);

mark the above edge as new;

end

Algorithm 1: Proposed IA operation.

The most common ﬁgure of merit is the weighted

expected cost of the actions taken by the IA as shown

in (4). The exponentially forgetting factor γ

essen-

tially stipulates that the effect of past errors tend to

have a negligible effect on later steps.

△

∑

k=1

(4)

An alternative metric is the expected weighted re-

ward to cost ratio of IA as shown in equation (5).

△

∑

k=1

(5)

Frequently the internal mechanics of an IA are

modeled as a ﬁnite state automaton (FSA) where the

transition between each possible state of the state vec-

tor s depends on the current vertex as well as on the

cost and rewards of the available actions. In this con-

text, the capacity and transitivity closure of this FSA

can be used as evaluation metrics of the complexity of

the underlying IA. Moreover, under the appropriate

conditions they may reﬂect the coding effort neces-

sary for creating the IA. The latter does not have to be

mandatorily implemented as an FSA, it only sufﬁces

that its internal logic can be translated to one while

their implementation is determined by technological

levels and the intended IA functionality. For instance,

an IA may well be implemented as a rule-based sys-

tem for AI explainability and accountability purposes.

As FSAs are limited by bounded rationality phe-

nomena, a single IA may not be sufﬁcient for certain

purposes, for example considerably suppressing or to-

tally preventing the functionality of a hostile IA. Such

scenarios typically require the cooperation of many

IAs for creating a distributed hive AI and are com-

monly modeled as games on graphs.

In this scenario, the performance metric of equa-

tion (5) is implicitly used with umiform unit costs for

either missing a latent edge between two vertices or

declaring that a non-existent edge exists.

3.1 Attributes

In order to train the algorithns determiming the ac-

tions and decisions of the proposed IA, a number of

graph structural metrics concerning vertex pairs are

used. These are also described in the GDSL Web site

of Neo4j

, namely its graph algorithms library.

• The common neighbors score h

(u, v) stemming

from the fundamental property of edge locality,

meaning the more neighbors two vertices share,

the more probable is that they are connected.

(u, v)

△

Γ(u) ∩ Γ(v)

(6)

• The preferential attachment score h

(u, v) relies

on the densiﬁcation property of dynamic graphs

stating that the higher degree a vertex has, the

more probable it is to attract new neighbors.

(u, v)

△

= deg (u)deg(v) (7)

• The number of total neighbors h

(u, v) is also de-

rived from the above stated property but takes a

different approach by evaluating the joint poten-

tial of a vertex pair to attract new neighbors.

(u, v)

△

= deg (u) + deg(v) (8)

• The Adamic-Adar index h

(u, v) evaluates the in-

formation theoretic potential for connections of

the common graph segment between the two ver-

tices instead of focusing to the vertices.

(u, v)

△

∑

s∈Γ(u)∩Γ(v)

log

Γ(s)

(9)

• The resource allocation metric h

(u, v) moves

along the similar line of reasoning and approxi-

mates the reciprocal of the number of connections

necessary to be established between them.

(u, v)

△

∑

s∈Γ(u)∩Γ(v)

Γ(s)

(10)

The attributes are collected using Cypher, the

ASCII art based query language of Neo4j which al-

lows access to every graph structural element. The

queries necessary for the IA to perform its task.

https://neo4j.com/docs/graph-data-science/current/alg

orithms/linkprediction/

Intelligent Agents with Graph Mining for Link Prediction over Neo4j

507

Instead of providing the learning algorithms with

the above attributes, they were given an averaged ver-

sion of them. Since different vertices have different

degrees, the harmonic mean of (11) is used:

h(u, v)

△

deg(u)

∑

s∈Γ(u)

h(s, v)

(11)

The approach of (11) relies heavily on the locality

property of the graphs. In other words, it exploits the

fact that if v is connected to u, then it is probable that

it will be also reconnected to some of its neighbors.

3.2 Learning Algorithms

The algorithms employed by the IA are the follow-

ing. Notice they are common and readily available in

a broad spectrum of platforms.

• Random Forest (RF).

• Decision Tree (DT).

• Logistic Regression (LR).

In addition to these ML algorithms, four feed for-

ward neural network (FFNN) architectures were also

employed by the IA to do link prediction.

• A p × 2p × 1 architecture where each layer uses

the SELU activation function and p is the number

of attributes as shown in equation (1) (NN1).

• A p × 5p × 1 architecture where each layer uses

the SELU activation function (NN2).

• A p × 2p × 2p × 1 where the input layer uses

RELU and the next ones SELU (NN3).

• A p × 5p × 5p × 1 where the input layer uses

RELU and the next ones SELU (NN4).

The scaled exponential linear unit (SELU) activa-

tion function

has a ﬂexible smooth form and can be

parameterized by a scaling factor β

as shown in (12).

ψ(u;β

)

△

(

u, u ≥ 0

− 1), u < 0

(12)

The rectiﬁed linear unit (ReLU) activation func-

tion

despite its seemingly simple form is very pop-

ular because of its adaptability and its easy interpre-

tation. Moreover, the lack of parameters signiﬁcantly

reduces training complexity.

ϕ(u)

△

(

u, u ≥ 0

0, u < 0

(13)

It should be noted that both SELU and RELU can

be easily found in many ML platforms.

www.tensorﬂow.org/api docs/python/tf/keras/activati

ons/selu

https://keras.io/api/layers/activations

4 RESULTS

Basic structural properties of the dataset obtained by

the Neo4j developer site are shown in table 3. In that

table positive examples refer to vertex pairs where a

latent edge exists, where negative ones refer to pairs

which are not actually linked. Observe that originally

there was a considerable imbalance between positive

and negative training examples and therefore random

downsampling took place.

Table 3: Dataset synopsis.

Property Value

Negative examples for training data 1580567

Positive examples for training data 105139

Negative examples downsampling 50085

Positive examples downsampling 50085

The benchmark dataset contains authors of scien-

tiﬁc papers and their publications over a range of sixty

years. In this scenario the objective of link prediction

is to discover and recommend potential co-authors in

order to boost scientiﬁc collaboration. In ﬁgure 2 the

number of papers entries is shown.

Communication between the Neo4j and the appli-

cation took place over py2neo, which is one of the

most popular Neo4j drivers for Python. It allows

sending dynamically formulated Cypher queries and

the reception of the results.

The results for each of the basic learning strate-

gies of RF, DT, and LR is shown in table 4. Therein

MAE and MSE denote mean absolute error and mean

squared error respectively. MSE is especially impor-

tant as it approximates the performance metric of (5).

Table 4: Performance metrics for the learning strategies.

Metric RF DT LR

Accuracy 0.963 0.963 0.936

Precision 0.965 0.962 0.947

Recall 0.960 0.964 0.924

MAE 0.037 0.037 0.064

MSE 0.037 0.037 0.064

F1 0.963 0.963 0.935

Observe that among these algorithms RF outper-

forms, even by a small margin, the other two. This can

be partly at least attributed to its robustness to outliers

and to its averaging nature which typically ensures a

more than adequate performance in ML settings.

The receiver operating characteristic (ROC) of an

ML model is deﬁned as a way to obtain the probability

that the ranking r (·) of any pair of patterns y and y

′

where y < y

′

is preserved under that model, namely

WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies

508

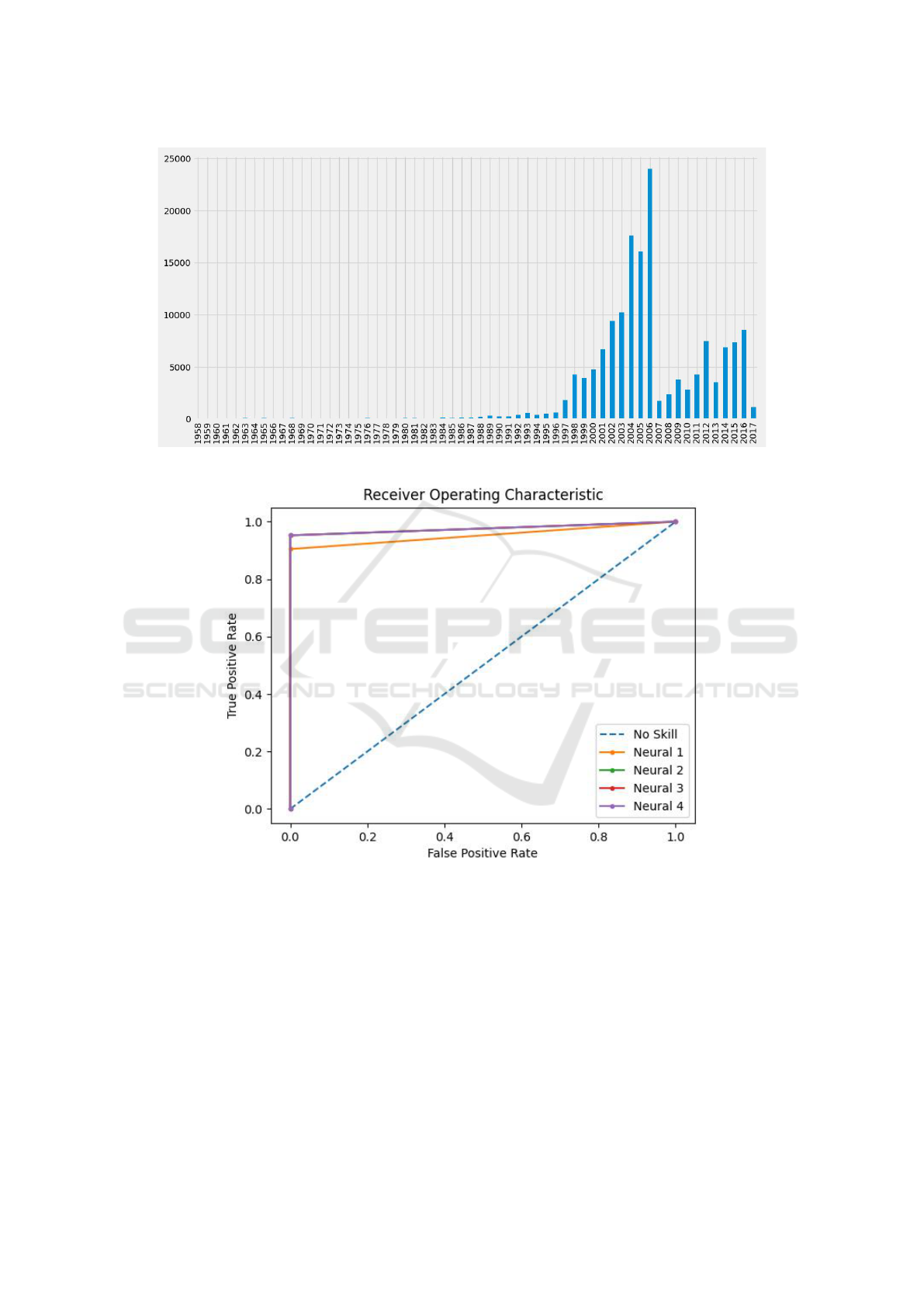
Figure 2: Entries per year.

Figure 3: ROC curves for the FFNN architectures.

r (y) < r (y

′

). Speciﬁcally, the area D under the ROC

curve yields this probability. This yields (14).

△

= prob



r (y) < r



′



y < y

′



(14)

In ﬁgure 3 the ROC curves for the four FFNN

architectures is shown. With the exception of NN1,

the remaining three architectures achieve comparable

performance. This can be explained by the fact that

NN2, NN3, and NN4 have more processing neurons

than NN1, allowing thus the discovery of more graph

structural patterns, especially those of higher order as

graphs are inherently distributed by nature and infor-

mation is typically not found in a single vertex but

instead it is locally spread.

5 CONCLUSIONS

This conference paper focuses on inteligent agent

(IA) design utilizing machine learning (ML) tech-

niques for link prediction. The benchmark dataset is

a graph containing collaborations between scientists.

Intelligent Agents with Graph Mining for Link Prediction over Neo4j

509

Therefore, in this setting link prediction can discover

and recommend potential co-authors, enhancing thus

research. The proposed IA uses an array of ML strate-

gies including random forest, decision tree, logistic

regression, and neural networks. These were trained

with graph structural attributes describing the poten-

tial of a pair of vertices to attract new neighbors as the

higher this potential is, the more probable the vertex

pair under consideration is to be connected. These

attributes include preferential attachment, Adamic-

Adar index, and resource allocation metric.

This work can be extended in a number of ways.

First and foremost, the IA can be tested in larger

graphs which have a greater variety of structural pat-

terns. Moreover, more ML algorithms can be applied

to the same local attributes. Alternatively, the entire

graph can be used in ML algorithms natively support-

ing two-dimensional data such as matrices and images

in order to address the link prediction problelm using

local and global patterns.

ACKNOWLEDGEMENTS

This work is part of Project 451, a long term re-

search initiative with a primary objective of devel-

oping novel, scalable, numerically stable, and inter-

pretable higher order analytics.

REFERENCES

Bedre, J. S. and Prasanna, P. (2022). A novel facial emotion

recognition scheme based on graph mining. In ICSCN,

pages 843–853. Springer.

Chen, M., Li, P., Wang, R., Xiang, Y., Huang, Z., Yu, Q.,

He, M., Liu, J., Wang, J., Su, M., et al. (2022). Multi-

functional ﬁber-enabled intelligent health agents. Ad-

vanced Materials, 34(52).

Chiatti, A., Bardaro, G., Motta, E., and Daga, E. (2022).

A spatial reasoning framework for commonsense rea-

soning in visually intelligent agents. In AIC. CEUR.

Dai, G., Zhu, Z., Fu, T., Wei, C., Wang, B., Li, X., Xie, Y.,

Yang, H., and Wang, Y. (2022). Dimmining: Pruning-

efﬁcient and parallel graph mining on near-memory-

computing. In Annual International Symposium on

Computer Architecture, pages 130–145.

Dong, Y., Ma, J., Wang, S., Chen, C., and Li, J. (2023).

Fairness in graph mining: A survey. IEEE Transac-

tions on Knowledge and Data Engineering.

Drakopoulos, G., Giannoukou, I., Mylonas, P., and Sioutas,

S. (2020a). A graph neural network for assessing the

affective coherence of Twitter graphs. In IEEE Big

Data, pages 3618–3627. IEEE.

Drakopoulos, G., Giannoukou, I., Sioutas, S., and Mylonas,

P. (2022). Self organizing maps for cultural content

delivery. NCAA.

Drakopoulos, G., Giotopoulos, K. C., Giannoukou, I., and

Sioutas, S. (2020b). Unsupervised discovery of se-

mantically aware communities with tensor Kruskal

decomposition: A case study in Twitter. In SMAP.

IEEE.

Drakopoulos, G. and Kafeza, E. (2020). One dimen-

sional cross-correlation methods for deterministic and

stochastic graph signals with a Twitter application in

Julia. In SEEDA-CECNSM. IEEE.

Drakopoulos, G., Kafeza, E., Mylonas, P., and Al Katheeri,

H. (2020c). Building trusted startup teams from

LinkedIn attributes: A higher order probabilistic anal-

ysis. In ICTAI, pages 867–874. IEEE.

Drakopoulos, G., Kafeza, E., Mylonas, P., and Iliadis, L.

(2021a). Transform-based graph topology similarity

metrics. NCAA, 33(23):16363–16375.

Drakopoulos, G., Kafeza, E., Mylonas, P., and Sioutas, S.

(2021b). A graph neural network for fuzzy Twitter

graphs. In Cong, G. and Ramanath, M., editors, CIKM

companion volume, volume 3052. CEUR-WS.org.

Drakopoulos, G., Kafeza, E., Mylonas, P., and Sioutas, S.

(2021c). Approximate high dimensional graph mining

with matrix polar factorization: A Twitter application.

In IEEE Big Data, pages 4441–4449. IEEE.

Drakopoulos, G., Kanavos, A., Tsolis, D., Mylonas, P., and

Sioutas, S. (2017). Towards a framework for tensor

ontologies over Neo4j: Representations and opera-

tions. In IISA. IEEE.

Drakopoulos, G. and Mylonas, P. (2022). A genetic algo-

rithm for Boolean semiring matrix factorization with

applications to graph mining. In Big Data. IEEE.

Elshan, E., Zierau, N., Engel, C., Janson, A., and Leimeis-

ter, J. M. (2022). Understanding the design elements

affecting user acceptance of intelligent agents: Past,

present and future. Information Systems Frontiers,

pages 1–32.

Gao, Z., Gama, F., and Ribeiro, A. (2022). Wide and deep

graph neural network with distributed online learning.

IEEE Transactions on Signal Processing, 70:3862–

3877.

Giraldo, J. H., Mahmood, A., Garcia-Garcia, B., Thanou,

D., and Bouwmans, T. (2022). Reconstruction of

time-varying graph signals via Sobolev smoothness.

IEEE Transactions on Signal and Information Pro-

cessing over Networks, 8:201–214.

Kaswan, K. S., Dhatterwal, J. S., and Balyan, A. (2022). In-

telligent agents based integration of machine learning

and case base reasoning system. In ICACITE, pages

1477–1481. IEEE.

Li, P., Shlezinger, N., Zhang, H., Wang, B., and Eldar, Y. C.

(2022a). Graph signal compression by joint quanti-

zation and sampling. IEEE Transactions on Signal

Processing.

Li, T., Zhou, Z., Li, S., Sun, C., Yan, R., and Chen, X.

(2022b). The emerging graph neural networks for in-

telligent fault diagnostics and prognostics: A guide-

line and a benchmark study. Mechanical Systems and

Signal Processing, 168.

WEBIST 2023 - 19th International Conference on Web Information Systems and Technologies

510

Lin, B., Cassee, N., Serebrenik, A., Bavota, G., Novielli, N.,

and Lanza, M. (2022). Opinion mining for software

development: A systematic literature review. TOSEM,

31(3):1–41.

Liu, J., Li, D., Gu, H., Lu, T., Zhang, P., Shang, L., and

Gu, N. (2023). Personalized graph signal processing

for collaborative ﬁltering. In Web Conference, pages

1264–1272. ACM.

Moussawi, S., Koufaris, M., and Benbunan-Fich, R. (2023).

The role of user perceptions of intelligence, anthropo-

morphism, and self-extension on continuance of use

of personal intelligent agents. European Journal of

Information Systems, 32(3):601–622.

Narumi, T. et al. (2022). Effect of attractive appearance

of intelligent agents on acceptance of uncertain in-

formation. In International Conference on Human-

Computer Interaction, pages 146–161. Springer.

Neﬂa, O., Brigui, I., Ozturk, M., and Viappiani, P. (2022).

Intelligent agents for multi-user preference elicitation.

In Advances in Deep Learning, Artiﬁcial Intelligence

and Robotics, pages 151–161. Springer.

Ortega, A. (2022). Introduction to graph signal processing.

Cambridge University Press.

Pirsa, S., Sani, I. K., and Mirtalebi, S. S. (2022). Nano-

biocomposite based color sensors: Investigation of

structure, function, and applications in intelligent food

packaging. Food Packaging and Shelf Life, 31.

Riedl, M. O. (2019). Human-centered artiﬁcial intelligence

and machine learning. Human behavior and emerging

technologies, 1(1):33–36.

Ruiz, L., Chamon, L. F., and Ribeiro, A. (2023). Trans-

ferability properties of graph neural networks. IEEE

Transactions on Signal Processing.

Shang, P., Liu, X., Yu, C., Yan, G., Xiang, Q., and Mi, X.

(2022). A new ensemble deep graph reinforcement

learning network for spatio-temporal trafﬁc volume

forecasting in a freeway network. Digital Signal Pro-

cessing, 123.

Shi, J. and Moura, J. M. (2022). Graph signal processing:

Dualizing GSP sampling in the vertex and spectral do-

mains. IEEE Transactions on Signal Processing.

Singh, M. (2022). Using natural language processing and

graph mining to explore inter-related requirements in

software artefacts. ACM SIGSOFT Software Engi-

neering Notes, 44(1):37–42.

Yoon, M., Gervet, T., Hooi, B., and Faloutsos, C. (2022).

Autonomous graph mining algorithm search with best

performance trade-off. Knowledge and Information

Systems, pages 1–32.

Zhao, X., Yao, J., Deng, W., Ding, P., Zhuang, J., and Liu,

Z. (2022). Multiscale deep graph convolutional net-

works for intelligent fault diagnosis of rotor-bearing

system under ﬂuctuating working conditions. IEEE

Transactions on Industrial Informatics, 19(1):166–

176.

Intelligent Agents with Graph Mining for Link Prediction over Neo4j

511