Differential Evolution Algorithm Based Hyper-Parameters Selection of

Convolutional Neural Network for Speech Command Recognition

Sandipan Dhar

1 a

, Anuvab Sen

2 b

, Aritra Bandyopadhyay

3 c

, Nanda Dulal Jana

1 d

Arjun Ghosh

1 e

and Zahra Sarayloo

4 f

Computer Science and Engineering, National Institute of Technology, Durgapur, West Bengal, India

Electronics and Telecommunication, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, India

Computer Science and Technology, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, India

School of Computer Science, University of Waterloo, Ontario, Canada

Keywords:

Differential Evolution Algorithm, Genetic Algorithm, Convolutional Neural Network, Hyper-parameters

Selection, Meta-heuristics, Speech Command Recognition, Deep Learning.

Abstract:

Speech Command Recognition (SCR), which deals with identiﬁcation of short uttered speech commands, is

crucial for various applications, including IoT devices and assistive technology. Despite the promise shown

by Convolutional Neural Networks (CNNs) in SCR tasks, their efﬁcacy relies heavily on hyperparameter

selection, which is typically laborious and time-consuming when done manually. This paper introduces a

hyperparameter selection method for CNNs based on the Differential Evolution (DE) algorithm, aiming to

enhance performance in SCR tasks. Training and testing with the Google Speech Command (GSC) dataset, the

proposed approach showed effectiveness in classifying speech commands. Moreover, a comparative analysis

with Genetic Algorithm-based selections and other deep CNN (DCNN) models highlighted the efﬁciency of

the proposed DE algorithm in hyperparameter selection for CNNs in SCR tasks.

1 INTRODUCTION

Speech Command Recognition (SCR) is a subﬁeld

of Automatic Speech Recognition (ASR) focused

on converting short spoken words into text (Pa-

tra et al., 2023). It’s widely used in Internet of

Things (IoT)-based smart home assistants, command-

controlled wheelchairs for blind and disabled people,

and AI-driven vehicles (Nanavati et al., 2021). Early

SCR systems primarily used Hidden Markov Mod-

els (HMMs) (Naithani et al., 2018), Gaussian Mixture

Models (GMMs) (Saravanan et al., 2020), and Multi-

Layered Perceptron models (MLPs) (Ahad et al.,

2002). Later, Recurrent Neural Networks (RNNs)

(Paul and Paul, 2021) and Long Short-Term Memory

networks (LSTMs) (Oruh et al., 2022) yielded signif-

https://orcid.org/0000-0002-3606-6664

https://orcid.org/0009-0001-8688-8287

https://orcid.org/0009-0003-5582-2431

https://orcid.org/0000-0003-0631-9912

https://orcid.org/0000-0003-1086-944X

https://orcid.org/0000-0001-9918-3625

icant improvements. However, Convolutional Neural

Networks (CNNs), effective in handling 2D data de-

pendencies, emerged as superior alternatives (Nana-

vati et al., 2021). Various input features have been

considered while dealing with SCR tasks, like using a

Depth-Wise Separable CNN (DS-CNN) for keyword

recognition with mel-frequency spectral coefﬁcients

(MFSS) as input feature (Sørensen et al., 2020), us-

ing mel-frequency cepstral coefﬁcients (MFCC) as in-

put for deploying a CNN for wheelchair control using

speech commands (Bakouri et al., 2022), smoothed-

spectrogram, mel-spectrogram, and cochleagram as

input features for CNN-based voice command detec-

tion (Sharan and Moir, 2018). Kubanek et al. pro-

posed a new approach where MFCC, time and spec-

trum are combined to be used as speech features for

the recognition of speech commands using DCNN

model (Kubanek et al., 2019). However, the perfor-

mance of all these CNNs is highly dependent on se-

lection of several crucial hyper-parameters.

CNN models have hyper-parameters like number

and type of convolution layers, ﬁlter count and size,

Dhar, S., Sen, A., Bandyopadhyay, A., Jana, N., Ghosh, A. and Sarayloo, Z.

Differential Evolution Algorithm Based Hyper-Parameters Selection of Convolutional Neural Network for Speech Command Recognition.

DOI: 10.5220/0012251500003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 315-322

ISBN: 978-989-758-674-3; ISSN: 2184-3236

315

pooling type, and activation function, which signif-

icantly inﬂuence performance in classiﬁcation tasks,

including SCR. Typically, hyper-parameters are man-

ually selected based on experience, a process that is

both time-consuming and tedious. Therefore, it be-

comes difﬁcult to obtain the optimal conﬁguration

of a CNN model within a reasonable cost (Elsken

et al., 2019; Liu et al., 2021; Ghosh et al., 2022;

Ghosh and Jana, 2022). The paper employs the Dif-

ferential Evolution (DE) algorithm (Das and Sugan-

than, 2011) (Sen et al., 2023c) (Sen et al., 2023b)

(Mazumder et al., 2023) (Sen et al., 2023a) to opti-

mize CNN hyper-parameters for SCR tasks. Each in-

dividual in the DE algorithm represents a viable CNN

architecture, with optimal hyper-parameters deter-

mined through standard DE operations like mutation,

crossover, and selection. Spectrograms are used as in-

put speech features for the CNN model. The dataset

considered in this work is the Google Speech Com-

mand (GSC) dataset (Warden, 2018). The proposed

DE algorithm-based hyper-parameters selection ap-

proach is compared with the Genetic Algorithm (GA)

(Katoch et al., 2021) based hyper-parameter selection,

as well as with state-of-the-art deep CNN (DCNN)

models namely ResNet-50, Inception-V3, Xception,

VGG-16 and VGG-19 for SCR task. The work main-

tains a consistent basic CNN architecture (with a ﬁxed

number of convolution, pooling, and fully connected

layers) for both DE and GA approaches while imple-

menting automatic hyper-parameter selection. Exper-

imental results demonstrate that the proposed method

outperforms others, achieving higher accuracy.

Rest of the paper is organized as follows. Sec-

tions 2 and 3 provide detailed overviews of the re-

lated work and preliminaries respectively. Section 4

includes the details of the dataset, training details and

experimental setups. In Section 5, the proposed ap-

proach is brieﬂy discussed. In Section 6, experimental

results are presented and discussed. Finally, Section 7

concludes the paper and provides some aspects of the

future research.

2 RELATED WORK

Hyperparameter optimization is a critical research

area for achieving high-performance deep learning

models. Techniques like Random Search, Grid

Search, Bayesian Optimization (Masum et al., 2021),

and Gradient-based Optimization (Maclaurin et al.,

2015) are used to ﬁnd optimal hyperparameter con-

ﬁgurations. Each method offers trade-offs in the

computational efﬁciency, exploration of search space,

and exploitation of discerned solutions. Genetic Al-

gorithms were ﬁrst utilized for modifying Convolu-

tional Neural Network architectures in late 1900’s,

subsequently instigating a gamut of applications in-

volving various nature-inspired algorithms in the do-

main of deep learning models. While many works

compare evolutionary algorithms on computational

models, no previous study comprehensively has ap-

plied evolutionary algorithms: Genetic Algorithm,

Differential Evolution, across Convolutional Neural

Networks architecture for isolated speech command

recognition. These algorithms stand out due to their

iterative population-based approaches, stochastic and

global search implementation, and versatility in op-

timizing various problems. In this context, this paper

aims to bridge the gap by conducting a comprehensive

exploration of the application of nature-inspired and

evolutionary algorithms, like Differential Evolution,

in optimizing DCNN architectures for SCR. By delv-

ing into the intricacies of how these algorithms inter-

act with lightweight CNN structures and comparing

the performance in SCR with that of DCNN models,

namely, VGG-16, VGG-19, Resnet-50, InceptionV3,

Xception, this study aims to uncover a clearer under-

standing of their advantages and the limitations for

the various other speech related tasks.

3 PRELIMINARIES

3.1 Differential Evolution (DE)

DE is a population-based optimization algorithm de-

signed for non-linear, multi-modal optimization prob-

lems (Das and Suganthan, 2011). It iteratively re-

ﬁnes a population of candidate solutions (individu-

als) through mutation, crossover, and selection opera-

tors, enhancing the individuals based on existing ones

within the population. In order to apply DE, ﬁrst a

population size of N individuals is created, and each

individual is represented by a d-dimensional vector x

(where i implies the i

individual). Thereafter, the

population is randomly initialized within the search

space. At each iteration, a new population with N

individuals are generated by applying the following

mutation, crossover and selection operators.

Mutation: In mutation operation, distinct individuals

from the population are selected. A widely used mu-

tation scheme is DE/rand/1, where three distinct in-

dividuals from the population are randomly selected.

Then, a mutant vector (also called donor vector) v

created as shown in Eq. (1),

= x

+ F ×



− x



. (1)

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

316

In Eq. (1), x

, x

, and x

are three distinct individ-

uals (here, g indicates generation). Whereas, r

, r

and r

means randomly selected indices, and F is the

scaling factor that controls the magnitude of the mu-

tation.

Crossover: In crossover operation, a trial vector u

is generated by combining the donor vector v

and

the original vector x

using crossover operation. The

crossover operation (binomial crossover) is explained

in details as follows,

j,i

(

j,i

i f j

rand

(0,1) ≤ CR or j = δ

j,i

Otherwise.

(2)

In this context, u

j,i

represents the j

dimension of

the i

individual at the g

generation. The crossover

rate is denoted by CR, and rand(0, 1) represents a ran-

domly generated number between 0 and 1. Addition-

ally, δ refers to a random dimension d selected from

the range (1,d) of u

Selection: In selection operation, the trial vector u

is compared with the original vector x

. If the ﬁtness

of u

is superior than x

, then replacement of x

with

is carried out in the next generation. Otherwise, x

is kept unchanged. The above three steps are repeated

until a stopping criterion is met (the stopping criterion

varies from problem to problem).

4 EXPERIMENTAL DETAILS

4.1 Dataset Description

The proposed DE-based hyper-parameters selection

approach is trained and tested on google speech com-

mand (GSC) dataset (Warden, 2018). In this work 8

speech commands from GSC dataset are considered

namely “down”, “go”, “left”, “no”, “right”, “stop”,

“up”, “yes”. Here, total 8000 speech samples are

considered by taking 1000 samples belonging to each

speech commands. The dataset is split into train-

ing, validation and test set. In this work, the model

is trained with 6400 training samples and 1000 vali-

dation samples. After the completion of training the

trained model is tested with 600 test samples. The

time span of each audio sample considered is of 1 sec-

ond or less and the sampling rate is 16kHz.

4.2 Experimental Setups

The experiments of this work are implemented in

Python 3.10.11 using three libraries as Tensorﬂow

2.11.0, Tensorﬂow built in Keras, and Numpy 1.22.

The audible speech data samples are preprocessed us-

ing Librosa 0.10.0. The experiments were performed

in a Google Colaboratory environment using A100

GPU.

5 PROPOSED APPROACH

This section explicitly describes the proposed DE

algorithm-based hyper-parameter selection of CNN

model for speech command recognition task. In the

pre-processing phase, each speech sample is con-

verted into mel-spectrogram (Akhter et al., 2022) of

shape 124 × 129, in order to make the input data com-

patible to work with 2D CNN. First, an overall frame-

work of the proposed method is presented followed by

the main components of the method. These include

encoding scheme, population initialization, ﬁtness

evaluation, mutation, crossover, and selection oper-

ation of DE, concerning the optimal hyper-parameter

selection for the CNN model.

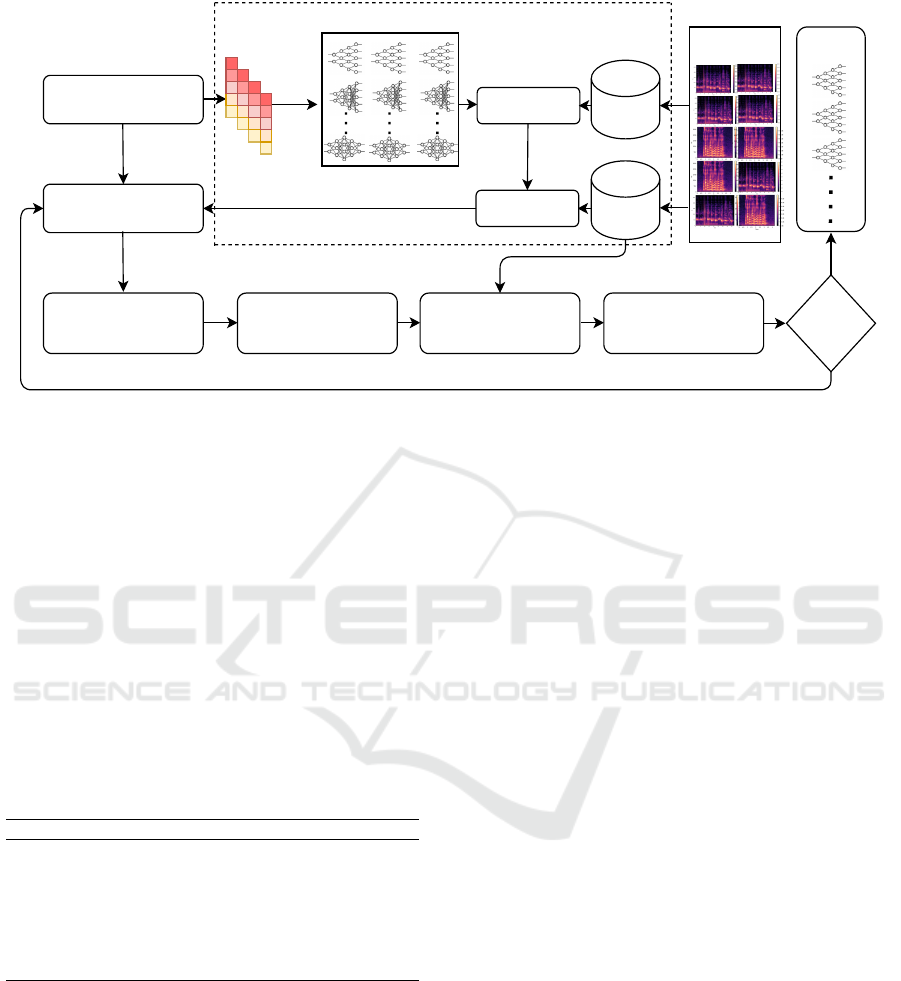
5.1 The Overall Framework

The overall framework of the proposed approach is

depicted in Fig. 1. The DE algorithm starts with a

population of N individuals, each representing a CNN

architecture which is trained on the training dataset

train

) and evaluated for ﬁtness on the validation

dataset (D

valid

) in terms of model accuracy. The asso-

ciated hyper-parameters of CNN models are evolved

through mutation and crossover operations of DE.

These processes are repeated with a maximum num-

ber of generations. The optimal hyper-parameters of

CNN architecture are selected from the best individ-

ual based on their ﬁtness value and tested on the test

dataset to determine the model’s ﬁnal performance.

5.2 Encoding Scheme

Designing an appropriate encoding process is a difﬁ-

cult task in any algorithm, as it determines how each

individual is represented as a CNN structure. To ad-

dress this, a standard layer-based encoding scheme is

proposed in this work. This adopts the widely popu-

lar VGG-16 CNN model design (Simonyan and Zis-

serman, 2014). The VGG-16 model is composed of

three types of layers - convolution, pooling, and fully

connected (FC) arranged sequentially. Each individ-

ual’s length is ﬁxed with a total of 16 layers, follow-

ing VGG-16 model. The hyper-parameters for each

layer are determined based on pre-deﬁned ranges for

the purpose of designing and training a CNN model.

Differential Evolution Algorithm Based Hyper-Parameters Selection of Convolutional Neural Network for Speech Command Recognition

317

Population Initialization

Population

Model Training

Fitness Evaluation

Training

Data

Validation

Data

Model

Performance

Dataset

Generate Donor

Vector Using

DE/best/1 Mutation

Trial Vector Generation

using Binomial Crossover

Fitness Evaluation

Selection for Next

Generation

Terminate?

Best

Individuals

Yes

Decoding

Figure 1: The working mechanism of the DE algorithm based hyper-parameters selection approach for the SCR task.

5.3 Population Initialization

The population in this context refers to the collec-

tion of individuals that are initially spread through-

out the search space. The population is denoted

as P, consists of N individuals represented as P =

,..., x

}. Every individual is regarded as a

CNN model architecture with a ﬁxed length similar to

the VGG-16 model architecture. In addition, the cor-

responding hyper-parameters of the CNN model are

initialized randomly within a set of pre-deﬁned ranges

deﬁned in Table 1.

Table 1: Hyper-parameters and their ranges considered in

the proposed work.

Hyper-parameters Hyper-parameters range

Convolution ﬁlter size {3×3, 5×5}

Number of ﬁlters {16, 32, 64, 128, 256, 512}

Activation function {‘ReLU’, ‘SELU’, ‘ELU’}

Optimization function {‘SGD’, ‘Adam’, ‘Adagrad’,

‘Adamax’}

Drop-out rate {0.1, 0.2, 0.3, 0.4, 0.5}

Number of neurons {128, 256, 512}

A layer-based approach is used to conﬁgure the

hyper-parameter of each layer type, including convo-

lution ﬁlter size, number of ﬁlters, activation function,

optimizer, drop-out value and number of neurons in

FC layers. In this work, the hyper-parameters of the

pooling layer are considered as same as the VGG-16

model. Fig.2 shows an example of a genotype along

with its corresponding phenotype.

5.4 Fitness Evaluation

In the proposed method, each individual in the popu-

lation is evaluated based on their ﬁtness. To calculate

the ﬁtness, every individual in the population P trans-

forms itself into a CNN architecture and trains it with

the training dataset D

train

. The trained model is then

evaluated on the validation dataset D

valid

using sparse

categorical cross-entropy (Dan et al., 2022) as the ﬁt-

ness function due to its excellent performance in the

SCR tasks.

5.5 Mutation

In DE, a mutant or donor vector is obtained by ap-

plying different mutant operations to the original vec-

tor of the current generation. In this study, the

DE/rand/1 mutation scheme is used for simplicity

and greater diversity in the hyper-parameters of CNN

architecture at each generation. During the muta-

tion phase, as described in Eq. (1), a basic differ-

ence calculation is employed to compare the hyper-

parameters of the chosen CNN model. In the pro-

posed approach, two individuals (x

̸= x

) are se-

lected randomly from the population P which are dif-

ferent from the original vector x

. Then, the difference

-x

) is calculated based on the hyper-parameter

values for each layer of CNN. After performing the

difference calculation, the range of hyper-parameters

for each layer is checked by boundary checking to

ensure that they fall within speciﬁed limits. Next,

the proposed approach selects another random indi-

vidual, denoted as x

and performs the computation

with (x

-x

) to generate a donor vector (also called

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

318

NOF

ACT

OPT

NON

index

index index

index

(a) Genotype

INPUT

OUTPUT

Convolution Layer Pooling Layer Fully-Connected Layer

NOF

ACT

OPT

NON

index

index index

index

index index

(b) Phenotype

Figure 2: An example of genotype with its phenotype. The acronym used in genotype is: FS (Convolution Filter Size),

NOF (Number of Filters), ACT (Activation function), OPT (Optimization function), DP (Drop-out rate), NON (Number of

Neurons).

a mutant vector) v

based on a scaling factor F. For

this purpose, a random number r[0,1] is generated for

each dimension of x

. If r ≤ F, the proposed method

chooses a layer from x

Otherwise, it selects a layer from (x

-x

). Eq.

(3) speciﬁes the mutation operation, where v

j,i

rep-

resents the j

dimension of the i

individual in the

population P.

j,i

(

j,r

i f r ≤ F

j,r

-x

j,r

| Otherwise

(3)

Since we cannot calculate (x

-x

) for activa-

tion functions, as there is no deﬁned “difference” be-

tween them, we follow an encoding and rounding off

strategy, encoding the activation functions with inte-

gers and then performing rounding off and boundary

checking while decoding.

5.6 Crossover

To boost population diversity, a crossover operation

follows the mutation operation in DE, exchanging

components between the donor vector v

j,i

and target

vector x

j,i

to form a new trial vector u

. Binomial

crossover is employed, with the trial vector forma-

tion guided by crossover rate CR and a random num-

ber δ. We deﬁnes δ value randomly one of the j

component of v

. Another random number j

rand

(0,1)

is assigned for each dimension ( j) of u

that has the

same length of v

. If the randomly generated number

rand

(0,1) is less than or equal to the crossover rate

CR, or if j is equal to δ, then the j

value from the

donor vector v

is selected. Otherwise, the j

value is

taken from the target vector x

The proposed crossover operation is mathemati-

cally represented in Eq. (4), where trial vector u

j,i

represents the j

dimension of the i

individual for

the target vector x

j,i



j,i

if j

rand

(0,1) ≤ CR or j = δ

j,i

Otherwise

(4)

5.7 Selection

The selection stage chooses either the target vector x

or trial vector u

for the next generation based on their

ﬁtness values f, ensuring a constant population size

across generations for stability. Each x

in the popu-

lation P is evaluated for its ﬁtness, denoted as f (x

using the ﬁtness function. Also, the ﬁtness of gener-

ated u

is calculated using the same ﬁtness function

as for each x

and represented as f (u

). For the sub-

sequent generation, i.e., (g + 1), the individual with

higher ﬁtness value is selected. Eq. (5) mathemati-

cally presents the proposed selection strategy used in

our proposed work.

g+1

(

i f f (x

) ≤ f (u

)

Otherwise

(5)

A pseudocode implementation of the proposed

Differential Evolution Algorithm is as follows:

6 RESULTS AND DISCUSSION

The parameters setting of the proposed work is based

on the literature review of the conventional DE (Das

and Suganthan, 2011) and deep learning (DL) (Guo

et al., 2016) implementations along with our limited

computational resources. The population size and

maximum generation are ﬁxed at 10 throughout the

proposed algorithm

. DE scaling factor is ﬁxed at 0.6.

Furthermore, to train the generated CNN models, we

have used Xavier weight initialization (Chang et al.,

2020) with the learning rate 0.001 due to its effective

utilization in the domain of DL. To enhance the train-

ing speed, we have incorporated batch normalization

(BN) (Ioffe and Szegedy, 2015) with a batch size of

32, along with a 25% dropout rate. The ﬁtness cal-

culation is conducted for each epoch throughout the

evaluation procedure. The ﬁnal CNN model archi-

Code implementation of the proposed work

is available at: https://github.com/Techie5879/

Hyperparameter-Optimization-CNN-Differential-Evolution

Differential Evolution Algorithm Based Hyper-Parameters Selection of Convolutional Neural Network for Speech Command Recognition

319

Algorithm: Differential Evolution.

Input : Population Size N = 15, Dimension

D, Scale Factor F, Crossover

Probability CR, Termination

Criterion

Output: Best individual

1 Initialize the population with N random

individuals in the search space;

2 while Termination Criterion is not met do

3 for each individual x

in the population

4 Select three distinct individuals x

, and x

from the population;

5 Generate a trial vector v

by mutating

, x

, and x

using the differential

weight F;

= x

+ F × (x

− x

) (6)

6 Perform crossover between x

and v

to produce a trial individual u

with

the crossover probability CR;

j,i



j,i

, if p

rand

(0,1) ≤ CR

j,i

else



(7)

7 if the ﬁtness of u

is better than the

ﬁtness of x

then

8 Replace x

with u

in the

population;

9 end

10 end

11 end

12 return the best individual in the ﬁnal

population;

tecture obtained from this proposed method is tested

using the test dataset to evaluate its performance.

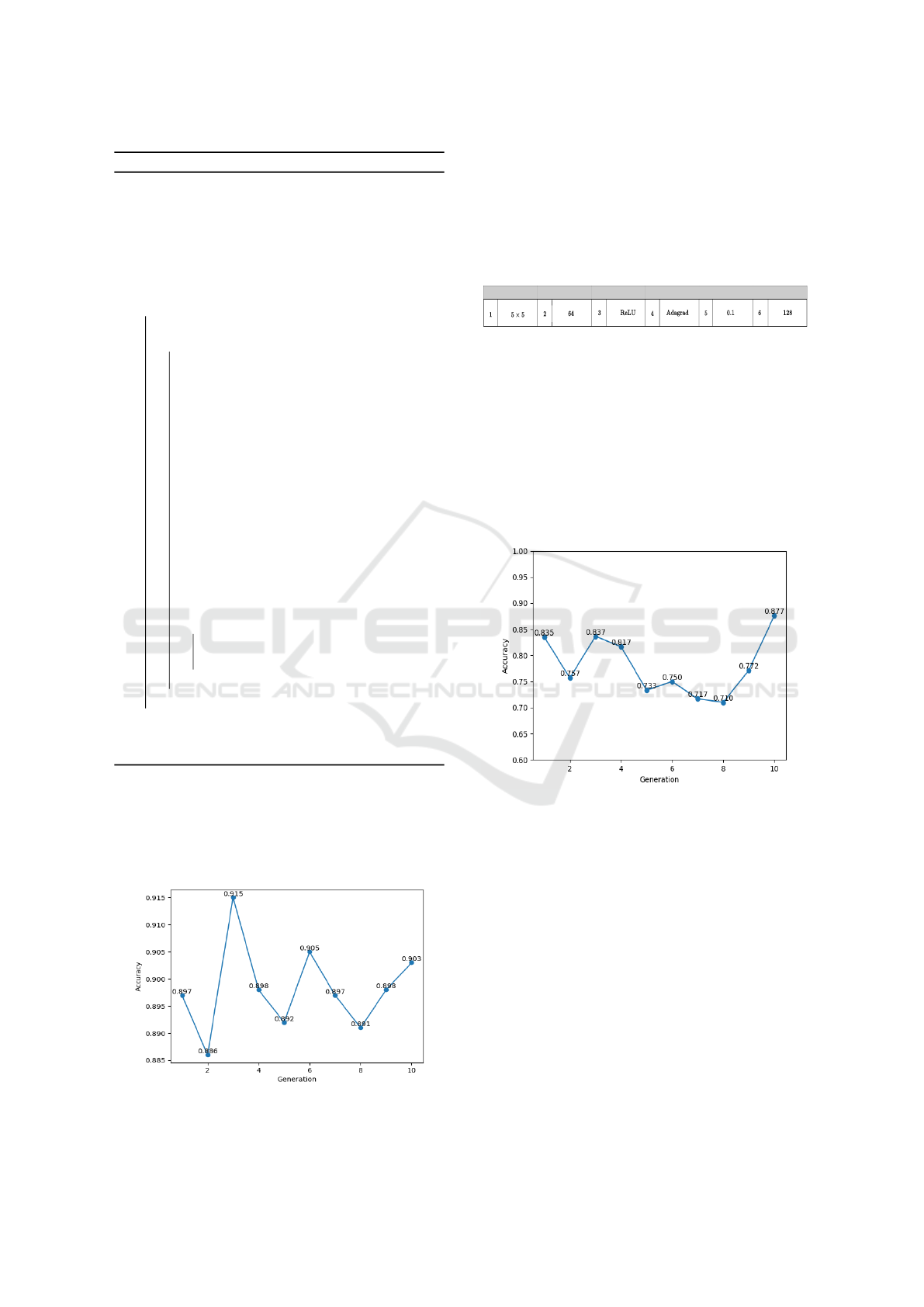
In Fig.3, the generation wise performance for

the best networks of the proposed DE-based hyper-

parameters selection approach are shown. The best

Figure 3: Generation wise accuracy plot for the proposed

DE-based hyper-parameters selection approach.

networks for each generation indicate the best selec-

tion of hyper parameters belonging to the respective

CNN networks. As shown in Fig.3, the highest test

accuracy obtained is 0.915 (i.e. 91.5%) for the gener-

ation number 3. In Fig.4, the hyper-parameters for the

CNN model are presented for which the highest accu-

racy is obtained. The proposed approach is also com-

NOF

ACT

OPT

NON

index

index index

index

Figure 4: Hyper-parameters of the best CNN model

(in terms of accuracy) obtained using DE-based hyper-

parameters selection approach.

pared with the GA-based hyper-parameter selection

approach. In GA based approach, each chromosome

is selected in each generation from the population size

15. The generation-wise accuracy plot for the GA-

based hyper-parameters selection approach is shown

in Fig.5. From Fig.5, it can be observed that the high-

est accuracy obtained is 0.877 (i.e. 87.7%) for the

generation number 10. In Fig.6, the hyper-parameters

Figure 5: Generation wise accuracy plot for the proposed

GA-based hyper-parameters selection approach.

for the CNN model are presented for which the high-

est accuracy is obtained. However, from both Fig.3

and Fig.5 it can be clearly observed that the perfor-

mance (in terms of accuracy) of the DE-based hyper-

parameter selection approach is better than the GA-

based hyper-parameter selection approach. The per-

formance of both DE and GA approaches are also

compared with ResNet-50, Inception-V3, Xception,

VGG-16, and VGG-19 models for the SCR task con-

sidering the test dataset.

Table 2 presents the average precision, recall, F1-

score, and test accuracy of all models considered,

highlighting the superior performance of the proposed

DE-based CNN model. While the ResNet-50 model

also performs signiﬁcantly better than other consid-

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

320

NOF

ACT

OPT

NON

index

index index

index

Figure 6: Hyper-parameters of the best CNN model

(in terms of accuracy) obtained using GA-based hyper-

parameters selection approach.

ered DCNN models, it is outshined by the proposed

model.

Table 2: Precision, Recall, F1-Score and Accuracy for all

the considered models (averaged over 10 runs).

Models Precision Recall F1-Sore Accuracy

ResNet-50 0.917 0.907 0.908 0.908

InceptionV3 0.892 0.887 0.884 0.886

Xception 0.804 0.802 0.802 0.808

VGG-16 0.828 0.820 0.819 0.823

VGG-19 0.798 0.789 0.789 0.795

GA-best 0.875 0.786 0.871 0.877

DE-best 0.916 0.914 0.913 0.915

However, from Table 2 it is clearly observed that

the accuracy of the CNN model obtained from the

proposed approach is higher than ResNet-50 model

for the SCR task. Fig.7 shows the confusion ma-

trix obtained from evaluating the model’s class wise

prediction accuracy for the DE approach on the test

dataset. From Fig.7, it can be concluded that the

Figure 7: Confusion matrix of the best model obtained from

the proposed approach.

CNN model obtained from the proposed approach has

shown signiﬁcant performance (in terms of accuracy)

for all the considered classes.

The superior performance of the DE-optimized

CNN model is due to its effective exploration of the

search space, utilizing parameter vector differences

to exploit promising regions for optimal solutions,

unlike genetic algorithms that may converge to lo-

cal minima. The mutation operator prevents early

convergence through random perturbations, while the

crossover operator accelerates convergence by ex-

changing useful features. The selection operator pre-

Table 3: Precision, Recall, F1-Score and Accuracy for all

the considered GSC Dataset Speech Commands.

Commands Precision Recall F1-Sore

left 0.871 0.971 0.918

down 0.952 0.821 0.882

stop 0.942 0.928 0.935

up 0.970 0.857 0.910

yes 0.965 0.988 0.976

right 0.938 0.987 0.962

go 0.831 0.862 0.846

no 0.859 0.897 0.877

serves the ﬁttest individuals, enhancing the quality of

solutions. Therefore, in Table 3 the class wise pre-

cision, recall, F1-score are also provided to show the

performance of the obtained CNN model for all the

considered speech commands of the GSC dataset.

7 CONCLUSION

This paper proposes an efﬁcient Differential Evolu-

tion (DE)-based approach for selecting CNN hyper-

parameters automatically, aiming to enhance Speech

Command Recognition (SCR) tasks. Unlike tedious

manual selection, DE, a global optimization algo-

rithm, avoids local optima entrapments common in

Grid Search, promoting more efﬁcient promoting

more efﬁcient global optimum identiﬁcation. Fur-

thermore, evolutionary algorithms like DE inherently

minimize user bias - when hyper-parameters are man-

ually selected, they are often inﬂuenced by an individ-

ual’s past experiences or preconceived notions, which

can skew the optimization process. The proposed

DE-based hyper-parameter selection approach out-

performed the GA-based approach and other consid-

ered DCNN models in SCR tasks. The improved per-

formance is attributed to DE’s superior search space

navigation and global maxima identiﬁcation abilities.

Unlike GA, DE requires fewer control parameters and

has demonstrated robustness across various optimiza-

tion problems. Additionally, the proposed approach

surpassed other DCNN models. Future work may

extend this approach to evolutionary algorithm-based

speech feature selection for diverse speech-based ap-

plications.

Differential Evolution Algorithm Based Hyper-Parameters Selection of Convolutional Neural Network for Speech Command Recognition

321

REFERENCES

Ahad, A., Fayyaz, A., and Mehmood, T. (2002). Speech

recognition using multilayer perceptron. In IEEE

Students Conference, ISCON ’02. Proceedings., vol-

ume 1, pages 103–109 vol.1.

Akhter, M. T., Banerjee, P., Dhar, S., and Jana, N. D.

(2022). An analysis of performance evaluation met-

rics for voice conversion models. In 2022 IEEE 19th

India Council International Conference (INDICON),

pages 1–6.

Bakouri, M., Alsehaimi, M., Ismail, H. F., Alshareef, K.,

Ganoun, A., Alqahtani, A., and Alharbi, Y. (2022).

Steering a robotic wheelchair based on voice recog-

nition system using convolutional neural networks.

Electronics, 11(1).

Chang, O., Flokas, L., and Lipson, H. (2020). Principled

weight initialization for hypernetworks. International

Conference on Learning Representations.

Dan, Z., Zhao, Y., Bi, X., Wu, L., and Ji, Q. (2022). Multi-

task transformer with adaptive cross-entropy loss for

multi-dialect speech recognition. Entropy, 24(10).

Das, S. and Suganthan, P. N. (2011). Differential evolution:

A survey of the state-of-the-art. IEEE Transactions on

Evolutionary Computation, 15(1):4–31.

Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural

architecture search: A survey. Journal of Machine

Learning Research, 20(55):1–21.

Ghosh, A. and Jana, N. D. (2022). Artiﬁcial bee colony

optimization based optimal convolutional neural net-

work architecture design. 2022 IEEE 19th India

Council International Conference (INDICON), pages

1–7.

Ghosh, A., Jana, N. D., Mallik, S., and Zhao, Z. (2022).

Designing optimal convolutional neural network ar-

chitecture using differential evolution algorithm. Pat-

terns, 3(9):100567.

Guo, Y., Liu, Y., Oerlemans, A., Lao, S., Wu, S., and Lew,

M. S. (2016). Deep learning for visual understanding:

A review. Neurocomputing, 187:27–48.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. International conference on machine

learning, pages 448–456.

Katoch, S., Chauhan, S. S., and Kumar, V. (2021). A review

on genetic algorithm: past, present, and future. Multi-

media Tools and Applications, 80(5):8091–8126.

Kubanek, M., Bobulski, J., and Kulawik, J. (2019). A

method of speech coding for speech recognition using

a convolutional neural network.

Liu, Y., Sun, Y., Xue, B., Zhang, M., Yen, G. G., and Tan,

K. C. (2021). A survey on evolutionary neural ar-

chitecture search. IEEE Transactions on Neural Net-

works and Learning Systems, pages 1–21.

Maclaurin, D., Duvenaud, D., and Adams, R. P. (2015).

Gradient-based hyperparameter optimization through

reversible learning.

Masum, M., Shahriar, H., Haddad, H., Faruk, M. J., Valero,

M., Khan, M. A., Rahman, M. A., Adnan, M. I., Cuz-

zocrea, A., and Wu, F. (2021). Bayesian hyperpa-

rameter optimization for deep neural network-based

network intrusion detection. 2021 IEEE International

Conference on Big Data (Big Data).

Mazumder, A., Sen, A., and Sen, U. (2023). Bench-

marking metaheuristic-integrated quantum approxi-

mate optimisation algorithm against quantum anneal-

ing for quadratic unconstrained binary optimization

problems.

Naithani, K., Thakkar, V. M., and Semwal, A. (2018).

English language speech recognition using mfcc and

hmm. In 2018 International Conference on Research

in Intelligent and Computing in Engineering (RICE),

pages 1–7.

Nanavati, R., Shah, S., and Joshi, M. (2021). Black box

attack on speech commands classiﬁcation model. In

2021 IEEE International Midwest Symposium on Cir-

cuits and Systems (MWSCAS), pages 109–111.

Oruh, J., Viriri, S., and Adegun, A. (2022). Long short-

term memory recurrent neural network for automatic

speech recognition. IEEE Access, 10:30069–30079.

Patra, A., Pandey, C., Palaniappan, K., and Sethy,

P. K. (2023). Convolutional neural network-enabling

speech command recognition. In Smys, S., Lafata,

P., Palanisamy, R., and Kamel, K. A., editors, Com-

puter Networks and Inventive Communication Tech-

nologies, pages 321–332, Singapore. Springer Nature

Singapore.

Paul, S. K. and Paul, R. R. (2021). Speech command recog-

nition system using deep recurrent neural networks. In

2021 5th International Conference on Electrical Engi-

neering and Information Communication Technology

(ICEEICT), pages 1–6.

Saravanan, P., Sri Ram, E., Jangiti, S., Ponmani, E., Ravi,

L., Subramaniyaswamy, V., Varadarajan, V., Kom-

mers, P., Piuri, V., and Subramaniyaswamy, V. (2020).

Ensemble gaussian mixture model-based special voice

command cognitive computing intelligent system. J.

Intell. Fuzzy Syst., 39(6):8181–8189.

Sen, A., Gupta, V., and Tang, C. (2023a). Differential evo-

lution algorithm based hyperparameter selection of

gated recurrent unit for electrical load forecasting.

Sen, A., Mazumder, A. R., Dutta, D., Sen, U., Syam,

P., and Dhar, S. (2023b). Comparative evaluation

of metaheuristic algorithms for hyperparameter selec-

tion in short-term weather forecasting. arXiv preprint

arXiv:2309.02600.

Sen, A., Mazumder, A. R., and Sen, U. (2023c). Differ-

ential evolution algorithm based hyper-parameters se-

lection of transformer neural network model for load

forecasting. arXiv preprint arXiv:2307.15299.

Sharan, R. V. and Moir, T. J. (2018). Acoustic event

recognition using cochleagram image and convolu-

tional neural networks. Applied Acoustics, 148.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

CoRR, abs/1409.1556.

Sørensen, P. M., Epp, B., and May, T. (2020). A depthwise

separable convolutional neural network for keyword

spotting on an embedded system. EURASIP Journal

on Audio, Speech, and Music Processing, 2020(1):10.

Warden, P. (2018). Speech commands: A dataset

for limited-vocabulary speech recognition. ArXiv,

abs/1804.03209.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

322