LQR Combined with Fuzzy Control for 2-DOF Planar Robot
Trajectories
A. Hernandez-Pineda
1
, I. Bezerra-Viana
1 a
, M. Marques-Simoes
1 b
and F. Bezerra Carvalho
2
1
Programa de P
´
os-Graduac¸
˜
ao em Engenharia El
´
etrica e Computac¸
˜
ao, Universidade Federal do Cear
´
a,
Rua Coronel Estanislau Frota-563, Sobral, Brazil
2
Programa de P
´
os-Graduac¸
˜
ao em Engenharia El
´
etrica e Computac¸
˜
ao, Universidade Federal do Cear
´
a, Sobral, Brazil
fl
Keywords:
Planar Robot Manipulator, LQR, Fuzzy Logic, Trajectory Control.
Abstract:
Some tasks of robotic manipulators are performed using control techniques for trajectory tracking. These tech-
niques ensure that the existing steady-state error between the desired and executed trajectories are close to zero.
This work proposes a hybrid control scheme that enhances a traditional control approach with computational
tuning optimization. The Linear Quadratic Regulator (LQR) controller is implemented by manipulating the
state variables of the plant to be controlled. The optimization of this controller is related to the weighting vari-
ables of the cost function. Computational tuning using fuzzy logic is applied to adjust the weighting variables
of LQR. The results demonstrate that the hybrid control optimal performance outperformed the traditional
LQR controller in the trajectory following task for the two-degree-of-freedom planar robotic manipulator.
1 INTRODUCTION
Robotics was developed with the intention of au-
tomating repetitive, complex, or precise tasks. Indus-
tries with robust processes found in robotics an al-
ternative for hazardous activities, avoiding risks for
their workers. Precision features offered by robotics
are valued in the medical field and in microcompo-
nent production. Operations and tasks like those pre-
viously mentioned are carried out by robots through
high-precision control strategies. Such strategies
are implemented in anthropomorphic manipulators to
correct the error difference between the obtained and
desired trajectories. The precision and stability de-
mands in robot trajectory tracking has led to inno-
vative control methodologies that rely or not on the
robot dynamic model.
In the first group, controllers such as the Com-
puted Torque Controller (CTC) (Garc
´
ıa et al., 2018),
the Sliding Mode Controller (SMC) (Nguyen, 2019),
the Linear Quadratic Regulator (LQR) Controller
(Mahil and Al-Durra, 2016), and the Model Pre-
dictive Controller (Wahrburg and Listmann, 2016)
Are not frequently used in robotic manipulators due
to its highly nonlinear model. In contrast, con-
a
https://orcid.org/0000-0002-0009-8330
b
https://orcid.org/0000-0002-7590-9898
trollers that independ of plant dynamic model, such as
the Proportional-Integral-Derivative (PID) Controller
(Kelly et al., 2005), Fuzzy Logic Controller (Ho et al.,
2007), Kinematic Analyzer via Neural Network (Shah
et al., 2011) and the hybrid controller of computerized
torque with fuzzy logic (Song et al., 2005) Are ro-
bust to the nonlinearity of robotics but most of them
require high computational resources. There are ap-
proaches that have been proposed to address nonlin-
earity in robotic controlling with low computational
resources, as the Robust Computed Torque Controller
(Kardo
ˇ
s, 2019), Robust Controller via Neural Net-
work Compensation (Li et al., 2005), and Computed
Torque Controller with Fuzzy Tuning (Pizarro-Lerma
et al., 2018). This third group comprises hybrid con-
trollers with low computational resources to deter-
mine the uncertainties presented by the nonlinearity
found in robotic systems. Precisely the non-linearity
of these MIMOS (multiple input - multiple output)
systems is the factor that makes the control and func-
tionality of robotic systems complex (Kumar et al.,
2023). In this context, this article proposes a hy-
brid strategy for anthropomorphic manipulators con-
trol based on the optimization, with computational
tuning, of a LQR controller. The latter is imple-
mented through the linearized dynamic model of the
plant, and the performance of this controller is linked
to the feedback matrix, which is calculated using the
Hernandez-Pineda, A., Bezerra-Viana, I., Marques-Simoes, M. and Carvalho Bezerra, F.
LQR Combined with Fuzzy Control for 2-DOF Planar Robot Trajectories.
DOI: 10.5220/0012258600003543
In Proceedings of the 20th Inter national Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 763-769
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
763

cost function values. Applying fuzzy logic to find the
weighting values of the cost function, it becomes pos-
sible to create a hybrid controller for trajectory track-
ing (Kudinov et al., 2020).
Methodologies based on fuzzy logic control are
capable of operating alongside the nonlinearities of
robotic systems, as presented in the work of (Sun
et al., 2023), thus improving the trajectory perfor-
mance of robotic arms. The difficulties of nonlin-
earity have also been discussed with hybrid methods
of fuzzy logic systems by Lypunov stability analysis
(An et al., 2023). In both works an implementation is
presented simply to implement fuzzy logic control to
complex systems. Furthermore, the openness of this
control methodology to be applied in tuning methods
is evident, making robust and reliable controls.
As a contribution, this article brings LQR-FL as
a proposal for controlling planar robotic manipulators
trajectories, and compares its performance to the clas-
sic LQR controller.
The structure of this work is as follows. Section II
contains the dynamics of the system in its state space
form. Section III presents the LQR controller and its
association with fuzzy logic. Section IV presents the
evaluation of the controllers and the comparison of
the results. Section V is dedicated to the conclusions.
2 DYNAMIC MODEL
The motion dynamics of the 2-DOF Planar Manipu-
lator is as follow:
M(θ)
¨
θ +V (θ,
˙
θ) + g = τ (1)
The dynamic analysis of energies is carried out
through the Lagrangian:
L = KE − PE (2)
where, KE is the kinetic energy and PE is system
potential energy. The Lagrangian is used to derive
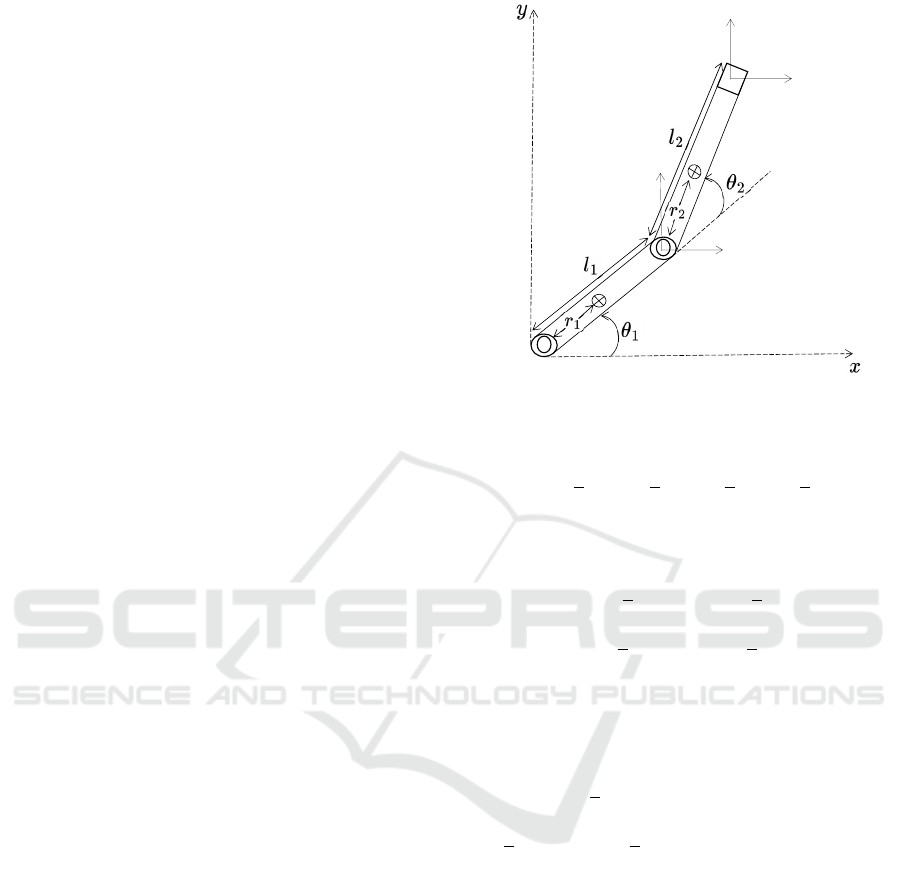
the dynamic model of the planar manipulator robot
shown in Figure 1, which is composed by masses m
1
and m
2
, lengths l
1
and l
2
, inertia tensors I
z1
and I
z2
,
and center of gravity r
1
and r
2
.
For each of the manipulator’s axes, the description
of linear displacement relative to the x/y coordinates
of the operating area is given by:
P
1
=


x
1
y
1
z
1


=


l
1
sin(θ
1
)
l
1
cos(θ
1
)
0


(3)
P
2
=


x
2
y
2
z
2


=


l
1
sin(θ
1
) + l
2
sin(θ
1
+ θ
2
)
l
1
cos(θ
1
) + l
2
cos(θ
1
+ θ
2
)
0


(4)
(
𝑚

,
𝐼


)
(
𝑚

,
𝐼


)
𝑥

𝑦

𝑥

𝑦

Figure 1: Two degrees of freedom planar manipulator.
The kinetic energy equation is:
KE =
1
2
m
1
v
2
1
+
1
2
I
z1
˙
θ
2
1
+
1
2
m
2
v
2
2
+
1
2
I
z2
˙
θ
2
2
(5)
Replacing velocities v
1
and v
2
with positions
derivatives of Equations 3 and 4, yields:
KE =
1
2
m
1
( ˙x
2
1
+ ˙y
2
1
) +
1
2
I
z1
˙
θ
2
1
+
1
2
m
2
( ˙x
2
2
+ ˙y
2
2
) +
1
2
I
z2
˙
θ
2
2
,
(6)
PE = m
1
g(˙z
2
1
) + m
2
g(˙z
2
2
). (7)
and replacing KE and PE of Equations 6 and 7 in
Equation 2 results:
L =
1
2
I
z1
[m
1
r
2
1
+ m
2
(l
2
1
+ r
2
2
+ 2l
1
r
2
C
2
)]
˙
θ
2
1
+
1
2
I
z2
[m
2
r
2
2
]
˙
θ
2
2
+
1
2
[m
2
2r
2
(l
1
C
2
+ d
2
)]
˙
θ
1
˙
θ
2
− g(0)
(8)
Applying partial derivatives to the Lagrangian
leads to the dynamic model of forces:

M
11
M
12
M
21
M
22

¨
θ
1
¨
θ
2

+

V
11
V
12
V
21
V
22

˙
θ
1
˙
θ
2

+

g
1
g
2

=

τ
1
τ
2

(9)
where,
M
11
= m
1
r
2
1
+ m
2
[l
2
1
+ r
2
2
+ 2l
1
r
2
cos(θ
2
)] + I
z1
+ Iz2,
M
12
= m
2
[r
2
2
+ l
1
r
2
cos(θ
2
)] + Iz2,
M
21
= m
2
[r
2
2
+ l
1
r
2
cos(θ
2
)] + Iz2,
M
22
= m
2
r
2
2
+ Iz2,
V
11
= −m
2
l
1
r
2
sin(θ
2
)
˙
θ
2
,
V
12
= −m
2
l
1
r
2
sin(θ
2
)[
˙
θ
1
+
˙
θ
2
],
V
21
= −m
2
l
1
r
2
sin(θ
2
)
˙
θ
1
,
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
764

V
22
= 0,
g
1
= 0,
g
2
= 0.
This planar manipulator has no vertical move-
ments; thus, the gravity value is zero. A system in
state space is represented by the expression :
˙x = Ax + Bu. (10)
The Equation 9, which represents the torque ex-
erted on the joints of the plane manipulator, is not lin-
ear. To express this system as a state space model, the
state variables are considered as follows:
x
1
= θ
1
, x
2
= θ
2
, x
3
=
˙
θ
1
, x
4
=
˙
θ
2
, (11)
˙x
1
=
˙
θ
1
, ˙x
2
=
˙
θ
2
, ˙x
3
=
¨
θ
1
, ˙x
4
=
¨
θ
2
. (12)
These are rewritten and associated with the exist-
ing torque equations for the joints:
˙x
1
= x
3
, (13)
˙x
2
= x
4
, (14)
˙x
3
(m
2
l
2
1
+ 2m
2
C
2
l
1
r
2
+ I
z1
+ I
z2
) =
τ
1
− (m
2
r
2
2
+ l
1
m
2
C
2
r
2
+ I
z2
)
¨
θ
2
+l
1
m
2
r
2
˙
θ
2
S
2
(
˙
θ
1
+
˙
θ
2
) + l
1
m
2
r
2
˙
θ
1
θ
2
S
2
, (15)
˙x
4
(m
2
r
2
+ I
z2
) = −τ
1
+ m
2
r
2
2
+ (l
1
m
2
S
2
)
˙
θ
2
1
r
2
+I
z2
+
¨
θ
1
+ (l
1
m
2
r
2
˙
θ
1
C
2
)
¨
θ
1
. (16)
The first-order Taylor series expansion of the dy-
namic Equations 13, 14, 15, and 16, results in the dy-
namic matrices A and B:
A =



0 0 1 0
0 0 0 1
0 A
32
A
33
A
34
0 A
42
A
43
0



, (17)
where,
A
32
=
σ
2
+ l
1
m
2
r
2
˙
θ
2
cos(θ
2
)(
˙
θ
1
+
˙
θ
2
) +l
1
m
2
r
2
˙
θ
1
˙
θ
2
cos(θ
2
)
σ
1
−

6Iz
2
5
− τ
1
+
6m
2
r
2
2
5
+
6l
1
m
2
r
2
cos(θ
2
)
5
− l
1
m
2
r
2
˙
θ
2
sin(θ
2
)(
˙
θ
1
+
˙
θ
2
) − l
1
m
2
r
2
˙
θ
1
˙
θ
2
sin(θ
2
)

2l
1
m
2
r
2
sin(θ
2
)
σ
2
1
A
33
=
2l
1
m
2
r
2
˙
θ
2
sin(θ
2
)
σ
1
A
42
=
σ
2
− l
1
m
2
r
2
˙
θ
2
1
cos(θ
2
)
σ
3
A
43
= −
2l
1
m
2
r
2
˙
θ
1
sin(θ
2
)
σ
3
σ
1
= m
2
l
1
2
+ 2m
2
cos(θ
2
)l
1
r
2
+ m
1
r
1
2
+ m
2
r
2
2
+ Iz
1
+ Iz
2
σ
2
=
6l
1
m
2
r
2
sin(θ
2
)
5
σ
3
= m
2
r
2
2
+ Iz
2
B =



0 0
0 0
B
31
0
0 B
42



. (18)
where,
B
31
=
1
m
2
l
1
2
+2m
2
cos(θ
2
)l
1
r
2
+m
1
r
1
2
+m
2
r
2
2
+Iz
1
+Iz
2
B
42
=
1
m
2
r
2
2
+Iz
2
3 CONTROLLER DESIGN
Nonlinearity leads to complex dynamic modeling
in robotic systems that challenges to design con-
trollers for the trajectories executed by the robot.
LQR was chosen in the design of 2-DOF planar ma-
nipulator trajectory controller, since this controller
addresses non-linearity issues linearizing the state
spaces (Teng Fong et al., 2015), (Lee et al., 2021).
For the adjustment techniques of the fuzzy logic
controller, there are different options that are chosen
according to the complexity and characteristics of the
system. One of the most common techniques is opti-
mization based on heuristics, such as gray wolf opti-
mization (GWO) implemented in the (Bojan-Dragos
et al., 2021). Also included in the set of heuristics
are optimization by genetic algorithms (GA) and par-
ticle swarm optimization presented in (Kumar et al.,
2023). Them also cites more traditional techniques
for the adjustment of fuzzy controllers such as the
Takagi and Sugeno adjustment or the Mamdani ad-
justment. This last adjustment technique to obtain the
relevant functions and fuzzification rules are used in
this work, because its methodology is obtained from
systems in state space.
3.1 LQR Controller
The LQR controller is designed using the state space
model obtained in Equations 17 and 18. The calcula-
tion of the gain satisfies the following the equation:
K = R
−1
B
T
P. (19)
LQR Combined with Fuzzy Control for 2-DOF Planar Robot Trajectories
765

−𝐾
u
𝑥
𝑥 = 𝐴𝑥 + 𝐵𝑢
Figure 2: Optimal Regulatory System.
in equation 19, B is the input vector, R is the
weighting matrix and P is the Riccati matrix. The R
matrix is filled with ones in its initialization, and its
solution follows:
A
T
P + PA + Q − PBR
−1
P = 0. (20)
The weighting matrix Q is given by,
Q = C
T
C. (21)
An optimal regulator system, can be designed ac-
cordingly to the Figure 2 (Ogata, 2010).
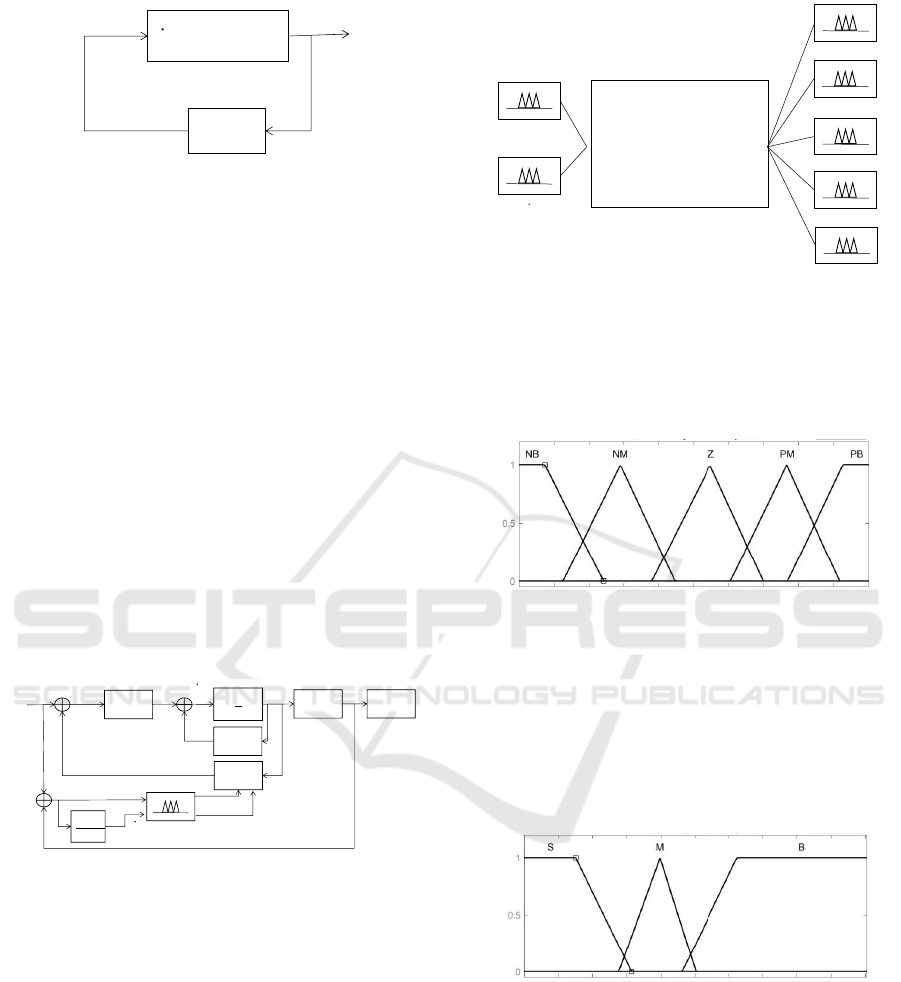
3.2 LQR-FL Controller
The creation of LQR-FL controller stems from the
premise of having an LQR controller implemented in
the plant to be controlled. Figure 3 illustrates that
fuzzy logic operates within a feedback loop parallel
to the operation of the base controller.



Robot

+





+
+
+
+
-

 

Fuzzy Logic




Figure 3: LQR control scheme using Fuzzy Logic.
This control methodology, when implemented
into planar manipulator trajectory control scheme,
takes as input the desired angular position calculated
through inverse kinematics. These controller deter-
mine the joint positions to execute the desired trajec-
tory.
The structure of the fuzzy controller, depicted in
Figure 4 employs membership functions (MFs) con-
sidering as inputs the error between the desired and
actual joint position e and its derivative ˙e. Meanwhile,
the MFs output are the elements of the main diagonal
of the matrix Q matrix and the optimal value of R.
The MFs input e and ˙e have different operating
ranges, yet the triangular and trapezoidal shapes of
their linguistic sets coincide, as depicted in Figure
System = Mamdani
Defuzzification = centroid
Rules = 25
𝑞

𝑅
𝑞

𝑞

𝑞

𝑒
𝑒
Figure 4: Fuzzy controller structure.
5. The proportionality of the linguistic sets negative
big (NB), negative medium (NM), zero (Z), positive
medium (PM) and positive big (PB) is adjustable to
obtain precise information in the inputs.
Current Variable
Name d_error
Type input
Range
[-0.1 0.1]
Display Range
[-0.1 0.1]
Current Membership Function (click on MF to select)
Name
Type
trimf
Params
181
plot points:
Help Close
Selected variable "d_error"
Figure 5: Membership functions of input variables.
The structure of the MFs shown in Figure 6 is im-
plemented in the five outputs of the fuzzy controller.
It’s evident that these output MFs are a simplified ver-
sion of the input MFs. The linguistic groups compos-
ing them are: small (S), medium (M), Big (B). Each
of these output MFs differs in the operating range
and the proportionality of each of the sets comprising
them.
Current Variable
Name q11
Type output
Range
[0 2.01]
Display Range
[0 2.01]
Current Membership Function (click on MF to select)
Name
Type
trimf
Params
181
plot points:
Help Close
Selected variable "q11"
Figure 6: Membership functions of input variables.
The fuzzy controller obtains the output values
through decisions that apply the rule base to the in-
put values it is receiving. Table 1. was constructed
based on the proposed controller in (Bekkar and Fer-
kous, 2023).
In the Table 1, position error input values as ver-
tical values. The horizontal of the table is related
to the rate of change of value. From this associa-
tion, the twenty-five operating rules of the fuzzy block
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
766

Table 1: Rule base.
In. ( ˙e)
q
1
, q
2
, q
3
, q
4
NB NM Z PM PB
*R
In.(e)
NB S,B,M,M M,M,M,M S,S,B,B B,M,S,S B,M,S,S
*B *M *B *S *S
NM B,B,S,M B,M,S,M M,M,S,M B,M,S,M B,M,S,M
*S *S *S *S *S
Z M,B,M,S B,B,S,S S,S,M,M B,B,S,S M,B,M,S
*M *M *B *M *M
PM B,M,S,M B,M,S,M M,M,S,M B,M,S,M B,B,B,S,M
*S *S *S *S *S
PB B,M,S,S B,M,S,S S,S,B,B M,M,M,M S,B,M,M
*S *S *B *M *B
are obtained. As a result, it is obtained the value of
(q
1
, q
2
, q
3
, q
4
) and (R).
4 RESULTS AND SIMULATION
In this study, trajectory control simulation is con-
ducted based on the model of a robotic arm shown
in Figure 1, The parameters of this two-degree-of-
freedom manipulator are those outlined in Table 2.
To design the LQR-FL controller, the parameters
in Table 3 are provided. The ranges of the input and
output membership functions are specified.
Table 2: Two degrees of freedom planar manipulator pa-
rameter values.
Parameter Value Units
l
1
0.26 m
l
1
0.38 m
r
1
0.13 m
r
2
0.19 m
m
1
0.53 kg
m
2
0.33 kg
I
z1
0.013 kg ∗ m
2
I
z2
0.016 kg ∗ m
2
g 0. m/s
2
4.1 Controller Parameters
The LQR controller is tuned choosing the weigh-
ing the matrix as, θ
1
= 0, θ
2
= 0,
˙
θ
1
= 0,
˙
θ
2
= 0,
Q=diag

1 1 0 0

e R=[1].
Therefore, both controllers are set to operate with the
dynamic input arrays of Equations 22 and 23, and the
output array of Equation 24.
A =



0 0 1 0
0 0 0 1
0 0.56 0 0
0 −0.69 0 0



(22)
B =



0 0
0 0
9.42 0
0 34.94



(23)
C =

1 0 0 0
0 1 0 0

(24)
4.2 Transient Response Analysis
The system has as inputs the unit impulse values for
each of the joints of the kinematic chain of the planar
manipulator. Controllers having this type of inputs
can be evaluated through transient response charac-
teristics. The Table 4 contains the parameters of delay
time (td), rise time (tr), peak time (tp) and accommo-
dation time (ts).
Table 4, shows that both controllers comply with
the desired positioning with respect to the input value
received. Showing a difference in the reduction of
time by the LQR-FL hybrid controller to reach the
desired position. The speed graphs for the LQR-FL
and LQR controllers are shown in Figures 7a and 7b
respectively. It agree with the fact that the speeds ex-
ecuted in the LQR-FL controller are faster.
Figure 7c and 7d graphs represents shorter travel
times with higher energy peaks for each of the joints
in the system. The higher energy peaks obtained with
the LQR-FL controller are the effect of better control
of the system energy for the same movement pres-
sure due to a computational tuning of the values of
the weighting matrices.
LQR Combined with Fuzzy Control for 2-DOF Planar Robot Trajectories
767

Table 3: LQR-FL Membership Features.
In / Out Fuzzy values obtained Range of M.F.
Error (e) (−1.2, 1.25)
Change rate ( ˙e) (−2.0, 2.25)
Q =



q
1
0 0 0
0 q
2
0 0
0 0 q
3
0
0 0 0 q
4






q
1
q
2
q
3
q
4






(0.98, 1.21)
(1.0, 1.1)
(0.05, 0.3)
(0.1, 0.4)



R R (0.8, 0.95)
Table 4: Transient response analysis.
Joint In real value td tr tp ts
n° deg deg s s s s
LQR-1 75 75.1 0.9 4 5 6
LQR-2 45 44.8 0.9 4 6 6.5
LQR-FL/1 75 75.1 0.5 1.8 2 2
LQR-FL/2 45 44.5 0.4 1.5 2.5 2.5
(a)
(b)
(c)
(d)
Figure 7: LQR position control.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
768

5 CONCLUSIONS
This study presents a methodology to enhance the
precision performance and steady-state behavior of a
robotic arm using LQR controller with computational
tuning. The LQR-FL hybrid control demonstrated to
operate with a smaller trajectory tracking error than
the one presented in the traditional LQR controller.
Therefore, the computational adjustment of the LQR
controller weighting matrices improved the simula-
tion performance in trajectory control.
5.1 Future Research
The performance of the controllers could be com-
pared in consideration of tolerances to disturbances
and noise and some comparative stability. An eval-
uation of the controllers with respect to trajectories
of greater complexity is as follows level that is being
worked to carry out this investigation.
REFERENCES
An, T., Zhu, X., Zhu, M., Ma, B., and Dong, B. (2023).
Fuzzy logic nonzero-sum game-based distributed ap-
proximated optimal control of modular robot manipu-
lators with human-robot collaboration. Neurocomput-
ing, 543:126276.
Bekkar, B. and Ferkous, K. (2023). Design of online fuzzy
tuning lqr controller applied to rotary single inverted
pendulum: Experimental validation. Arabian Journal
for Science and Engineering, 48(5):6957–6972.
Bojan-Dragos, C.-A., Precup, R.-E., Preitl, S., Roman, R.-
C., Hedrea, E.-L., and Szedlak-Stinean, A.-I. (2021).
Gwo-based optimal tuning of type-1 and type-2 fuzzy
controllers for electromagnetic actuated clutch sys-
tems. IFAC-PapersOnLine, 54(4):189–194.
Garc
´
ıa, J. J. A., Castellanos, E. I., and Santana, L. H.
(2018). Control por modelo din
´
amico inverso de
simulador de conducci
´
on de 2 grados de libertad.
ITEGAM-JETIA, 4(13):59–65.
Ho, H., Wong, Y.-K., and Rad, A. B. (2007). Robust fuzzy
tracking control for robotic manipulators. Simulation
Modelling Practice and Theory, 15(7):801–816.
Kardo
ˇ
s, J. (2019). Robust computed torque method of robot
tracking control. In 2019 22nd International Con-
ference on Process Control (PC19), pages 102–107.
IEEE.
Kelly, R., Davila, V. S., and Perez, J. A. L. (2005). Control
of robot manipulators in joint space. Springer Science
& Business Media.
Kudinov, Y., Duvanov, E., Kudinov, I., Pashchenko,
A., Pashchenko, F., Pikina, G., Andryushin, A.,
Arakelyan, E., and Mezin, S. (2020). Construction
and analysis of adaptive fuzzy linear quadratic regula-
tor. In Journal of Physics: Conference Series, volume
1683, page 042065. IOP Publishing.
Kumar, A., Raj, R., Kumar, A., and Verma, B. (2023).
Design of a novel mixed interval type-2 fuzzy logic
controller for 2-dof robot manipulator with payload.
Engineering Applications of Artificial Intelligence,
123:106329.
Lee, T. S., Alandoli, E. A., and Vijayakumar, V. (2021).
2-dof robot modelling by simmechanics and pd-fl in-
tegrated controller for position control and trajectory
tracking. F1000Research, 10:1045.
Li, Y., Liu, G., Hong, T., and Liu, K. (2005). Robust control
of a two-link flexible manipulator with quasi-static de-
flection compensation using neural networks. Journal
of Intelligent and Robotic Systems, 44:263–276.
Mahil, S. M. and Al-Durra, A. (2016). Modeling analysis
and simulation of 2-dof robotic manipulator. In 2016
IEEE 59th International Midwest Symposium on Cir-
cuits and Systems (MWSCAS), pages 1–4. IEEE.
Nguyen, T.-T. (2019). Sliding mode control-based sys-
tem for the two-link robot arm. International Jour-
nal of Electrical and Computer Engineering (IJECE),
9(4):2771–2778.
Ogata, K. (2010). Modern control engineering fifth edition.
Prentice Hall.
Pizarro-Lerma, A., Garc
´
ıa-Hern
´
andez, R., and Santib
´
a
˜
nez,
V. (2018). Fine-tuning of a fuzzy computed-torque
control for a 2-dof robot via genetic algorithms. IFAC-
papersonline, 51(13):326–331.
Shah, J., Rattan, S., and Nakra, B. (2011). Kinematic
analysis of 2-dof planer robot using artificial neural
network. International Journal of Mechanical and
Mechatronics Engineering, 5(9):1720–1723.
Song, Z., Yi, J., Zhao, D., and Li, X. (2005). A com-
puted torque controller for uncertain robotic manip-
ulator systems: Fuzzy approach. Fuzzy sets and sys-
tems, 154(2):208–226.
Sun, Y., Liang, X., and Wan, Y. (2023). Tracking control
of robot manipulator with friction compensation using
time-delay control and an adaptive fuzzy logic system.
In Actuators, volume 12, page 184. MDPI.
Teng Fong, T., Jamaludin, Z., Bani Hashim, A. Y., and Rah-
man, M. A. A. (2015). Design and analysis of linear
quadratic regulator for a non-linear positioning sys-
tem. Applied Mechanics and Materials, 761:227–232.
Wahrburg, A. and Listmann, K. (2016). Mpc-based admit-
tance control for robotic manipulators. In 2016 IEEE
55th Conference on Decision and Control (CDC),
pages 7548–7554. IEEE.
LQR Combined with Fuzzy Control for 2-DOF Planar Robot Trajectories
769