On the Value of Combiners in Heterogeneous Ensemble Effort

Estimation

Mohamed Hosni

MOSI Research Team, ENSAM, University Moulay Ismail of Meknes, Meknes, Morocco

Keywords:

Ensemble Effort Estimation, Software Development Effort Estimation, Combiners, Non-Linear Rule.

Abstract:

Effectively managing a software project to deliver a high-quality product primarily depends on accurately es-

timating the effort required throughout the software development lifecycle. Various effort estimation methods

have been proposed in the literature, including machine learning (ML) techniques. Previous attempts have

aimed to provide accurate estimates of software development effort estimation (SDEE) using individual esti-

mation techniques. However, the literature on SDEE suggests that there is no commonly superior estimation

technique applicable to all software project contexts. Consequently, the idea of using an ensemble approach

emerged. An ensemble combines multiple estimators using a speciﬁc combination rule. This approach has

been investigated extensively in the past decade, with overall results indicating that it can yield better perfor-

mance compared to other estimation approaches. However, not all aspects of ensemble methods have been

thoroughly explored in the literature, particularly the combination rule used to generate the ensemble’s output.

Therefore, this paper aims to shed light on this approach by investigating both types of combiners: three lin-

ear and four non-linear. The ensemble learners employed in this study were K-Nearest Neighbors, Decision

Trees, Support Vector Regression, and Artiﬁcial Neural Networks. The grid search technique was employed

to tune the hyperparameters for both the learners and the non-linear combiners. Six datasets were utilized

for the empirical analysis. The overall results were satisfactory, as they indicated that the ensemble and single

techniques exhibited similar predictive properties, and the ensemble with a non-linear rule demonstrated better

performance.

1 INTRODUCTION

Software development effort estimation plays a cru-

cial role in software project management, as it in-

volves estimating the amount of effort required to de-

velop a new software project (Wen et al., 2012). Ac-

curately estimating the effort needed during the early

stages of the software lifecycle is essential for ensur-

ing project success. Both underestimation and over-

estimation can lead to project failure (Minku and Yao,

2013c). Over the past four decades, researchers have

proposed and evaluated various approaches to pro-

vide accurate effort estimates for software develop-

ment. These approaches can be generally classiﬁed

into three categories (Jorgensen and Shepperd, 2006):

expert judgment, algorithmic models, and machine

learning (ML). In recent years, there has been a signif-

icant increase in research on the use of ML techniques

for software development effort estimation (Ali and

Gravino, 2019). ML techniques assume a non-linear

https://orcid.org/0000-0001-7336-4276

relationship between the dependent variable (effort)

and independent variables, and they aim to model this

relationship based on historical software projects.

Despite the availability of numerous software ef-

fort estimation models, it is still necessary to inves-

tigate novel models to improve the accuracy of these

estimates. One recent approach proposed and eval-

uated in the literature is ensemble effort estimation

(EEE), which combines multiple effort estimators to

provide more accurate estimates compared to using

a single technique (Idri et al., 2016). The existing

literature on software development effort estimation

categorizes EEE techniques into two types: homoge-

neous EEE and heterogeneous EEE. Homogeneous

EEE refers to an ensemble that combines different

variants of the same SDEE methods or a combina-

tion of one ensemble learning technique (such as Bag-

ging, Boosting, or Random Subspace) and one single

technique. Heterogeneous EEE, on the other hand, in-

volves an ensemble that incorporates at least two dif-

ferent SDEE techniques (Azzeh et al., 2015; Braga

Hosni, M.

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation.

DOI: 10.5220/0012259300003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 153-163

ISBN: 978-989-758-671-2; ISSN: 2184-3228

153

et al., 2007b; Elish, 2013; Kocaguneli et al., 2009;

Minku and Yao, 2013b; Wu et al., 2013).

Idri et al. conducted a systematic literature review

(SLR) to gather evidence on the use of EEE in SDEE

(Idri et al., 2016). Their review included 24 papers

published between 2000 and 2016. The review re-

vealed that the homogeneous type of ensemble was

the most investigated in the literature. ML techniques,

particularly Artiﬁcial Neural Networks (ANN) and

decision trees (DTs), were frequently employed in

constructing this new approach. In terms of accuracy,

the overall results indicated that the performance of

the ensemble approach was superior to that of sin-

gle techniques. Additionally, the review identiﬁed 20

combination rules used to generate the ﬁnal output

of the ensemble methods, with linear rules being the

most extensively investigated. A similar conclusion

was drawn in the review conducted by Carbal et al.

(de A. Cabral et al., 2023), which updated the ﬁnd-

ings of Idri et al.

Despite the existence of various EEE techniques

proposed in the literature, certain aspects, particularly

the utilization of non-linear combiners, have not been

adequately explored. The reviews conducted by Idri

et al. and Carbal et al. both indicated that linear

combiners were predominantly employed for joining

the outputs of single techniques in both homogeneous

and heterogeneous ensembles. However, there is a

lack of evidence regarding the effectiveness of non-

linear combiners. Thus, the objective of this paper is

to address this gap by investigating the use of several

non-linear combiners and assessing whether they can

potentially outperform linear rules in terms of perfor-

mance.

This paper speciﬁcally introduces a heterogeneous

ensemble approach that incorporates four widely

recognized ML techniques: K-Nearest Neighbors

(KNN), Support Vector Regression (SVR), Multilayer

Perceptron Neural Networks (MLP), and DT. The ob-

jective is to estimate the effort required for develop-

ing a new software system using both linear and non-

linear combiners. The linear rules employed in the

study include average, median, and inverse ranked

weighted mean. On the other hand, the non-linear

rules involve four combiners: MLP, KNN, DT, and

SVR. The proposed ensemble is evaluated using six

established datasets and various performance criteria.

The study addresses three research questions (RQs):

• (RQ1): Does the heterogeneous ensemble outper-

form its base ML methods irrespective of the com-

bination rule used?

• (RQ2): Among the two types of combiners uti-

lized, which one yields accurate estimates for the

proposed ensemble?

• (RQ3): Among the seven combiners employed,

which one demonstrates superior accuracy for the

proposed heterogeneous ensemble?

The key features of this paper are as follows:

• Exploration of a heterogeneous ensemble based

on four ML techniques widely used in the ﬁeld

of SDEE.

• Investigation of three different linear and four

non-linear rules to drive the ensemble outputs.

• Evaluation of the predictive capabilities of both

single techniques and the heterogeneous ensemble

using six well-known datasets.

The remaining sections of this paper are organized as

follows: Section 2 provides a review of related work

on EEE. Section 3 gives an overview of the techniques

used. Section 4 describes the experimental design.

Section 5 presents and discusses the results. Section 6

outlines the limitations. Conclusions and future work

are given in the last section.

2 RELATED WORK

This section begins by providing a brief description of

the EEE approach and an overview of prior research

conducted in the ﬁeld of SDEE examining this ap-

proach.

EEE involves aggregating the output of multiple

effort prediction techniques using a speciﬁc combina-

tion rule. This approach has been extensively stud-

ied in various domains (Hosni et al., 2021a; Nguyen

et al., 2014; Sewak et al., 2007; Hosni et al., 2018a).

It is employed to leverage the strengths of individual

techniques and compensate for their weaknesses, ulti-

mately leading to more accurate estimates. While sev-

eral studies have explored this approach in the context

of SDEE, the number of research works in this area is

still relatively limited compared to studies focusing

on single techniques (de A. Cabral et al., 2023). For

instance, a review conducted by Carbal et al. identi-

ﬁed only 54 research papers on EEE in SDEE.

A SLR by Idri et al. investigated the use of ensem-

ble methods in SDEE. The review analyzed 24 papers

published between 2000 and 2016, and the main ﬁnd-

ings were as follows:

• Homogeneous ensembles were the most com-

monly investigated, appearing in 17 out of 24 pa-

pers.

• Machine learning techniques, particularly ANN

and DTs, were the most frequently employed in

ensemble construction, with both techniques be-

ing studied in 50% of the selected papers.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

154

• Twenty combination rules were utilized to gener-

ate the ﬁnal output of ensemble methods, falling

into two categories: linear and non-linear rules.

However, linear rules were the most extensively

explored.

• Heterogeneous ensembles were explored in only 9

papers, using 12 different ML techniques as base

models. DT and KNN were the most commonly

utilized techniques.

• Heterogeneous ensembles demonstrated better

performance than their individual members, with

improved Mean and Median Magnitude of Rela-

tive Error (MMRE, MdMRE), Prediction within

25% (Pred(25)).

• Overall, ensemble methods outperformed single

techniques in terms of performance.

A recent SLR by Cabral et al. aimed to update the ev-

idence on ensemble methods in SDEE between 2016

and 2022. The main ﬁndings conﬁrmed those of Idri

et al. (Idri et al., 2016), including:

• Homogeneous ensembles remained the most

prevalent in effort estimation, but the use of het-

erogeneous ensembles had increased over time.

• Machine learning models, particularly neural net-

works (such as MLP), were the most commonly

used techniques in constructing both homoge-

neous and heterogeneous ensembles. Regression

trees and similarity-based models were also fre-

quently employed.

• A total of 18 combination rules were identiﬁed

and categorized into linear and non-linear types,

with linear rules being the most commonly em-

ployed.

• Homogeneous ensembles using the mean as the

combiner rule achieved the highest accuracy.

• Heterogeneous ensembles using the median as the

combination rule achieved the highest accuracy.

The review by Carbal et al. (de A. Cabral et al.,

2023) also highlighted the need for investigating new

combination rules and determining whether any rule

can outperform the median in heterogeneous ensem-

bles. Several recommendations and research gaps

were identiﬁed in their review.

3 SDEE TECHNIQUES USED: AN

OVERVIEW

This section presents an overview of the four ML

techniques used in this paper.

3.1 K-Nearest Neighbor

KNN is a non-parametric technique utilized for clas-

siﬁcation and regression tasks. It is a straightforward

ML method. KNN determines the effort required for

a new software project by assessing its similarity to

historical projects based on certain measurements. In

this approach, the estimation for a new project is de-

rived by considering the efforts expended on the K

most similar historical projects, employing usually

the arithmetic mean method (Kocaguneli et al., 2011;

Mendes et al., 2002).

3.2 Multilayer Perceptron

MLP neural networks are neural networks that oper-

ate in a feed-forward manner, enabling them to tackle

classiﬁcation and regression tasks. This architecture

consists of at least three layers: an input layer, one or

more hidden layers, and an output layer. The number

of neurons in the input layer aligns with the dimen-

sionality of the feature space, while the size of the

output layer varies depending on the speciﬁc problem

being addressed. Several research studies have ex-

plored the utilization of MLPs in SDEE (Araujo et al.,

2010; Berlin et al., 2009).

3.3 Support Vector Regression

SVR is a regression method that utilizes the principles

of support vector machines. The SVR implementa-

tion was initially proposed by Cortes and Vapnik in

1996 and introduced to the realm of SDEE by Oliveira

in 2006 (Oliveira, 2006). This technique is founded

on statistical learning theory and offers a powerful ap-

proach for solving regression problems. Several stud-

ies investigated this technique in SDEE (Braga et al.,

2007a; Oliveira et al., 2010). To effectively employ

SVR, it is necessary to ﬁne-tune various parameters

(Hosni et al., 2018b), including the choice of kernel,

kernel parameters, complexity parameter, and the tol-

erance for deviations.

3.4 Decision Trees

DTs are a form of supervised learning techniques

used for both classiﬁcation and regression purposes.

DT creates a model with the aim of predicting the

value of the dependent variable by extracting rules

from the independent variables in the data. In this

paper, the CART variant was used. Different variants

of DTs were investigated in SDEE ﬁeld (Braga et al.,

2007b; Hosni et al., 2021b; Kocaguneli et al., 2011;

Song et al., 2013; Minku and Yao, 2013c).

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation

155

4 EXPERIMENTAL DESIGN

This section provides details about the experimental

design followed to carry out the experiments raised

in this paper. It starts with listing the performance

metrics and statistical tests used to assess the perfor-

mance accuracy of the proposed predictive models.

Thereafter, the grid search hyperparameters optimiza-

tion technique used to tune the parameters setting of

the individual and the non-linear combination rules

and the list of datasets selected for the empirical pur-

pose are detailed. Finally, the methodology used to

construct ensemble is described.

4.1 Performance Measures and

Statistical Test

Previous SLRs focusing on SDEE-based ML tech-

niques have stated that the primary performance met-

rics used to evaluate the effectiveness of software ef-

fort predictor models are the MMRE and Pred (0.25)

(Wen et al., 2012; Hosni and Idri, 2018), both of

which are based on the magnitude of relative error

(MRE). Nevertheless, the MRE criterion has faced

criticism for its inherent bias towards underestima-

tion, thus diminishing its suitability as a measure

of accuracy (Miyazaki et al., 1991; Myrtveit et al.,

2005). To avoid this shortcoming, we used other per-

formance metrics proposed in the literature, namely:

Mean Absolute Error (MAE), Mean Balanced Rel-

ative Error (MBRE), Mean Inverted Balanced Rela-

tive Error (MIBRE) which are considered less vener-

able to bias and asymmetry, along with their median

values, and Logarithmic Standard Deviation (LSD)

(Miyazaki et al., 1991; Minku and Yao, 2013a; Minku

and Yao, 2013c).

We compared the reasonability of the proposed

technique against the baseline estimator proposed by

Shepperd and MacDonell (Shepperd and MacDonell,

2012) using the Standardized Accuracy (SA) and Ef-

fect Size (∆). The SA can be understood as a measure

that quantiﬁes the improvement of a prediction tech-

nique (P

) over random guessing (P

) by indicating

the ratio between the two. To assess the probability of

non-random estimation, we employed the 5% quantile

of the random guessing distribution. The Effect Size

criterion is utilized to determine whether the predic-

tions made by a model are the result of chance or if

there is a signiﬁcant improvement over the baseline

estimator.

Equations (1)-(13) displays the mathematical for-

mulas of the performance used.

= |e

−

| (1)

Pred(0.25) =

100

∑

i=1

(

1 if

6 0.25

0 otherwise

(2)

MAE =

∑

i=1

(3)

MdAE = Median(AE

, AE

, ·· · , AE

) (4)

BRE =

min(e

)

(5)

IBRE =

max(e

)

(6)

MdBRE = Median(BRE

, ·· · , BRE

) (7)

MdIBRE = Median(IBRE

, ·· · , IBRE

) (8)

MBRE =

∑

i=1

min(e

)

(9)

MIBRE =

∑

i=1

max(e

)

(10)

LSD =

∑

i=1

(λ

)

n − 1

(11)

SA = 1 −

MAE

(12)

4 =

MAE

− MAE

(13)

where:

• e

and ˆe

are the actual and predicted effort for the

ith project.

• MAE

represents the average value of 10000

runs of random guessing estimator.

• MAE

average value of absolute error committed

by i estimation technique.

• S

represents the standard deviation value of the

baseline estimator.

• λ

= ln(e

) − ln(

• s

variance of the λ

For evaluation, we utilize leave-one-out cross vali-

dation (LOOCV), a cross-validation technique where

the target project is excluded from the dataset and

estimated using the remaining projects (Quenouille,

1956). For the statistical test, we employ the Scott-

Knott (SK) test based on the AE of the predictive

models (Scott and Knott, 1974).

4.2 Hyperparameters Optimization

Previous studies in the ﬁeld of SDEE have extensively

discussed the settings of hyperparameters for predic-

tive models (Hosni et al., 2018b; Song et al., 2013).

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

156

These studies have highlighted the importance of em-

ploying optimization techniques to improve the accu-

racy of these models. It has been observed that the ac-

curacy of ML SDEE techniques can vary across dif-

ferent datasets (Elish et al., 2013). Therefore, using

the same parameter settings for a given technique may

lead to incorrect assessments of predictive capability.

To address this, we employ the grid search optimiza-

tion method to determine the optimal parameters for

the selected models. Table 1 presents the predeﬁned

search space for the optimal parameter values for each

ML technique.

In addition, for the non-linear combiners used to

combine the individual estimates provided by the en-

semble constituents, we utilize the grid search tech-

nique to optimize their hyperparameter values. The

range of these parameters is listed in Table 2.

4.3 Dataset Used

To assess the predictive capabilities of the proposed

ensembles, we chose six datasets that offer a diverse

range of sizes and features (Azzeh et al., 2015). This

selection allows for a comprehensive analysis of the

results. The datasets were obtained from two repos-

itories: the PRedictOr Models In Software Engineer-

ing (PROMISE) data repository and the International

Software Benchmarking Standards Group (ISBSG)

data repository. Five datasets, namely Albrecht, CO-

COMO81, Desharnais, Kemerer, and Miyazaki, were

obtained from the PROMISE repository. Addition-

ally, one dataset was selected from the ISBSG R8

dataset.

Table 3 provides an overview of the six chosen

datasets, including details such as dataset size, num-

ber of attributes, and descriptive statistics of effort

(minimum, maximum, mean, and median).

4.4 Methodology Used

This subsection outlines the methodology employed

for constructing and evaluating both the single tech-

niques and the heterogeneous ensembles. The steps

followed for each dataset are as follows:

For Single Techniques:

• Step 1: Build the four single ML techniques

(KNN, SVR, MLP, and DT) using the grid

search optimization technique with 10-fold cross-

validation.

• Step 2: Select the optimal parameter values that

result in the lowest MAE for each single tech-

nique.

• Step 3: Assess the reasonability of the optimized

predictive models based on the SA and effect size,

ensuring they outperform the 5% quantile of ran-

dom guessing.

• Step 4: Report the performance metrics (MAE,

MdAE, MIBRE, MdIBRE, MBRE, MdBRE,

LSD, Pred( 25)) of the selected ML techniques us-

ing the LOOCV technique.

• Step 5: Rank the ML techniques using Borda

count voting system based on eight performance

criteria.

For Ensemble Methods:

• Step 1: Construct the heterogeneous ensemble us-

ing the four single techniques and seven combi-

nation rules: average (AVR), median (MED), in-

verse ranked weighted mean (IRWM), MLP, DT,

SVR, and KNN.

• Step 2: Report the performance of the proposed

ensemble in terms of the eight performance cri-

teria (MAE, MdAE, MIBRE, MdIBRE, MBRE,

MdBRE, LSD, Pred(25)) using the LOOCV tech-

nique.

• Step 3: Rank the developed techniques (both sin-

gle and ensemble) based on the eight performance

criteria using the Borda count voting system.

• Step 4: Cluster the constructed techniques (en-

semble and single) using the Scott-Knott test

based on AE.

5 EMPIRICAL RESULTS

This section presents the empirical results of the ex-

periments conducted in this paper. The experiments

were carried out using various tools, with Python and

its associated libraries being utilized to execute the

experiments. Additionally, the R programming lan-

guage was employed to perform the Scott-Knott test.

5.1 Evaluation of Single ML Techniques

The evaluation process begins by constructing indi-

vidual ML techniques using the grid search optimiza-

tion technique. This step aims to identify the optimal

parameters for each ML technique in each dataset.

The performance of each technique depends on two

main factors: parameter settings and the input dataset.

The objective function to optimize is the MAE, aim-

ing for the lowest MAE. It should be noted that dif-

ferent optimal hyperparameter values were identiﬁed

for the same method in each dataset.

Next, we construct the ML techniques using the

identiﬁed parameters through the LOOCV technique.

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation

157

Table 1: Hyperparameter search space for techniques.

Technique Search space

KNN

n neighbors: [1 to 11]

weights: {’uniform’, ’distance’},

metric:[’euclidean’, ’manhattan’, ’cityblock’, ’minkowski’]

SVR

kernel: [’rbf’, ’poly’],

C: [5, 10, 20, 30, 40, 50, 100],

epsilon: [0.0001, 0.001, 0.01, 0.1],

degree: [2, 3, 4, 5, 6],

gamma: [0.0001, 0.001, 0.01, 0.1]

MLP

hidden layer sizes: [(8,), (8,16), (8, 16, 32), (8,16,32,64)],

activation: [’relu’, ’tanh’, ’identity’, ’logistic’],

solver: [’adam’, ’lbfgs’, ’sgd’],

learning rate: [’constant’, ’adaptive’, ’invscaling’],

criterion: [’squared error’, ’friedman mse’, ’absolute error’, ’poisson’],

max depth: [None] + (1 to number of features),

max features: [None, ’sqrt’, ’log2’]

Table 2: Hyperparameter search space for the combiners.

Combiner Search space

KNN

n neighbors’: [1 to 4],

weights’: [’uniform’, ’distance’],

metric’: [’euclidean’]

SVR

kernel: [’rbf’, ’poly’],

C: [5, 10, 20, 30, 40, 50, 100],

epsilon: [0.0001, 0.001, 0.01, 0.1],

degree: [2, 3, 4, 5, 6],

gamma: [0.0001, 0.001, 0.01, 0.1]

MLP

hidden layer sizes: [(4,), (4,8)],

activation: [’relu’, ’tanh’, ’identity’, ’logistic’],

solver: [’adam’, ’lbfgs’, ’sgd’],

learning rate: [’constant’, ’adaptive’, ’invscaling’],

criterion: [’absolute error’],

max depth: [1, 4]

The ﬁrst evaluation step involves assessing the rea-

sonability of the predictions generated by the four ML

techniques. To achieve this, we compare the perfor-

mance of our estimators against a baseline estima-

tor. This baseline estimator was created by conduct-

ing multiple random guessing runs. The performance

criterion used is the SA indicator.

As shown in Table 4, all techniques generated bet-

ter estimates than the 5% quantile of random guess-

ing. In fact, all techniques performed at least 50%

better than random guessing across all datasets, ex-

cept for the SVR technique in Desharnais dataset.

Additionally, the KNN technique outperformed the

baseline estimator in the Albrecht, COCOMO, De-

sharnais, and ISBSG datasets. Furthermore, in terms

of effect size, all techniques exhibited a signiﬁcant

improvement over random guessing, with |∆| > 0.8.

Therefore, we can conﬁdently state that the proposed

techniques are genuinely predictive and not merely

guessing.

However, it is important to note that this initial

evaluation step is not sufﬁcient to draw conclusions

about the predictive capabilities of the effort estima-

tors. It only veriﬁes whether these techniques perform

better than a baseline estimator. Further analysis is

required to make deﬁnitive conclusions regarding the

predictive capabilities of the effort estimator.

The next step involves evaluating the performance

accuracy of the proposed techniques using multiple

indicators. Each indicator captures a different aspect

of performance accuracy. It is important to note that

a predictive technique may have a contradictory rank-

ing based on different performance criteria, leading to

instability and inconclusive results regarding the ac-

tual performance of a given technique. To address

this, we employ a ﬁnal ranking method called the

Borda Count, which utilizes the rankings of each tech-

nique according to each indicator. This voting system

is widely used in the literature of SDEE. The ﬁnal

rankings for all datasets are presented in Table 5.

As observed, there is no single technique that con-

sistently outperforms the others across all datasets.

For example, the MLP, DT, and KNN techniques were

ranked ﬁrst in two datasets each. However, the DT

and MLP techniques were ranked last in one dataset

each (Albrecht and COCOMO, respectively). The

SVR technique, on the other hand, was consistently

ranked last in four datasets and third in the remain-

ing two datasets. Therefore, we can conclude that the

SVR technique is the least effective among the four

techniques used in this study. Additionally, the DT

technique achieved the second position in the rank-

ings three times, while the KNN technique achieved

it twice, and the MLP technique achieved it once.

In summary, there is no single technique that can be

considered the most accurate overall. Even if a tech-

nique performs better than random guessing in terms

of the SA indicator and effect size, it does not guaran-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

158

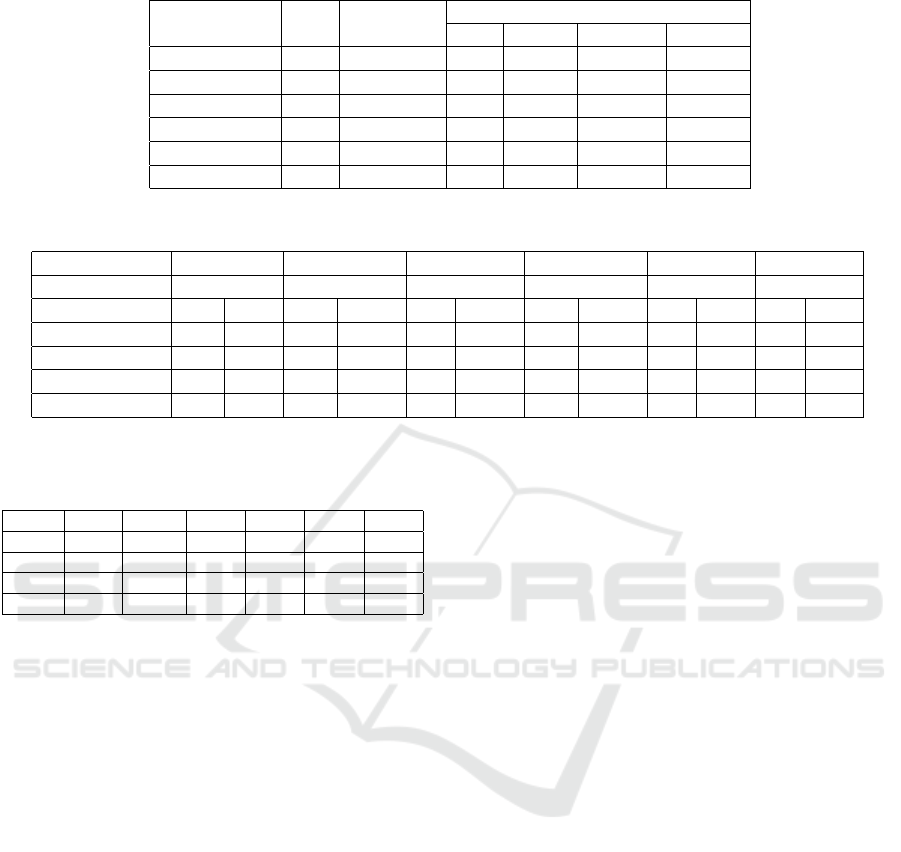
Table 3: Datasets characteristics.

Dataset Size #Features

Effort

Min Max Mean Median

Albrecht 24 7 0.5 105 21.87 11

COCOMO81 252 13 6 11400 683.44 98

Desharnais 77 12 546 23940 4833.90 3542

ISBSG 148 10 24 60270 6242.60 2461

Kemerer 15 7 23 1107 219.24 130

Miyazaki 48 8 5.6 1586 87.47 38

Table 4: Reasonability assessment of the SDEE techniques.

Dataset Albrecht COCOMO Desharnais ISBSG Kemerer Miyazaki

SA5% (in %) 30 15 15 13 34 34

Technique SA ∆ SA ∆ SA ∆ SA ∆ SA ∆ SA ∆

KNN 100 5.05 100 10.23 50 5.34 100 11.57 60 2.33 66 2.40

SVR 82 4.16 48 4.90 36 3.87 38 4.36 54 2.07 55 1.98

MLP 100 5.06 80 8.22 54 5.76 67 7.79 92 3.56 86 3.13

DT 86 4.37 100 10.23 58 6.15 71 8.25 87 3.38 90 3.28

tee its superiority across different accuracy indicators.

Table 5: Ranking of the four ML technique.

Rank Alb. COC. Des. ISB. Kem. Miy.

1 MLP KNN DT KNN MLP DT

2 KNN DT MLP DT DT KNN

3 SVR SVR KNN MLP KNN MLP

4 DT MLP SVR SVR SVR SVR

5.2 Evaluating Ensemble Methods

The next step involves constructing our proposed en-

semble, which is a heterogeneous ensemble based on

the four optimized ML techniques. We utilize two

types of combiners: three linear rules (average, me-

dian, and inverse ranked weighted mean) and four

non-linear rules (KNN, SVR, MLP, and DT). For clar-

ity, we use the following abbreviations:

• Ensemble with Average combiner: EAVG

• Ensemble with Median combiner: EMED

• Ensemble with IRWM: EIRWM

• Ensemble with MLP combiner: EMLP

• Ensemble with KNN combiner: EKNN

• Ensemble with DT combiner: EDT

• Ensemble with SVR combiner: ESVR

The non-linear rules were optimized using the grid

search optimization technique, considering the pa-

rameters range speciﬁed in Table 1. The proposed

ensembles yield improved estimates compared to the

5% quantile of random guessing, as shown in Table 6.

Furthermore, all ensemble techniques, regardless of

the combiner used, exhibit a signiﬁcant improvement

over the baseline estimator, with ∆ values exceeding

0.8.

In the next step, we evaluate the proposed ensem-

ble using eight accuracy indicators and determine the

ﬁnal rankings for both the single techniques and the

ensemble using a voting system technique. The ﬁnal

rankings are presented in Table 7.

The rankings reveal that the ensemble using KNN

as the combiner achieved ﬁrst place in three datasets:

Desharnais, ISBSG, and Miyazaki. On the other

hand, ESVR consistently ranked last in three datasets

and attained the 10th position in two datasets. More-

over, in the Albrecht dataset, both MLP and KNN sin-

gle techniques outperformed the ensemble methods.

Similarly, in the COCOMO dataset, KNN and DT

single techniques were more accurate than the ensem-

bles. In the ISBSG dataset, the KNN technique out-

performed the majority of ensembles. In the Miyazaki

dataset, the DT technique outperformed ﬁve out of

seven ensembles.

The key ﬁndings that can be drawn from this eval-

uation are that single methods can achieve competi-

tive performance similar to the ensemble methods and

that the ESVR technique remains the weakest ensem-

ble technique among those developed in this study.

Additionally, it is important to note that there is no

single approach, either single or ensemble, that can

be considered the best across all datasets, as the rank-

ings vary from one dataset to another. Therefore, a

more in-depth analysis of the software factors should

be conducted to identify an effective estimator tech-

nique that performs well in diverse circumstances.

Regarding the combination rules, the overall re-

sults suggest that non-linear rules can generate more

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation

159

Table 6: Reasonability evaluation of ensemble methods.

Dataset Albrecht COCOMO Desharnais ISBSG Kemerer Miyazaki

SA5% (in %) 30 15 15 13 34 34

Technique SA ∆ SA ∆ SA ∆ SA ∆ SA ∆ SA ∆

EAVR 93 4.71 83 8.50 54 5.78 74 8.57 75 2.91 76 2.75

EMED 97 4.91 94 9.63 55 5.82 79 9.09 78 2.99 79 2.85

EIRWM 96 4.87 91 9.36 57 6.08 82 9.49 82 3.18 82 2.98

EMLP 100 5.05 100 10.23 58 6.18 100 11.57 92 3.55 90 3.28

EKNN 100 5.05 100 10.23 62 6.56 100 11.57 69 2.66 100 3.62

EDT 94 4.77 93 9.53 51 5.45 91 10.59 91 3.52 88 3.21

ESVR 95 4.80 50 5.11 39 4.10 38 4.38 52 2.01 51 1.84

accurate results than linear rules, as they were ranked

higher than ensembles using linear rules. Speciﬁ-

cally, KNN and MLP stand out as the best combiners,

achieving better rankings in four datasets compared to

the other combiners.

Table 7: Techniques ranking.

Rank Alb. COC. Des. ISB. Kem. Miy.

1 MLP KNN EKNN EKNN MLP EKNN

2 EMLP DT EIRWM KNN EMLP EMLP

3 EKNN EMLP DT EMLP EDT DT

4 KNN EKNN EMLP EDT EIRWM EIRWM

5 EMED EMED EAVR EIRWM DT EDT

6 EIRWM EIRWM EMED EMED EAVR EMED

7 ESVR EDT MLP EAVR EMED EAVR

8 EDT EAVR EDT DT EKNN KNN

9 EAVR SVR KNN MLP KNN MLP

10 SVR ESVR ESVR SVR SVR SVR

11 DT MLP SVR ESVR ESVR ESVR

To further validate our conclusions regarding the

combiners, we conducted clustering of the ensemble

techniques using the SK test based on the AE. Ta-

ble 8 presents the clusters identiﬁed in each dataset.

The ensemble method using KNN as the combiner be-

longed to the best cluster in four out of six datasets,

followed by the ensemble using MLP as the com-

biner. Additionally, the ensemble utilizing DT as the

combiner was part of the best cluster in two datasets.

Conversely, none of the linear combiners, except for

the Desharnais dataset, were included in the best clus-

ter. Hence, we can conﬁdently conclude that the non-

linear rules, particularly KNN and MLP, are the pre-

ferred combiners among those utilized in this study.

These non-linear rules consistently enabled the en-

semble to generate statistically superior results.

Table 8: SK test for the ensemble methods.

Rank Alb. COC. Des. ISB. Kem. Miy.

EAVR 7 5 1 5 3 3

EDT 6 4 1 3 1 2

EIRWM 4 4 1 4 2 3

EKNN 2 1 1 1 4 1

EMED 3 3 1 4 3 3

EMLP 1 2 1 2 1 2

ESVR 5 5 2 6 5 4

To assess the statistical signiﬁcance of the pro-

posed techniques, we conducted a statistical analysis

using the SK test. The AE of the 11 estimation tech-

niques served as input for this test. Table 9 presents

the identiﬁed clusters in each dataset, and Figs. 1-

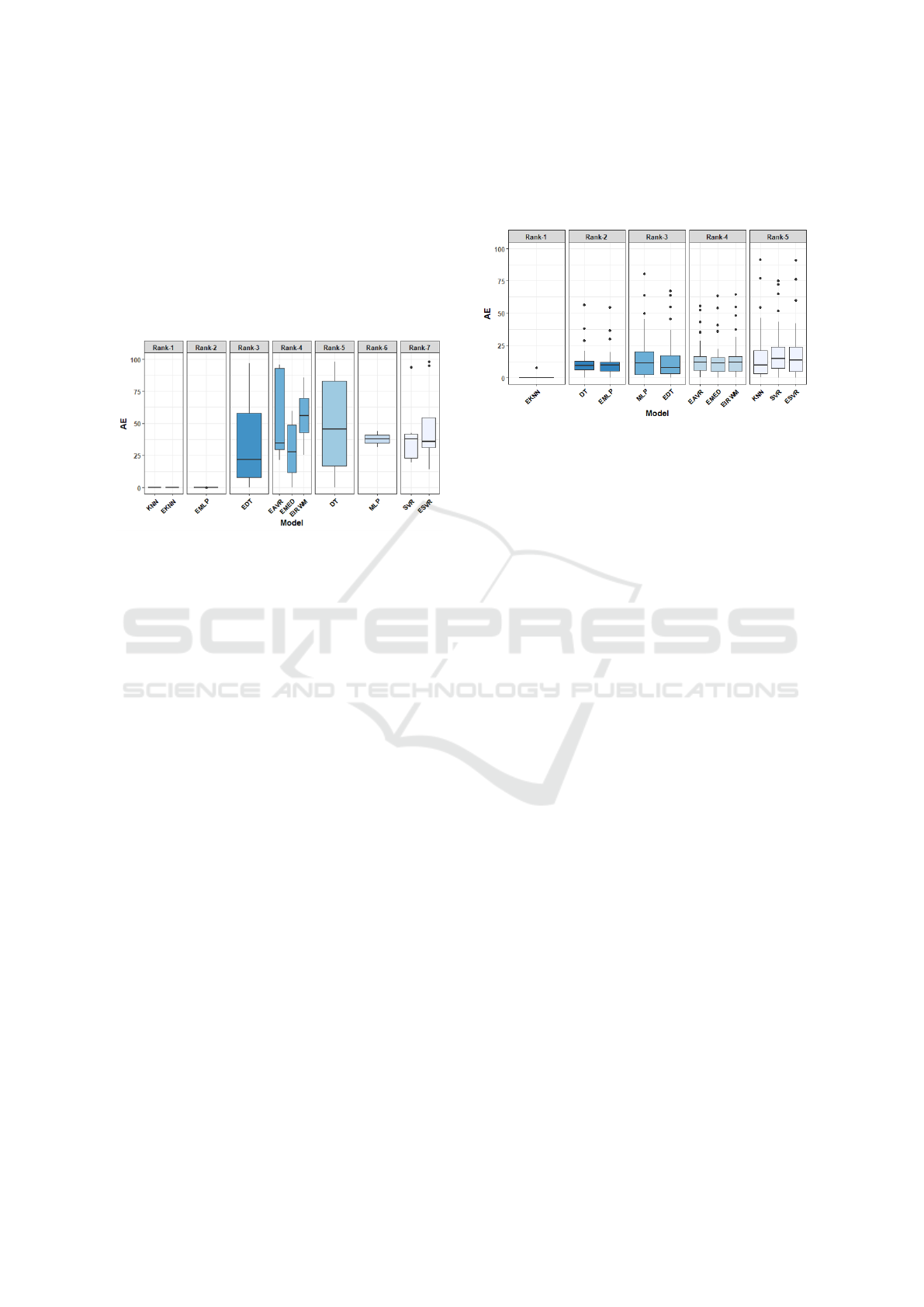
2 illustrate the output of the SK test for the ISBSG

and Miyazaki dataset (other ﬁgures are excluded due

to space limitations). Notably, varying numbers of

clusters were identiﬁed in each dataset. The Albrecht

dataset exhibited the largest number of clusters, with

a total of ten. Each cluster consisted of only one tech-

nique, except for the best cluster, which encompassed

the MLP and EMLP techniques. The worst cluster

in this dataset comprised the DT technique. In the

COCOMO dataset, six clusters were identiﬁed, with

the best cluster including the KNN, EMLP, and KNN

techniques. In the Desharnais dataset, two clusters

were identiﬁed, with the best cluster encompassing

all techniques except the SVR and ESVR techniques.

Among the seven clusters identiﬁed in the ISBSG

dataset, the best one included the KNN and EKNN

techniques. The Kemerer dataset yielded six identi-

ﬁed clusters, with the MLP, EMLP, and EDT tech-

niques ranking as the best. Finally, in the Miyazaki

dataset, ﬁve clusters were generated, with the EKNN

technique emerging as the best approach.

Table 9: Identiﬁed clusters by SK test.

Rank Alb. COC. Des. ISB. Kem. Miy.

DT 9 2 1 5 2 2

EAVR 8 5 1 4 4 4

EDT 7 4 1 3 1 3

EIRWM 5 4 1 4 3 4

EKNN 2 1 1 1 5 1

EMED 4 3 1 4 4 4

EMLP 1 1 1 2 1 2

ESVR 6 5 2 7 6 5

KNN 3 1 1 1 5 5

MLP 1 5 1 6 1 3

SVR 10 6 2 7 6 5

The obtained results, except for the Miyazaki

dataset, suggest that there is no signiﬁcant evidence

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

160

indicating the superiority of one technique over an-

other. This implies that the ensemble techniques ex-

hibit similar predictive capabilities as the single tech-

niques. However, there is conﬁrmation regarding the

combination rules: the non-linear rules, with the ex-

ception of the SVR combiner, consistently demon-

strate better performance compared to the linear rules.

This is evident from their inclusion in the best cluster

across all datasets, either as all three non-linear rules

or at least one of them.

Figure 1: Output of SK test in ISBSG dataset.

6 THREATS TO VALIDITY

In this section, we focus on discussing potential chal-

lenges to the validity of the conclusions drawn in this

empirical study. We identify three speciﬁc types of

threats to the validity of the ﬁndings:

Internal Validity: is a critical aspect of any empiri-

cal study. In fact, we adopted the LOOCV technique

to assess the predictive capabilities of the effort es-

timators. In fact, this approach tends to yield lower

bias and high variance estimate. Moreover, using this

approach we guarantee the replication of the empiri-

cal results obtained in contrast to cross validation or

holdout techniques.

External Validity: concerns the deﬁnition of the va-

lidity perimeter of the obtained results. In fact, the

proposed techniques, and their empirical assessment

concern only the ﬁeld of SDEE. Moreover, in this

study we tried to employ several datasets that have

different characteristics and collected from different

resources.

Construct Validity: the performance criteria are an

essential aspect of the assessment process of the es-

timation techniques. Using biased criteria led to the

generating of wrong conclusions. In this paper, eight

unbiased metrics were used for the assessment pur-

pose. These criteria are wieldy used in the literature

of SDEE. Concerning the hyperparameters values, we

used grid search optimization technique to ﬁne-tune

the hyperparameters settings for the employed tech-

niques. The use of other optimization techniques may

generate different results and therefore different con-

clusions.

Figure 2: Output of SK test in Miyazaki dataset.

7 CONCLUSIONS AND FUTURE

WORK

This paper focuses on the utilization of non-linear

combiners to determine the ﬁnal output of a Hetero-

geneous EEE based on four commonly used ML tech-

niques in SDEE literature. The hyperparameters of

these techniques were ﬁne-tuned using the grid search

optimization technique. Seven combiners were em-

ployed to combine the individual estimates within the

proposed ensemble. Three linear rules, namely aver-

age, median, and inverse ranked weighted mean, were

utilized based on their wide application in EEE lit-

erature. Additionally, four non-linear rules, namely

MLP, KNN, SVR, and DT, were incorporated. The

hyperparameters of the non-linear combiners were

optimized using the grid search technique. The em-

pirical evaluation was conducted on six datasets us-

ing the LOOCV technique. Multiple unbiased perfor-

mance indicators were employed for assessment pur-

poses. The key ﬁndings related to the three RQs ad-

dressed in this paper are summarized as follows:

• (RQ1): The overall results indicate that there is

no compelling evidence supporting the superior-

ity of the proposed heterogeneous ensemble over

its base learners. However, certain ensembles ex-

hibited better predictive capabilities than individ-

ual members and were outperformed by others.

Furthermore, based on the SK test, it was ob-

served that all the best clusters identiﬁed in all

datasets consisted of a combination of both sin-

gle and ensemble approaches. Therefore, it can

be concluded that both techniques share similar

predictive capabilities.

• (RQ2): The empirical analysis reveals that en-

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation

161

sembles employing non-linear rules yield more

accurate estimations compared to those utilizing

linear combiners.

• (RQ3): The KNN and MLP combiners appear

to be more suitable for combining estimates pro-

vided by the proposed combinations of single

techniques. Moreover, the SK test demonstrates

that the best cluster in all datasets exclusively

comprises non-linear rules, particularly the KNN

and MLP rules.

Future research directions will explore the use of dif-

ferent single estimators for constructing ensembles

and investigate the effectiveness of other non-linear

rules to develop accurate and stable EEE models.

Additionally, investigating datasets containing mixed

types of features (e.g., numerical and categorical) is

crucial to assess the efﬁcacy of the proposed ensem-

ble methodology.

REFERENCES

Ali, A. and Gravino, C. (2019). A systematic literature

review of software effort prediction using machine

learning methods. Journal of software: evolution and

process, 31(10):e2211.

Araujo, R. d. A., de Oliveira, A. L., and Soares, S.

(2010). Hybrid intelligent design of morphological-

rank-linear perceptrons for software development cost

estimation. In 2010 22nd IEEE International Confer-

ence on Tools with Artiﬁcial Intelligence, volume 1,

pages 160–167. IEEE.

Azzeh, M., Nassif, A. B., and Minku, L. L. (2015). An

empirical evaluation of ensemble adjustment methods

for analogy-based effort estimation. Journal of Sys-

tems and Software, 103:36–52.

Berlin, S., Raz, T., Glezer, C., and Zviran, M. (2009). Com-

parison of estimation methods of cost and duration

in it projects. Information and software technology,

51(4):738–748.

Braga, P. L., Oliveira, A. L., and Meira, S. R. (2007a). Soft-

ware effort estimation using machine learning tech-

niques with robust conﬁdence intervals. In 7th inter-

national conference on hybrid intelligent systems (HIS

2007), pages 352–357. IEEE.

Braga, P. L., Oliveira, A. L., Ribeiro, G. H., and Meira, S. R.

(2007b). Bagging predictors for estimation of soft-

ware project effort. In 2007 international joint con-

ference on neural networks, pages 1595–1600. IEEE.

de A. Cabral, J. T. H., Oliveira, A. L., and da Silva, F. Q.

(2023). Ensemble effort estimation: An updated and

extended systematic literature review. Journal of Sys-

tems and Software, 195:111542.

Elish, M. O. (2013). Assessment of voting ensemble for

estimating software development effort. In 2013 IEEE

Symposium on Computational Intelligence and Data

Mining (CIDM), pages 316–321. IEEE.

Elish, M. O., Helmy, T., Hussain, M. I., et al. (2013). Empir-

ical study of homogeneous and heterogeneous ensem-

ble models for software development effort estima-

tion. Mathematical Problems in Engineering, 2013.

Hosni, M., Carrillo de Gea, J. M., Idri, A., El Bajta, M.,

Fern

andez Alem

an, J. L., Garc

ıa-Mateos, G., and Ab-

nane, I. (2021a). A systematic mapping study for en-

semble classiﬁcation methods in cardiovascular dis-

ease. Artiﬁcial Intelligence Review, 54:2827–2861.

Hosni, M. and Idri, A. (2018). Software development ef-

fort estimation using feature selection techniques. In

SoMeT, pages 439–452.

Hosni, M., Idri, A., and Abran, A. (2018a). Improved ef-

fort estimation of heterogeneous ensembles using ﬁl-

ter feature selection. In ICSOFT, pages 439–446.

Hosni, M., Idri, A., and Abran, A. (2021b). On the value of

ﬁlter feature selection techniques in homogeneous en-

sembles effort estimation. Journal of Software: Evo-

lution and Process, 33(6):e2343.

Hosni, M., Idri, A., Abran, A., and Nassif, A. B. (2018b).

On the value of parameter tuning in heterogeneous en-

sembles effort estimation. Soft Computing, 22:5977–

6010.

Idri, A., Hosni, M., and Abran, A. (2016). Systematic liter-

ature review of ensemble effort estimation. Journal of

Systems and Software, 118:151–175.

Jorgensen, M. and Shepperd, M. (2006). A systematic re-

view of software development cost estimation stud-

ies. IEEE Transactions on software engineering,

33(1):33–53.

Kocaguneli, E., Kultur, Y., and Bener, A. (2009). Com-

bining multiple learners induced on multiple datasets

for software effort prediction. In International Sym-

posium on Software Reliability Engineering (ISSRE).

Kocaguneli, E., Menzies, T., and Keung, J. W. (2011). On

the value of ensemble effort estimation. IEEE Trans-

actions on Software Engineering, 38(6):1403–1416.

Mendes, E., Watson, I., Triggs, C., Mosley, N., and Coun-

sell, S. (2002). A comparison of development ef-

fort estimation techniques for web hypermedia appli-

cations. In Proceedings Eighth IEEE Symposium on

Software Metrics, pages 131–140. IEEE.

Minku, L. L. and Yao, X. (2013a). An analysis of multi-

objective evolutionary algorithms for training ensem-

ble models based on different performance measures

in software effort estimation. In Proceedings of the

9th international conference on predictive models in

software engineering, pages 1–10.

Minku, L. L. and Yao, X. (2013b). Ensembles and locality:

Insight on improving software effort estimation. Infor-

mation and Software Technology, 55(8):1512–1528.

Minku, L. L. and Yao, X. (2013c). Software effort esti-

mation as a multiobjective learning problem. ACM

Transactions on Software Engineering and Methodol-

ogy (TOSEM), 22(4):1–32.

Miyazaki, Y., Takanou, A., Nozaki, H., Nakagawa, N., and

Okada, K. (1991). Method to estimate parameter val-

ues in software prediction models. Information and

Software Technology, 33(3):239–243.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

162

Myrtveit, I., Stensrud, E., and Shepperd, M. (2005). Reli-

ability and validity in comparative studies of software

prediction models. IEEE Transactions on Software

Engineering, 31(5):380–391.

Nguyen, T. T., Liew, A. W.-C., Tran, M. T., and Nguyen,

M. P. (2014). Combining multi classiﬁers based

on a genetic algorithm–a gaussian mixture model

framework. In Intelligent Computing Methodologies:

10th International Conference, ICIC 2014, Taiyuan,

China, August 3-6, 2014. Proceedings 10, pages 56–

67. Springer.

Oliveira, A. L. (2006). Estimation of software project ef-

fort with support vector regression. Neurocomputing,

69(13-15):1749–1753.

Oliveira, A. L., Braga, P. L., Lima, R. M., and Corn

elio,

M. L. (2010). Ga-based method for feature selection

and parameters optimization for machine learning re-

gression applied to software effort estimation. infor-

mation and Software Technology, 52(11):1155–1166.

Quenouille, M. H. (1956). Notes on bias in estimation.

Biometrika, 43(3/4):353–360.

Scott, A. J. and Knott, M. (1974). A cluster analysis method

for grouping means in the analysis of variance. Bio-

metrics, pages 507–512.

Sewak, M., Vaidya, P., Chan, C.-C., and Duan, Z.-H.

(2007). Svm approach to breast cancer classiﬁcation.

In Second international multi-symposiums on com-

puter and computational sciences (IMSCCS 2007),

pages 32–37. IEEE.

Shepperd, M. and MacDonell, S. (2012). Evaluating pre-

diction systems in software project estimation. Infor-

mation and Software Technology, 54(8):820–827.

Song, L., Minku, L. L., and Yao, X. (2013). The impact of

parameter tuning on software effort estimation using

learning machines. In Proceedings of the 9th inter-

national conference on predictive models in software

engineering, pages 1–10.

Wen, J., Li, S., Lin, Z., Hu, Y., and Huang, C. (2012). Sys-

tematic literature review of machine learning based

software development effort estimation models. In-

formation and Software Technology, 54(1):41–59.

Wu, D., Li, J., and Liang, Y. (2013). Linear combination of

multiple case-based reasoning with optimized weight

for software effort estimation. The Journal of Super-

computing, 64:898–918.

On the Value of Combiners in Heterogeneous Ensemble Effort Estimation

163