GANMCMCRO: A Generative Adversarial Network Markov Chain

Monte Carlo Random Oversampling Algorithm for Imbalance

Datasets

Najmeh Abedzadeh and Matthew Jacobs

EECS Dept., School of Engineering, Catholic University of America, Washington, DC, U.S.A.

Keywords: Imbalanced Datasets, Machine Learning, Random Oversampling, Markov Chain Monte Carlo, Generative

Adversarial Networks.

Abstract: Machine learning techniques have showcased their adeptness in identifying patterns within data, yet their

efficacy diminishes when dealing with imbalanced datasets—a pervasive concern, especially apparent in the

realm of Intrusion Detection Systems (IDS). IDS, pivotal for monitoring malicious activities in networks or

systems, requires strategic interventions to address dataset imbalances and increase machine learning model

accuracy. Of note, imbalanced IDS datasets harbour covert cyber-attacks amid their substantial imbalances,

intricately complicating detection for conventional machine learning methods. This study introduces novel

algorithms designed to rectify imbalances within IDS datasets. The first algorithm, named Markov Chain

Monte Carlo Random Oversampling (MCMCRO), seamlessly integrates Markov Chain Monte Carlo

(MCMC) and Random Oversampling techniques to systematically synthesize fresh data. Additionally,

MCMCRO's novel data synthesis capability is harnessed within the Generative Adversarial Network

framework to formulate the second algorithm, GANMCMCRO (Generative Adversarial Networks Markov

Chain Monte Carlo Random Oversampling). This framework augments the potency of MCMCRO's data

generation function within the data generator model. An evaluation conducted on the CSE-CIC-IDS2018

Dataset substantiates the efficacy of both algorithms. MCMCRO showcases a recall of 0.66, precision of 1,

an F1 score of 0.79, and an overall accuracy of 0.91. Similarly, GANMCMCRO attains a recall of 0.81,

precision of 0.82, an F1 score of 0.81, and an overall accuracy of 0.88, providing compelling evidence of their

prowess in mitigating the challenges posed by imbalanced datasets. This research advances the field by

introducing innovative techniques that demonstrate substantial potential in enhancing the accuracy of machine

learning models for imbalanced data domains, particularly IDS datasets.

1 INTRODUCTION

In today's dynamic cybersecurity landscape,

protecting networks against evolving cyber threats

remains paramount. Intrusion Detection Systems

(IDS) play a critical role in identifying and mitigating

malicious activities within network environments

(Vij and Saini, 2021). This study focuses on network-

based intrusion detection systems (NIDS) specialized

in detecting external threats aiming to breach network

defences. IDS employ two primary protective

approaches: location-based defence, guarding

networks or hosts against attacks, and data-centric

defence, preserving data integrity amidst a range of

malicious activities.

Among diverse cybersecurity methodologies,

machine learning uses historical data to refine threat

detection models (Seeber and Rodosek, 2015),

However, machine learning-based IDS face

challenges in training accurate models due to

imbalanced datasets, where certain classes are

underrepresented, skewing model performance.

Consequently, research efforts concentrate on

addressing this issue to enhance algorithm efficacy.

With escalating cyber threats, detection systems

must anticipate established and emerging risks.

Intricate networks and the internet provide a backdrop

for adversaries to blend with legitimate activities

(Abedzadeh and Jacobs, 2022). Thus, IDS

frameworks need to adapt to evolving landscapes and

attack vectors. Intrusion detection primarily falls into

two paradigms: signature-based and anomaly-based.

Abedzadeh, N. and Jacobs, M.

GANMCMCRO: A Generative Adversarial Network Markov Chain Monte Carlo Random Oversampling Algorithm for Imbalance Datasets.

DOI: 10.5220/0012259600003584

In Proceedings of the 19th International Conference on Web Information Systems and Technologies (WEBIST 2023), pages 587-594

ISBN: 978-989-758-672-9; ISSN: 2184-3252

587

Signature-based IDS identify known threats using

predefined patterns or signatures, while anomaly-

based methods focus on deviations from norms,

uncovering unexpected events or behaviours. By

learning typical benign behaviours, anomaly-based

IDS identify anomalies, presenting a more adaptive

approach compared to traditional methods.

Based on our comprehensive survey of various

resampling algorithms aimed at mitigating

imbalanced IDS datasets, it was observed that only a

singular study has explored the utilization of Markov

Chain Monte Carlo (MCMC) and Generative

Adversarial Network (GAN) methodologies for this

purpose (Abedzadeh and Jacobs, 2022). The

outcomes of this study indicated that the individual

application of MCMC, random oversampling, or

GAN techniques to the CSE-CIC-IDS2018 dataset

yielded insufficient outcomes in rectifying the

inherent data imbalance compared with Logistic

Regression (LgR). Consequently, to address this gap,

our paper introduces a novel approach termed

Generative Adversarial Networks Markov Chain

Monte Carlo random oversampling

(GANMCMCRO), wherein various combinations of

these methods, along with random oversampling, are

explored to determine if their integration can lead to

performance improvements.

This study forges ahead by introducing two novel

resampling strategies. Firstly, the innovative MCMC

algorithm is introduced, which generates synthetic

data using a distinctive methodology that merges

MCMC and random oversampling techniques.

Testing tests underscore its superiority over extant

resampling methods. Secondly, the MCMCRO

function takes canter stage as the data generator

within GANMCMCRO—a framework that

assimilates MCMCRO's synthesized data within a

GAN model. Importantly, GANMCMCRO's data

generator employs MCMCRO instead of random

data, signifying a distinctive methodology.

The contribution of this work includes two facets:

1) The introduction of MCMCRO, a novel

imbalanced dataset resampling technique.

2) The implementation of GANMCMCRO, an

innovative framework that seamlessly integrates

MCMCRO-generated data into a GAN model for

novel model training.

Finally, a comprehensive evaluation that

benchmarks the performance of MCMCRO and

GANMCMCRO against established algorithms,

further solidifying their efficacy and innovation

within the realm of imbalanced dataset handling and

intrusion detection.

2 RELATED WORKS

The application of machine learning, Deep Learning,

and Reinforcement Learning has been widely

explored in various research papers to address the

challenge of imbalanced datasets (Abedzadeh and

Jacobs, 2023). This is particularly relevant in IDSs

where these methodologies are leveraged for

detecting malicious cyber-attacks. While these

algorithms have been employed for such purposes,

the imbalance in IDS datasets has garnered limited

attention in comparison. (Abedzadeh and Jacobs,

2022) conducted a comprehensive survey to explore

techniques aimed at addressing imbalance within IDS

datasets. Their work, delved into the intricacies of

handling imbalanced data, shedding light on the

methods prevalent in the domain. Meanwhile,

(Subiksha et al., 2021) provided a critical perspective

on the landscape of machine learning techniques for

IDS by conducting a survey focused on the CSE-CIC

IDS dataset. Remarkably, their findings indicated that

merely a minority of examined IDS research (18%)

ventured into the creation of novel algorithms to

rectify dataset imbalance, with the majority opting for

established methodologies.

(Liu et al., 2020) undertook a comprehensive

investigation into classification algorithms,

encompassing a diverse range including Random

Forest, Support Vector Machine (SVM), XGBoost,

LSTM, Mini-VGGNet, and AlexNet. In their study,

they introduced the innovative Difficult Set Sampling

Technique (DSSTE) to effectively mitigate the

challenge of dataset imbalance. This approach

involves a meticulous division of the dataset into

distinct 'easy' and 'difficult' subsets, strategically

leveraging the Edited Nearest Neighbour (ENN)

algorithm. The 'difficult' subset consists of instances

that share striking similarities, rendering their

differentiation challenging, while the 'easy' subset

comprises instances that are more discernible. By

employing K-Means clustering on the 'easy' subset

and intelligently compressing majority samples, the

authors iteratively merged the refined dataset with a

minority subset extracted from the 'difficult' set. This

systematic approach yielded promising results,

achieving an accuracy of 0.8284 and F1-score of

0.8166 on the NSL-KDD dataset.

(Akila et al., 2019) proposed a hybrid sampling

technique for addressing imbalanced datasets,

integrating oversampling using Synthetic Minority

Over-sampling Technique (SMOTE) and

undersampling through the ENN technique. The

proposed approach was rigorously evaluated on the

NSL-KDD dataset with various classifiers including

DMMLACS 2023 - 3rd International Special Session on Data Mining and Machine Learning Applications for Cyber Security

588

Random Forest, SVM, and Naive Bayes. The hybrid

method exhibited remarkable performance metrics,

achieving accuracy of 98.17%, precision of 96.32%,

recall of 99.84%, and F1-score of 97.02%.

Additionally, Generative Adversarial Networks

(GANs) have been applied in various domains,

including balancing datasets. (Shi et al., 2021)

introduced Sample Equalization for Intrusion

Detection System (SE-IDS), which employs GANs

for balancing industrial network datasets. They

employed a filtering mechanism to under-sample the

majority class, achieving impressive results with

AUC of 99.12, macro F1 of 98.10, macro recall of

97.23, and macro precision of 99.03. In parallel

endeavours, the CSE-CIC-IDS2018 dataset

witnessed separate applications of MCMC and GANs

as resampling techniques, with their efficacy

benchmarked against LgR as a reference. While LgR

showcased peak performance without resampling,

achieving notable accuracy (0.88), precision (0.88),

and recall (0.99), MCMC and GANs emerged as

alternative approaches for addressing data imbalance.

However, their standalone outcomes underscored the

insufficiency of MCMC and GANs as individual

resampling strategies (Abedzadeh and Jacobs, 2022)

Inspired by these findings, we embarked on an

exploration to synergize MCMC, oversampling, and

GANs in a novel framework—GANMCMCRO. This

endeavour aims to ascertain whether their combined

potential could pave the way for effective resampling

of imbalanced IDS datasets, an avenue hitherto

unexplored by existing methodologies.

3 METHODOLLOGY

3.1 Dataset

The CSE-CIC-IDS2018 dataset

(SOLARMAINFRAME, 2018) widely recognized in

the field of IDS, comprises 10 distinct files that capture

network traffic over varying timestamps which was

simulated during early 2018. It exhibits a diverse range

of network traffic attributes, including features related

to packet sizes, durations, protocols, and source-

destination pairs. Notably, this dataset is derived from

a variety of network-based attacks, including DoS,

DDoS, and port scanning. Each file, generated from

network traffic of a single day, encompasses

approximately 79 attributes. The dataset's binary

classification categorizes instances as either benign or

infiltration, maintaining an imbalanced distribution

with a ratio of 1 infiltration instance to 8 benign

instances. For the present study, the dataset dated

02/28/2018 is chosen for evaluation due to its

pronounced class imbalance, containing 540,568

benign instances and 68,462 infiltration instances.

3.2 Pre-Processing

Pre-processing involves addressing missing values

and outliers, followed by the encoding of categorical

data. Subsequently, dimensionality reduction is

carried out using the forward selection algorithm

(Galit, et al., 2019). This iterative method starts with

an empty feature set and gradually incorporates the

most significant variables, employing a Regression

algorithm to select attributes with statistically

significant (p<0.05) and high R^2 values, indicative

of their relevance to the binary classification label

(benign or infiltration). It is noteworthy that the steps

are not applied to the test set, or any other new

unlabelled data that require classification. Upon

employing this algorithm on the CSE-CIC-IDS2018

Dataset, a subset of 38 variables out of the original 79

is retained. Then, a standardization and normalization

process are applied to the data, with the label column

being encoded as 0 for Benign and 1 for Infiltration

instances. Ultimately, the data is partitioned into a

training set comprising 60% of the data and a testing

set encompassing 40%, thereby facilitating the testing

of the proposed models and the number of records did

not change after pre-processing.

3.3 Method

This section explains the MCMC algorithm, the

MCMCRO algorithm, and the GANMCMCRO

framework in a clear manner, highlighting their

unique features. In selecting the machine learning

algorithms for our experimentation on the CSE-CIC-

IDS2018 dataset, we aimed to cover a diverse range

of approaches commonly used in the field of intrusion

detection systems. The choice of algorithms was

based on their popularity in previous research studies,

as well as their potential suitability for the task at

hand. The parameters were selected through a

combination of empirical experimentation and

established best practices recommended in relevant

research. Figure 1 illustrates the method's steps,

starting from initial data preparation to achieving a

well-suited dataset for Machine Learning. We use the

Python programming language for implementation,

in line with current practices.

The process begins by dividing the pre-processed

training data into categorical and continuous parts.

The innovative MCMCRO algorithm generates data

using two strategies. Random Sampling is used for

GANMCMCRO: A Generative Adversarial Network Markov Chain Monte Carlo Random Oversampling Algorithm for Imbalance Datasets

589

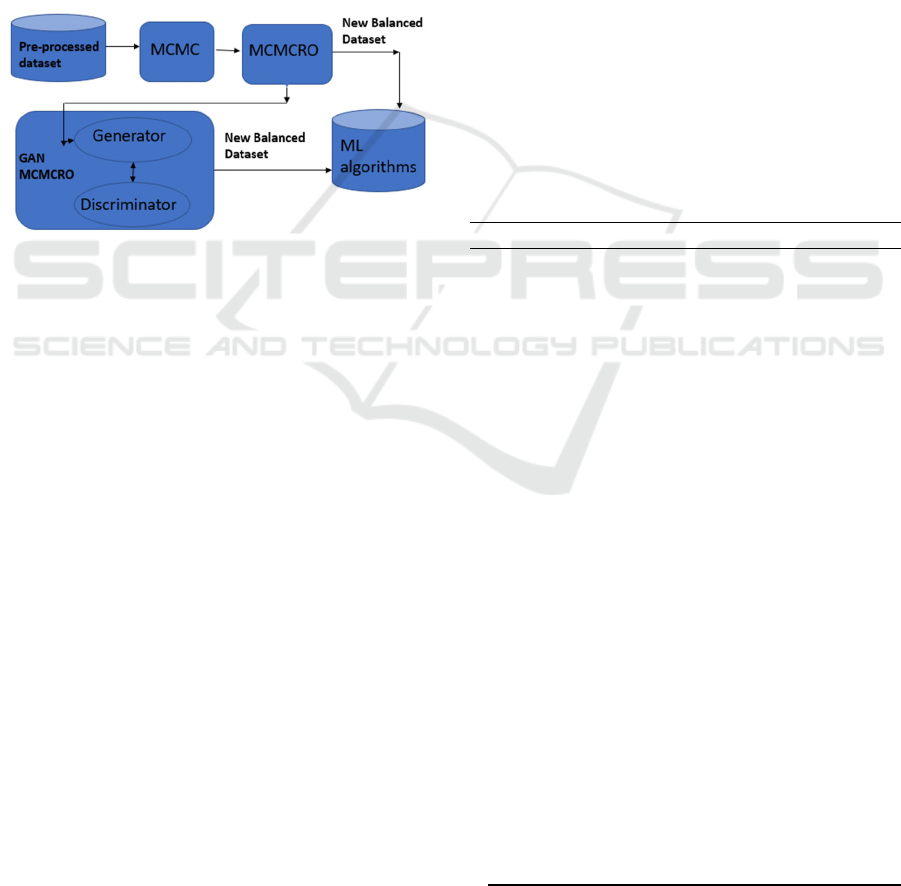
the categorical part, while the MCMC technique is

applied to the continuous part. The MCMCRO

algorithm skilfully combines these distinct datasets,

introducing a fresh approach for creating balanced

datasets.

Building on this, the GANMCMCRO framework

takes things further by taking the MCMCRO

algorithm into the generator module of the GAN

algorithm as an input, pushing the field's boundaries.

Both MCMCRO and GANMCMCRO are conceived

as novel contributions in the realm of resampling

algorithms designed explicitly for addressing the

dataset imbalance in the context of IDS. Subsequent

sections (1, 2, and 3) delve into the nuanced

descriptions of each algorithm.

Figure 1: The process of MCMCRO and GANMCMCRO.

3.3.1 MCMC Algorithm

The MCMC algorithm is a way to estimate data

patterns using probability and sampling methods

(Jason, 2019) It helps to gather related samples,

which is different from the separate sampling in

regular Monte Carlo (Rosenbluth, 2023). Leveraging

the Metropolis-Hastings (MH) algorithm (Metropolis

and Ulam, 1949) a pivotal MCMC implementation,

the procedure exhibits a complexity ranging from

lower bound O(d) to upper bound O(d^2), contingent

upon the dimensionality of the parameter space,

denoted as 'd'. The MH algorithm is particularly

useful when direct calculation of next state

probability distribution is unfeasible. Within this

project, the MH algorithm is harnessed for MCMC

realization (Moukarzel, 2018). The algorithm's

involves drawing a sample from a symmetric

distribution, evaluating the likelihood of the

generated data within the distribution, and

subsequently confirming acceptance based on the

fidelity of the new data's selection from the

distribution. Crucially, the logarithm of both the prior

and likelihood functions is employed for acceptance

or rejection determination, assuring numerical

stability and preventing underflow issues.

3.3.2 MCMCRO Algorithm

The MCMCRO algorithm combines the strengths of

both methodologies, strategically leveraging MCMC

for continuous variables and harnessing random

oversampling for categorical counterparts. The

algorithm's intricate mechanics are detailed below.

Experimental testing underscored the inadequacy of

solely oversampling the CSE-CIC-IDS2018 dataset,

as random data generation might not yield substantial

performance improvements (Abedzadeh and Jacobs,

2022). Consequently, the MCMCRO of algorithm

emerges as a solution, seamlessly fusing MCMC and

random oversampling strategies. For categorical

variables, MCMCRO artfully selects values from the

category list, while continuous data undergoes

MCMC-based synthesis, as elucidated in the Method

section. The algorithm's complexity mirrors that of

MCMC, with a lower bound of O(d) and an upper

bound of O(d^2), where 'd' represents the dimension

of the parameter space for continuous variables.

Simultaneously, the time complexity for categorical

variables remains optimal at O(1). Subsequently, the

data synthesized by the MCMCRO algorithm

Algorithm 1: The proposed MCMCRO algorithm.

Input: minority data

Output: newly generated data for the minority class

1. Select Minority Data:

1.1. Identify and isolate the minority class

instances from the dataset.

2. Generate Synthetic Data:

For each variable in the dataset, perform the

following steps:

2.1. Categorical Column:

If the current variable is categorical:

Randomly select one category from the pre-

existing data.

Since the data points are independent, random

selection of a category is appropriate for

generating new instances.

2.2. Continuous Column:

Else, if the current variable is continuous:

Apply the Markov Chain Monte Carlo (MCMC)

algorithm to generate synthetic data.

MCMC techniques leverage the current data

distribution to generate new points that

approximate the distribution.

3. Append Generated Data:

Incorporate the newly generated synthetic data

into the original dataset. This integration enriches

the dataset with artificial instances that align with

the minority class characteristics.

DMMLACS 2023 - 3rd International Special Session on Data Mining and Machine Learning Applications for Cyber Security

590

seamlessly integrates into the GANMCMCRO

framework, serving as pivotal input for training both

generator and discriminator models while iteratively

refining their weight updates. This methodological

integration epitomizes the distinctive contribution of

this work detailed in Algorithm 1.

3.3.3 GANMCMCRO Algorithm

The GANMCMCRO framework combines GANs

and the new MCMCRO resampling algorithm in a

unique way, introducing an innovative approach, as

outlined in Algorithm 2. GANs, an exemplar of

unsupervised Deep Learning, orchestrate a dynamic

interplay between two adversarial Deep Neural

Networks (DNNs) (Goodfellow et al., 2014).

Algorithm 2: The GANMCMCRO algorithm.

input: original dataset,

output: rained generator model

1. Define Discriminator:

1.1. Create a Neural Network model with 128 nodes.

1.2. Set 100 epochs for training.

1.3. Use the Dense function.

1.4. Implement LeakyReLU activation with an alpha

of 0.2.

1.5. LeakyReLU helps mitigate the dying ReLU

problem.

2. Define Generator:

2.1. Create a Neural Network model with 128 nodes.

2.2. Set 100 epochs for training.

2.3. Use the Dense function.

2.4. Implement LeakyReLU activation with an alpha

of 0.2.

3. Create Combined Model:

3.1. Build a sequential model by combining the

generator and discriminator.

3.2. Utilize the Adam optimizer.

3.3. Adam adjusts learning rates for each network

weight [15].

3.4. This model will be used to update the generator.

4. Load Original Dataset:

4.1. Import data from the original dataset for training.

5. Training Phase:

5.1. Train Discriminator:

5.1.1. Train discriminator using real data from the

dataset.

5.2. Train Generator:

5.2.1. Train generator using data generated by the

MCMCRO algorithm.

5.3. Save Generator Model:

5.3.1. Save the trained generator model for future use.

The generator crafts synthetic data by interpolating

training data, while the discriminator undertakes the

intricate task of distinguishing between authentic and

generated data (Jason, 2019). The generator operates

under a probabilistic framework, crafting data to

deceive the discriminator to minimize the

discrepancy between predicted and expected

outcomes through a minmax equation given in

Equation 1 (Jason, 2019). The inherent challenge of

GANs lies in maintaining equilibrium between the

networks, as the convergence speeds of the two

DNNs can diverge (Zhang, 2017).

𝑚𝑖𝑛𝑚𝑎𝑥𝑉



𝐺,𝐷



= 𝐸



[𝑙𝑜𝑔𝐷



𝑥



+ 𝐸



[log



1−𝐷𝐺



𝑧







]

Equation 1 minmax algorithm

The GANMCMCRO framework harnesses the

innovative MCMCRO resampling algorithm for data

generation within the GAN paradigm. By training the

discriminator on genuine data and employing the

MCMCRO algorithm within the generator, the

GANMCMCRO approach forges a symbiotic

relationship that optimally leverages both

methodologies. This symbiosis ultimately culminates

in the generation of a discriminator-enhanced

generator model, capable of engendering synthetic

data closely aligned with authentic instances. The

resultant generator model, honed through the unique

GANMCMCRO framework, emerges as a potent tool

for data synthesis. Upon training, the framework

amalgamates the newly generated data with the

original dataset, harmonizing the distribution to

rectify imbalances. This innovative data balancing

methodology is rigorously evaluated in the

subsequent sections through an array of machine

learning algorithms, demonstrating its contribution in

addressing the pivotal issue of imbalanced datasets.

3.4 Testing

To test our approach's effectiveness, we undertake a

rigorous evaluation of both MCMCRO and

GANMCMCRO using the CSE-CIC-IDS2018

dataset. Past studies have emphasized the limited

superiority of conventional methods like MCMC,

GAN, and random oversampling in comparison to

LgR on the IDS dataset (Abedzadeh and Jacobs,

2022). Our focus shifts to a comparative assessment

involving notable machine learning algorithms,

including LgR to ascertain the suitability of the

MCMC and GAN combination, as a new systematic

resampling technique for imbalanced datasets.

GANMCMCRO: A Generative Adversarial Network Markov Chain Monte Carlo Random Oversampling Algorithm for Imbalance Datasets

591

3.4.1 MCMCRO Testing

The testing process initiates with the dataset division

into distinct training and testing subsets. Within this

framework, we thoroughly train various machine

learning algorithms—Decision Tree (DT), Random

Forest (RF), LgR, Bagging (Bag), Extra Tree (ET), K

Nearest Neighbour (KNN), Linear SVC (LSVC),

Linear Discriminant Analysis (LDA), and Easy

Ensemble (EE)—on the training subset, focusing on

highlighting MCMCRO's impact. Parameters for all

algorithms remain at their default settings. Following

this training phase, each model undergoes a

comprehensive testing procedure to classify the

testing subset. The assessment includes accuracy,

precision, recall, F1 score, temporal efficiency, and t-

test (p-value) analysis. Accuracy shows out of all the

activities the system looked at, how many did it get

right? Precision represents when the system says

there's an intrusion, how often is it actually correct?

F1 Score finds a good balance between avoiding false

positives (wrongly identifying normal activity as

intrusion) and false negatives (missing actual

intrusions). Recall shows out of all the actual

intrusions.

3.4.2 GANMCMCRO Testing

Similar analyses are conducted for the

GANMCMCRO algorithm, employing consistent

dataset partitioning and assessing performance on

distinct training and testing sets. We present results

with and without the GANMCMCRO algorithm,

comparing classification metrics for the best and

worst-performing machine learning algorithms under

both scenarios

4 EXPERIMENTS

4.1 MCMCRO Testing

The discernible strides achieved through the

MCMCRO algorithm are most evident in the

substantial improvement witnessed across crucial

performance indices. This comprehensive

comparison is depicted in Table 1, wherein we

showcase the classification metrics of machine

learning algorithms both with and without the

MCMCRO algorithm applied to the CSE-CIC-

IDS2018 Dataset which was described in the

Methodology section.

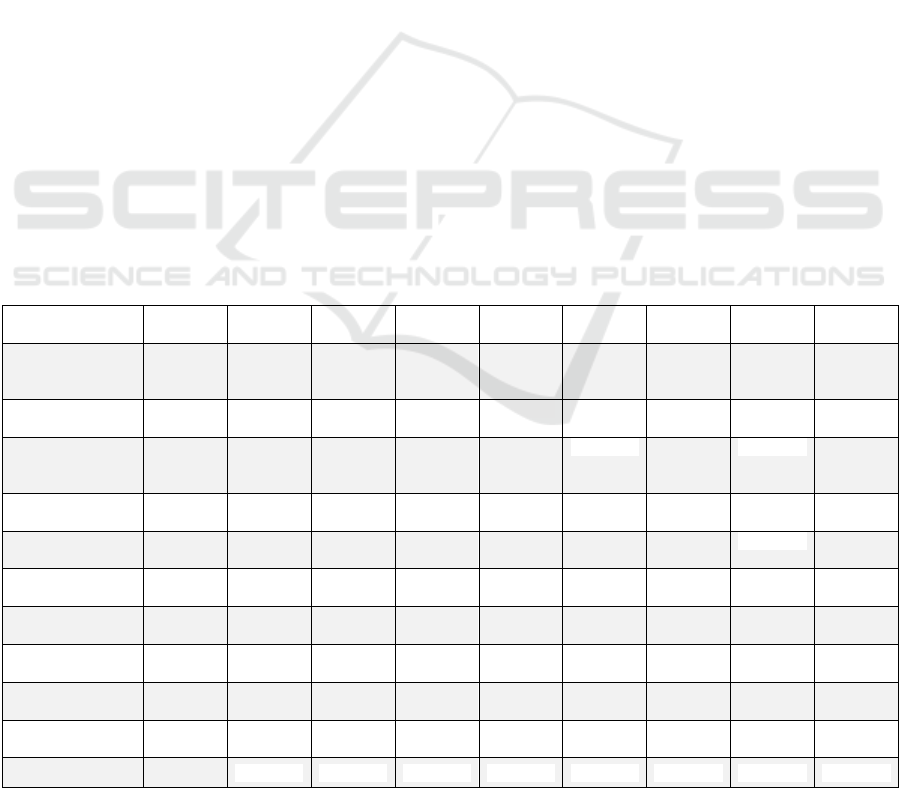
Table 1: Comparing accuracy, precision, recall, F1 score, and time of machine learning Algorithms with/without MCMCRO

algorithm. The machine learning algorithms are Decision Tree (DT), Logistic Regression (LgR), Bagging Classifier (Bag),

Random Forest (RF), Extra Tree (ET), K Nearest Neighbor (KNN), Linear SVC (LSVC), Easy Ensemble (EE), and Linear

Discriminant Analysis (LDA). Yellow highlights the best performance and blue highlights the worst performance.

Parameters/Algo

rithms

DT LgR Bag RF ET KNN LSVC LDA EE

accuracy

without

MCMCRO

0.83 0.81 0.84 0.86 0.83 0.88 0.89 0.89 0.48

accuracy with

MCMCRO

0.86 0.87 0.87 0.89 0.87 0.90 0.91 0.91 0.91

precision

without

MCMCRO

0.50 0.47 0.49 0.49 0.48 0.54

0.47 0.47

0.53

precision with

MCMCRO

0.82 0.94 00.86 0.88 0.84 0.91 0.94 0.94 0.94

F1 score without

MCMCRO

0.50 0.47 0.49 0.49 0.48 0.49 0.47 0.47

0.42

F1 score with

MCMCRO

0.81 0.87 0.83 0.84 0.82 0.86 0.87 0.87 0.87

recall without

MCMCRO

0.50 0.47 0.49 0.50 0.49 0.51 0.50 0.50 0.58

recall with

MCMCRO

0.80 0.83 0.81 0.82 0.81 0.83 0.83 0.83 0.83

time without

MCMCRO

17.99 0.50 112.59 187.05 93.74 1513.09 32.38 1.95 123.37

time with

MCMCRO

0.0384 18.51 69.99 112.58 74.98 25.00 94.51 1.94 311.97

t-test

0.042 0.038 0.044 0.045 0.039 0.049 0.054 0.054 0.004

DMMLACS 2023 - 3rd International Special Session on Data Mining and Machine Learning Applications for Cyber Security

592

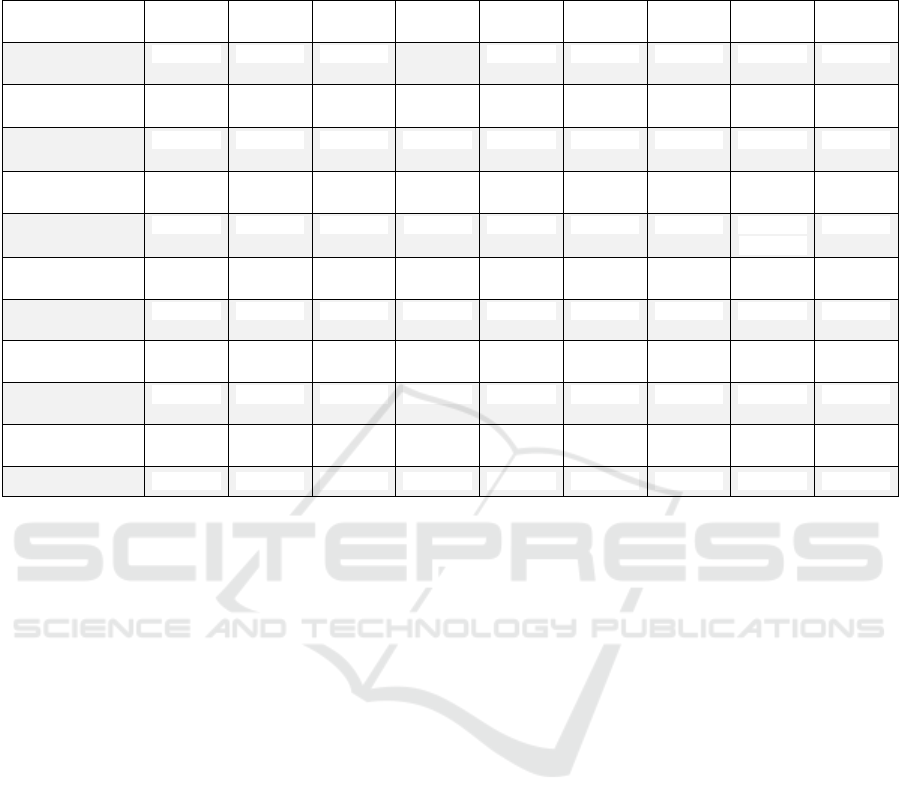
Table 2: Comparing accuracy, precision, recall, F1 score, and time of machine learning Algorithms with/without

GANMCMCRO algorithm. The machine learning algorithms are Decision Tree (DT), Logistic Regression (LgR), Bagging

Classifier (Bag), Random Forest (RF), E.

Parameters/Algo

rithms

DT LgR Bag RF ET KNN LSVC LDA EE

accuracy without

GANMCMCRO

0.83 0.89 0.84 0.86 0.83 0.88 0.89 0.89 0.48

accuracy with

GANMCMCRO

0.81 0.86 0.85 0.87 0.85 0.76 0.86 0.83 0.88

precision without

GANMCMCRO

0.50 0.47 0.49 0.49 0.48 0.54

0.47 0.47

0.53

precision with

GANMCMCRO

0.79 0.84 0.83 0.85 0.82 0.73 0.84 0.80 0.87

F1 score without

GANMCMCRO

0.50 0.47 0.49 0.49 0.48 0.49 0.47 0.47

0.42

F1 score with

GANMCMCRO

0.78 0.83 0.83 0.85 0.83 0.73 0.83 0.81 0.86

recall without

GANMCMCRO

0.50 0.50 0.49 0.50 0.49 0.51 0.50 0.50 0.58

recall with

GANMCMCRO

0.77 0.83 0.84 0.85 0.84 0.73 0.83 0.82 0.86

time without

GANMCMCRO

17.99 5.95 112.59 187.05 93.74 1513.09 32.38 1.95 123.37

time with

GANMCMCRO

29.60 5.35 223.49 371.23 125.55 9038.73 94.57 2.23 597.04

t-test

0.072 0.075 0.053 0.053 0.048 0.216 0.075 0.097 0.002

4.2 GANMCMCRO Testing

A detailed dissection of the accuracy shifts, before

and after the GANMCMCRO algorithm's application,

underscores LgR, LDA, and LSVC as pre-

GANMCMCRO leaders, achieving an accuracy of

0.89 as detailed in Table 2. However, the post-

GANMCMCRO landscape redefines excellence,

with EE commanding an accuracy of 0.88, thereby

setting a new benchmark. Precision disparities

manifest as KNN exhibits pre-GANMCMCRO

superiority with a precision of 0.54, while EE ascends

as the post-GANMCMCRO victor with a resolute

precision of 0.87.

5 DISCUSSION

Within this paper, a pioneering contribution is

unveiled through the introduction of two novel

resampling algorithms named MCMCRO and

GANMCMCRO, further augmenting its potential.

While our proposed algorithms exhibit significant

promise, it's noteworthy to mention a current

limitation regarding their computational time. The

findings of the previous research (Abedzadeh and

Jacobs, 2022) revealed notable metrics, with the LgR

algorithm trained on different data from the same

dataset achieving an accuracy of 0.88, precision of

0.88, and a commendable recall of 0.99. This proved

to be the highest performance level compared with

MCMC, random oversampling, and GAN. In the

present study, we undertake a comprehensive

comparison between our results obtained with the

LgR algorithm before and after the implementation of

both the MCMCRO and GANMCMCMRO

resampling techniques. The primary aim of this

analysis is to discern the potential enhancement that

these resampling methodologies can bring to the

performance of machine learning algorithms,

specifically the LgR algorithm. By evaluating the

changes in performance metrics following the

application of these techniques, we seek to provide

insights into the effectiveness and impact of these

resampling strategies on model performance and

overall predictive capabilities.

A pivotal aspect of our work lies in the

performance evaluation of different machine learning

algorithms under the influence of MCMCRO and

GANMCMCRO. The outcome of this analysis

highlights the commendable performance of linear

discriminant analysis as the optimal machine learning

algorithm within the MCMCRO context and easy

ensemble within the GANMCMCRO context.

GANMCMCRO: A Generative Adversarial Network Markov Chain Monte Carlo Random Oversampling Algorithm for Imbalance Datasets

593

6 CONCLUSION

In the realm of Intrusion Detection Systems (IDS), a

critical bastion safeguarding vulnerable network

environments from various covert attacks, the

challenge arises from these threats' ability to mimic

legitimate network actions. This proves to be a

significant hurdle for machine learning algorithms,

which struggle due to the scarcity of malicious

instances for effective training. In response, this study

introduces pioneering solutions: the MCMCRO and

GANMCMCRO algorithms. MCMCRO creatively

tackles imbalanced datasets by generating synthetic

data, achieving equilibrium in the CSE-CIC-IDS2018

Dataset. Expanding on this, the GANMCMCRO

framework blends MCMCRO with GANs,

augmenting data generation and balance.

The impact of these innovations resonates in

experimental outcomes. Integrating MCMCRO with

linear discriminant analysis redefines Infiltration

activity detection, yielding substantial precision,

recall, F1 score, and accuracy enhancements. These

advancements are statistically significant (p<0.054),

reflecting the potency of the approach. Beyond

compatibility with diverse machine learning

algorithms, the optimized integration within

GANMCMCRO showcases adaptability and

effectiveness, as seen in the results applying

MCMCRO and GANMCMCRO to the CSE-CIC-

IDS2018 Dataset alongside Easy Ensemble.

In the landscape of IDS and imbalanced data

handling, these contributions mark a pioneering

milestone, forging innovative pathways for network

security. With an anticipation of future extensions to

complex datasets, this approach empowers machine

learning algorithms for precise network defence.

REFERENCES

C. Vij and H. Saini, “Intrusion Detection Systems:

Conceptual Study and Review,” 2021 6

International

Conference on Signal Processing, Computing and

Control (ISPCC), 2021, pp. 694-700.

S. Seeber and G.D. Rodosek, “Towards an adaptive and

effective IDS using OpenFlow”, IFIP International

Conference on Autonomous Infrastructure

Management and Security, pp. 134-139, 2015, June.

N. Abedzadeh, M. Jacobs, “A Survey in Techniques for

Imbalanced IDS datasets,” ICICCS 2022: 16.

International Conference on Intelligent Computing and

Control Systems, August 08-09, 2022, in Montreal,

Canada.

N. Abedzadeh, M. Jacobs, “Using Markov Chain Monte

Carlo Algorithm for Sampling Imbalance Binary IDS

datasets,” 12

International Workshop on Security,

Privacy, Trust for Internet of Things (IoTSPT) at the

ICCCN 2022, IEEE, July 2022 in Hawaii.

N. Abedzadeh, M. Jacobs, “A Reinforcement Learning

Framework with Oversampling and Undersampling

Algorithms for Intrusion Detection System,” AIADFSB

journal of Applied Sciences, 2023.

Subiksha Srinivasa Gopalan1, Dharshini Ravikumar1, Dino

Linekar, Ali Raza1, Maheen Hasib, “Balancing

Approaches towards ML for IDS: A Survey for the

CSE-CIC IDS dataset,” 2020 International Conference

on Communications, Signal Processing, and their

Applications (ICCSPA), IEEE, 2021.

Lan Liu 1, Pengcheng Wang, Jun Lin, and Langzhou Liu,

“Intrusion Detection of Imbalanced Network Traffic

Based on Machine Learning and Deep Learning,” IEEE

access, 2020.

Akila, R., Elayaraja, E., & Sudha, A. (2019). Handling

Imbalanced Intrusion Detection System Data using

Hybrid Sampling and Machine Learning Techniques.

International Journal of Computer Applications,

975(8887), 13-17.

P. Shi, X. Chen, X. Kong and X. Cao, "SE-IDS: A Sample

Equalization Method for Intrusion Detection in

Industrial Control System," 2021 36th Youth Academic

Annual Conference of Chinese Association of

Automation (YAC), Nanchang, China, 2021, pp. 189-

195, doi: 10.1109/YAC53711.2021.9486601.

SOLARMAINFRAME, "IDS 2018 Intrusion CSVs (CSE-

CIC-IDS2018)," https://www.kaggle.com/datasets/

solarmainframe/ids-intrusion-csv, 2018.

Galit Shmueli, Peter C. Bruce, Peter Gedeck, Nitin R. Patel,

“Data Mining for Business Analytics: Concepts,

Techniques and Applications in Python”, Mathematics,

Nov 5, 2019.

Jason Brownlee, "A Gentle Introduction to Markov Chain

Monte Carlo for Probability,”, https://machinelearning

mastery.com/markov-chain-monte-carlo-for-probabili

ty/, 2019

M. N. Rosenbluth, “in The Monte Carlo Method in the

Physical Sciences”, edited by J. E. Gubernatis

(American Institute of Physics), New York, 200

N. Metropolis and S. Ulam, “The Monte Carlo method,” J.

Am. Stat. Assoc., vol. 44, no. 247, pp. 335–341, 1949.

Joseph Moukarzel, “From Scratch: Bayesian Inference,

Markov Chain Monte Carlo and Metropolis Hastings,

in python,” https://towardsdatascience.com/from-

scratch-bayesian-inference-markov-chain-monte-

carlo-and-metropolis-hastings-in-python-

ef21a29e25a, Nov 2018.

Goodfellow et al, Generative Adversarial Networks (2014)

Jason Brownlee, “How to Develop a Conditional GAN

(cGAN) From Scratch”, https://machinelearningmaste

ry.com/how-to-develop-a-conditional-generative-adve

rsarial-network-from-scratch/, July 2019

H. Zhang, C. Luo, X. Yu, and P. Ren, “Mcmc based

generative adversarial networks for handwritten

numeral augmentation,” in Proc. Int. Conf. Commun.

Signal Process. Syst., 2017, pp. 2702–2710.

DMMLACS 2023 - 3rd International Special Session on Data Mining and Machine Learning Applications for Cyber Security

594