Improving Reward Estimation in Goal-Conditioned Imitation Learning

with Counterfactual Data and Structural Causal Models

Mohamed Khalil Jabri

1,2,3,4

, Panagiotis Papadakis

1,4

, Ehsan Abbasnejad

2,3,4

, Gilles Coppin

1,4

and Javen Shi

2,3,4

IMT Atlantique, Lab-STICC, UMR CNRS 6285, F-29238 Brest, France

The University of Adelaide, Adelaide, Australia

Australian Institute for Machine Learning, Adelaide, Australia

IRL CROSSING, CNRS, Adelaide, Australia

Keywords:

Imitation Learning, Causality, Structural Causal Models (SCMs), Counterfactual Reasoning.

Abstract:

Imitation learning has emerged as a pragmatic alternative to reinforcement learning for teaching agents to

execute speciﬁc tasks, mitigating the complexity associated with reward engineering. However, the deploy-

ment of imitation learning in real-world scenarios is hampered by numerous challenges. Often, the scarcity

and expense of demonstration data hinder the effectiveness of imitation learning algorithms. In this paper, we

present a novel approach to enhance the sample efﬁciency of goal-conditioned imitation learning. Leveraging

the principles of causality, we harness structural causal models as a formalism to generate counterfactual data.

These counterfactual instances are used as additional training data, effectively improving the learning process.

By incorporating causal insights, our method demonstrates its ability to improve imitation learning efﬁciency

by capitalizing on generated counterfactual data. Through experiments on simulated robotic manipulation

tasks, such as pushing, moving, and sliding objects, we showcase how our approach allows for the learning of

better reward functions resulting in improved performance with a limited number of demonstrations, paving

the way for a more practical and effective implementation of imitation learning in real-world scenarios.

1 INTRODUCTION

The pursuit of training autonomous agents to per-

form tasks efﬁciently and effectively remains a fun-

damental challenge. While reinforcement learning

has made signiﬁcant strides (Sutton and Barto, 2018),

it is often plagued by the reliance on reward engi-

neering, making it impractical for real-world applica-

tions. One promising alternative is imitation learning,

a paradigm that offers notable advantages over rein-

forcement learning, as it alleviates the arduous task of

reward engineering and improves data efﬁciency by

reducing the need for extensive trial and error.

Despite its promise, however, imitation learning is

not without limitations. Acquiring expert demonstra-

tions can be a prohibitively expensive and resource-

intensive process, cumbersome or even unfeasible. In

turn, the reliance on a limited number of demonstra-

tions often leads to suboptimal performance or results

in catastrophic failures when the training data is not

sufﬁciently representative of the task’s complexity.

In recent years, there has been a growing recog-

nition of the role of causality in improving learning-

based approaches (Sch

olkopf, 2019) (Kaddour et al.,

2022). Causality, the study of cause-and-effect rela-

tionships, has emerged as a powerful tool for gaining

a deeper understanding of how agents interact with

their environments. It provides a framework for rea-

soning about the consequences of different actions

and interventions, which offers the potential to en-

hance the robustness and efﬁciency of learning.

This work presents a novel causal approach to im-

prove the learning of policies from limited demonstra-

tions in goal-conditioned settings, leveraging causal-

ity by learning Structural Causal Models (SCMs) that

represent the expert’s behavior within its environ-

ment. We harness the learned SCM to generate coun-

terfactual data that simulate what would have hap-

pened had the expert pursued different goals. The

counterfactual data serves as supplementary training

data for goal-conditioned imitation learning, allowing

agents to learn more effectively with less data.

The key contributions of this work include 1) for-

mulating a methodology to learn the SCM of high-

level expert-environment interactions (section 3.2.1),

2) using SCM to generate counterfactual data that

Jabri, M., Papadakis, P., Abbasnejad, E., Coppin, G. and Shi, J.

Improving Reward Estimation in Goal-Conditioned Imitation Learning with Counterfactual Data and Structural Causal Models.

DOI: 10.5220/0012268200003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 329-337

ISBN: 978-989-758-670-5; ISSN: 2184-2809

329

correspond to alternative goals and actions (section

3.2.2), and 3) demonstrating how the counterfactual

data could serve as additional training data to improve

learning (section 4.2). We evaluate our method in a

series of simulated robotic manipulation tasks con-

sisting of pushing, moving and sliding objects with

a 7-DoF robotic arm. Experiments demonstrate that

our method is able to improve goal-conditioned, gen-

erative adversarial imitation learning, especially when

few demonstrations are available. The obtained re-

sults shed light on the potential of causality to ad-

dress fundamental challenges in imitation learning

and to advance the capabilities of autonomous agents

in learning complex tasks.

2 BACKGROUND

2.1 Imitation Learning

Imitation learning enables agents to acquire skills by

imitating expert behavior rather than relying on trial

and error. Several key approaches have emerged in

imitation learning. Behavior cloning involves learn-

ing a policy that mimics the actions of an expert

based on observed state-action pairs (Bain and Sam-

mut, 1999). Inverse reinforcement learning (Russell,

1998) (Mnih et al., 2013) (Silver et al., 2016) aims to

recover the underlying reward function from expert

demonstrations, allowing agents to generalize beyond

speciﬁc trajectories. Generative Adversarial Imitation

Learning (GAIL) (Ho and Ermon, 2016) bypasses this

intermediate step and directly learns the policy from

demonstrations by formulating imitation learning as

a two-player minimax game between a discriminator

D and the policy π. The discriminator aims to distin-

guish between expert trajectories and agent-generated

trajectories, while the policy generator seeks to pro-

duce trajectories that are indistinguishable from ex-

pert data.

Goal-Conditioned Imitation Learning. In goal-

conditioned imitation learning (Liu et al., 2022), each

task or trajectory is uniquely characterized by a dis-

tinct goal state. Thus, the policy is conditioned

on both the observed states and designated goals,

namely, as π : S × G → A.

One common challenge in goal-conditioned set-

tings is sparse rewards (Hare, 2019), typically taking

on a binary form that denotes goal attainment. This

poses a substantial challenge for traditional reinforce-

ment learning (RL) methods due to the absence of in-

formative reward signals in unsuccessful trajectories.

Hindsight Experience Replay (HER) (Andrychowicz

et al., 2017) offers a remedy to this problem by intro-

ducing a relabeling trick that reinterprets unsuccessful

trajectories as valuable learning experience. By treat-

ing these trajectories as successful ones with different

goal states, i.e. states that were actually achieved, the

policy is able to learn from its failures which drasti-

cally improves sample efﬁciency in RL.

GoalGAIL (Ding et al., 2019) combines GAIL

with HER relabeling strategy, which yields notable

improvements in learning efﬁciency and makes it a

compelling approach for goal-conditioned imitation

learning. Our proposed approach extends GoalGAIL

by leveraging counterfactual data to improve reward

learning efﬁciency.

2.2 Structural Causal Models (SCMs)

Structural Causal Models (SCMs) (Pearl et al., 2000)

offer a formal framework for modeling causal re-

lationships in a system. At the core of SCMs lie

two fundamental types of variables: endogenous

and exogenous. Exogenous variables represent un-

controllable external factors and serve as indepen-

dent sources of variation. Endogenous variables, on

the other hand, represent outcomes inﬂuenced by

other variables within the model through structural

equations, capturing the system’s internal dynamics.

These equations usually take the following form:

= f

(Parents(X

),U

) (1)

where X

and U

denote endogenous and exogenous

variables respectively, f

is a deterministic function

specifying the causal dependencies between the vari-

ables, and Parents(X) denotes the variables that have

a direct causal effect on X. An SCM is typically as-

sociated with a Directed Acyclic Graph (DAG) as a

graphical representation of the causal system, where

the nodes correspond to variables, and the directed

edges indicate causal dependencies.

2.3 Counterfactual Reasoning with

SCMs

Structural Causal Models (SCMs) offer a formal

framework for conducting counterfactual reasoning

(Pearl, 2013). The process of counterfactual reason-

ing with SCMs involves three essential steps.

• Abduction: This step consists in recovering the

values of exogenous variables within the SCM

based on the observed evidence.

• Intervention: Once exogenous variables are in-

ferred, we modify the SCM by intervening on one

or more variables of interest. This represents a

LICARSA 2023 - Special Session on Learning in Control and Robotic Systems Applications

330

hypothetical change to the system, allowing to ex-

plore ”what if” scenarios.

• Prediction: We can predict the counterfactual

outcome of interest using the updated structural

equations within the modiﬁed SCM.

3 CAUSAL MECHANISM AND

COUNTERFACTUAL

REASONING

3.1 Problem Formulation

In this work, we consider a goal-conditioned

Markov Decision Process (MDP) deﬁned by a tuple

(S, G, A, P, R, γ), where S denotes the state space, A

the action space, G ⊂ S the goal space, P(s

t+1

, a

)

the transition dynamics, R(s

, a

, g

) the true reward

function indicating whether the goal was achieved and

0 < γ < 1 the discount factor.

Given a set of N expert trajectories D

{(s

, a

, g

), 0 ⩽ t ⩽ T }

1⩽i⩽N

, our goal is to learn a

policy π that matches the distribution of the trajecto-

ries in the demonstrations by optimizing the following

objective:

min

max

[logD(s, g, a)] + E

[log(1 − D(s, g, a))]

(2)

where π

denotes the expert policy and D a discrimi-

nator that outputs a score for each tuple (s, g, a).

In goal-conditioned settings, the policy is typi-

cally conditioned on the current state and the goal. In

this work, we make the choice of introducing a latent

variable denoted m

, which we refer to as the moti-

vator. m

is causally affected by both s

and g and

represents the intermediate relative goal at state s

relation to achieving the absolute goal g.

From a causal perspective, the concept of interme-

diate relative goal is more informative to the agent.

The policy is therefore conditioned on m

instead of

, g

). One could argue that m would naturally corre-

spond to the intermediate features learned by a neural

policy. However, this is not the case in our formu-

lation. To understand this, let us start by depicting

the SCM that we assume and its corresponding causal

graph.

We assume that our SCM satisﬁes the following

structural equation, as shown in the causal graph in

Figure 1:

= f

, g, u

) (3)

where u

denotes the exogenous variable capturing the

external factors affecting the system as explained in

section 2.2.

For simplicity, we omit time indexes for all vari-

ables in the remainder of this work, which should

not introduce any ambiguity. Our goal is to learn

the causal mechanism governing the generation of

m, which corresponds to the above equation. Subse-

quently, we want to learn a policy conditioned on the

motivator m. Details on how to learn the SCM and

generate counterfactual data are provided in section

3.2 (section 4 describes how we leverage the learned

SCM and the counterfactual data to learn the policy).

We therefore separate the processes of learning the

structural equation of m and the policy π. Learning

the former can be thought of as learning a high-level

causal policy whose role is to generate abstract rel-

ative subgoals. The reason we choose to learn the

causal model for a high-level policy is that it is sim-

pler and easier than learning ﬁne-grained causal rela-

tionships directly linking the state and goal pairs to

actions, given a limited amount of expert data. To

make an analogy, this can be thought of as learning

the overall directions in a robot navigation problem

instead of learning speciﬁc ﬁne-grained actions such

as controlling the forces applied by the robot actua-

tors.

This results in two beneﬁts. First, once the SCM is

learned, one can reason counterfactually about what

would have happened had the goal been different.

This allows us to generate high-level counterfactual

policy demonstrations in the form of (s, g, m). By

conditioning the policy on counterfactual motivators,

one can indirectly obtain counterfactual actions un-

der a given policy. Second, by conditioning on m,

we are separating policy training from the process of

identifying relevant causal features. Neural networks

are known for their tendency to learn spurious corre-

lations rather than task-relevant features (Shah et al.,

2020). By learning the causal mechanism of m and

conditioning the policy on it, we are limiting the ex-

posure of the policy to spurious features, as these will

rather be captured by the exogenous variable u.

3.2 SCM Learning and Counterfactuals

Generation

Given the SCM in equation (3), one could reason

counterfactually for what would have been the action

taken by the agent had its motivator been different. At

a given timestep t, given an observed triplet (s, g, a),

we want to predict the counterfactual motivator for an

alternative goal g′ and infer the agent action given that

motivator under the current policy.

Recall the three steps involved in the counterfac-

tual reasoning process (see section 2.3). The ﬁrst

step consists of recovering the noise variable from

Improving Reward Estimation in Goal-Conditioned Imitation Learning with Counterfactual Data and Structural Causal Models

331

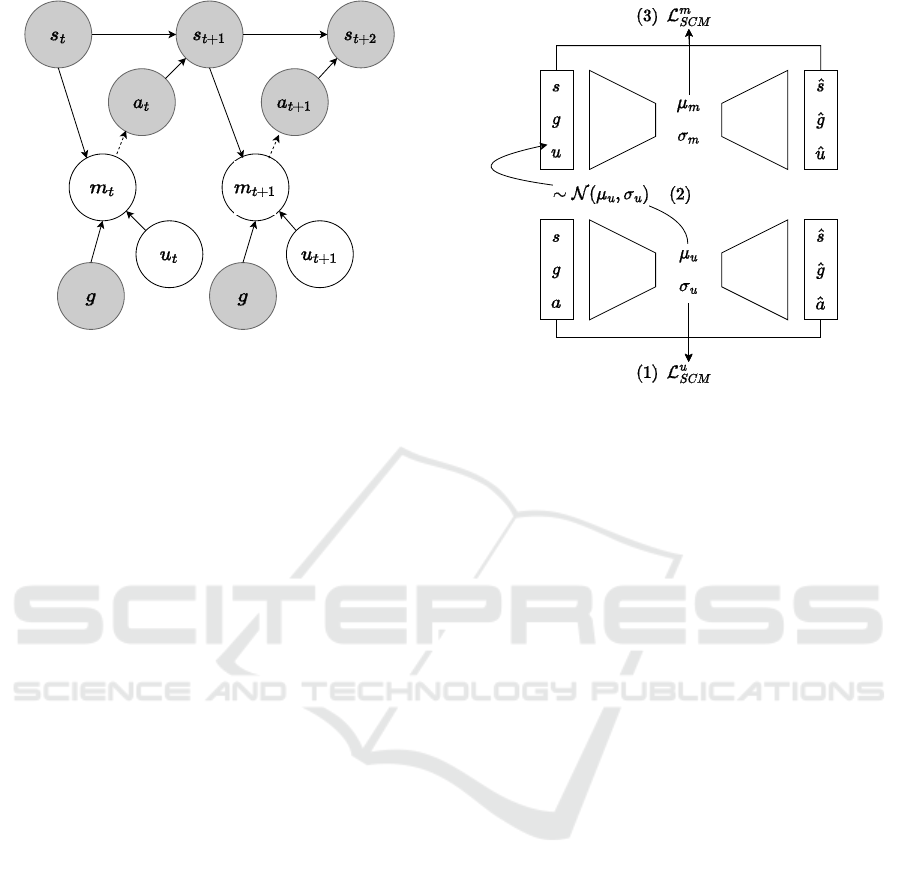
Figure 1: The causal graph describing the expert trajec-

tories’ generation process between t and t + 2. Solid and

dashed lines denote causal and conditional dependence, re-

spectively. Shaded nodes are observed variables.

the observed evidence, which corresponds in our case

to (s,g, a). Thus, we need to learn an inverse map-

ping from these observed variables to the indepen-

dent noise term u which we assume follows a standard

normal distribution. Similarly, to be able to perform

the second and third steps, it is necessary to approx-

imate the structural function f

in equation (3). To

capture the causal relationship between the variables,

both functions need to be learned simultaneously so

as to capture the joint distribution p(m,u|s, g, a).

3.2.1 Learning the SCM

We cast the learning of both functions in a dou-

ble Variational Autoencoder (VAE) (Kingma and

Welling, 2013) setting, allowing us to approximate

the two functions concurrently.

The encoders of the VAEs parameterize the

mean and log-variance of two Gaussian distribu-

tions: q

(m|s, g, u) = N (µ

(s, g, u), σ

(s, g, u)) and

(u|s, g, a) = N (µ

(s, g, a), σ

(s, g, a)). The corre-

sponding decoders are deﬁned as d

(m) = (ˆs, ˆg, ˆu)

and d

(u) = ( ˆs, ˆg, ˆa). Let D

SCM

be a set of trajecto-

ries used to learn the SCM (we discuss in section 4.1

the choice of the training trajectories for the SCM).

To learn the SCM from the observed trajectories in

SCM

, we alternate between optimizing the following

two losses:

SCM

= E

u∼q

(u|s,g,a),s,g,a∼D

SCM

||(d

(u)−(s, g, a))||

KL(q

(u|s, g, a)∥N (0, 1)) (4)

Figure 2: The three steps of the SCM learning loop: (1)

Update u’s VAE. (2) Sample u batch from the updated dis-

tribution. (3) Update m’s VAE.

SCM

= E

m∼q

(m|s,g,u),u∼q

(u|s,g,a),s,g,a∼D

SCM

||(d

(m) − (s, g, u))||

KL(q

(m|s, g, u)∥N (0, 1)) (5)

In each iteration, we sample a u batch from the

updated distribution q

(s, g, a) to use as input to the

VAE corresponding to m. This is essential to learn

the dependencies between the exogenous variable m

and the motivator m. Figure 2 summarizes the SCM

learning steps.

3.2.2 Generating Counterfactual Data

Once we have approximated the SCM, we can gen-

erate counterfactual data points following the steps

in section 2.3. Let e

and e

denote the func-

tions giving the deterministic VAEs’ outputs, i.e. the

learned distributions’ means: e

(s, g, u) = µ

(s, g, u)

and e

(s, g, a) = µ

(s, g, a). For a given triplet (s, g, a),

we denote the corresponding motivator as m

s,g

(s, g, e

(s, g, a)). Given an alternative goal g

′

, we

denote the corresponding counterfactual motivator as

′

s,g

. To predict m

′

s,g

, we use e

to recover the noise

term from the observed evidence (s, g, a) and we in-

ject it in the structural equation (3) where we also set

the goal to g′. The predicted counterfactual motivator

can then be written as:

′

s,g

= e

(s, g

′

, e

(s, g, a)) (6)

Figure 3 summarizes the counterfactual data genera-

tion steps.

LICARSA 2023 - Special Session on Learning in Control and Robotic Systems Applications

332

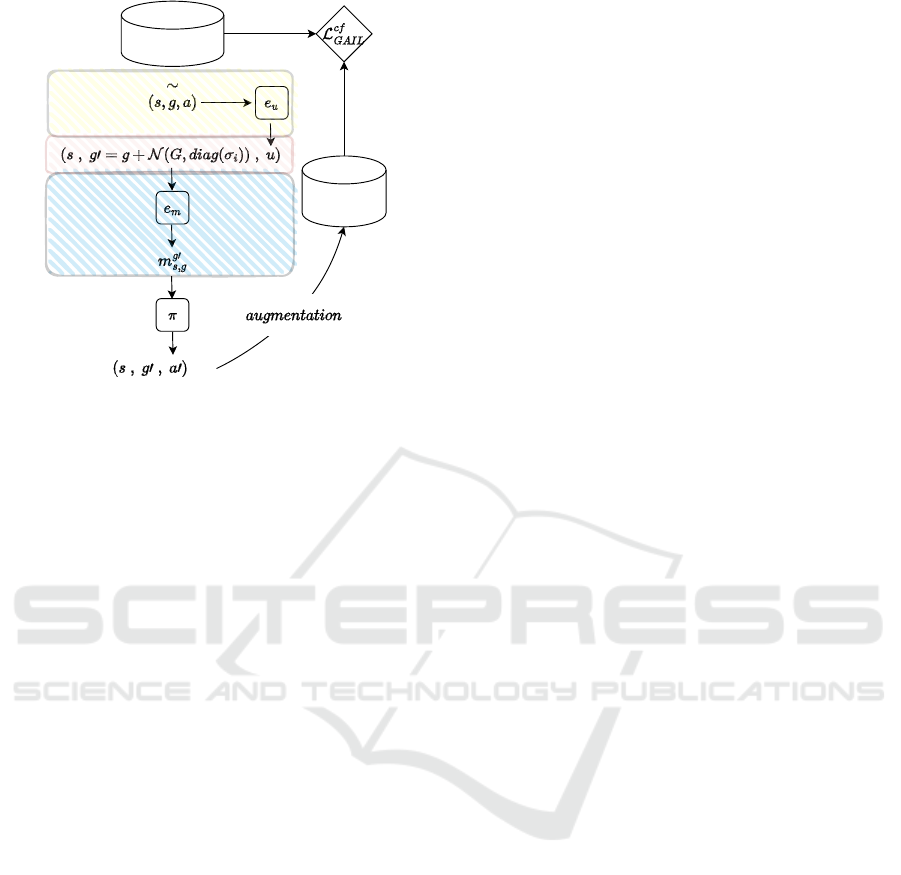
demonstrations

policy

trajectories

Figure 3: Counterfactual data generation: The yellow, red

and blue boxes denote the abduction, intervention and pre-

diction steps respectively.

4 POLICY LEARNING WITH

CAUSAL REASONING

We base our approach on GoalGAIL. GoalGAIL op-

timizes equation (2) by alternating between two steps:

learning the reward function and optimizing the pol-

icy. In the ﬁrst step, the discriminator is trained to

minimize the GAIL loss:

GAIL

= E

s,g,a∼D

[logD(s, g, a)] +

s,g,a∼D

[log(1 − D(s, g, a))] (7)

where D

denotes the trajectories generated by the

current version of the policy, i.e. the on-policy data.

For the second step, the policy is optimized using any

RL algorithm, with respect to the following reward

r = D(s, g, a).

In our approach, we start by pretraining the SCM

from expert demonstrations. Then, as we learn the

policy and the reward, we keep ﬁnetuning the learned

SCM. The learned SCM is used at each step to gener-

ate counterfactual data for reward learning. For pol-

icy learning, the only difference is that it is no longer

conditioned on the state-goal pairs but rather on the

causal motivator learned by the SCM. In the follow-

ing, we detail each of these three steps.

4.1 Pretraining and Finetuning the

SCM

At the beginning of the learning process, we want

to capture all the causal information in the available

demonstrations. We ﬁt the two VAEs discussed in

3.2 on the expert demonstrations. In this step, D

SCM

in equations (4) and (5) is set to D

. However, the

available demonstrations are usually limited and in-

sufﬁcient to learn complex patterns of the SCM. To

alleviate this problem, at each iteration, we ﬁnetune

the VAEs on data from both the expert demonstrations

and the trajectories generated by the current policy.

SCM

is then set to D

∪D

. As we update the policy,

the quality of its trajectories improves, which beneﬁts

the SCM. Policy trajectories prevent the SCM from

overﬁtting to the limited demonstration data without

decreasing the performance.

4.2 Learning the Reward with

Counterfactual Demonstrations

In GoalGAIL, the discriminator is optimized to learn

to distinguish expert trajectories from those generated

by the policy. While adversarial imitation learning

provides a direct way to learn from demonstrations

and bypass the intermediate step in IRL, they inher-

ently suffer from the instability of the learning pro-

cess as in GANs (Arjovsky and Bottou, 2017). Such

a problem is even more severe in adversarial imitation

learning because 1) expert data is very limited and 2)

the generator, i.e. the policy, is trained by policy gra-

dient (Sutton et al., 1999) and not by simple gradient

descent as in GANs. Adversarial training of GANs

is unstable because it requires a balance between the

discriminator and the policy, which is hard to achieve,

especially at the beginning of the learning. In early it-

erations, the trajectories generated by the policy are

random, which makes them easily distinguishable by

the discriminator. This leads to having a too-powerful

discriminator, making its feedback uninformative for

the policy. Another problem is that of mode collapse.

Mode collapse occurs when the generator, i.e. the pol-

icy, outputs a narrow set of trajectories instead of ex-

ploring the whole policy space. This problem is more

likely to occur when the training data is limited.

We show that counterfactual examples can help

mitigate the problems mentioned above. Since the

SCM learns the expert behavior, it is natural to gener-

ate counterfactuals from expert demonstrations rather

than policy rollouts. An intuitive way to use these

counterfactual examples is to add them as supplemen-

tary demonstrations. However, it is more efﬁcient to

use such counterfactual demonstrations to augment

policy data. In fact, given the low quality of coun-

terfactuals compared to real expert demonstrations,

adding them to the demonstrations may in fact de-

crease the performance. However, these counterfac-

tuals could serve well as policy data.

Improving Reward Estimation in Goal-Conditioned Imitation Learning with Counterfactual Data and Structural Causal Models

333

To understand the intuition behind such a claim,

we should recall that the counterfactual data is more

difﬁcult to classify for the discriminator because it

resembles the expert demonstrations at the motivator

level. This can mitigate the ﬁrst problem mentioned

above by preventing the discriminator from being too

powerful in classifying trajectories. This is in line

with work in supervised learning showing that learn-

ing from difﬁcult examples is more efﬁcient (Robin-

son et al., 2021). Furthermore, by adding counterfac-

tuals, the policy data becomes more diverse, which

helps prevent mode collapse. It is also worth not-

ing that as the policy improves, the quality of coun-

terfactuals improves, and classifying them becomes

even more difﬁcult. The discriminator output then be-

comes more and more informative for the policy. We

show in the experiments that this allows learning bet-

ter reward functions.

The modiﬁed GAIL loss then becomes:

c f

GAIL

= E

s,g,a∼D

∪D

logD(s, g, a)+

s,g,a∼D

expert

log(1 − D(s, a, g)) (8)

where D

denotes the counterfactual policy data.

This corresponds to D

with every data point rela-

beled counterfactually as explained in 3.2 using alter-

native goals sampled by adding Gaussian noise with

variance σ

to the original ones: D

= {(s, g′, a′ =

π(s, m

g′

s,g

), g′ ∼ N (g, diag(σ)), (s, g) ∼ D

}

4.3 Learning the Policy

The policy is optimized using an RL algorithm with

respect to the reward output by the discriminator. To

beneﬁt from HER, we use an off-policy algorithm,

namely DDPG (Lillicrap et al., 2015), as in the origi-

nal GoalGAIL work. In our setting, the policy input is

no longer the state and goal pairs, but rather the mo-

tivator m inferred from (s, g, u). When learning the

SCM, u is sampled from the distribution output by

the u’s VAE encoder for a given (s, g, a) triple. How-

ever, when learning the policy or interacting with the

environment, we only have access to (s, g). We over-

come this problem by using the average mean output

by u’s VAE encoder across all the trajectories gener-

ated by both the policy and the expert. We denote this

inference noise term as µ

∗

. The predicted actions then

become a = π(e

(s, g, µ

∗

)). Consequently, DDPG’s

Q-function becomes:

= E

(s,g,a,s

′

)∼R

[(Q(s, g, a)−

(D(s, g, a) + γQ(s

′

, π(s

′

, g, π(s

′

, g, µ

∗

))))

] (9)

where s

′

denotes the next state reached after taking

action a in state s and R denotes the policy replay

buffer containing all the trajectories generated by the

policy since the beginning of the learning. Similarly,

DDPG’s policy objective becomes:

= E

s∼π

[Q(s, π(s, g, µ

∗

))] (10)

Algorithm 1 summarizes the entire approach.

Input: Random π, Demonstrations set D

Empty buffers R , D

SCM

and D

// SCM pretraining

SCM

← D

for k=1 to n do

Update SCM using eq. (4) and (5)

end

// Policy Learning Loop

for k=1 to m do

// Interaction with the

Environment

← {(s, g, a) ∼ π}

R ← R ∪ D

// SCM Finetuning

SCM

← D

∪ D

Update SCM using eq. (4) and (5)

// Counterfactuals Generation

← {(s, g′, a′ = π(s, m

g′

s,g

), g′ ∼

N (g, diag(σ)), (s, g) ∼ D

}

// Reward Update

Minimize L

c f

GAIL

in eq. (8)

// Policy Update

Update Q-function using eq. (9)

Update π using eq. (10)

end

Algorithm 1: Overview of the proposed approach.

5 EXPERIMENTAL RESULTS

We conduct experiments in a simulated environment

featuring a 7-DoF Fetch Mobile Manipulator arm

with a two-ﬁngered parallel gripper (Plappert et al.,

2018). We tackle three diverse manipulation tasks.

1) Push: The agent’s mission is to move a box by

pushing it along a table, guiding it to reach a prede-

termined goal position. 2) Pick and Place: The agent

has to grasp a box from a table using its gripper and

then move it to a designated goal position. 3) Push:

The agent’s task is to hit a puck resting on a table in

such a way that it slides and comes to a halt at the

speciﬁc goal position.

Our experiments aim to address three key ques-

tions. 1) Does our method improve the agent’s per-

formance compared to the baseline (GoalGAIL)? 2)

What impact does the incorporation of counterfactual

data have on the learned reward function? 3) Can

LICARSA 2023 - Special Session on Learning in Control and Robotic Systems Applications

334

our method perform efﬁciently with fewer demonstra-

tions?

5.1 Sample Efﬁciency

To assess the effectiveness of our approach, we

present in Figure 4 the learning curves for each of the

three tasks with 10 expert demonstrations. The curves

illustrate the success rate achieved by both GoalGAIL

and our method over the course of the training. The

success rate is computed over 10 test episodes, and the

curves show the mean and standard deviation of the

results averaged over 5 independent random seeds.

The obtained learning curves show that our

method consistently outperforms GoalGAIL in terms

of both ﬁnal success rate and convergence speed

across all three tasks. This suggests that the perfor-

mance gain can be attributed to our method’s abil-

ity to leverage counterfactual data. To gain deeper

insights into how the counterfactual data affects the

learning process, we examine the difference between

the reward functions learned by our method and the

baseline.

5.2 Learned Rewards with

Counterfactuals

In this section, we focus our analysis on the Pick and

Place task with 10 expert demonstrations. We dissect

the inﬂuence of counterfactual data on the learned re-

ward function.

Figure 5 presents the evolving reward distribu-

tions learned by the discriminator in both our method

and the baseline for expert demonstrations and trajec-

tories generated by the policy. The plotted reward

distributions unveil several noteworthy observations.

Firstly, our method exhibits a reward distribution that

is notably ﬂatter and less skewed compared to the

baseline. Furthermore, our approach tends to out-

put rewards that are generally less optimistic over-

all. This is evident when examining the distribu-

tion centroids at convergence for expert demonstra-

tions, where our method’s reward distribution cen-

ters around approximately 0.6 (Figure 5c), in contrast

to the baseline’s which centers around approximately

0.9 (Figure 5a). Similarly, for policy-generated trajec-

tories, our method’s rewards span the whole reward

space (Figure 5d) while the baseline’s rewards are

predominantly concentrated above 0.5 (Figure 5b).

These observations suggest that counterfactual

data acts as a regularizer preventing the overestima-

tion of the reward. Due to the way we generate coun-

terfactual data using the learned SCM, its quality re-

sembles that of the expert demonstrations, preventing

the discriminator from conﬁdently distinguishing be-

tween the two. This in turn curbs the discriminator’s

tendency to assign overly optimistic rewards as we

can observe with the baseline. The resulting reward

distribution makes the discriminator’s feedback more

informative to the policy which explains the improved

performance and expedited convergence observed in

our approach.

We further examine the reward dynamics across

various trajectory types: expert demonstrations, suc-

cessful policy trajectories, and failed policy trajecto-

ries. We randomly select one representative trajectory

from each category and plot the reward predictions

generated by both GoalGAIL and our method at each

timestep along these trajectories. The obtained results

shown in Figure 6 are in line with the earlier observa-

tions regarding the more conservative nature of the

reward in our method compared to the baseline. Ad-

ditionally, our approach maintains a higher degree of

reward consistency throughout the trajectory, in con-

trast to the baseline’s oscillatory reward predictions.

5.3 Low Data Regime

In this section, we conduct experiments to assess the

robustness of our method in the face of a reduced

number of demonstrations. In Figure 7, we present

the success rate achieved at convergence for the Pick

and Place task, averaged across 5 independent runs,

as we vary the number of expert demonstrations given

to the agent. The results show that our method con-

sistently outperforms the baseline. More importantly,

our method exhibits a milder decline in performance

as the number of demonstrations decreases when con-

trasted with the baseline.

6 CONCLUSION

In this paper, we have presented a novel approach to

enhance the efﬁciency and effectiveness of genera-

tive adversarial imitation learning in goal-conditioned

tasks. Our method leverages the power of Structural

Causal Models to improve the learning process. By

learning the causal mechanism governing a high-level

behavior policy of the demonstrator, we are able to

generate counterfactual data that we use as additional

training data for the reward function. Our experi-

ments show that the incorporation of counterfactual

data mitigates reward overestimation and improves

its informativeness for policy learning. This results

in superior performance and faster convergence com-

pared to the baseline. Moreover, our methods perform

well in scenarios with limited expert demonstrations

Improving Reward Estimation in Goal-Conditioned Imitation Learning with Counterfactual Data and Structural Causal Models

335

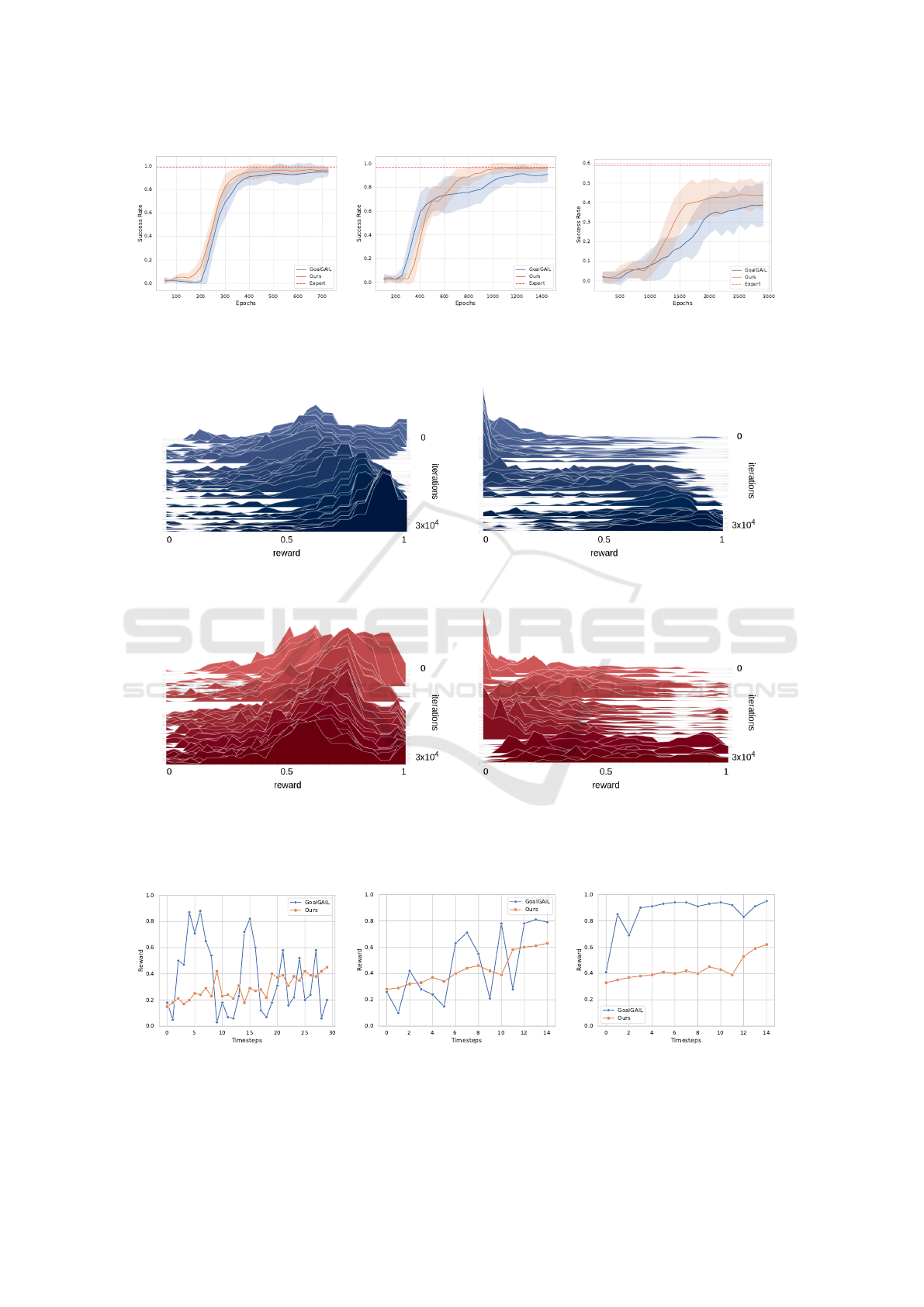
(a) Push. (b) Pick and Place. (c) Slide.

Figure 4: Learning curves of our approach and the baseline for different tasks: Our approach boosts the ﬁnal performance of

GoalGAIL and accelerates convergence across all three tasks.

(a) GoalGAIL reward distribution

for expert demonstrations.

(b) GoalGAIL reward distribution

for policy trajectories.

for expert demonstrations.

(d) Our approach’s reward distribution

for policy trajectories.

Figure 5: The distribution of the rewards learned by our approach and the baseline: Our method mitigates reward overestima-

tion and demonstrates ﬂatter, less skewed reward distributions for both expert demonstrations and policy trajectories.

(a) Failed trajectory. (b) Successful trajectory. (c) Expert demonstration.

Figure 6: Reward predictions by our approach and the baseline for different types of trajectories: The reward output from our

method exhibits greater consistency throughout trajectory execution.

LICARSA 2023 - Special Session on Learning in Control and Robotic Systems Applications

336

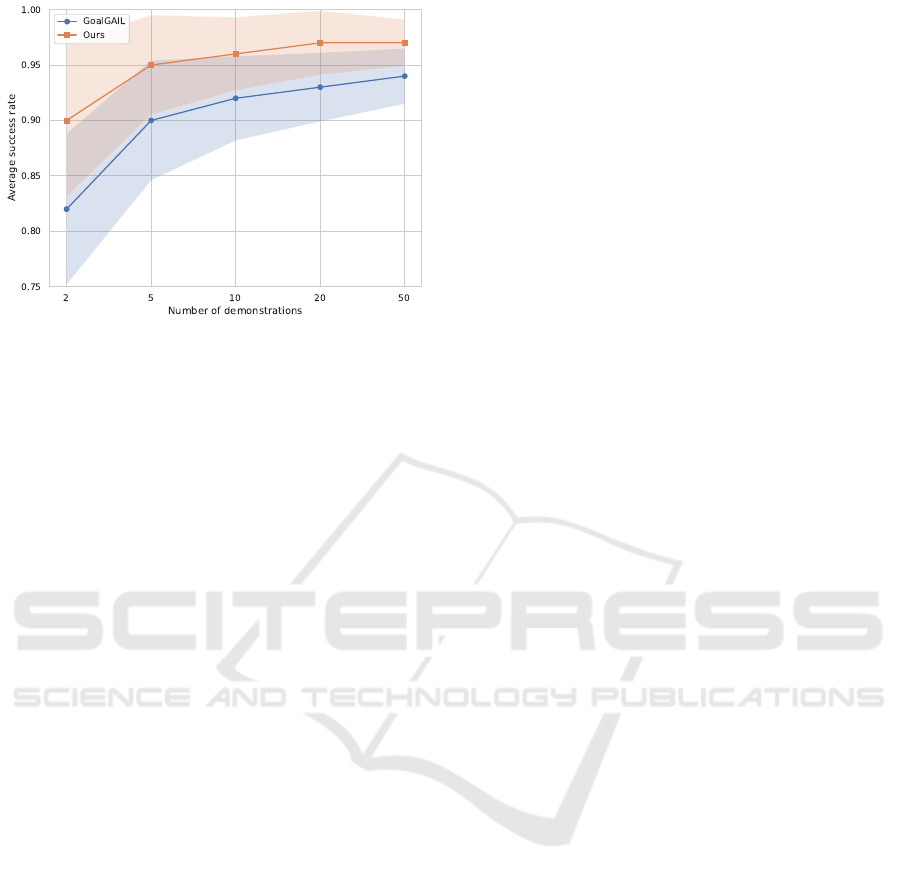
Figure 7: Average success rate for different numbers of

demonstrations: Our method is more resilient to the de-

crease of the number of demonstrations.

and make a step toward achieving more reliable imi-

tation learning using causality.

ACKNOWLEDGEMENTS

This work was funded in part by the region of Brittany

under the ROGAN project. We are grateful for their

support, which made this research possible.

REFERENCES

Andrychowicz, M., Wolski, F., Ray, A., Schneider, J., Fong,

R., Welinder, P., McGrew, B., Tobin, J., Pieter Abbeel,

O., and Zaremba, W. (2017). Hindsight experience re-

play. Advances in neural information processing sys-

tems, 30.

Arjovsky, M. and Bottou, L. (2017). Towards principled

methods for training generative adversarial networks.

arXiv preprint arXiv:1701.04862.

Bain, M. and Sammut, C. (1999). A framework for be-

havioural cloning. In Machine Intelligence 15, Intel-

ligent Agents [St. Catherine’s College, Oxford, July

1995], page 103–129, GBR. Oxford University.

Ding, Y., Florensa, C., Abbeel, P., and Phielipp, M. (2019).

Goal-conditioned imitation learning. Advances in

neural information processing systems, 32.

Hare, J. (2019). Dealing with sparse rewards in reinforce-

ment learning. arXiv preprint arXiv:1910.09281.

Ho, J. and Ermon, S. (2016). Generative adversarial imi-

tation learning. Advances in neural information pro-

cessing systems, 29.

Kaddour, J., Lynch, A., Liu, Q., Kusner, M. J., and Silva, R.

(2022). Causal machine learning: A survey and open

problems. arXiv preprint arXiv:2206.15475.

Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-

ational bayes. arXiv preprint arXiv:1312.6114.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-

uous control with deep reinforcement learning. arXiv

preprint arXiv:1509.02971.

Liu, M., Zhu, M., and Zhang, W. (2022). Goal-

conditioned reinforcement learning: Problems and so-

lutions. arXiv preprint arXiv:2201.08299.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312.5602.

Pearl, J. (2013). Structural counterfactuals: A brief intro-

duction. Cognitive science, 37(6):977–985.

Pearl, J. et al. (2000). Models, reasoning and inference.

Cambridge, UK: CambridgeUniversityPress, 19(2):3.

Plappert, M., Andrychowicz, M., Ray, A., McGrew, B.,

Baker, B., Powell, G., Schneider, J., Tobin, J.,

Chociej, M., Welinder, P., Kumar, V., and Zaremba,

W. (2018). Multi-goal reinforcement learning: Chal-

lenging robotics environments and request for re-

search. CoRR, abs/1802.09464.

Robinson, J. D., Chuang, C.-Y., Sra, S., and Jegelka, S.

(2021). Contrastive learning with hard negative sam-

ples. In International Conference on Learning Repre-

sentations.

Russell, S. (1998). Learning agents for uncertain environ-

ments. In Proceedings of the eleventh annual confer-

ence on Computational learning theory, pages 101–

103.

Sch

olkopf, B. (2019). Causality for machine learning.

CoRR, abs/1911.10500.

Shah, H., Tamuly, K., Raghunathan, A., Jain, P., and Netra-

palli, P. (2020). The pitfalls of simplicity bias in neural

networks. Advances in Neural Information Processing

Systems, 33:9573–9585.

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,

Van Den Driessche, G., Schrittwieser, J., Antonoglou,

I., Panneershelvam, V., Lanctot, M., et al. (2016).

Mastering the game of go with deep neural networks

and tree search. nature, 529(7587):484–489.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-

ing: An introduction. MIT press.

Sutton, R. S., McAllester, D., Singh, S., and Mansour, Y.

(1999). Policy gradient methods for reinforcement

learning with function approximation. Advances in

neural information processing systems, 12.

Improving Reward Estimation in Goal-Conditioned Imitation Learning with Counterfactual Data and Structural Causal Models

337