
A Reliable and Energy-Efficient Federated Learning in Computing
Force Network
Shizhan Lan
1,2
, Zhenyu Wang
2
, Yuxuan Long
2,*
and Weichao Kong
2
1
China Mobile Guangxi Branch Co., Ltd, Nanning, China
2
South China University of Technology, Guangzhou, China
Keywords: Federated Learning, Computing Force Network, Optimization.
Abstract: A Computing Force Network (CFN) is a distributed computing network that utilizes distributed computing
power to solve complex computational problems. Unlike traditional computing networks that centralize
resources in a single location, CFNs distribute processing power across an interconnected network of
devices. The intelligent devices within CFNs possess computational capabilities and carry varying quantities
of private training samples. Due to CFNs being provided by different service providers, private data
between devices cannot be directly shared, which makes it challenging to train models directly using the
private data. Federated Learning (FL) emerges as a novel distributed training paradigm that enables
distributed model training while preserving user privacy. This paper presents a K-Means-based
communication-assured federated learning algorithm for CFNs. It allows for federated training tasks under
non-iid conditions and selects reliable clients for communication in each round to ensure algorithm
convergence. Experimental results demonstrate the superior performance of our algorithm compared to the-
state-of-arts.
1
INTRODUCTION
With the advancement of information technology
and the improvement of infrastructure,
computational power and networking are
increasingly converging. A new emerging concept
called computational power network has been
proposed by IETF and ETSI. The computational
power network refers to a means of effectively
allocating computational and storage resources
among the cloud, edge, and end devices through
networking, based on the pervasive development of
computational capabilities. This allocation aims to
enhance the quality of business services and the user
experience. Emerging artificial intelligence
technologies, represented by ChatGPT, are
profoundly transforming our lives and modes of
production. However, these artificial intelligence
technologies consume significant amounts of
computational resources (Shi X, 2022)-(Gu J, 2022).
The computational power network leverages the
pervasive computational resources of the cloud,
edge, and end devices to provide robust
computational support for artificial intelligence
technologies.
Recently, Federated Learning (FL) has emerged
as a distributed learning paradigm within the
computational power network, which aims to
analyze and process non-iid data. In the
computational power network, edge devices possess
not only computational resources but also different
data samples (such as smart surveillance cameras
and intelligent streetlights) from the Internet of
Things (IoT) devices. FL can collaboratively train a
highly generalized global model by leveraging the
intelligent edge devices while ensuring the privacy
and security of private data (Sun, 2023)-(Jing Y,
2022). This approach effectively alleviates the
pressure of big data in the IoT and improves
resource utilization.
However, the data samples carried by intelligent
edge devices in the computational power network
exhibit heterogeneity, often characterized as non-
independent and identically distributed (non-iid).
This heterogeneity severely impacts the training
quality of the global model in FL and may even lead
to the failure of convergence. Additionally, the
computational power network integrates
communication environments from various
scenarios (Chen, 2020)-(Kong, 2022). In wireless
mobile communication environments, data
Lan, S., Wang, Z., Long, Y. and Kong, W.
A Reliable and Energy-Efficient Federated Learning in Computing Force Network.
DOI: 10.5220/0012275700003807
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (ANIT 2023), pages 117-124
ISBN: 978-989-758-677-4
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
117

transmission is susceptible to packet loss, and high
packet loss rates can result in the loss of gradients
uploaded by clients during FL training, significantly
affecting the convergence of the global model. This
article makes the following contributions:
1) We propose an optimization problem under
multiple constraint conditions.
2) We propose a communication-reliable
clustering FL algorithm.
3) Our research experiments demonstrate that the
proposed method outperforms the existing state-of-
the-art approaches.
2
SYSTEM MODEL
The architecture of AI based on computing power
networks can be divided into three components: the
infrastructure of integrated computing and
networking, the unified operation and
multidimensional scheduling management layer, and
the distributed and collaborative AI application
platform.
Firstly, the integrated computing and networking
infrastructure is a core component of the AI
computing power network. It encompasses various
types of computing resources, such as high-
performance computing servers, GPU clusters, edge
computing devices, and so forth. These computing
resources are interconnected through a network,
forming a unified computing platform. The
integrated computing and networking infrastructure
possesses high scalability and elasticity, enabling
dynamic allocation of computing resources based on
demand to meet the computational requirements of
AI tasks at different scales and complexities.
Secondly, the unified operation and
multidimensional scheduling management layer
serve as the management and scheduling plane of
the AI computing power network. It is responsible
for the unified management and scheduling of
computing resources within the integrated
computing and networking infrastructure, aiming to
achieve efficient resource utilization and rational
task allocation. This layer encompasses various
management and scheduling algorithms that enable
intelligent resource allocation and task scheduling
based on factors such as task priorities, resource
availability, and performance requirements. Through
the unified operation and multidimensional
scheduling management, the AI computing power
network can maximize the utilization of computing
resources, reduce task waiting time, and enhance
overall computational efficiency.
Finally, the distributed and collaborative AI
application plane is the application layer of the AI
computing power network. It involves collaborative
computing and data sharing among multiple
participants. In this plane, participants can share
their computing resources and data, and engage in
collaborative computing to achieve more complex
and advanced AI applications. Large-scale
distributed and collaborative computing necessitates
addressing issues of data security and privacy
protection to ensure the security of data sharing and
computational processes among participants.
Federated learning applications are deployed within
this layer.
2.1 Federated Learning Framework
Based on CFN
As described in the previous section, federated
learning applications are deployed in the distributed
AI application layer, involving multiple service
providers. In this layer, there is a central server
manager overseeing different federated learning
clients. Different federated learning participants
carry distinct data samples, which are considered
private and cannot be shared with other participants.
Each participant can choose to train a private model
using their local data and then upload their model
parameters to the central server for weighted
aggregation with the model parameters of other
participants. This collaborative training process aims
to create a globally generalized model with
enhanced performance.
In the CFN scenario, we consider the mobile
devices can collect the images, LiDAR data and
IMU data as the training samples (Cui Q, 2022)-(Yu
Z, 2020). We assume that mobile device V
collects a
matrix X
=[x
,x
,...,x
] input data, where
K
is the number of training samples of mobile
device 𝑉
. For simplicity, the label of samples can be
denoted as 𝑌
= [𝑦
, 𝑦
,...,𝑦
]. Moreover, we
denote 𝑤
as the weight related to the local FL
model that trained by samples 𝑥
.
The whole training process can be divided into
three phases:
1) Training Task assignment: Firstly, the edge
server will select a set of mobile devices 𝒱⊆𝑉 to
participate in federated learning. Then, the edge
server conforms the relevant parameters, such as the
object of training task and the initialization
parameters. Finally, edge server sends the model to
the FL participants.
2) Local Training: Each client in 𝒱 download the
model from edge server, and uses its samples to train
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
118

the model. The purpose of local training is to find
optimal parameters of local model after t iterations
which minimizing the loss function:
𝑤
∗
=argmin
𝐿(𝑤
, 𝑥
, 𝑦
)
(1)
Then, the client uploads the local model 𝑤
to
the edge server.
3) Edge Aggregation: The edge server will
calculate the weighted average of received local
model from the participated client in 𝒱 , and uses
them to update global model (Duan M, 2019):
𝕃(w
,x
,y
) =
|𝒱|
L(w
,x
,y
)
|𝒱|
(2)
Repeat the steps of 2 and 3 until the global model
coverage.
2.2 Transmission Model
The transmission model contains two phases, uplink
and downlink. We assume that each vehicle
equipped with an on-board unit(OBU), which can
communication with CFN server with orthogonal
frequency division multiple access (OFDMA)
technique (Hard A, 2018). The uplink transmission
rate and transmission time can be formulated as:
𝑟
= 𝐵
𝑙𝑜𝑔(1+
)
(3)
𝑇
=
|
|
|
|
(4)
Where 𝐵
is the bandwidth, and 𝑃
is the
transmission power. 𝑑
is the Euclidean distance
between 𝑉 and CFN server. 𝜁
is the Rayleigh
channel coefficient with a complex Gaussian
distribution. a is the path-loss exponent and 𝑁
is the
power noise. 𝑤
is the size of local model
parameters of 𝑉 in 𝑇
global iterations. Since the
action of vehicle upload data to CFN is
instantaneous rather than continuous, the uplink
transmission energy consumption is related to the
instantaneous power for 𝑉 to transmit local model
parameters:
𝐸
=
𝜁
𝑃
(5)
Where 𝜁
is the transmission energy
consumption factor. Similarly, the downlink data is
the CFN server broadcasts the training model to the
vehicles which are selected to participate in
federated learning, and the download date rate and
the model download time are given by:
𝑟
= 𝐵
𝑙𝑜𝑔(1+
)
(6)
𝑇
=
|
|
|
|
(7)
Where 𝐵
is the bandwidth of CFN server
broadcast the global model to each 𝑉
, and 𝑃
is the
transmission power of the CFN server. And the
energy consumption of downlink transmission is
given by:
𝐸
=
𝜁
𝑃
(8)
2.3 Packet Error Rates
In the real wireless scenario, the data packet maybe
lost while the vehicle download or upload model.
For simplicity, we assume that the global model and
the model parameters can be packed in a package
respectively. The packet error rate is denoted as:
𝑞
=
𝔼
(1 −𝑒𝑥𝑝(−
))
(9)
Where 𝔼
(·) is the expectation with respect to
ℎ
, and ℎ
= 𝜁
𝑑
. m is a waterfall threshold.
Since the transmission power of CFN is large
enough, the packet error rate of downlink can be
ignore.
2.4 Problem Formulation
In this work, we formulate an optimization problem
to minimize total latency and energy cost of vehicle
in FL. Moreover, we consider the maximum latency
and energy consumption that user can tolerate, the
model quality and the packet error as constraints. In
particular, we optimize the client selected set that
participate in FL, the transmission power of client
𝑃 =(𝑃
, 𝑃
,...,𝑃
), the OBU computation resources
𝑓
=(𝑓
, 𝑓
,..., 𝑓
) to minimize the model
transmission and computation time and energy
consumption in FL. Since the VEC updates the
global model after the aggregation phase, the actual
time cost is:
𝑇
=argmin
∈𝒱
( 𝑇
+ 𝑇
)
(10)
However, the form of 𝑇
is non-smooth and
non-linear, which is difficult to be solved with
optimization techniques. Thus, we take the
expectation total time cost, which is the average of
𝑇
:
𝔼(𝑇
)=
|𝒱|
𝑎
( 𝑇
+ 𝑇
)
|𝒱|
(11)
Where 𝑎
∈ {0,1} and 𝑎
=1 indicates that
client 𝑉
is selected to participate in FL, otherwise
A Reliable and Energy-Efficient Federated Learning in Computing Force Network
119

𝑎
= 0. Similarly, the expectation of total energy
cost is given by:
𝔼(𝐸
)=
|𝒱|
𝑎
( 𝐸
+ 𝐸
)
|𝒱|
(12)
Above of all, the optimization problem is given by:
𝑃1: min
,
𝔼(𝐸
+ 𝑇
)
)
s.t
𝔸
𝔸
≤𝜀 (C1)
s.t 𝑇
+ 𝑇
≤ 𝑡
(C2)
s.t 𝐸
≤ 𝐸
(C3)
s.t 0 ≤𝑃
≤ 𝑃
(C4)
𝔸 = 𝐾
(1 −𝑎
+ 𝑞
𝑎
)
|𝒱|
(13)
Where 𝑃
and 𝐸
are the maximum
transmission power of 𝑉
and the maximum energy
consumption that user can tolerate for federated
learning, respectively. We utilize the convergence
result into approximate the convergence constraint
of federated learning in wireless communication
environment, which is demonstrated as (C1). (C2) is
the latency constraint, the total time cost can not
exceed the time that 𝑉
driving within the coverage
of CFN. (C3) is the energy constraint, which
regulates total energy cost in federated learning must
satisfy user requirements. (C4) is the physical limit
of 𝑉
transmission power.
This problem is a mixed integer programming
problem that cannot be solved using conventional
optimization techniques. Firstly, we assume that all
clients are selected to participate in federated
training, which means 𝑎
=1 The original problem is
then transformed into a standard optimization
problem. By utilizing the Hessian matrix, we can
prove the convexity of the transformed problem,
making it amenable to optimization techniques. We
can optimize the problem and substitute the obtained
solution back into the original problem. By
employing linear programming, we can determine
the set of clients selected to participate in the
federated training task.
2.5 Federated Clustering Problem
In this section, we formalize the problem of
federated clustering aggregated learning. In
federated learning, N clients collaborate to train a
shared global model. Let i denote the index of a
client. Each client i maintains an arbitrary local
dataset 𝐷
. We choose the classical cross-entropy as
the training loss function
In scenarios where the data is sampled by
individual clients from their respective distributions,
the overall data distribution, denoted as 𝑃
, emerges
as a composite of all local data distributions.
Mathematically, it can be expressed as 𝑃 =
∑
𝑤
𝑃
.
Here, each client's weight in the aggregation
depends on the size of their local dataset. In the ideal
case of Independent and Identically Distributed (IID)
data, it is assumed that all clients' data, represented
by 𝑃
, follows the same distribution. However,
practical applications often deviate from the IID
assumption. In such cases, for different clients i and
j, their respective data distributions are not equal.
This situation is commonly referred to as a Non-
Independent and Non-Identically Distributed (Non-
IID) data distribution.
The presence of non-IID data prevents the global
model 𝜃 from attaining the minimum empirical loss
function 𝐿 across all clients. As a result, there has
been an increased interest in exploring personalized
solutions. Prior research has primarily concentrated
on integrating personalized insights gleaned from
clients' local data into the overarching shared global
model (Luo B, 2021). However, as highlighted
earlier, in highly diverse settings, relying solely on a
single global model may prove to be inefficient. To
tackle this challenge, we suggest the utilization of
multiple shared global models distributed among
clients. More specifically, we advocate the use of
multiple federated sub-models.
In a formal sense, we introduce a collection of K
global models, with each global model being shared
among a distinct group of clients. Within each client
group, there exists a single global model. These
global meta-models serve as the basis with well-
initialized parameters for the individual models.
Consequently, clients have the flexibility to select
the global model that aligns most effectively with
their respective local data distributions, facilitating
personalized execution. This reshapes our global
objective as follows
min
∈,
∈
ℒ
([𝜙
, 𝜗
]; 𝐷
)
(13)
where 𝑔 represents the identification of the
global model for the 𝑖-th client, 𝛷 represents the
parameter space of the global model, and 𝐺
represents the set of client indices in the k-th group.
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
120
3
SOLUTION
In this section, we present the overall framework of
the algorithm. Firstly, we have the client selection
phase. In this phase, the parameter server collects
information from each client, such as the number of
samples carried by each client, available computing
resources, and communication transmission power,
among others. In wireless networks, communication
links are often unreliable, and there is a certain
probability of data loss. In severe cases, it can
prevent the convergence of federated learning
training. Therefore, we need to consider the
reliability of federated training in wireless
environments to ensure its convergence. This paper
proposes a client selection algorithm based on
optimization principles. We initially assume that all
clients participate in federated training and then
optimize the transmission power of each client. The
client set participating in federated learning is then
determined based on convergence conditions.
The whole process of our algorithm is proposed
as follows:
Al
g
orithm 1: Pro
p
rosed FL in CFN.
1. Input: The data size of FL model, 𝑷
𝒏
𝒎𝒂𝒙
and
the task distribution of each mobile device,
related network and energy lllll parameters.
2. Output: 𝑷
𝒏
∗
, 𝒂
𝒏
∗
, 𝜽
𝒏
∗
3. Initialize variable: set 𝒂
𝒏
=1
4. Obtain 𝑷
𝒏
∗
by solving the original problem.
5. Put 𝑷
𝒏
∗
into original problem, and obtain 𝒂
𝒏
∗
6. Selecting client according to 𝒂
𝒏
∗
7. Encoding the tasks representation of each
client
8. Using K-mean clustering problem to group the
selected clients by tasks representation
9. Each group start local training
10. group uploads parameters and aggregates
model in the group server
11. Central server performs a aggregation for each
group.
12. Central server broadcasts group model to its
clients.
13. Repet step 9 to 12 until global model is
conver
g
ence
The initialization phase involves a
comprehensive approach to capturing the
relationships between clients. Initially, we employ
an autoencoder to acquire task representations from
each client, facilitating the subsequent grouping of
clients based on these representations. To
accomplish this, each client retrieves the
autoencoder's architecture from the server. The
autoencoder's primary objective is to distill low-
dimensional vectors, known as task representations,
from local data. Subsequently, clients transmit these
task representations to the server, where they serve
as input for the K-Means clustering algorithm. As a
result, we obtain K cluster centers, which play a
pivotal role in identifying client groups during the
federated optimization phase. Furthermore, it's
noteworthy that the meta-models within each group
share the same model initialization.
The aggregation phase involves optimizing the
models within each group. Without loss of
generality, this phase follows the standard process of
federated learning. Specifically, each client first
downloads the corresponding group's model from
the server and performs local optimization of the
group's model using its local data. Additionally, we
utilize a pre-trained encoder to obtain task
representations of the training data. Finally, the
clients send the updated group meta-models and task
representations to the server. The server completes
the grouping process by measuring and comparing
the similarity between task representations and the K
cluster centers. Subsequently, the server performs
model aggregation for each group to obtain new
global models for the next round of communication.
This process is repeated until certain termination
criteria are met, such as a finite number of
communication rounds.
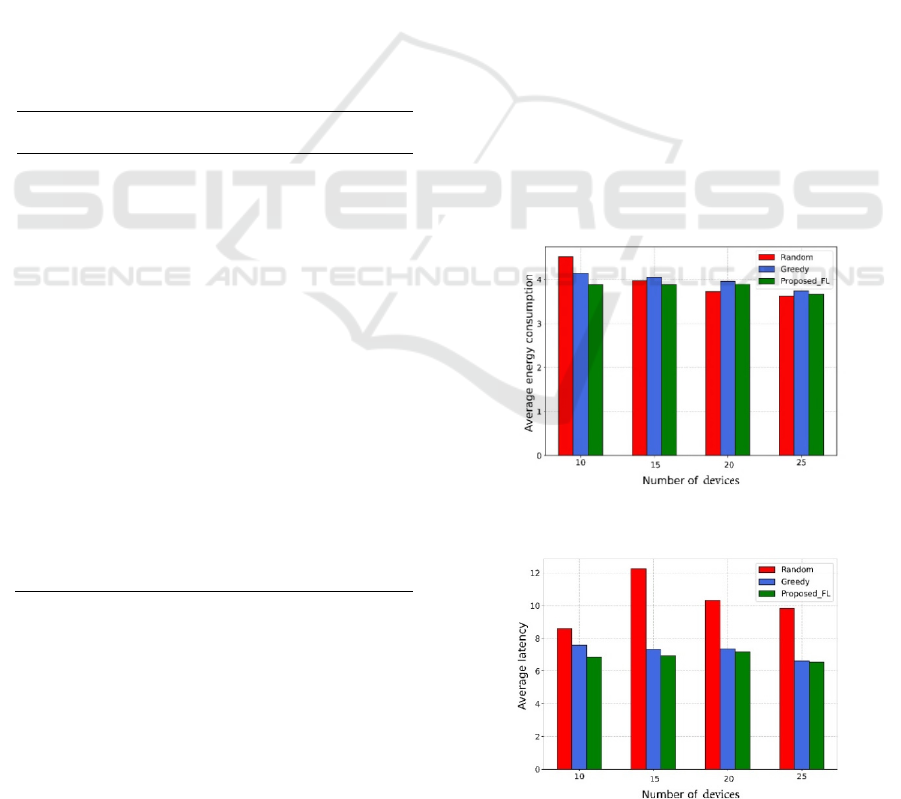
Figure 1: 𝐸
with different algorithm.
Figure 2: 𝑇
with different algorithm.
A Reliable and Energy-Efficient Federated Learning in Computing Force Network
121
4
SIMULATION
In this section, we evaluate the performance of the
proposed FL algorithm. First, we introduce the
settings of the experiment parameters and
environment. Then, we analyze the accuracy rate of
proposed FL algorithm, and compared the latency
and energy cost with the baseline. Finally, a series of
comparative experiments show that our algorithm
can significantly reduce total latency and energy
consumption.
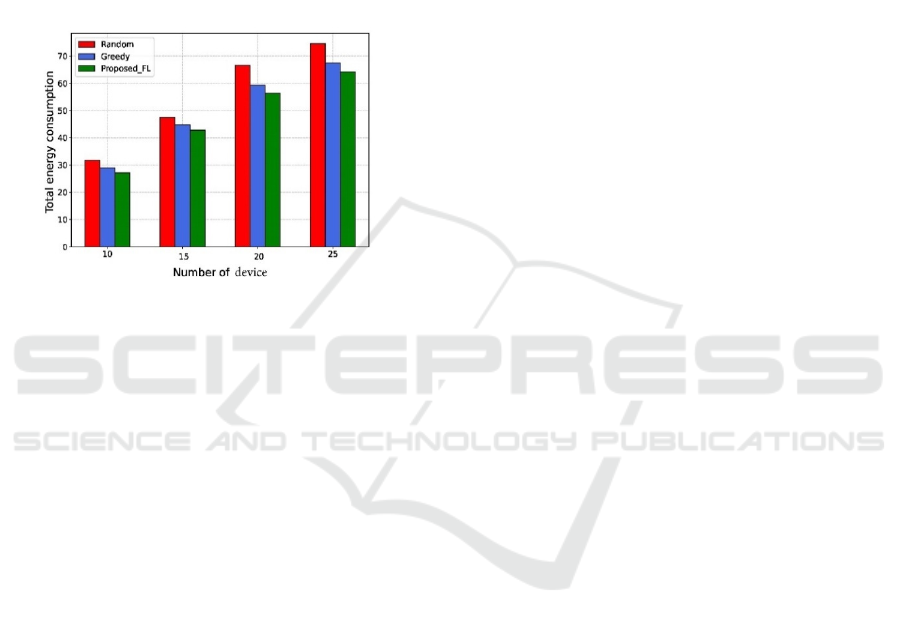
Figure 3: 𝐸
with different algorithm.
The experiments are simulated in a Python-based
desktop with 16 GB memory. The CPU is Intel Core
i7-8700, and the proposed FL algorithms is
simulated by using an open source Python machine
learning library Pytorch. The MNIST and Cifar-10
datasets are used in this simulation.
The MNIST dataset is a standard benchmark
dataset in machine learning and computer vision. It
consists of 60,000 training images and 10,000
testing images of handwritten digits (0-9). Each
grayscale image is 28x28 pixels. MNIST is widely
used for evaluating image classification algorithms
due to its balanced distribution and accessibility,
making it an essential resource for research and
development in the field.
The CIFAR-10 dataset is a well-known
benchmark dataset in the field of computer vision
and machine learning. It consists of 60,000 color
images, with each image belonging to one of ten
classes, namely airplane, automobile, bird, cat, deer,
dog, frog, horse, ship, and truck. The dataset is
divided into 50,000 training images and 10,000
testing images, each of size 32x32 pixels. CIFAR-10
has been widely used for evaluating and comparing
various image classification algorithms due to its
diverse object categories and realistic images,
making it an important resource for research and
development in computer vision.
4.1 Latency and Energy Consumption
Fig. 1, Fig. 2 and Fig. 3 present the latency and
energy cost of the algorithms with different number
of devices in MNIST dataset. We can find that the
average energy consumption of all algorithms
decreases as the number of vehicles increases.
Because the impact of high-energy devices on the
average energy consumption decreases as the
number of devices increases
As shown in Fig. 2, the average latency of
proposed FL is significantly lower than the random
algorithm, and it is the lowest one whatever the
number of device is. It is worth mentioning that the
transmission power and computation resources of
greed algorithm is given by proposed FL. Therefore,
the difference in performance between the greedy
algorithm and the proposed FL is not particularly
pronounced. However, the performance of the
proposed FL is still better than greedy algorithm
with different number of device, and it completely
proves that it is importance to optimize the set of
device selection.
Fig. 3 presents the total energy consumption of all
algorithms. Obviously, our proposed FL save the
most energy in different number of vehicles, and the
energy consumption of proposed FL is about 14%
lower than random algorithm when the number of
device is 25. This is because the proposed FL will
not blindly increase the number of FL-tasks device.
Compared to greedy algorithm, we can know that
the proposed FL can effectively reduce energy
consumption by the proper selection.
4.2 Accuracy
In this section, we compare the proposed federated
learning algorithm with the baseline algorithms,
FedAvg and the popular FL algorithm, Per-FedAvg.
We conduct our evaluation on the CIFAR-10 dataset.
To create non-i.i.d. (independent and identically
distributed) data, we divide the CIFAR-10 dataset
into 20 sets, with varying numbers of samples in
each set, as shown in Table 1. Our proposed
algorithm achieves significantly higher accuracy
compared to the other two algorithms. It improves
the accuracy by approximately 25% compared to
FedAvg and around 50% compared to Per-FedAvg.
Why does Per-FedAvg perform poorly in this
case? This can be attributed to the fact that Per-
FedAvg is suitable for small-sample learning and
works best when the learning task is not very
challenging. Typically, it performs well only on the
MNIST dataset. FedAvg, on the other hand, is a
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
122

classical federated learning algorithm. However, in
our experiment, we intentionally set the CIFAR-10
dataset as non-i.i.d., where the private datasets of
different clients have minimal or no intersection.
This lack of intersection leads to suboptimal
performance of FedAvg.
Table 1: Main Notation.
Method Test accuracy of No-iid Cifar-10
Per-Fedavg
21.45%
30.15%
40.13%
Fedavg
Proposed-FL
In contrast, our proposed federated learning
algorithm groups clients based on their data
distributions, effectively mitigating the impact of
non-i.i.d. data. The experimental results demonstrate
that our algorithm significantly improves the
accuracy of the global model.
5
CONCLUSION
In this paper, we investigate a novel distributed
learning framework that enables the implementation
of FL algorithms in CFN. We formulate a MIP
problem that considers device velocity, wireless
packet transmission errors, resources allocation and
client selection for minimization of FL learning
time, energy consumption and training loss. To
address this problem, we utilize Lagrangian
multiplier method and gradient method to iteratively
calculate the optimal transmission power and on-
board CPU frequency under the given clients
selection. Then, we put above results into primal
problem and slack the 0-1 selection variables, which
transforms the primal problem into LP problem, and
it can be solved by multiple optimization techniques.
The numerical results illustrate that the performance
of the proposed FL algorithm significantly
outperforms other baseline algorithms in terms of
average latency and total energy consumption.
Moreover, the performance of proposed FL is more
stable and efficient with the different number of
devices.
REFERENCES
Shi X, Li Q, Wang D, et al. Mobile Computing Force
Network (MCFN): Computing and Network
Convergence Supporting Integrated Communication
Service[C]//2022 International Conference on Service
Science (ICSS). IEEE, 2022: 131-136.
https://doi.org/10.1109/ICSS55994.2022.00028
Dong Y, Guan C, Chen Y, et al. Optimization of Service
Scheduling in Computing Force Network[C]//2022
International Conference on Service Science (ICSS).
IEEE, 2022: 147-153. https://doi.org/10.1109/
ICSS55994.2022.00031
Gu J, Feng J, Xu H, et al. Research on Terminal-Side
Computing Force Network Based on Massive
Terminals[J]. Electronics, 2022, 11(13): 2108.
https://doi.org/10.3390/electronics11132108
Sun W, Zhao Y, Ma W, et al. Accelerating Convergence
of Federated Learning in MEC with Dynamic
Community[J]. IEEE Transactions on Mobile
Computing, 2023. https://doi.org/10.1109/TMC
.2023.3241770
Xu Z, Li D, Liang W, et al. Energy or accuracy? Near-
optimal user selection and aggregator placement for
federated learning in MEC[J]. IEEE Transactions on
Mobile Computing, 2023. https://doi.org/10.1109
/TMC.2023.3262829
Jing Y, Wang J, Jiang C, et al. Satellite MEC with
Federated Learning: Architectures, Technologies, and
Challenges[J]. IEEE Network, 2022, 36(5): 106-112.
https://doi.org/10.1109/MNET.001.2200202
Chen M, Yang Z, Saad W, et al. A joint learning and
communications framework for federated learning over
wireless networks[J]. IEEE Transactions on Wireless
Communications, 2020, 20(1): 269-283.
https://doi.org/10.1109/TWC.2022.3168538
Wang Z, Zhou Z, Zhang H, et al. AI-based cloud-edge-
device collaboration in 6G space-air-ground integrated
power IoT[J]. IEEE Wireless Communications, 2022,
29(1): 16-23. https://doi.org/10.1109/MWC.001.00254
Kong X, Wu Y, Wang H, et al. Edge Computing for
Internet of Everything: A Survey[J]. IEEE Internet of
Things Journal, 2022, 9(23): 23472-23485.
https://doi.org/10.1109/JIOT.2022.3200431
Cui Q, Hu X, Ni W, et al. Vehicular mobility patterns and
their applications to Internet-of-Vehicles: a
comprehensive survey[J]. Science China Information
Sciences, 2022, 65(11): 211301.
https://doi.org/10.1007/s11432-021-3487-x
AlNagar Y, Hosny S, El-Sherif A A. Towards mobility-
aware proactive caching for vehicular ad hoc
networks[C]//2019 IEEE Wireless Communications
and Networking Conference Workshop (WCNCW).
IEEE, 2019: 1-6. https://doi.org/10.1109/WCN
CW.2019.8902903
Yu Z, Hu J, Min G, et al. Mobility-aware proactive edge
caching for connected vehicles using federated
learning[J]. IEEE Transactions on Intelligent
Transportation Systems, 2020, 22(8): 5341-5351.
https://doi.org/10.1109/TITS.2020.3017474
Duan M, Liu D, Chen X, et al. Astraea: Self-balancing
federated learning for improving classification
accuracy of mobile deep learning applications[C]//2019
IEEE 37th international conference on computer design
(ICCD). IEEE, 2019: 246-254. https://doi.org/
10.1109/ICCD46524.2019.00038
A Reliable and Energy-Efficient Federated Learning in Computing Force Network
123

Hard A, Rao K, Mathews R, et al. Federated learning for
mobile keyboard prediction[J]. arXiv preprint
arXiv:1811.03604, 2018. https://doi.org/10.48550/
arXiv.1811.03604
Luo B, Li X, Wang S, et al. Cost-effective federated
learning design[C]//IEEE INFOCOM 2021-IEEE Conf.
on Computer Communications. IEEE, 2021: 1-10.
https://doi.org/10.1109/INFOCOM42981.2021.9488679
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
124
