Calculation Method for Harmonic Impedance of System Side Based

on Data Fusion

Hangya Xu, Jinshuai Zhao and Kun Zheng

Sichuan University, Chengdu, China

Keywords: Harmonic Impedance Calculation, Fast Independent Component Analysis, Fluctuation Method Method,

Kalman Filtering, Data Fusion.

Abstract: Starting from the existing Independent Component Analysis (ICA) method and Fluctuation Method, this

paper explores the advantages and disadvantages of these two methods in calculating harmonic impedance.

Combining the strengths of both methods, a data fusion-based harmonic impedance calculation method is

proposed. The proposed method maintains high computational accuracy even in the presence of unstable

background harmonics and correlated source signals on both sides of the Point of Common Coupling (PCC).

The accuracy and effectiveness of the proposed method are verified through simulation experiments,

providing theoretical guidance for subsequent harmonic mitigation efforts.

INTRODUCTION

With the increasing integration of nonlinear loads

such as rectifiers, arc furnaces, variable frequency

devices, and electrified railways, the distortion of

system voltage and current waveforms caused by

harmonic pollution has become a serious concern.

To effectively allocate pollution responsibility and

suppress harmonic pollution, accurately calculate the

harmonic impedance of system side has become a

pressing issue (Liu Yi., Wang Yang, Li Fengxiang.).

Fast independent component analysis (ICA)

and Fluctuation Method are widely employed for

assessing harmonic emission levels (Li Xiangqun,

Du Wenlong, Meng Lingling). However, the former

relies heavily on weak correlation between the

system side and customer side, leading to significant

measurement errors when there is a strong

correlation between them. The latter requires stable

background harmonics, and substantial measurement

errors occur when the background harmonics

fluctuate dramatically.

Therefore, in this paper, the concept of data

fusion is introduced, and a data fusion-based method

for calculating harmonic impedance is proposed.

This method combines the characteristics of

FastICA (Independent Component Analysis) and the

Fluctuation Method method (Wang

Shichmmmmmmmmmao, Li Yang, Wang

Qianggang), achieving high computational accuracy

even in scenarios with fluctuating background

harmonics and strong correlation between the

system side and customer side. In practical

applications of Kalman filtering, the covariance

matrices of input noise and measurement noise are

often empirically determined, which introduces

calculation errors. This paper presents a method for

estimating the hyperparameters of the covariance

matrices of input noise and measurement noise to

accurately estimate them, thereby improving the

accuracy of Kalman filtering in practical

applications (Wang Qianggang, Xia Wei, Wang

Jingcai). Finally, simulation analysis demonstrates

that compared to FastICA and the Fluctuation

method, the proposed method in this paper combines

the advantages of both methods, expanding the

applicable range and computational accuracy.

FASTICA ALGORITHM

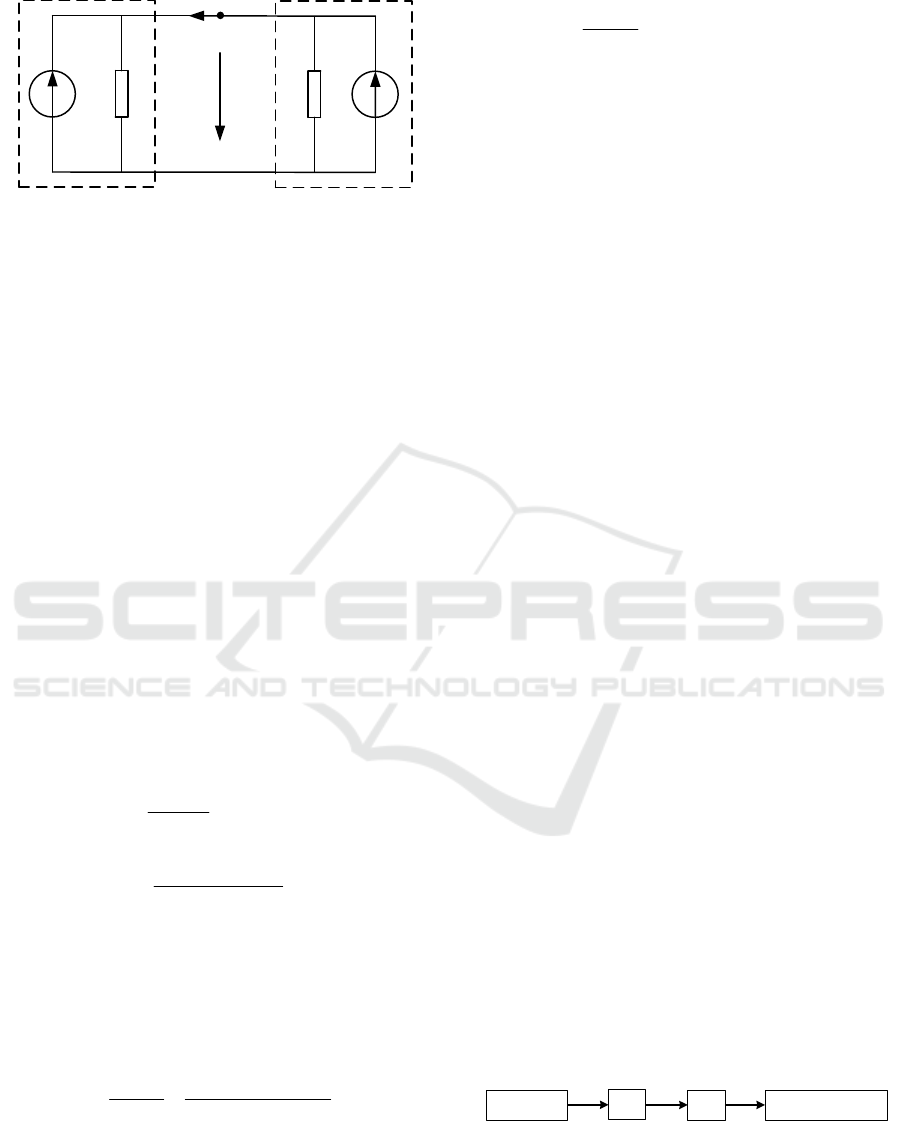
2.1 Norton Equivalent Circuit

In harmonic analysis, the Norton equivalent circuit

is commonly used as a theoretical model. The power

grid is divided into two parts, the customer side and

the system side, at the Point of Common Coupling

(PCC). The Norton equivalent circuit is illustrated in

Figure 1 (Wang Jingcai, 2015).

Xu, H., Zhao, J. and Zheng, K.

Calculation Method for Harmonic Impedance of System Side Based on Data Fusion.

DOI: 10.5220/0012276100003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 143-147

ISBN: 978-989-758-677-4

143

IΔ

pcc

UΔ

PCC

Customer side

System side

Figure 1: Harmonic Equivalent Model of System Side and

customer side.

2.2 Fluctuation Method

This method starts from analyzing the fluctuation

characteristics of the fluctuation magnitude at the

point of common coupling (PCC). Based on the ratio

of the fluctuation magnitude between the harmonic

voltage and current at the PCC point, the harmonic

impedance of the system is estimated.

The harmonic emission level of the user is

estimated based on the measured values at the PCC

point. The harmonic impedance on the system side

depends on the short-circuit capacity of the system,

which can be considered constant in a short period

of time. The variation in the customer-side harmonic

current can reflect the variation in the customer-side

harmonic impedance. Therefore, when analyzing the

fluctuations on the system side and the customer

side, only the changes in the system-side harmonic

current and the customer-side harmonic current need

to be considered. Mathematically, this can be

expressed as (

Gong Hualin, 2010):

...

()

pcc

UII

Δ= Δ+Δ

(1)

cc ss

pcc

IZ IZ

Δ−Δ

Δ=

(2)

The harmonic voltage fluctuation characteristic

at the point of common coupling (PCC), defined as

KhVA, is the ratio of the fluctuation magnitude of

the harmonic voltage at the PCC point to the

fluctuation magnitude of the harmonic current on the

common bus. Its value is given by:

.. .

pcc

hVA

pcc

cs sc

IIZIZ

Δ+Δ

ΔΔ−Δ

(3)

When analyzing the fluctuations at the point of

common coupling (PCC) caused by fluctuations on

the system side or the customer side:

, 0

pcc

hVA

pcc



Δ=







−Δ=



(4)

The geometric interpretation of KhVA is the

slope of the harmonic voltage-current characteristic

curve. As indicated by the above equation, the ratio

of the harmonic current and harmonic voltage

fluctuations at the PCC point can be used to estimate

the harmonic impedance on both sides of the PCC

point. Based on the sign of the harmonic voltage

fluctuation characteristic at the PCC point, the

obtained result can be identified as either the

harmonic impedance on the system side or the

harmonic impedance on the customer side. When the

real part of the harmonic voltage fluctuation

characteristic at the PCC point is positive, the result

corresponds to the harmonic impedance on the

system side. Conversely, when the real part of the

harmonic voltage fluctuation characteristic at the

PCC point is negative, the result corresponds to the

negative value of the harmonic impedance on the

customer side.

INDEPENDENT COMPONENT

ANALYSIS (ICA)

Independent Component Analysis (ICA) is a novel

blind source separation technique that has emerged

in recent years. It separates mixed signals by

exploiting the independence or weak correlation of

the source signals. It primarily utilizes the

independence between the fluctuation magnitudes of

the customer-side harmonic sources and the

system-side harmonic sources. In the absence of

knowledge about the source signals, an appropriate

separation matrix is obtained through iterative

calculations. This matrix is then used to separate

independent signal components from the measured

data at the point of common coupling (PCC). These

separated components exhibit a high degree of

correlation with the source signals.

The basic steps of the ICA algorithm are

illustrated in Figure 2 (Zhao Xi, 2015).

FastICA

Independent

components

PCC point

harmonic voltage

and c urrent data

Least square

method

Linear

relationship

sx sy

ZjZ

−−

Mixing

coefficient

Measurement

volume

System side harmonic

edanc e

Figure 2: Basic steps of ICA algorithm.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

144

DATA FUSION STRATEGY

BASED ON KALMAN

FILTERING

FastICA exhibits strong resistance to background

harmonic disturbances but has high requirements for

the mutual independence of signals. This limitation

can result in situations where the separated source

signals do not perfectly match the true source

signals, leading to errors in calculating the harmonic

impedance on the system side.

On the other hand, the fluctuation method is

simple to operate and does not require mutual

independence of the data, but it has poor resistance

to background harmonic fluctuations, making it

challenging to apply in practical situations. In order

to overcome the limitations of FastICA and the

fluctuation method, this paper proposes a data fusion

strategy based on Kalman filtering for calculating

harmonic impedance.

The proposed strategy applies the concept of data

fusion to the calculation of harmonic impedance. It

aims to overcome the limitations of FastICA and the

fluctuation method. By employing Kalman filtering

techniques, the strategy combines information from

different sources to improve the accuracy of

harmonic impedance estimation.

Considering the state-space model of a linear

discrete dynamic system:

() ( 1) ( 1)Xk AXk Wk=−+Γ−

(5)

() () ()

kHXkVk=+

(6)

K represents discrete time; X(k) and Z(k)

represent the state variable and measurement

variable, respectively; W(k-1) and V(k) denote the

input noise and measurement noise, respectively; Γ

represents the noise driving matrix; A is the state

transition matrix; H is the observation matrix.

Assuming that the input noise and measurement

noise are mutually independent with zero means,

their covariance matrices are denoted as Q and R,

respectively. The statistical characteristics of the

noise can be described as follows:

{()}0

{()} 0

{() ()}0

() { () ()}

() {() ()}

()~(0,)

EW k

EV k

EW kV j

Qk EW kW j

kEVkVj

PW Q

PV R











(7)

When neglecting the noise errors, the prior

prediction value can be obtained, and its

mathematical expression is given by:

𝑥





= 𝐴𝑥



(8)

kmea k

−

(9)

𝑥





represents the prior state prediction value at

time k, and 𝑥



represents the measurement

prediction value.

The final prediction value of the Kalman filter at

time k can be expressed as:

𝑥



= 𝑥





+ 𝐾



(𝑧



−𝐻



𝑥





)

(10)

represents the Kalman gain,

[0, ]

−

∈

The prediction error e

and the prior error

−

can be expressed as:

kkk

exx=−

(11)

kkk

exx

−−

=−

(12)

When the variance of the error is minimized, the

final prediction value is closest to the true value. The

covariance matrix of the error, P

, is given by:

ˆˆ

()()

kkk kkkk

PEee Exxxx

 

==−−

 

(13)

Then

PH R

−

(14)

To address the issue of increased error in Kalman

filtering caused by using empirical values for Q and

R, this paper proposes a hyperparameter estimation

method for the covariance matrices of the input

noise and measurement noise. This method aims to

determine the covariance matrix Q of the input noise

and the covariance matrix R of the measurement

noise.

Assuming that the computational error e is given by:

jsz

eZ Z

−−

=−

(15)

S-j

represents the computed value of the

harmonic impedance on the system side, and Z

S-z

represents the true value of the harmonic impedance

on the system side.

The variance of the error e is given by:

jsz

eZ Z

−−

=−

(16)

S-j

represents the computed value of the

harmonic impedance on the system side, and Z

S-z

represents the true value of the harmonic impedance

on the system side. The variance of the error e is

given by:

() ( )

jsz

VAR e VAR Z Z

−−

=−

(17)

In the process of calculating the harmonic

impedance, Z

S-z

is considered constant and can be

Calculation Method for Harmonic Impedance of System Side Based on Data Fusion

145

treated as a constant. According to the variance

propagation theorem:

() ( ) ( )

jsz sj

VAR e VAR Z Z VAR Z

−− −

=−=

(18)

Therefore, the values of the covariance matrix Q

for input noise and the covariance matrix R for

measurement noise can be determined based on the

variances of the computed results obtained from

FastICA and the fluctuation method.

In summary, Kalman filtering consists of three

main parts: prediction, correction, and update. The

computation process is shown in Figure 3, and the

specific steps are as follows:

Step 1: Obtain the prior state prediction value

𝑥





, measurement prediction value 𝑥



covariance matrix Q for input noise, and covariance

matrix R for measurement noise. These values can

be obtained using FastICA and the fluctuation

method, where the prior state prediction value and

measurement prediction value are computed results

from FastICA and the fluctuation method,

respectively.

Step 2: Calculate the prior error covariance

matrix

−

, according to equation (13).

Step 3: Calculate the Kalman gain K

using

equation (14).

Step 4: Update the error covariance matrix P

()

kkk

PIKHP

−

=−

(19)

Step 5: Set k = k + 1 and repeat Step 2.

Step 6: Output the final prediction value.

The updated error covariance matrix is used to

filter the signals at time k+1. In the subsequent

iterations, the predicted values gradually approach

the true values. The smaller the error between the

computed results and the true values, the smaller the

error generated by the Kalman filter.

Final

The FastICA method calculation

results and

Fluctuation method calculation

results.

Begin

Compute the prior error covariance

matrix .

Obtain the prior state prediction value ,measurement

prediction value ,

noise covariance matrix Q and measurement

noisecovariance matrix R.

kmea

−

Calculate the Kalman gain .

The final predicted value at time .

Update error covariance matrix .

Output the final predicted value.

k=k+1.

Figure 3: Kalman filter calculation flow chart.

CONCLUSION

In this study, a data fusion approach was introduced

to combine the advantages of FastICA and the

Fluctuation Method, resulting in a harmonic

impedance calculation method based on data fusion.

This method demonstrates high computational

accuracy when dealing with intense background

harmonic fluctuations and strong correlation

between the system side and customer side.

Furthermore, considering the empirical values

commonly used for the covariance matrices of input

and measurement noise in practical engineering

applications of Kalman filtering, which can

introduce calculation errors and affect convergence

speed, a hyperparameter estimation method for the

covariance matrices of input and measurement noise

was proposed to accurately estimate these matrices.

Through simulation analysis and real-world

cases, it was demonstrated that the proposed method,

compared to FastICA and the Fluctuation Method,

combines the strengths of both methods, thereby

expanding the applicability range and improving

computational accuracy.

REFERENCES

Liu Yi. Harm of Harmonics and Suppression Strategy for

Harmonic Pollution(J). Low Voltage Apparatus,

2007(16):48-52.

Wang Yang, Tang Wenchu, Zhao Jinshuai, et al.

Harmonic Pollution Partition Method Based on

kDBA++ Clustering Algorithm[J]. Advanced

Engineering Sciences, 2023,55(2):84-96.

Li Fengxiang. Eliminate the Harmonic Pollution to Insure

Safe Running of Electric Power Systems[J]. China

Safety Science Journal, 2004,14(9):77-80.

Li Xiangqun, Wu Yaping, Zhuang Xufei, et al. A Method

for Narrowband Interference Suppression in Partial

Discharge Signal Combining Generalized S-transform

and Fast Independent Component Analysis[J]. Modern

Electric Power, 2022,39(5):597-604.

Du Wenlong, Yang Honggeng, Ma Xiaoyang.

Harmonic/Interharmonic Spectrum Separation

Algorithm Based on Fast Independent Component

Analysis[J]. Automation of Electric Power Systems ,

2020,44(13):115-122.

Meng Lingling, Sun Changdong, Wang Xiaodong.

Harmonic/Interharmonic Detection A Detection

Method for Harmonic/Inter-harmonic Based on

Eigenvalue Decomposition and Fast Independent

Component Analysis[J]. Automation of Electric Power

Systems, 2012,36(5):61-66.

Wang Shichao, Shen Shen, Li Yang, et al. A Fluctuation

Quantity Based Method to Evaluate Estimation

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

146

Precision of Harmonic Impedance Amplitude at

System Side[J]. Power System Technology,

2012,36(5):145-149.

Li Yang, Liu Zifa, Wang Shichao. Feasibility research on

the selection strategy of critical current data in the

fluctuation method[J]. Journal of North China Electric

Power University, 2012,39(2):28-33,38.

Wang Qianggang, Zhou Yiyao, Liao Jianquan, et al.

Review on Power Quality in DC Distribution

Network[J]. Automation of Electric Power Systems,

2023,47(7):193-207.

Xia Wei, Cai Wenting, Liu Yang, et al. Multi-source

heterogeneous data fusion of a distribution network

based on a joint Kalman filter[J]. Power System

Protection and Control, 2022,50(10):180-187.

Wang Jingcai, Li Yan, Xu Tianqi. Detection of False Data

in Smart Grid Based on Extended Kalman Filter[J].

Smart Power, 2022,50(3):50-56.

Gong Hualin, Xiao Xianyong, Liu Yamei, et al. A Method

for Assessing Customer Harmonic Emission Level

Based on the Dominant Fluctuation Filtering

Principle[J]. Proceedings of the CSEE,

2010,30(4):22-27.

Zhao Xi, Yang Honggeng. Method of Calculating

System-side Harmonic Impedance Based on

FastICA[J]. Automation of Electric Power Systems,

2015(23):139-144,151.

Calculation Method for Harmonic Impedance of System Side Based on Data Fusion

147