Heterogeneous Resource Scheduling Method based on Energy

Optimization under Price Constraints in Computing Force Network

Shizhan Lan

, Zhenyu Wang

, Weichao Kong

and Yuxuan Long

China Mobile Guangxi Branch Co., Ltd, Nanning, China

South China University of Technology, Guangzhou, China

Keywords: Computing Force Network, Workflow Scheduling, Price-Sensitive.

Abstract: With the development of Computing Force Network (CFN), more and more resources are deployed in CFN

which dynamically provide computing resources according to users' needs. In the CFN environment,

scheduling workflow under deadline constraints is one of the fundamental issues. The number and size of

heterogeneous resources in the CFN are gradually increasing, and the required costs are also constantly

rising. As a result, it is necessary to consider users' budget limits while also reducing the energy

consumption of end-side devices and edge servers. Aiming at workflow scheduling on time, cost, and

energy consumption constraints, a scheduling algorithm that combines with NSGA-II is used to optimize

scheduling time, cost, and energy consumption, with price as a soft constraint to ensure that the cost stays

within the budget and the schedule is completed before the deadline while minimizing energy consumption.

Our algorithm is validated by four typical scientific workflows, and the experimental results show that our

algorithm can reduce the average energy consumption by 14.8%, and compared to the GPR-HEFT method,

the average energy consumption can be reduced by 20.5%.

INTRODUCTION

In recent years, the computing infrastructure has

undergone a significant transformation, moving

from a centralized cloud-based model to a

distributed architecture that includes the cloud, edge,

and end-side computing (

F. Liang, 2018). The cloud,

represented by large-scale data centers, serves as the

foundation of cloud computing, offering users the

ability to store and process data through grid-based

access to interconnected computers and servers.

However, the rise of Multi-access Edge Computing

(MEC) has shifted the focus towards bringing

computing capabilities closer to the data source,

addressing the limitations of latency and data

volume associated with centralized cloud computing

(

Ahmad, S. Lembo, 2022). MEC enables the analysis

and processing of data generated by Internet of

Things (IoT) devices at the network edge, enhancing

efficiency and security by eliminating the need to

transmit data to remote cloud data centers.

Additionally, the end-side computing encompasses

various devices with networking and computing

capabilities, such as PCs, smartphones, smart TVs,

home set-top boxes, and IoT devices like smart

meters for water and electricity (

Baek, 2020). The

proliferation of these terminal devices in the era of

the Internet of Things presents an opportunity for

leveraging their collective computing power through

shared computing resources (

B. Baek, 2020). By

aggregating the idle computational resources of

these devices, computing power sharing can be

achieved, opening up new possibilities for

distributed computing. These advancements in

computing infrastructure offer potential for

improved performance, reduced latency, enhanced

security, and efficient utilization of computing

resources. Researchers and industry professionals

are actively exploring the opportunities and

challenges associated with distributed computing

models to harness the benefits of cloud, edge, and

end-side computing in various domains.

With the increasing adoption of the three-level

computing architecture comprising cloud, edge, and

end-side, computing power is no longer confined to

centralized data centers but is distributed across

various locations at the edge and end-side. However,

realizing the full potential of these distributed

computing resources requires a robust network

infrastructure that enables seamless interconnection

and collaboration among the computing nodes. To

address this challenge, the concept of the Computing

Fabric Network (CFN) has been introduced. The

194

Lan, S., Wang, Z., Kong, W. and Long, Y.

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network.

DOI: 10.5220/0012277500003807

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 2nd International Seminar on Artiﬁcial Intelligence, Networking and Information Technology (ANIT 2023), pages 194-203

ISBN: 978-989-758-677-4

CFN seeks to establish a network framework that

facilitates the sharing, scheduling, utilization, and

collaboration of computing resources across the

distributed computing nodes. By enabling effective

communication and coordination among these

nodes, the CFN ensures that the computing power

available at the edge and end-side can be harnessed

efficiently and effectively. This concept holds great

promise in unlocking the full potential of the three-

level computing architecture and driving the

development of innovative applications and services.

In the CFN, there are various heterogeneous

resources in addition to computing power and

storage space. Heterogeneous resources refer to

different computing resources, such as CPUs, GPUs,

FPGAs, etc., with different computing capabilities

and characteristics. In the CFN (Seo, 2022), the use

of heterogeneous resources can better meet the needs

of different computing tasks and improve computing

efficiency and flexibility.

Energy consumption of end-side devices is a

crucial factor in computing scheduling, as these

devices usually have limited computing power and

storage space and need to complete various

computing tasks through the CFN (Zhu, 2020). In

computing scheduling, considering the energy

consumption of end-side devices can help to

maximize the battery life of devices, increase device

usage time, and improve usage efficiency (Djigal,

2021).

The energy consumption of end-side devices is

closely related to computing scheduling. In

computing scheduling, tasks need to be assigned to

different computing nodes for execution, and these

computing nodes often require a significant amount

of energy to complete computing tasks. If the

computing scheduling is unreasonable, it can cause

some computing nodes to have a high workload,

resulting in excessive energy consumption and

affecting the performance and efficiency of the

entire CFN (Wang, 2021). Therefore, computing

scheduling needs to consider the energy

consumption of end-side devices to maximize the

reduction of computing node energy consumption

and improve the energy efficiency performance of

the entire CFN.

To reduce energy consumption, computing

scheduling can adopt various measures, such as task

merging, node sleep, load balancing, etc. Task

merging can merge multiple small tasks into one

large task, reducing nodes’ startup and shutdown

time and lowering energy consumption (Yadav,

2020). Node sleep can put idle nodes to sleep to

reduce energy consumption. Load balancing can

evenly distribute tasks to different computing nodes,

avoiding high workload on some nodes and thereby

reducing energy consumption.

The contributions of this paper are summarized

as follows:

According to the CFN scenario, the resource

scheduling problem was defined in a three-tiered

collaborative environment of cloud, edge, and

terminal, and a resource scheduling stability model

based on energy consumption and price sensitivity

was constructed.

A refined NSGA-II algorithm is introduced in

this study, leveraging the resource scheduling model

in the Computing Fabric Network (CFN).

Alongside, a novel elite selection method is

employed to efficiently match services with tasks,

while considering cost, energy consumption, and

execution time. The approach prioritizes selecting

the best-suited service within budget and deadline

limitations, leading to cost reduction without

compromising success rates under various strict

constraints.

Extensive simulation experiments were

performed to evaluate the effectiveness of the

proposed algorithm, comparing it against four state-

of-the-art methods. The obtained results demonstrate

that the proposed algorithm consistently achieves

successful scheduling under all imposed constraints

across all tested scenarios.

The remaining sections of the paper are as

follows: Section II provides a review and discussion

of the related work. Section III models the workflow

scheduling problem in the CFN environment.

Section IV presents the proposed optimization

algorithm in detail. Section V provides the specific

simulation settings and results, summarizes our work

and points out the next steps.

RELATED WORK

Currently, there are increasing numbers of workflow

scheduling algorithms proposed for cloud

computing, which can be mainly classified into three

types: heuristic algorithms, meta-heuristic

algorithms, and reinforcement learning-based

algorithms.

Heuristic algorithms have been extensively

researched as a method for workflow scheduling,

offering time-saving benefits by traversing tasks

from the entry to the exit of the workflow.

Researchers have made notable contributions in this

area. Durillo et al. (

Durillo, 2014) analyzed the multi-

objective heterogeneous earliest finish time

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network

195

(MOHEFT) algorithm, a Pareto-based list

scheduling heuristic that provides a set of trade-off

optimal solutions to users. Poola et al. (Poola, 2014)

proposed a robust scheduling algorithm that utilizes

a resource allocation strategy to schedule workflow

tasks on heterogeneous cloud resources, aiming to

minimize both completion time and cost. Faragardi

et al. (Faragardi, 2020) introduced GPR-HEFT, a

cost-benefit-driven resource allocation method for

minimizing makespan in budget-constrained cloud

environments. They considered different cost-benefit

ratios among resource instances and proposed an

improved version of the HEFT algorithm that

schedules tasks on a fixed subset of resource

instances. They optimized the calculation of the

earliest finish time using an insertion strategy and

sought a balance between instance renewal and

budget constraints. However, while heuristic

algorithms provide specific rules for task scheduling

with lower time complexity, they face challenges in

handling uncertainty in real-world scheduling

scenarios and may not yield solutions close to

optimality.

Meta-heuristic algorithms have gained significant

popularity for scheduling workflows in the cloud due

to their ability to find global optimal solutions while

minimizing completion time and monetary cost.

These algorithms operate based on a set of guiding

principles or strategies. Deb et al. (K. Deb, 2002)

proposed the Non-dominated Sorting Genetic

Algorithm II (NSGA-II), which is a generational

evolutionary algorithm that employs Pareto sorting

and crowding distance density estimation. Coello et

al. (Coello, 2004) introduced the Multi-Objective

Particle Swarm Optimization algorithm (MOPSO),

which incorporates Pareto dominance into Particle

Swarm Optimization (PSO) to handle multi-

objective optimization problems. These meta-

heuristic algorithms partially overcome the

limitations of heuristic approaches and can generate

near-optimal solutions. However, their high time

complexity poses challenges for their widespread

and deep application. These algorithms often require

a large number of iterations in the evolutionary

process to obtain good solutions, resulting in high

computational costs and long convergence times.

SOLUTIONS

3.1 Workflow Model

The workflow is represented by a directed acyclic

graph (DAG), G=(T, E), where T represents a set of

nodes, 𝑇 ={𝑡



, 𝑡



, 𝑡



...𝑡



} , and each node is a

microservice. In addition, E represents a set of edges

between tasks, 𝐸 ={𝑒

,

|𝑡



, 𝑡



∈𝑇} , where these

edges are control or data dependencies, and the

amount of data transferred between 𝑡



and 𝑡



denoted by 𝐶𝑅

,

. If microservice 𝑡



depends on

microservice 𝑡



, then 𝑒

,

is 1, otherwise 𝑒

,

is 0.

There are M different combinations of computing

resources in the entire CFN,

𝑃 ={𝑝



, 𝑝



, 𝑝



...𝑝



} ,

where 𝑝



{𝐶𝑃𝑈



, 𝐺𝑃𝑈



, 𝐴𝑆𝐼𝐶



, 𝐹𝑃𝐺𝐴



, 𝑀𝐸𝑀𝑂𝑅𝑌



, 𝐵𝐴𝑁𝐷𝑊𝐼𝑇𝐻



|𝑖∈𝑀}

represents the number of heterogeneous resources

provided by different resource combinations.

The processing capacity of different computing

resource combinations varies, and 𝐸𝑥𝑒𝑐𝑇𝑖𝑚𝑒

,

used to represent the execution time of 𝑡



on 𝑝



. If

resource combination A takes less time to execute

the same task than B, then A is faster than B. The

reasons for this may be: (1) the MIPS rate of the

virtual processors of instance types is higher. (2)

there are more virtual cores. (3) the memory size and

storage capacity are larger, and the storage access

time is faster.

3.2 Energy Consumption Model

Consider the following three types of energy

consumption: (1) energy consumption when running

tasks on computing resource combinations; (2)

energy consumption when computing resource

combinations are idle; (3) energy consumption of

communication links. Assuming that the hardware

facilities support DVFS technology (

S. Wang, 2017),

the system-level power model used in (Y. Chen,

2018

) and (Z. Long, 2020) is adopted, and the power

estimation at running frequency f is shown in

Formula 1:

𝑃



𝑓



= 𝑃



+ ℎ



𝑃



+ 𝑃





= 𝑃



+ ℎ𝑃



+ 𝐶



∗𝑓





(1)

Where 𝑃



is the static power, which is always

present by default and can only be eliminated by

turning off the entire system's power; h is the system

state, indicating whether the current system is

consuming dynamic power. When the system is in

an active state, h=1; otherwise, h=0. 𝑃



represents

the frequency-independent dynamic power, which

can only be eliminated by putting the system into

sleep mode; 𝑃



represents the frequency-dependent

dynamic power (

Y. Chen, 2018); 𝐶



represents the

effective switching capacitance; m represents the

dynamic power exponent, and its value should not

be less than 2.

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

196

In this study, the static power 𝑃



is not considered

in the computation. For various types of

heterogeneous resources in the CFN, such as FPGA

and ASIC, the mainstream calculation method for

their power consumption is to follow the

computation form of CPU, which consists of three

parts: chip static power, design static power, and

design dynamic power (Xu, 2016)(Taghinezhad-

Niar A., 2020). The power consumption of the first

two parts depends on the FPGA chip itself, so the

main focus is still on the dynamic power

consumption as the variable to be considered in the

computation:

𝑃



= 𝑃



+ 𝛼𝐶𝑉



𝑓

(2)

3.3 Cost Model

Cloud computing resources are composed of a set of

virtual machines with different unit prices.

Therefore, let 𝐶𝑜𝑠𝑡(𝑡



, 𝑝



, 𝑓



, ℎ) denote the

execution cost of task 𝑡



running on node 𝑝



with

𝑓

,

, which can be expressed as:

𝐶𝑜𝑠𝑡

(

𝑡



, 𝑝



, 𝑓



, ℎ

)

= 𝑤

,

× 𝑝𝑟𝑖𝑐𝑒





,



,

(3)

Where 𝑝𝑟𝑖𝑐𝑒



is the unit execution price of a task

on node 𝑝



. The total execution cost of a DAG

application can be calculated as follows:

𝐶𝑜𝑠𝑡

(

𝐺

)



𝐶𝑜𝑠𝑡

(

𝑡



)







𝐶𝑜𝑠𝑡

(

𝑡



, 𝑝



, 𝑓



, ℎ

)





(

)

3.4 Optimization Model

This study considers completing the scheduling

before the deadline while minimizing energy

consumption as much as possible while ensuring that

the cost is within the budget. The optimization

model can be formulated as follows:

𝑀𝑖𝑛𝐹

(

𝑋

)

= 𝑀𝑖𝑛𝑀𝑎𝑘𝑒𝑠𝑝𝑎𝑛

(

𝑋

)

+ 𝐸𝑛𝑒𝑟𝑔𝑦𝐶𝑜𝑛𝑠𝑢𝑚𝑝𝑡𝑖𝑜𝑛

(

𝑋

)(

)

𝑠. 𝑡 𝑋

,





= 1, ∀𝑖 ∈



1, 𝑁



, 𝑋

,

∈ {0,1}.

𝑇𝑎𝑠𝑘

,

≤𝐶𝑢𝑟𝑟𝑁𝑜𝑑𝑒

,

, ∀𝑖 ∈



1, 𝑁



, ∀𝑗 ∈



1,4



𝐶𝑜𝑠𝑡

(

𝐺

)

−𝐵𝑢𝑑𝑔𝑒𝑡



≤𝑞, ∀𝑖 ∈



1, 𝑁



3.5 Baseline

The Spread algorithm is an innovative approach for

solving multi-objective heterogeneous earliest finish

time scheduling problems. It is a Pareto-based list

scheduling heuristic algorithm that offers users a

range of trade-off optimal solutions. The Binpack

algorithm, on the other hand, proposes a robust

scheduling approach that incorporates a resource

allocation strategy. It schedules workflow tasks onto

a set of heterogeneous cloud resources while

minimizing both the maximum completion time and

cost. GPR-HEFT, a greedy heuristic method, takes

into account resource allocation under budget

constraints. To establish a baseline for comparison,

the essence of these three algorithms was

reproduced, and energy and time calculations were

incorporated into the algorithms.

3.6 Algorithm Based on NSGA-II

The workflow scheduling problem is a typical multi-

objective optimization problem, and it is also NP-

Hard. Traditional single-objective optimization

algorithms cannot solve multi-objective optimization

problems. Non-Dominated Sorting Genetic

Algorithm (NSGA) is a commonly used method for

solving multi-objective optimization problems.

However, NSGA has drawbacks such as high

computational complexity and the inability to

perform elite selection.

To address these issues, Deb et al. proposed the

NSGA-II algorithm in (

K. Deb, 2002), which

improves on NSGA in the following ways: (1)

proposes a fast non-dominated sorting method, (2)

introduces the concept of crowding distance and

crowding distance sorting, and (3) introduces an

elite selection strategy. In NSGA-II, a portion of the

best solutions is retained in each offspring to ensure

the algorithm maintains diversity in the search space

and accelerates convergence. Therefore, NSGA-II

has significant improvements over NSGA in terms

of algorithm efficiency, diversity in the search space,

offspring quality, and convergence speed. NSGA-II

is an effective method for solving multi-objective

optimization problems, and this paper will also

design a workflow scheduling algorithm based on

NSGA-II to solve the microservice scheduling

problem in the CFN.

The algorithm takes as input a set of user tasks

and a set of computing nodes, and outputs the Pareto

front. The following is the algorithm and its

flowchart.

Algorithm 1 The proposed algorithm

Input: Input the initial population size, number of generations to run the algorithm,

number of offspring, crossover and mutation rates, and fitness function.

Output: Return the final population, non-dominated solutions or Pareto front,

diversity of the population, convergence performance, and execution time.

1. Initialize population P(0) with N individuals randomly

2. for each generation G = 1 to T do

3. M = 2N offspring created through crossover and mutation of P(G-1)

4. Q = P(G-1) ∪ M

5. Compute non-domination of Q

6. Assign a rank to each individual based on the non-domination levels

7. Perform crowding distance calculation for each individual

8. Create a new population P(G) by selecting the best individuals based on

their rank and crowding distance

9. end for

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network

197

The input of the proposed algorithm is a set of

user tasks and a set of computing nodes, and the

output is the Pareto front.

4 EXPERIMENT

To ensure reproducibility and statistical significance,

simulation methods were employed to evaluate the

proposed method. Conducting repeatable

experiments in a real data center or cloud platform

can be challenging. Therefore, a simulation

approach was adopted, enabling a substantial

number of experiments to be conducted across

various application configurations. This approach

allows for rigorous testing and analysis, resulting in

more reliable and statistically significant results.

The purpose of the experiment is to verify the

superiority of the improved algorithm over other

algorithms in the same optimization indicators,

including energy consumption, cost, and scheduling

delay. In terms of hardware, a physical machine with

an Intel(R) Core(TM) i5-1135G7 @ 2.40GHz

processor and running the Windows 11 operating

system was used for the experiment.

CYBERSHAKE LIGO

MONTAGE GENOME

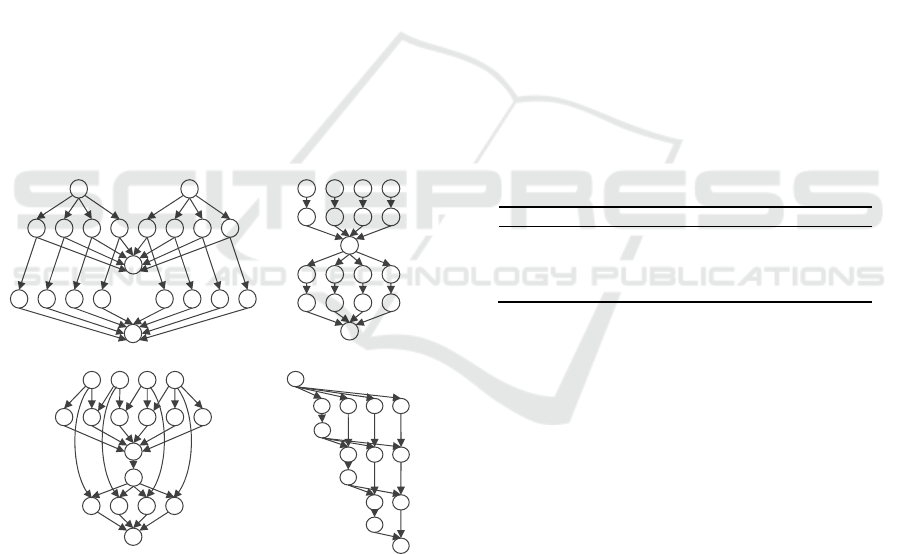
Figure 1: Four kinds of workflow diagrams.

4.1 Dataset

The simulation incorporated four commonly used

scientific workflow models: CYBERSHAKE,

GENOME, LIGO, and MONTAGE. Figure 1

illustrates the smaller workflow structures of each

application. CYBERSHAKE is a data-intensive

workflow that places high demands on memory and

CPU resources. It plays a significant role in

modeling seismic disasters in a particular region.

GENOME is designed for automating various

genome sequencing operations, essentially serving

as a data processing pipeline. LIGO is utilized for

the detection and analysis of gravitational waves in

physics. It primarily requires substantial CPU

resources.MONTAGE is an astronomy workflow

model used to generate customized sky mosaics. In

MONTAGE, most tasks are I/O-intensive and do not

necessitate high CPU processing capabilities

(Gideon Juve, 2012).

In our experiment, we assume that the CFN

provides six types of virtual machines, each with

different resource and price characteristics.Each

virtual machine has different attribute values that are

randomly generated based on the resource

requirements of the dataset. The pricing was based

on the existing Alibaba Cloud pricing for cloud

resources. For the resource requirements, the same

dataset as (S. Tao, 2023) was used.

The parameters of the algorithm greatly affect the

performance of the algorithm. Table 1 is the

parameters used in the implementation of the

algorithm.

Table 1: NSGA-II parameter setting.

Paramete

Valu e

Population size 80

Number of iterations 100

Cross probability 1

Mutation probability 0.1

The performance metric employed to evaluate the

different algorithms on various workflows is the

normalized cost. The normalized cost is calculated

as the ratio of the cost of the current solution to the

cost of the cheapest solution. In the cheapest

solution, all tasks are scheduled on the cheapest

virtual machine, resulting in the minimum cost. The

total execution time and cost of the cheapest solution

are denoted as 𝑀



and 𝐶



, respectively. Similarly, in

the fastest scheduling solution, all tasks are

scheduled on the fastest virtual machine. The HEFT

algorithm is used to determine the fastest scheduling

method in our experiment. The total execution time

and cost of the fastest solution are denoted as 𝑀



and 𝐶



, respectively. To control the variation of the

deadline, a deadline factor µ is introduced, with µ ∈

[0,1]. The deadline for each repeated experiment can

be calculated based on the value of µ. This allows

for the assessment of algorithm performance under

different deadline constraints.

𝑀𝑎𝑘𝑒𝑠𝑝𝑎𝑛 = 𝑀



+ 𝑀



−𝑀



× 𝜇

(

)

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

198

For certain workflows, the cost can be much

higher due to their special structures, making it

difficult to show differences when considering

budget constraints. To overcome this problem, a

budget factor λ (λ∈[0,1]) is introduced to represent

the looseness of the budget. To make it easier to

control the factor, we set λ = 1−µ and calculate the

budget based on λ.

𝐵𝑢𝑑𝑔𝑒𝑡 = 𝐶



+ 𝐶



−𝐶



× λ

(

)

A higher value of µ indicates looser deadline

constraints and stricter budget constraints. In such

cases, the scheduling method is more likely to

prioritize slower services to meet the budget

restrictions. On the other hand, a higher value of λ

increases the likelihood of the scheduling method

selecting faster services, as it emphasizes meeting

tighter deadline constraints.

The success rate measurement was employed to

assess the effectiveness of each method in

generating solutions that satisfy the given

constraints. It is determined by dividing the number

of successful plans by the total number of plans

evaluated. This metric provides an indication of how

well each method performs in meeting the specified

constraints and achieving satisfactory outcomes.

4.2 Results Analysis

The experiment employed the total delay of

scheduling and the energy consumption of resources

as evaluation indicators for microservice scheduling.

These indicators were calculated using formulas 2

and 4, respectively. To assess the performance of the

proposed algorithm, benchmark methods such as

Spread, Binpack, and GPR-HEFT were utilized.

These methods are well-established optimization

techniques in the field of workflow scheduling.

Considering the stochastic nature of certain

properties of the methods, the experiments were

conducted using datasets of different sizes (50, 100,

200). Each experiment was repeated 10 times to

obtain average values, ensuring the reliability and

robustness of the results.

To comprehensively assess the effectiveness of

each method under varying degrees of constraints,

the evaluation process began by setting µ and λ to

small values to evaluate performance under strict

constraints. Subsequently, µ and λ were varied

within the range of [0.005, 0.03] with a step size of

0.005. The average success rate of each method

under different configurations is depicted in Figures

2 and 3. These figures provide insights into the

performance of each method across a range of

constraint settings, allowing for a comprehensive

evaluation of their ability to generate effective

solutions.

(a) CYBERSHAKE (b) LIGO

Figure 2: The average scheduling success rate of each

workflow data under the deadline constraint.

(a) CYBERSHAKE (b) LIGO

Figure 3: The average scheduling success rate of each

workflow data under budget constraints

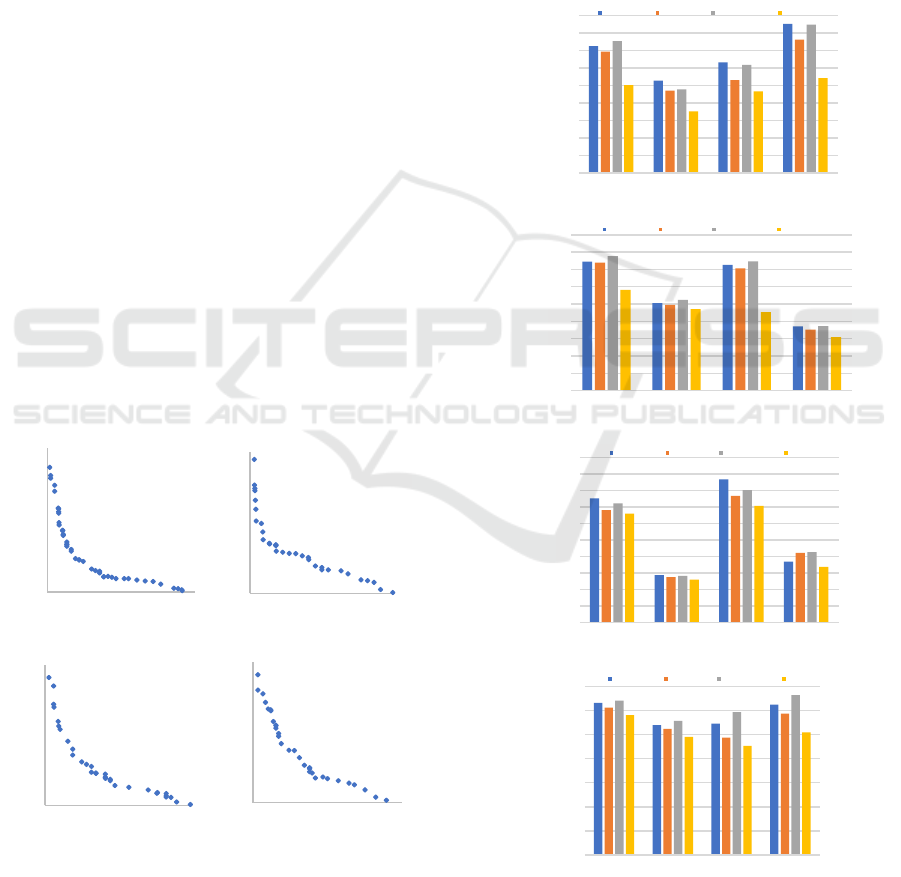
As shown in Figure 2, as the deadline factor µ

increases and the budget factor λ decreases, the

success rate of each method also increases, and

when µ equals 0.025, all methods can achieve a

success rate of 100%. The Spread method does not

perform well on every workflow. When used on

CYBERSHAKE and LIGO, it can quickly reach

100%, but performs the worst on GENOME. When

µ is less than 0.025, the Binpack method cannot

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Deadline Factor 𝜇

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Deadline Factor 𝜇

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Deadline Factor 𝜇

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Deadline Factor 𝜇

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Budget Factor λ

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Budget Factor λ

Binpack Spread GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Budget Factor λ

Binpack Spread

GPR-HEFT NSGA-II

0,2

0,4

0,6

0,8

0 0,005 0,01 0,015 0,02

Success rate

Budget Factor λ

Binpack Spread GPR-HEFT NSGA-II

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network

199

complete the scheduling 100% and performs

relatively poorly on GENOME and LIGO. the GPR-

HEFT method performs better than the first two

methods, but there are still cases where it cannot

complete scheduling when the deadline constraints

are strict. The proposed agorithm performs the best

in terms of performance and can successfully

schedule under all workflows in this experiment.

As depicted in Figure 3, an interesting

observation is that when the budget factor λ is

extremely small, only our proposed method

consistently achieves a 100% success rate across all

workflows. In contrast, the Binpack method fails to

satisfy the constraints in most cases, achieving a

100% success rate only for GENOME when λ

exceeds 0.02. The Spread method performs well for

MONTAGE, reaching a 100% success rate in every

case. However, it struggles to satisfy the constraints

when the budget is at its minimum for MONTAGE.

On the other hand, the Binpack method

demonstrates robustness, with a relatively stable

success rate at small values of µ and λ. The

performance of GPR-HEFT under budget constraints

remains steady, with a success rate that gradually

increases as the budget constraint becomes more

stringent. This aligns with the design intention of the

GPR-HEFT algorithm. Overall, these findings shed

light on the comparative performance of different

methods under varying constraint settings and

highlight the strengths and limitations of each

approach.

(a) CYBERSHAKE (b) LIGO

(

)

MONTAGE

(

)

GENOME

Figure 4: The number of tasks is 100 when the NSGA-II

algorithm Vilfredo Pareto front.

Figure 4 shows the Pareto front of the proposed

algorithm for four different workflow datasets with a

task count of 100. It can be seen that for the four

different datasets, our algorithm can converge

quickly and obtain a set of Pareto front solutions for

selection, with a moderate number of solutions that

are evenly distributed.

Figures 5 and 6 show the comparison of delay

and energy consumption of three algorithms under

different task counts in four datasets. From the

figure, it can be seen that as the number of

microservices increases, the overall delay continues

(a)10

(b) 50

(d) 200

Figure 5: The energy consumption of the four algorithms

was compared with the data from different tasks.

129

139

149

159

169

179

189

199

209

219

229

179 189 199 209

The consumption of energy

makespan

339

359

379

399

419

439

459

479

499

118 123 128 133 138

The consumption of energy

makespan

129

139

149

159

169

179

189

179 189 199 209

The consumption of energy

makespan

129

139

149

159

169

179

189

183 198 213 228

The consumption of energy

makespan

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

100

150

200

250

300

350

400

450

500

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

100

200

300

400

500

600

700

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

200

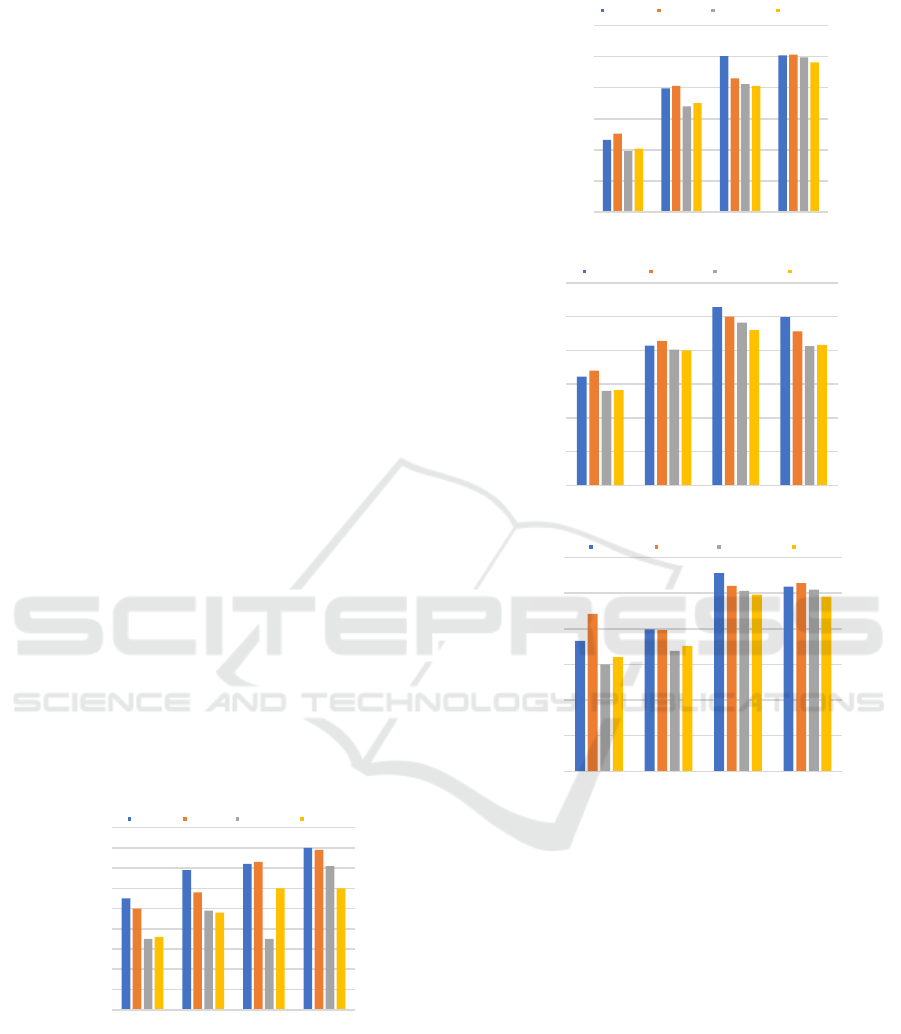
to increase, and the proposed algorithm has a much

lower delay than the Spread algorithm, slightly

lower than the Binpack algorithm. This is because

Spread always schedules microservices to different

nodes, resulting in an increase in microservice data

transmission. Binpack schedules microservices to

one node, reducing this delay. Due to its greedy

strategy, the GPR-HEFT method often falls into

local optima during the search process, resulting in

overall inefficiency, while our algorithm has global

search capabilities and can find globally optimal

solutions to some extent. In terms of load balance,

our algorithm has significant improvements

compared to the above two algorithms. The

experimental results show that the proposed

algorithm optimizes both scheduling delay and

energy consumption, effectively ensuring the QoS of

user applications.

In summary, the LIGO workflow's complex

topological structures may limit the impact of

NSGA-II in the elite selection step, leading to a less

significant reduction in scheduling execution costs.

In the CYBERSHAKE workflow, tasks with

numerous parent tasks but no intermediate child

tasks can be scheduled flexibly, with their execution

having a varying impact on the overall plan

depending on the constraints and budget. The

GENOME workflow, with its simpler structure and

consistent scheduling order, exhibits similar cost and

energy consumption patterns across different

scheduling methods. These observations emphasize

the role of workflow characteristics in influencing

scheduling method performance and highlight the

specific challenges posed by each workflow.

(a) 10

(b) 50

(d) 200

Figure 6. Under the data of different tasks, the Makespan

of the three algorithms is compared.

In summary, the proposed algorithm performs well

on each dataset with different numbers of tasks, as

shown in Figure 5. On the four datasets, the

scheduling energy consumption of the NSGA-II

algorithm is on average 19.4% lower than Binpack,

14.8% lower than Spread, and 20.5% lower than

GPR-HEFT. Especially on the MONTAGE dataset,

the average energy consumption is 24.7% lower than

Binpack. In Figure 6, the NSGA-II method still has

an advantage in scheduling delay, with an average

delay that is 15.4% lower than Binpack, 14.1%

lower than Spread, and 3.7% lower than GPR-

HEFT. Especially on the CYBERSHAKE dataset,

the average scheduling time is 23.7% lower than

Spread.

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

100

150

200

250

300

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

100

150

200

250

300

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

100

150

200

250

300

CYBERSHAKE LIGO MONTAGE GENOME

Binpack Spread GPR-HEFT NSGA-II

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network

201

Regarding scheduling delay, our method also

performs well. Figure 6 shows the average

scheduling delay of the four methods on four

datasets. The scheduling delay of our algorithm is on

average 15.4% lower than Binpack, 14.1% lower

than Spread, and 3.7% lower than GPR-HEFT.

Especially on the CYBERSHAKE dataset, the

average scheduling time of our method is 23.7%

lower than that of Spread.

5 CONCLUSION

In this article, we analyzed the scheduling problem

of workflow in the existing CFN environment and

found that energy consumption and price constraints

are important in the scheduling process in a real

environment. Therefore, we concluded that the

scheduling problem in the CFN is a multi-objective

optimization problem. Then, we modeled the

energy-aware and price-sensitive scheduling

problem in the CFN.

A comparative analysis between the proposed

algorithm and existing algorithms showed that the

proposed algorithm achieved the highest success

rate, satisfying constraints with low energy

consumption, especially under tight constraints. It

also maintained good performance as the constraints

became looser. The algorithm performed

exceptionally well on the CYBERSHAKE dataset,

with a consistently lower average Makespan

compared to other algorithms. In summary, the

comparative analysis demonstrated the superior

performance of the proposed algorithm in terms of

success rate, constraint satisfaction, energy

consumption, and Makespan. This highlights its

potential as a promising solution for microservice

scheduling.

In future research, we plan to enhance the update

strategy of the algorithm to improve convergence

speed and achieve better results across workflow

processes. Our goal is to optimize the algorithm's

efficiency, enabling faster generation of high-quality

solutions. We will also focus on refining the

comprehensive budget allocation and service

selection methods, particularly for relaxed constraint

conditions. This will allow the algorithm to be

applied effectively in a wider range of real-world

scenarios with varying constraints and budget

allocations. By addressing these areas, we aim to

advance the algorithm's performance, expand its

applicability, and contribute to the field of

microservice scheduling research.

REFERENCES

F. Liang, W. Yu, D. An, A Survey on Big Data Market:

Pricing, Trading and Protection[J], IEEE Access. 2018,

6: 15132-15154. https://doi.org/10.1109/ACCESS.

2018.2806881

I. Ahmad, S. Lembo, F. Rodriguez, Security of Micro MEC

in 6G: A Brief Overview[C], 2022 IEEE 19th Annual

Consumer Communications & Networking Conference

(CCNC) 2022, 332-337. https://doi.org/10.1109/CCNC4

9033.2022.9700577

B. Baek, J. Lee, Y. Peng, Three Dynamic Pricing Schemes

for Resource Allocation of Edge Computing for IoT

Environment[J], IEEE Internet of Things Journal. 2020,

7 (5): 4292-4303. https://doi.org/10.1109/JIOT.2020.

2966627

H. Seo, H. Oh, J. K. Choi, Differential Pricing-Based Task

Offloading for Delay-Sensitive IoT Applications in

Mobile Edge Computing System[J], IEEE Internet of

Things Journal. 2022. 9 (19): 19116-19131. https://

doi.org/10.1109/JIOT.2022.3163820

J. Zhu, X. Li, R. Ruiz, Scheduling Periodical Multi-Stage

Jobs With Fuzziness to Elastic Cloud Resources[J],

IEEE Transactions on Parallel and Distributed Systems.

2020, 31 (12): 2819-2833. https://doi.org/10.1109/TP

DS.2020.3004134

H. Djigal, J. Feng, J. Lu, J. Ge, An Efficient Algorithm for

Scientific Workflow Scheduling in Heterogeneous

Computing Systems[J], IEEE Transactions on Parallel

and Distributed Systems. 2021, 32 (5): 1057-1071.

https://doi.org/10.1109/TPDS.2020.3041829

Y. Wang and X. Zuo, An Effective Cloud Workflow

Scheduling Approach Combining PSO and Idle Time

Slot-Aware Rules[J], IEEE/CAA Journal of

Automatica Sinica. 2021, 8 (5): 1079-1094. https://

doi.org/10.1109/JAS.2021.1003982

Yadav, R., Zhang, W. Li, K., An adaptive heuristic for

managing energy consumption and overloaded hosts in

a cloud data center[J], Wireless Networks. 2020, 26 (3):

1905–1919.https://doi.org/10.1007/s11276-018-1874-1

Durillo, J.J., Prodan, R., Multi-objective workflow

scheduling in Amazon EC2[J], Cluster Computing.

2014, 17 (2): 169–189. https://doi.org/10.1007/s10586-

013-0325-0

D. Poola, S. K. Garg, R. Buyya, Robust Scheduling of

Scientific Workflows with Deadline and Budget

Constraints in Clouds[C], 2014 IEEE 28th

International Conf. on Advanced Information

Networking and Applications. 2014, 2819-2833.

https://doi.org/10.1109/AINA.2014.105

K. Deb, A. Pratap, S. Agarwal, A fast and elitist

multiobjective genetic algorithm: NSGA-II Constraints

in Clouds[J], IEEE Transactions on Evolutionary

Computation. 2002, 6 (2): 182-197. https://doi.org/10.

1109/4235.996017

C. A. C. Coello, G. T. Pulido, M. S. Lechuga, Handling

multiple objectives with particle swarm

optimization[J], IEEE Transactions on Evolutionary

Computation. 2004, 8 (3): 256-279. https://doi.

org/10.1109/TEVC.2004.826067

ANIT 2023 - The International Seminar on Artiﬁcial Intelligence, Networking and Information Technology

202

S. Tao, Y. Xia, L. Ye, DB-ACO: A Deadline-Budget

Constrained Ant Colony Optimization for Workflow

Scheduling in Clouds[J], IEEE Transactions on

Automation Science and Engineering. 2023, 1–16.

https://doi.org/10.1109/TASE.2023.3247973

H. R. Faragardi, M. R. Saleh Sedghpour, S. Fazliahmadi,

GRP-HEFT: A Budget-Constrained Resource

Provisioning Scheme for Workflow Scheduling in IaaS

Clouds[J], IEEE Transactions on Parallel and

Distributed Systems. 2020, 31 (6): 1239-1254.

https://doi.org/10.1109/TPDS.2019. 2961098

Gideon Juve, Ann Chervenak, Ewa Deelman, Taheri,

Handling, Characterizing and profiling scientific

workflows[J], Future Generation Computer Systems.

2013, 29 (3): 682–692.

https://doi.org/10.1016/j.future.2012.08.015

S. Wang, Z. Qian, J. Yuan, A DVFS Based Energy-

Efficient Tasks Scheduling in a Data Center[J], IEEE

Access. 2017, 5: 13090-13102.

https://doi.org/10.1109/ACCESS.2017.2724598

Y. Chen, G. Xie, R. Li, Reducing Energy Consumption

With Cost Budget Using Available Budget

Preassignment in Heterogeneous Cloud Computing

Systems[J], IEEE Access. 2018, 6: 20572-20583.

https://doi.org/10.1109/ACCESS.2018.2825648

Z. Long, Z. Li, S. Ahmad, Efficient scientific workflow

scheduling for deadline-constrained parallel tasks in

cloud computing environments[J], IEEE Transactions

on Evolutionary Computation. 2020, 531: 31-46.

https://doi.org/10.1016/j.ins.2020.04.039

X. Xu, W. Dou, X. Zhang, An Energy-Aware Resource

Allocation Method for Scientific Workflow Executions

in Cloud Environment[J], IEEE Transactions on Cloud

Computing. 2016, 4 (2): 166-179.

https://doi.org/10.1109/TCC.2015.2453966

Taghinezhad-Niar A., Pashazadeh S., Taheri, Handling,

Workflow scheduling of scientific workflows under

simultaneous deadline and budget constraints[J],

Cluster Computing. 2021, 24 (4): 3449–3467.

https://doi.org/10.1007/s10586-021-03314-3

Heterogeneous Resource Scheduling Method Based on Energy Optimization Under Price Constraints in Computing Force Network

203