
General Studies on Electromagnetic Wave Transmission Behaviors
with the High-Speed Dielectric Interface
Zeming Zhuang, Yetong Hu and Yi Jin
*
Department of Physics, University of Jinan, Jinan, China
Keywords: High-Speed Moving Interface, Electromagnetic Wave, Fresnel’s Law, Half-Wave Loss.
Abstract: The propagation of electromagnetic wave with high-speed moving medium is very complex and one of the
important research contents of electromagnetic wave theory. It can not only reveal the characteristics of
electromagnetic waves themselves and the properties of the medium, but also has important application value.
In this paper, the laws of reflection and refraction of electromagnetic waves at the interface of high-speed
moving medium are derived by using the Special Relativity transformation relations of electromagnetic field
quantities and four-dimensional wave vectors between different inertial systems. Meanwhile the phenomena
of total reflection, Brewster’s angle and half-wave loss, etc. are discussed in detail, and some new useful
results are obtained.
1 INTRODUCTION
The problem of the reflection and refraction of
electromagnetic waves (the following are referred to
as waves for simplicity) at the motion interface is
fundamental to the electrodynamics transmission and
has been valued by people for a long time, which is
widely used in optics, radar engineering, radio
astronomy and other aspects (Jean Van Bladel, 1984),
and is also one of the core theories of remote sensing
technology (Li Jindong, 2018). However, due to the
excessive complexity, the problem mentioned above
are rarely involved in classical electrodynamics
textbooks (Guo Shuohong, 2008) in which the
reflection and refraction laws with static interface
have been discussed in more detail. Although it has
been studied in some literatures, it is only discussed
from some special angles that are easy to solve, such
as the wave is incident from a vacuum to a medium
moving parallel or perpendicular to the interface
(Wen Shengle et al., 2001; Wei Renhuai et al., 2009),
etc, but does not give universal solutions, especially
the case that the medium interface moves along any
direction.
The studies in this paper are mainly based on
Lorentz transformation in Special Relativity and
Maxwell's electromagnetic theory, taking plane wave
as the research object for which has many advantages
in theoretical research. Firstly, the case of incidence
from vacuum to medium is discussed detailedly, and
the reflection and refraction laws of waves at high-
speed moving interface with arbitrary direction are
obtained. Then it is extended to medium to medium.
Finally the half-wave loss, total reflection and
Brewster’s angle, etc. are discussed in detail.
2 SOME USEFUL RELATIVISTIC
TRANSFORMATIONS
Here we take laboratory system as Σ and the system
at rest relative to the motion interface as Σ'. The
incidence of plane wave from vacuum to medium is
considered. In Σ, the electric field strength and wave
vector of waves, normal direction vector and motion
velocity of the interface, and relative refractive index
of medium are E
⃗
i
, k
⃗
i
, n
⃗
, v⃗ and n
f
respectively. The
Lorentz transformations from Σ to Σ' of the electric
field strength, wave vector and frequency of waves
are as Eq.(1).
E
⃗
' = γ
E
⃗
+v⃗ × B
⃗
-
γ
γ+1
v⃗
v⃗∙E
⃗
c
2
, k
⃗
' = k
⃗
+
γ -1
k
⃗
∙v⃗
v⃗
|
v⃗
|
2
-
γω
c
2
v⃗, ω'= γ
k
⃗
i
c-v⃗∙k
⃗
i
(1)
For n
⃗
' in Σ', n
//
r
//
+ n
⊥
r
⊥
+ c=0 and
n'
//
r'
//
+ n'
⊥
r'
⊥
+ c'=0 are obtained by the
decomposition of plane equations n
⃗
∙r⃗ + c = 0 in Σ
and n
⃗
'∙r⃗' + c'=0 in Σ' into parallel and perpendicular
to the velocity direction. By the length contraction,
the Lorentz transformation of n
⃗
' can be written as
Eq.(2).
Zhuang, Z., Hu, Y. and Jin, Y.
General Studies on Electromagnetic Wave Transmission Behaviors with the High-Speed Dielectric Interface.
DOI: 10.5220/0012280400003807
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (ANIT 2023), pages 257-261
ISBN: 978-989-758-677-4
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
257

n
⃗
'=n
⃗
+
1
γ
-1
n
⃗
∙v⃗
v⃗
|
v⃗
|
2
(2)
3 ELECTROMAGNETIC WAVE
IN Σ'
In this section, the electric field strength, magnetic
induction strength and wave vector of reflected and
refracted waves in Σ' will be obtained.
3.1 Wave Vector in Σ'
The wave vectors k
⃗
i
', k
⃗
R
' and k
⃗
T
' are taken to
analyse in the direction parallel and perpendicular to
n
⃗
' . Decomposition of k
⃗
i
' into parallel and
perpendicular
to n
⃗
' gets k
⃗
i
'
//
=k
⃗
i
'∙n
⃗
'n
⃗
'/
|
n
⃗
'
|
2
and k
⃗
i
'
⊥
=k
⃗
i
'-k
⃗
i
'
//
.
For k
⃗
R
' , k
⃗
R
'
//
= -k
⃗
i
'
//
and k
⃗
R
'
⊥
= k
⃗
i
'
⊥
can be obtained
from the reflection law in static system (Guo
Shuohong, 2008). For k
⃗
T
' , combining ω=k
⃗
i
c and
the equal magnitude of the frequency of wave in
different medium, k
⃗
T
'
//
2
+k
⃗
T
'
⊥
2
=k
⃗
T
'
2
=n
f
2
ω'
2
/c
2
=
n
f
2
k
⃗
i
'
2
= n
f
2
k
⃗
i
'
//
2
+k
⃗
i
'
⊥
2
can be obtained. The
Snell’s law in Σ' is n
f
=sinθ'/cosα', where θ' is the
incident angle and α' is the refraction angle.
Combining above equations we can get k
⃗
T
'
⊥
=k
⃗
i
'
⊥
.
Since k
⃗
T
'
⊥
and k
⃗
i
'
⊥
are both in the incident plane
and perpendicular to n
⃗
', they are parallel. Then Eq.
(3) about k
⃗
R
' and k
⃗
T
' are as the following.
k
⃗
R
' = k
⃗
i
'-2
k
⃗
i
'⋅n
⃗
'
n
⃗
'
|
n
⃗
'
|
2
, k
⃗
T
'=k
⃗
i
'+
n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
+
k
⃗
i
'⋅n
⃗
'
2
-
k
⃗
i
'⋅n
⃗
'
n
⃗
'
|
n
⃗
'
|
2
(3)
According to the reflection law θ'=φ', the
trigonometric functions of the incident angle θ',
reflection angle φ' and refraction angle α' can be
written as Eq.(4).
⎩
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎧
sinθ'=sinφ'=
k
⃗
i
'
⊥
k
⃗
i
'
=
|
n
⃗
'
|
2
k
⃗
i
'
2
-k
⃗
i
'∙n
⃗
'
2
|
n
⃗
'
|
k
⃗
i
'
, sinα'=
k
⃗
T
'
⊥
k
⃗
T
'
=
k
⃗
i
'
⊥
n
f
k
⃗
i
'
=
|
n
⃗
'
|
2
k
⃗
i
'
2
-k
⃗
i
'∙n
⃗
'
2
n
f
|
n
⃗
'
|
k
⃗
i
'
cosθ'=cosφ'=
k
⃗
i
'
//
k
⃗
i
'
=
k
⃗
i
'∙n
⃗
'
|
n
⃗
'
|
k
⃗
i
'
, cosα'=
k
⃗
T
'
//
k
⃗
T
'
=
n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
+k
⃗
i
'∙n
⃗
'
2
n
f
|
n
⃗
'
|
k
⃗
i
'
tanθ'=tanφ'=
sinθ'
cosθ'
=
|
n
⃗
'
|
2
k
⃗
i
'
2
-k
⃗
i
'∙n
⃗
'
2
k
⃗
i
'∙n
⃗
'
, tanα'=
sinα'
cosα'
=
|
n
⃗
'
|
2
k
⃗
i
'
2
-k
⃗
i
'∙n
⃗
'
2
n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
+k
⃗
i
'∙n
⃗
'
2
(4)
3.2 Electric Field Strength in Σ'
The normal direction of the incident plane in Σ' is
denoted as m
⃗
'=k
⃗
i
'×n
⃗
'/k
⃗
i
'×n
⃗
'. Because Fresnel’s law
(Guo Shuohong, 2008) studies the reflection and
refraction coefficients relevant to the s and p
components of waves, we need to know the
magnitude of the s and p components E
i
'
⊥
and E
i
'
//
of
the incident waves, where the direction of E
⃗
i
'
⊥
is
along the normal direction m
⃗
'. Then E
i
'
⊥
and E
i
'
//
can be written as Eq.(5) by using B
⃗
=k
⃗
×E
⃗
/ω.
E
i
'
⊥
=E
⃗
i
'∙m
⃗
'=E
⃗
i
'∙
k
⃗
i
'×n
⃗
'
k
⃗
i
'×n
⃗
'
, E
i
'
//
=E
⃗
i
'∙
m
⃗
'×
k
⃗
i
'
k
⃗
i
'
=E
⃗
i
'∙
k
⃗
i
'×n
⃗
'×k
⃗
i
'
k
⃗
i
'×n
⃗
'×k
⃗
i
'
(5)
Fresnel’s law in Σ' is as Eq.(6).
⎩
⎪
⎨
⎪
⎧
E
R
'
⊥
E
i
'
⊥
= -
sinθ'cosα'-cosθ'sinα'
sinθ'cosα'+cosθ'sinα'
,
E
R
'
//
E
i
'
//
=
1-tanθ'tanα'
tanθ'-tanα'
1+tanθ'tanα'
tanθ'+tanα'
E
T
'
⊥
E
i
'
⊥
=
2cosθ'sinα'
sinθ'cosα'+cosθ'sinα'
,
E
T
'
//
E
i
'
//
=
2cosθ'sinα'
sinθ'cosα'+cosθ'sinα'
cosθ'cosα'+sinθ'sinα'
(6)
Substituting the Eq.(4) into (6), E
R
'
⊥
, E
T
'
⊥
, E
R
'
//
and E
T
'
//
can be obtained as Eq.(7),
⎩
⎪
⎨
⎪
⎧
E
R
'
⊥
= -
a
-
a
+
E
i
'
⊥
, E
R
'
//
=
b
-
b
+
a
-
a
+
E
i
'
//
E
T
'
⊥
=
a
+
-a
-
a
+
E
i
'
⊥
, E
T
'
//
=n
f
2
b
+
-b
-
+
a
+
-a
-
2
4b
+
a
+
-a
-
a
+
E
i
'
//
(7)
Where a
±
= n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
+k
⃗
i
'∙n
⃗
'
2
1/2
±k
⃗
i
'∙n
⃗
',
b
±
=k
⃗
i
'∙n
⃗
'n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
+k
⃗
i
'∙n
⃗
'
2
1/2
±
|
n
⃗
'
|
2
k
⃗
i
'
2
-k
⃗
i
'∙n
⃗
'
2
.
Finally, from Eq.(5)-(7), electric field strengths in
Σ' are written as Eq.(8). And the magnetic induction
strength in Σ' can be written by using B
⃗
=k
⃗
×E
⃗
/ω as
Eq.(9).
E
⃗
R
' =E
R
'
//
k
⃗
i
'×n
⃗
'×k
⃗
R
'
k
⃗
i
'×n
⃗
'×k
⃗
R
'
+E
R
'
⊥
k
⃗
i
'×n
⃗
'
k
⃗
i
'×n
⃗
'
, E
⃗
T
' =E
T
'
//
k
⃗
i
'×n
⃗
'×k
⃗
T
'
k
⃗
i
'×n
⃗
'×k
⃗
T
'
+E
T
'
⊥
k
⃗
i
'×n
⃗
'
k
⃗
i
'×n
⃗
'
(8)
B
⃗
R
'=
1
ω'
E
R
'
//
k
⃗
i
'
2
k
⃗
i
'×n
⃗
'
k
⃗
i
'×n
⃗
'×k
⃗
R
'
-E
R
'
⊥
k
⃗
i
'×n
⃗
'×k
⃗
R
'
k
⃗
i
'×n
⃗
'
,
B
⃗
T
'=
1
ω'
E
T
'
//
n
f
2
k
⃗
i
'
2
k
⃗
i
'×n
⃗
'
k
⃗
i
'×n
⃗
'×k
⃗
T
'
-E
T
'
⊥
k
⃗
i
'×n
⃗
'×k
⃗
T
'
k
⃗
i
'×n
⃗
'
(9)
4 ELECTROMAGNETIC WAVE
IN Σ
In this section, we will give the electric field strength
and wave vector of the reflected and refracted waves
in Σ based on the results in section III, and then the
reflection coefficient, refraction coefficient, half-
wave loss, total reflection law and Brewster’s law will
be analyzed in detail.
4.1 Electric Field Strength and Wave
Vector in Σ
Because both incident and reflected waves are in
vacuum, the Lorentz transformations of the electric
field strength and wave vector of reflected wave in
Eq.(10) are familiar as the incident wave.
E
⃗
R
= γ
E
⃗
R
'-v⃗×B
⃗
R
'-
γ
γ+1
v⃗
v⃗∙E
⃗
R
'
c
2
, k
⃗
R
= k
⃗
R
'+(γ -1)
k
⃗
R
'∙v⃗
v⃗
|
v⃗
|
2
+
γω'
c
2
v⃗ (10)
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
258
The Lorentz transformation of wave vector of the
refracted wave is the same as the incident wave for it
is independent of the medium. However, when there
is a medium, the Lorentz transformation of electric
field strength E
⃗
should be replaced by the Lorentz
transformation of electric displacement vector D
⃗
.
The Lorentz transformation of D
⃗
along the X-axis
direction has been given in reference (Liu Liao et al.,
2008). Analogously to the Lorentz transformation of
E
⃗
, the Lorentz transformation of D
⃗
along any
direction is written as
D
⃗
'=γD
⃗
+v⃗×H
⃗
/c
2
-γv⃗v⃗⋅D
⃗
/(γ+1)/c
2
. Where D
⃗
=εE
⃗
,
H
⃗
=B
⃗
/μ , ε and μ are permittivity and magnetic
permeability in the relative static medium
respectively, and μ≈μ
0
for the ordinary linear medium.
By wave velocity v=(με)
−1/2
, vacuum light velocity
c=(μ
0
ε
0
)
−1/2
and n
f
=c/v, we can get E
⃗
T
and k
⃗
T
as in
Eq.(11).
k
⃗
T
= k
⃗
T
'+(γ -1)
k
⃗
T
'∙v⃗v⃗
|
v⃗
|
2
+
γω'
c
2
v⃗, E
⃗
T
=
D
⃗
T
ε
=
D
⃗
T
ε
0
n
f
2
= γ E
⃗
T
'-
1
n
f
2
v⃗×B
⃗
T
'-
γ
γ+1
v⃗v⃗∙E
⃗
T
'
c
2
(11)
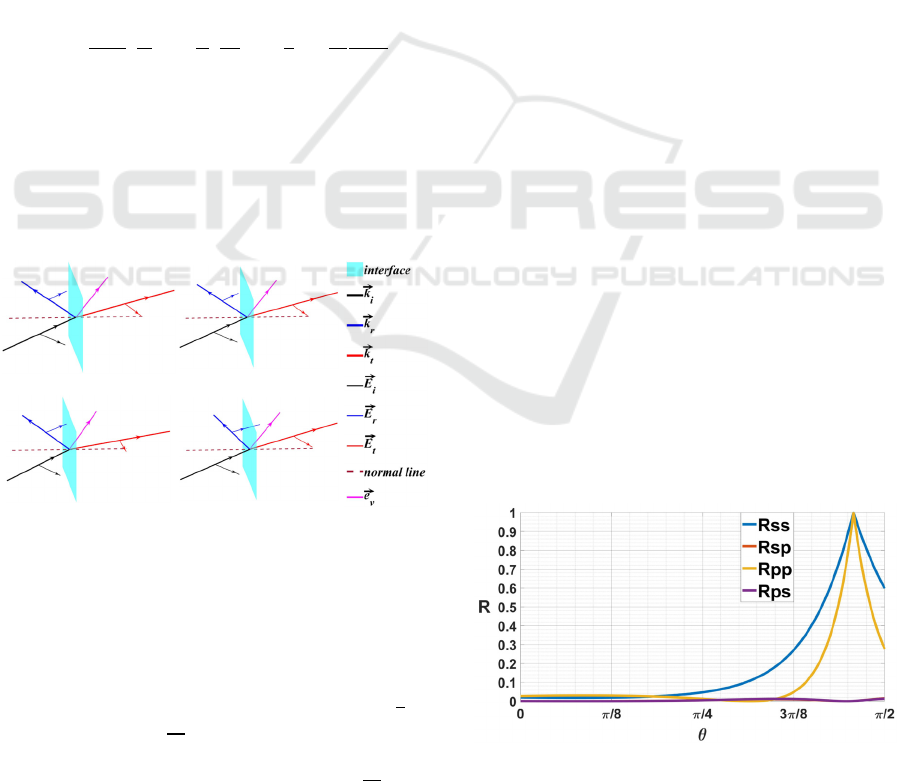
The above results can be demonstrated visually in
Fig.1. Fig.1 (a) vs. (c) and (d) show the refractive
index of medium and the speed of the interface have
the significant influence on the reflected and refracted
waves respectively. While it can be seen from Fig.1
(a) vs. (b) that frequency ω has no effect on the
reflected and refracted waves.
(a) (b)
(c) (d)
Figure 1. Demonstration of incident, reflected and refracted
waves from at the interface between vacuum and the
moving medium. The subscript i, R and T represent
incident, reflected and refracted waves respectively, and the
relative length represents the absolute value of
corresponding vector. n
⃗
and e⃗
v
represent the normal
direction and motion direction of the interface respectively.
The conditions of (a) are ω=2π∙50kHz,
E
⃗
i
=e⃗
x
+e⃗
y
-2e⃗
z
(V/m) , n
f
=1.5, e⃗
ki
=e⃗
x
+e⃗
y
+e⃗
z
/
√
3 ,
v⃗=0.5ce⃗
x
+2e⃗
y
+3e⃗
z
/
√
14 (m/s) and n
⃗
=e⃗
x
, while the
conditions of (b, c, d) vary only in (b) ω=2π∙500kHz, (c)
n
f
=2.5 and (d) v⃗=0.75ce⃗
x
+2e⃗
y
+3e⃗
z
/
√
14 (m/s)
separately.
Combining ω=k
⃗
i
c and Eq.(1),
k
⃗
i
'=ω
e⃗
ki
+
γ -1
e⃗
ki
∙v⃗
v⃗/
|
v⃗
|
2
-γv⃗/c
/c is obtained. It is
obvious that the direction of the incident wave in Σ' is
independent of ω. Through the analysis of Eq.(4) and
(6), it can be seen that k
⃗
i
' has no effect on Eq.(6).
Considering Eq.(8), it can be concluded that ω has no
effect on electric field strength direction of the
reflected and refracted waves. Then the frequency of
wave has no effect on the electric field strength of the
reflected and refracted waves.
4.2 Coefficients of Reflection and
Transmission
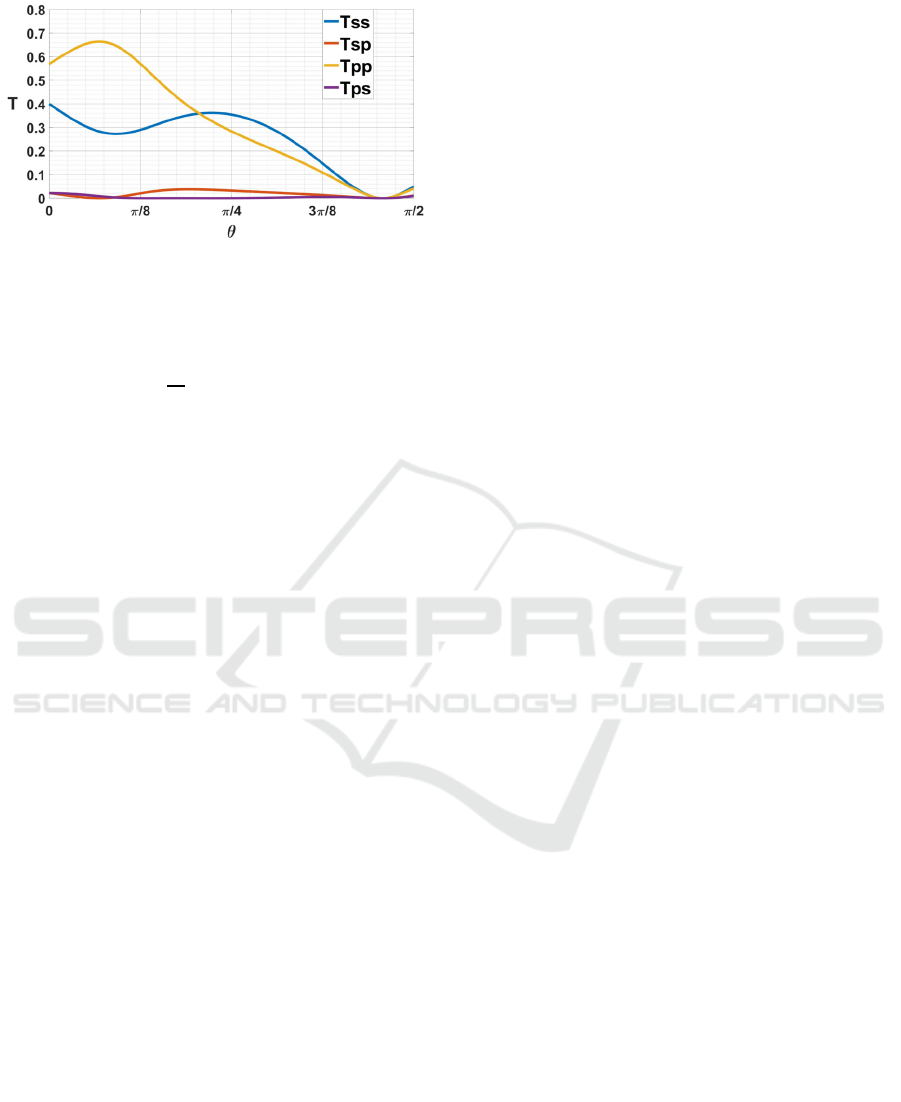
In order to show more clearly the electric field
strengths of the reflected and refracted waves, we make
the curve of reflection coefficient R and refraction
coefficient T with the change of incident angle θ as
Fig.2. Among them, there are four cases of reflection
coefficient and refraction coefficient respectively.
According to ω=k
⃗
i
c and Eq.(1), when electric field
strength and wave vector are transformed between Σ
and Σ', the magnitude and direction of the transformed
electric field strength and wave vector are affected by
v⃗. Thus, reflected and refracted waves will exist p (s)
wave component when the incident wave is just s (p)
wave. Hence the reflected and refracted waves would
have different polarization types from the incident
wave, just like Faraday effect and Kerr effect which are
caused by some characteristics of special media.
Therefore, R and T can be divided into R
αβ
and T
αβ
respectively, where α, β=s, p. R
αβ
(T
αβ
) refers to the
ratio of the intensity of the β wave of reflected
(refracted) wave to the intensity of the α wave of
incident wave, where R
αβ
=E
Rα
2
/E
iβ
2
and T
αβ
=E
Tα
2
/E
iβ
2
.
As can be seen from the Fig.2, R
αβ
and T
αβ
, α=β are
significantly greater than R
αβ
and T
αβ
, α≠β in most
angle ranges.
(a)
General Studies on Electromagnetic Wave Transmission Behaviors with the High-Speed Dielectric Interface
259
(b)
Figure 2. The relation of (a) reflection coefficient R and (b)
refraction coefficient T with the incident angle θ, where the
incident wave of ω=2π∙50kHz, E
⃗
i
=e⃗
x
+e⃗
y
-2e⃗
z
(V/m) and
wave vector in the XOY plane are reflected and refracted at
the interface of n
⃗
=e⃗
x
, n
f
=1.5 and
v⃗=0.5ce⃗
x
+2e⃗
y
+3e⃗
z
/
√
14 (m/s).
4.3 Half-Wave Loss, Total Reflection
and Brewster’s Law
Half-wave loss, total reflection and Brewster’s law
are the classical behaviors of waves at interface. The
influence of high-speed moving interface on these
phenomena are discussed in the following. According
to the first formula of Eq.(7), the requirement for half-
wave loss is
n
f
2
-1
|
n
⃗
'
|
2
k
⃗
i
'
2
>0 .
It is obvious that
when n
f
>1 there is half-wave loss between the
incident and the reflected waves. Therefore, the
condition of half-wave loss at the moving interface is
the same as stationary interface. According to Eq.(3),
when k
⃗
T
'
//
2
≤0, the wave vector in the medium along
the normal direction is imaginary and the total
reflection would happen. The critical angle condition
for satisfying total reflection is sinθ'≥n
f
. The
meaningful condition for the above is n
f
<1, while
here is no total reflection of incident from vacuum to
medium. In other word, the incident wave should be
from the optically denser medium to the thinner one.
Total reflection critical angle θ' increases with n
f
. The
Brewster’s law says that the component of electric
field strength parallel to incident plane in reflected
wave is vanishing, that is to say, E
R
'
//
=0 and E
R
'
⊥
≠0.
The Brewster’s angle condition of cosθ'
b
=[n
f
2
/(n
f
2
+1)]
1/4
can be obtained by substituting θ'≠α',
E
R
'
//
=0 and E
R
'
⊥
≠0 into Eq.(4), and cosθ' (θ')
increases (decreases) with n
f
.
5 FURTHER DISCUSSION ON
INCIDENCE FROM ONE
MEDIUM TO ANOTHER
The incidence from vacuum to medium has been
studied in former sections, and the case of one
medium to another would be discussed based on the
above. There are two points which should be
considered here: firstly, the Lorentz transformation of
the field strength of the incident and reflected waves
should use D
⃗
instead of E
⃗
; secondly, when the
phenomenon of dispersion is considered, the relative
refractive index has the relation with the interface
velocity, and then it will affect the rule of half-wave
loss, total reflection and Brewster’s phenomenon.
5.1 Effect on Fresnel’s Law
The Lorentz transformation of the field strength in
medium is different from the one in vacuum. When
wave spreads in medium, it is only need to rewrite the
Lorentz transformations E
⃗
i
to E
⃗
i
' and E
⃗
R
' to E
⃗
R
by imitating the second formula in Eq.(11), and no
other equations need to be changed. The Fresnel’s law
of wave incident from one medium to another and the
interface moving at high speed can be obtained.
5.2 Effect on Half-Wave Loss, Total
Reflection and Brewster’s Law
The relative refractive index of medium to vacuum is
greater than 1 surely, but the one between two media
may have all kinds of possible values. In this paper,
the reflection and refraction of waves at interface are
analyzed from Σ'. The equations for reflection and
refraction laws in Σ are derived by using the equations
for reflection and refraction laws in Σ'. However, the
reflected and refracted behaviors of wave at interface
is related to the relative refractive index concerned
with two media. And the n
f
in the previous sections
also should have relation with the wave frequency ω'
in Σ', that is n
f
= n
f
(ω'), hence the conditions of half-
wave loss, total reflection and Brewster’s law in
section IV are also related to n
f
(ω'). The relation
between the refractive index of medium and the
wavelength in vacuum satisfies the Cauchy’s
dispersion formula n
f
(λ')=A+B/λ'
2
+C/λ'
4
[7], which is
rewritten as n
f
(ω')=A+Bω'
2
/(4π
2
c
2
) +Cω'
4
/(16π
4
c
4
) by
using λ'=2πc/ω', where λ' and ω' are wavelength and
frequency in Σ' and A, B and C are the coefficients
determined by experiments. Eq.(1) shows that the ω'
of the wave changes with v⃗, and the range of ω'
ANIT 2023 - The International Seminar on Artificial Intelligence, Networking and Information Technology
260

is γk
⃗
i
c-v
≤ω'≤γk
⃗
i
c+v
, or γ
1-β
ω≤ω'≤γ
1+β
ω.
Suppose there exist two suitable media 1 and 2, and
their refractive indexes satisfy the following
conditions: the ω' is smaller but greater than γ(1−β)ω,
and the refractive indexes of the two media meet
n
f1
(ω')<n
f2
(ω'). In other word, the relative refractive
index n
f21
>1. With the increase of ω', when ω' is
greater but less than γ(1+β)ω, the refractive indexes
of the two media can meet n
f1
(ω')>n
f2
(ω'), that is, the
relative refractive index n
f21
<1. There is a special case
of n
f21
=1 between the two cases. When the media are
determined, both n
f1
(ω'), n
f2
(ω') and n
f21
are uniquely
determined by ω', while ω' is determined by ω and v⃗
according to Eq.(1). Hence v⃗ is bound to affect the
laws of half-wave loss, critical angle of total
reflection, and Brewster’s angle. However, the
relations of refractive indexes and wave frequencies
are so complex in fact, and it is difficult to have a
unified theoretical formula to describe for different
media. This is another interesting subject valuable to
investigate deeply in the next.
6 CONCLUSION
In this paper, the problem of electromagnetic waves
transmission at high-speed interface moving in any
direction has been studied extensively. Firstly, the
case of incidence from vacuum to medium is
discussed, and the reflection and refraction laws are
obtained by Lorentz transformation, Snell’s law and
Fresnel’s law, which are different vastly from the
laws in static system. Besides the half-wave loss, total
reflection and Brewster’s law are analyzed.
Furthermore, the case of incidence from one medium
to another is also discussed. In the specific
application, according to the method and theoretical
formula in this paper, the final results needed can be
obtained by numerical calculation by substituting
concrete conditions like ω, n
f
and v⃗.
ACKNOWLEDGMENTS
This work is supported by Research Project on
Undergraduate Teaching Reform of Higher
Education of Shandong Province (Z2021036), Group
Theory Curriculum Ideological and Political
Education Demonstration Project of Shandong
Province, Research Project on Teaching Reform of
Postgraduate Education of Shandong Province
(SDYJG19038), Quality Course Construction of
Colleges and Universities in Shandong Province
(JPKC201311), and Shandong Students’ innovation
and entrepreneurship training program 2023.
REFERENCES
Jean Van Bladel. Relativity and engineering[M]. Springer-
Verlag Berlin Heidelberg, 1984.
Li Jindong. Satellite Remote Sensing Technology: Volume
one[M]. Beijing Institute of Technology Press, 2018.
Guo Shuohong. Electrodynamics[M]. Higher Education
Press, 2008.
Wen Shengle, Yi Huixian. Fresnel formulas of a medium
surface in motion[J]. College Physics, 2001, (11): 4-7.
https://doi.org/10.16854/j.cnki.1000-0712.2001.11.002
Wei Renhuai, Zhu Mengzheng. Study on the refraction
behavior of plane electromagnetic wave at the interface
of moving medium[J]. Journal of Mudanjiang Normal
University (Natural Sciences Edition), 2009, (04): 10-
12.
https://doi.org/10.13815/j.cnki.jmtc(ns).2009.04.028
Liu Liao, Fei Baojun, Zhang Yunzhong. Special Theory of
Relativity[M]. Science Press, 2008.
Zhu Jianyue, Chen Qian. Spectral Analysis and Cauchy
Dispersion Formula Research Based on Spectrometer
Experiment[J]. Physical Experiment of College, 2016,
29 (02):41-43. https://doi.org/10.14139/j.cnki.cn22-
1228.2016.002.011
General Studies on Electromagnetic Wave Transmission Behaviors with the High-Speed Dielectric Interface
261
